Next Article in Journal
Comparison between Germinated Seed and Isolated Microspore EMS Mutagenesis in Chinese Cabbage (Brassica rapa L. ssp. pekinensis)
Previous Article in Journal
Russeting of Fruits: Etiology and Management
Previous Article in Special Issue
Cluster-Zone Leaf Removal and GA3 Application at Early Flowering Reduce Bunch Compactness and Yield per Vine in Vitis vinifera cv. Pinot Gris
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Horticulturae
Volume 8
Issue 3
10.3390/horticulturae8030233
horticulturae-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Multicultivar Approach for Grape Bunch Weight Estimation Using Image Analysis

by
Gonçalo Victorino
1,*,
Carlos Poblete-Echeverría
2 and
Carlos M. Lopes
1
1
LEAF—Linking Landscape, Environment, Agriculture and Food, Instituto Superior de Agronomia, Universidade de Lisboa, Tapada da Ajuda, 1349-017 Lisbon, Portugal
2
Department of Viticulture and Oenology, Faculty of AgriSciences, SAGWRI—South African Grape and Wine Research Institute, Stellenbosch University, Private Bag X1, Matieland 7602, South Africa
*
Author to whom correspondence should be addressed.
Horticulturae 2022, 8(3), 233; https://doi.org/10.3390/horticulturae8030233
Submission received: 31 January 2022 / Revised: 28 February 2022 / Accepted: 3 March 2022 / Published: 8 March 2022
(This article belongs to the Special Issue Advances in Viticulture Production)
Browse Figures
Versions Notes

Abstract

:
The determination of bunch features that are relevant for bunch weight estimation is an important step in automatic vineyard yield estimation using image analysis. The conversion of 2D image features into mass can be highly dependent on grapevine cultivar, as the bunch morphology varies greatly. This paper aims to explore the relationships between bunch weight and bunch features obtained from image analysis considering a multicultivar approach. A set of 192 bunches from four cultivars, collected at sites located in Portugal and South Africa, were imaged using a conventional digital RGB camera, followed by image analysis, where several bunch features were extracted, along with physical measurements performed in laboratory conditions. Image data features were explored as predictors of bunch weight, individually and in a multiple stepwise regression analysis, which were then tested on 37% of the data. The results show that the variables bunch area and visible berries are good predictors of bunch weight (R2 ranging from 0.72 to 0.90); however, the simple regression lines fitted between these predictors and the response variable presented significantly different slopes among cultivars, indicating cultivar dependency. The elected multiple regression model used a combination of four variables: bunch area, bunch perimeter, visible berry number, and average berry area. The regression analysis between the actual and estimated bunch weight yielded a R2 = 0.91 on the test set. Our results are an important step towards automatic yield estimation in the vineyard, as they increase the possibility of applying image-based approaches using a generalized model, independent of the cultivar.

1. Introduction

Grapevine yield estimation is a subject of utmost importance for the wine and vine business [1]. Accurately estimating the amount of fruit in the vineyard can provide advantages to the farmer regarding harvest logistics, cellar management, wine stock management, and even marketing strategies [2]. However, spatial and temporal variability in vineyard blocks [3,4,5] make this task extremely challenging [6]. Current commercial methods are based on manual bunch sampling, which is destructive, laborious, and time-consuming. In general, all standard methods are dependent on bunch weight, either measured or historical, and are then extrapolated for the entire vineyard or plot. Conventional methods usually present errors close to 30%, depending on sampling methods and vineyard variability [7].
Recently, sensor-based technology has been developed to address the challenge of bunch weight estimation [8]. In particular, image analysis has shown the most promising results regarding this topic. If used thoroughly, it has the potential of inspecting a great number of bunches or vines in a short period of time, resorting less to the extrapolation of data, thus being less prone to errors caused by spatial and temporal variability. Victorino et al. [9] showed that several bunch features are highly correlated with bunch weight, highlighting bunch volume, bunch projected area, and visible berry number in a two-dimensional image. These yield components have also been discussed in other works such as Dunn and Martin [2] and Diago et al. [10].
Bunch area (or pixels) has been explored to estimate bunch or vine yield by Lopes et al. [11] and Milella et al. [12]. In the last case, the authors proposed an automatic bunch segmentation using convolutional neural networks for pixel classification. Three-dimensional data (RGB-D images) have also been used to estimated bunch weight and compared to two-dimensional imaging, on cv. Syrah [13]. The authors concluded that although 3D data outperformed 2D in a controlled lab environment (R2 = 0.89 with RGB, compared to 0.95 with RGB-D, observed vs. estimated data), in field conditions, at a vine level, 3D data were not as reliable (R2 = 0.88 with RGB, compared to 0.59 with RGB-D, observed vs. estimated data).
An automatic berry counting algorithm was developed by Aquino et al. [14], where the number of visible berries in two-dimensional vine images was used to estimate bunch weight and vine yield on several cultivars, by multiplying the berry number by historical berry weight data. In this case, the images were collected at night using artificial lighting and the method achieved a R2 value of 0.78 between the observed and estimated yield. Liu et al. [15] developed a fast, calibration-free algorithm for berry counting. The algorithm uses two-dimensional bunch images taken in field conditions with an artificial background and attempts to reconstruct the bunch in three-dimensions, estimating the occluded berries. The authors used this reconstruction to estimate bunch weight, obtaining an accuracy of 92% in two cultivars [15]. Other works used similar approaches, most including machine learning techniques, to achieve the same goal in different cultivars and conditions [1,15,16,17,18]. However, the relationship between bunch area or visible berries and bunch weight presented different results in multivariate scenarios (e.g., [1,16]), the first being mentioned to be cultivar-dependent in previous research [10,19]. Furthermore, in a 2D bunch image, as only a fraction of berries is visible, and an intermediate step (estimation of total berry number) is needed before estimating bunch weight. The relationship between visible berries and total berries is also cultivar dependent, as it depends on the shape of the bunch [20].
OIV [21] describes different ways to characterize grape bunch morphologic traits through code descriptors. Some of these codes describe the following traits (e.g.,):
  • Code 202: bunch length;
  • Code 203: bunch width;
  • Code 204: bunch compactness;
  • Code 208: bunch shape;
  • Code 220: berry length;
  • Code 221: berry width;
  • Code 222: berry size uniformity;
All these traits can vary among cultivars and even within bunches of the same cultivar, and can have an impact when trying to convert bunch image features into bunch weight. Even though several studies have successfully estimated bunch weight using image analysis [22,23,24], this task still poses several challenges. The main challenges are linked to the following: (i) image background noise and need for using complex algorithms or artificial backgrounds to avoid or remove it [10]; (ii) 2D imaging of a 3D object, which neglects berries that are occluded by other berries or vegetation [25]; and (iii) cultivar dependency, as most relationships between bunch weight and other bunch features changes with the cultivar mainly due to differences in bunch architecture [26,27]. Bunch features like bunch size or bunch compactness can also vary when subject to different management practices or edaphoclimatic conditions [28].
Considering the above-mentioned challenges, in this study, we do not intend to develop a ready-to-use yield estimation protocol. Our main objective is to explore the relationships between bunch weight and bunch features obtained from 2D image analysis in four different cultivars (multicultivar approach). To address the challenge of cultivar dependency, a simplified protocol is proposed, which focuses on using features that have already been proven to be able to be automatically extracted from images, and attempting to reach the best performing model for multicultivar bunch weight estimation.

2. Materials and Methods

2.1. Site Characterization and Trial Description

The experiment was performed in two vineyards located in different countries from different hemispheres: Portugal (Site PT) and South Africa (Site SA).
The PT site is an experimental vineyard located in the Lisbon winegrowing region, at Instituto Superior de Agronomia campus, Lisbon, Portugal (38°42′24.61″ N, 9°11′05.53″ W). It is located 70 m above sea level and includes two different plots with spur pruned vines trained on a vertical shoot positioning trellis system with two pairs of movable wires. In the PT site, the season presented a dry spring (119 mm of precipitation from March to June) and a very dry and warm summer (17 mm of precipitation and average mean temperature of 20.6 °C, from June to September). The first plot included two drip-irrigated white Portuguese autochthonous cultivars (Encruzado and Arinto) grafted onto 1103 Paulsen rootstock, planted in 2006. Both cultivars were trained on a unilateral Royat cordon and were spaced 1.0 m within and 2.5 m between north−south oriented rows. Water was supplied with a drip irrigation system, which was managed using a soil water probe. Readily available water was maintained until veraison, at which point stress was applied by allowing the soil water to reach values below the refill point. The refill point was defined using predawn leaf water potential thresholds established for white wines at our site (~−0.3 MPa). The second plot was rainfed and consisted of the cultivar Syrah (grafted onto 140 Ruggeri rootstock) planted in 1999. Plants were trained on a bilateral Royat cordon and spaced 1.2 m within and 2.5 m between north−south oriented rows. In both plots, the soil was a clay loam with 1.6% organic matter and a pH of 7.8 [29].
The SA site is a commercial Cabernet Sauvignon vineyard located at Stellenbosch wine region in the Western Cape, South Africa (33°54′10.4″ S, 18°55′12.9″ E), 430 m above sea level. Plants were grafted onto 101-14 MGt (101-14 Millardet et de Grasset) rootstock, spur-pruned, and trained on a vertical shoot positioning trellis system with two pairs of movable wires. Vines were planted in 2003 on a bilateral Royat cordon and spaced 2.0 m within and 2.5 m between north−south oriented rows. Water was supplied with a drip irrigation system and irrigation was managed within commercial standards using the midday stem water potential with a threshold for water stress conditions of −0.9 MPa as an indicator. At the SA site, the season presented a spring with an average rainfall (205 mm of precipitation from September until December 2020) and a warm summer with some precipitation (~100 mm of precipitation and an average temperature of 21 °C from December until April).

2.2. Data Set

The PT site data were collected during the 2019 season, near harvest (August 2019). Samples of 48, 71, and 60 bunches of cvs. Arinto, Encruzado, and Syrah, respectively, were collected from four different plants per cultivar, located randomly across the vineyard (Figure 1A–C).
As shown in the example of Figure 1C, the bunches from cultivar Syrah were uncommonly loose compared to the typical Syrah bunch as a result of a lower fruit set caused by unfavorable weather conditions during flowering. A black metal spring was used as scale (5 cm wide) on images collected at the PT site (Figure 1A–C), while a black square (3 cm2) was used at the SA site (Figure 1D).
The SA site data were collected during the 2020–2021 season, near harvest (March 2021). A sample of 96 bunches from 16 different vines of the cultivar Cabernet Sauvignon (hereinafter referred to as Cabernet) located across the vineyard was collected and taken to lab conditions.
Different numbers of bunches were analyzed for different cultivars and sites. However, to prevent possible modelling bias from different sample sizes, each sample was reduced to the lowest number of bunches, 48 from cv. Arinto, using a randomized selection process. A complete description of the collected data set is presented in Table 1.

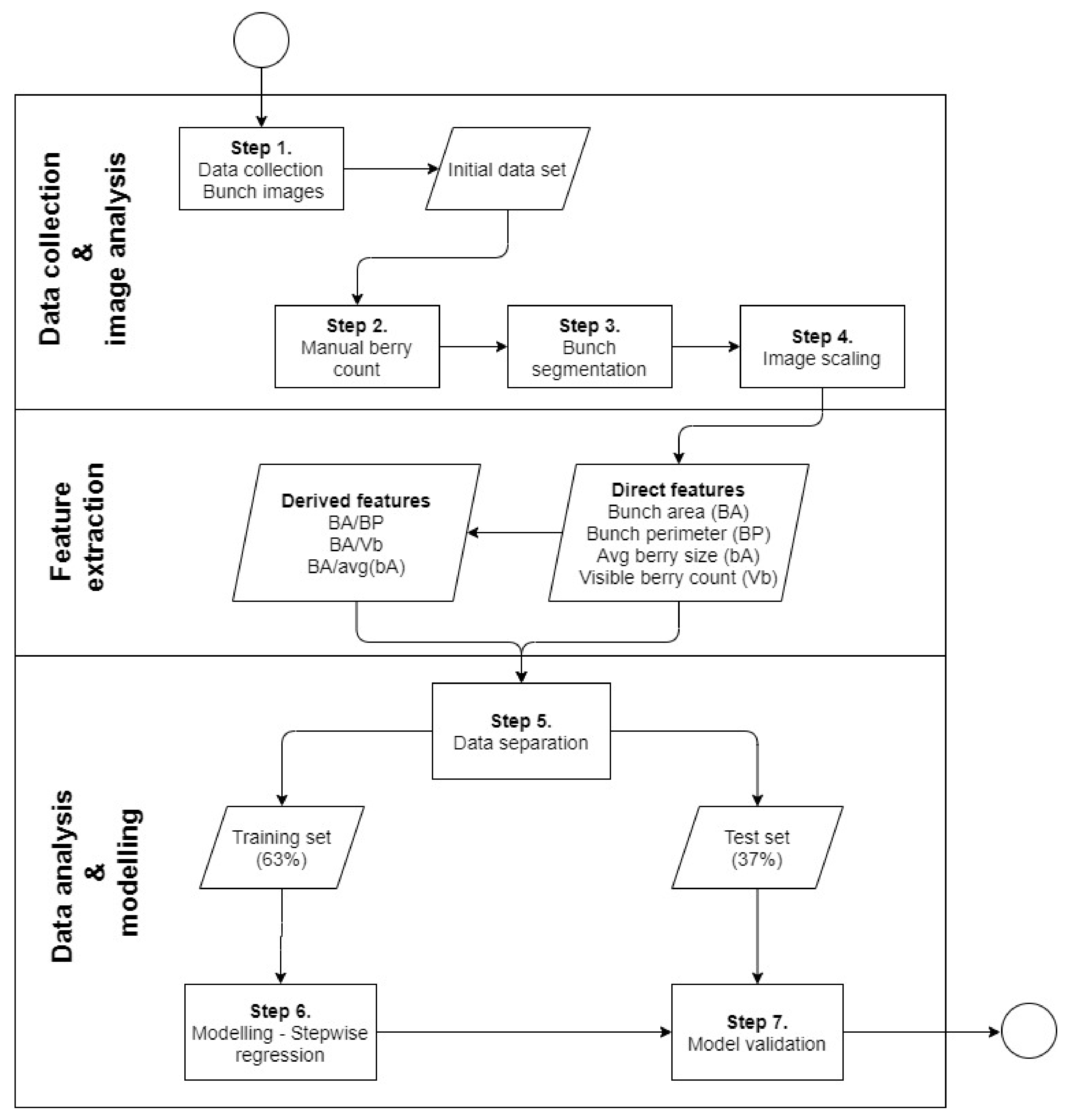
2.3. Data Collection and Image Analysis

At the PT site, bunch images were collected, in lab conditions, using a commercial camera (Nikkon D5200, Nikon Inc., Melville, NY, USA) mounted on a tripod, approximately 50 cm away from the hanging bunches. A blue background was used to prevent noise caused by surrounding objects and to improve color thresholding for bunch segmentation. At the SA site, the image collection methods were similar, except for the background color, which was white, in order to improve the color contrast, particularly with red grape cultivars. In the lab, at both sites, all bunches were weighed (Bw), imaged (hung by the peduncle, in a random position), and the total number of berries per bunch were counted (Tb).
Image analysis was performed using a customized script written in Matlab (R2020a, The Mathworks, Natick, MA, USA) and using ImageJ (version 1.44p, National Institutes of Health, USA). From each bunch image, the following variables were extracted: bunch projected area (BA; cm2), bunch perimeter (BP; cm), average berry area (bA, cm2), and visible berry number (Vb). BA and BP were estimated using a color threshold tool in the L*a*b color space, adapted to each image type (e.g., different cultivars, background, or lighting conditions). This process was performed in a loop for all cases, and all images were inspected individually after processing. bA was estimated from a subsample of three full berries (fully visible) of each bunch that were selected manually in the image. This number of berries was used in order to keep the methodology simplified, so as to possibly automate it in the future, and was representative of each bunch. The bA was then computed using Matlab’s Hough transform function (hough function), which is designed to detect lines (or curves) in an image [30]. Vb was obtained manually from the images, by clicking each berry in the image and marking the berries already counted. In all cases where it made sense, pixels were converted into cm2 using references in the image with known dimensions (black spring in PT images and black square in SA images; Figure 1). The description of the image analysis sequence is presented in Figure 2. Bunch compactness was visually evaluated from the images, with a panel of eight judges, according to OIV descriptor n°204 [21], which classifies bunches into five categories, based on the mobility of the berries and the visibility of the pedicels, namely: very loose (class 1), loose (class 3), medium (class 5), dense (class 7), and very dense (class 9).

2.4. Data Analysis

In addition to the original variables obtained from the bunches and bunch images (BA, BP, bA, and Vb), three other derived variables were calculated:
  • ratio between bunch area and visible berries (BA_Vb), which represents the average area occupied by each visible berry;
  • ratio between bunch area and bunch perimeter (BA_BP), which represents the relationship between the area that berries occupy and their perimeter, and;
  • ratio between bunch area and the average bA of each variety (BA_avg(bA)), which represents the average number of berries per unit of bunch area.
The original data set was divided into a training set (with 63% of the data) and test set (with 37% of the data) in a full random mode, for each cultivar, using a customized code in RStudio (ver. 1.2.5, RStudio team). This splitting process was compared with a cross-validation procedure, providing the same results in terms of the selection of variables and similar regression coefficients. The training set was used to establish the relationship between the analyzed variables (described above) and to train the regression model (Figure 2). A simple linear regression analysis was used to evaluate the relationships between bunch weight and the remaining bunch features. This analysis was performed separately per cultivar in order to explore the potential differences among them. A Student’s t-test was used to compare the slope between each regression line.
The general multiple model was obtained by a stepwise regression procedure using the R® function stepAIC from the package MASS [31], which selects the best model based on its Akaike information criterion (AIC) value. The coefficient of determination (R2), root mean squared percentage error (RMSPE), bias, and modelling efficiency (EF), were the deviance measures used to evaluate the model performance.

3. Results

3.1. Characterization of Bunch Features

Table 2 presents the average values of the main bunch features obtained during data collection for all of the studied cultivars. All parameters were obtained via image analysis, except for Bw and Tb, which were obtained manually, in lab conditions.
cv. Arinto presented the heaviest bunches, by far, while cv. Syrah presented the lowest ones. Cultivars Cabernet and Encruzado presented similar weights among them. Similar results were observed for the total berry number (Tb), except for Encruzado, which showed lower Tb values than Cabernet. Bunch area followed the same trend as Tb, also with cv. Encruzado presenting values nearly as low as cv. Syrah. Bunch perimeter did not follow the same trend, with the highest values being observed on cv. Cabernet and the lowest on cv. Encruzado, while cv. Arinto and Syrah presented similar values. The Arinto cultivar showed the highest number of visible berries, followed by Cabernet, while Encruzado and Syrah presented the lowest values. The largest berries were observed on the cultivar Encruzado, followed by Arinto, while Syrah and Cabernet presented the smallest values. Regarding bunch compactness notations, cvs. Arinto, Cabernet, and Encruzado presented the same mode (7—dense bunch), while cv. Syrah presented a mode of 3 (loose bunch). All of the analyzed variables showed high coefficients of variation within the same cultivar, between 30% and 62%, with the lowest being for BP and the highest for Bw and Tb.

3.2. Relationships between Image Features and Bunch Weight

Figure 3 presents the linear regressions between all image-based features (predictors) and bunch weight, while Table 3 presents the respective regression equations, for R2 and RMSPE. The average berry area did not have a significant relationship with bunch weight (R2 = 0.02 on the combined data set) and thus was not showcased in Table 3. However, bA is still an important feature for the objective of this work, as shown in the Discussion section.
The results show that linear regressions between bunch weight and bunch area presented high and significant R2 for all cultivars and combined data, with the highest R2 being observed for cv. Cabernet. The same cultivar also presented the lowest RMSPE (Table 3). However, the regression lines between cvs. for this relationship presented significantly different slopes among each other (Figure 3A), except between cvs. Encruzado and Arinto. The same trends were true for the visible berries and bunch weight regression models, in this case with cvs. Syrah and Cabernet also presenting an equal slope between their regression lines (Figure 3B). The regression lines for the relationship between Bw and BP presented slope differences among cultivars that mirrored the ones mentioned for visible berries, in this case even more clearly (Figure 3C), with the slopes from cvs. Encruzado and Arinto being approximately six to eight times larger than the slopes from the cvs. Syrah and Cabernet regression lines.

3.3. Multiple Regression Model

In order to test the hypothesis that bunch weight can be estimated, regardless of cultivar and bunch shape, all the assessed variables were included in a forward stepwise regression analysis. In sum, for this analysis, all image-based features, both original and computed ratios, were considered. Table 4 shows the variable selection summary of the forward stepwise regression analysis. The first variable selected was Vb with a high partial R2, followed by BA_BP, which contributed an additional 10% to the model R2. The variables BA_avg(bA), BA, and BP were also added to the model, but with a lower contribution, with 3% in total. In the last step, the function excluded BA_BP to avoid collinearity issues, with the final model retaining the same R2 and a lower AIC. The final multiple regression model is presented in Equation (1).
Bw = −31.451 + 4.008 × BA − 1.596 × BP + 3.055 × Vb − 3.644 × BA_avg(bA)
Figure 4 presents the relationship between the observed and estimated values of bunch weight using the model described in Equation (1) on the training and test sets, with all of the cultivars combined. Visual observation showed a good agreement between the data on both sets, which were corroborated by the statistical measures of validation shown in Table 5.
Table 5 shows the results of the linear regressions between the actual and estimated bunch weight in the test set using the model described in Equation (1), separated for each cultivar and for all of the cultivars combined. All cases presented a high and significant R2, with the highest coefficient being shown for the cvs. Encruzado, Arinto, and combined data sets. These two cultivars also presented a regression model with an RMSPE below 20%, while the combined data presented a slightly higher RMSPE value, but still below 30%. The Cabernet cultivar regression model achieved a lower R2, which was still high and significant, and higher than the one shown by cv. Syrah. The elected model (Equation (1)) showed the lowest absolute bias on the data set for cv. Encruzado, while the highest bias was observed for cv. Syrah, with a tendency to overestimate Bw for cvs. Arinto and Syrah and for the combined data. The data sets of cvs. Arinto, Encruzado, and the combined data presented the highest EF values (all above 0.80), followed by cv. Cabernet. All regression lines presented slope and intercept values not significantly different from 1 and 0, respectively, except for cv. Syrah. The cv. Syrah presented a high RMSPE, which, along with its lower R2, low EF, and high bias (>20%) indicated that this data set was where the model described in Equation (1) achieved the worst results.

4. Discussion

To date, several works have focused on developing accurate and automatic ways to identify grapevine yield components such as berries and grape bunches in 2D images for yield estimation purposes [2,24,32]. However, past research has not focused on optimizing the intermediate step for converting what is identified in the image into mass (bunch weight or total plant weight). This task can be challenging to generalize considering the morphological variability of the fruit within and between different cultivars [26,33].
In our study, when comparing the performance of the predictors Vb and BA when estimating the bunch weight, we found that, despite the similar range of values of R2 and RMSPE, the highest and lowest R2 of the regression models were not always found on the same cv. Data set. Indeed, while the models based on the predictor BA showed the highest R2 in the cv. Cabernet data set and the lowest in the combined data set, the models based on the predictor Vb had the highest R2 in the cvs. Arinto and Encruzado data sets and the lowest in the cv. Syrah. The good agreement between these bunch features and bunch weight was similar to the results presented in previous research [1,34], but, to the best of our knowledge, have never been used together in the same estimation model.
A visual observation of the scatter plot (Figure 3) shows that BW presents a linear trend with BA (Figure 3A) and BP (Figure 3C), where power relationships would be expected. The geometrical differences from the relationship between the weight and area or perimeter of a sphere might be caused by occluded berries and irregular depth along the bunch (e.g., varying bunch compactness). On a single berry, regression lines with power equations would probably have the best modeling performance, however, with a whole bunch, the same perimeter or area might be associated with a portion of the bunch that has an indefinite number of berries behind the visible ones, resulting in a changing depth. Regarding the use of BP to predict BW, we observed a lower fit when compared to the models based on BA and Vb. This can be explained by the fact that BP can vary greatly even in cases of similar bunch weight (Table 2), possibly due to different bunch shapes. However, by providing information on bunch morphology, BP can be an important variable to be included in a multiple regression model and, hence, add accuracy to a generalized weight estimation model.
Bunch features assessed in our work (Table 2) present many interactions between each other and among cultivars, that might hint towards indicators of bunch morphology. For example, cv. Encruzado presents a higher average berry area and a much heavier average bunch than cv. Syrah. At the same time, both cvs. had almost the same total berry number, showing the importance of berry size when estimating bunch weight using berry number as an estimator. This has been previously explored in [15], either by using historical data or through direct measurements of the average berry weight. Berry weight automatic estimation was explored in Mirbod et al. [35] and Roscher et al. [36] using the automatically obtained average berry area. Another example that reinforces the need to use more than one bunch feature in the models for BW estimation is, again, in the case of cv. Encruzado, where the average BA was almost as low as for cv. Syrah, even though the cv. Syrah bunches were much lighter. Further examples can be given, like the case of the average BP of cv. Syrah, which presented the second-highest value, even though, again, this cultivar presented much smaller bunches than the other cultivars. A final example that hints at the possible bunch morphology differences that can be obtained by comparing berry attributes of cv. Encruzado and cv. Syrah is that both cvs. presented a similar average number of visible berries, but cv. Encruzado showed an average berry size that was almost twice that of cv. Syrah. Most of these observations can be corroborated visually, by inspecting the bunch images. These observations indicate that many of these bunch features can help differentiate bunch shapes and architectural traits when analyzed together and, in return, add accuracy to the bunch weight estimation models, as was briefly mentioned by Di Gennaro et al. [24] and Ivorra et al. [33]. Furthermore, because the mentioned bunch features (bunch area, bunch perimeter, and average berry area) were all possible to be obtained automatically from images, it was considered relevant to use such features as predictors of bunch weight, even though they might not always show high correlations between them. This was the reason behind the computing of the derived features of BA_BP, BA_Vb, and BA_avg(bA). In addition, in this way, the shape differences could even be automatically identified on different bunches of the same cultivar in cases of internal variability, and would not require any previous context for the algorithm to be effective for different cultivars.
In our results, BA_BP and BA_avg(bA) presented high and significant Pearson correlation coefficients with OIV bunch compactness indexes (code 204) of 0.73 and 0.60, respectively. As this is a complex trait by itself and goes beyond the scope of this work, it was not further explored. However, this correlation shows that the ratios between these variables can indeed be interesting to classify bunch architectural traits, as mentioned above. In sum, and to further elucidate on the rationale behind these ratios, for BA_BP, if an example is considered for two bunches with the same area, one loose and the other compact, it is possible to understand that the loose one would have a higher perimeter. This would happen as more cases of whole berries would be considered instead of clustered ones, thus having a lower BA_BP ratio, just as it would have a lower OIV bunch compactness index (code 204). On the other hand, BA_avg(bA) relates to the average amount of berries per unit of area, which also increases or decreases, depending on bunch compactness. These relationships, to the best of our knowledge, have never been explored for the bunch weight estimation. Their variables are key in a multiple regression analysis that attempts to estimate the weight for several bunch shapes. A similar approach was explored in [20], where the authors explored several bunch features and achieved a multicultivar method to estimate bunch compactness. However, most of the features used in this work were difficult to achieve through automatic image analysis.
The stepwise regression analysis computed in this study (Table 4) selected all original features (BA, BP, and Vb), except bA, which was included within the ratio of BA_avg(bA). The variable Vb was the first to be selected with a very high partial R2, reinforcing what was observed in the simple linear regressions analyzed above, and in accordance with what has previously been reported in other works for different cultivars [1,22]. The ratio for BA_BP also presented a high contribution to the stepwise regression model, possibly because it includes the other main bunch trait that explain Bw (BA), and also because of what this ratio represents regarding bunch morphology, as mentioned above. In the end, this ratio was removed from the model (last step of the stepwise regression model), but the two variables remained, indicating the importance of their interaction, even when BP showed a low R2 with Bw. It is important to highlight that all studied variables were not extracted at the cost of any extra labor, as they were all features that could be obtained automatically from images [12,15,33,37].
The selected model (Equation (1)) presented a very good fit, with the test set (Table 5) being effective at estimating the bunch weight of different cultivars with a very distinct bunch morphology, presenting an increase in R2 of 20%, 14%, and 35% compared to models that used the single predictors BA, Vb, or BP, respectively, on the combined data set (Table 3). In cvs. Arinto and Syrah, the model overestimated Bw, possibly for different reasons. In the case of cv. Arinto, the differences in bunch shape might be the main issue. With bigger and wider bunches, this cultivar presents a higher portion of extremities that have different berry occlusion rates than the center of the bunch, which was not considered by the model. The overestimation of Bw for cv. Syrah was possibly related to the fact that this cultivar presented much lighter bunches than the other cultivars. With the model being fitted with three other cultivars that present an average bunch between 161g and 424 g, an overestimation was expected for bunches with less than half the average weight, probably because of the same reasons mentioned for cv. Arinto. The model did not achieve higher R2 values for the cvs. Cabernet or Syrah than the ones presented by a cultivar-specific model based only on BA (Table 3). Furthermore, especially in the case of cv. Syrah, the resulting RMSPE was above 60%. Despite the good overall model performance, when working with cv. Syrah, better results could still be obtained with the simpler approaches, using a cultivar-specific model. However, as explained above, in this study, the cv. Syrah showed abnormal bunch feature values. For this reason, it is relevant to continue this research and study this approach with more cultivars from different sites and different seasons.
The best bunch weight estimation results were obtained for cultivars that presented higher slopes on all single relationships, as shown in Figure 3 (cvs. Arinto and Encruzado). This behavior might be explained by the fact that cvs. Encruzado and Arinto bunches presented a lower bunch area, visible berry number, and bunch perimeter per unit of bunch weight, which might indicate that there was a higher bunch density and consequent more berry by berry occlusion. In fact, cv. Arinto showe an average of 37% of visible berries per bunch, while cvs. Cabernet, Encruzado, and Syrah presented 53%, 57%, and 66%, respectively. This makes sense, as the Arinto bunches were very large and had increased dimensions in all axes. On the other hand, even though cv. Encruzado did not present the same trend in berry visibility, this cultivar presented the largest average berry area, which could also cause a higher percentage of berry occlusion by other berries, and in return, could be the reason behind the higher slopes of the relationships shown in Figure 3. Furthermore, heavier bunches presented a slightly higher weight estimation error on both the training and test sets (Figure 4), which, again, could be caused by the fact that on bigger bunches, there was a higher fraction of berry-by-berry occlusion (63.2%, 46.8%, 43.5% and 34.5% of the average occluded berries on bunches of cvs. Arinto, Cabernet, Encruzado, and Syrah, respectively). The elected model presented a final RMSPE = 25.9%, which is very promising considering the great variability in average bunch weight among the cvs. Arinto (434 g) and Syrah (72 g).
In our work, differences among years and sites were not explored, as our data were limited in this regard. However, both spatial and temporal variability are caused by differences in the number and/or weight of the bunches [38]. Hence, bunch weight estimation methods that achieve accurate results on varying bunch shapes and sizes, such as the ones presented in this work (Table 2), are likely to also be accurate between sites and at different years.
As mentioned before, all of the analyzed features could be collected from a vine image of a realistic, vineyard scenario [12,15,34,37]. However, we predict that the application of the studied approach in such conditions would be subject to several challenges/adaptations, such as (i) image resolution, which would be particularly important to extract features such as bunch perimeter and visible berries, as these require more detail and, thus, higher resolution if images are to be taken from a larger distance; (ii) bunch occlusion by leaves, where recent works have explored ways to estimate the occluded bunches [39,40], but this challenge still remains unsolved; (iii) extracting features from occluded bunches, as even if occluded bunches are estimated, it will be impossible to have their corresponding exact area, visible berries or perimeter, and ratios between these features on the visible portion of the bunches can be a better option; and (iv) robust segmentation methods, as this challenge lies in the step before the weight estimation (segmentation step), being crucial for a vineyard scenario.

5. Conclusions

To obtain a generalized, accurate model for grape bunch weight, this paper compared the explanatory potential of several image-based bunch features for estimating bunch weight of four grapevine cultivars. Several simple linear regression models between the studied bunch features and bunch weight presented a strong goodness of fit, showing that bunch weight could be estimated based on single image-based variables, corroborating what has been reported in recent research. However, the resulting regression models were significantly different from each other, depending on the grapevine cultivar. Along with the original image features, other derived features were computed to attempt to explain the bunch morphological differences. The resulting model used a combination of bunch area, bunch perimeter, visible berry number, and average berry area, and presented strong goodness of fit when estimating bunch weight on the test set, which included cultivars with very different bunch shapes. The generalized model did not achieve satisfactory results for cv. Syrah, which, in this study, showcased unusual small bunches. Our results are an important step towards automatic yield estimation in the vineyard, as the possibility of applying image-based approaches in a generalized way that is independent of grape cultivar is increased. Further research needs to confirm the outputs with other cultivars, different sites, and seasons. From a practical point of view, the application of this methodology in field conditions should be explored.

Author Contributions

Conceptualization, G.V., C.P.-E. and C.M.L.; methodology, G.V., C.P.-E. and C.M.L.; software, G.V and C.P.-E.; writing—original draft preparation, G.V.; writing—review and editing, G.V., C.P.-E. and C.M.L.; visualization, G.V., C.P.-E. and C.M.L.; supervision, C.P.-E. and C.M.L.; project administration, C.P.-E. and C.M.L. All authors have read and agreed to the published version of the manuscript.

Funding

G.V. was supported by PhD grant SFRH/BD/132305/2017, sponsored by FCT—Fundação para a Ciência e a Tecnologia. His mobility to the University of Stellenbosch was supported by the Rise vWise project, grant agreement ID: 872394, sponsored by the European Community’s Horizon 2020 Program. The field experiment in South Africa was supported by WINETECH through the research program “Grapevine production with limited water resources”, project Fship Water 1.

Data Availability Statement

Not applicable.

Acknowledgments

We gratefully acknowledge the valuable contributions of Beatrice Carmignani, Giuseppe Samà, Luigi Mauro, Ruben Bonaria, Jaco Luus, Sally Duncan, Someleze Mbiza, Anke Berry and Stenford Matsikidze, who helped with data collection and overall teamwork, which made this research possible.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Nuske, S.; Achar, S.; Bates, T.; Narasimhan, S.; Singh, S. Yield Estimation in Vineyards by Visual Grape Detection. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 2352–2358. [Google Scholar]
  2. Dunn, G.M.; Martin, S.R. Yield prediction from digital image analysis: A technique with potential for vineyard assessments prior to harvest. Aust. J. Grape Wine Res. 2008, 10, 196–198. [Google Scholar] [CrossRef]
  3. Bramley, R.; Ouzman, J.; Boss, P. Variation in vine vigour, grape yield and vineyard soils and topography as indicators of variation in the chemical composition of grapes, wine and wine sensory attributes. Aust. J. Grape Wine Res. 2011, 17, 217–229. [Google Scholar] [CrossRef]
  4. Victorino, G.; Braga, R.; Lopes, C.M. The effect of topography on the spatial variability of grapevine vegetative and repro-ductive components. In Proceedings of the I Congresso Luso-Brasileiro de Horticultura, Lisbon, Portugal, 1–4 November 2017; pp. 510–516. Available online: https://aph.aphorticultura.pt/wp-content/uploads/2019/10/the_effect_of_topography_on.pdf (accessed on 6 March 2022).
  5. Jasse, A.; Berry, A.; Aleixandre-Tudo, J.L.; Poblete-Echeverría, C. Intra-block spatial and temporal variability of plant water status and its effect on grape and wine parameters. Agric. Water Manag. 2020, 246, 106696. [Google Scholar] [CrossRef]
  6. Taylor, J.; Dresser, J.; Hickey, C.; Nuske, S.; Bates, T. Considerations on spatial crop load mapping. Aust. J. Grape Wine Res. 2018, 25, 144–155. [Google Scholar] [CrossRef]
  7. Carrillo, E.; Matese, A.; Rousseau, J.; Tisseyre, B. Use of multi-spectral airborne imagery to improve yield sampling in viticulture. Precis. Agric. 2015, 17, 74–92. [Google Scholar] [CrossRef]
  8. Seng, K.P.; Ang, L.-M.; Schmidtke, L.M.; Rogiers, S.Y. Computer Vision and Machine Learning for Viticulture Technology. IEEE Access 2018, 6, 67494–67510. [Google Scholar] [CrossRef]
  9. Victorino, G.F.; Braga, R.; Santos-Victor, J.; Lopes, C.M. Yield components detection and image-based indicators for non-invasive grapevine yield prediction at different phenological phases. OENO One 2020, 54, 833–848. [Google Scholar] [CrossRef]
  10. Diago, M.P.; Tardáguila, J.; Aleixos, N.; Millán, B.; Prats-Montalban, J.M.; Cubero, S.; Blasco, J. Assessment of cluster yield components by image analysis. J. Sci. Food Agric. 2014, 95, 1274–1282. [Google Scholar] [CrossRef] [Green Version]
  11. Lopes, C.M.; Graça, J.; Sastre, J.; Reyes, M.; Guzmán, R.; Braga, R.; Monteiro, A.; Pinto, P.A. Vineyard Yeld Estimation by VINBOT Robot—Preliminary Results with the White Variety Viosinho. In Proceedings 11th International Terroir Congres; Jones, G., Doran, N., Eds.; Southern Oregon University: Ashland, OR, USA, 2016; pp. 458–463. [Google Scholar]
  12. Milella, A.; Marani, R.; Petitti, A.; Reina, G. In-field high throughput grapevine phenotyping with a consumer-grade depth camera. Comput. Electron. Agric. 2018, 156, 293–306. [Google Scholar] [CrossRef]
  13. Hacking, C.; Poona, N.; Manzan, N.; Poblete-Echeverría, C. Investigating 2-D and 3-D Proximal Remote Sensing Techniques for Vineyard Yield Estimation. Sensors 2019, 19, 3652. [Google Scholar] [CrossRef] [Green Version]
  14. Aquino, A.; Barrio, I.; Diago, M.-P.; Millan, B.; Tardaguila, J. vitisBerry: An Android-smartphone application to early evaluate the number of grapevine berries by means of image analysis. Comput. Electron. Agric. 2018, 148, 19–28. [Google Scholar] [CrossRef]
  15. Liu, S.; Zeng, X.; Whitty, M. A vision-based robust grape berry counting algorithm for fast calibration-free bunch weight estimation in the field. Comput. Electron. Agric. 2020, 173, 105360. [Google Scholar] [CrossRef]
  16. Aquino, A.; Millan, B.; Diago, M.-P.; Tardaguila, J. Automated early yield prediction in vineyards from on-the-go image acquisition. Comput. Electron. Agric. 2018, 144, 26–36. [Google Scholar] [CrossRef]
  17. Maimaitiyiming, M.; Sagan, V.; Sidike, P.; Kwasniewski, M.T. Dual Activation Function-Based Extreme Learning Machine (ELM) for Estimating Grapevine Berry Yield and Quality. Remote Sens. 2019, 11, 740. [Google Scholar] [CrossRef] [Green Version]
  18. Zabawa, L.; Kicherer, A.; Klingbeil, L.; Milioto, A.; Topfer, R.; Kuhlmann, H.; Roscher, R. Detection of Single Grapevine Berries in Images Using Fully Convolutional Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–17 June 2019; 2019; pp. 2571–2579. [Google Scholar] [CrossRef] [Green Version]
  19. Zhang, Z.; Zou, L.; Ren, C.; Ren, F.; Wang, Y.; Fan, P.; Li, S.; Liang, Z. VvSWEET10 mediates sugar accumulation in grapes. Genes 2019, 10, 255. [Google Scholar] [CrossRef] [Green Version]
  20. Tello, J.; Aguirrezábal, R.; Hernáiz, S.; Larreina, B.; Montemayor, M.; Vaquero, E.; Ibáñez, J. Multicultivar and multivariate study of the natural variation for grapevine bunch compactness. Aust. J. Grape Wine Res. 2015, 21, 277–289. [Google Scholar] [CrossRef]
  21. OIV Descriptor List for Grape Varieties and Vitis Species (2nd Edition). Available online: http://www.oiv.int/en/technical-standards-and-documents/description-of-grape-varieties/oiv-descriptor-list-for-grape-varieties-and-vitis-species-2nd-edition (accessed on 6 March 2022).
  22. Font, D.; Tresanchez, M.; Martínez, D.; Moreno, J.; Clotet, E.; Palacín, J. Vineyard Yield Estimation Based on the Analysis of High Resolution Images Obtained with Artificial Illumination at Night. Sensors 2015, 15, 8284–8301. [Google Scholar] [CrossRef] [Green Version]
  23. Herrero-Huerta, M.; González-Aguilera, D.; Rodríguez-Gonzálvez, P.; Hernández-López, D. Vineyard yield estimation by automatic 3D bunch modelling in field conditions. Comput. Electron. Agric. 2015, 110, 17–26. [Google Scholar] [CrossRef]
  24. Di Gennaro, S.F.; Toscano, P.; Cinat, P.; Berton, A.; Matese, A. A Low-Cost and Unsupervised Image Recognition Methodology for Yield Estimation in a Vineyard. Front. Plant Sci. 2019, 10, 559. [Google Scholar] [CrossRef] [Green Version]
  25. Nuske, S.; Gupta, K.; Narasimhan, S.; Singh, S. Modeling and calibrating visual yield estimates in vineyards. In Field and Service Robotics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 92, pp. 343–356. [Google Scholar] [CrossRef] [Green Version]
  26. Tello, J.; Cubero, S.; Blasco, J.; Tardáguila, J.; Aleixos, N.; Ibáñez, J. Application of 2D and 3D image technologies to characterise morphological attributes of grapevine clusters. J. Sci. Food Agric. 2016, 96, 4575–4583. [Google Scholar] [CrossRef] [Green Version]
  27. Cubero, S.; Diago, M.; Blasco, J.; Tardaguila, J.; Prats-Montalbán, J.; Ibáñez, J.; Tello, J.; Aleixos, N. A new method for assessment of bunch compactness using automated image analysis. Aust. J. Grape Wine Res. 2015, 21, 101–109. [Google Scholar] [CrossRef] [Green Version]
  28. Smart, R.E.; Turkington, C.R.; Evans, J.C. Grapevine Response to Furrow and Trickle Irrigation. Am. J. Enol. Vitic. 1974, 25, 62–66. [Google Scholar]
  29. Teixeira, G.; Monteiro, A.; Santos, C.; Lopes, C. Leaf morphoanatomy traits in white grapevine cultivars with distinct geographical origin. Ciência Técnica Vitivinícola 2018, 33, 90–101. [Google Scholar] [CrossRef] [Green Version]
  30. Duda, R.O.; Hart, P.E. Use of the Hough transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
  31. Venables, W.N.; Ripley, B.D. Tree-based Methods. In Modern Applied Statistics with S-Plus; Springer: New York, NY, USA, 1997; pp. 413–430. [Google Scholar] [CrossRef]
  32. Nuske, S.; Achar, S.; Gupta, K.; Narasimhan, S.; Singh, S. Visual Yield Estimation in Vineyards: Experiments with Different Varietals and Calibration Procedures; CMURI-TR-11-39; Carnegie Mellon University: Pittsburgh, PA, USA, 2011; p. 27. [Google Scholar]
  33. Ivorra, E.; Sánchez, A.; Camarasa, J.; Diago, M.; Tardaguila, J. Assessment of grape cluster yield components based on 3D descriptors using stereo vision. Food Control 2015, 50, 273–282. [Google Scholar] [CrossRef] [Green Version]
  34. Hacking, C.; Poona, N.; Poblete-Echeverria, C. Vineyard yield estimation using 2-D proximal sensing: A multitemporal approach. OENO One 2020, 54, 793–812. [Google Scholar] [CrossRef]
  35. Mirbod, O.; Yoder, L.; Nuske, S. Automated measurement of berry size in images. IFAC-Pap. OnLine 2016, 49, 79–84. [Google Scholar] [CrossRef]
  36. Roscher, R.; Herzog, K.; Kunkel, A.; Kicherer, A.; Töpfer, R.; Förstner, W. Automated image analysis framework for high-throughput determination of grapevine berry sizes using conditional random fields. Comput. Electron. Agric. 2014, 100, 148–158. [Google Scholar] [CrossRef] [Green Version]
  37. Aquino, A.; Diago, M.P.; Millán, B.; Tardaguila, J. A new methodology for estimating the grapevine-berry number per cluster using image analysis. Biosyst. Eng. 2017, 156, 80–95. [Google Scholar] [CrossRef]
  38. Clingeleffer, P. Crop Development, Crop Estimation and Crop Control to Secure Quality and Production of Major Wine Grape Varieties: A National Approach. Final Rep. Grape Wine Res. Dev. Corp. 2001, 148. Available online: http://hdl.handle.net/102.100.100/201731?index=1 (accessed on 6 March 2022).
  39. Kierdorf, J.; Weber, I.; Kicherer, A.; Zabawa, L.; Drees, L.; Roscher, R. Behind the Leaves—Estimation of Occluded Grapevine Berries with Conditional Generative Adversarial Networks. arXiv 2021, arXiv:2105.10325. Available online: http://rs.ipb.uni-bonn.de/wp-content/papercite-data/pdf/kierdorf2021behind.pdf (accessed on 6 March 2022).
  40. Parr, B.; Legg, M.; Bradley, S.; Alam, F. Occluded Grape Cluster Detection and Vine Canopy Visualisation Using an Ultrasonic Phased Array. Sensors 2021, 21, 2182. [Google Scholar] [CrossRef] [PubMed]
Horticulturae 08 00233 g001 550
Figure 1. Bunch images collected in lab conditions from cultivars Arinto (A), Encruzado (B), and Syrah (C) at the PT site in 2019 and cultivar Cabernet Sauvignon (D) at the SA site in 2021.
Figure 1. Bunch images collected in lab conditions from cultivars Arinto (A), Encruzado (B), and Syrah (C) at the PT site in 2019 and cultivar Cabernet Sauvignon (D) at the SA site in 2021.
Horticulturae 08 00233 g001
Horticulturae 08 00233 g002 550
Figure 2. Flowchart describing the work’s methodology from data collection to modelling.
Figure 2. Flowchart describing the work’s methodology from data collection to modelling.
Horticulturae 08 00233 g002
Horticulturae 08 00233 g003 550
Figure 3. Scatter plots showing the fitted linear relationships between bunch weight (predictor) and bunch area (A), visible berry number (B), bunch perimeter (C), and average berry area (D) on the training data set. Marker colors: green squares = Arinto; purple diamonds = Cabernet; blue circles = Encruzado; red triangles = Syrah. Different letters near the regression lines indicate significant differences among slopes according to Student’s T-test at p ≤ 0.05. When R2 is not significant, regression lines are not shown on the plot.
Figure 3. Scatter plots showing the fitted linear relationships between bunch weight (predictor) and bunch area (A), visible berry number (B), bunch perimeter (C), and average berry area (D) on the training data set. Marker colors: green squares = Arinto; purple diamonds = Cabernet; blue circles = Encruzado; red triangles = Syrah. Different letters near the regression lines indicate significant differences among slopes according to Student’s T-test at p ≤ 0.05. When R2 is not significant, regression lines are not shown on the plot.
Horticulturae 08 00233 g003
Horticulturae 08 00233 g004 550
Figure 4. Regression analysis between estimated bunch weight (predictor) and observed bunch weight for the training and test sets. Marker colors: green squares = Arinto; purple diamonds = Cabernet; blue circles = Encruzado; red triangles = Syrah.
Figure 4. Regression analysis between estimated bunch weight (predictor) and observed bunch weight for the training and test sets. Marker colors: green squares = Arinto; purple diamonds = Cabernet; blue circles = Encruzado; red triangles = Syrah.
Horticulturae 08 00233 g004
Table
Table 1. Description of the data set collected for the four studied cultivars.
Table 1. Description of the data set collected for the four studied cultivars.
CultivarVine AgeSiteN° of BunchesVine Spacing
Row × Interrow; m)		Training SystemPruning SystemIrrigation
Arinto13PT481.0 × 2.5VSPUnilateral RoyatDeficit drip
Cabernet18SA482.0 × 2.5VSPBilateral RoyatDrip
Encruzado13PT481.0 × 2.5VSPUnilateral RoyatDeficit drip
Syrah20PT481.3 × 2.5VSPBilateral RoyatRainfed
VSP: vertical shoot positioning.
Table
Table 2. Average ± standard error for the main variables analyzed in the full data set (n = 48 per cultivar). Bunch compactness notations (CI) are the mode of the observations based on the OIV descriptor n°204 [21].
Table 2. Average ± standard error for the main variables analyzed in the full data set (n = 48 per cultivar). Bunch compactness notations (CI) are the mode of the observations based on the OIV descriptor n°204 [21].
CultivarBw (g)Tb (n°)BA (cm2)BP (cm)Vb (n°)bA (cm2)CI
Arinto423.5 ± 26.9293.6 ± 18.9107.8 ± 5.562.3 ± 2.3108.0 ± 5.41.6 ± 0.17
Cabernet160.6 ± 10.4152.5 ± 9.285.7 ± 4.284.8 ± 4.581.2 ± 3.71.3 ± 0.17
Encruzado173.0 ± 15.482.3 ± 7.160.0 ± 3.943.2 ± 1.746.5 ± 2.72.3 ± 0.17
Syrah72.7 ± 6.571.4 ± 5.950.6 ± 4.268.7 ± 4.146.8 ± 2.91.2 ± 0.13
Bw: bunch weight; Tb: total berry number; BA: bunch area; BP: bunch perimeter; Vb: visible berry number; bA: average berry area. CI = 7: dense bunch; CI = 3: loose bunch. n = 48 per cultivar.
Table
Table 3. Fitted models resulting from the linear regression between bunch weight (Bw; g; predictor) over bunch area (BA; cm2), visible berry number (Vb), total berry number (Tb), and bunch perimeter (BP; cm), and respective statistical deviance measures for each of the four cultivars (n = 30) and for the combined data (n = 120) on the training set.
Table 3. Fitted models resulting from the linear regression between bunch weight (Bw; g; predictor) over bunch area (BA; cm2), visible berry number (Vb), total berry number (Tb), and bunch perimeter (BP; cm), and respective statistical deviance measures for each of the four cultivars (n = 30) and for the combined data (n = 120) on the training set.
PredictorCultivarEquationR2RMSPE (%)
BAArintoBw = 4.388 × BA − 56.0590.81 ***18.2
CabernetBw = 2.238 × BA − 34.3080.90 ***12.7
EncruzadoBw = 3.632 × BA − 44.3000.74 ***31.3
SyrahBw = 1.222 × BA + 9.4930.86 ***19.7
CombinedBw = 3.897 × BA − 91.0600.71 ***45.0
VbArintoBw = 4.427 × Vb − 65.3950.86 ***15.4
CabernetBw = 2.085 × Vb − 12.5930.72 ***21.1
EncruzadoBw = 5.257 × Vb − 77.6390.86 ***23.0
SyrahBw = 2.055 × Vb − 18.9190.73 ***27.6
CombinedBw = 4.066 × Vb − 81.1250.77 ***39.8
BPArintoBw = 8.838 × BP − 143.4400.55 ***28.0
CabernetBw = 1.220 × BP + 53.9870.25 ***34.8
EncruzadoBw = 6.603 × BP − 105.4000.19 *54.7
SyrahBw = 1.215 × BP − 7.8570.56 ***35.1
CombinedBw = 1.524 × BP + 111.9000.04 *81.6
*, *** p < 0.05 and 0.001, respectively.
Table
Table 4. Variable selection summary of the forward stepwise regression analysis, on the training set; between bunch weight (predictor) and bunch area (BA); bunch perimeter (BP); visible berry number (Vb); average berry area (bA); and the ratios between BA and BP (BA_BP), BA and Vb (BA_Vb), and BA and average berry area (BA_avg(bA)).
Table 4. Variable selection summary of the forward stepwise regression analysis, on the training set; between bunch weight (predictor) and bunch area (BA); bunch perimeter (BP); visible berry number (Vb); average berry area (bA); and the ratios between BA and BP (BA_BP), BA and Vb (BA_Vb), and BA and average berry area (BA_avg(bA)).
StepVariableSelectionAICR2Adj-R2
1VbAdded1394.50.780.77
2BA_BPAdded1319.80.880.88
3BA_avg(bA)Added1308.00.900.89
4BAAdded1294.60.910.91
5BPAdded1286.60.920.91
6BA_BPRemoved1285.10.920.91
AIC = Akaike information criteria. All R2 and Adj–R2 are statistically significant (p < 0.001).
Table
Table 5. Linear regression models between estimated bunch weight (predictor) and actual bunch weight (response) on the test set, respective statistical measures of validation, and t-test for slope and intercept analysis.
Table 5. Linear regression models between estimated bunch weight (predictor) and actual bunch weight (response) on the test set, respective statistical measures of validation, and t-test for slope and intercept analysis.
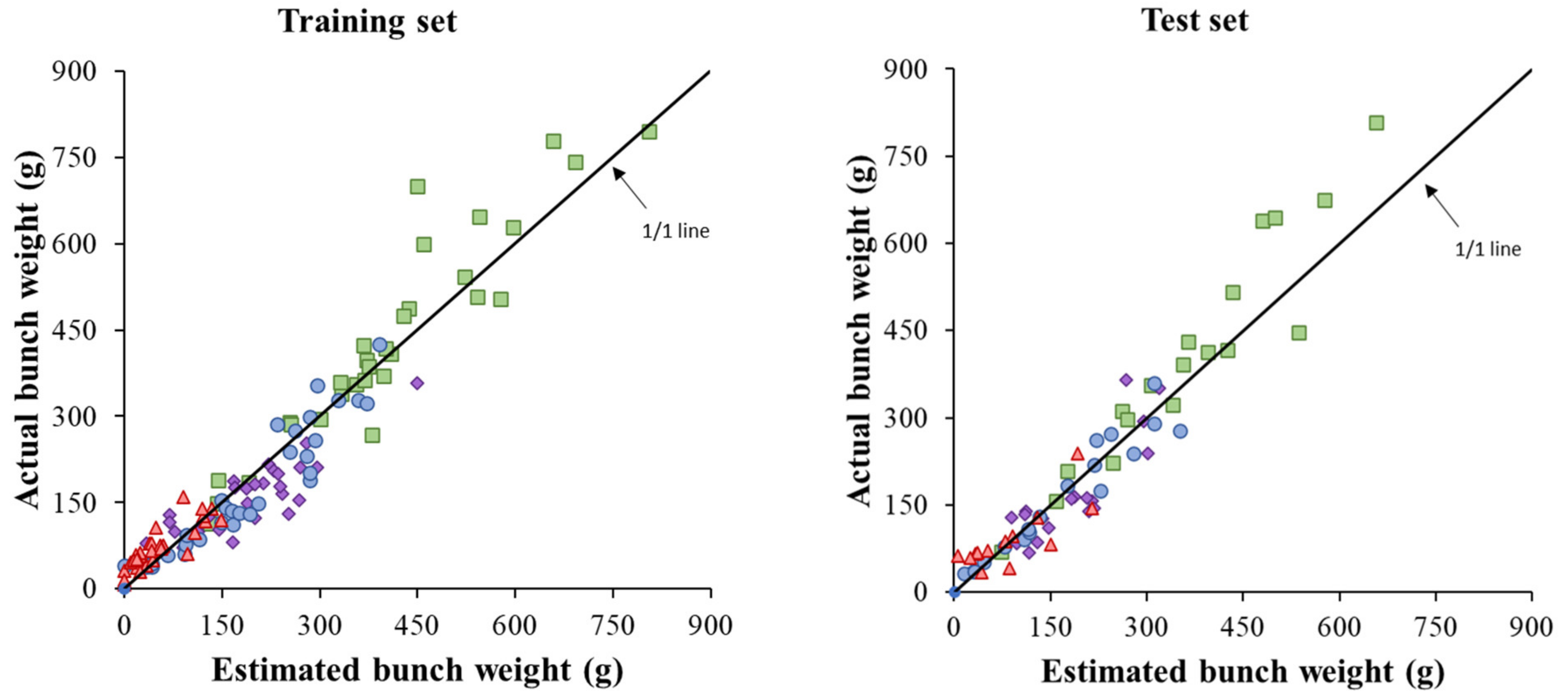
Data SetLinear RegressionR2RMSPE (%)Bias (%)EF
1 Slope2 Intercept
Arinto1.202 *−30.520 n.s.0.91 ***19.010.60.83
Cabernet0.996 n.s.−15.577 n.s.0.72 ***27.8−9.60.69
Encruzado0.924 n.s.−8.719 n.s.0.92 ***18.3−2.40.91
Syrah0.599 ***−39.822 ***0.70 ***60.523.00.28
Combined1.073 n.s.−4.184 n.s.0.91 ***25.94.90.91
1t-test for slope = 1; 2t-test for intercept = 0; n.s. = not significant; *, *** p < 0.05 and 0.001, respectively. R2: coefficient of determination; RMSPE: root mean square percentage error; EF: modelling efficiency.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Victorino, G.; Poblete-Echeverría, C.; Lopes, C.M. A Multicultivar Approach for Grape Bunch Weight Estimation Using Image Analysis. Horticulturae 2022, 8, 233. https://doi.org/10.3390/horticulturae8030233

AMA Style

Victorino G, Poblete-Echeverría C, Lopes CM. A Multicultivar Approach for Grape Bunch Weight Estimation Using Image Analysis. Horticulturae. 2022; 8(3):233. https://doi.org/10.3390/horticulturae8030233

Chicago/Turabian Style

Victorino, Gonçalo, Carlos Poblete-Echeverría, and Carlos M. Lopes. 2022. "A Multicultivar Approach for Grape Bunch Weight Estimation Using Image Analysis" Horticulturae 8, no. 3: 233. https://doi.org/10.3390/horticulturae8030233

APA Style

Victorino, G., Poblete-Echeverría, C., & Lopes, C. M. (2022). A Multicultivar Approach for Grape Bunch Weight Estimation Using Image Analysis. Horticulturae, 8(3), 233. https://doi.org/10.3390/horticulturae8030233

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop