Kinetic Analysis of Gluconacetobacter diazotrophicus Cultivated on a Bench Scale: Modeling the Effect of pH and Design of a Sucrose-Based Medium
Abstract
1. Introduction
2. Materials and Methods
2.1. Microorganism
2.2. Inoculum Preparation
2.3. Cultivation Conditions for Culture Medium Design
2.4. Screening of Medium Components
2.5. One-Factor Design
2.6. Submerged Cultivation on a Bench Scale
2.7. Analytical Methods
3. Model Development
3.1. Model Formulation
3.2. Preliminary Modeling and Fitting
3.3. First Modeling Approach
3.4. Second Modeling Approach
3.5. Statement of the Fitting Procedure
- The parameters of biomass and µ models are estimated on biomass measurements by minimization of SSE (18); in the µ model (6), the [H+] values are obtained by interpolation of the experimental [H+] data, and the signal is computed as well, whereas the pH definition is [42];
- The parameters of hydrogen models (17a) and (17b) are estimated on measurements of pH and biomass concentration via least squares, using Equation (19), with the values of computed in the previous step;
- The parameters of the biomass model (1) and specific growth rate model (6) are estimated on biomass measurements by minimization of the SSE (18); in the specific growth rate model (6), the [H+] values are obtained by using the hydrogen models (17a) and (17b) fitted in the previous step, instead of using interpolation.
4. Results and Discussion
4.1. Cultivation of Gluconacetobacter Diazotrophicus on a Laboratory Scale
4.2. Key Components of the Culture Medium
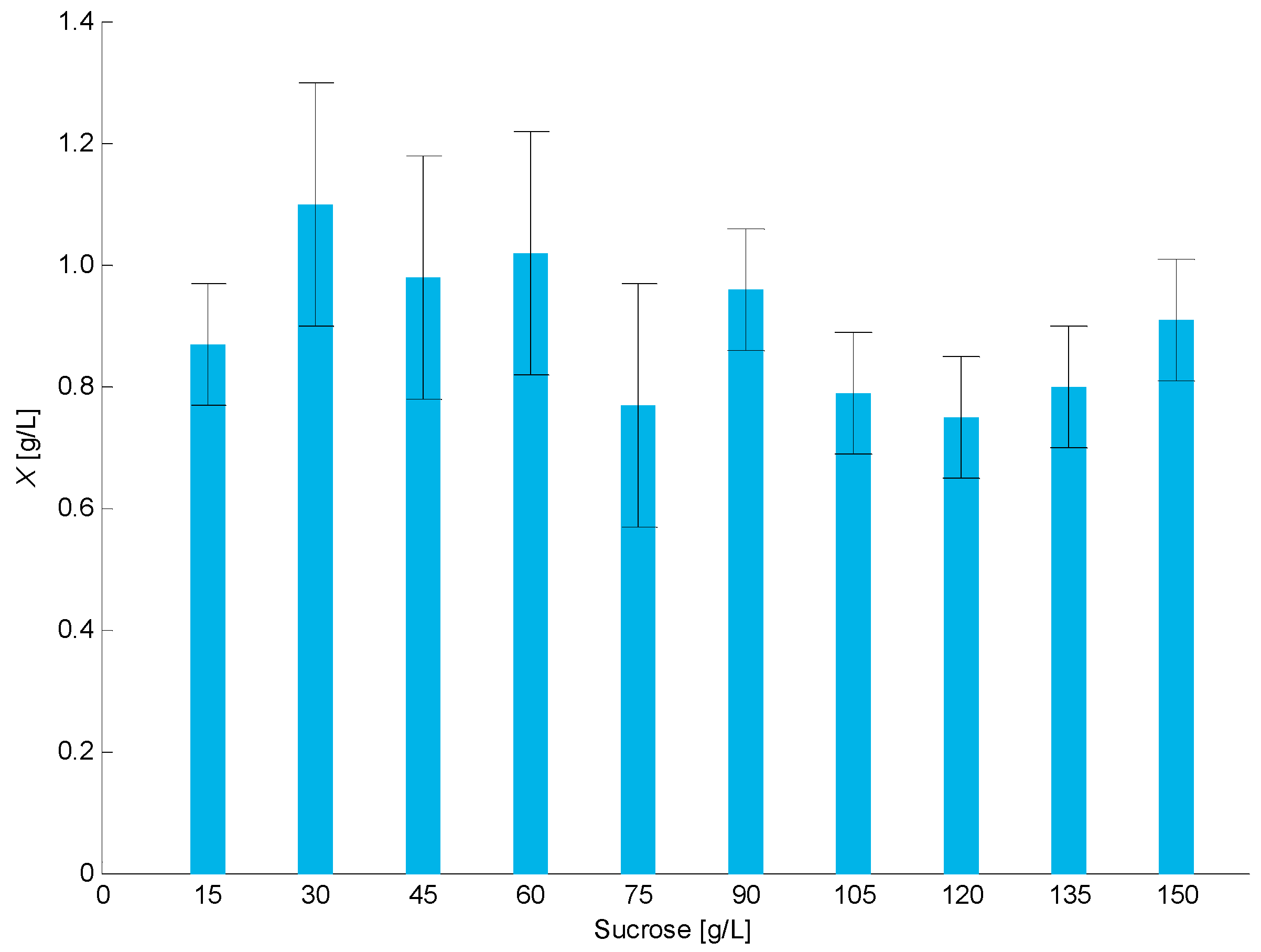
4.3. Definition of Carbon Source Concentration
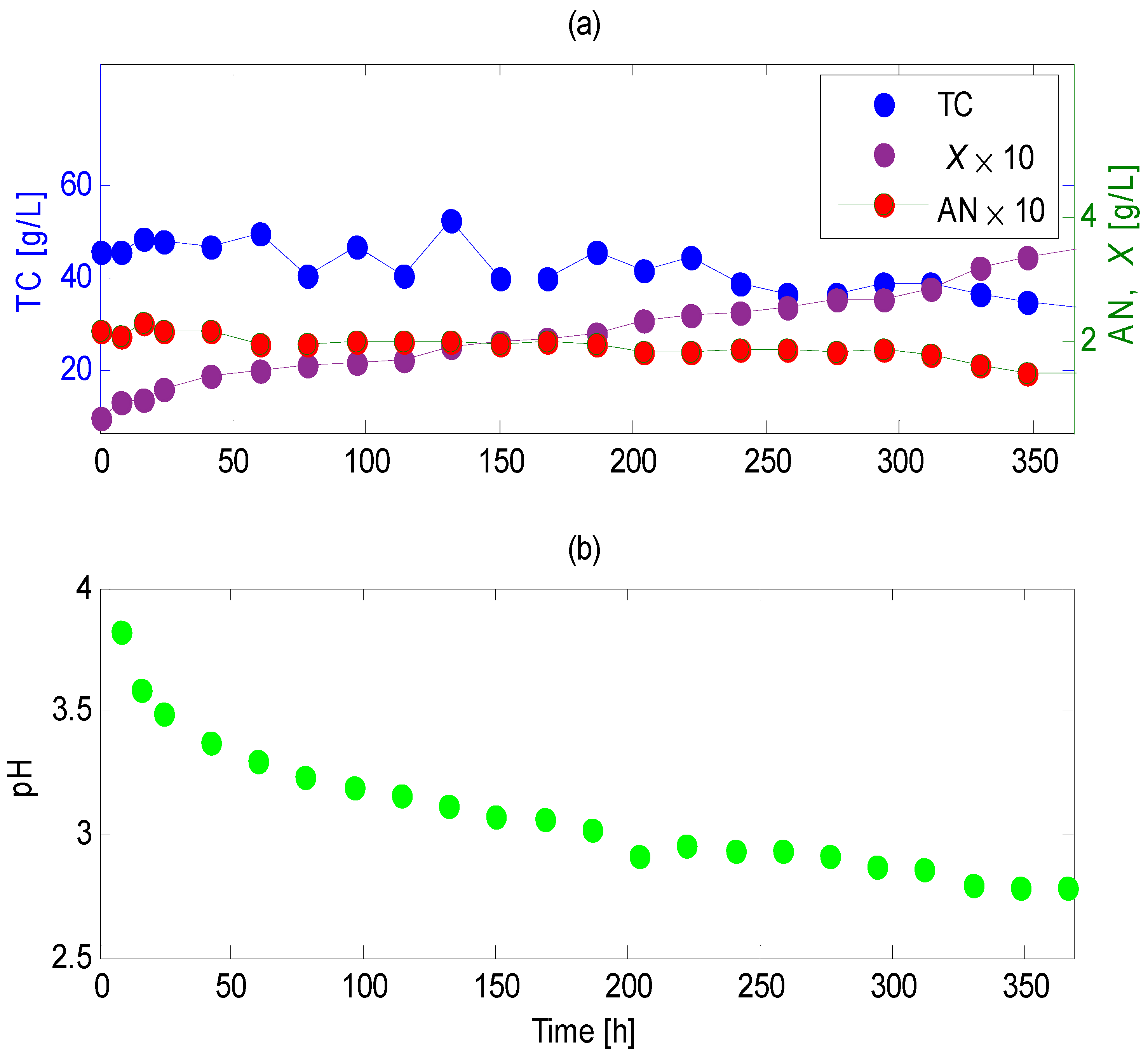
4.4. Bench-Scale Submerged Cultivation
4.5. Fitting of the Kinetic Model
4.5.1. Fitting of First Approach Models
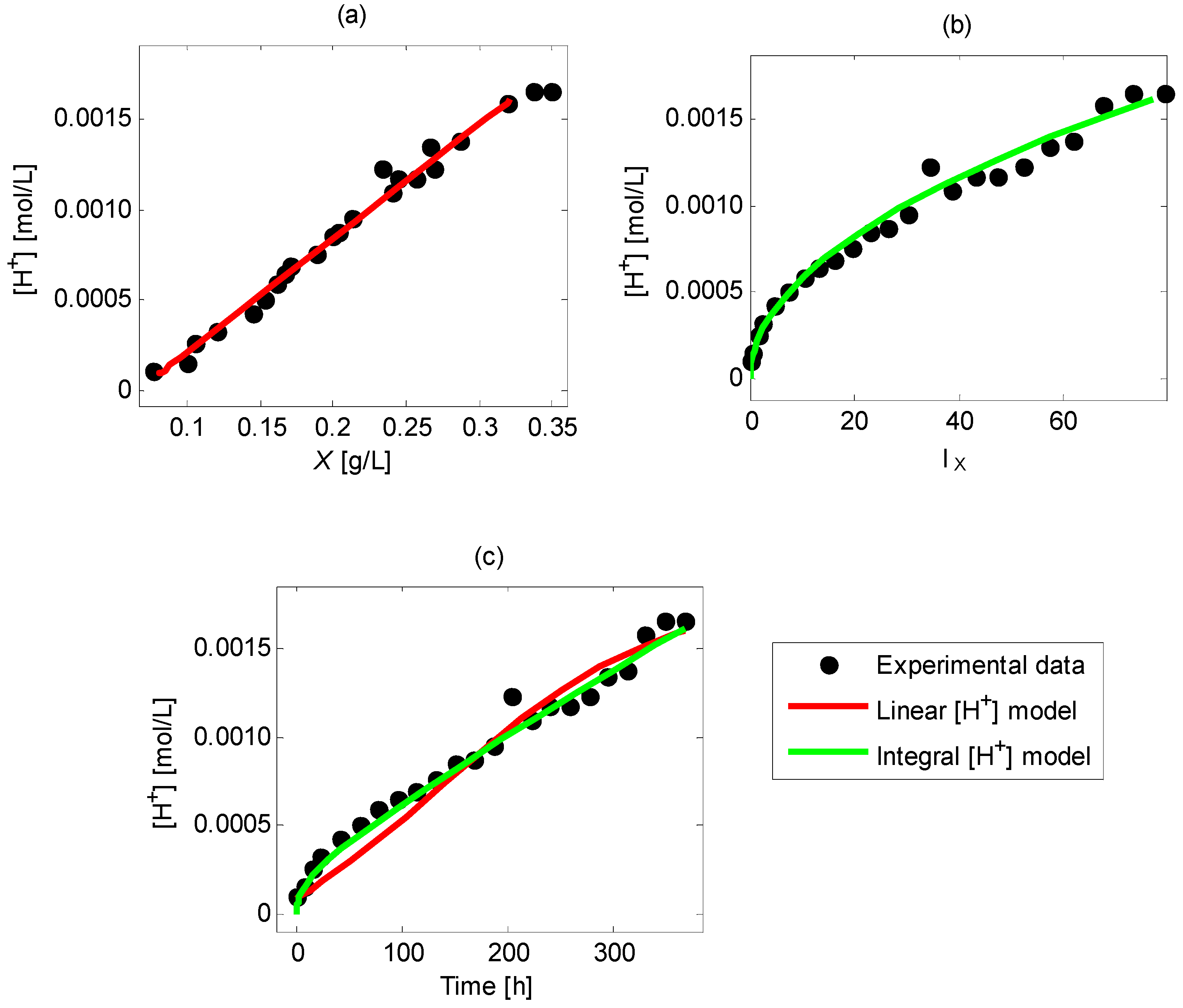
4.5.2. Fitting of Second Approach Models
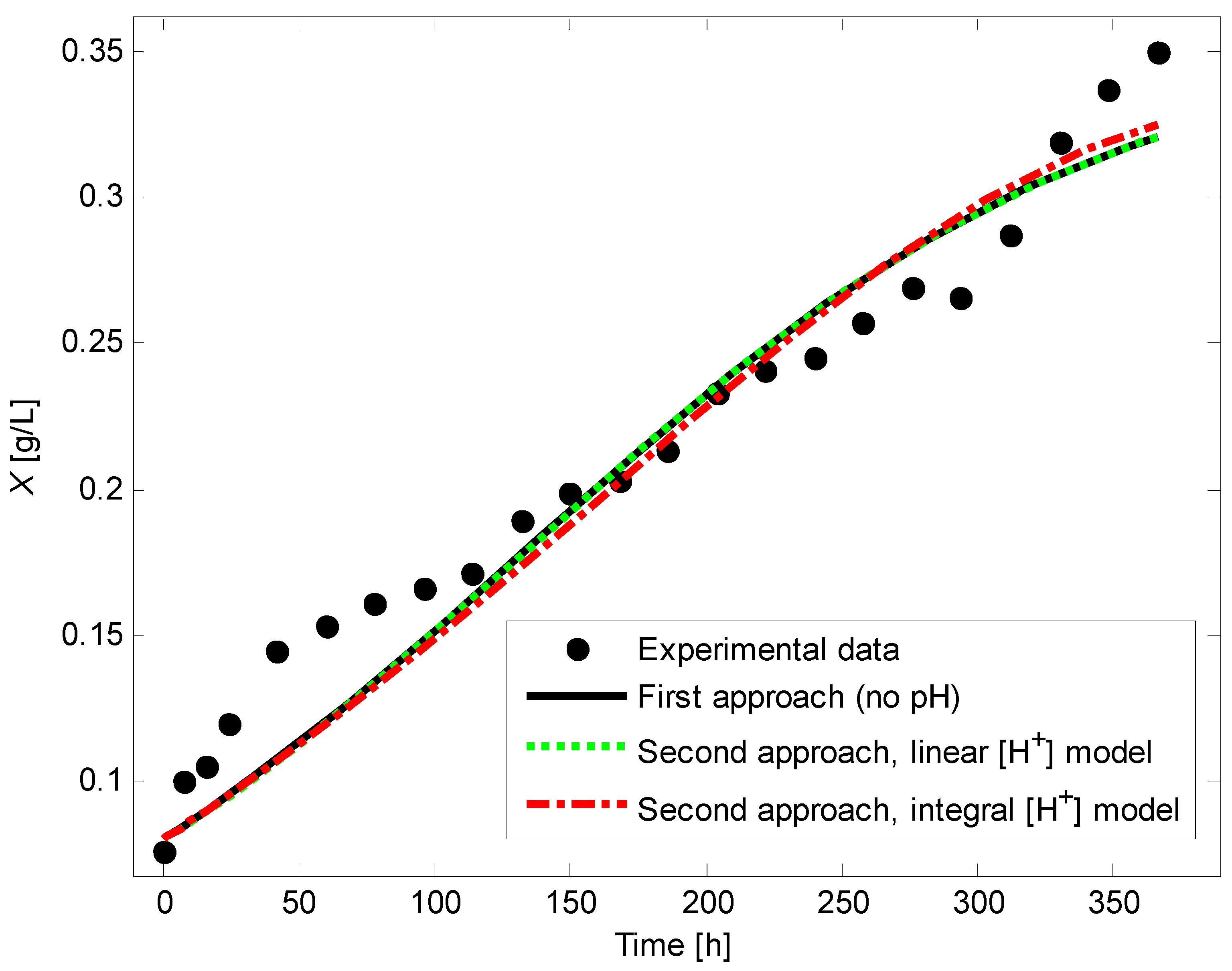
4.6. Comparison of Model Fitting via First and Second Approaches
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Overview of Scientific Literature on Modeling Approaches for the Relationship between Hydrogen Ions, Acids, Bases, and Buffer
- The Wiener models [24].
Appendix B. Equation of pH for the Case of External Addition of Acids/Bases/Buffer Compounds
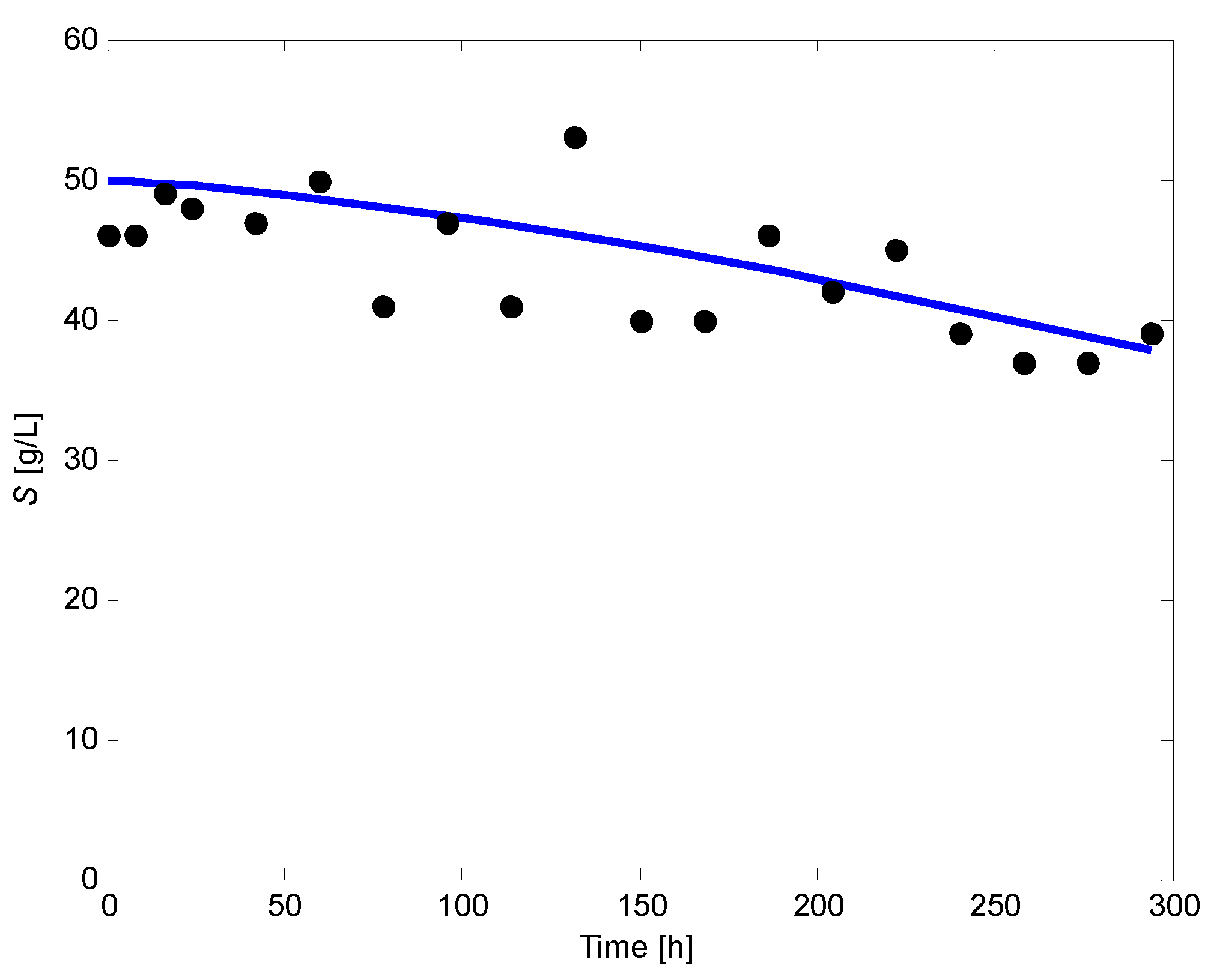
Appendix C. Fitting of Substrate Concentration
References
- Moreno Reséndez, A.; Carda Mendoza, V.; Reyes Carrillo, J.L.; Vásquez Arroyo, J.; Cano Ríos, P. Plant growth promoting rhizobacteria: A biofertilization alternative for sustainable agriculture. Rev. Colomb. Biotecnol. 2018, 20, 68–83. [Google Scholar] [CrossRef]
- Rojas, M.; Hernández, A.; Rives, N.; Tejera, B.; Acebo, Y.; Heydrich, M. Antisera production to detect indoleacetic acid in cultures of plant-growth promoting bacteria. Acta Biol. Colomb. 2012, 17, 271–280. [Google Scholar]
- Acurio Vásconez, R.D.; Mamarandi Mossot, J.E.; Ojeda Shagñay, A.G.; Tenorio Moya, E.M.; Chiluisa Utreras, V.P.; Vaca Suquillo, I.Á. Evaluation of Bacillus spp. as plant growth-promoting rhizobacteria (PGPR) in broccoli (Brassica oleracea var. italica) and lettuce (Lactuca sativa). Cienc. Tecnol. Agropecuaria. 2020, 21, e1465. [Google Scholar] [CrossRef]
- Nieto-Penalver, C.G.; Savino, M.J.; Bertini, E.V.; Sánchez, L.A.; de Figueroa, L.I. Gluconic acid produced by Gluconacetobacter diazotrophicus Pal5 possesses antimicrobial properties. Res. Microbiol. 2014, 165, 549–558. [Google Scholar] [CrossRef] [PubMed]
- Murumkar, D.; Nalawade, S.; Indi, D.; Pawar, S. Response of sugarcane seed plot to microbial inoculation by Gluconacetobacter diazotrophicus and phosphate-solubilizing bacteria. Sugar. Tech. 2017, 19, 26–32. [Google Scholar] [CrossRef]
- de Oliveira, T.R.A.; Gravina, G.A.; da Cruz, D.P.; Silva, N.D.; de Oliveira, G.H.F.; de Sant’Anna, C.Q.; Magalhães, M.M.; Berbert-Molina, M.A.; Neto, F.A. The performance of bean pod lineage inoculated with Gluconacetobacter diazotrophicus PAL5. Sci. Hortic. 2019, 249, 65–70. [Google Scholar] [CrossRef]
- Restrepo, G.M.; Sánchez, Ó.J.; Marulanda, S.M.; Galeano, N.F.; Taborda, G. Evaluation of plant-growth promoting properties of Gluconacetobacter diazotrophicus and Gluconacetobacter sacchari isolated from sugarcane and tomato in West Central region of Colombia. Afr. J. Biotechnol. 2017, 16, 1619–1629. [Google Scholar]
- Ferreira, C.M.; Soares, H.M.; Soares, E.V. Promising bacterial genera for agricultural practices: An insight on plant growth-promoting properties and microbial safety aspects. Sci. Total Environ. 2019, 682, 779–799. [Google Scholar] [CrossRef]
- Botta, A.L.; Santacecilia, A.; Ercole, C.; Cacchio, P.; Del Gallo, M. In vitro and in vivo inoculation of four endophytic bacteria on Lycopersicon esculentum. New Biotechnol. 2013, 30, 666–674. [Google Scholar] [CrossRef]
- Restrepo, G.M.; Ceballos, N.; Valencia, L.F.; Sánchez, Ó.J. Plant growth promotion by Gluconacetobacter diazotrophicus and its interaction with genotype and phosphorus availability in tomato seedlings. Org. Agric. 2021, 11, 601–614. [Google Scholar] [CrossRef]
- Cavalcante, V.A.; Döbereiner, J. A new acid-tolerant nitrogen-fixing bacterium associated with sugar cane. Plant Soil 1988, 108, 23–31. [Google Scholar] [CrossRef]
- Reis, V.M.; Olivares, F.L.; Döbereiner, J. Improved methodology for isolation of Acetobacter diazotrophicus and confirmation of its endophytic habitat. World J. Microbiol. Biotechnol. 1994, 10, 401–405. [Google Scholar] [CrossRef] [PubMed]
- Molinari, M.L.; Boiardi, J.L. Levans production by Gluconacetobacter diazotrophicus. Electron. J. Biotechnol. 2013, 16, 7. [Google Scholar] [CrossRef]
- Ríos Rocafull, Y.; Sánchez López, M.; Dibut Álvarez, B.; Ortega García, M.; Tejeda González, G.; Rodríguez Sánchez, J.; Rojas Badía, M. The culture medium effect in plant growth promotion activity of Gluconacetobacter diazotrophicus in carrot and sugar beet. Rev. Bio Cienc. 2019, 6, e470. [Google Scholar] [CrossRef]
- Dent, D.R.; Patel, D.; Devine, G. Novel Strain of Gluconacetobacter diazotrophicus (Gd) and Use Thereof in Agriculture. United Kingdom Patent No. 2558094, 22 April 2020. [Google Scholar]
- Triplett, E.W.; Kaeppler, S.M.; Chelius, M.K. Klebsiella pneumoniae Inoculants for Enhancing Plant Growth. United States Patent No. 7393678, 1 July 2008. [Google Scholar]
- Vessey, J.K.; Fei, H.; Abudureheman, A. Use of Gluconacetobacter with Reduced Use of Nitrogen Fertilizer to Improve Beet Crop Production. United States Patent No. 8252720, 28 August 2012. [Google Scholar]
- Boniolo, F.S.; Nunes, M.C.O.; Berbert de Molina, M.A. Processo Tecnológico Para a Produção de Biomassa Bacteriana e Produtos de Fermentação de Gluconacetobacter diazotrophicus. Brazil Patent No. Application PI0917666-7, 13 March 2012. [Google Scholar]
- Rincón, A.; Cuéllar, J.A.; Valencia, L.F.; Sánchez, O.J. Kinetics of Gluconacetobacter diazotrophicus growth using cane molasses and sucrose: Assessment of kinetic models. Acta Biol. Colomb. 2019, 24, 38–57. [Google Scholar]
- Attwood, M.; Van Dijken, J.; Pronk, J. Glucose metabolism and gluconic acid production by Acetobacter diazotrophicus. J. Ferment. Bioeng. 1991, 72, 101–105. [Google Scholar] [CrossRef]
- Luna, M.F. Características fisiológicas de Gluconacetobacter diazotrophicus: Importancia funcional de la oxidación periplasmática de aldosas. Ph.D. Thesis, Departamento de Ciencias Biológicas, Universidad Nacional de la Plata, La Plata, Argentina, 2003; 134p. [Google Scholar]
- Luna, M.F.; Boiardi, J.L. Growth yields and glucose metabolism of N2-fixing Gluconacetobacter diazotrophicus at different culture pH values. World J. Microbiol. Biotechnol. 2008, 24, 587–590. [Google Scholar] [CrossRef]
- Molinari, M.L. Producción de exopolisacáridos tipo fructooligosacáridos por Gluconacetobacter diazotrophicus. PhD Thesis, Doctorado en Ciencias Exactas; Departamento de Química, Universidad Nacional de la Plata: La Plata, Argentina, 2011; 153p. [Google Scholar]
- Aliskan, I. Adaptive model predictive control for Wiener nonlinear systems. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 361–377. [Google Scholar] [CrossRef]
- Panda, A.; Panda, R.C. Adaptive nonlinear model-based control scheme implemented on the nonlinear processes. Nonlinear Dyn. 2018, 91, 2735–2753. [Google Scholar] [CrossRef]
- Nicolai, B.; Van Impe, J.; Verlinden, B.; Martens, T.; Vandewalle, J.; De Baerdemaeker, J. Predictive modelling of surface growth of lactic acid bacteria in vacuum-packed meat. Food Microbiol. 1993, 10, 229–238. [Google Scholar] [CrossRef]
- Spann, R.; Roca, C.; Kold, D.; Lantz, A.E.; Gernaey, K.V.; Sin, G. A probabilistic model-based soft sensor to monitor lactic acid bacteria fermentations. Biochem. Eng. J. 2018, 135, 49–60. [Google Scholar] [CrossRef]
- Duarte-Mermoud, M.A.; Rojo, F.A.; Pérez, R. Experimental evaluation of combined model reference adaptive controller in a pH regulation process. Int. J. Adapt. Control. Signal Process. 2002, 16, 85–106. [Google Scholar] [CrossRef]
- Lee, S.; Sung, S.W.; Lee, J. In-line mixer pH system for the identification of titration curve. Int. J. Control. Autom. Syst. 2013, 11, 442–449. [Google Scholar] [CrossRef]
- Vereecken, K.M.; Van Impe, J.F. Analysis and practical implementation of a model for combined growth and metabolite production of lactic acid bacteria. Int. J. Food Microbiol. 2002, 73, 239–250. [Google Scholar] [CrossRef]
- Hall, R.C.; Seborg, D.E. Modelling and self-tuning control of a multivariable ph neutralization process Part I: Modelling and multiloop control. In Proceedings of the 1989 American Control Conference, Pittsburgh, PA, USA, 21–23 June 1989; IEEE: Pittsburgh, PA, USA, 1989; pp. 1822–1827. [Google Scholar]
- McAvoy, T.J.; Hsu, E.; Lowenthal, S. Dynamics of pH in controlled stirred tank reactor. Ind. Eng. Chem. Process Des. Dev. 1972, 11, 68–70. [Google Scholar] [CrossRef]
- Boniolo, F.S.; Rodrigues, R.C.; Delatorre, E.O.; da Silveira, M.M.; Flores, V.M.Q.; Berbert-Molina, M.A. Glycine betaine enhances growth of nitrogen-fixing bacteria Gluconacetobacter diazotrophicus PAL5 under saline stress conditions. Curr. Microbiol. 2009, 59, 593–599. [Google Scholar] [CrossRef]
- Luna, M.; Bernardelli, C.; Galar, M.; Boiardi, J. Glucose metabolism in batch and continuous cultures of Gluconacetobacter diazotrophicus PAL 3. Curr. Microbiol. 2006, 52, 163–168. [Google Scholar] [CrossRef]
- Stephan, M.P.; Oliveira, M.; Teixeira, K.R.S.; Martinez-Drets, G.; Döbereiner, J. Physiology and dinitrogen fixation of Acetobacter diazotrophicus. FEMS Microbiol. Lett. 1991, 77, 67–72. [Google Scholar] [CrossRef][Green Version]
- Plackett, R.L.; Burman, J.P. The design of optimum multifactorial experiments. Biometrika 1946, 33, 305–325. [Google Scholar] [CrossRef]
- Feng, Y.; Li, W.; Wu, X.; Cheng, J.; Ma, S. Statistical optimization of media for mycelial growth and exo-polysaccharide production by Lentinus edodes and a kinetic model study of two growth morphologies. Biochem. Eng. J. 2010, 49, 104–112. [Google Scholar] [CrossRef]
- Herbert, D.; Phipps, P.J.; Strange, R.E. Chemical analysis of microbial cells. In Methods in Microbiology; Norris, J.R., Ribbons, D.W., Eds.; Academic Press: New York, NY, USA, 1971; pp. 265–272. [Google Scholar]
- DuBois, M.; Gilles, K.; Hamilton, J.; Rebers, P.; Smith, F. Colorimetric method for determination of sugars and related substances. Anal. Chem. 1956, 28, 350–356. [Google Scholar] [CrossRef]
- Wheaterburn, M.W. Phenol hypoclorite reaction determination of ammonia. Anal. Chem. 1967, 39, 971–974. [Google Scholar] [CrossRef]
- Lara, C.; Villalba, M.; Oviedo, L. Non-symbiotic bacterial diazotrophs from agricultural crops of San Carlos. Córdoba, Colombia. Rev. Colomb. Biotecnol. 2007, 9, 6–14. [Google Scholar]
- Poschet, F.; Vereecken, K.; Geeraerd, A.; Nicolaï, B.; Van Impe, J. Analysis of a novel class of predictive microbial growth models and application to coculture growth. Int. J. Food Microbiol. 2005, 100, 107–124. [Google Scholar] [CrossRef] [PubMed]
- Belfares, L.; Perrier, M.; Ramsay, B.A.; Ramsay, J.A.; Jolicoeur, M.; Chavarie, C. Multi-inhibition kinetic model for the growth of Alcaligenes eutrophus. Can. J. Microbiol. 1995, 41, 249–256. [Google Scholar] [CrossRef]
- de Andrade, R.R.; Maugeri Filho, F.; Maciel Filho, R.; da Costa, A.C. Kinetics of ethanol production from sugarcane bagasse enzymatic hydrolysate concentrated with molasses under cell recycle. Bioresour. Technol. 2013, 130, 351–359. [Google Scholar] [CrossRef]
- Cañete-Rodríguez, A.; Santos-Dueñas, I.; Jimenez-Hornero, J.; Torija-Martinez, M.; Mas, A.; García-García, I. An approach for estimating the maximum specific growth rate of Gluconobacter japonicus in strawberry purée without cell concentration data. Biochem. Eng. J. 2016, 105, 314–320. [Google Scholar] [CrossRef]
- Gordeeva, Y.L.; Rudakovskaya, E.; Gordeeva, E.; Borodkin, A. Mathematical modeling of biotechnological process of lactic acid production by batch fermentation: A review. Theor. Found. Chem. Eng. 2017, 51, 282–298. [Google Scholar] [CrossRef]
- Antwi, M.; Theys, T.; Bernaerts, K.; Van Impe, J.; Geeraerd, A. Validation of a model for growth of Lactococcus lactis and Listeria innocua in a structured gel system: Effect of monopotassium phosphate. Int. J. Food Microbiol. 2008, 125, 320–329. [Google Scholar] [CrossRef]
- Vereecken, K.; Devlieghere, F.; Bockstaele, A.; Debevere, J.; Van Impe, J. A model for lactic acid-induced inhibition of Yersinia enterocolitica in mono-and coculture with Lactobacillus sakei. Food Microbiol. 2003, 20, 701–713. [Google Scholar] [CrossRef]
- Luedeking, R.; Piret, E.L. A kinetic study of the lactic acid fermentation. Batch process at controlled pH. J. Biochem. Microbiol. Technol. Eng. 1959, 1, 393–412. [Google Scholar] [CrossRef]
- Cangussu, A.S.R.; Cruz, P.A.; Aguiar, R.W.S.; Santos, G.R.; Campos, F.S.; Sobrinho, E.M.; Brandi, I.V.; Viana, K.F.; Nogueira, P.A.; Passos, F.J. Prediction of fermentative parameters from mathematical modeling using thermotolerant probiotic yeast. Bioresour. Technol. Rep. 2020, 11, 100522. [Google Scholar] [CrossRef]
- De Bhowmick, G.; Sen, R.; Sarmah, A.K. Analysis of growth and intracellular product synthesis dynamics of a microalga cultivated in wastewater cocktail as medium. Biochem. Eng. J. 2019, 149, 107253. [Google Scholar] [CrossRef]
- Sanjay, K.; Anand, A.P.; Veeranki, V.D.; Kannan, P. Kinetics of growth on dual substrates, production of novel glutaminase-free L-asparaginase and substrates utilization by Pectobacterium carotovorum MTCC 1428 in a batch bioreactor. Korean J. Chem. Eng. 2017, 34, 118–126. [Google Scholar] [CrossRef]
- Motulsky, H.; Christopoulos, A. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Akkermans, S.; Van Impe, J.F. Mechanistic modelling of the inhibitory effect of pH on microbial growth. Food Microbiol. 2018, 72, 214–219. [Google Scholar] [CrossRef]
- Baty, F.; Delignette-Muller, M.-L. Estimating the bacterial lag time: Which model, which precision? Int. J. Food Microbiol. 2004, 91, 261–277. [Google Scholar] [CrossRef]
- Donaldson, J.R.; Schnabel, R.B. Computational experience with confidence regions and confidence intervals for nonlinear least squares. Technometrics 1987, 29, 67–82. [Google Scholar] [CrossRef]
- Åström, K.; Wittenmark, B. Adaptive Control. Reading ea; Addison Wesley Publishing Comp: Boston, MA, USA, 1995. [Google Scholar]
- Flores-Encarnación, M.; Contreras-Zentella, M.; Soto-Urzua, L.; Aguilar, G.; Baca, B.; Escamilla, J. The respiratory system and diazotrophic activity of Acetobacter diazotrophicus PAL5. J. Bacteriol. 1999, 181, 6987–6995. [Google Scholar] [CrossRef]
- Stephan, M.P.; Teixeira, K.R.S.; Döbereiner, J. Nitrogen fixation physiology of Acetobacter nitrocaptans: Effect of oxygen, pH and carbon source on respiration and nitrogenase activity. In Proceedings of the 7th International Congress on Nitrogen Fixation; Nitrogen Fixation: Hundred years after, Cologne, Germany, 13–20 March 1988; p. 207. [Google Scholar]
- Bashan, Y.; Kamnev, A.A.; de-Bashan, L.E. Tricalcium phosphate is inappropriate as a universal selection factor for isolating and testing phosphate-solubilizing bacteria that enhance plant growth: A proposal for an alternative procedure. Biol. Fertil. Soils 2013, 49, 465–479. [Google Scholar] [CrossRef]
- Pizarro, O. Obtención de condiciones de elaboración de vinagre de arándanos (Vaccinium corymbosum) utilizando torta de prensa Ingeniería de Alimentos. In Escuela de Ingeniería de Alimentos; Universidad Austral de Chile: Valdivia, Spain, 2005; p. 81. [Google Scholar]
- Meneses, C.; Vassoler, R.; Rouws, L.; de Araújo, J.; Soares, M.; Baldani, J.I. Produção e Quantificação de Exopolissaccarídeos Sintetizados por Gluconacetobacter Diazotrophicus PAL5 em meio de cultivo líquido; Comunicado Técnico; Embrapa: Seropedica, RJ, USA, 2009; pp. 1–6. [Google Scholar]
- Rodrigues, E.P.; Coelho, M.S.; Soares, C.d.P.; Vidal, M.S.; Araújo, J.L.; Baldani, J.I. Identificação e Quantificação de Compostos Indólicos no Sobrenadante de Gluconacetobacter Diazotrophicus, Cultivada em Meio Liquido, por Cromatografia Líquida de Alta Eficiência (HPLC). 2009. Available online: https://www.embrapa.br/busca-de-publicacoes/-/publicacao/664190/identificacao-e-quantificacao-de-compostos-indolicos-no-sobrenadante-de-gluconacetobacter-diazotrophicus-cultivada-em-meio-liquido-por-cromatografia-liquida-de-alta-eficiencia-hplc (accessed on 7 June 2023).
- Balannec, B.; Bouguettoucha, A.; Amrane, A. Unstructured model for batch cultures without pH control of Lactobacillus helveticus—Inhibitory effect of the undissociated lactic acid. Biochem. Eng. J. 2007, 35, 289–294. [Google Scholar] [CrossRef]
- Ellouze, M.; Pichaud, M.; Bonaiti, C.; Coroller, L.; Couvert, O.; Thuault, D.; Vaillant, R. Modelling pH evolution and lactic acid production in the growth medium of a lactic acid bacterium: Application to set a biological TTI. Int. J. Food Microbiol. 2008, 128, 101–107. [Google Scholar] [CrossRef] [PubMed]
- Alkamil, E.H.; Al-Dabooni, S.; Abbas, A.K.; Flori, R.; Wunsch II, D.C. Learning from experience: An automatic pH neutralization system using hybrid fuzzy system and neural network. Procedia Comput. Sci. 2018, 140, 206–215. [Google Scholar] [CrossRef]
- Ebrahimpour, M.; Yu, W.; Young, B. Artificial neural network modelling for cream cheese fermentation pH prediction at lab and industrial scales. Food Bioprod. Process. 2021, 126, 81–89. [Google Scholar] [CrossRef]
- Wright, R.A.; Kravaris, C. Nonlinear control of pH processes using the strong acid equivalent. Ind. Eng. Chem. Res. 1991, 30, 1561–1572. [Google Scholar] [CrossRef]
- Birol, G.; Ündey, C.; Cinar, A. A modular simulation package for fed-batch fermentation: Penicillin production. Comput. Chem. Eng. 2002, 26, 1553–1565. [Google Scholar] [CrossRef]
- Henson, M.A.; Seborg, D.E. Adaptive nonlinear control of a pH neutralization process. IEEE Trans. Control. Syst. Technol. 1994, 2, 169–182. [Google Scholar] [CrossRef]
- Antwi, M.; Bernaerts, K.; Van Impe, J.; Geeraerd, A.H. Modelling the combined effects of structured food model system and lactic acid on Listeria innocua and Lactococcus lactis growth in mono-and coculture. Int. J. Food Microbiol. 2007, 120, 71–84. [Google Scholar] [CrossRef]


| N. | Component | Amount for 1 L | Concentration (g/L) |
|---|---|---|---|
| 1 | White sugar | 100 g | 100 |
| 2 | K2HPO4 (10% solution) | 2 mL | 0.02 |
| 3 | KH2PO4 (10% solution) | 6 mL | 0.06 |
| 4 | MgSO4·7H2O (10% solution) | 2 mL | 0.02 |
| 5 | CaCl2·2H2O (1% solution) | 2 mL | 0.002 |
| 6 | Na2MoO4·2H2O (0,1% solution) | 2 mL | 0.0002 |
| 7 | FeCl3·6H2O (1% solution) | 1 mL | 0.001 |
| 8 | (NH4)2SO4 | 1 g | 1 |
| Coded Factor | Factor | Experimental Range (g/L) | |
|---|---|---|---|
| Low Level (−1) | High Level (+1) | ||
| Z1 | Sucrose | 70 | 130 |
| Z2 | K2HPO4 | 0.005 | 0.035 |
| Z3 | KH2PO4 | 0.045 | 0.075 |
| Z4 | MgSO4·7H2O | 0.005 | 0.035 |
| Z5 | CaCl2·2H2O | 0.0005 | 0.0035 |
| Z6 | Na2MoO4·2H2O | 0.00005 | 0.00035 |
| Z7 | FeCl3·6H2O | 0.0001 | 0.0019 |
| Z8 | (NH4)2SO4 | 0.1 | 1.9 |
| Z9–Z11 | Dummy factors | - | - |
| N. | Coded Factors | Biomass (g/L) 1 | Standard Deviation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | Z9 | Z10 | Z11 | |||
| 1 | +1 | −1 | +1 | +1 | +1 | +1 | +1 | −1 | −1 | −1 | −1 | 0.83 | 0.20 |
| 2 | +1 | +1 | −1 | +1 | −1 | +1 | −1 | +1 | −1 | +1 | −1 | 1.08 | 0.32 |
| 3 | −1 | +1 | +1 | −1 | −1 | +1 | +1 | +1 | −1 | −1 | +1 | 1.10 | 0.23 |
| 4 | −1 | +1 | +1 | +1 | +1 | −1 | −1 | −1 | −1 | +1 | +1 | 1.17 | 0.11 |
| 5 | −1 | −1 | +1 | −1 | +1 | +1 | −1 | +1 | +1 | +1 | −1 | 1.10 | 0.04 |
| 6 | −1 | −1 | −1 | +1 | −1 | +1 | +1 | −1 | +1 | +1 | +1 | 1.42 | 0.63 |
| 7 | +1 | −1 | +1 | +1 | −1 | −1 | −1 | +1 | +1 | −1 | +1 | 1.11 | 0.20 |
| 8 | −1 | +1 | −1 | +1 | +1 | −1 | +1 | +1 | +1 | −1 | −1 | 1.28 | 0.19 |
| 9 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 1.32 | 0.22 |
| 10 | +1 | +1 | −1 | −1 | +1 | +1 | −1 | −1 | +1 | −1 | +1 | 1.35 | 0.43 |
| 11 | +1 | +1 | +1 | −1 | −1 | −1 | +1 | −1 | +1 | +1 | −1 | 1.15 | 0.17 |
| 12 | +1 | −1 | −1 | −1 | +1 | −1 | +1 | +1 | −1 | +1 | +1 | 1.19 | 0.24 |
| Source | Chi-Squared | Degrees of Freedom | t-Value | Mean Squared Deviation | p-Value |
|---|---|---|---|---|---|
| Z1 | 1.370723 | 1 | 2.032245 | 7.097078 | 0.2416877 |
| Z2 | 0.272593 | 1 | 2.032245 | 7.212022 | 0.6015979 |
| Z3 | 2.604274 | 1 | 2.032245 | 6.965699 | 0.1065760 |
| Z4 | 1.261836 | 1 | 2.032245 | 7.108559 | 0.2613038 |
| Z5 | 0.002253 | 1 | 2.032245 | 7.240039 | 0.9621434 |
| Z6 | 1.766220 | 1 | 2.032245 | 7.055222 | 0.1838505 |
| Z7 | 0.361454 | 1 | 2.032245 | 7.202788 | 0.5476996 |
| Z8 | 0.012265 | 1 | 2.032245 | 7.239003 | 0.9118151 |
| Contrast | Difference | +/− Limits | Lower Limit | Higher Limit |
|---|---|---|---|---|
| 15–30 | −0.22601 | 0.132147 | −0.358157 | −0.093863 |
| 15–60 | −0.14268 | 0.132147 | −0.274827 | −0.010533 |
| 30–75 | 0.32433 | 0.132147 | 0.192183 | 0.456477 |
| 30–90 | 0.13634 | 0.132147 | 0.004193 | 0.268487 |
| 30–105 | 0.31333 | 0.132147 | 0.181183 | 0.445477 |
| 30–120 | 0.35267 | 0.132147 | 0.220523 | 0.484817 |
| 30–135 | 0.29701 | 0.132147 | 0.164863 | 0.429157 |
| 30–150 | 0.187 | 0.132147 | 0.054853 | 0.319147 |
| 45–75 | 0.20699 | 0.132147 | 0.074843 | 0.339137 |
| 45–105 | 0.19599 | 0.132147 | 0.063843 | 0.328137 |
| 45–120 | 0.23533 | 0.132147 | 0.103183 | 0.367477 |
| 45–135 | 0.17967 | 0.132147 | 0.047523 | 0.311817 |
| 60–75 | 0.241 | 0.132147 | 0.108853 | 0.373147 |
| 60–105 | 0.23 | 0.132147 | 0.097853 | 0.362147 |
| 60–120 | 0.26934 | 0.132147 | 0.137193 | 0.401487 |
| 60–135 | 0.21368 | 0.132147 | 0.081533 | 0.345827 |
| 75–90 | −0.18799 | 0.132147 | −0.320137 | −0.055843 |
| 75–150 | −0.13733 | 0.132147 | −0.269477 | −0.005183 |
| 90–105 | 0.17699 | 0.132147 | 0.044843 | 0.309137 |
| 90–120 | 0.21633 | 0.132147 | 0.084183 | 0.348477 |
| 90–135 | 0.16067 | 0.132147 | 0.028523 | 0.292817 |
| 120–150 | −0.16567 | 0.132147 | −0.297817 | −0.033523 |
| Modeling Approach and Model | Parameter and R2 | Value |
|---|---|---|
| First modeling approach; biomass model (1) and µ model (20) | µmax | 0.0093 ± 0.0017 h−1 |
| Xmax | 0.3578 ± 0.0503 g/L | |
| R2 (for biomass concentration over time) | 0.9364 | |
| Second modeling approach; hydrogen model (21) | θ1 | 0.0665 ± 0.0093 |
| θ2 | 158.5 ± 9.1 | |
| R2 (for H+ concentration as a function of biomass concentration) | 0.9841 | |
| Second modeling approach; hydrogen model (22) | θ | 29,449,609 ± 1,652,515 |
| R2 (for H+ concentration as a function of the integral of biomass concentration) | 0.9811 | |
| Second modeling approach; biomass model (1) and µ model (23), with [H+] provided by the hydrogen model (21) | µmax | 0.0076 ± 0.0012 h−1 |
| Hmax | 0.00184 ± 0.00032 mol/L (corresponds to pHmin = 2.735) | |
| R2 (for biomass concentration over time) | 0.9364 | |
| Second modeling approach; biomass model (1) and µ model (23), with [H+] provided by the hydrogen model (22) | µmax | 0.0078 ± 0.0010 h−1 |
| Hmax | 0.00181 ± 0.00027 mol/L | |
| R2 (for biomass concentration over time) | 0.9357 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Restrepo, G.M.; Rincón, A.; Sánchez, Ó.J. Kinetic Analysis of Gluconacetobacter diazotrophicus Cultivated on a Bench Scale: Modeling the Effect of pH and Design of a Sucrose-Based Medium. Fermentation 2023, 9, 705. https://doi.org/10.3390/fermentation9080705
Restrepo GM, Rincón A, Sánchez ÓJ. Kinetic Analysis of Gluconacetobacter diazotrophicus Cultivated on a Bench Scale: Modeling the Effect of pH and Design of a Sucrose-Based Medium. Fermentation. 2023; 9(8):705. https://doi.org/10.3390/fermentation9080705
Chicago/Turabian StyleRestrepo, Gloria M., Alejandro Rincón, and Óscar J. Sánchez. 2023. "Kinetic Analysis of Gluconacetobacter diazotrophicus Cultivated on a Bench Scale: Modeling the Effect of pH and Design of a Sucrose-Based Medium" Fermentation 9, no. 8: 705. https://doi.org/10.3390/fermentation9080705
APA StyleRestrepo, G. M., Rincón, A., & Sánchez, Ó. J. (2023). Kinetic Analysis of Gluconacetobacter diazotrophicus Cultivated on a Bench Scale: Modeling the Effect of pH and Design of a Sucrose-Based Medium. Fermentation, 9(8), 705. https://doi.org/10.3390/fermentation9080705







