Abstract
Syngas (mixture of CO, H2 and CO2) fermentation suffers from mass transfer limitation due to low solubility of CO and H2 in the liquid medium. Therefore, it is critical to characterize the mass transfer in syngas fermentation reactors to guide in delivery of syngas to the microorganisms. The objective of this study is to measure and predict the overall volumetric mass transfer coefficient, kLa for O2 at various operating conditions in a 7-L sparged and non-sparged continuous stirred-tank reactor (CSTR). Measurements indicated that the kLa for O2 increased with an increase in air flow rate and agitation speed. However, kLa for O2 decreased with the increase in the headspace pressure. The highest kLa for O2 with air sparged in the CSTR was 116 h−1 at 600 sccm, 900 rpm, 101 kPa, and 3 L working volume. Backmixing of the headspace N2 in the sparged CSTR reduced the observed kLa. The mass transfer model predicted the kLa for O2 within 10% of the experimental values. The model was extended to predict the kLa for syngas components CO, CO2 and H2, which will guide in selecting operating conditions that minimize power input to the bioreactor and maximize the syngas conversion efficiency.
1. Introduction
Liquid biofuels (e.g., bioethanol and biobutanol) can be produced from lignocellulosic feedstocks using biochemical or hybrid thermochemical-biological processes, which alleviates the heavy dependence on crude oil and avoid competition with food crops [1,2]. Biochemical conversion platform of lignocellulosic biomass to biofuels requires pretreatment, enzymatic hydrolysis, and detoxification of hydrolysate to obtain fermentable sugars (i.e., glucose and xylose) before fermentation, resulting in energy intensive and economically unfavorable processing [3]. The hybrid process involves gasification of lignocellulosic feedstocks to synthesis gases (syngas, mixture of CO, H2 and CO2) regardless of biomass composition and origin, followed by fermentation of syngas to biofuel [4]. Based on a process simulation model, the hybrid process has the potential to produce biofuels with higher yield from same amount of biomass compared to biochemical platform [5]. This process can achieve 440 L ethanol/Mg biomass compared to 340 L ethanol/Mg biomass in the biochemical platform due to utilization of all components of the biomass, including lignin, to make ethanol [6].
Microbial catalysts such as Clostridium carboxidivorans, Alkalibaculum bacchi, Clostridium ragsdalei and Clostridium ljungdahlii have been used in the production of ethanol, butanol and hexanol from syngas [7,8,9,10]. One bottleneck during syngas fermentation is gas-liquid mas transfer limitation due to the low solubility of the gaseous substrates CO and H2 in the liquid medium [11]. Mass transfer limitations occur when cells have the capacity to process more gas than the bioreactor can supply. The resistance of gaseous substrate diffusion at the gas-liquid interface was recognized as the limiting step in syngas fermentation [12,13]. Gaseous substrate mass transfer limitation results in low cell concentration and low productivity, making the process not economically feasible [14]. Therefore, it is necessary to characterize and model the mass transfer in the bioreactor used for syngas fermentation to understand how to overcome mass transfer limitation of the gaseous substrates, CO and H2. In addition, modeling improves understanding of the process behavior and assists in bioreactor design, process control and optimization of operating conditions to maximize productivity and reduce costs to meet the requirements for commercial fermentation [5].
The mass transfer characteristics of several types of bioreactors, including the continuously stirred tank reactor (CSTR), trickle bed reactor (TBR), hollow fiber membrane reactor (HFR), bubble column reactor (BCR), monolith biofilm reactor (MBR), horizontal rotating packed bed biofilm (h-RPB) reactor, and airlift reactor have been reported [11,13,15,16,17,18,19]. These studies estimated the volumetric mass transfer coefficient via an air-water system, or sparging syngas into medium with and without fermentation. The HFR and TBR were reported to have higher volumetric mass transfer coefficients (kLa) than the CSTR. Besides, the effect of internal pressure and gas/liquid interface area on the CO mass transfer rate in an HFR was investigated and an increase in CO mass transfer rate was observed [20]. Another study reported that for syngas fermentation in an external HFR, the membrane surface area was found to be the most significant factor in the enhancement of CO mass transfer rates [21].
Recently, a new model predicting kLa of CO and H2 in a HFR had also been developed [22]. However, when considered for syngas fermentation, each reactor has its own advantages and disadvantages in terms of operation and scale up [15]. The CSTR, as a conventional reactor, has been more extensively studied and applied in industrial fermentation processes than the HFR and TBR [11,15]. In addition, the CSTR operation is simpler than other types of reactors and can provide good mixing capability and high mass transfer rates, but requires high power consumption, which becomes an issue for large reactors due to high power cost. Moreover, the HFR operation can suffer from membrane fouling, and the pump for liquid recirculation requires external power input [15,23,24]. The TBR increases gas and liquid contact by forming a thin liquid film on the packing; however, an external pump is required to circulate the liquid to the TBR [15,17]. Issues related to scale up and operation parameters of various bioreactors for syngas fermentation have been recently addressed [13,15,25,26,27].
Most mass transfer studies in syngas fermentation using CSTR investigated operating parameters such as gas flow rate and agitation speed at a fixed working volume and mostly in unpressurised reactors [15,28,29]. Only a few studies have investigated the effect of elevated pressure on the mass transfer rates in a bioreactor. The effect of increased air pressure on the O2 mass transfer rate in a stirred bioreactor was studied and a correlation has been presented [30,31]. CO and H2 solubility and the driving force for mass transfer increase with elevated CO and H2 partial pressures in the headspace [12]. The incorporation of various liquid working volumes and pressures will provide a more accurate description of mass transfer characteristics of the CSTR for syngas fermentation. For large-scale syngas fermentation, the headspace pressure, gas flow rate, the power consumption, and reactor working volume are critical parameters for estimating the feasibility of fermentation process. The incorporation of these parameters into one model will help determine the operational parameters and meet the microbial kinetics requirement for syngas fermentation. No such models have been reported in the literature. In addition, backmixing of syngas components (CO and H2) from the headspace into the fermentation medium can increase the gas substrate’s retention time and improve gas conversion efficiency. The increase in the headspace pressure in the bioreactor at high agitation can increase the headspace gas backmixing. However, no reports were found on the effect of headspace gas backmixing on mass transfer for syngas fermentation reactors.
Typically, mass transfer characteristics of reactors are performed using a dynamic method with an air-water system due to simplicity of setup that only requires a dissolved oxygen (DO) probe [32]. The objectives of the present study were to experimentally investigate and model the kLa for O2 in an air-water system at various gas flow rates, headspace pressures, agitation speeds, and working volumes using a 7-L CSTR. In addition, the effect of backmixing of headspace gas on kLa was studied in non-sparged and sparged conditions. Moreover, a correlation of kLa with power consumption and gas flow rate was developed. Finally, the kLa for syngas components CO, CO2 and H2 were estimated from kLa for O2 based on the penetration or surface renewal theory [33,34].
2. Materials and Methods
2.1. CSTR Configuration and Operating Conditions
A 7-L Bioflo 415 CSTR (New Brunswick Scientific Co., Edison, NJ, USA) was used, which is 14.6 cm in diameter and 41.9 cm in length (Figure 1). The configuration of the CSTR followed the suggestions by Bakker and Myers [35]. Four baffles, each 1.3 cm in width and 34.6 cm in length, were used to avoid liquid vortices. Two working volumes of 3 and 5.6 L of water at 43% and 80% of the total CSTR volume, respectively, were examined. The number of impellers mounted on the drive shaft was based on the ratio of gassed liquid level to the CSTR diameter [35]. Thus, two six-blade Rushton impellers were chosen with the 3 L working volume (Figure 1). For the 5.6 L working volume, three impellers were used consisting of two six-blade Rushton impellers and one curved three-blade marine impeller pumping downward (Figure 1). The downward marine impeller was selected to increase the gas retention time in the liquid and increase mass transfer area. The distance between all impellers was equal to the impeller diameter.
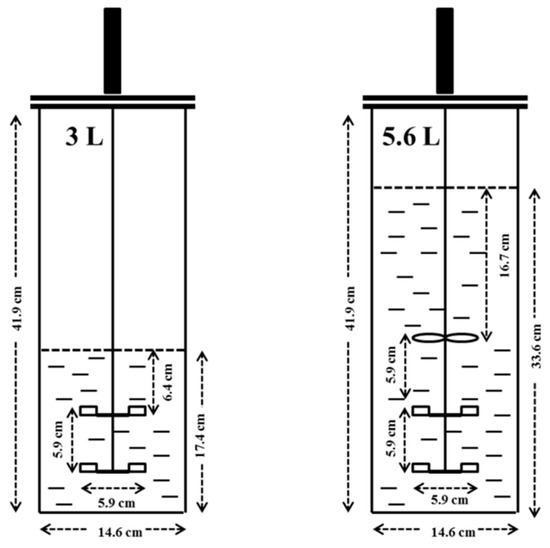
Figure 1.
7-L Bioflo 415 continuous stirred-tank reactor (CSTR) with the 3 and 5.6 L working volumes and impellers configuration.
The setup for the mass transfer study in the CSTR is shown in Figure 2. N2 or air (UHP/Zero grade, Stillwater Steel Co., Stillwater, OK, USA) was fed to the CSTR using a microsparger with 10–15 µm pore size (New Brunswick Scientific Co.). The inlet N2 and air flow rates were controlled by two separate thermal mass flow controllers (MFC) (Burkert, Charlotte, NC, USA). Two 0.2 µm pore size gas filters (New Brunswick Scientific Co.) were used in the inlet and outlet gas lines. The CSTR temperature was controlled at 37 °C by a water heating jacket. A dissolved oxygen (DO) probe (InPro 6830, Mettler Toledo, Columbus, OH, USA) was used to measure % DO saturation.
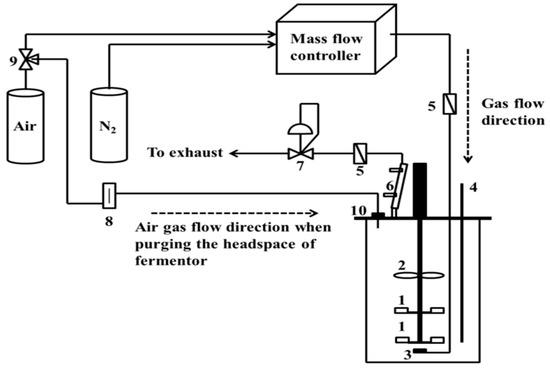
Figure 2.
Bioflo 415 CSTR setup. (1) Rushton impellers, (2) marine impeller, (3) microsparger, (4) dissolved oxygen (DO) probe, (5) 0.2 µm gas filters, (6) condenser, (7) backpressure regulator valve, (8) rotameter, (9) two-way valve, and (10) headspace septum used with purging the headspace.
At the beginning of the experiment, the CSTR was first filled with deionized (DI) water to the required working volume (3 or 5.6 L). The temperature was set at 37 °C similar to syngas fermentation temperature. N2 was then sparged into the CSTR at 1000 sccm (standard cubic centimeters per minute, 20 °C and 101 kPa) to remove dissolved O2 from the DI water with the agitation speed set at 900 rpm and headspace pressure of 101 kPa. The high N2 flow rate and agitation speed were used to shorten the O2 stripping time. Three headspace pressures (101, 150 and 240 kPa) were studied. When % DO in the DI water was less than 0.2%, the headspace pressure was set at the desired pressure using a backpressure regulator. Then, N2 flow rate and agitation speed were adjusted to the desired conditions. When the headspace pressure was stable at the required set point, N2 flow was stopped and air flow was started at the desired flow rate. Three air flow rates of 90, 150, and 600 sccm were tested. The agitation speeds examined were 150, 300, 450, 600, 750, and 900 rpm. The DO probe was calibrated at each tested pressure to 100% DO by saturating the DI water with sparging air at 1000 sccm and 900 rpm. This eliminates the differences in the saturated % DO at various headspace pressures. The % DO values did not exceed 100% saturation. The changes in the % DO in the DI water during aeration were recorded every 12 s by the Biocommand software (New Brunswick Scientific Co.) for the estimation of kLa. When the % DO in the water reached saturation, air flow was stopped. Experiments were performed in duplicates.
The effect of backmixing of gas from the headspace on kLa in a non-sparged and sparged CSTR was also examined. Backmixing experiments started by first calibrating the DO probe as mentioned earlier. The O2 in the DI water in the bioreactor was stripped by flowing 1000 sccm N2 at 101 kPa until the % DO was near 0%. Then, N2 flow and agitation were stopped. To replace the N2 in the CSTR headspace, the headspace was flushed with air at 1000 sccm for 2 min at 101 kPa by inserting a needle into the headplate septum as shown in Figure 2. After 2 min, the pressure inside the CSTR was set at the test value of 101, 150 or 240 kPa by closing the backpressure regulator valve. Two agitation speeds (150 and 900 rpm) and two working volumes (3 and 5.6 L) were examined in the non-sparged CSTR. Agitation was started immediately when the headspace pressure reached the required value. During the backmixing experiment with non-sparged CSTR, no air was sparged in the DI water and the CSTR exhaust was completely closed by the backpressure regulator valve (Figure 2). The backmixing experiment with the sparged CSTR was performed with the 3 L working volume and air sparged in the DI water at 600 sccm and 900 rpm. The backpressure regulator valve was adjusted to keep the pressure in the headspace at the desired value.
2.2. Calculations
2.2.1. Overall Volumetric Mass Transfer Coefficient
The overall volumetric mass transfer coefficient, kLa, was estimated by the following equation [15,32]:
where, kL is liquid film mass transfer coefficient (m h−1), a is gas-liquid interfacial area per unit volume (a=A/VL) (m−1), A is the mass transfer area (m2), VL is the liquid working volume in the CSTR (m3), kLa is overall volumetric mass transfer coefficient (h−1), CS is the saturated DO concentration in the liquid (mol m−3), CL is the DO concentration in the bulk liquid (mol m−3), and t is time (h). CL/CS is replaced by % DO/100 [15]. For calculating the kLa in non-sparged CSTR at various pressures, CS in Equation (1) was replaced by equilibrium saturated % DO at the examined pressure. The kLa value for O2 was estimated from the linear slope of ln(1- CL/CS) versus t when % DO was between 20% and 80% of saturation level.
2.2.2. Volumetric Flow Rate at Various Headspace Pressures
The molar and volumetric air flow rates at various pressures and 37 °C were calculated using Equations (2) to (5) that included estimation of the pressure in the headspace and water hydraulic head above the microsparger in the CSTR [36]:
where, ρa is air density at 20 °C (kg m−3), Ma is air molecular weight (g mol−1), VNIST is air flow rate (m3 min−1) at standard National Institute of Science and Technology (NIST) conditions (20 °C, 101.3 kPa) set using the thermal mass flow controller (MFC), na is air molar flow rate from MFC (mol min−1), PHP is the hydraulic pressure above the microsparger (kPa), ρw is water density (kg m−3), g is gravitational acceleration (m s−2), h is the distance between the microsparger and liquid surface (m), PHS is the headspace pressure (kPa), Ptotal is the total pressure in the CSTR (kPa), Qg is the air volumetric flow rate (mL min−1), R is the ideal gas constant (L kPa mol−1 K−1), T310K is the temperature used (310 K).
2.2.3. Power Consumption
The impellers used were two six-blade Rushton impellers for the 3 L working volume, and one marine impeller plus two six-blade Rushton impellers for the 5.6 L working volume. The marine impeller was estimated to have a power number at 40% of a single Rushton impeller [34]. The power number (Np) of a single six-blade Rushton impeller was reported to be 5.5 [35]. Thus, the calculated power number for the marine impeller of 2.2 was chosen. The power consumption of all impellers above a microsparger was calculated using Equations (6) to (10) as suggested [35]
where NA is aeration number (dimensionless), NFr is Froude number (dimensionless), Qg is the air volumetric flow rate (mL min−1), g is gravity acceleration (m·s−2), Pu is the ungassed power consumption of a single impeller (W), Np is power number of a single Rushton impeller or marine impeller (dimensionless), N is the impeller rotational speed (s−1), D is the diameter of impeller (m), Pg,lower is gassed power consumption of the single impeller mounted directly above the microsparger (W), µ is water dynamic viscosity (Pa·s), Pg,upper is the power consumption of upper impellers not mounted directly above the gas sparger (W), A = 5.3 exp[−5.4(D/T)]; B = 0.47(D/T)1.3; C = 0.64−1.1(D/T); E = 0.25. D is the impeller diameter (m) and T is the tank diameter (m).
For the second Rushton impeller and marine impeller above the microsparger, the power consumption was calculated from Equation (10) [35]. The total power consumption under gassed condition, Pg, is the additive power consumption from all impellers mounted on the shaft. For the 3 L working volume, Pg equals to the power consumption of one Rushton impeller directly above the microsparger calculated using Equation (9) plus the power consumption of the second Rushton impeller calculated using Equation (10). However, for the 5.6 L working volume, the total power consumption, Pg, equals the power consumed by one Rushton impeller directly above the microsparger calculated using Equation (9) plus the power consumed by the second Rushton and third marine impellers calculated using Equation (10).
2.2.4. Mass Transfer Model of a 7-L CSTR
There are many reports in literature that described various correlations of the volumetric mass transfer coefficient, kLa, at different operating parameters. However, the most used correlation for kLa is expressed in terms of power input per unit volume and superficial gas velocity [32,35,37,38]. The overall volumetric mass transfer coefficient typically follows the model below [35]:
where Pg is the total impeller power consumption under gassed condition (W), α, β and c are model parameters, VL is the liquid working volume (m3), vg is superficial gas velocity (m s−1). The model parameters α, β and c in Equation (11) were estimated based on the volumetric flow rates at 37 °C, agitation speeds, and working volumes used in the present study. The least square approach and SOLVER function in EXCEL (Microsoft, Redmond, WA, USA) were used to estimate the model parameters α, β and c.
The kLa for CO, CO2 and H2, were calculated from the measured kLa for O2 using the penetration or surface renewal theory based on their diffusivities in the fermentation broth. The kLa for gas species i can be calculated from kLa for gas species j, using the following equation [33,34]:
where Di and Dj are the diffusivities of gas species i and j (O2). In water, the diffusivities of CO, CO2 and H2 were 107%, 90%, and 212%, respectively, of the O2 diffusivity at 37 °C [15]. Thus, the ratios of (kLa)i/(kLa)O2 for CO, CO2 and H2 based on their diffusivities are 1.03, 0.95 and 1.46, respectively.
2.2.5. Statistical Analysis
T-TEST procedure was performed using SAS Release 9.3 (Cary, NC, USA) to determine the statistical differences in the kLa for O2 between when the headspace was flushed with air for 2 and 12 min in the non-sparged CSTR during the backmixing experiment at 95% confidence level. Also, the statistical differences of the kLa for O2 in the backmixing study in the sparged CSTR with and without air flushing of the headspace were also determined by T-TEST procedure using SAS.
3. Results and Discussion
3.1. Effect of Agitation Speed, Pressure and Gas Flow Rate on kLa
The effects of agitation speed, headspace pressure, and gas flow rate on the kLa for O2 with the 3 L and 5.6 L working volumes in the air-water system are shown in Figure 3. The kLa for O2 increased as agitation speed increased at fixed air flow rate, headspace pressure and working volume. Also, the mass transfer of O2 into the DI water was improved with increasing air flow rate. The highest measured kLa for O2 was 116.2 h−1 at 600 sccm, 900 rpm and 101 kPa with 3 L working volume (Figure 3). The measured kLa values for O2 in 3 L working volume were generally 6% to 50% higher than with 5.6 L working volume at similar standard air flow rates, headspace pressures and all agitation speeds except at 900 rpm. At 900 rpm, the measured kLa for O2 was generally 10% to 50% lower in the 3 L working volume than in the 5.6 L working volume at headspace pressures of 150 and 240 kPa and flow rates 90 and 150 sccm. The decrease in the measured kLa for O2 at these conditions was due to the backmixing of N2 and O2 depleted air from the headspace into the water.
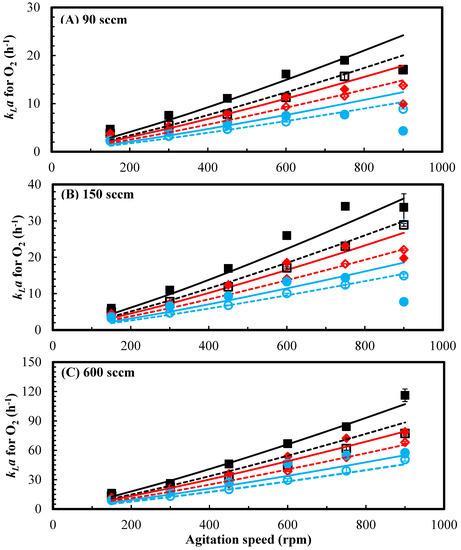
Figure 3.
kLa for O2 in air water system at standard flow rates in standard cubic centimeters per minute, sccm, (A) 90 sccm, (B) 150 sccm and (C) 600 sccm and headspace pressures of 101 kPa (■), 150 kPa (♦) and 240 kPa (●) in 3 L (experimental data in solid symbols, model predictions in solid lines) and 5.6 L (experimental data in open symbols, model predictions in dash lines) working volumes. Error bars not visible are smaller than the symbols.
As mentioned earlier, one of the challenges of syngas fermentation process is the mass transfer limitation due to low solubility of CO and H2 in the fermentation medium. Mass transfer can be increased by increasing the agitation speed and gas flow rate. In addition, the increase in headspace pressure improves molar mass transfer by increasing the driving force. Thus, it is important to determine the effect of headspace pressure on kLa in sparged and non-sparged CSTRs to guide in reactor operation. The kLa for O2 was the highest at the lowest headspace pressure of 101 kPa compared to 150 and 240 kPa at the same agitation speed, working volume and standard air flow rate in sccm. This decrease in kLa is caused by lower volumetric gas flow at higher pressure. Estimated air flow rates at 37 °C and headspace pressures of 150 and 240 kPa were 32% and 57%, respectively, lower than at 101 kPa. Thus, the actual volumetric gas flow rate that results from elevated headspace pressure should be considered in kLa estimation. The hydraulic head above the microsparger should also be considered in the estimation of kLa values in large fermentor. The decrease in volumetric air flow rate reduces the air superficial velocity, vg (m s−1), as calculated from Equation (13), resulting in reduced kLa in Equation (11).
The measured kLa for O2 in the sparged CSTR with 3 L working volume decreased from 10% to 50% when the agitation speed increased from 750 to 900 rpm and air flow rate was below 600 sccm (Figure 3). However, the measured kLa for O2 with the 3 L working volume increased when the agitation speed was increased from 750 to 900 rpm at air flow rate of 600 sccm. The phenomenon of decreasing kLa for O2 was not observed with the 5.6 L working volume even at 900 rpm. The decrease in measured kLa in the 3 L working volume was attributed to severe backmixing of N2 in the headspace into water and O2 stripping from water, which increased the time for DO concentration reaching saturation values. There was 2.9 times more N2 initially present in the headspace in the sparged CSTR with the 3 L working volume compared to the 5.6 L working volume, which caused higher effect of backmixing on kLa in the 3 L working volume. In addition, the amounts of N2 in the headspace at 150 and 250 kPa were 1.5 times and 2.4 times, respectively, higher than at 101 kPa. The measured kLa for O2 at air flow rate of 600 sccm, 900 rpm and 101 kPa in the 3 L working volume increased from the kLa measurement at 750 rpm because the high air flow rate increased the O2 content in the headspace over four times faster than at 90 and 150 sccm. The measured kLa for O2 remained almost constant at 600 sccm with the headspace pressures of 150 and 240 kPa when the agitation speed was increased from 750 to 900 rpm with the 3 L working volume (Figure 3). This was due to lower volumetric air flow rates at 150 and 240 kPa, which could not flush N2 from headspace as fast as at 101 kPa.
3.2. Effect of Headspace Backmixing on kLa
The effect of backmixing from the headspace containing air on the kLa for O2 in non-sparged CSTR and 3 L and 5.6 L working volumes was evaluated at agitation speeds of 150 and 900 rpm and headspace pressures of 101, 150 and 240 kPa (Table 1). In this set of experiments, the headspace was purged with air at 1000 sccm for 2 min and pressure was set at the desired value. During the test at each condition, the inlet and outlet CSTR gas lines were completely closed. Results showed that the effect of backmixing of air from the headspace on the kLa for O2 in the 5.6 L working volume was negligible compared to 3 L working volume (Table 1). For the CSTR with 3 L working volume at 150 rpm and headspace pressures between 101 and 240 kPa, the backmixing of air from the headspace was low, resulting in kLa values for O2 below 1.3 h−1. However, the kLa for O2 increased from 0.7 h−1 to 67.3 h−1 due to backmixing of air from the headspace when the agitation speed was increased from 150 rpm to 900 rpm at 101 kPa. Moreover, the kLa for O2 in the non-sparged CSTR at 900 rpm increased by 77% with the increase in the air pressure in the headspace from 101 to 240 kPa in the 3 L working volume. This explains the decrease in the kLa for O2 when air was sparged into the water with initial N2 headspace was due to backmixing of N2 from the headspace at 900 rpm with pressures of 150 and 240 kPa at air flow rates of 90 and 150 sccm (Figure 3).

Table 1.
Effect of headspace pressure and backmixing at 150 and 900 rpm on kLa for O2 in a non-sparged CSTR with 3 and 5.6 L working volumes.
In addition to the higher headspace volume with the 3 L working volume, the high kLa from backmixing at 900 rpm was attributed to the impeller arrangement in the CSTR. The distance from the top impeller to the liquid surface was 6.4 cm in the 3 L working volume (Figure 1). However, there was 16.7 cm between the top impeller and the liquid surface in the 5.6 L working volume. No vortex was observed in the 5.6 L working volume at 900 rpm. However, a vortex formed between the water surface and the top impeller in the 3 L working volume, drawing gas from the headspace to circulate in the liquid.
To determine the effect of the headspace flushing time on backmixing and estimation of kLa for O2, the headspace in the CSTR with 3 L working volume was flushed with air for 2 and 12 min at 1000 sccm. Flushing the CSTR headspace for 2 min at 1000 sccm represented about 50% of the headspace volume with the 3 L working volume. However, using O2 saturation when each run reached equilibrium as % DO for Cs in Eq. 1 corrected for the lower initial concentration of O2 in the headspace that resulted from low purging time. In addition, the results showed that there was no statistical difference (p > 0.05) between the headspace flushing times (Table 1). Thus, 2 min was sufficient to flush the headspace with air to evaluate the backmixing effect on the kLa for O2.
The estimation of kLa from Equation (1) assumes a constant O2 concentration at the gas/liquid interface, Cs. However, O2 transferred into the water is removed from the headspace gas lowering the O2 concentration at the interface. The change of O2 concentration in the headspace was estimated by the O2 mass balance and the equilibrium O2 saturation (% DO) to be 2% and 9% for the 3 and 5.6 L working volumes, respectively. The mass transfer driving force for O2 transfer was estimated by the logarithmic mean of the initial difference of partial pressure in the gas and 0 kPa in the water, and a low terminal partial pressure difference of 0.2 kPa between the gas and the near equilibrium saturation of the water. This estimation shows the average driving force increases with pressure. This suggests that the increase in observed kLa for O2 in the non-sparged CSTR due to backmixing with increased pressure resulted from increased driving force.
The backmixing effect with the 5.6 L working volume was less than 2 h−1. Therefore, the subsequent experiments on effect of backmixing were done with the 3 L working volume. In this set of experiments, the headspace was flushed with air before air was sparged in water through the CSTR inlet sparger to evaluate if the backmixing of air affects the kLa for O2 in the 3 L working volume at 600 sccm and 900 rpm and various headspace pressures.
The kLa for O2 increased between 20% and 48% when the headspace was flushed with air before flowing air into the CSTR compared to no air flushing (i.e., only N2 in the headspace) (Table 2). The kLa for O2 were 32% and 50% lower at 150 kPa and 240 kPa, respectively, compared to 101 kPa when the headspace was not initially flushed with air (Table 2). However, when the headspace was flushed with air, the kLa values for O2 were 16% and 41% lower at 150 kPa and 240 kPa, respectively, than at 101 kPa. This was due to 32% and 57% lower superficial gas velocities at 150 and 240 kPa, respectively, compared to 101 kPa. In addition, the differences in kLa values for O2 were lower when the headspace was flushed with air at 150 and 240 kPa compared to 101 kPa since higher initial O2 content in the headspace added to the rate of O2 saturation compared to stripping of O2 by the N2 headspace.

Table 2.
Effect of headspace pressure and backmixing on kLa for O2 in a sparged CSTR with 3 L working volume at standard air flow rate of 600 sccm and 900 rpm.
Utilizing the backmixing effect can be useful in syngas fermentation. Under low syngas conversion, the unutilized gas in the headspace can be entrained back into the medium, thus improving mass transfer and conversion of syngas components such as CO and H2 into products. However, if conversion of CO and H2 was high, the inert gas such as N2 from the producer gas derived from biomass [39] in the headspace can reduce the kLa for CO or H2 at high agitation speed due to backmixing. Thus, it would be beneficial to operate the syngas fermentation at low agitation speed, and high working volume to alleviate the backmixing effect when the syngas conversion efficiency is high. However, other factors such as gas flow rate, gas uptake rate, and agitation speed should be considered in evaluating the benefits of backmixing on syngas fermentation.
3.3. Model Predictions of kLa for O2
Equation (11) was used to predict the kLa for O2 at air flow rates (90, 150 and 600 sccm), various agitation speeds (150 to 900 rpm), working volumes (3 and 5.6 L) and headspace pressures (101, 150 and 240 kPa). Based on the experimental data, the air flow rates at standard condition in sccm were converted using Equations (2) to (5) into the corresponding volumetric flow rates in mL min−1 at 37 °C and the various hydraulic heads and headspace pressures used. The power consumption per unit volume (Pg/VL) and superficial velocity were calculated using Equations (6) to (10) and (13). Using the experimental data, the constants α, β and c in Equation (11) were determined and the kLa for O2 can be estimated using Equation (14).
The parameters α and β in Equation (11) were reported in the range of 0.3 to 0.7 and 0.0 to 1.0, respectively, and the variance of these parameters was due to measurement error and the configuration of stirred tank reactors [11,40].
In the present study, the values of α and β parameters of 0.39 and 0.79, respectively, were within the previously reported range. As shown in Figure 3, there were less than 10% variation between the experimental data and model predictions of the kLa for O2 in the CSTR with 5.6 L working volume. When agitation speeds were low, mainly 150 to 600 rpm in 3 L working volume, less than 10% variation between the experimental and predicted kLa values for O2 were observed. However, there were 30% to 60% variation between the experimental and predicted kLa values for O2 in the 3 L working volume at low standard flow rate 90 and 150 sccm and agitation speed above 750 rpm. This was due to the backmixing of N2 that lowered the observed kLa deviating from model predictions. The superficial gas velocity vg in Equation (11) was determined using the volumetric flow rate at 37 °C as shown in Equation (13). Higher headspace pressures for the same standard flow rate in sccm resulted in lower volumetric flow rates in mL min−1 at 37 °C and lower vg and kLa. The model predictions of kLa for O2 were compared with the experimental results at various agitation speeds and volumetric flow rates (Figure 4). In addition, the model predictions of the kLa for O2 were plotted versus experimental data, which were mostly within 10% of variance (Figure 5). The R2 value for model predictions of the experimental data was 0.97, indicating a very good fit.
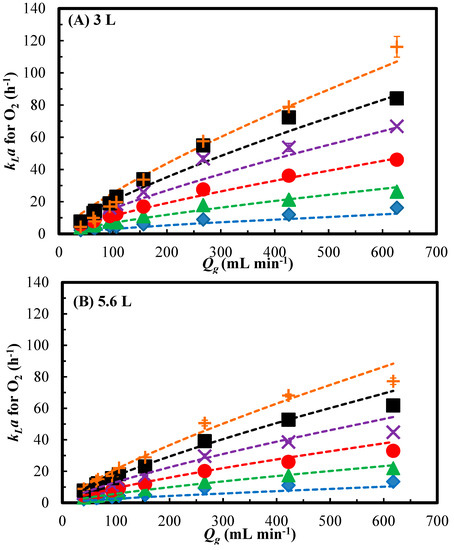
Figure 4.
Experimental and predicted kLa for O2 in (A) 3 L and (B) 5.6 L working volumes in the 7 L Bioflo 415 CSTR at volumetric flow rates between 40 mL min−1 to 630 mL min−1 and 37 °C and various agitation speeds: 150 rpm (♦), 300 rpm (▲), 450 rpm (●), 600 rpm (×), 750 rpm (■) and 900 rpm (+); model prediction (dash lines). Error bars not visible are smaller than the symbols.
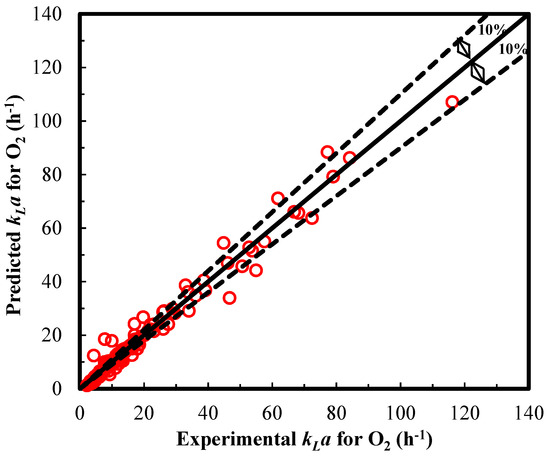
Figure 5.
Predicted versus experimental kLa for O2 at volumetric flow rates between 40 mL min−1 to 630 mL min−1 and 37 °C, agitation speeds range from 150 rpm to 900 rpm in the 3 L and 5.6 L working volumes.
The 3 and 5.6 L working volumes used were 43% and 80% of the total bioreactor volume (7 L), respectively. It is desired to operate the bioreactor at high working volume to increase the amount of products produced. However, factors such as power consumption and foam formation should be considered when selecting the working volume. The power per unit volume, Pg/VL, was calculated using Equations (6) to (10). Increasing the agitation speed from 150 to 900 rpm increased power consumption from 33 to 8181 W m−3 and from 21 to 5216 W m−3 in the 3 L and 5.6 L working volumes, respectively. The Pg/VL slightly decreased (no more than 8%) when air flow rate was increased from 90 to 600 sccm and headspace pressure was increased from 101 to 240 kPa. This showed that the increase in flow rate and headspace pressure within the tested ranges had small effects on Pg/VL.
Although the predicted kLa for O2 in 3 L working volume was from 6% to 50% higher than in 5.6 L working volume at similar operating conditions, the Pg/VL consumed in 5.6 L working volume was about 37% lower than in 3 L working volume indicating the advantage of using higher working volumes in terms of power consumption. In addition, when high conversion efficiencies of CO, CO2 and H2 in 3 L working volume were to be attained, the backmixing of N2 from producer gas [39] would diminish the advantage of using this working volume with higher kLa than the 5.6 L working volume.
3.4. Model Predictions of kLa for CO, CO2 and H2
Syngas fermentation is a strictly anaerobic fermentation process which excludes O2 in the process. It is more convenient to measure the kLa for O2 using an air-water system for the simplicity of the method and then predict the kLa for CO, CO2 and H2. The kLa for CO, CO2 and H2 were calculated from the model prediction of kLa for O2 (Equation (14)) based on the penetration or surface renewal theory [33,34] as shown in Equations (15) to (17).
Based on Equations (15) to (17), the kLa for CO was 6% higher and 30% lower than the kLa for CO2 and H2, respectively, at all similar operating conditions. For syngas fermentation in a CSTR, the kLa for CO, CO2 and H2 can be estimated if the bioreactor size, number and type of impellers, working volume, agitation speeds, headspace and hydraulic pressures and gas flow rates are known.
Syngas fermentation in CSTR requires high power input to obtain high kLa. [11,15] Therefore, CSTR operating conditions should be carefully selected to reduce the power input to make the process more economically feasible. As shown in Figure 6, the predicted kLa for O2 increased with the increase in the Pg/VL. The trends of kLa for O2 were similar in 3 and 5.6 L working volumes at the same standard flow rate and headspace pressure. The kLa values for O2 increased by over four times when the flow rate was increased from 90 to 600 sccm at the same headspace pressure and Pg/VL. Therefore, higher kLa for O2 can be realized by increasing the air flow rate without increasing the Pg/VL. However, while increasing gas flow rate during syngas fermentation increases kLa, this can reduce syngas conversion efficiency when gas transfer rate exceeds the kinetic capacity of the cells. High cell concentrations are required to increase the gas conversion efficiency at high gas flow rates. Increased cell concentration in the fermentor was successfully demonstrated using membrane module for cell recycle [41,42]. Moreover, the increase in the headspace pressure from 101 to 240 kPa decreased the kLa for O2 by 48% at similar Pg/VL. This means that higher Pg/VL is required to achieve the same kLa for O2 at higher pressure, offsetting the higher driving force gained at high pressure. The change of kLa for O2 as a function of Pg/VL would be similar to kLa for CO, CO2 and H2 during syngas fermentation. When operating syngas fermentation bioreactors, Equations (15) to (17) are useful to predict the mass transfer capacity for CO, CO2 and H2 based on the uptake ability of the culture used, and therefore can guide in setting the operating conditions to minimize Pg/VL and maximize gas conversion efficiency.
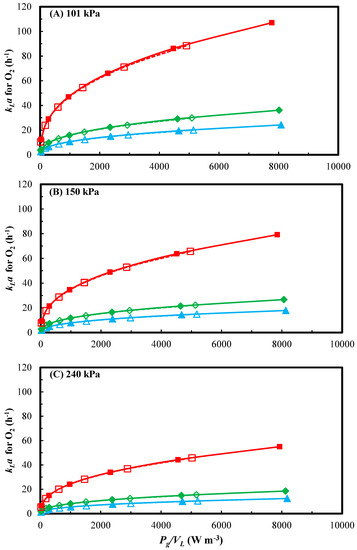
Figure 6.
Profiles of predicted kLa for O2 with Pg/VL at various headspace pressures (A) 101 kPa (B) 150 kPa (C) 240 kPa and 90 sccm (▲), 150 sccm (♦) and 600 sccm (■) in 3 L working volume (solid symbol and solid line) and 5.6 L working volume (open symbol and dash line).
kLa values for different reactors using air and syngas components were reported by various research groups (Table 3). Based on Equation (12), kLa for CO is 1.03 the kLa for O2. However, it is difficult to compare kLa values based on the same gas accurately because of the different reactors and operating parameters used and unreported data about reactor volume, gas and liquid flow rates, pressure and agitation (Table 3). However, a comparison of the data from the literature showed that the kLa values of the HFR and TBR reactors were greatly higher than in various reported CSTRs [15,20,43,44]. HFR reactors showed remarkably high kLa values (about 1000 h−1), which depended on the type of the membrane, surface area to unit volume, gas flow rate and pressure [15,24,43]. An increase in the gas pressure in the HFR increased the kLa [20,43]. However, an increase in the gas pressure in the CSTR decreased kLa due to lower volumetric gas flow rate at high pressure (Table 3). The kLa values reported for CSTRs in Table 3 were below 160 h−1 [18,45,46]. However, the kLa values for the TBR, air-lift and MBR coupled with CSTR were 421, 130 and 450 h−1, respectively [15,16,47].

Table 3.
Mass transfer coefficient kLa in different bioreactors and operating parameters.
The present study showed that kLa values in the CSTR increased by increasing the gas flow rate and agitation speed (Figure 3). In addition, the kLa values in sparged CSTR increased with a decrease in the headspace pressure. However, the kLa values in non-sparged CSTR increased with an increase in the headspace pressure and agitation due to increased backmixing (Table 1). These results provide guidance in design, operation, and scale up of syngas fermentation reactors.
4. Conclusions
The kLa for O2 was increased by increasing the air flow rates and agitation speeds in the 7-L Bioflo 415 CSTR with the 3 and 5.6 L working volumes. The increase in headspace pressure decreased the kLa for O2 due to lower volumetric gas flow rate at high pressure. The highest kLa for O2 was 116 h−1, which was obtained at 600 sccm, 900 rpm and 101 kPa with the 3 L working volume. Backmixing from the headspace in the non-sparged CSTR at 900 rpm with the 3 L working volume increased kLa. The highest kLa for O2 due to backmixing in the non-sparged CSTR was 119 h-1, attained at 900 rpm and headspace air pressure of 240 kPa. A mass transfer model was developed and the model predicted the experimental kLa values for O2 within 10%. Also, the model predicts an increase in kLa for O2 with an increase in the gas flow rate without increasing the power consumption per unit volume (Pg/VL). The model was extended to predict the kLa values for syngas components CO, CO2, and H2, which can provide crucial insights for setting operating conditions in the CSTR to minimize Pg/VL and increase gas conversion efficiency.
Author Contributions
Conceptualization: H.K.A., K.L. and J.R.P.; methodology: H.K.A., K.L. and J.R.P.; software, K.L. and J.R.P.; validation, K.L. and J.R.P.; data analysis and interpretation: H.K.A., K.L. and J.R.P.; resources: H.K.A., and R.L.H.; writing, review and editing: K.L., H.K.A., J.R.P., X.S., S.M. and R.L.H.; supervision: H.K.A.; funding acquisition: H.K.A. and R.L.H.
Funding
This research was funded by USDA-NIFA Special Research Grant Award USDA-NIFA 34447-20772, Sun Grant Program—South Center No. DOTS59-07-G-00053, USDA–NIFA Project No. OKL03005, and Oklahoma Agricultural Experiment Station.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | Gas-liquid interfacial area per unit volume (m−1) |
| A, B, C and E Parameters in Equations (9) and (10) | |
| CL | Bulk dissolved oxygen (DO) concentration in the liquid (mol m−3) |
| CS | Saturated dissolved oxygen (DO) concentration (mol m−3) |
| D | Impeller diameter (m) |
| Di and Dj | Diffusivities of gas species i and j in water (cm2 s−1) |
| DO | Dissolved oxygen (%) |
| g | Gravitational acceleration (m s−2) |
| h | Distance of microsparger from the surface of liquid (m) |
| kL | Liquid film mass transfer coefficient (m h−1) |
| kLa | Overall volumetric mass transfer coefficient (h−1) |
| Ma | Molecular weight of air (g mol−1) |
| MFC | Mass flow controller |
| na | Molar air flow rate (mol min−1) |
| N | Rotation speed of impeller (s−1) |
| NA | Aeration number (dimensionless) |
| NFr | Froude number (dimensionless) |
| NIST | National Institute of Science and Technology |
| Np | Power number of single Rushton impeller or marine impeller (dimensionless) |
| PHS | Headspace pressure (kPa) |
| PHP | Liquid pressure above the microsparger (kPa) |
| Ptotal | Total pressure in the CSTR (kPa) |
| Pg | Total impeller power consumption at gassed condition (W) |
| Pg,lower | Gassed power consumption of single impeller mounted directly above microsparger (W) |
| Pg,upper | Gassed power consumption for impellers not directly installed above microsparger (W) |
| Pg/VL | Power consumption per unit volume (W m−3) |
| Pu | Ungassed power consumption of single impeller (W) |
| Qg | Volumetric air flow rate at the applied pressure and 37 °C (mL min−1) |
| R | Ideal gas law constant (L kPa mol−1 K−1) |
| t | Time (h) |
| T | Tank diameter (m) |
| TNIST | NIST standard temperature of 293.15 K |
| vg | Superficial gas velocity (m s−1) |
| VL | Liquid working volume in CSTR (m3) |
| VNIST | Volumetric flow rate of air at standard NIST conditions (m3 min−1) |
| α, β and c | Model parameters in Equation (11) |
| ρa | Air density (kg m−3) |
| ρw | Water density (kg m−3) |
| µ | Dynamic viscosity of water (Pa s) |
References
- Ibrahim, M.F.; Ramli, N.; Kamal Bahrin, E.; Abd-Aziz, S. Cellulosic biobutanol by Clostridia: Challenges and improvements. Renew. Sust. Energ. Rev. 2017, 79, 1241–1254. [Google Scholar] [CrossRef]
- Devarapalli, M.; Atiyeh, H.K. A review of conversion processes for bioethanol production with a focus on syngas fermentation. Biofuel Res. J. 2015, 2, 268–280. [Google Scholar]
- Liu, K.; Atiyeh, H.K.; Pardo-Planas, O.; Ezeji, T.C.; Ujor, V.; Overton, J.C.; Berning, K.; Wilkins, M.R.; Tanner, R.S. Butanol production from hydrothermolysis-pretreated switchgrass: Quantification of inhibitors and detoxification of hydrolyzate. Bioresour. Technol. 2015, 189, 292–301. [Google Scholar] [CrossRef] [PubMed]
- Ramachandriya, K.D.; Kundiyana, D.K.; Sharma, A.M.; Kumar, A.; Atiyeh, H.K.; Huhnke, R.L.; Wilkins, M.R. Critical factors affecting the integration of biomass gasification and syngas fermentation technology. AIMS Bioeng. 2016, 3, 188–210. [Google Scholar] [CrossRef]
- Pardo-Planas, O.; Atiyeh, H.K.; Phillips, J.R.; Aichele, C.P.; Mohammad, S. Process simulation of ethanol production from biomass gasification and syngas fermentation. Bioresour. Technol. 2017, 245, 925–932. [Google Scholar] [CrossRef] [PubMed]
- Tanner, R.S. Production of ethanol from synthesis gas. In Bioenergy; Wall, J.D., Harwood, C.S., Demain, A.L., Eds.; American Society of Microbiology: Washington, DC, USA, 2008; pp. 147–151. [Google Scholar]
- Wilkins, M.R.; Atiyeh, H.K. Microbial production of ethanol from carbon monoxide. Curr. Opin. Biotechnol. 2011, 22, 326–330. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Atiyeh, H.K.; Tanner, R.S.; Wilkins, M.R.; Huhnke, R.L. Fermentative production of ethanol from syngas using novel moderately alkaliphilic strains of Alkalibaculum bacchi. Bioresour. Technol. 2012, 104, 336–341. [Google Scholar]
- Phillips, J.R.; Atiyeh, H.K.; Tanner, R.S.; Torres, J.R.; Saxena, J.; Wilkins, M.R.; Huhnke, R.L. Butanol and hexanol production in Clostridium carboxidivorans syngas fermentation: Medium development and culture techniques. Bioresour. Technol. 2015, 190, 114–121. [Google Scholar] [CrossRef]
- Sun, X.; Atiyeh, H.K.; Kumar, A.; Zhang, H.; Tanner, R.S. Biochar enhanced ethanol and butanol production by Clostridium carboxidivorans from syngas. Bioresour. Technol. 2018, 265, 128–138. [Google Scholar] [CrossRef]
- Bredwell, M.D.; Srivastava, P.; Worden, R.M. Reactor design issues for synthesis-gas fermentations. Biotechnol. Prog. 1999, 15, 834–844. [Google Scholar]
- Klasson, K.T.; Ackerson, M.D.; Clausen, E.C.; Gaddy, J.L. Biological conversion of coal and coal-derived synthesis gas. Fuel 1993, 72, 1673–1678. [Google Scholar] [CrossRef]
- Munasinghe, P.C.; Khanal, S.K. Biomass-derived syngas fermentation into biofuels: Opportunities and challenges. Bioresour. Technol. 2010, 101, 5013–5022. [Google Scholar] [CrossRef] [PubMed]
- Vega, J.L.; Antorrena, G.M.; Clausen, E.C.; Gaddy, J.L. Study of gaseous substrate fermentations: Carbon monoxide conversion to acetate. 2. Continuous culture. Biotechnol. Bioeng. 1989, 34, 785–793. [Google Scholar] [CrossRef] [PubMed]
- Orgill, J.J.; Atiyeh, H.K.; Devarapalli, M.; Phillips, J.R.; Lewis, R.S.; Huhnke, R.L. A comparison of mass transfer coefficients between trickle-bed, hollow fiber membrane and stirred tank reactors. Bioresour. Technol. 2013, 133, 340–346. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Brown, R.; Wen, Z. Enhancing mass transfer and ethanol production in syngas fermentation of Clostridium carboxidivorans P7 through a monolithic biofilm reactor. Appl. Energ. 2014, 136, 68–76. [Google Scholar] [CrossRef]
- Devarapalli, M.; Atiyeh, H.K.; Phillips, J.R.; Lewis, R.S.; Huhnke, R.L. Ethanol production during semi-continuous syngas fermentation in a trickle bed reactor using Clostridium ragsdalei. Bioresour. Technol. 2016, 209, 56–65. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Brown, R.C.; Wen, Z. Syngas fermentation by Clostridium carboxidivorans P7 in a horizontal rotating packed bed biofilm reactor with enhanced ethanol production. Appl. Energ. 2017, 187, 585–594. [Google Scholar] [CrossRef]
- Jang, N.; Yasin, M.; Park, S.; Lovitt, R.W.; Chang, I.S. Determination of volumetric gas–liquid mass transfer coefficient of carbon monoxide in a batch cultivation system using kinetic simulations. Bioresour. Technol. 2017, 239, 387–393. [Google Scholar] [CrossRef] [PubMed]
- Yasin, M.; Park, S.; Jeong, Y.; Lee, E.Y.; Lee, J.; Chang, I.S. Effect of internal pressure and gas/liquid interface area on the CO mass transfer coefficient using hollow fibre membranes as a high mass transfer gas diffusing system for microbial syngas fermentation. Bioresour. Technol. 2014, 169, 637–643. [Google Scholar] [CrossRef]
- Lee, P.-H.; Ni, S.-Q.; Chang, S.-Y.; Sung, S.; Kim, S.-H. Enhancement of carbon monoxide mass transfer using an innovative external hollow fiber membrane (HFM) diffuser for syngas fermentation: Experimental studies and model development. Chem. Eng. J. 2012, 184, 268–277. [Google Scholar] [CrossRef]
- Orgill, J.J.; Abboud, M.C.; Atiyeh, H.K.; Devarapalli, M.; Sun, X.; Lewis, R.S. Measurement and prediction of mass transfer coefficients for syngas constituents in a hollow fiber reactor. Bioresour. Technol. 2019, 276, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Liew, F.M.; Koöpke, M.; Simpson, S.D. Gas fermentation for commercial biofuels production. In Liquid, Gaseous and Solid Biofuels; Fang, Z., Ed.; InTech: London, UK, 2013; pp. 125–173. [Google Scholar]
- Shen, Y.; Brown, R.; Wen, Z. Syngas fermentation of Clostridium carboxidivoran P7 in a hollow fiber membrane biofilm reactor: Evaluating the mass transfer coefficient and ethanol production performance. Biochem. Eng. J. 2014, 85, 21–29. [Google Scholar] [CrossRef]
- Abubackar, H.N.; Veiga, M.C.; Kennes, C. Biological conversion of carbon monoxide: Rich syngas or waste gases to bioethanol. BiofuelsBioprod. Biorefin. 2011, 5, 93–114. [Google Scholar] [CrossRef]
- Yasin, M.; Jeong, Y.; Park, S.; Jeong, J.; Lee, E.Y.; Lovitt, R.W.; Kim, B.H.; Lee, J.; Chang, I.S. Microbial synthesis gas utilization and ways to resolve kinetic and mass-transfer limitations. Bioresour. Technol. 2015, 177, 361–374. [Google Scholar] [CrossRef] [PubMed]
- Asimakopoulos, K.; Gavala, H.N.; Skiadas, I.V. Reactor systems for syngas fermentation processes: A review. Chem. Eng. J. 2018, 348, 732–744. [Google Scholar] [CrossRef]
- Klasson, K.T.; Ackerson, M.D.; Clausen, E.C.; Gaddy, J.L. Bioreactors for synthesis gas fermentations. Resour. Conserv. Recy. 1991, 5, 145–165. [Google Scholar] [CrossRef]
- Younesi, H.; Najafpour, G.; Ku Ismail, K.S.; Mohamed, A.R.; Kamaruddin, A.H. Biohydrogen production in a continuous stirred tank bioreactor from synthesis gas by anaerobic photosynthetic bacterium: Rhodopirillum rubrum. Bioresour. Technol. 2008, 99, 2612–2619. [Google Scholar] [CrossRef]
- Lopes, M.; Belo, I.; Mota, M. Over-pressurized bioreactors: Application to microbial cell cultures. Biotechnol. Prog. 2014, 30, 767–775. [Google Scholar] [CrossRef]
- Lopes, M.; Mota, M.; Belo, I. Oxygen Mass Transfer Rate in a Pressurized Lab-Scale Stirred Bioreactor. Chem. Eng. Technol. 2013, 36, 1779–1784. [Google Scholar] [CrossRef]
- Shuler, M.L.; Fikret, K. Bioprocess Engineering: Basic Concepts, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2002; p. 576. [Google Scholar]
- Kawase, Y.; Halard, B.; Moo-Young, M. Liquid-phase mass transfer coefficients in bioreactors. Biotechnol. Bioeng. 1992, 39, 1133–1140. [Google Scholar] [CrossRef]
- McCabe, W.L.; Smith, J.C. Unit Operations of Chemcial Engineering, 7th ed.; Mcgraw-Hill Inc.: New York, NY, USA, 2005; p. 1007. [Google Scholar]
- Bakker, A.; Smith, J.; Myers, K. How to disperse gases in liquids. Chem. Eng. 1994, 101, 98–104. [Google Scholar]
- Munson, B.R.; Young, D.F.; Okiishi, T.H.; Huebsch, W.W. Fundamentals of Fluid Mechanics, 6th ed.; Willey: Hoboken, NJ, USA, 2009; p. 784. [Google Scholar]
- Lee, J.M. Biochemcial Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1992; p. 240. [Google Scholar]
- Blanch, H.W.; Clark, d.S. Biochemcial Engineering; Marcel Dekker, Inc: New York, NY, USA, 1997; p. 702. [Google Scholar]
- Ahmed, A.; Cateni, B.G.; Huhnke, R.L.; Lewis, R.S. Effects of biomass-generated producer gas constituents on cell growth, product distribution and hydrogenase activity of Clostridium carboxidivorans P7T. Biomass Bioenergy 2006, 30, 665–672. [Google Scholar] [CrossRef]
- Stenberg, O.; Andersson, B. Gas-liquid mass transfer in agitated vessels—II. Modelling of gas-liquid mass transfer. Chem. Eng. Sci. 1988, 43, 725–730. [Google Scholar] [CrossRef]
- Liu, K.; Atiyeh, H.K.; Stevenson, B.S.; Tanner, R.S.; Wilkins, M.R.; Huhnke, R.L. Continuous syngas fermentation for the production of ethanol, n-propanol and n-butanol. Bioresour. Technol. 2014, 151, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.; Klasson, K.; Clausen, E.; Gaddy, J. Biological production of ethanol from coal synthesis gas. Appl. Biochem. Biotechnol. 1993, 39, 559–571. [Google Scholar] [CrossRef]
- Munasinghe, P.C.; Khanal, S.K. Syngas fermentation to biofuel: Evaluation of carbon monoxide mass transfer and analytical modeling using a composite hollow fiber (CHF) membrane bioreactor. Bioresour. Technol. 2012, 122, 130–136. [Google Scholar] [CrossRef] [PubMed]
- Jang, N.; Yasin, M.; Kang, H.; Lee, Y.; Park, G.W.; Park, S.; Chang, I.S. Bubble coalescence suppression driven carbon monoxide (CO)-water mass transfer increase by electrolyte addition in a hollow fiber membrane bioreactor (HFMBR) for microbial CO conversion to ethanol. Bioresour. Technol. 2018, 263, 375–384. [Google Scholar] [CrossRef]
- Riggs, S.S.; Heindel, T.J. Measuring Carbon Monoxide Gas—Liquid Mass Transfer in a Stirred Tank Reactor for Syngas Fermentation. Biotechnol. Prog. 2006, 22, 903–906. [Google Scholar] [CrossRef]
- Ungerman, A.J.; Heindel, T.J. Carbon Monoxide Mass Transfer for Syngas Fermentation in a Stirred Tank Reactor with Dual Impeller Configurations. Biotechnol. Prog. 2007, 23, 613–620. [Google Scholar] [CrossRef]
- Munasinghe, P.C.; Khanal, S.K. Evaluation of hydrogen and carbon monoxide mass transfer and a correlation between the myoglobin-protein bioassay and gas chromatography method for carbon monoxide determination. Rsc Adv. 2014, 4, 37575–37581. [Google Scholar] [CrossRef]
- Munasinghe, P.C.; Khanal, S.K. Syngas fermentation to biofuel: Evaluation of carbon monoxide mass transfer coefficient (kLa) in different reactor configurations. Biotechnol. Prog. 2010, 26, 1616–1621. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).