End-User Software for Efficient Sensor Placement in Jacketed Wine Tanks
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model
Balance Equations
2.2. Software Implementation
2.3. Case Definition
2.4. Geometry and Mesh Generation
2.5. Boundary Conditions
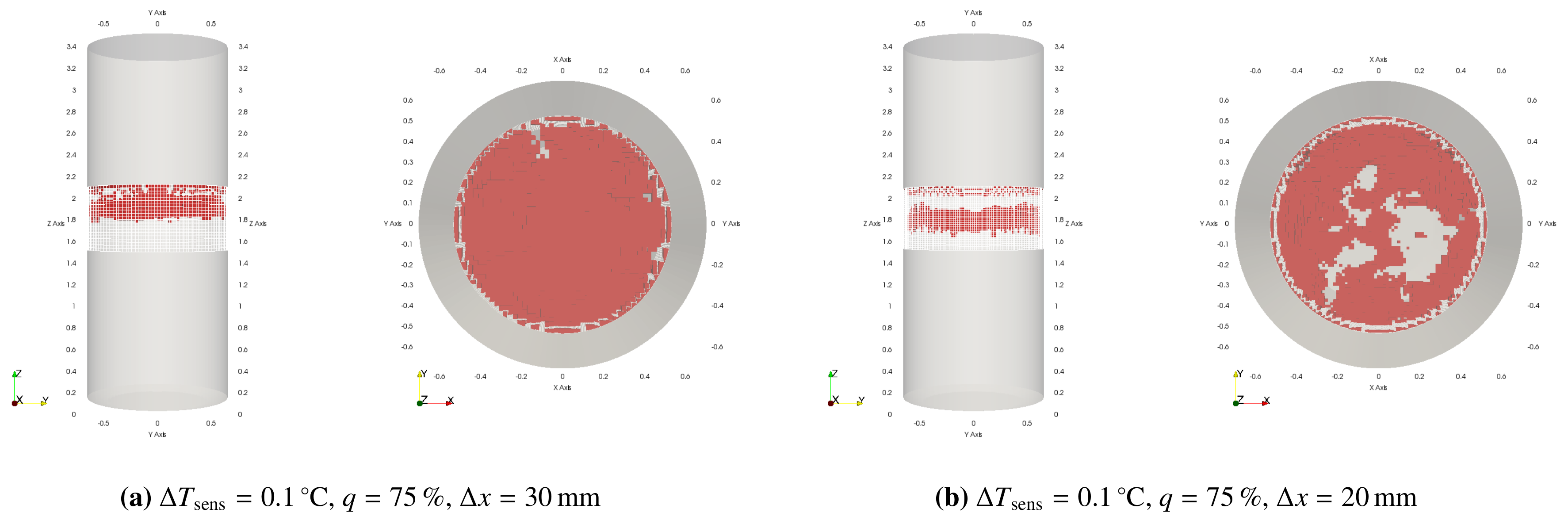
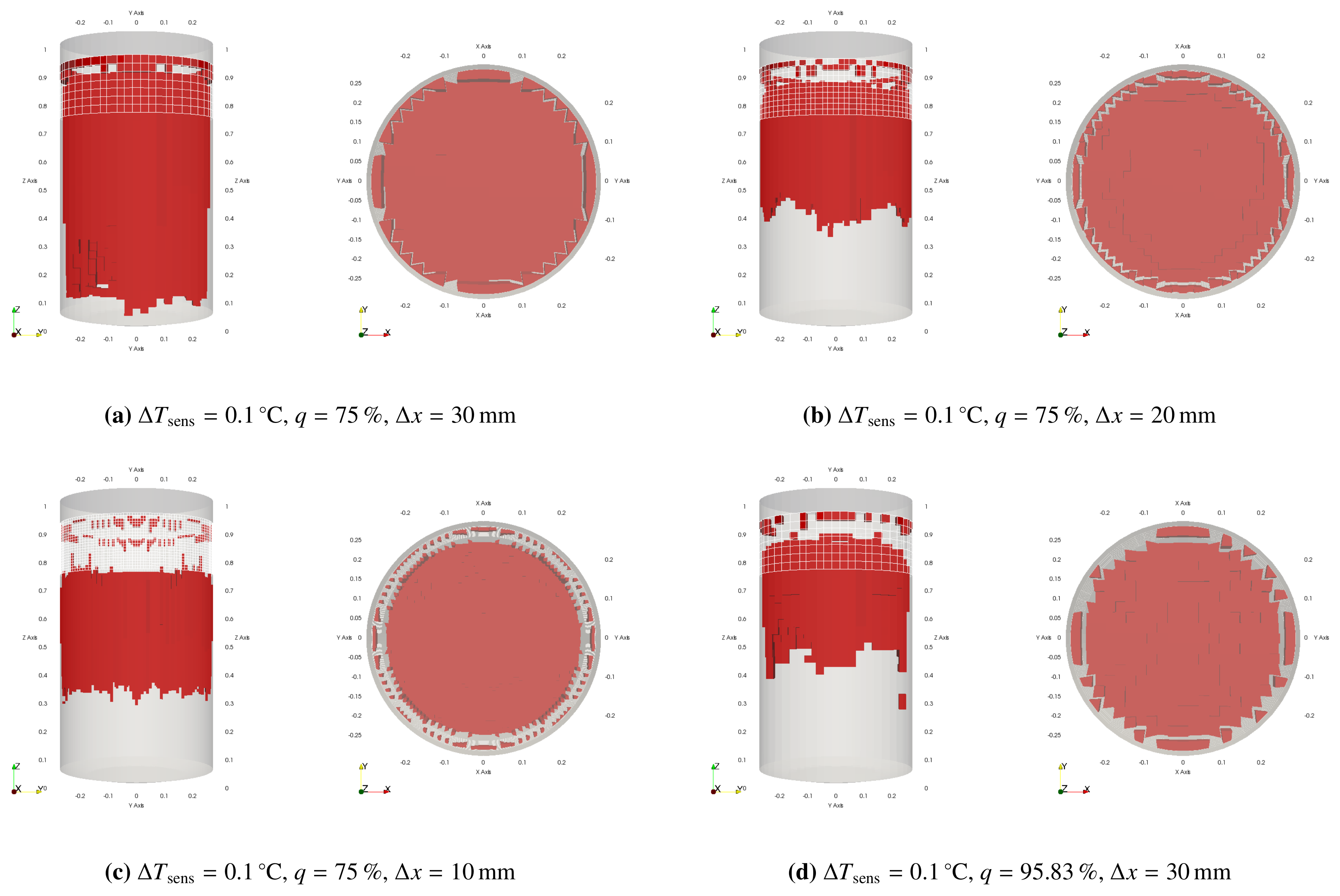
2.6. Identification of Sensor Locations
2.7. Case Studies
3. Results and Discussion
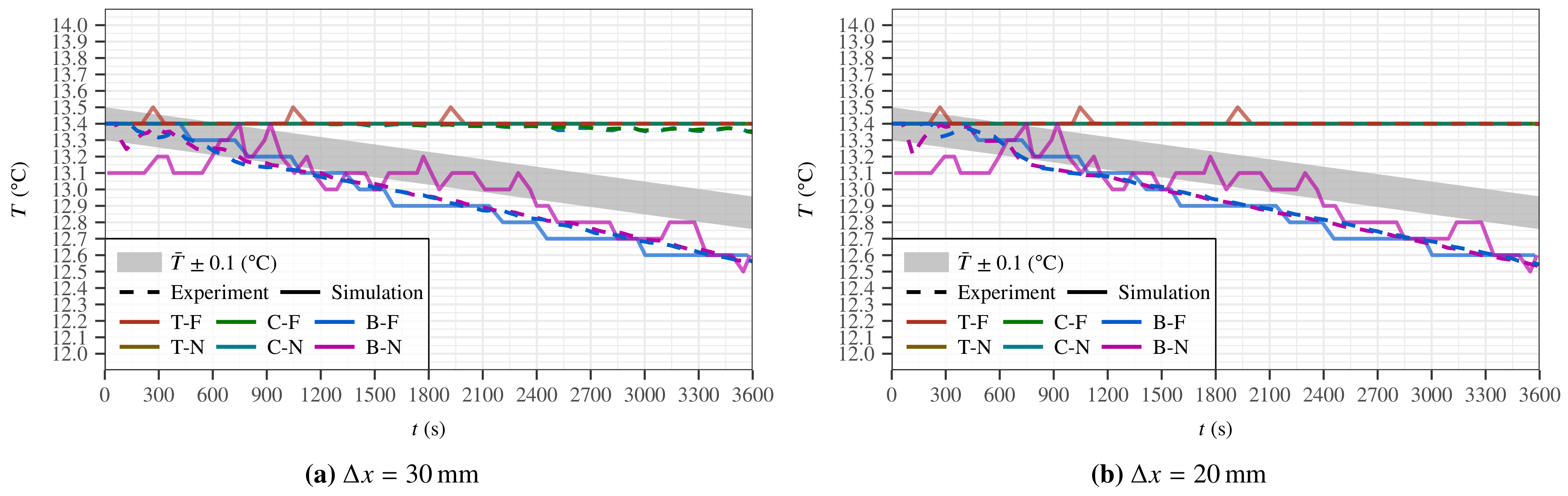
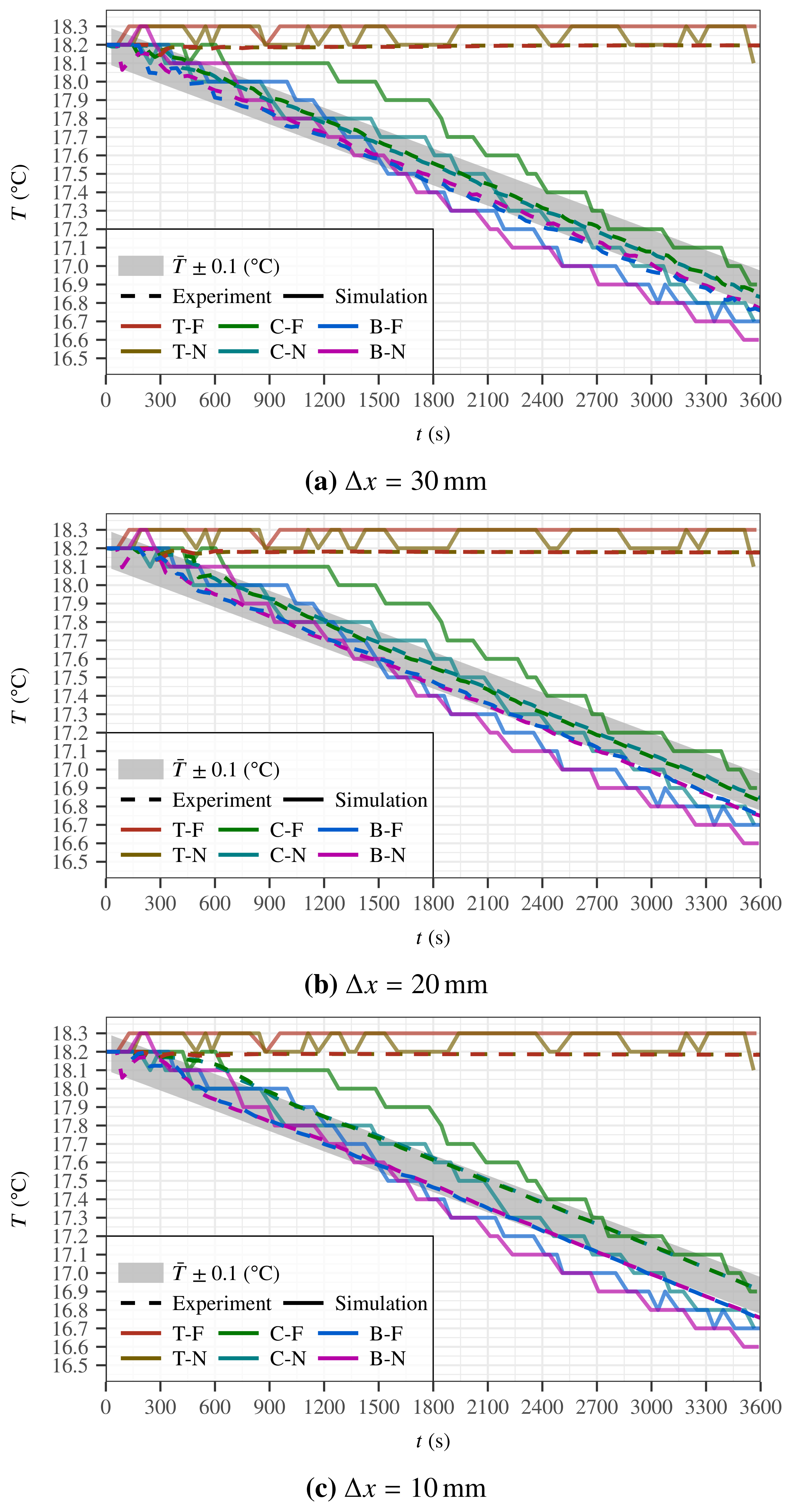
3.1. Case Studies
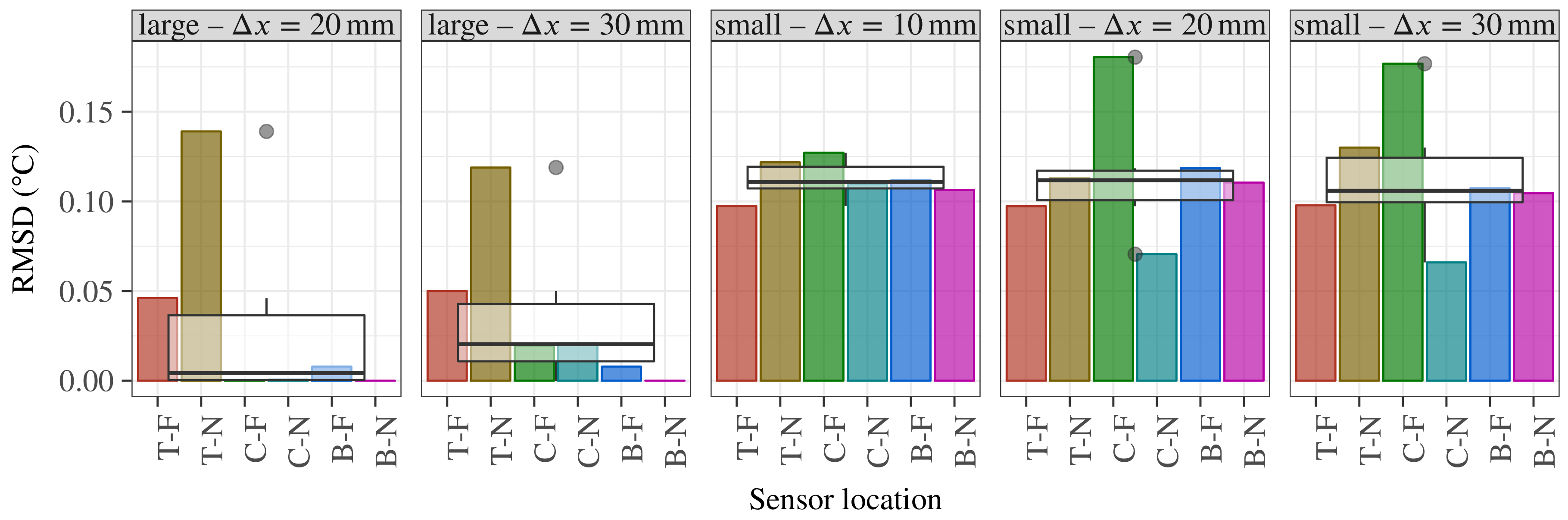
3.2. Sensor Location Scenarios
3.3. Computational Costs
3.4. Summary of Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| specific heat capacity (J kg−1 K−1) | |
| tank diameter (m) | |
| sediment fraction (m3 m−3) | |
| gravitational acceleration (m s−2) | |
| Boussinesq gravity (m s−2) | |
| jacket height (m) | |
| cooling jacket distance from tank height (m) | |
| tank height (m) | |
| p | pressure (Pa) |
| Pr | Prandtl number (-) |
| turbulent Prandtl number (-) | |
| Rate of heat flow from ambient air to the liquid (W) | |
| cooling power (W) | |
| rate of heat flow (W) | |
| q | percentage of valid measurements (%) |
| T | temperature (K) |
| cell center temperature (K) | |
| cooling rate (°C h−1) | |
| accepted temperature tolerance (mm) | |
| boundary face temperature (K) | |
| initial fluid temperature (°C) | |
| local reference temperature gradient (K) | |
| reference temperature (K) | |
| measurement interval of the temperature sensor (s) | |
| simulation duration (s) | |
| velocity (m s−1) | |
| V | liquid volume (m3) |
| grid cell size (mm) | |
| Greek symbols | |
| thermal expansion coefficient (K−1) | |
| face-to-cell distance (m) | |
| thermal conductivity (W m−1 K−1) | |
| kinematic viscosity (m2 s−1) | |
| turbulent kinematic viscosity (m2 s−1) | |
| cone angle (°) | |
| density (kg m−3) | |
| Subscripts | |
| c | linear cooling |
| f | linear face |
| L | linear large tank |
| S | linear small tank |
| x | linear cell |
| Acronyms | |
| CFD | computational fluid dynamics |
References
- Boulton, R.; Singleton, V.; Bisson, L.; Kunkee, R. Heating and Cooling Applications. In Principles and Practices of Winemaking; Springer: New York, NY, USA, 1999; pp. 492–520. [Google Scholar] [CrossRef]
- Molina, A.; Swiegers, J.; Varela, C.; Pretorius, I.; Agosin, E. Influence of wine fermentation temperature on the synthesis of yeast-derived volatile aroma compounds. Appl. Microbiol. Biotechnol. 2007, 77, 675–687. [Google Scholar] [CrossRef] [PubMed]
- Masneuf-Pomarède, I.; Mansour, C.; Murat, M.L.; Tominaga, T.; Dubourdieu, D. Influence of fermentation temperature on volatile thiols concentrations in Sauvignon blanc wines. Int. J. Food Microbiol. 2006, 108, 385–390. [Google Scholar] [CrossRef] [PubMed]
- Beltran, G.; Novo, M.; Guillamón, J.M.; Mas, A.; Rozès, N. Effect of fermentation temperature and culture media on the yeast lipid composition and wine volatile compounds. Int. J. Food Microbiol. 2008, 121, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Torija, M.; Rozès, N.; Poblet, M.; Guillamón, J.M.; Mas, A. Effects of fermentation temperature on the strain population of Saccharomyces cerevisiae. Int. J. Food Microbiol. 2003, 80, 47–53. [Google Scholar] [CrossRef]
- Bisson, L.F. Stuck and Sluggish Fermentations. Am. J. Enol. Vitic. 1999, 50, 107–119. [Google Scholar]
- Benitez, J.G.; Macias, V.P.; Gorostiaga, P.S.; Lopez, R.V.; Rodriguez, L.P. Comparison of electrodialysis and cold treatment on an industrial scale for tartrate stabilization of sherry wines. J. Food Eng. 2003, 58, 373–378. [Google Scholar] [CrossRef]
- Jourdes, M.; Michel, J.; Saucier, C.; Quideau, S.; Teissedre, P.L. Identification, amounts, and kinetics of extraction of C-glucosidic ellagitannins during wine aging in oak barrels or in stainless steel tanks with oak chips. Anal. Bioanal. Chem. 2011, 401, 1531. [Google Scholar] [CrossRef] [PubMed]
- Forsyth, K.; Roget, W.; O’Brien, V. Improving Winery Refrigeration Efficiency, Final Report, Project Number AWR 0902; The Australian Wine Research Institute: Adelaide, Australia, 2012. [Google Scholar]
- Soccol, C.R.; Pandey, A.; Larroche, C. Fermentation Processes Engineering in the Food Industry; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Schmidt, D.; Velten, K. Numerical simulation of bubble flow homogenization in industrial scale wine fermentations. Food Bioprod. Process. 2016, 100, 102–117. [Google Scholar] [CrossRef]
- Zenteno, M.I.; Pérez-Correa, J.R.; Gelmi, C.A.; Agosin, E. Modeling temperature gradients in wine fermentation tanks. J. Food Eng. 2010, 99, 40–48. [Google Scholar] [CrossRef]
- Vlassides, S.; Block, D.E. Evaluation of cell concentration profiles and mixing in unagitated wine fermentors. Am. J. Enol. Vitic. 2000, 51, 73–80. [Google Scholar]
- Han, Y.; Wang, R.; Dai, Y. Thermal stratification within the water tank. Renew. Sustain. Energy Rev. 2009, 13, 1014–1026. [Google Scholar] [CrossRef]
- Takamoto, Y.; Saito, Y. Thermal Convection in Cylindro-Conical Tanks During the Early Cooling Process. J. Inst. Brew. 2003, 109, 80–83. [Google Scholar] [CrossRef]
- Meironke, H.; Kasch, D.; Sieg, R. Determining the thermal flow structure inside fermenters with different shapes using Ultrasonic Doppler Velocimetry. In Proceedings of the 10th International Symposium on Ultrasonic Doppler Methods for Fluid Mechanics and Fluid Engineering, Tokyo, Japan, 28–30 September 2016; pp. 125–128. [Google Scholar]
- Schandelmaier, B. Gärsteuerung 2013—Ob groß oder klein—Pillow plates müssen sein. Das Dtsch. Weinmagazin 2013, 20, 30–36. [Google Scholar]
- Morakul, S.; Mouret, J.R.; Nicolle, P.; Trelea, I.C.; Sablayrolles, J.M.; Athes, V. Modelling of the gas–liquid partitioning of aroma compounds during wine alcoholic fermentation and prediction of aroma losses. Process Biochem. 2011, 46, 1125–1131. [Google Scholar] [CrossRef]
- Galitzky, C.; Worrell, E.; Healy, P.; Zechiel, S. Benchmarking and self-assessment in the wine industry. In Proceedings of the 2005 ACEEE Summer Study on Energy Efficiency in Industry, West Point, NY, USA, 19–22 July 2005. [Google Scholar]
- Perez-Coello, M.; Gonzalez-Vinas, M.; Garcia-Romero, E.; Diaz-Maroto, M.; Cabezudo, M. Influence of storage temperature on the volatile compounds of young white wines. Food Control 2003, 14, 301–306. [Google Scholar] [CrossRef]
- Joyeux, A.; Lafon-Lafourcade, S.; Ribéreau-Gayon, P. Evolution of acetic acid bacteria during fermentation and storage of wine. Appl. Environ. Microbiol. 1984, 48, 153–156. [Google Scholar] [PubMed]
- Lafon-Lafourcade, S.; Carre, E.; Ribéreau-Gayon, P. Occurrence of lactic acid bacteria during the different stages of vinification and conservation of wines. Appl. Environ. Microbiol. 1983, 46, 874–880. [Google Scholar] [PubMed]
- Boquete, L.; Cambralla, R.; Rodríguez-Ascariz, J.; Miguel-Jiménez, J.; Cantos-Frontela, J.; Dongil, J. Portable system for temperature monitoring in all phases of wine production. ISA Trans. 2010, 49, 270–276. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Skouroumounis, G.K.; Monro, T.M.; Taylor, D. Distributed Wireless Monitoring System for Ullage and Temperature in Wine Barrels. Sensors 2015, 15, 19495–19506. [Google Scholar] [CrossRef] [PubMed]
- Cañete, E.; Chen, J.; Martín, C.; Rubio, B. Smart Winery: A Real-Time Monitoring System for Structural Health and Ullage in Fino Style Wine Casks. Sensors 2018, 18, 803. [Google Scholar] [CrossRef] [PubMed]
- Ranasinghe, D.C.; Falkner, N.J.; Chao, P.; Hao, W. Wireless sensing platform for remote monitoring and control of wine fermentation. In Proceedings of the 2013 IEEE Eighth International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Melbourne, VIC, Australia, 2–5 April 2013; pp. 503–508. [Google Scholar]
- Sainz, B.; Antolín, J.; López-Coronado, M.; Castro, C.D. A Novel Low-Cost Sensor Prototype for Monitoring Temperature during Wine Fermentation in Tanks. Sensors 2013, 13, 2848–2861. [Google Scholar] [CrossRef] [PubMed]
- Di Gennaro, S.F.; Matese, A.; Mancin, M.; Primicerio, J.; Palliotti, A. An Open-Source and Low-Cost Monitoring System for Precision Enology. Sensors 2014, 14, 23388–23397. [Google Scholar] [CrossRef] [PubMed]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Rodríguez, I.; Castro, J.; Pérez-Segarra, C.; Oliva, A. Unsteady numerical simulation of the cooling process of vertical storage tanks under laminar natural convection. Int. J. Therm. Sci. 2009, 48, 708–721. [Google Scholar] [CrossRef]
- Papanicolaou, E.; Belessiotis, V. Transient natural convection in a cylindrical enclosure at high Rayleigh numbers. Int. J. Heat Mass Trans. 2002, 45, 1425–1444. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Chang, W.; Cheng, J.; Allaire, J.; Xie, Y.; McPherson, J. Shiny: Web Application Framework for R. R Package Version 1.0.3. 2017. Available online: https://cran.r-project.org/package=shiny (accessed on 24 May 2018).
- CEA/DEN, EDF R&D, O.C. SALOME Geometry User’s Guide. CEA/DEN, EDF R&D, OPEN CASCADE, 2016. Available online: http://docs.salome-platform.org/7/gui/GEOM/ (accessed on 24 May 2018).
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An End-User Tool for Large Data Visualization; Visualization Handbook; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Günther, M.; Velten, K. Mathematische Modellbildung und Simulation; Wiley-VCH: Berlin, Germeny, 2014. [Google Scholar]
- Velten, K.; Müller, J.; Schmidt, D. New methods to optimize wine production at all stages from vineyard to bottle. BIO Web Conf. 2015, 5, 02013. [Google Scholar] [CrossRef]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2009. [Google Scholar]
- Urbanek, S.; Horner, J. Cairo: R Graphics Device Using Cairo Graphics Library for Creating High-Quality Bitmap (PNG, JPEG, TIFF), vector (PDF, SVG, PostScript) and Display (X11 and Win32) Output. R Package Version 1.5-9. 2015. Available online: https://cran.r-project.org/package=Cairo (accessed on 24 May 2018).
- Bengtsson, H. Future: Unified Parallel and Distributed Processing in R for Everyone. R Package Version 1.5.0. 2017. Available online: https://cran.r-project.org/package=future (accessed on 24 May 2018).
- Greenshields, C. OpenFOAM User Guide, v5 ed.; CFD Direct Ltd.: Reading, UK, 2017; Available online: https://cfd.direct/openfoam/user-guide/ (accessed on 24 May 2018).
- De Moura, M.D.; Júnior, A.C. Heat Transfer by Natural ConvectIon in 3D Enclosures. In Proceedings of the ENCIT 2012, Rio de Janeiro, Brazil, 18–22 November 2012. [Google Scholar]
- Corzo, S.F.; Ramajo, D.E.; Nigro, N.M. CFD model of a moderator tank for a pressure vessel PHWR nuclear power plant. Appl. Therm. Eng. 2016, 107, 975–986. [Google Scholar] [CrossRef]
- McQuillan, F.J.; Culham, J.R.; Yovanovich, M.M. Properties of Some Gases and Liquids at One Atmosphere; Technical Report; Microelectronics Heat Transfer Laboratory Report UW/MHTL 8407 G-02; Microelectronics Heat Transfer Laboratory, University of Waterloo: Waterloo, ON, Canada, 1984. [Google Scholar]
- Wagner, W.; Pruß, A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Velten, K. Mathematical Modeling and Simulation: Introduction for Scientists and Engineers; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Safikhani, H.; Hajiloo, A.; Ranjbar, M. Modeling and multi-objective optimization of cyclone separators using CFD and genetic algorithms. Comput. Chem. Eng. 2011, 35, 1064–1071. [Google Scholar] [CrossRef]

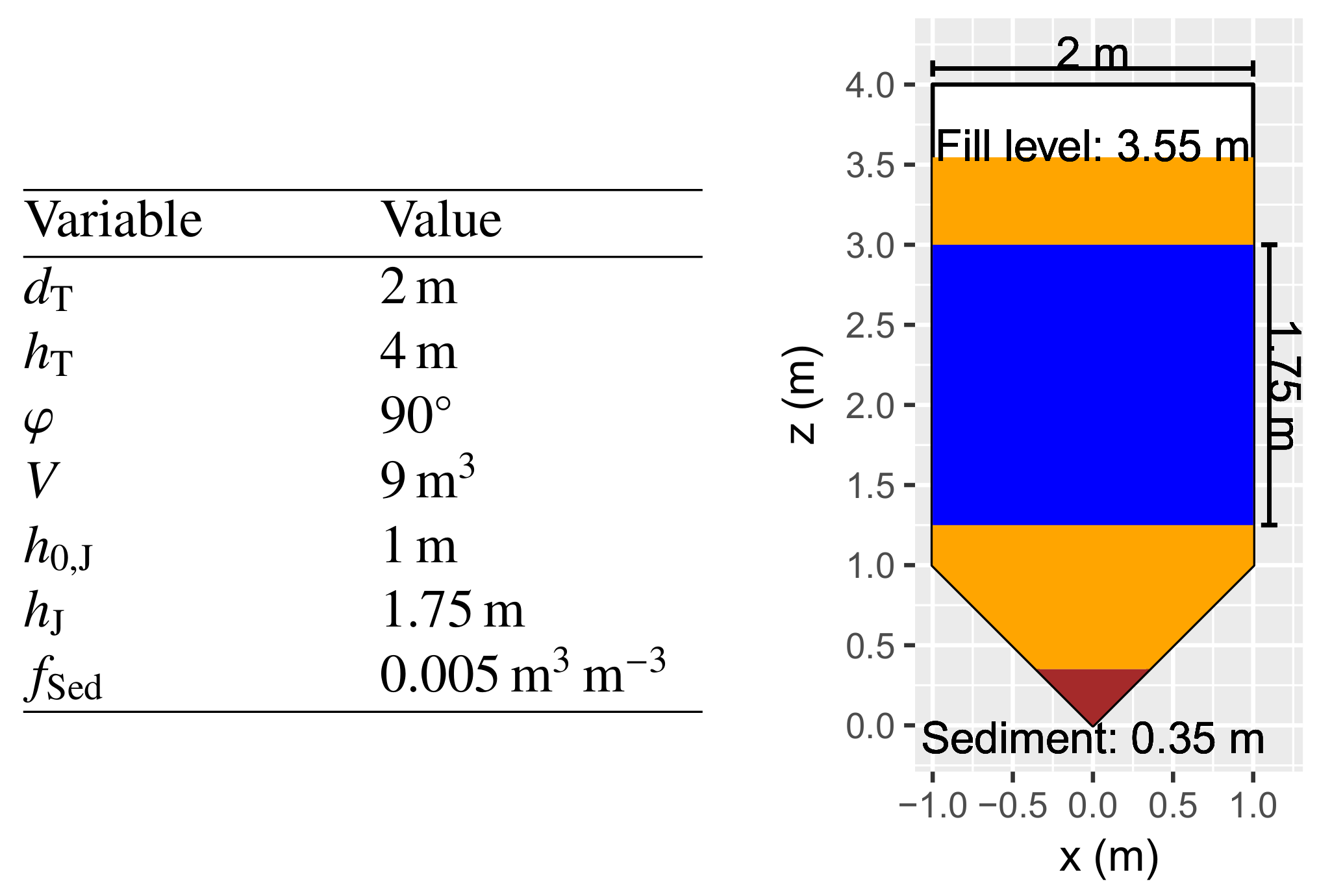
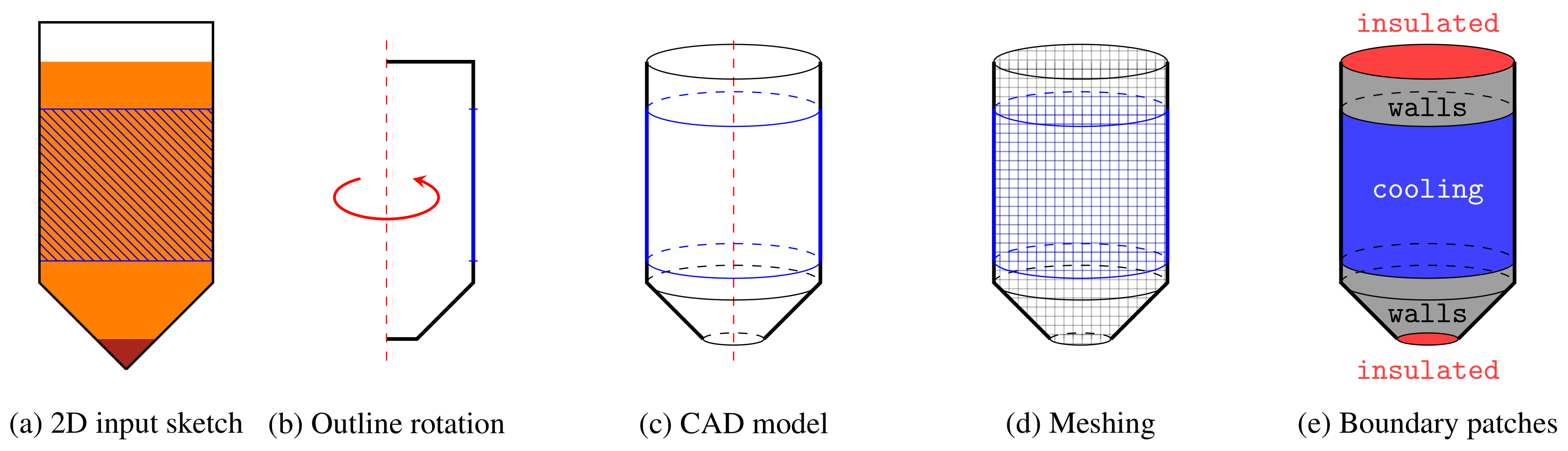
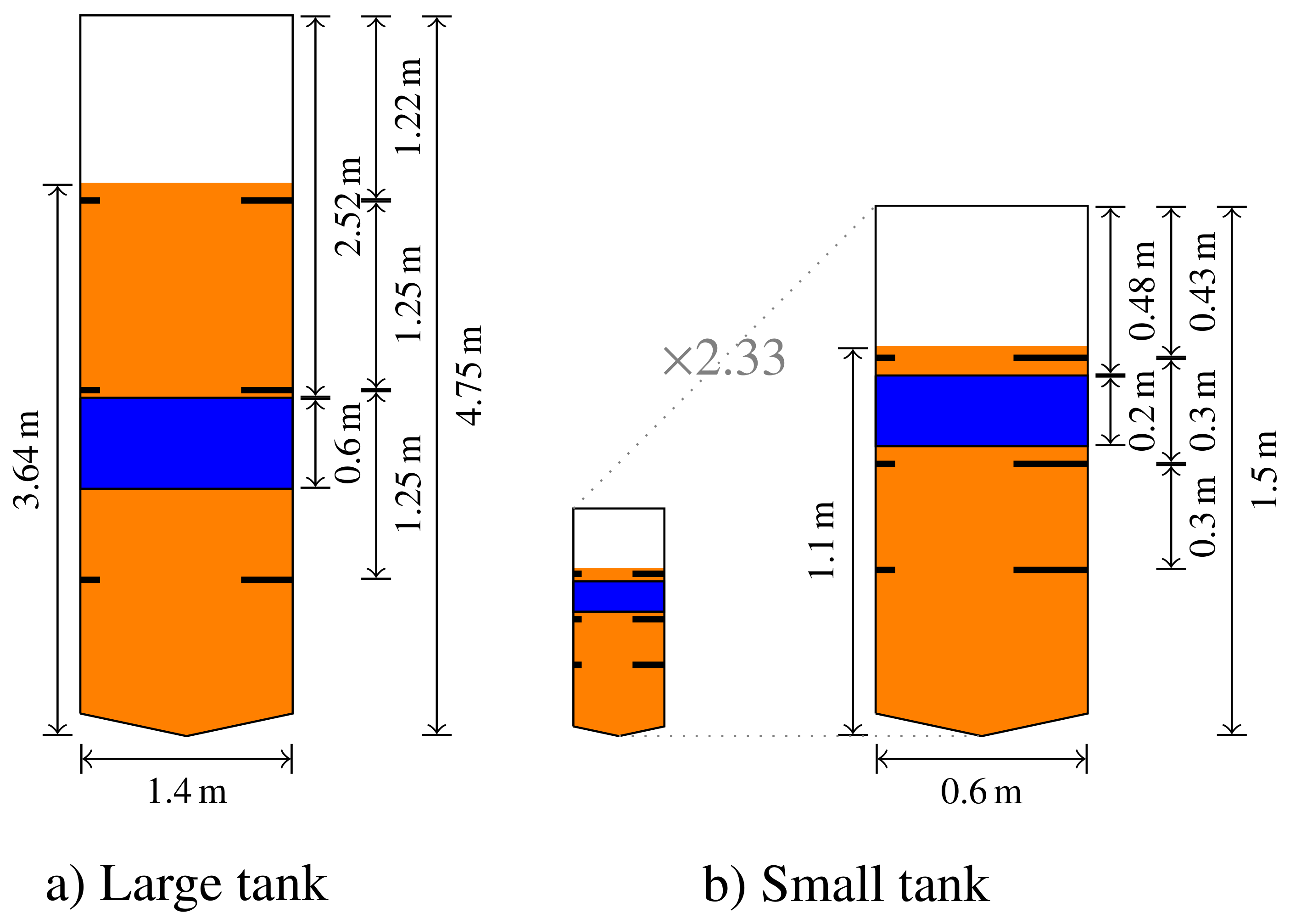
| Variable | Value |
|---|---|
| 3960 J kg−1 K−1 | |
| 970 kg m−3 | |
| 1.6 × 10−6 m2 s−1 | |
| 207 × 10−6 K−1 | |
| 0.6 W m−1 K−1 |
| Variable | Small Tank | Large Tank |
|---|---|---|
| 0.6 m | 1.4 m | |
| 1.5 m | 4.75 m | |
| 156° | 156° | |
| 0.3 m3 | 5.42 m3 | |
| 0.48 m | 2.52 m | |
| 0.2 m | 0.6 m | |
| 0.005 m3 m−3 | 0.005 m3 m−3 |
| Δx | Grid Cells | Cores a | Simulation Time (min) | ||
|---|---|---|---|---|---|
| Real Time | Single Core | ||||
| small | 30 mm | 12,805 | 3 | 3.73 | 11.19 |
| 20 mm | 40,154 | 18 | 8.92 | 160.56 | |
| 10 mm | 310,252 | 18 | 157.25 | 2830.5 | |
| large | 30 mm | 214,036 | 3 | 729.47 | 2188.4 |
| 20 mm | 714,920 | 15 | 1207.35 | 21,735.54 | |
| Case studies | - Successful validation of CFD simulations against experimental temperature progression in 300 L and 5420 L jacketed wine tanks. - Pre-installed sensor locations not well suited to monitor bulk mean temperature. |
| Sensor locations | - Efficient sensor location depends on fill level and cooling jacket position. - More variability in height than in depth (distance to wall) |
| Computational costs | - Computational times of less than one day already lead to sufficient results. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, D.; Freund, M.; Velten, K. End-User Software for Efficient Sensor Placement in Jacketed Wine Tanks. Fermentation 2018, 4, 42. https://doi.org/10.3390/fermentation4020042
Schmidt D, Freund M, Velten K. End-User Software for Efficient Sensor Placement in Jacketed Wine Tanks. Fermentation. 2018; 4(2):42. https://doi.org/10.3390/fermentation4020042
Chicago/Turabian StyleSchmidt, Dominik, Maximilian Freund, and Kai Velten. 2018. "End-User Software for Efficient Sensor Placement in Jacketed Wine Tanks" Fermentation 4, no. 2: 42. https://doi.org/10.3390/fermentation4020042
APA StyleSchmidt, D., Freund, M., & Velten, K. (2018). End-User Software for Efficient Sensor Placement in Jacketed Wine Tanks. Fermentation, 4(2), 42. https://doi.org/10.3390/fermentation4020042





