Design Considerations and Flow Characteristics for Couette-Type Blood-Shear Devices
Abstract
1. Introduction
2. Physiological Considerations
2.1. Non-Physiological Shear-Induced Blood Trauma in Stents
2.2. Non-Physiological Shear-Induced Blood Trauma in Valves
2.3. Non-Physiological Shear-Induced Blood Trauma in Mechanical Circulatory Support Devices
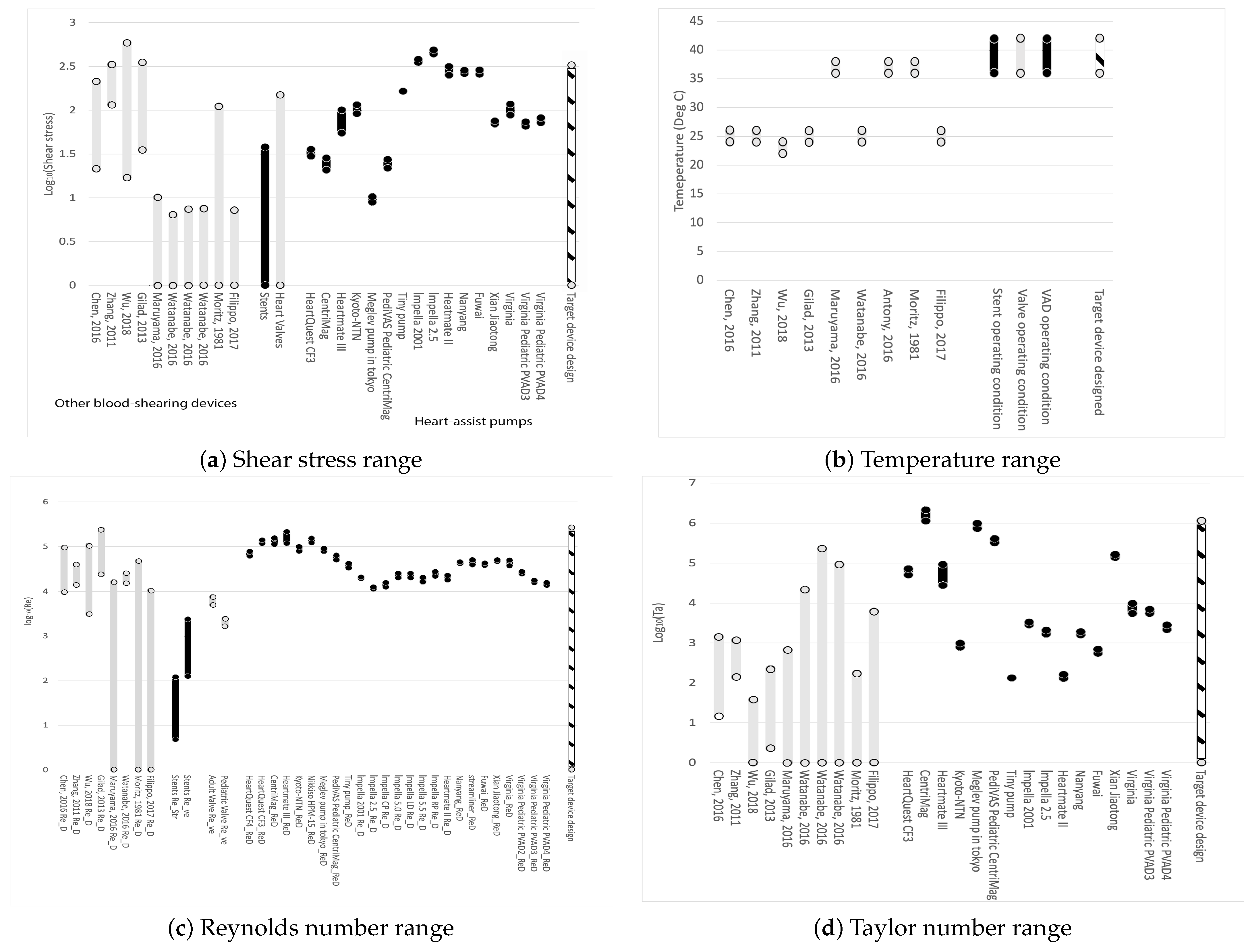
3. Ranges of Reynolds Numbers and Taylor Numbers for Blood Trauma Testing Devices
| Pump Name | References | Impeller Diameters (mm) D | Gap (mm) d | Flow Rate (Liter/Min) | Pressure (mmHg) | Speed (rpm) | at | at | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimum | Maximum | Optimum | Maximum | Optimum | Maximum | Design rpm | Maximum rpm | Design rpm | Maximum rpm | ||||
| Adult pumps | |||||||||||||
| HeartQuest CF4/Levacor | [95] | 44.45 | 6.0 | 10 | 100 | 190 | 2000 | 2500 | 62,072 | 77,590 | |||
| HeartQuest CF3/Levacor | [95,96] | 61 | 7.62 0.75 | 6.0 | 13.26 | 100 | 2000 | 2400 | 116,900 | 140,280 | 50,746 | 73,074 | |
| CentriMag | [97,98] [95] | 42.4 | 1.5 | 5.0 | 9.9 | 352 | 600 | 4000 | 5500 | 112,956 | 155,315 | 1,128,727 | 2,133,999 |
| HeartMate III | [95,99,100,101] | 50 | 0.5–1 | 7.0 | 10 | 90 | 120 | 3000 | 5500 | 117,809 | 215,984 | 27,730 | 93,204 |
| UltraMag | [95] | 1.0–3.0 | 6.0 | 5000–7000 | 9000 | ||||||||
| Kyoto-NTN | [95,102] | 50 | 0.2 | 6.5 | 120 | 2000 | 78,540 | 788 | |||||
| Nikkiso HPM-15 | [95,103,104] | 50 | 5.0 | 300 | 3100 | 121,740 | |||||||
| HVAD | [101] | 0.05 | |||||||||||
| Meglev pump developed in Tokyo Medical and Dental University | [95,105] | 51.2 | 2 | 6.0 | 7.6 | 105 | 140 | 1900 | 2200 | 78,237 | 90,590 | 728,947 | 977,315 |
| Pediatric pumps | |||||||||||||
| PediVAS Pediatric CentriMag | [95] | 27.2 | 1 | 3.0 | 200 | 5500 | 63,918 | 405,623 | |||||
| TinyPump | [95] | 30 | 0.1 | 2.0 | 4.0 | 86 | 120 | 3000 | 3000 | 42,412 | 42,412 | 133 | 133 |
| Pump Name | References | Impeller Diameters (mm) D | Gap (mm) d | Flow Rate (Liter/min) | Pressure (mmHg) | Speed (rpm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimum | Maximum | Optimum | Maximum | Optimum | Maximum | Design rpm | Maximum rpm | Design rpm | Maximum rpm | ||||
| Adult pumps | |||||||||||||
| Impella (2001) | [95] | <6.4 | 0.1 | 5.2 | 30,000 | 32,500 | 19,301 | 20,910 | 2839 | 3332 | |||
| Impella 2.5 | [95,106] | <4 | 0.075 | 2.4 | 2.7 | 50 | 45,000 | 50,000 | 11,309 | 12,566 | 1684 | 2079 | |
| Impella CP | [107] | <4.67 | 3.7 | 46,000 | 15,758 | ||||||||
| Impella 5.0 | [108] | <7 | 5.3 | 33,000 | 25,399 | ||||||||
| Impella LD | [108] | <7 | 5.3 | 33,000 | 25,399 | ||||||||
| Impella 5.5 | [109] | <6.3 | 5.5 | 33,000 | 20,573 | ||||||||
| Impella RP | [110] | <7.3 | 4.4 | 33,000 | 27,623 | ||||||||
| HeartMate II | [65,101] | 12 | 0.07 | 8000 | 18,095 | 129 | |||||||
| Nanyang Technological University | [95] | 15.6 | 0.12 | 5.14 | 8.5 | 100 | 120 | 11,000 | 12,000 | 42,049 | 45,872 | 1607 | 1913 |
| Streamliner | [95] | 19 | 6.0 | 15.0 | 140 | 260 | 7000 | 9000 | 39,694 | 51,035 | |||
| FuWai | [95] | 17.5 | 0.1 | 6.0 | 8.0 | 110 | 150 | 8000 | 9000 | 39,694 | 51,035 | 552 | 698 |
| Xian Jiaotong | [95] | 15.8 | 0.5 | 5.0 | 7.0 | 100 | 150 | 12,000 | 13,000 | 47,055 | 50,977 | 140,203 | 164,544 |
| Virginia LEV-VAD | [95] | 20 | 0.25 | 6.0 | 10.0 | 100 | 160 | 6000 | 8000 | 37,699 | 50,265 | 5546 | 9859 |
| Pediatric pumps | |||||||||||||
| Virginia Pediatric PVAD PVAD2 | [95] | 14 | 1.5 | 3.0 | 72 | 95 | 8000 | 9000 | 24,630 | 27,709 | |||
| Virginia Pediatric PVAD3 | [95] | 11.2 | 0.25 | 1.5 | 3.0 | 70 | 95 | 8000 | 9000 | 15,763 | 17,734 | 5521 | 6987 |
| Virginia Pediatric PVAD4 | [95] | 11.2 | 0.2–0.4 | 1.5 | 4.0 | 70 | 95 | 7000 | 8000 | 13,792 | 15,763 | 2164 | 2826 |
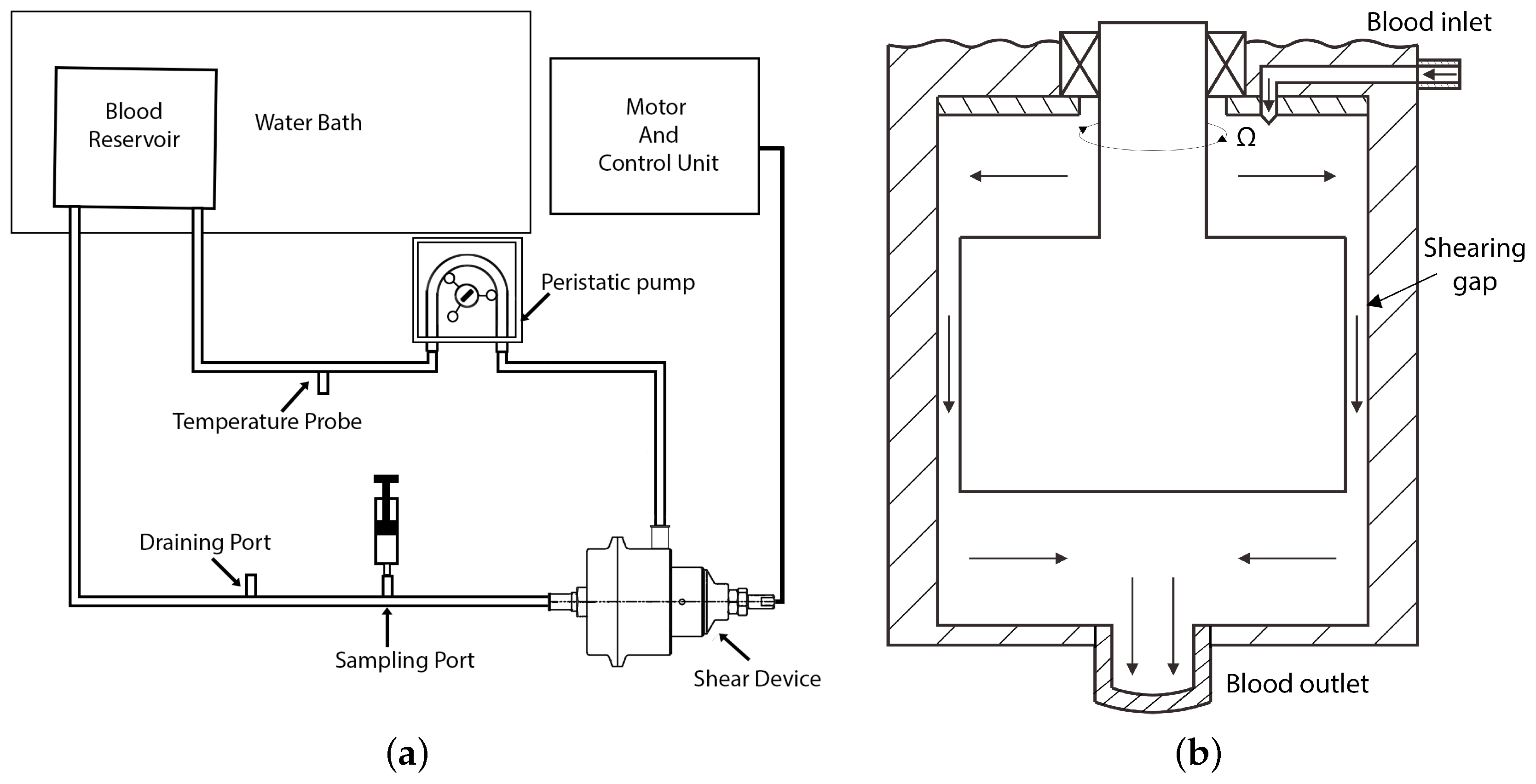
4. Considerations for Blood-Shearing Couette-Type Devices
4.1. Shear Stress Considerations
4.2. Temperature Considerations
4.3. Reynolds Number Considerations
4.4. Taylor Number Considerations
4.5. Basic Geometry
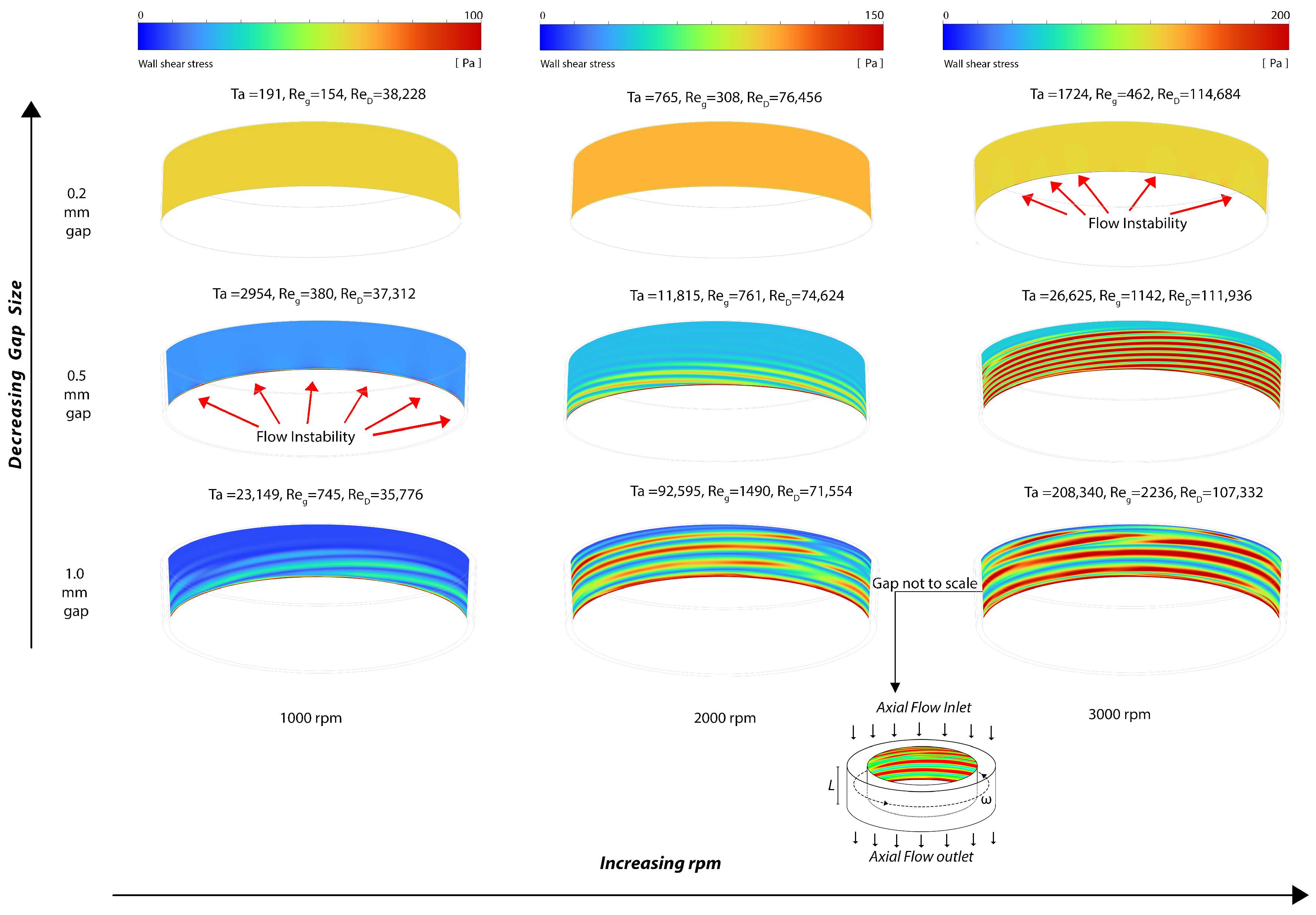
5. Numerical Simulation of Representative Flow Fields
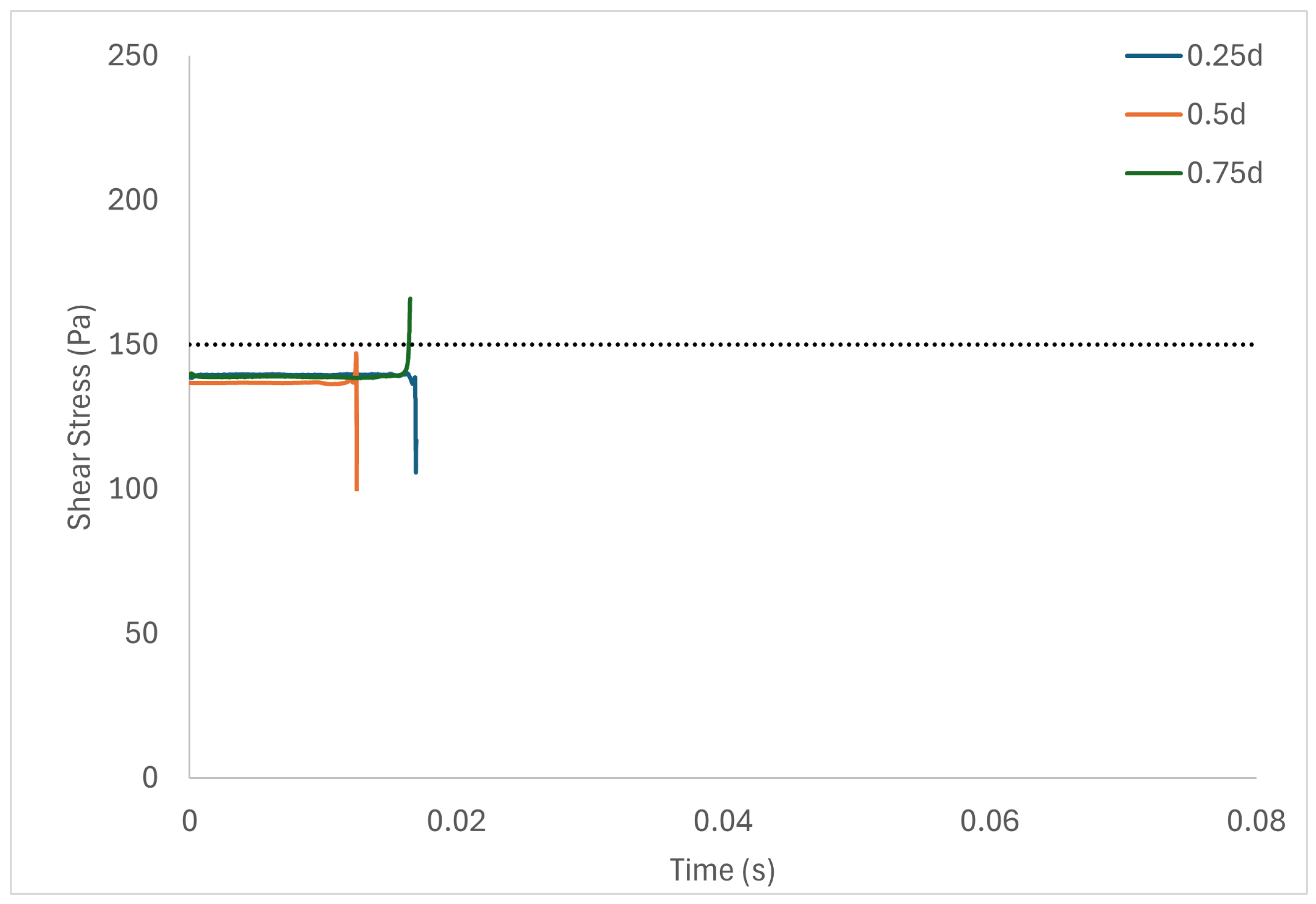
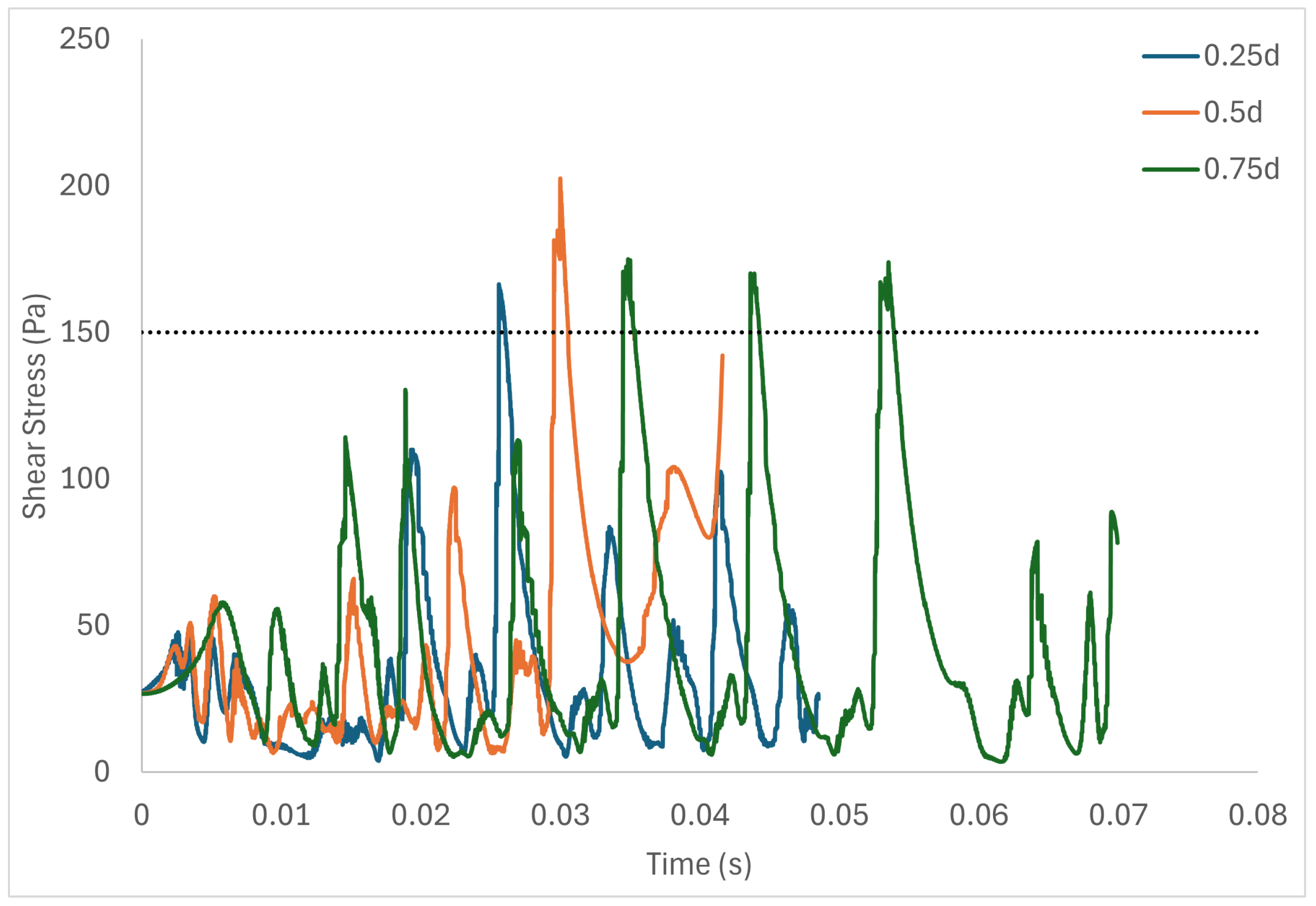
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin | |
| D | Diameter [m] |
| d | Radial gap size [m] |
| L | Height [m] |
| R | Radius [m] |
| Reynolds number | |
| Taylor number | |
| u | Velocity [m s−1] |
| Greek | |
| Dynamic viscosity [kg m−1 s−1 or Pa·s] | |
| Rotation speed [s−1] | |
| Density [kg m−3] | |
| Deviatoric stress [kg m−1 s−2] |
| Superscripts and subscripts | |
| D | Diameter |
| g | Radial gap |
| in | Inner rotor |
| R | Radius |
| str | Strut |
| ve | Vessel |
References
- Girdhar, G.; Bluestein, D. Biological effects of dynamic shear stress in cardiovascular pathologies and devices. Expert Rev. Med. Devices 2008, 5, 167–181. [Google Scholar] [CrossRef] [PubMed]
- LaDisa, J.; Guler, I.; Olson, L.; Hettrick, D.; Kersten, J.; Warltier, D.; Pagel, P. Three-Dimensional Computational Fluid Dynamics Modeling of Alterations in Coronary Wall Shear Stress Produced by Stent Implantation. Ann. Biomed. Eng. 2003, 31, 972–980. [Google Scholar] [CrossRef] [PubMed]
- LaDisa, J.; Olson, L.; Douglas, H.A.; Warltier, D.; Kersten, J.; Pagel, P. Alterations in regional vascular geometry produced by theoretical stent implantation influence distributions of wall shear stress: Analysis of a curved coronary artery using 3D computational fluid dynamics modeling. Biomed. Eng. Online 2006, 5, 40. [Google Scholar] [CrossRef]
- LaDisa, J.; Olson, L.; Hettrick, D.; Warltier, D.; Kersten, J.; Pagel, P. Axial stent strut angle influences wall shear stress after stent implantation: Analysis using 3D computational fluid dynamics models of stent foreshortening. Biomed. Eng. Online 2005, 4, 59. [Google Scholar] [CrossRef] [PubMed]
- Charonko, J.; Karri, S.; Schmieg, J.; Prabhu, S.; Vlachos, P. In Vitro, Time-Resolved PIV Comparison of the Effect of Stent Design on Wall Shear Stress. Ann. Biomed. Eng. 2009, 37, 1310–1321. [Google Scholar] [CrossRef]
- Stone, P.; Coskun, A.; Croce, K. Evolving insights into the role of local shear stress in late stent failure from neoatherosclerosis formation and plaque destabilization. Int. J. Cardiol. 2018, 272, 45–46. [Google Scholar] [CrossRef] [PubMed]
- Cutlip, D.E.; Nakazawa, G.; Krucoff, M.W.; Vorpahl, M.; Mehran, R.; Finn, A.V.; Vranckx, P.; Kimmelstiel, C.; Berger, C.; Petersen, J.L.; et al. Autopsy Validation Study of the Academic Research Consortium Stent Thrombosis Definition. JACC Cardiovasc. Interv. 2011, 4, 554–559. [Google Scholar] [CrossRef]
- Papafaklis, M.; Bourantas, C.; Theodorakis, P.; Katsouras, C.; Fotiadis, D.; Michalis, L. Relationship of shear stress with in-stent restenosis: Bare metal stenting and the effect of brachytherapy. Int. J. Cardiol. 2008, 134, 25–32. [Google Scholar] [CrossRef]
- Wentzel, J.J.; Krams, R.; Schuurbiers, J.C.H.; Oomen, J.A.; Kloet, J.; van der Giessen, W.J.; Serruys, P.W.; Slager, C.J. Relationship between Neointimal Thickness and Shear Stress after Wallstent Implantation in Human Coronary Arteries. Circulation 2001, 103, 1740–1745. [Google Scholar] [CrossRef]
- Stone, P.H.; Coskun, A.U.; Kinlay, S.; Clark, M.E.; Sonka, M.; Wahle, A.; Ilegbusi, O.J.; Yeghiazarians, Y.; Popma, J.J.; Orav, J.; et al. Effect of Endothelial Shear Stress on the Progression of Coronary Artery Disease, Vascular Remodeling, and In-Stent Restenosis in Humans. Circulation 2003, 108, 438–444. [Google Scholar] [CrossRef]
- Papafaklis, M.I.; Bourantas, C.V.; Theodorakis, P.E.; Katsouras, C.S.; Naka, K.K.; Fotiadis, D.I.; Michalis, L.K. The Effect of Shear Stress on Neointimal Response Following Sirolimus- and Paclitaxel-Eluting Stent Implantation Compared with Bare-Metal Stents in Humans. JACC Cardiovasc. Interv. 2010, 3, 1181–1189. [Google Scholar] [CrossRef] [PubMed]
- Economou, F.; Katranas, S.; Giannoglou, G.; Gemitzis, K.; Styliadis, I.; Efthimiadis, G.; Karvounis, H.; Ziakas, A. Impact of stent implantation on endothelial shear stress. Herz 2016, 42, 505–508. [Google Scholar] [CrossRef]
- Carlier, S.; van Damme, L.V.; Blommerde, C.P.; Wentzel, J.; van Langehove, G.; Verheye, S.; Kockx, M.; Knaapen, M.; Cheng, C.; Gijsen, F.; et al. Augmentation of Wall Shear Stress Inhibits Neointimal Hyperplasia After Stent Implantation: Inhibition Through Reduction of Inflammation? Circ. J. Am. Heart Assoc. 2003, 107, 2741–2746. [Google Scholar] [CrossRef] [PubMed]
- Wentzel, J.J.; Whelan, D.M.; van der Giessen, W.J.; van Beusekom, H.M.; Andhyiswara, I.; Serruys, P.W.; Slager, C.J.; Krams, R. Coronary stent implantation changes 3-D vessel geometry and 3-D shear stress distribution. J. Biomech. 2000, 33, 1287–1295. [Google Scholar] [CrossRef] [PubMed]
- Shishido, K.; Antoniadis, A.P.; Takahashi, S.; Tsuda, M.; Mizuno, S.; Andreou, I.; Papafaklis, M.I.; Coskun, A.U.; O’Brien, C.; Feldman, C.L.; et al. Effects of Low Endothelial Shear Stress after Stent Implantation on Subsequent Neointimal Hyperplasia and Clinical Outcomes in Humans. J. Am. Heart Assoc. 2016, 5, e002949. [Google Scholar] [CrossRef] [PubMed]
- Jiménez, J.M.; Davies, P.F. Hemodynamically Driven Stent Strut Design. Ann. Biomed. Eng. 2009, 37, 1483–1494. [Google Scholar] [CrossRef] [PubMed]
- Mejìa, J.; Ruzzeh, B.; Mongrain, R.; Leask, R.; Bertrand, O. Evaluation of the effect of stent strut profile on shear stress distribution using statistical moments. Biomed. Eng. Online 2009, 8, 8. [Google Scholar] [CrossRef] [PubMed]
- Kokkalis, E.; Aristokleous, N.; Houston, J. Haemodynamics and Flow Modification Stents for Peripheral Arterial Disease: A Review. Ann. Biomed. Eng. 2015, 44, 466–476. [Google Scholar] [CrossRef]
- Peacock, J.; Hankins, S.; Jones, T.; Lutz, R. Flow instabilities induced by coronary artery stents: Assessment with an in vitro pulse duplicator. J. Biomech. 1995, 28, 17–26. [Google Scholar] [CrossRef]
- Hofma, S.; Whelan, D.; van Beusekom, H.; Verdouw, P.; van der Giessen, W. Increasing arterial wall injury after long-term implantation of two types of stent in a porcine coronary model. Eur. Heart J. 1998, 19, 601–609. [Google Scholar] [CrossRef]
- Hu, Z.Y.; Chen, S.L.; Zhang, J.J.; Shan, S.J.; Liu, Z.Z.; Ye, F.; Kan, J.; Xu, H.M.; Nguyen, K.; Kwan, T.; et al. Distribution and Magnitude of Shear Stress after Coronary Bifurcation Lesions Stenting with the Classical Crush Technique: A New Predictor for In-Stent Restenosis. J. Interv. Cardiol. 2010, 23, 330–340. [Google Scholar] [CrossRef] [PubMed]
- Ng, J.; Bourantas, C.V.; Torii, R.; Ang, H.Y.; Tenekecioglu, E.; Serruys, P.W.; Foin, N. Local Hemodynamic Forces After Stenting. Arterioscler. Thromb. Vasc. Biol. 2017, 37, 2231–2242. [Google Scholar] [CrossRef] [PubMed]
- Jenei, C.; Balogh, E.; Szabó, G.; Dézsi, C.; Koszegi, Z. Wall shear stress in the development of in-stent restenosis revisited. A critical review of clinical data on shear stress after intracoronary stent implantation. Cardiol. J. 2016, 23, 365–373. [Google Scholar] [CrossRef] [PubMed]
- Koskinas, K.C.; Chatzizisis, Y.S.; Antoniadis, A.P.; Giannoglou, G.D. Role of Endothelial Shear Stress in Stent Restenosis and Thrombosis: Pathophysiologic Mechanisms and Implications for Clinical Translation. J. Am. Coll. Cardiol. 2012, 59, 1337–1349. [Google Scholar] [CrossRef]
- Azari, S.; Rezapour, A.; Omidi, N.; Alipour, V.; Tajdini, M.; Sadeghian, S.; Bragazzi, N.L. A systematic review of the cost-effectiveness of heart valve replacement with a mechanical versus biological prosthesis in patients with heart valvular disease. Heart Fail. Rev. 2020, 25, 495–503. [Google Scholar] [CrossRef]
- Li, R.L.; Russ, J.; Paschalides, C.; Ferrari, G.; Waisman, H.; Kysar, J.W.; Kalfa, D. Mechanical considerations for polymeric heart valve development: Biomechanics, materials, design and manufacturing. Biomaterials 2019, 225, 119493. [Google Scholar] [CrossRef]
- Baldwin, A.C.W.; Tolis, G. Tissue Valve Degeneration and Mechanical Valve Failure. Curr. Treat. Options Cardiovasc. Med. 2019, 21, 33. [Google Scholar] [CrossRef]
- David, T. How to Decide Between a Bioprosthetic and Mechanical Valve. Can. J. Cardiol. 2020, 37, 1121–1123. [Google Scholar] [CrossRef]
- Dasi, L.P.; Simon, H.A.; Sucosky, P.; Yoganathan, A.P. Fluid mechanics of artificial heart valves. Clin. Exp. Pharmacol. Physiol. 2009, 36, 225–237. [Google Scholar] [CrossRef]
- Barakat, M.; Dvir, D.; Azadani, A.N. Fluid Dynamic Characterization of Transcatheter Aortic Valves Using Particle Image Velocimetry. Artif. Organs 2018, 42, E357–E368. [Google Scholar] [CrossRef]
- Gürsoy, M.O.; Kalçık, M.; Yesin, M.; Karakoyun, S.; Bayam, E.; Gündüz, S.; Özkan, M. A global perspective on mechanical prosthetic heart valve thrombosis: Diagnostic and therapeutic challenges. Anatol. J. Cardiol. 2016, 16, 980–989. [Google Scholar] [PubMed]
- Boloori_Zadeh, P.; Corbett, S.C.; Nayeb-Hashemi, H. Effects of fluid flow shear rate and surface roughness on the calcification of polymeric heart valve leaflet. Mater. Sci. Eng. C 2013, 33, 2770–2775. [Google Scholar] [CrossRef] [PubMed]
- Lim, W.Y.; Lloyd, G.; Bhattacharyya, S. Mechanical and surgical bioprosthetic valve thrombosis. Heart 2017, 103, 1934–1941. [Google Scholar] [CrossRef]
- Mirsadraee, S.; Sellers, S.; Duncan, A.; Hamadanchi, A.; Gorog, D. Bioprosthetic valve thrombosis and degeneration following transcatheter aortic valve implantation (TAVI). Clin. Radiol. 2021, 76, 73.e39–73.e47. [Google Scholar] [CrossRef]
- Hatoum, H.; Gooden, S.; Heitkemper, M.; Blum, K.M.; Zakko, J.; Bocks, M.; Yi, T.; Wu, Y.L.; Wang, Y.; Breuer, C.K.; et al. Fetal Transcatheter Trileaflet Heart Valve Hemodynamics: Implications of Scaling on Valve Mechanics and Turbulence. Ann. Biomed. Eng. 2020, 48, 1683–1693. [Google Scholar] [CrossRef]
- Laflamme, J.; Puri, R.; Urena, M.; Laflamme, L.; DeLarochellière, H.; Abdul-Jawad Altisent, O.; del Trigo, M.; Campelo-Parada, F.; DeLarochellière, R.; Paradis, J.M.; et al. Incidence and Risk Factors of Hemolysis after Transcatheter Aortic Valve Implantation With a Balloon-Expandable Valve. Am. J. Cardiol. 2015, 115, 1574–1579. [Google Scholar] [CrossRef]
- Hedayat, M.; Borazjani, I. Comparison of platelet activation through hinge vs bulk flow in bileaflet mechanical heart valves. J. Biomech. 2019, 83, 280–290. [Google Scholar] [CrossRef]
- Krafczyk, M.; Tölke, J.; Rank, E.; Schulz, M. Two-dimensional simulation of fluidñstructure interaction using lattice-Boltzmann methods. Comput. Struct. 2001, 79, 2031–2037. [Google Scholar] [CrossRef]
- Gilmanov, A.; Sotiropoulos, F. Comparative hemodynamics in an aorta with bicuspid and trileaflet valves. Theor. Comput. Fluid Dyn. 2016, 30, 67–85. [Google Scholar] [CrossRef]
- Kang, Y.; Hwang, H.Y.; Sohn, S.; Choi, J.W.; Kim, K.H.; Kim, K.B. Fifteen-Year Outcomes After Bioprosthetic and Mechanical Tricuspid Valve Replacement. Ann. Thorac. Surg. 2020, 110, 1564–1571. [Google Scholar] [CrossRef]
- IJsselhof, R.J.; Slieker, M.G.; Hazekamp, M.G.; Accord, R.; van Wetten, H.; Haas, F.; Schoof, P.H. Mitral Valve Replacement with the 15-mm Mechanical Valve: A 20-Year Multicenter Experience. Ann. Thorac. Surg. 2020, 110, 956–961. [Google Scholar] [CrossRef] [PubMed]
- Vu, V.; May-Newman, K. Bileaflet Prosthesis Design and Orientation Affect Fluid Shear, Residence Time, and Thrombus Formation. J. Cardiothorac. Vasc. Anesth. 2019, 33, 2870–2872. [Google Scholar] [CrossRef] [PubMed]
- Yoganathan, A.P.; Corcoran, W.H.; Harrison, E.C.; Carl, J.R. The Björk-Shiley aortic prosthesis: Flow characteristics, thrombus formation and tissue overgrowth. Circulation 1978, 58, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Choi, H.; Kweon, J.; Yang, D.H.; Kim, Y.H. Effects of pannus formation on the flow around a bileaflet mechanical heart valve. PLoS ONE 2020, 15, e0234341. [Google Scholar] [CrossRef] [PubMed]
- Darwazah, A.K. Recurrent pannus formation causing prosthetic aortic valve dysfunction: Is excision without valve re-replacement applicable? J. Cardiothorac. Surg. 2012, 7, 62. [Google Scholar] [CrossRef] [PubMed]
- Ha, H.; Koo, H.J.; Huh, H.K.; Kim, G.B.; Kweon, J.; Kim, N.; Kim, Y.H.; Kang, J.W.; Lim, T.H.; Song, J.K.; et al. Effect of pannus formation on the prosthetic heart valve: In vitro demonstration using particle image velocimetry. PLoS ONE 2018, 13, e0199792. [Google Scholar] [CrossRef]
- Karakoyun, S.; Ozan Gürsoy, M.; Yesin, M.; Kalçik, M.; Astarcioglu, M.A.; Gündüz, S.; Emrah Oguz, A.; Çoban Kökten, S.; Nimet Karadayi, A.; Tuncer, A.; et al. Histopathological and Immunohistochemical Evaluation of Pannus Tissue in Patients with Prosthetic Valve Dysfunction. J. Heart Valve Dis. 2016, 25, 104–111. [Google Scholar]
- Weidemann, H.; Müller, K.M.; Hennig, E.; Meissler, M.; Bücherl, E.S. Experience with Vascular Grafts in total Artificial Heart Replacement. Int. J. Artif. Organs 1990, 13, 288–292. [Google Scholar] [CrossRef]
- May-Newman, K.; Montes, R.; Campos, J.; Marquez-Maya, N.; Vu, V.; Zebrowski, E.; Motomura, T.; Benkowski, R. Reducing regional flow stasis and improving intraventricular hemodynamics with a tipless inflow cannula design: An in vitro flow visualization study using the EVAHEART LVAD. Artif. Organs 2019, 43, 834–848. [Google Scholar] [CrossRef]
- Hatoum, H.; Dollery, J.; Lilly, S.M.; Crestanello, J.A.; Dasi, L.P. Effect of severe bioprosthetic valve tissue ingrowth and inflow calcification on valve-in-valve performance. J. Biomech. 2018, 74, 171–179. [Google Scholar] [CrossRef]
- Misawa, Y. Valve-related complications after mechanical heart valve implantation. Surg. Today 2015, 45, 1205–1209. [Google Scholar] [CrossRef] [PubMed]
- Starling, R.C.; Moazami, N.; Silvestry, S.C.; Ewald, G.; Rogers, J.G.; Milano, C.A.; Rame, J.E.; Acker, M.A.; Blackstone, E.H.; Ehrlinger, J.; et al. Unexpected Abrupt Increase in Left Ventricular Assist Device Thrombosis. N. Engl. J. Med. 2014, 370, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.E.; Haglund, N.A.; Tricarico, N.M.; Matafonov, A.; Gailani, D.; Maltais, S. Immediate Recovery of Acquired von Willebrand Syndrome After Left Ventricular Assist Device Explantation: Implications for Heart Transplantation. ASAIO J. 2015, 61, e1–e4. [Google Scholar] [CrossRef] [PubMed]
- National Heart Lung and Blood Institute. The Diagnosis, Evaluation and Management of von Willebrand Disease. 2007. Available online: https://www.nhlbi.nih.gov/sites/default/files/media/docs/vwd.pdf (accessed on 22 June 2024).
- Meyer, A.L.; Malehsa, D.; Budde, U.; Bara, C.; Haverich, A.; Strueber, M. Acquired von Willebrand Syndrome in Patients With a Centrifugal or Axial Continuous Flow Left Ventricular Assist Device. JACC Heart Fail. 2014, 2, 141–145. [Google Scholar] [CrossRef] [PubMed]
- Uriel, N.; Pak, S.W.; Jorde, U.P.; Jude, B.; Susen, S.; Vincentelli, A.; Ennezat, P.V.; Cappleman, S.; Naka, Y.; Mancini, D. Acquired von Willebrand Syndrome After Continuous-Flow Mechanical Device Support Contributes to a High Prevalence of Bleeding During Long-Term Support and at the Time of Transplantation. J. Am. Coll. Cardiol. 2010, 56, 1207–1213. [Google Scholar] [CrossRef] [PubMed]
- Bartoli, C.R.; Zhang, D.; Kang, J.; Hennessy-Strahs, S.; Restle, D.; Howard, J.; Redline, G.; Bermudez, C.; Atluri, P.; Acker, M.A. Clinical and In Vitro Evidence That Subclinical Hemolysis Contributes to LVAD Thrombosis. Ann. Thorac. Surg. 2018, 105, 807–814. [Google Scholar] [CrossRef] [PubMed]
- Slepian, M.J.; Sheriff, J.; Hutchinson, M.; Tran, P.; Bajaj, N.; Garcia, J.G.; Saavedra, S.S.; Bluestein, D. Shear-mediated platelet activation in the free flow: Perspectives on the emerging spectrum of cell mechanobiological mechanisms mediating cardiovascular implant thrombosis. J. Biomech. 2017, 50, 20–25. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.T.; Yang, F.; Wu, J.; Aubry, N.; Massoudi, M.; Antaki, J.F. High fidelity computational simulation of thrombus formation in Thoratec HeartMate II continuous flow ventricular assist device. Sci. Rep. 2013, 6, 38025. [Google Scholar] [CrossRef]
- Nobili, M.; Sheriff, J.; Morbiducci, U.; Redaelli, A.; Bluestein, D. Platelet Activation Due to Hemodynamic Shear Stresses: Damage Accumulation Model and Comparison to In Vitro Measurements. ASAIO J. 2008, 54, 64–72. [Google Scholar] [CrossRef]
- Chiu, W.C.; Girdhar, G.; Xenos, M.; Alemu, Y.; Soares, J.S.; Einav, S.; Bluestein, D. Thromboresistance Comparison of the HeartMate II Ventricular Assist Device With the Device Thrombogenicity Emulation-Optimized HeartAssist 5 VAD. J. Biomech. Eng. 2014, 136, C0210141–C0210149. [Google Scholar] [CrossRef]
- Kang, J.; Zhang, D.M.; Restle, D.J.; Kallel, F.; Acker, M.A.; Atluri, P.; Bartoli, C.R. Reduced continuous-flow left ventricular assist device speed does not decrease von Willebrand factor degradation. J. Thorac. Cardiovasc. Surg. 2016, 151, 1747–1754.e1. [Google Scholar] [CrossRef] [PubMed]
- Meyer, A.L.; Kuehn, C.; Weidemann, J.; Malehsa, D.; Bara, C.; Fischer, S.; Haverich, A.; Strüber, M. Thrombus formation in a HeartMate II left ventricular assist device. J. Thorac. Cardiovasc. Surg. 2008, 135, 203–204. [Google Scholar] [CrossRef] [PubMed]
- Jessen, S.L.; Kaulfus, C.N.; Chorpenning, K.; Ginn-Hedman, A.M.; Tamez, D.; Weeks, B.R. Histologic features of thrombosis events with a centrifugal left ventricular assist device. J. Heart Lung Transplant. 2021, 40, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Rowlands, G.W.; Antaki, J.F. High-speed visualization of ingested, ejected, adherent, and disintegrated thrombus in contemporary ventricular assist devices. Artif. Organs 2020, 44, E459–E469. [Google Scholar] [CrossRef] [PubMed]
- Schmitto, J.D.; Pya, Y.; Zimpfer, D.; Krabatsch, T.; Garbade, J.; Rao, V.; Morshuis, M.; Beyersdorf, F.; Marasco, S.; Sood, P.; et al. Long-term evaluation of a fully magnetically levitated circulatory support device for advanced heart failure—Two-year results from the HeartMate 3 CE Mark Study. Eur. J. Heart Fail. 2019, 21, 90–97. [Google Scholar] [CrossRef] [PubMed]
- Kalathiya, R.J.; Houston, B.A.; Chaisson, J.M.; Grimm, J.C.; Stevens, G.R.; Sciortino, C.M.; Shah, A.S.; Whitman, G.J.R.; Russell, S.D.; Tedford, R.J. Cardiac Index Declines During Long-Term Left Ventricular Device Support. Artif. Organs 2016, 40, 1105–1112. [Google Scholar] [CrossRef] [PubMed]
- Kawamura, A.; Toda, K.; Sawa, Y. First clinical experience with the double cuff tipless inflow cannula in the EVAHEART left ventricular assist system: Case report. Artif. Organs 2020, 44, 436–437. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, M.; Nonaka, K.; Linneweber, J.; Kawahito, S.; Ohtsuka, G.; Nakata, K.i.; Takano, T.; Schulte-Eistrup, S.; Glueck, J.; Schima, H.; et al. Development of the NEDO Implantable Ventricular Assist Device with Gyro Centrifugal Pump. Artif. Organs 2000, 24, 459–467. [Google Scholar] [CrossRef]
- Abe, Y.; Chinzei, T.; Isoyama, T.; Ono, T.; Mochizuki, S.; Saito, I.; Iwasaki, K.; Ishimaru, M.; Karita, T.; Kuono, A.; et al. One Month Survival with the Undulation Pump Total Artificial Heart in a Goat. Artif. Organs 2001, 25, 69–71. [Google Scholar]
- Khayata, M.; ElAmm, C.A.; Sareyyupoglu, B.; Zacharias, M.; Oliveira, G.H.; Medalion, B. HeartMate II pump exchange with HeartMate III implantation to the descending aorta. J. Card. Surg. 2019, 34, 47–49. [Google Scholar] [CrossRef]
- Drews, T.; Stepanenko, A.; Dandel, M.; Buz, S.; Lehmkuhl, H.B.; Hetzer, R. Mechanical circulatory support in patients of advanced age. Eur. J. Heart Fail. 2010, 12, 990–994. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.; Ichikawa, S.; Asai, T.; Motomura, T.; Hata, A.; Ito, S.; Shinohara, T.; Tsujimura, S.; Glueck, J.A.; Oestmann, D.J.; et al. Centrifugal Blood Pump with a Hydraulically-levitated Impeller for a Permanently Implantable Biventricular Assist Device. Artif. Organs 2004, 28, 556–563. [Google Scholar] [CrossRef]
- Ichikawa, S.; Nonaka, K.; Motomura, T.; Ishitoya, H.; Watanabe, K.; Ashizawa, S.; Shinohara, T.; Sumikura, H.; Ichihashi, F.; Oestmann, D.; et al. Antithrombogenicity of the Gyro Permanently Implantable Pump with the RPM Dynamic Suspension System for the Impeller. Artif. Organs 2003, 27, 865–869. [Google Scholar] [CrossRef] [PubMed]
- Fumoto, H.; Shiose, A.; Flick, C.R.; Noble, L.D.; Dudzinski, D.T.; Casas, F.; Takaseya, T.; Arakawa, Y.; Fukamachi, K.; Smith, W.A.; et al. Short-Term In Vivo Performance of the Cleveland Clinic PediPump Left Ventricular Assist Device. Artif. Organs 2014, 38, 374–382. [Google Scholar] [CrossRef] [PubMed]
- Tomaszewski, M.; Sybilski, K.; Baranowski, P.; Malachowski, J. Experimental and numerical flow analysis through arteries with stent using particle image velocimetry and computational fluid dynamics method. Biocybern. Biomed. Eng. 2020, 40, 740–751. [Google Scholar] [CrossRef]
- Mutlu, O.; Olcay, A.B.; Bilgin, C.; Hakyemez, B. Evaluating the Effectiveness of 2 Different Flow Diverter Stents Based on the Stagnation Region Formation in an Aneurysm Sac Using Lagrangian Coherent Structure. World Neurosurg. 2019, 127, e727–e737. [Google Scholar] [CrossRef] [PubMed]
- Kolachalama, V.B.; Levine, E.G.; Edelman, E.R. Luminal flow amplifies stent-based drug deposition in arterial bifurcations. PLoS ONE 2009, 4, e8105. [Google Scholar] [CrossRef]
- Boghi, A.; Venuta, I.D.; Gori, F. Three-dimensional numerical simulation of a failed coronary stent implant at different degrees of residual stenosis. Part II: Apparent viscosity and wall permeability. Numer. Heat Transf. Part A Appl. 2017, 71, 653–665. [Google Scholar] [CrossRef]
- Boghi, A.; Gori, F. Numerical Simulation of Blood Flow through Different Stents in Stenosed and Non-Stenosed Vessels. Numer. Heat Transf. Part A Appl. 2015, 68, 225–242. [Google Scholar] [CrossRef]
- Kabinejadian, F.; Cui, F.; Su, B.; Danpinid, A.; Ho, P.; Leo, H.L. Effects of a carotid covered stent with a novel membrane design on the blood flow regime and hemodynamic parameters distribution at the carotid artery bifurcation. Med. Biol. Eng. Comput. 2015, 53, 165–177. [Google Scholar] [CrossRef]
- Lam, S.K.; Fung, G.S.K.; Cheng, S.W.K.; Chow, K.W. A computational study on the biomechanical factors related to stent-graft models in the thoracic aorta. Med. Biol. Eng. Comput. 2008, 46, 1129–1138. [Google Scholar] [CrossRef] [PubMed]
- Rajani, B.; Kandasamy, A.; Majumdar, S. Numerical simulation of laminar flow past a circular cylinder. Appl. Math. Model. 2009, 33, 1228–1247. [Google Scholar] [CrossRef]
- Lee, J.H.; Scotten, L.N.; Hunt, R.; Caranasos, T.G.; Vavalle, J.P.; Griffith, B.E. Bioprosthetic aortic valve diameter and thickness are directly related to leaflet fluttering: Results from a combined experimental and computational modeling study. JTCVS Open 2020, 6, 50–81. [Google Scholar] [CrossRef] [PubMed]
- Hutchison, C.; Sullivan, P.; Ethier, C.R. Measurements of steady flow through a bileaflet mechanical heart valve using stereoscopic PIV. Med. Biol. Eng. Comput. 2011, 49, 325–335. [Google Scholar] [CrossRef]
- Basri, A.A.; Zuber, M.; Basri, E.I.; Zakaria, M.S.; Aziz, A.F.A.; Tamagawa, M.; Ahmad, K.A. Fluid Structure Interaction on Paravalvular Leakage of Transcatheter Aortic Valve Implantation Related to Aortic Stenosis: A Patient-Specific Case. Comput. Math. Methods Med. 2020, 2020, 9163085. [Google Scholar] [CrossRef]
- Hasler, D.; Obrist, D. Three-dimensional flow structures past a bio-prosthetic valve in an in-vitro model of the aortic root. PLoS ONE 2018, 13, e0194384. [Google Scholar] [CrossRef]
- De Vita, F.; de Tullio, M.D.; Verzicco, R. Numerical simulation of the non-Newtonian blood flow through a mechanical aortic valve. Theor. Comput. Fluid Dyn. 2016, 30, 129–138. [Google Scholar] [CrossRef]
- Suzuki, I.; Shiraishi, Y.; Yabe, S.; Tsuboko, Y.; Sugai, T.K.; Matsue, K.; Kameyama, T.; Saijo, Y.; Tanaka, T.; Okamoto, Y.; et al. Engineering analysis of the effects of bulging sinuses in a newly designed pediatric pulmonary heart valve on hemodynamic function. J. Artif. Organs 2012, 15, 49–56. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, P.; Rezaienia, M.A.; Rahideh, A.; Keeble, T.R.; Rothman, M.T.; Korakianitis, T. In vitro cardiovascular system emulator (Bioreactor) for the simulation of normal and diseased conditions with and without mechanical circulatory support. Artif. Organs 2013, 37, 549–560. [Google Scholar] [CrossRef]
- Korakianitis, T.; Rezaienia, M.A.; Paul, G.; Rahideh, A.; Rothman, M.T.; Mozafari, S. Optimization of Centrifugal Pump Characteristic Dimensions for Mechanical Circulatory Support Devices. ASAIO J. 2016, 62, 545–551. [Google Scholar] [CrossRef]
- Korakianitis, T.; Rezaienia, M.A.; Paul, G.; Avital, E.J.; Rothman, M.T.; Mozafari, S. Optimization of Axial Pump Characteristic Dimensions and Induced Hemolysis for Mechanical Circulatory Support Devices. ASAIO J. 2018, 64, 727–734. [Google Scholar] [CrossRef]
- Shu, F.; Tian, R.; Vandenberghe, S.; Antaki, J.F. Experimental Study of Micro-Scale Taylor Vortices Within a Co-Axial Mixed-Flow Blood Pump. Artif. Organs 2016, 40, 1071–1078. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.Y.; Yang, K.S. Numerical study of TaylorñCouette flow with an axial flow. Comput. Fluids 2004, 33, 97–118. [Google Scholar] [CrossRef]
- Fraser, K.H.; Taskin, M.E.; Griffith, B.P.; Wu, Z.J. The use of computational fluid dynamics in the development of ventricular assist devices. Med. Eng. Phys. 2011, 33, 263–280. [Google Scholar] [CrossRef]
- Bearnson, G.; Diegel, P.; Khanwilkar, P.; Allaire, P.; Ludlow, J.; Cooley, D.; Long, J.; Kumar, B.A.; Pantalos, G.; Wood, H.; et al. Progress on the heartquest VAD—A centrifugal pump with magnetically suspended rotor. ASAIO J. 2000, 46, 192. [Google Scholar] [CrossRef]
- Zhang, J.; Gellman, B.; Koert, A.; Dasse, K.A.; Gilbert, R.J.; Griffith, B.P.; Wu, Z.J. Computational and Experimental Evaluation of the Fluid Dynamics and Hemocompatibility of the CentriMag Blood Pump. Artif. Organs 2006, 30, 168–177. [Google Scholar] [CrossRef]
- Chan, C.H.; Pieper, I.L.; Hambly, R.; Radley, G.; Jones, A.; Friedmann, Y.; Hawkins, K.M.; Westaby, S.; Foster, G.; Thornton, C.A. The CentriMag Centrifugal Blood Pump as a Benchmark for In Vitro Testing of Hemocompatibility in Implantable Ventricular Assist Devices. Artif. Organs 2015, 39, 93–101. [Google Scholar] [CrossRef]
- Potapov, E.; Kukucka, M.; Falk, V.; Krabatsch, T. Off-pump implantation of the HeartMate 3 left ventricular assist device through bilateral thoracotomy approach. J. Thorac. Cardiovasc. Surg. 2016, 153, 104–105. [Google Scholar] [CrossRef]
- Bourque, K.; Cotter, C.; Dague, C.; Harjes, D.; Dur, O.; Duhamel, J.; Spink, K.; Walsh, K.; Burke, E. Design Rationale and Pre-Clinical Evaluation of the HeartMate 3 Left Ventricular Assist System for Hemocompatibility. ASAIO J. 2016, 62, 1. [Google Scholar] [CrossRef]
- Shah, P.; Tantry, U.S.; Bliden, K.P.; Gurbel, P.A. Bleeding and thrombosis associated with ventricular assist device therapy. J. Heart Lung Transplant. 2017, 36, 1164–1173. [Google Scholar] [CrossRef] [PubMed]
- Akamatsu, T.; Tsukiya, T.; Nishimura, K.; Park, C.H.; Nakazeki, T. Recent Studies of the Centrifugal Blood Pump with a Magnetically Suspended Impeller. Artif. Organs 1995, 19, 631–634. [Google Scholar] [CrossRef]
- Song, X.; Throckmorton, A.L.; Wood, H.G.; Antaki, J.; Olsen, D.B. Quantitative Evaluation of Blood Damage in a Centrifugal VAD by Computational Fluid Dynamics. J. Fluids-Eng.-Trans. ASME Fluids Eng. 2004, 126, 410–418. [Google Scholar] [CrossRef]
- Naito, K.; Suenaga, E.; Cao, Z.L.; Suda, H.; Ueno, T.; Natsuaki, M.; Itoh, T. Comparative Hemolysis Study of Clinically Available Centrifugal Pumps. Artif. Organs 1996, 20, 560–563. [Google Scholar] [CrossRef] [PubMed]
- Asama, J.; Shinshi, T.; Hoshi, H.; Takatani, S.; Shimokohbe, A. A Compact Highly Efficient and Low Hemolytic Centrifugal Blood Pump With a Magnetically Levitated Impeller. Artif. Organs 2006, 30, 160–167. [Google Scholar] [CrossRef] [PubMed]
- Zein, R.; Patel, C.; Mercado-Alamo, A.; Schreiber, T.; Kaki, A. A Review of the Impella Devices. Interv. Cardiol. 2022, 17, e05. [Google Scholar] [CrossRef]
- ABIOMED. Impella CP with SmartAssist for Use during Cardiogenic Shock and High-Risk PCI; ABIOMED: Danvers, MA, USA, 2020. [Google Scholar]
- ABIOMED. Impella Ventricular Support Systems for Use during Cardiogenic Shock and High-Risk PCI; ABIOMED: Danvers, MA, USA, 2018. [Google Scholar]
- ABIOMED. Impella 5.5 with SmartAssist For Use during Cardiogenic Shock and High-Risk PCI; ABIOMED: Danvers, MA, USA, 2024. [Google Scholar]
- ABIOMED. Impella RP with the Automated Impella Controller; ABIOMED: Danvers, MA, USA, 2012. [Google Scholar]
- Moritz, M.W.; Sutera, S.P.; Joist, J. Factors influencing shear-induced platelet alterations: Platelet lysis is independent of platelet aggregation and release. Thromb. Res. 1981, 22, 445–455. [Google Scholar] [CrossRef]
- Zhang, T.; Taskin, M.E.; Fang, H.B.; Pampori, A.; Jarvik, R.; Griffith, B.P.; Wu, Z.J. Study of Flow-Induced Hemolysis Using Novel Couette-Type Blood-Shearing Devices. Artif. Organs 2011, 35, 1180–1186. [Google Scholar] [CrossRef] [PubMed]
- Arwatz, G.; Smits, A. A viscoelastic model of shear-induced hemolysis in laminar flow. Biorheology 2013, 50, 45–55. [Google Scholar] [CrossRef]
- Chen, Z.; Mondal, N.K.; Ding, J.; Koenig, S.C.; Slaughter, M.S.; Wu, Z.J. Paradoxical Effect of Nonphysiological Shear Stress on Platelets and von Willebrand Factor. Artif. Organs 2016, 40, 659–668. [Google Scholar] [CrossRef]
- Maruyama, O.; Kosaka, R.; Nishida, M.; Yamane, T.; Tatsumi, E.; Taenaka, Y. In Vitro Thrombogenesis Resulting from Decreased Shear Rate and Blood Coagulability. Int. J. Artif. Organs 2016, 39, 194–199. [Google Scholar] [CrossRef]
- Watanabe, N.; Ueda, S.; Nagashima, K.; Oguri, T.; Mita, T. Ratio of surface roughness to flow scale as additional parameter for shear-induced hemolysis. Int. J. Artif. Organs 2016, 39, 205–210. [Google Scholar] [CrossRef] [PubMed]
- Mcnamee, A.; Tansley, G.; Sabapathy, S.; Simmonds, M. Biphasic impairment of erythrocyte deformability in response to repeated, short duration exposures of supraphysiological, subhaemolytic shear stress. Biorheology 2016, 53, 1–13. [Google Scholar] [CrossRef]
- Consolo, F.; Sheriff, J.; Gorla, S.; Magri, N.; Bluestein, D.; Pappalardo, F.; Slepian, M.; Fiore, G.; Redaelli, A. High Frequency Components of Hemodynamic Shear Stress Profiles are a Major Determinant of Shear-Mediated Platelet Activation in Therapeutic Blood Recirculating Devices. Sci. Rep. 2017, 7, 4994. [Google Scholar] [CrossRef] [PubMed]
- Dimasi, A.; Rasponi, M.; Consolo, F.; Fiore, G.B.; Bluestein, D.; Slepian, M.J.; Redaelli, A. Microfludic platforms for the evaluation of anti-platelet agent efficacy under hyper-shear conditions associated with ventricular assist devices. Med. Eng. Phys. 2017, 48, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Boehning, F.; Groß-Hardt, S.; Hsu, P.L. On the Accuracy of Hemolysis Models in Couette-Type Blood Shearing Devices. Artif. Organs 2018, 42, E290–E303. [Google Scholar] [CrossRef] [PubMed]
- Cinar, Y.; Senyol, A.M.; Duman, K. Blood viscosity and blood pressure: Role of temperature and hyperglycemia. Am. J. Hypertens. 2001, 14, 433–438. [Google Scholar]
- Krisher, J.A.; Malinauskas, R.A.; Day, S.W. The effect of blood viscosity on shear-induced hemolysis using a magnetically levitated shearing device. Artif. Organs 2022, 46, 1027–1039. [Google Scholar] [CrossRef]
- Dou, H.S.; Khoo, B.C.; Yeo, K.S. Instability of Taylor–Couette flow between concentric rotating cylinders. Int. J. Therm. Sci. 2008, 47, 1422–1435. [Google Scholar] [CrossRef]
- Alexander, T.; Chen, X.; Avital, E.J.; Imran, S.; Mujtaba, M.A.; Isbell, T.S.; Jain, A.; Jin, H.; Hinkle, P. Hemolysis from Energy Consumed in Fluid Dissipation in High-Shear Blood Flow. In Submitted to Artificial Organs; Saint Louis University Cardiovascular Flows Lab report 2024-CVFL-03; Wiley: Hoboken, NJ, USA, 2024. [Google Scholar]
- Fardin, M.A.; Perge, C.; Taberlet, N. “The hydrogen atom of fluid dynamics”—Introduction to the Taylor–Couette flow for soft matter scientists. Soft Matter 2014, 10, 3523–3535. [Google Scholar] [CrossRef]
- Liu, H.; Lan, L.; Abrigo, J.; Ip, H.L.; Soo, Y.; Zheng, D.; Wong, K.S.; Wang, D.; Shi, L.; Leung, T.W.; et al. Comparison of Newtonian and Non-newtonian Fluid Models in Blood Flow Simulation in Patients with Intracranial Arterial Stenosis. Front. Physiol. 2021, 12, 718540. [Google Scholar] [CrossRef]
- Cho, Y.I.; Kensey, K.R. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef]
- Fraser, K.H.; Zhang, T.; Taskin, M.E.; Griffith, B.P.; Wu, Z.J. A Quantitative Comparison of Mechanical Blood Damage Parameters in Rotary Ventricular Assist Devices: Shear Stress, Exposure Time and Hemolysis Index. J. Biomech. Eng. 2012, 134, 081002. [Google Scholar] [CrossRef] [PubMed]
- Baskurt, O.K.; Meiselman, H.J. Red blood cell mechanical stability test. Clin. Hemorheol. Microcirc. 2013, 55, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Beris, A.N.; Horner, J.S.; Jariwala, S.; Armstrong, M.J.; Wagner, N.J. Recent advances in blood rheology: A review. Soft Matter 2021, 17, 10591–10613. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Ji, C.; Avital, E.; Kaliviotis, E.; Munjiza, A.; Williams, J. An Investigation on the Aggregation and Rheodynamics of Human Red Blood Cells Using High Performance Computations. Scientifica 2017, 2017, 6524156. [Google Scholar] [CrossRef] [PubMed]


| Vessel Diameter (mm) | Blood Velocity u (m/s) | Strut Height h (m) | Ref. | ||
|---|---|---|---|---|---|
| 3.2 | 0.97 | 140 | 931 | 40.74 | [76] |
| 3.2 | 2.49 (exercise) | 140 | 2390 | 104.58 | [76] |
| 3.2 | 0.97 | 50 | 931 | 14.55 | [76] |
| 3.2 | 2.49 (exercise) | 50 | 2390 | 37.35 | [76] |
| 9.5 | 0.3125 | 890 | [77] | ||
| 3.03 | 0.31 | 100 | 282 | 9.3 | [78] |
| 3.03 | 0.533 (centerline) | 100 | 484 | 15.99 | [78] |
| 96 | [3] | ||||
| 2.6 | 0.16 | 100 | 124.8 | 4.8 | [79] |
| 8 | 0.25 | 122 | 600 | 9.15 | [80] |
| 8 | 0.3 (peak systolic) | 720 | [81] | ||
| 3.5 | 0.2 | 210 | [21] | ||
| 20 | 0.2 | 1200 | [82] | ||
| 0.45 | 150 | 20.25 | [19] | ||
| 2.7 | 150 | 121.5 | [19] |
| Reference | ||
|---|---|---|
| Adult valves | 5000–7600 | [44,84,85,86,87,88] |
| Pediatric valves | 1639–2454 | [89] |
| Parameter | Value |
|---|---|
| Housing (outer cylinder) radius | 25 mm |
| 1st inner rotor radius | 24.8 mm |
| 2nd inner rotor radius | 24.5 mm |
| 3rd inner rotor radius | 24.5 mm |
| Height of the shearing region | 10 mm |
| Operating speed range | 0 rpm–7000 rpm |
| Flow rate | 1 lt/min |
| range | 0–116 |
| range | 0–5.2 |
| range | 0–1200 |
| Volume for Stress Larger than 150 Pa (mm3) | 1000 rpm | 2000 rpm | 3000 rpm |
|---|---|---|---|
| 0.2 mm gap | 0.00 | 0.00 | 2.38 |
| 0.5 mm gap | 0.29 | 1.13 | 64.82 |
| 1.0 mm gap | 0.30 | 1.82 | 49.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Avital, E.J.; Imran, S.; Abbas, M.M.; Hinkle, P.; Alexander, T. Design Considerations and Flow Characteristics for Couette-Type Blood-Shear Devices. Fluids 2024, 9, 157. https://doi.org/10.3390/fluids9070157
Chen X, Avital EJ, Imran S, Abbas MM, Hinkle P, Alexander T. Design Considerations and Flow Characteristics for Couette-Type Blood-Shear Devices. Fluids. 2024; 9(7):157. https://doi.org/10.3390/fluids9070157
Chicago/Turabian StyleChen, Xingbang, Eldad J. Avital, Shahid Imran, Muhammad Mujtaba Abbas, Patrick Hinkle, and Theodosios Alexander. 2024. "Design Considerations and Flow Characteristics for Couette-Type Blood-Shear Devices" Fluids 9, no. 7: 157. https://doi.org/10.3390/fluids9070157
APA StyleChen, X., Avital, E. J., Imran, S., Abbas, M. M., Hinkle, P., & Alexander, T. (2024). Design Considerations and Flow Characteristics for Couette-Type Blood-Shear Devices. Fluids, 9(7), 157. https://doi.org/10.3390/fluids9070157








