Shedding of Cavitation Clouds in an Orifice Nozzle
Abstract
1. Introduction
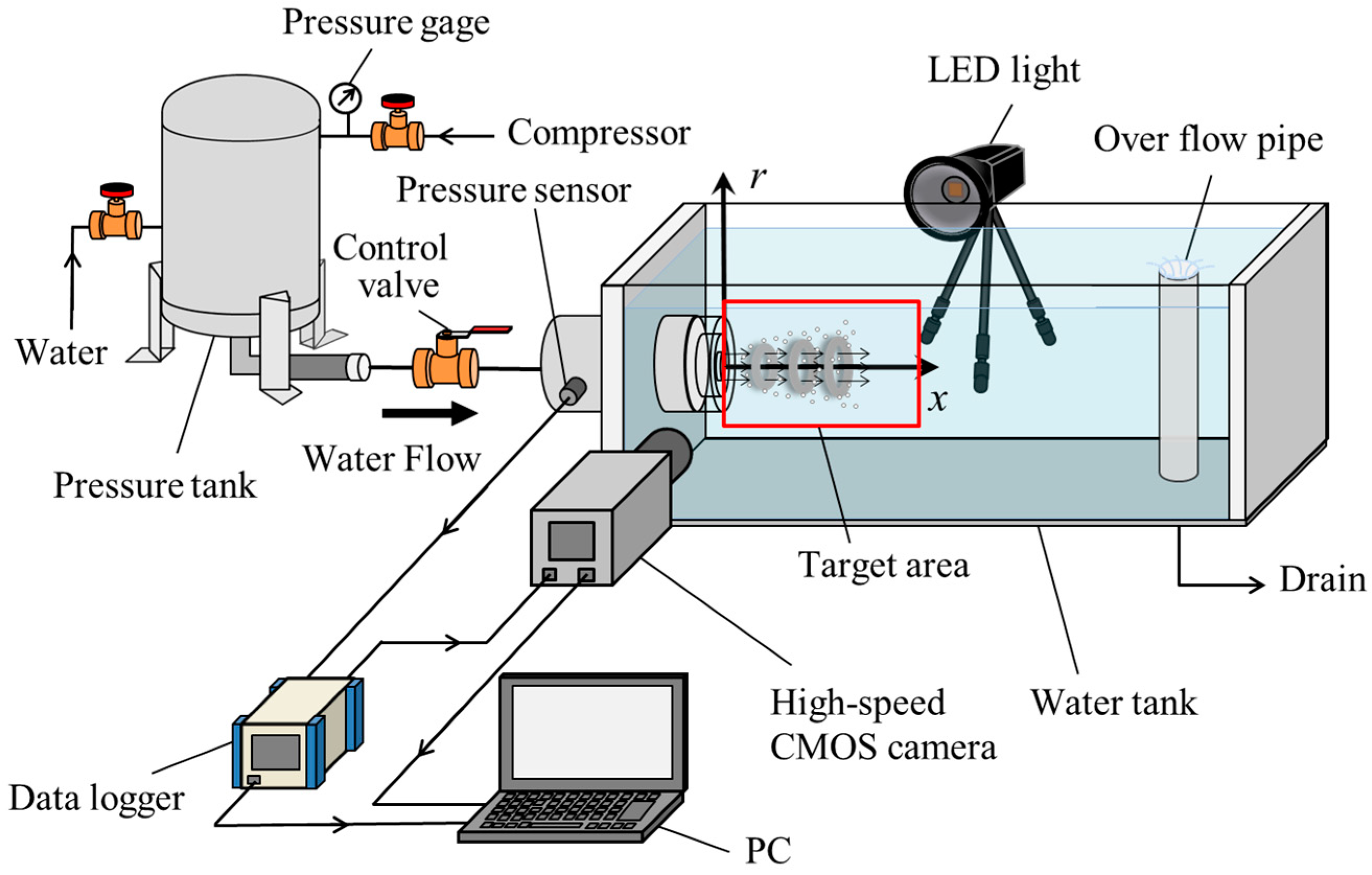
2. Experimental Apparatus and Method
3. Results and Discussions
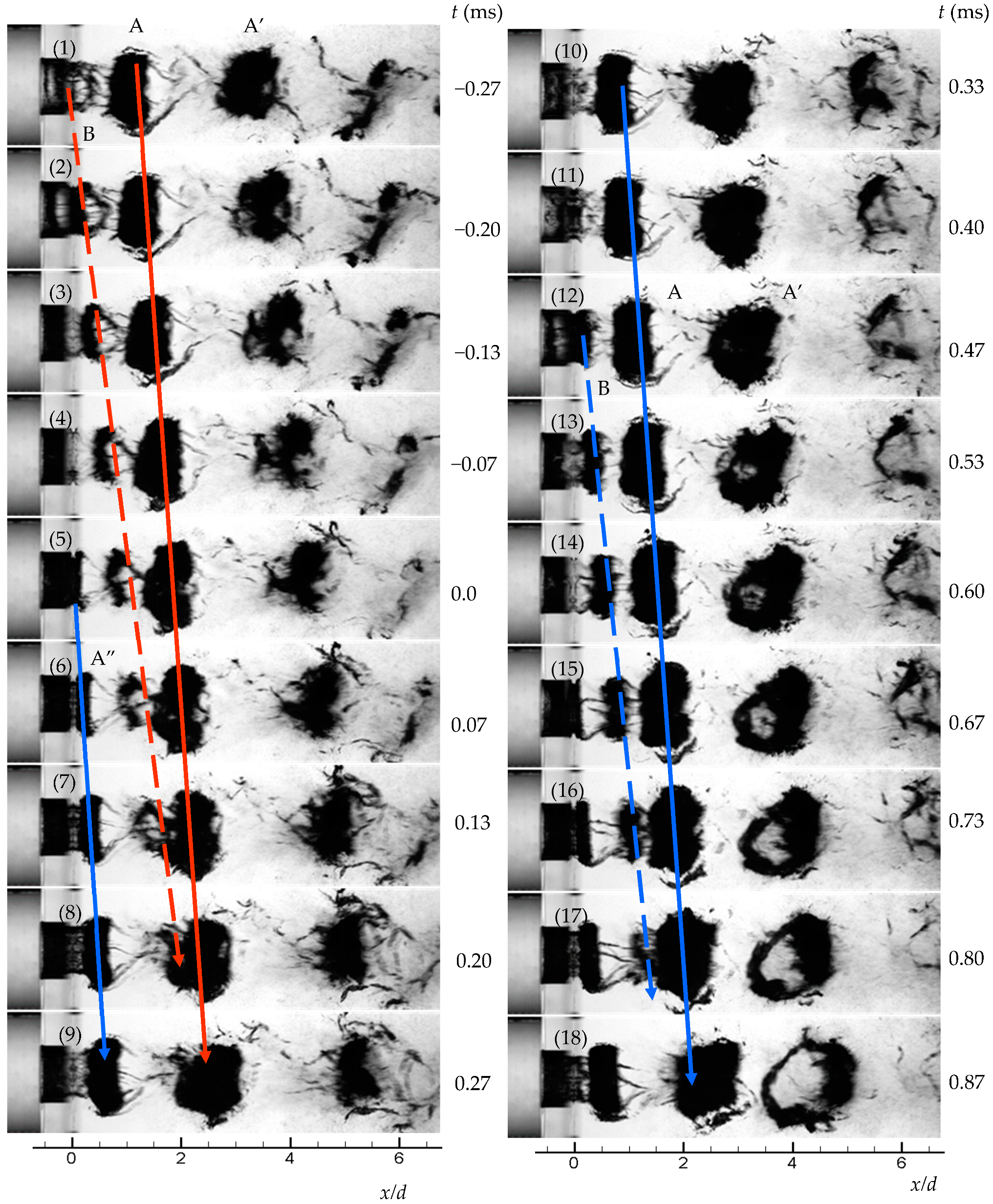
3.1. Instantaneous Flow Visualization
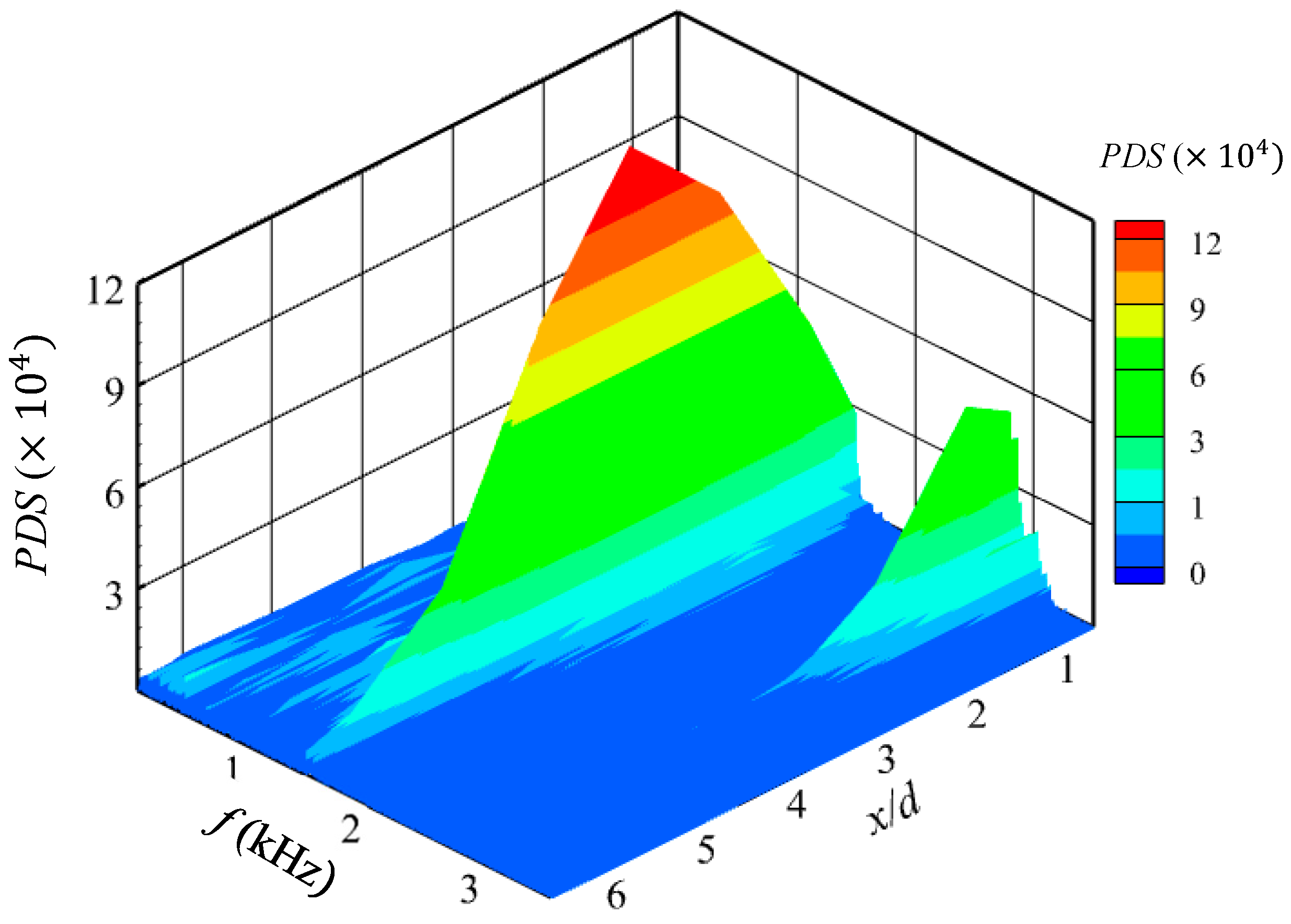
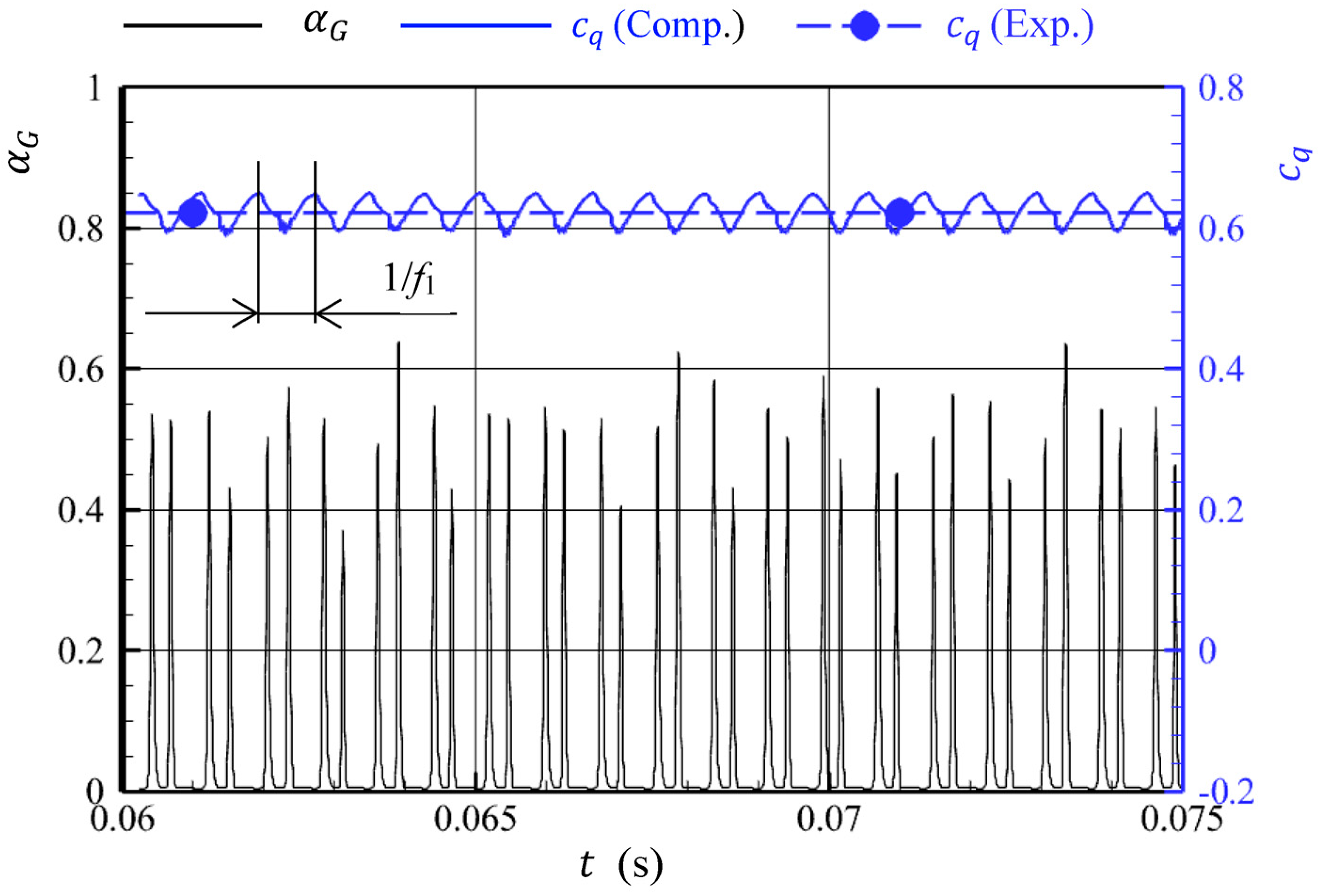
3.2. Periodicity of Cavitation Cloud Shedding
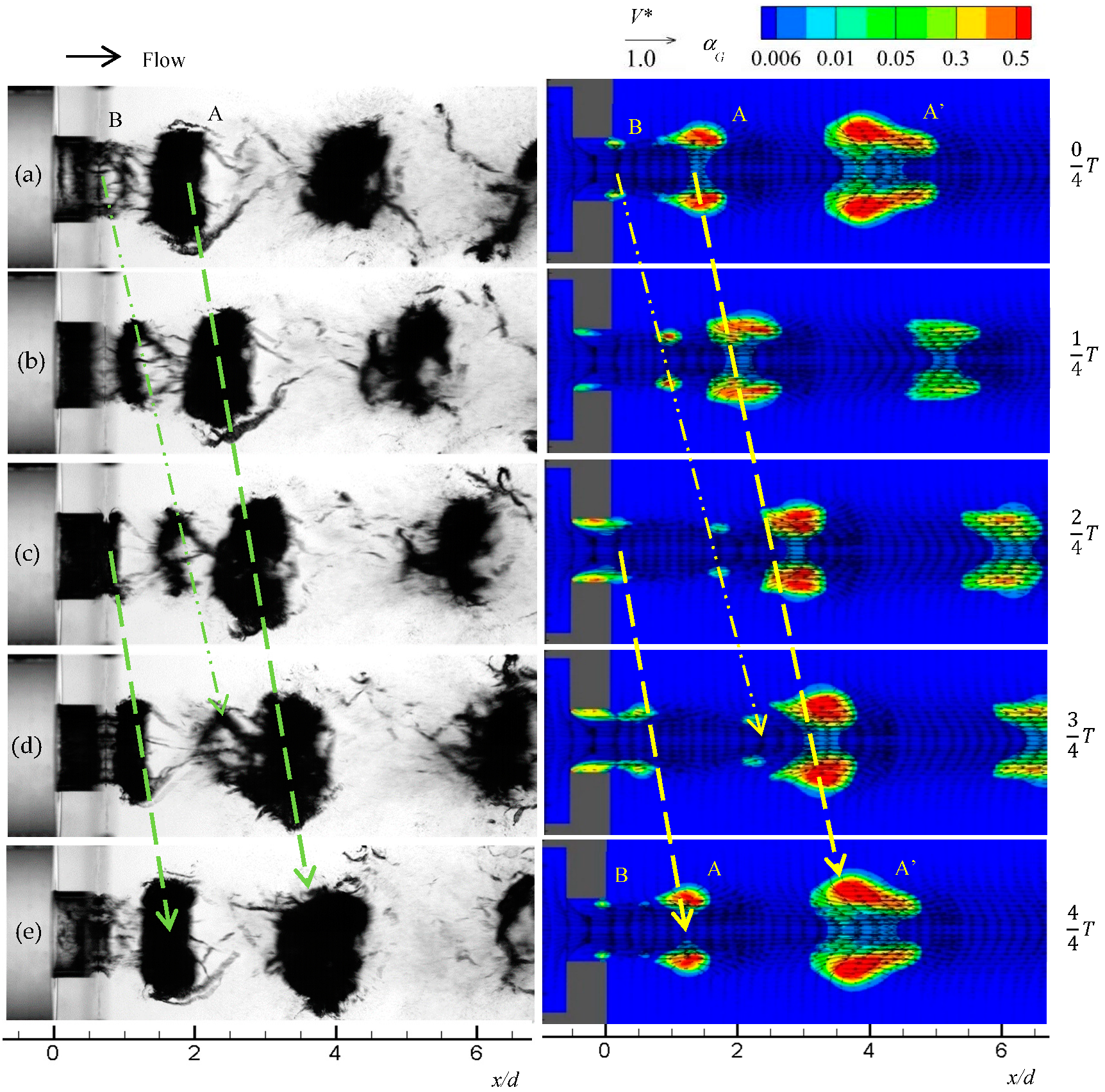
3.3. Mechanism of Cavitation Cloud Shedding
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Howell, J.; Ham, E.; Jung, S. Ultrasonic Bubble Cleaner as a Sustainable Solution. Fluids 2023, 8, 291. [Google Scholar] [CrossRef]
- Kalumuck, K.M.; Chahine, G.L. The use of cavitating jets to oxidize organic compounds in water. J. Fluids Eng. 2000, 122, 465–470. [Google Scholar] [CrossRef]
- Hutli, E.A.F.; Nedeljkovic, M.S.; Radovic, N.A.; Bonyár, A. The relation between the high speed submerged cavitating jet behaviour and the cavitation erosion process. Int. J. Multiph. Flow 2016, 83, 27–38. [Google Scholar] [CrossRef]
- Safaei, S.; Mehring, C. Effect of Dissolved Carbon Dioxide on Cavitation in a Circular Orifice. Fluids 2024, 9, 41. [Google Scholar] [CrossRef]
- Cui, Y.; Zhao, M.; Ding, Q.; Cheng, B. Study on Dynamic Evolution and Erosion Characteristics of Cavitation Clouds in Submerged Cavitating Water Jets. J. Mar. Sci. Eng. 2024, 12, 641. [Google Scholar] [CrossRef]
- Soyama, H. Cavitating jet: A review. Appl. Sci. 2020, 10, 7280. [Google Scholar] [CrossRef]
- Mohod, A.V.; Teixeira, A.C.S.C.; Bagal, M.V.; Gogate, P.R.; Giudici, R. Degradation of organic pollutants from wastewater using hydrodynamic cavitation: A review. J. Environ. Chem. Eng. 2023, 11, 109773. [Google Scholar] [CrossRef]
- Michael, M.; Wright, B.E.; Dropkin, A.; Truscott, T.T. Cavitation of a submerged jet. Exp. Fluids 2013, 54, 1541–1543. [Google Scholar]
- Peng, K.; Tian, S.; Li, G.; Huang, Z.; Zhang, Z. Cavitation in water jet under high ambient pressure conditions. Exp. Therm. Fluid Sci. 2017, 89, 9–18. [Google Scholar] [CrossRef]
- Peng, G.; Itou, T.; Oguma, Y.; Shimizu, S. Effect of ventilation on the velocity decay of cavitating submerged water jet. In Fluid-Structure-Sound Interactions and Control; Zhou, Y., Lucey, A.D., Liu, Y., Huang, L., Eds.; Springer: London, UK, 2018; Volume 9, pp. 93–98. [Google Scholar]
- Ullas, P.K.; Dhiman Chatterjee, S. Vengadesan; Experimental study on the effect of throat length in the dynamics of internal unsteady cavitating flow. Phys. Fluids 2023, 35, 023332. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, B.; Zhang, H.; Wu, Q.; Wang, G. Experimental investigation into fluid–structure interaction of cavitating flow. Phys. Fluids 2021, 33, 093307. [Google Scholar] [CrossRef]
- Huang, S.; Huang, J.; He, K. Research on Erosion Effect of Various Submerged Cavitating Jet Nozzles and Design of Self-Rotating Cleaning Device. Appl. Sci. 2024, 14, 1433. [Google Scholar] [CrossRef]
- Ge, M.; Manikkam, P.; Ghossein, J.; Subramanian, R.; Coutier-Delgosha, O.; Zhang, G. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254, 124426. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, G.; Petkovšek, M.; Kunpeng Long, K.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean. Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Hutli, E.A.F.; Nedeljkovic, M.S. Frequency in shedding/discharging cavitation clouds determined by visualization of a submerged cavitating jet. J. Fluids Eng. 2008, 130, 021304. [Google Scholar] [CrossRef]
- Franc, J.P.; Michel, J.M. Fundamentals of Cavitation; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 1–55. [Google Scholar]
- Podbevšek, D.; Petkovšek, M.; Ohl, C.D.; Dular, M. Kelvin-Helmholtz instability governs the cavitation cloud shedding in Venturi microchannel. Int. J. Multiph. Flow 2021, 142, 103700. [Google Scholar] [CrossRef]
- Peng, G.; Yang, C.; Oguma, Y.; Shimizu, S. Numerical analysis of cavitation cloud shedding in a submerged water. J. Hydrodyn. 2016, 28, 986–993. [Google Scholar] [CrossRef]
- Cruz-Ávila, M.; León-Ruiz, J.; Carvajal-Mariscal, I.; Klapp, J. CFD turbulence models assessment for the cavitation phenomenon in a rectangular profile Venturi tube. Fluids 2024, 9, 71. [Google Scholar] [CrossRef]
- Oishi, T.; Peng, Y.; Ji, H.; Peng, G. Numerical simulations of cavitating water jet by an improved cavitation model of compressible mixture flow with an emphasis on phase change effects. Phys. Fluids 2023, 35, 073333. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy-viscosity model for high Reynolds number turbulent flows—Model development and validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Peng, G.; Wakui, A.; Oguma, Y.; Shimizu, S.; Ji, H. Periodic behavior of cavitation cloud shedding in submerged water jets issuing from a sheathed pipe nozzle. J. Flow Control Meas. Vis. 2018, 6, 15–26. [Google Scholar] [CrossRef]
- Lin, Y.; Kadivar, E.; Moctar, O. Experimental study of the cavitation effects on hydrodynamic behavior of a circular cylinder at different cavitation regimes. Fluids 2023, 8, 162. [Google Scholar] [CrossRef]
- Nishimura, A.; Takakuwa, O.; Soyama, H. Similarity law on shedding frequency of cavitation cloud induced by a cavitating jet. J. Fluid Sci. Technol. 2012, 7, 405–420. [Google Scholar] [CrossRef][Green Version]
- Liu, H.; Kang, C.; Zhang, W.; Zhang, T. Flow structures and cavitation in submerged waterjet at high jet pressure. Exp. Therm. Fluid Sci. 2017, 88, 504–512. [Google Scholar] [CrossRef]
- Liu, B.; Pan, Y.; Ma, F. Pulse pressure loading and erosion pattern of cavitating jet. Eng. Appl. Comput. Fluid Mech. 2019, 14, 136–150. [Google Scholar] [CrossRef]
- Nurick, W.H. Orifice cavitation and its effect on spray mixing. J. Fluids Eng. 1976, 98, 681–687. [Google Scholar] [CrossRef]

| (MPa) | (m/s) | ) | (s−1) | (s−1) | ||
|---|---|---|---|---|---|---|
| 0.3 | 20.3 | 0.7 | 1161 | 0.29 | 2322 | 0.57 |
| 0.4 | 24.9 | 0.8 | 1443 | 0.29 | 2856 | 0.57 |
| 0.5 | 28.6 | 0.9 | 1373 | 0.24 | 2725 | 0.48 |
| 0.6 | 32.0 | 1.0 | 1483 | 0.23 | 2791 | 0.44 |
| 0.7 | 35.0 | 1.1 | 1545 | 0.22 | 3076 | 0.44 |
| 0.8 | 37.8 | 1.2 | 1571 | 0.21 | 3124 | 0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onishi, T.; Li, K.; Ji, H.; Peng, G. Shedding of Cavitation Clouds in an Orifice Nozzle. Fluids 2024, 9, 156. https://doi.org/10.3390/fluids9070156
Onishi T, Li K, Ji H, Peng G. Shedding of Cavitation Clouds in an Orifice Nozzle. Fluids. 2024; 9(7):156. https://doi.org/10.3390/fluids9070156
Chicago/Turabian StyleOnishi, Taihei, Kaizheng Li, Hong Ji, and Guoyi Peng. 2024. "Shedding of Cavitation Clouds in an Orifice Nozzle" Fluids 9, no. 7: 156. https://doi.org/10.3390/fluids9070156
APA StyleOnishi, T., Li, K., Ji, H., & Peng, G. (2024). Shedding of Cavitation Clouds in an Orifice Nozzle. Fluids, 9(7), 156. https://doi.org/10.3390/fluids9070156







