CFD Analysis of Ultra-High-Performance Concrete Rheological Tests

Abstract

This study connects and compares the results from two different rheological measurement techniques, namely, the slump test and rotational rheometry, on UHPC (Ultra-High-Performance Concrete) through the use of commercially available numerical simulation software ANSYS Fluent 2022 R2. The workability and resulting mechanical properties of the UHPC (a material used in construction) are highly dependent on its rheology and, hence, also on the composition and level of homogeneity of the assessed mixture. It is generally understood that the most suitable rheological model for concrete mixtures is the Hershel–Bulkley model. However, obtaining reliable rheological data is complicated as the wide-gap rotational rheometers developed for concrete show bias in their measurements even on precise laboratory equipment, while common industrial tests, such as the slump test, do not produce the usual shear rate–shear stress relation and, hence, do not allow for more complex analysis. Recently, a new methodology for the rheological measurement of non-Newtonian fluids that utilises a simple power input–rotation speed measurement was published. However, in this study, only model liquids were evaluated, and the method was not validated for more complex fluids such as pastes. Therefore, it was the goal of this study to show this method’s suitability for fine pastes through a comparison with the slump test, using numerical simulation.

1. Introduction

Obtaining precise information on the rheological properties of a UHPC mixture is important for the construction industry, as it affects the workability, consistency, and plasticity of the mixture [1] and the final mechanical properties of the concrete structure [2]. It is well-documented that UHPC can be differentiated into two groups according to the level of yield stress. The first group is characterised by Newtonian or pseudoplastic characteristics with an indistinct yield stress, and the second group is represented by mixtures exhibiting nonlinear characteristics with significant yield stress [3]. Hence, models that can describe such behaviour, such as the Bingham (1) [4,5,6] or Herschel–Bulkley (HB) (2) model [4,6,7], are often used. However, the three-parameter HB model is often too complex, as the yield stress can be insignificantly small; hence, a simpler Power Law (PL) model can be used instead (3) [3]. However, such a simplification may not be suitable for the slow low-shear-stress flows that are often seen in construction.

$$\tau ={\tau }_0+\eta \dot{\gamma }$$

(1)

$$\tau ={\tau }_0+K{\dot{\gamma }}^n$$

(2)

$$\tau =C{\dot{\gamma }}^n,$$

(3)

Here, K is the flow consistency index of the HB model (Pa/s), n is the flow behaviour index (−), γ is the shear rate (1/s), η is the apparent viscosity (Pa·s), τ is the shear stress (Pa), and τ₀ is the yield shear stress (Pa), which are valid only for positive values of the shear rate.

These models are also utilised in the numerical simulation of concrete flow [4,8,9,10], as they are already implemented in the most common commercial CFD solvers such as Ansys Fluent, OpenFoam, or STAR-CCM+. However, it is difficult to obtain precise rheological data, as none of the regularly used methods are superior to the others; all display a weakness. For example, one of the common methods used in mortar testing is the so-called slump test. Its simplistic nature allows for a swift assessment of the mixture, and it is thus suitable for infield testing. Its main disadvantage, however, is its one-factor nature, as it only provides information related to the yield stress [11]; this is only one term in the viscosity models generally used for the description of UHPC. Thus, it produces only limited insights into the fluid behaviour. To obtain data for more complex rheological models, a different measurement method must be adopted. One of the most common methods used to measure viscosity is rotational rheometry. Although versatile, it often requires laboratory equipment and is thus far less practical. Moreover, the traditional Narrow-Gap Couette geometry defined by DIN EN ISO 3219 [12] is unsuitable for suspensions with large or dense particles due to sedimentation, wall slip, and small differences between the diameter of the particle and the size of the gap. To overcome these problems, a measurement method that utilises the power input characteristics in the creep region of a known agitator with the Metzner–Otto relation [13] between the effective shear rate and rotation speed for non-Newtonian fluids was suggested by Dostál et al. [3]. A similar methodology is often used to measure the viscosity of more complex systems utilising screw agitators [3], helical ribbons [14,15], or anchor agitators [16,17]. The weakness of these methods is hidden in the imprecise nature of the agitator constants, which may vary between agitators of the same type due to imperfections during manufacture, measurement errors, and their intertwined nature. For screw agitators, the Metzner–Otto constant k can vary between 16.82 [18] and 77 [19]; for helical ribbons, it varies between 16.1 [20] and 38 [21]; and for anchor agitators, it varies between 25 and 30 [22]. However, these imprecisions have a significant effect on the results of the viscosity measurements. The validation of these measurements is usually performed through a comparison with model fluids that are Newtonian and non-Newtonian in character and have known rheological properties. These could be defined either by the manufacturer or set on a different rheometer with a suitable geometry (usually a narrow gap or cone and plane). This methodology is still applicable for suspensions with a very small particle size (substantially smaller than the measurement geometry), but it fails when used for suspensions with large aggregates such as concrete [23]. To allow for larger aggregates, a different geometry with a wider gap must be adopted, which is, in principal, similar to the method presented by Dostal et al. [3]. Such designs, however, are rarely adopted in industry, where a simple slump test is still preferred [23]. Moreover, complex fluid behaviours such as thixotropy or particle settlement may also influence the measurement results [24]. For these reasons, it is important to determine whether the coefficients of the viscosity models gained through the method of Dostal et al. [3] adequately describe the behaviour of the real mixture. For this purpose, we adopted a method similar to that used by other researchers [4,8,9]; through a comparison of the experimental and numerical simulations of a slump test, we tested whether the rheological parameters produced by Dostal et al. [3] replicate a similar concrete spread.

2. Materials and Methods

The methodology of the rheological experiments, the data, and their evaluation were previously published by Dostal et al. [3]. The parameters of the various rheological experiments on which the numerical comparison is based are presented in

Table 1. Rheological parameters of various UHPC mixtures published by [3].

Mixture	K (Pa sn)	n (−)	τ0 (Pa)	TS0 (mm)
Mixture 1	138.3	0.839	13.4	240 × 240
	152.9	0.782
Mixture 2	34	0.89	1.5	310 × 310
	35.53	0.864
Mixture 3	91.8	1.027	14.7	230 × 240
	95.3	1	12.3

Source: data published by [3]. Note: K—flow consistency index of HB model, n—flow behaviour index, τ₀—yield shear stress, T_S0—initial size of the spilled concrete. The precision of the experimental spread is about ±5 mm.

. Their measurement was performed according to EN 12350-8 [25]. A cone with defined internal dimensions according to EN 1015-3 [26] (illustrated in Figure 1) was placed on a clean wetted surface, filled with concrete mixture, and quickly lifted. This enabled the spreading of concrete over time to the surrounding volume, creating a roughly circular spillage with outer diameter d. The diameter of the spillage was measured over time with time intervals depending on the properties of the mixture. In the case of Dostal et al. [3], these measurements were conducted at 120 s, 600 s, and 1500 s. Only the mixtures for which all data were available were used, as they seemed more reliable. The CFD (computational fluid dynamics) simulation was performed in ANSYS Fluent 2022 R2. As it is hard to numerically incorporate the divergence of the viscosity to infinity at values of shear stress below the yield stress, Fluent 2022 R2 utilises the bi-viscous model first published by Tanner and Milthorpeta [27]; as the name suggests, it utilises two viscosity slopes, where one is substantially steeper than the other. According to the Fluent User’s Guide, these apparent viscosities are defined by Functions (4) and (5).

$$\eta =\frac{{\tau }_0}{\dot{\gamma }}+K{\dot{\gamma }}^{n-1}\mathrm{for}\dot{\gamma }>{\dot{\gamma }}_C$$

(4)

$$\eta =\frac{{\tau }_0\left(2-\frac{\dot{\gamma }}{{\dot{\gamma }}_C}\right)}{{\dot{\gamma }}_C}+K{\dot{\gamma }}^{n-1}\left[\left(2-n\right)+\left(n-1\right)\frac{\dot{\gamma }}{{\dot{\gamma }}_C}\right]$$

(5)

To fulfil the condition of τ₀, the value of γ_C was chosen as 0.001 s⁻¹, which was deemed sufficiently close to 0 without triggering the divergence to infinity problem. The geometry of the initial volume was the same as the inside of the small Hägermann cone defined by EN 1015-3 and is illustrated along with measured dimensions in Figure 1.

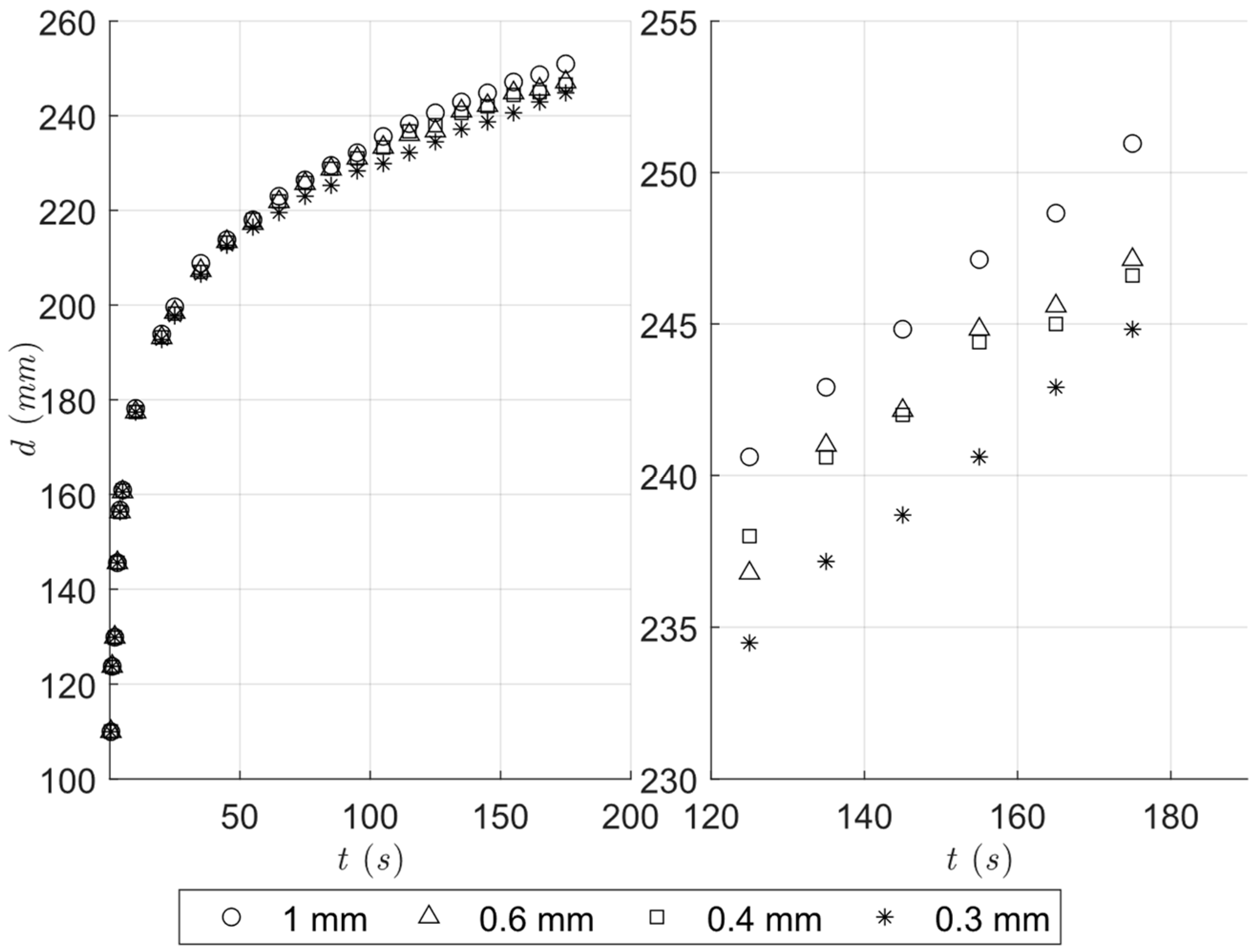
The axisymmetric nature of the problem was utilised to save time and energy. Therefore, the simulated geometry was a 2D axisymmetric slice composed of the mortar volume and air. The effect of the cone movement was also neglected, as its effect was deemed insignificant, and it would not necessarily replicate the experiment. For this geometry, a 2D mesh was created in Ansys Meshing with Physics Preference CFD and Solver Preference Fluent. To obtain a more uniform, better-quality mesh, Mapped Face Meshing was applied to the 2 faces using the quadrilateral mesh method. A default growth rate of 1.2 was used, with the default curvature capture enabled. The mesh quality was evaluated primarily using the skewness metric with the target skewness set to 0.5. The tested element sizes were 1 mm, 0.6 mm, 0.4 mm, and 0.3 mm. All the created meshes reached very similar quality. The worst quality was reached with the 0.6 mm element size mesh with a maximum skewness of 0.186 and an average of 0.071. This quality is well within the recommended interval for the 2D Fluent solver, which is defined in the User Manual. A quality 2D mesh has a skewness value of 0.1 and should not reach values above 0.5. Other mesh metrics were within the desired values with a minimal orthogonal quality of 0.96 and highest aspect ratio of 1.26. The comparison of the speed of the concrete spread, depending on the different mesh element sizes, is presented in Figure 2. It is apparent from the figure that the mesh size did not significantly affect the spread speed, as the curves are relatively close together. However, as the mesh sensitivity, due to the high computational time, was evaluated only on Mixture 1 and only with the Power Law model, for the main bulk of the simulations, a relatively fine mesh size of 0.4 mm was used to reduce the probability of it significantly affecting the precision of the results. The meshed geometry with different regions and boundary conditions is presented in Figure 3.

The simulation was set up as a 2D Axisymmetric Multiphase Transient problem with a gravitational acceleration of 9.81 m/s² in the direction of the axis. Fluent 2022 R2 standardly solves the conservation of mass (6) and momentum (7) and (8) equations. The 2D Axisymmetric problem is therefore defined by the following set of 3 main equations:

$$\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x}\left(\rho v_x\right)+\frac{\partial }{\partial r}\left(\rho v_r\right)+\frac{\rho v_r}{r}=S_m$$

(6)

$$\begin{gathered} \frac{\partial }{\partial t}\left(\rho v_x\right)+\frac{1}{r}\frac{\partial }{\partial x}\left(r\rho v_x{v}_x\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r\rho v_r{v}_x\right)=-\frac{\partial p}{\partial x} \\ +\frac{1}{r}\frac{\partial }{\partial x}\left[r\eta \left(2\frac{\partial v_x}{\partial x}-\frac{2}{3}\left(\nabla ·\overrightarrow{v}\right)\right)\right] \\ +\frac{1}{r}\frac{\partial }{\partial r}\left[r\eta \left(\frac{\partial v_x}{\partial r}+\frac{\partial v_r}{\partial x}\right)\right]+F_x \end{gathered}$$

(7)

$$\begin{gathered} \frac{\partial }{\partial t}\left(\rho v_r\right)+\frac{1}{r}\frac{\partial }{\partial x}\left(r\rho v_x{v}_r\right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r\rho v_r{v}_r\right)=-\frac{\partial p}{\partial r} \\ +\frac{1}{r}\frac{\partial }{\partial x}\left[r\eta \left(\frac{\partial v_r}{\partial x}+\frac{\partial v_x}{\partial r}\right)\right] \\ +\frac{1}{r}\frac{\partial }{\partial r}\left[r\eta \left(2\frac{\partial v_r}{\partial r}-\frac{2}{3}\left(\nabla ·\overrightarrow{v}\right)\right)\right] \\ -2\eta \frac{V_r}{r^2}+\frac{2}{3}\frac{\eta }{r}\left(\nabla ·\overrightarrow{v}\right)+\rho \frac{v_x^2}{r}+F_r, \end{gathered}$$

(8)

Here, $\nabla ·\overrightarrow{v}=\frac{\partial v_x}{\partial x}+\frac{\partial v_r}{\partial r}+\frac{V_r}{r}$; ρ is the density of the fluid; t is the time; x and r are the axial and radial coordinates, respectively; v_i is the velocity in the direction of subscript i; S_m is a mass source (here, 0); F_x is the momentum source term in the axial direction (here, g·ρ, where g is the gravitational acceleration); and F_r is the momentum source term in the radial direction (here, 0).

As a multiphase model, the Euler–Euler type Volume of Fluid (VOF) was selected, as the system comprises two immiscible fluids with a clearly defined boundary between the two. The explicit version of this model was selected due to its suitability for fluids with large differences in density [4], better precision, and suitability for transient problems as per the Fluent User Guide, with the default settings, sharp interface, and 2 Eulerian phases, with no phase interaction. As the model introduces additional unknown variables, namely, the volume fraction of one or more phases α_q, the set of equations must be expanded by f − 1 equations, where f is the number of phases. The Fluent 2022 R2 utilises the time-dependent explicit formulation defined in Equation (9).

$$\frac{{\alpha }_q^{n+1}{\rho }_q^{n+1}-{\alpha }_q^n{\rho }_q^n}{∆t}V+{\sum }_f\left({\rho }_q{U}_f^n{\alpha }_{q,f}^n\right)=\left[{\sum }_{p=1}^n\left({\dot{m}}_{pq}-{\dot{m}}_{qp}\right)+S_{{\alpha }_q}\right]V,$$

(9)

Here, n is the previous time step index, q is the index of the solved phase, p is the index of another phase, α_q,f is the volume fraction of the qth phase on face f, U_f is the volume flux through face f, ṁ_qp is the mass transfer from phase q to phase p, S_α is the source term of phase q (in our case, 0), and V is the volume of the cell.

For fluids, the default air model and the user-defined concrete model with the viscosity model parameters from Table 1 were used. Initially, the effect of the different viscosity models was tested. For this simulation, Mixture 1 was selected, as it displayed high yield stress and had data available for both the HB and PL models.

When compared, there seemed to be a small difference between the precision of the two models, as both were within a reasonable error margin from the experimental results. Therefore, the simpler PL model was used for the subsequent simulation of Mixture 2. For all simulations, a pressure-based solver was selected with the laminar viscous model. This model was chosen based on the observation of the real experiment, during which the highest spread speed was around 1.75 mm/s. Combined with the expected apparent viscosity, it was reasonable to assume that the case would be laminar. The boundary conditions of the model were selected as follows: the axis boundary condition on the axis of the mortar to allow an axisymmetric approach, an internal boundary on the interface between the initial concrete volume and the air volume, the outlet boundary condition on the top of the box with allowed back flow, and a wall boundary with no slip condition and no roughness assigned on the remaining two sides of the box. The no roughness option was chosen, as it corresponds to the initial state of the test plate, which is commonly oiled/watered before the beginning of the slump test. The solution used the standard SIMPLE method due to its robustness when compared to SIMPLEC and its suitability for multiphase problems. The default settings of the method were used with the default controls. All residual monitors were increased to 1 × 10⁻⁵ for higher accuracy. The computation was standardly initialised and subsequently patched to correspond to the initial state of the experiment in terms of the initial volume fractions in the various regions. Initially, shorter time steps were tried, as the fluid was expected to cross a cell every 0.2 s. However, during the initial decomposition of the cone, faster movement must have occurred, as the method diverged during the first simulated second with time steps lower than 0.001 s. To be on the safe side, the final time step of 0.0001 s was used for all simulations with a maximum of 50 iterations per time step. The total number of time steps was set to 1,800,000, resulting in 180 s of simulation. However, to test how much the change in time step affected the precision of the simulation, a test run with a 0.001 time step was also performed with Mixture 1. The usual time delay between the start of the experiment and the first experimental measurement was approximately 120 s [3]. An additional 60 s was added to see how the trend further evolved and to enable extrapolation to the 10 and 25 min experimental measurements. During these timescales, curing of the mixture should not have affected its viscosity, and therefore, a similar trend should have been preserved. The simulation progress was evaluated using CFDPost with a varying time increment. Progress was visually analysed using the concentration contour with 3 contours and the zebra colour palette. This setting allowed for a simple evaluation of the spread distance using the Microsoft PowerToys v0.76.0 utility. The number of pixels between the axel and the farthest point of the contour was measured at the set time interval using the measurement tool. The value was then rescaled using the known initial distance between the axel and the base of the cone. An illustration of this process is presented in Figure 4.

3. Results and Discussion

Initially, apart from the mesh size, the influence of the rheological model and of the time step were explored. These simulations of Mixture 1 are presented in Figure 5. In this figure, the imprecision of the experimental results, presented by Dostál et al. at around ±5 mm, is represented by the larger than usual symbol. From these results, it is apparent that the simulation with the PL model tends to be more optimistic, resulting in a faster spread after the initial cone decomposition, while the simulation with the HB model has a slightly faster spread at the beginning but then slows down. The probable cause is the lower apparent viscosity of the HB model during the initial cone decomposition, as the shear stress needs to be substantially high for the yield stress to significantly affect the flow. This changes after the subsequent slowdown, where the yield stress is thought to have a major influence on the flow. However, it is hard to assess from these simulations which model is better suited, as both were within the 10% error margin of the experimentally measured data. To determine how the system evolved at longer spread times, the data were fit with a simple logarithmic model.

The resulting extrapolations seem to correspond well with the simulated results and are reasonably close to the 10 and 25 min experimental measurements but may only be used as an illustration of the supposed trend. We are of the opinion that further slowdown would occur if the length of the simulation was expanded. However, we are unsure how well would this be represented by the Power Law model due to its lack of yield shear stress, which, along with surface tension, is supposed to have the greatest effect [6]. Thus, from a computational point of view, it is better to use the less-demanding PL model for faster computation. Regarding the effect of the time step size, the results were close between the two settings, suggesting that a larger time step may be used, as it allows for swifter calculations with a negligible difference in precision.

As the convergence is limited by the time step during the initial few seconds where the swift cone decomposition occurs, it is reasonable to assume that through the adaptive time step, which would allow for larger time steps in the subsequent slower spread, the simulation may be expedited.

Subsequently, other mixtures were tested. Their simulated spread is presented in Figure 6, Figure 7 and Figure 8 with a 10% error interval (dotted line). Similar to that in Figure 5, the error of the experimental method is represented by the larger than usual symbol. These figures show that the experimental results are within the error margin of the simulated spreads, thus showing that the simulation methodology is replicable. Such results show that the simulation successfully predicts the expected behaviour of the UHCP mixture when provided with the correct rheological models. Thus, it connects the two completely independent techniques for the rheological evaluation of concrete mixtures and demonstrates that the new rheological measurement method proposed by Dostál et al. [3] is also suitable for fine-grained suspensions, such as UHCP mixtures. This methodology is an improvement over the current method published by [4], which only estimates rheological behaviour based on spread results. All the presented results are available in data form in Table S1 in Supplementary Materials.

The spread speed of Mixtures 1 and 3 is nearly identical, although their model constants suggest different behaviour (as is apparent from Table 1). This would suggest that pure simulations of concrete spread are insufficient for the correlation of the model constants for our UHPC concretes, which spread very slowly, as suggested by Choi et al. [4] or Shien and Kim [8], as one spread curve could be described by multiple rheological models. This may be further exacerbated by the usually utilised short simulation time (10–20 s), where differences between models may not arise, especially for mixtures displaying high yield shear stress. Here, the simple solution of extending the simulation time seems too computationally expensive, as similar results can be obtained through experimental work, as shown by numerous authors [6,28,29].

Finally, faster computing methods that can utilise GPU computation such as Lattice–Boltzmann or discrete element methods should be considered, especially for the simulation of fibre-reinforced concrete, where the behaviour of the fluid is strongly influenced by the fibres and aggregates [30,31,32].

4. Conclusions

It was shown in a previous publication by Dostál et al. [3] that the rheological properties of simple non-Newtonian fluids can be successfully explored using the measurement of the power input and the rotation speed of standard agitators. However, there was doubt about its suitability for more complex systems, such as suspensions and pastes. This study shows the suitability of their methodology for more complex non-Newtonian materials represented here by fine-grained suspensions of UHPC.

This study further shows that numerical simulation can be successfully used to compare and validate independent rheological measurements. Comparative simulations of the proposed models show that the PL model may be used instead of the HB model with similar imprecision. The main difference between the models seems to occur in the latter spreading of the concrete after the initial decline (after the first 5 to 10 s). In this second period, the effect of the yield stress seems to be significant, as it restricts the flow, resulting in a slower spread of the concrete. Therefore, the HB model seems to provide more pessimistic results, while the PL model is more optimistic. However, overall, the rheological models seem to favour a more pessimistic view, as the simulated spreads were generally slower than the one measured experimentally. Thus, it is recommended, if suitable, to use the Power Law model, as its simpler nature allows for substantially faster computation and is more on the optimistic side. The HB model should be used either when the fluid displays significant yield stress (higher than the tested mixtures) or when the flow is very slow with low values of shear stress. Other significant savings may be found in the adoption of the adaptive time step, as small time steps are only necessary during the first few seconds of the simulation, while larger time steps may be used during the latter stages of simulation. This result also suggests that the often-utilised validation simulations of the Hägermann cone, which are shorter than 15 s, may display false positivity for UHPC mixtures with a long spread time, as some of the parameters of the viscosity model significantly influence the flow in latter stages of the cone decomposition. Additionally, it was shown that rotational rheology, which utilises well-described agitators, may be adapted for the measurement of the rheological properties of UHPC mixtures to a reasonable degree of accuracy. The main benefit of this measurement method is its suitability for suspensions containing large particles, such as sand or reinforcing fibres, which prohibit the use of the traditional narrow-gap Couette geometry found on the most common rotational rheometers. Therefore, it enables the study of these more complex suspensions, which would allow for the better design of equipment and work procedures, which could subsequently facilitate the better distribution of the reinforcement fibres and, thus, better mechanical properties of the cured concrete.