Abstract
We review and extend the theory of ideal, homogeneous, incompressible, magnetohydrodynamic (MHD) turbulence. The theory contains a solution to the ‘dynamo problem’, i.e., the problem of determining how a planetary or stellar body produces a global dipole magnetic field. We extend the theory to the case of ideal MHD turbulence with a mean magnetic field that is aligned with a rotation axis. The existing theory is also extended by developing the thermodynamics of ideal MHD turbulence based on entropy. A mathematical model is created by Fourier transforming the MHD equations and dynamical variables, resulting in a dynamical system consisting of the independent Fourier coefficients of the velocity and magnetic fields. This dynamical system has a large but finite-dimensional phase space in which the phase flow is divergenceless in the ideal case. There may be several constants of the motion, in addition to energy, which depend on the presence, or lack thereof, of a mean magnetic field or system rotation or both imposed on the magnetofluid; this leads to five different cases of MHD turbulence that must be considered. The constants of the motion (ideal invariants)—the most important being energy and magnetic helicity—are used to construct canonical probability densities and partition functions that enable ensemble predictions to be made. These predictions are compared with time averages from numerical simulations to test whether or not the system is ergodic. In the cases most pertinent to planets and stars, nonergodicity is observed at the largest length-scales and occurs when the components of the dipole field become quasi-stationary and dipole energy is directly proportional to magnetic helicity. This nonergodicity is evident in the thermodynamics, while dipole alignment with a rotation axis may be seen as the result of dynamical symmetry breaking, i.e., ‘broken ergodicity’. The relevance of ideal theoretical results to real (forced, dissipative) MHD turbulence is shown through numerical simulation. Again, an important result is a statistical solution of the ‘dynamo problem’.
1. Introduction
Our purpose here is to review the statistical mechanics of ideal, homogeneous magnetohydrodynamic (MHD) turbulence and to show how this leads to a solution to the so-called dynamo problem. We also develop new theoretical results in the case of a turbulent magnetofluid in which the rotation axis and mean magnetic field are parallel. Numerical simulation will be used to verify the theory of ideal MHD turbulence and to show how these results apply to real, i.e., forced and dissipative, MHD turbulence.
Planets and stars generally rotate and possess a strong, quasi-stationary, mostly dipole magnetic field, i.e., a magnetic coherent structure. Over a hundred years ago, it was conjectured that internal magnetic fields coupled to fluid motions within the Sun and the Earth were responsible for creating and maintaining their respective global magnetic dipole fields [1]. Deducing the mechanism for this came to be called the ‘dynamo problem’. A heat flux from deep inside induces MHD turbulence in planetary liquid cores and stellar interiors and because of their large size, the flow has high Reynolds number and is convectively forced. If such planets and stars are stable for long periods of time, their interiors, where their global magnetic fields originate, are in states of quasi-equilibrium with statistical characteristics that have become quasi-stationary, which warrants the application of statistical mechanics, as we will do here. These relatively stable interiors may be contrasted to coronal mass ejections, for example, whose transient nature, if it evolves too quickly, may not allow equilibrium statistical mechanics to be applied in a global sense.
Almost seventy years ago, it was recognized that for ‘the dynamo problem, that is …the problem of generating and maintaining magnetic fields which draw their energy from the mechanical energy of the fluid, the nonlinear character of the equations is altogether essential’, as it produces ‘turbulence, the most conspicuous of the nonlinear phenomena of fluid dynamics’ [2]. More recently, numerical simulations of the geodynamo [3,4,5] established that MHD processes within the Earth’s liquid core were capable of creating a magnetic field similar to the actual geomagnetic field, including reversals of the dominant dipole component. There have been many laboratory experiments [6,7] also and some have shown the growth of self-generated magnetic fields, i.e., dynamo action [8,9,10].
Even though computer codes based on the MHD equations have been successful in simulating the geodynamo, and various experiments have shown a dynamo effect, the fundamental MHD origin of a quasi-steady, dominant, geomagnetic dipole field remained a theoretical mystery [11]—the so-called ‘dynamo problem’. There have been several approaches over the years to solve this mystery—that it is purely due to rotation [12]—many, many unsuccessful attempts to find a kinematic dynamo theory [13,14,15,16,17,18,19,20,21,22,23], and mean-field-electrodynamics (MFE) [24,25,26], but MFE is non-viable because it is essentially a circular argument [27]. It has long been acknowledged [2,28,29,30,31,32] that turbulence is a factor in dynamo action but the focus was usually on the small-scales of turbulence and the connection with a largest-scale magnetic field was not really understood. We believe that a true understanding of how turbulence is connected to dynamo action lies in the statistical theory of MHD turbulence, the details of which will be reviewed here.
To a high order of accuracy, the regions inside planets and stars that contain turbulent magnetofluid can be modeled as spherical shells. Since planetary and stellar Reynolds numbers are large, we can initially consider the magnetofluid to be ideal, i.e., without dissipation, although we can add viscosity and magnetic diffusivity later to test the applicability of ideal theory to reality. We will treat the magnetofluid as incompressible, as is commonly the case in geodynamo simulations [3,4,5]. This assumes, of course, that changes in fluid density do not significantly affect the magnetic field evolution equation (except through transport coefficients, which are absent in the ideal case) and it is the dynamic magnetic field that is of primary interest here.
Various boundary conditions (b.c.s) exist and can be applied to a spherical shell but these are of secondary importance in the ideal case. In the case of the geodynamo, it is not even clear what the outer core boundaries actually look like [33]. In previous analysis of ideal MHD turbulence in a spherical shell [34], normal components of both velocity and magnetic field were assumed to be zero on the boundaries. Velocity and magnetic fields were expanded in terms of spherical Bessel functions and spherical harmonics. These expansions involved so-called Chandrasekhar-Kendall (C-K) eigenfunctions [35], which have been used for analysis [36], as well as for numerical simulations of MHD turbulence [37,38], although these simulations were, and still are, of very low resolution. Rather than boundary conditions, which are uncertain, our primary focus is on turbulence and, in particular, on its statistical description.
As it turns out, ideal MHD turbulence statistical mechanics takes essentially the same form in spherical shell models as it does in a model magnetofluid that is contained in a periodic box (where velocity and magnetic fields are represented by Fourier series and there are no boundaries) [34]. Thus, a periodic box model is a surrogate for a spherical shell model. A further reason, and one of great practical importance, is that numerical simulations using Fourier transform methods allow for the much larger grid-sizes needed to adequately test the statistical theory of ideal MHD turbulence, since it has been shown that a large-enough grid-size is needed [39,40], but one that is not so large that long-term MHD processes remain undiscovered.
Thus, homogeneous, incompressible MHD turbulence in a periodic box with sufficient resolution is the model we choose to examine. Fourier transformation of the MHD equations leads to a nonlinear dynamical system with a huge number of interacting Fourier coefficients, analogous to a gas containing many atoms (except that there is no compressibility). In the case of an ideal gas, statistical methods lead to predictions of equipartition of energy amongst the atoms. In the case of MHD turbulence, however, a lack of equipartition can and does occur [41], in which a few largest-scale modes contain much greater energy than any of the smaller-scale modes [42,43]. A critical difference between an ideal gas and ideal MHD turbulence is that the former only has one ideal invariant, the energy, while the latter can have up to two more ideal invariants in addition to energy. Since probability densities are based on the ideal invariants a system has, the statistical theory of ideal MHD turbulence differs significantly from that of an ideal gas.
When these largest-scale modes in a turbulent magnetofluid become large enough, they also become quasi-stationary [42,43] and, if there is rotation, will align themselves with the rotation axis of the system [27,44,45]. These largest scale modes comprise the ‘dipole’ in MHD turbulence. This is the case for planets and stars which can be rotating, but have no externally applied constant (mean) magnetic field. If there is an externally imposed mean magnetic field in an experimental apparatus, however, equipartition can occur, as long as the mean magnetic field and rotation axis are not parallel; if they are parallel, a weak dynamo action can occur. In total, there are five Cases of MHD turbulence that are differentiated by the number and kind of ideal invariants that each Case has; these are listed in Table 1. Along with the energy E, these ideal invariants may include magnetic helicity , cross helicity [46] or parallel helicity [47]. These ideal invariants will be defined presently.

Table 1.
Cases with different ideal invariants for ideal MHD turbulence. The ‘parallel helicity’ of Case IV is and occurs when , i.e., is parallel to .
Here, we will review ideal MHD statistical theory, which predicts [48,49], for Cases I and II of Table 1, a large-scale magnetic field that is quasi-stationary with a ‘dipole’ energy that is related to the magnetic helicity and the wavenumber of the largest-scale modes, by the expression
The separation of dipole components from turbulent dynamics will also be explicitly seen in the thermodynamics of ideal MHD turbulence. Equation (1) may be viewed as an ‘ideal MHD law’ analogous to the ideal gas law; there is a similar result in Case IV, involving parallel helicity and also total energy E, though there appears to be much less ‘dipole’ energy. The turbulent MHD relation (1) may be reminiscent of the relation between total magnetic energy and in a relaxed, non-turbulent ‘Taylor state’ [50], where is minimized through dissipation while is held constant, so that ; however, in the ideal result (1), does not appear and is not required to be a minimum with respect to (and generally is not). As it turns out, (1) also seems to apply to dissipative and forced MHD turbulence in which energy and other ideal invariants achieve quasi-stationarity.
As will be seen, the appearance of a quasi-stationary dipole component of the magnetic field in the most geophysically and astrophysically pertinent Cases, i.e., I and especially II, indicates nonergodicity in MHD turbulence, which is very apparent in numerical simulations and also manifests itself in the Earth’s geomagnetic dipole field. This nonergodicity can be viewed as being due to a statistically expected symmetry being dynamically broken, i.e., ‘broken ergodicity’. Again, these results survive the addition of forcing and dissipation to the magnetofluid as has been shown in previous studies of helically forced, dissipative MHD turbulence [27,44,45]. We will also present similar evidence here.
Next, we review the mathematical model, statistical mechanics, thermodynamics, and numerical procedure, as well as present new theoretical results, along with new computational results drawn from ideal and real and simulations. These are followed by a discussion of these results and their great relevance to the dynamo problem. All this leads to our conclusion that the statistical mechanics of MHD turbulence contains a solution to the ‘dynamo problem’.
2. Review of Ideal MHD Statistical Mechanics
In this section, we summarize the results that appear in more detail in previous papers [48,49], which also have further references. With regard to MHD general references, there are several good books available, if needed [51,52,53].
2.1. Basic Equations
The non-dimensional form of the 3-D incompressible MHD equations in a rotating frame of reference with constant angular velocity and mean magnetic field (i.e., constant in space and time) can be written as
Here, and are the turbulent velocity and magnetic fields, respectively. Velocity and magnetic fields are solenoidal: , as is appropriate for laboratory experiments and the Earth’s outer core [3]. The vorticity and electric current density are defined by
Non-dimensional density does not appear in (2) because it equals unity. The symbols in (2) and in (3) are shorthand for and , i.e., the inverses of the kinetic and magnetic Reynolds numbers, respectively. In the dimensional form of the equations, is the kinematic viscosity, while is the magnetic diffusivity and for ideal MHD turbulence. Again, we avoid the complication of boundary conditions by placing the magnetofluid in a periodic box and expanding the various fields in terms of Fourier series.
2.2. Fourier Representation
Discrete Fourier transforms for and , connecting -space to -space, are
Here, N is the number of grid points in each -space dimension, so we have a grid of points. The set of positions and wave vectors (modes) appearing in (5) and (6) are
The components and , , are integers. The satisfy , while the integers lie in the range and ; thus, there are points in both spaces. The Fourier coefficients and are nonzero only for , where .
In -space, the requirements become . Thus, and have two independent complex vector coefficients each, which can be defined [54,55] as follows: First, determine a coordinate system for each by starting with a unit vector ; then choosing a unit vector orthogonal to ; the remaining unit vector is a vector product of the first two, forming a right-handed orthonormal basis for each :
In terms of the defined above, the Fourier vector coefficients are
Equivalent, but perhaps more useful, is the helical representation:
Here, the positive and negative helicity unit vectors and components are
Note that . The orthonormality properties of the are
An important property of the helical unit vectors concerns the curl operation:
The velocity, vorticity, magnetic field and current are, in helical form,
As can be seen, the helical ± components of vorticity and current are directly connected to velocity and magnetic field ± helical components.
2.3. A Dynamical System
The Fourier-transformed 3-D MHD equations are found by placing expansions for and of the form (5) into (2) and (3). The result is a set of coupled, nonlinear ordinary differential equations that represents a dynamical system in the sense of [56]:
The nonlinear terms denoted by are vector convolutions:
The double summation in (24) is over all wavevectors and inside the truncation volume in -space that satisfy .
Note that as defined in (24) is a summation that does not include or ; this applies to all of the appearing in (22) and (23). Thus, the components of flow in phase space and satisfy, for ideal MHD (),
This result is a ‘Liouville theorem’ and is essential for defining the probability density D in the phase space of ideal MHD turbulence, as will be seen in Section 4.
2.4. Linear Modes
The dynamic Equations (22) and (23) be can linearized and put into a matrix form:
The eigenmodes of this linear system are
The matrix elements , , and eigenfrequencies , , are
Knowing the frequencies allows us to remove sinusoidal behavior from these variables, in order that the nonlinear dynamics are more clearly seen.
3. Global Quantities
There are various important global quantities that can be expressed as averages over either -space or, equivalently, -space. The volume average of a quantity multiplied by a quantity as , is
Using (32), the volume-averaged energy E, enstrophy , mean-squared current J, cross helicity , magnetic helicity , and mean-squared vector potential A (the last two defined in terms of the magnetic vector potential , where , ) are
When in (22) and (23), E is always an invariant integral. Referring to Table 1: If , then and are also ideal invariants of MHD turbulence; this is Case I. If but , then is no longer an ideal invariant but is; this is Case II. If bur , then is no longer be an ideal invariant but is. When , the helicity is the additional invariant; this is Case IV. If and , but , then only E is an invariant. (For hydrodynamic turbulence, and E are ideal invariants).
The total energy E, cross helicity , magnetic helicity , and parallel helicity comprise a set of possible invariants for the Cases in Table 1. They are explicitly represented in -space by the quadratic forms:
Here and in simulations, these are dimensionless quantities, and we normally set the energy to initially, though this may drift a little bit due to round-off and time-differencing error in ideal simulations. In forced, dissipative simulations, there is an algorithm that tries to keep be adjusting the energy input at each time step. The quadratic forms (36), (39), (40), and (41) are used to define the phase space probability density, as will now be discussed.
4. Statistical Mechanics
Here, we review the statistical mechanics of ideal, homogeneous MHD turbulence. We draw on standard developments of statistical mechanics, such as may be found in [57,58,59], concerning canonical ensembles and expectation values, and of dynamical systems, as presented by [56]. Equations (22) and (23) are a finite dynamical system with phase space whose coordinates are the independent real and imaginary components of and , ; a phase point in represents a possible state of the dynamical system. Canonical ensemble expectation values may be taken once we have a probability density for . ( will generally have a large-dimension, in practice, determined by balancing grid-size and run-time. For example, if and the number of independent is 459,916, then the phase space has dimension 3,679,328.)
As pointed out by [60], when , the system has a Liouville theorem, as will be shown, in a phase space that represents a canonical ensemble where the probability density depends on constants of the motion. Again, these constants, also known as ideal invariants, are the energy E, the magnetic helicity (if ) and the cross helicity (if ), while if , the parallel helicity is an ideal invariant. Since there is Liouville’s theorem for ideal MHD turbulence, the phase space distribution function is a constant of the motion; however, it is also a function of the phase space variables and . The only way it can be both is that is a function of other constants of the motion, e.g., . The only functional form possible for is then
Here, , , and are initially undetermined constants called ‘inverse temperatures’.
If we normalize with the appropriate choice of , we have the probability density function in . The ‘partition function’ Z is
Here, E, and are given by (36), (39) and (40), respectively; for the Cases in Table 1, I: ; II: , ; III: , ; IV: ; and V: .
Using the basic expressions for and , (43) and (44) become
In the product above, the notation means that only independent modes are included, i.e., if is included, then is not. Also, , and , i.e., the factors have been absorbed. Note that the modal phase space volume element is 8-dimensional and the limits on each variable are from to ∞.
Initially [60], the dynamical system (22) and (23) was thought to be ergodic, an assumption that was unchallenged in the early work on ideal MHD turbulence [41,61,62]. It was finally challenged by [42], when apparent non-ergodicity was first noticed and reported, and confirmed later [43]. As already mentioned, this non-ergodicity is actually ‘broken ergodicity’ [63]; a review of broken ergodicity for 2-D and 3-D ideal MHD and hydrodynamic turbulence models is given by [40].
In general, there is no reason to expect ergodicity in any dynamical system, as this can only be determined by experimentation or numerical simulation. This is because ensemble averages are taken over all probable realizations while a single experiment or simulation only produces one dynamical realization. Remember that ergodicity is defined as the equivalence of statistical ensemble predictions with statistics drawn from a single dynamical realization; sometimes this definition is unappreciated and incorrect conclusions result [64]. In addition, one must use large enough grid-sizes in simulations (see [40]) since turbulence is high-dimensional; otherwise, nonergodic behavior will be missed in the low-dimensional simulations [65].
Expectation values can be determined using the probability density function (44) once , , and are determined. Given a quantity Q, the expectation value is defined by
For example, velocity and magnetic field coefficients are predicted to be zero mean random variables:
The second-order moments and , where or I denotes real or imaginary parts, can also be determined by integration [40,41,43]; these are given in Table 2. Similarly, the cross terms and , which appear in the cross and magnetic helicity, can also be determined:
Note that these expectation values and those in Table 2 depend on , , and , which are still undetermined. (Expectation values related to Case IV will presented in Section 6).

In the ideal case, the ideal invariants E, (if ), and (if ) or (if and are nonzero and parallel), should have time-independent values , , and , as the case may be, that are equal to their expectation values:
Requiring that the relations in (52) for the different cases in Table 1 be true, we use these values to determine the ‘inverse temperatures’ , , and . While (49) is an ‘ergodic hypothesis’, (52) is actually an a priori axiom on which the theory of ideal MHD turbulence is based, though justified by a posteriori numerical results.
5. Cases I, II, III and V
In this section, as alternative to the approach leading to Equation (45), we use a model covariance matrix to develop the necessary statistical formulation. This is then applied to Cases I, II, III and V of Table 1; these cases can be treated in a unified manner by analyzing Case I and then reducing this to Cases II, III and V in a straightforward manner. Case IV is more involved and will considered in Section 6.
Placing the -space representation of E, , and , as given in (36)–(40), into the PDF (44) gives an expression that contains modal 4×4 Hermitian covariance matrices in the argument of the exponential:
Here, is the Hermitian adjoint ( means transpose) of the column vector , where
The Hermitian (here, real and symmetric) 4 × 4 covariance matrix is
Again, the circumflex indicates division by : , and .
Although the in (55) can also be expressed as 8 × 8 real symmetric matrices and the as 8 × 1 real arrays [41], finding eigenvalues and eigenvariables is facilitated by using the 4 × 4 matrices and 4 × 1 complex arrays , along with the properties of block matrices given by [66].
The real, symmetric matrices can be diagonalized (and more easily than the Hermitian matrices used previously [39,40]) to yield the modal PDFs,
The eigenvalues are also written with a circumflex to indicate division by , just as for , and . When we find the , the modal partition function given in (45) will be seen to be .
Implicit in the form of given above is the transformation , where SU(4) is a unitary transformation matrix (see below). Explicitly, is
The energy expectation values for the complex eigenvariables , , are
This energy contains equal contributions from the real and imaginary parts of . The exact forms of the and in terms of , and will be presented next.
5.1. Eigenvariables
The eigenvariables in (57) can be determined for ideal MHD turbulence through a modal unitary transformation [34,39,40]. In the general case (nonrotating with zero mean magnetic field), the transformation matrix and the transformation itself are
Using (54), (58) and (60), the results of the transformation are
Above, with for ; the functions and are
In terms of , as defined above, the eigenvalues () are determined by a similarity transformation of (55) using (60):
Explicitly, the eigenvalues , , are
Again, we define , and . Using and forming the product reproduces in (45).
Although it appears that the eigenvalues given above are functions of the undetermined quantities , and , there is only one unknown to be determined: . Summing over the entries in Table 2, and using (50) and (51), tells us that
Here, for . From Table 2, it is clear that and ; thus, in the expression for we have . The linear Equation (69) can be solved to yield
Noting that and are pseudoscalars, we see that and are also pseudoscalars and that and ; thus, the probability density (53) is explicitly invariant under a parity or charge or time transformation. The Equation (70) pertain to Cases I ( and ), II ( and ), III ( and ) and V (). Again, Case IV, where and , with , will be treated separately later.
5.2. Entropy
The entropy functional is ; using (53), (57), (67) and (68), we find (again, )
Above, the sum over means, again, that only independent modes are included (if , then not ). The fact that there is only one unknown quantity in (70) means that the entropy functional (71) depends only on the one variable . As discussed by [57], finding the (single) minimum of gives us the value that sets the values of , and , as well as the system entropy . Note that must be the minimum of because maximizes the probability of the equilibrium states that lie on the ‘surface of constant energy’ in phase space [57]; hence, is called the entropy functional, while is called the entropy.
We first consider Case I and describe the procedure for finding a formula for the approximate value of . From this formula, we can find the one for Case II by setting . Cases III and V both have and (70) tells us immediately that in these cases.
To simplify the upcoming formulas, we will assume that , again, implying that . For Case I, the first derivative of the entropy functional (71) with respect to is
The denominators for the terms in are positive because the arguments of the logarithms in (71), as well as in (70), are all positive; also, from (37) and (40), we see that . For the Fourier case we are discussing here, , and for the spherical shell model of the outer core developed by [34], .
For purposes of illustration, let us recall some Case I and Case II examples. In recent ideal MHD turbulence simulations [48], Case I Run 1 had , while Case II Runs 2a and 2b had and 4.69, respectively. As for real, i.e., forced and dissipative, MHD turbulence simulations [27], using time averages , , for , , , in order to determine , we found for Case I run NM02c, , while for Case II run NM06c, . For these ideal MHD runs, , while for the real MHD runs, and 1.03. (These results indicated that ideal MHD statistical theory is applicable to Case I and Case II real MHD turbulence).
The important point here is that ideal or dissipative, driven magnetofluids with no mean magnetic field, i.e., Cases I and II of Table 1, tend to have . Here, for ideal MHD, we will assume that for simplicity, as it is the terms that are critical. There are 3 independent Fourier modes with smallest wavenumber , so the summation can be broken up into the following:
Above, the first term on the right is negative, while all the rest are positive because for . (Even if , so that there were a few more negative terms, the following development would still be valid). Also, all the terms in are positive. In the limit that ,
Requiring that is equivalent to requiring that ; from the relations given above, we see that three of negative terms (the “dipole” part, corresponding to the smallest wavenumber, ) must balance a very large number of positive terms. (For a spherically symmetric shell, there are also three independent modes at [34]; the following results apply with the substitution ).
Putting the expressions in (76) into leads to
Defining the small quantity , we obtain the cubic equation,
We always have , but in the non-rotating Case I (, ), we also have , so that (approximately) if ; or if .
Equation (78) can be solved by a perturbation expansion , where will be the root of a cubic polynomial and a rational function of . For Case I, the procedure can be implemented analytically or numerically, but we will forgo this here. Instead, we now consider the rotating Case II (, ) which applies to essentially all planets and stars. In this case, (78) becomes much easier to solve once we set .
5.3. Case II, Rotating MHD
First, we show explicitly that the entropy functional (71) for Case II has a minimum at . We use (72)–(74) with to find that the second derivative of (71) at is
It can be shown that is the only minimum of in the range and is thus unique.
Second, setting in (78) leads, to first order in a small parameter ,
This approximation is used here for theoretical development, but when exactness is required, is determined from (77) by numerically finding the minimum of corresponding to and for a given run, as well as if .
From the expression (80) for , we can also determine the expectation value of the kinetic energy, , as well as of the difference :
We will now use these results to show how the positive magnetic helicity eigenvariable has an energy expectation value of , which is independent of ; all of the other eigenvariables have expected energies . This will allow us to explain the large-scale coherent magnet structures (i.e., quasi-stationary dipole fields) that spontaneously arise within a turbulent magnetofluid such as is found in the Earth’s outer core.
5.4. Temperature
In a rotating frame of reference, Case II of Table 1, so that , for which . Assuming , so that and thus and , (61)–(64) become:
Remember that the dynamical variables and carry negative and positive kinetic helicity, respectively, while and carry negative and positive magnetic helicity, respectively. If the magnitudes of (83) are constant, they are essentially the same as the linear modes (see Section 2.4) for Case II. For Case III, (29) and (61)–(64) become Elsässer variables [2], while in Case V, the two sets of eigenvariables are generally different, though Elsässer variables may be associated with certain values of , i.e., those with . In Case V, the expectation values of all the variables (83) are the same.
For Case II, we take the limit , so and the eigenvariables are as given in (83), while the eigenvalues (67) and (68) become
In the rotating case, and are determined by putting from (80) into their respective expressions as given in (70) with ; the result is
Using (81) and (82), as well as , and , we have
The first equation above tells us that the temperature of the system is, using ,
Thermodynamically, ; here, we have and . However, we can express our results thermodynamically as well as statistically, showing the origin of (87).
Using (81), (82) and (84), as well as setting ,
We now remove the constant terms and define the equilibrium entropy as
Here, the are ‘chemical potentials’ and the are the number of independent that satisfy . The numbers jump around as increases; for example,
Furthermore, we have whenever [67].
The differential of (88), taken as a function of and (the and are numerical constants) is
Here, T is temperature and is the ‘helicon-magnetic-susceptibility’. In the next section we will see that is the ‘dipole energy’ , so that is the turbulent energy . Setting Boltzmann’s constant , the average energy per degree of freedom is manifestly , i.e., the turbulent energy divided by minus six degrees of freedom, these six being , and , which are those associated with the dipole, and not part of the turbulent dynamics.
5.5. Energy Expectation Values
Here, we will see that this energy goes into six (dipole) components. Using (85), along with (81), (82), and (84), gives us the unnormalized eigenvalues , up to leading order:
The eigenvariables have real (R) and imaginary (I) parts, i.e., , with real and imaginary parts having the same expectation values. The associated energies of the real (R) and imaginary (I) parts are
As defined in (83), the index refers to negative and to positive kinetic helicity coefficients; similarly, the index refers to negative and to positive magnetic helicity coefficients. The relations (93) and (94) tell us that the expected energies with respect to helicity are
The sum of these over independent modes is plus a term ∼O(). An important result can be seen in (100): summing over the three modes tells us where the non-turbulent energy goes: into what we will call the ‘dipole’ energy ; summing up all the remaining modal energies (97)–(99) gives the residual turbulent energy :
Thus, in a compact, rotating, turbulent magnetofluid with no mean magnetic field, the energy in the dipole is equal to the magnetic helicity. (In a spherical shell model, the dipole energy is [34]; here, since the components of are integers as defined in Section 2.2).
Again, for cubical periodic boxes or symmetrical spherical shells, the three lowest-wavenumber modes are expected to have the same energy. However, for the non-rotating case, and especially for the rotating case, there is always some dynamical symmetry breaking so that one of the lowest-wavenumber modes dominates dynamically, as will be discussed further shortly.
The statistical results given above are directly related to Case II of Table 1, but also apply approximately to Case I if is small compared to . In Case III, is not an ideal invariant but is and the predictions for the energies of the eigenvariables (61)–(64), which are now Elsässer variables, are
Here, we have used (70) along with . In Case V, all the eigenvariables are predicted to have the same energy, which is given in (102) by setting . The statistical predictions for Case IV are discussed in the next section.
6. Case IV, Parallel Helicity
MHD turbulence with mean magnetic field parallel to rotation axis, for which parallel helicity is an ideal invariant, has been investigated before. Parallel helicity was first introduced [47] as part of a general study of all the Cases in Table 1. After this its relation to weak turbulence [68], two-fluid effects [69] and inverse cascades [70] was studied. Here, we fully develop the statistical mechanics of Case IV MHD turbulence for the first time.
for Case IV in Table 1 can be determined by first setting where ; we will also set , so that . In this Case, Equation (69) become
The invariant parallel helicity is, again, and the variable whose value we must determine is . Solving Equation (103), we get, instead of the simpler looking set in Equation (70),
The denominator for above must be positive: . This leads to two inequalities:
These strict inequalities as we cannot allow , at which value , and we would have . Other limits can be found by squaring both sides in (106) and (107) to get
Here, the upper symbol of ≷ or ≶ corresponds to and the lower symbol corresponds to . The limits on corresponding to and are then
For Case IV, where ; here, for definiteness, we will choose ; we will also choose , so that and thus . The eigenvalues (67) and (68) then become
We have used (65) here, so that ; the have no z or dependence.
The exact value of must be determined by numerically finding the minimum of the entropy functional (71), which we write here as
The evaluation of analytically to find a good approximation for would seem complicated since the that appear in the eigenvalues (111) and (112) are themselves function of . However, consider the that appear in (105) and take their derivatives with respect to :
Clearly and within their respective ranges of . We then have
Thus, we can use instead of to find . Note that the requirement means that and are implicit functions of each other and that one corresponds to one .
We can now find an approximate value for by differentiating (113) and using from (105), along with (111) and (112):
This derivative cannot equal zero unless one or more of the terms within parentheses is negative. Since the denominators must always satisfy , some of the numerators must be negative. The values of k for which becomes negative satisfy (since , )
If , then the first term within the parentheses of (116) is negative for all , while if , then all the last terms are also negative for all ; the middle two terms are clearly always positive.
However, if , then there are only a few negative first terms to negate the positive terms within the parentheses, in which case at least one of the negative terms must be very large. This must be the first term at , because it has the smallest possible denominator of all the terms; this leads to
We can find by putting the approximate in (118) into (116) an using the fact that as , and solving for to get
Again, , where , and this result applies only when .
Again, ignoring constant terms and terms of order , we define the equilibrium entropy for as
The differential of (123) gives us (remember that )
Here, we see that the temperature , and that as increases, T and decrease.
Referring to (59), along with (111) and (112), we see that the energies of the eigenmodes are
Now, using (118) and (119), these expressions become,
We can sum these over the respective ranges, assuming that K and thus are very, very large, using the fact that , to get, for the ‘dipole energy’ and the residual, ‘non-dipole energy’ , the following:
Algebraic manipulation of (133) confirms that :
This result follows because .
7. Broken Ergodicity and Broken Symmetry
Here, we discuss the differences between the eigenvariables and all the other eigenvariables with regard to their dynamical behavior. Broken ergodicity is expressed when some of the variables have very large mean values dynamically compared to their standard deviations, which obviously gives rise to a coherent structure in -space; broken symmetry is expressed as the random orientations that this coherent structure can take. This creation of larg-scale coherent structure is essentially a dynamo process that is inherent in MHD turbulence. Because of its relevance for rotating planets and stars, we will focus on Case II, where and , so that .
7.1. Broken Ergodicity, Case II
We continue with the results developed in Section 5.3, where and we chose and . The expectation values (97)–(100) yield rms values , so that
Looking at (83), we see and . In (b), the expected magnitude is just the standard deviation because the associated mean of may be taken as zero. In (a), however, the expected magnitude may represent the magnitude of the mean of , rather than its standard deviation, since it becomes quasi-stationary for the following reasons.
Consider the modal dynamic Equation (22) with and (23) with :
Again, the nonlinear terms denoted by are vector convolutions:
Now, assume that is very large so that the variables in (136) are also very large. The dipole field and associated current will be
The remainder, or random, parts of and are
In Case II, all the and all the except for are random variables of magnitude and zero-mean value.
Thus, in (137), because , we have and can then use (139) to write
Using (136a,b) as size estimates, we see that the rms values of the first two terms on the right are larger than the third term , which is of the same size as in (22).
In (138), can be written as
Again using (136a,b), we also see that the rms value of the first term on the right is larger than the second term.
Using these estimates, the rms sizes of the right sides of (137) and (138) appear to be
From these and (136), we obtain
What this implies dynamically is that, in equilibrium, the ‘dipole’ eigenvariables , when they are large, have, on average, fluctuations in magnitude comparable in size to the other , which are, on average, all very small. In particular, the fluctuations of these other are of the same size as their rms magnitudes and so they behave like zero-mean random variables, as expected. However, the rms values of one or more of the are so large compared to their fluctuations that they exhibit nonergodic behavior, i.e., they have relatively large mean values over very long durations, i.e., the exhibit ‘broken ergodicity’. This phenomenon will be made clearer in the next subsection, where we discuss ‘broken symmetry’.
7.2. Broken Symmetry
Again, we use the results developed in Section 5.3, where and we chose and . In Section 5.3, we saw that, dynamically, the magnitudes of a ‘dipole’ eigenvariables , where , could become very large. Now we show that at least one of the becomes effectively constant over a long time because fluctuations in its component values are very small. Often, one of the , for , or does not become as large as predicted by (99). These predictions are just average values over the ensemble and to see what is really going on we must consider the sum of the expectation values . Again, the smallest wavenumber occurs for the wavevectors , or . The ensemble prediction (100) tells us that the three complex vector coefficients are very large and unique from those with ; using the , we can define a six component vector in a 6-D real space or a three component vector in a complex 3-D space; for compactness, we define a vector and dot product in a 3-D complex space:
The endpoint of is, for the reasons given in Section 7.1, a quasi-stationary point on the surface of the hypersphere of radius in a 6-D subspace of the -D phase space . Thus, although (136a) predicts that all , for , will have the same magnitude, this is an ensemble average and does not take into account that will become quasi-stationary. Once it is quasi-stationary, a unitary transformation of phase space can point in any direction in its 6-D space that we choose, at least for the non-rotating Case I; in the rotating Case II, of course, there is a preferred direction due to axisymmetry and dipole alignment with the rotation axis although with small fluctuations. To reiterate, canonical ensemble predictions can give us mean-squared expectation values (100), but cannot predict the direction of in Case I; broken ergodicity occurs because of dynamically broken symmetry. The appearance of broken ergodicity has been noted many times before [40,42,43,71], as has the phenomenon of broken symmetry [71]; here, we see how these aspects of MHD turbulence are connected.
In equilibrium, the magnitudes of the , for , and , are often not that different from each other in non-rotating ideal MHD Case I but may vary appreciably when rotation is imposed, i.e., Case II, where the eigenfunction with parallel to has essentially all the dipole energy, as we have consistently seen numerically. In the real case of forced, dissipative MHD turbulence, this phenomenon is also observed numerically, although some mechanisms of forcing and dissipation may disrupt this process, as seen in Figure 7 of [27].
The generation of quasi-stationary, energetic dipole magnetic fields, along with dipole moment alignment with the rotation axis, seems fairly ubiquitous in numerical simulations, as well as in planets and stars. The theory of ideal MHD turbulence and its relevance to real MHD turbulence at the largest scales appears to be a viable explanation of these planetary and stellar phenomena.
8. Numerical Procedure
A Fourier spectral transform method based on the Fast Fourier Transform (FFT) algorithm [72] was used on an grid with either or . The minimum wave number is and the maximum wave number is for and for . In the ideal runs, de-aliasing [73] was performed, but not in the forced, dissipative runs. Time-integration was performed with a third-order Adams–Bashforth–Adams–Moulton method [74] with a time-step of for and for . Initial, non-equilibrium magnetic and kinetic modal energy values (spectra) were , where . Viscosity and magnetic diffusivity are set to zero in the ideal runs and typically in the forced, dissipative runs. A maximum grid size of was used so that a single-core MHD run could be completed in a reasonable amount of time with the resources available, which was the Hopper Cluster at George Mason University, where each simulation ran at sec per for an ideal run and sec for a forced, dissipative run, while each simulation ran at sec for an ideal run and sec for a forced, dissipative run. Thus, a single ideal run of s requires about 36 weeks of cpu time, for example. The ratio in run-times between the and per is 12.1, which is very close to the expected ratio for an FFT transform method of .
The computer simulations covering the five Cases in Table 1 are identified in Table 3, Table 4 and Table 5. The ideal invariants associated with each Case are quadratic forms (global quantities) with terms that are scalar products of the vector Fourier coefficients and , with , as defined in Section 3. The partial differential equations for MHD in -space are given by (2) and (3), while the transformed set of ordinary differential equations in -space are given by (22) and (23). The set of equations in -space is a finite dynamical system as discussed in Section 2.3. The -space Equations (22) and (23) were numerically integrated to advance the and , as described above.

Table 3.
Time averages and standard deviations (avg±std) for various global quantities over the last half of each run are given below for six ideal MHD turbulence long-time runs 1, 2a, 2b, 3, 4, and 5. These global quantities are: energy E, kinetic energy , magnetic energy (compared with ), mean squared vector potential A, kinetic helicity , magnetic helicity , cross helicity , parallel helicity , enstrophy and mean squared current J. The ‘dipole angle’ , defined in (156), shows alignment with the rotation axis; it would be if all components were equal.

Table 4.
here, so that none of these runs has an invariant . Time averages and standard deviations (avg±std) for various global quantities over the 15% near the end of these forced dissipative runs, where for each. and are the squares of the relative forcing amplitudes, i.e., the relative amount kinetic and magnetic energy injected to keep the total energy ; the wavenumber at which energy is injected is . The global quantities below are: energy E, kinetic energy , magnetic energy (compared with ), mean squared vector potential A, kinetic helicity , magnetic helicity , cross helicity , parallel helicity , enstrophy , and mean squared current J. The ‘dipole angle’ , defined in (156), shows alignment with the rotation axis; it would be if all components were equal.

Table 5.
Parallel helicity runs. Time averages and standard deviations (avg±std) for various global quantities for the forced dissipative run GDpar; for comparison, the statistics for ideal Run 4 are also given below; also, the statistics for ideal Run P0 (averaged over the last half of the run) and those for forced, dissipative Run P1 (averaged over to 3100) are given. These global quantities are: energy E, kinetic energy , magnetic energy (compared with ), mean squared vector potential A, kinetic helicity , magnetic helicity , cross helicity , parallel helicity , enstrophy and mean squared current J. The ‘dipole angle’ , defined in (156), shows alignment or not with the rotation axis; it would be if all components were equal.
As seen in Table 1, the ideal invariants of ideal MHD turbulence are the volume-averaged energy E and magnetic helicity when , as well as the cross helicity when and when . In a numerical simulation of ideal MHD turbulence, these ideal invariants typically have a standard deviation of less than 1% per million time-steps, while kinetic helicity , though an invariant for ideal hydrodynamic turbulence [75], falls to zero very quickly and then has small fluctuations about that value, as Table 3 shows. However, if there is strong helical kinetic forcing, can become relatively large, as Table 4 shows.
8.1. Forcing and Dissipation
Forcing is implemented at wavenumber , specifically at wavevectors , by setting the kinetic and magnetic coefficients and to have, at each time-step, the form:
The indices j, n, and m are cyclic permutations of x, y, and z. These coefficients are set independently of the time-integration scheme applied to the k-space versions of (2) and (3), by prescribing their values in the manner above. The factors and are for positive and for negative kinetic or magnetic helicity forcing. The factor adjusted itself at each time-step to keep the total energy density close to unity. The forcing wavenumber was set to 32 (or 16) as this seemed large enough to allow Fourier modes at the smallest wavenumber (largest length-scale) to develop naturally, while providing enough modes with for a direct cascade to smaller length-scales and ultimate dissipation to occur. The phases in (151) and (152) were and , i.e., linear with time with a period of unity.
Dissipation is introduced by setting in (22) and in (23) to nonzero values. These values were usually set to but were changed and then reset for one run (GDpar), as discussed in the next section, to see the effects this disruption might cause. The level of forcing and dissipation must, of course, come into balance and this typically occurs after a short period of adjustment.
9. Computational Results
For each run in Table 3, the quantities that are supposed to be conserved were, in fact, conserved. These runs are fully turbulent and their transition to turbulence was described previously [48,49]; here, the run-times are considerably extended. There are two further sets of runs whose statistics are given in Table 4 and Table 5 that will also be discussed.
For all the runs presented here, the values of all the and with were saved every 0.1 units of simulation time t (i.e., every 200 s for the runs and every 100 s for runs). From the saved data, components of the vectors and can be transformed into helical components , , and , as discussed in Section 2.2. These are useful, but can be further transformed into cyclic linear modes whose non-cyclic factors are , , and , as defined in Section 2.4. If there were no nonlinear interactions in the MHD equations, the would be complex constants; however, the MHD equations are nonlinear, so the may wander around with time. Since we have recorded data that can give us the time-histories of these for , we can plot their trajectories on a complex plane and clearly see the nature of ideal (or real) MHD turbulence, at least at the larger length-scales (i.e., smaller wave numbers k). These ‘phase portraits’ are projections of the dynamical trajectory in the high-dimensional phase space onto a 2-D plane which enables us to visualize the concepts of coherent structure, broken ergodicity, and broken symmetry (please see Section 7 for a review of these concepts). For the runs discussed here, some phase portraits are shown in Figure 1, Figure 2 and Figure 3. Next, we discuss Figure 1 and Figure 2, while Figure 3 will be discussed a little later.
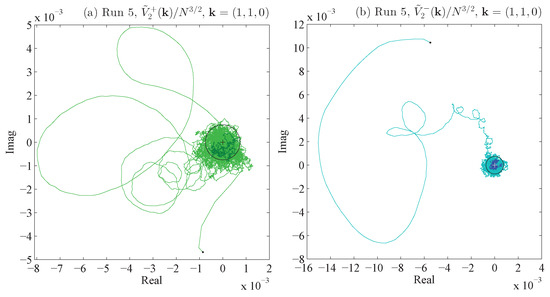
Figure 1.
Ideal Run 5 coefficient trajectories with initial values signified by a black dot: (a) , ; (b) , . The black circles indicate the predicted standard deviation and the darker parts of the trajectories indicate the last 5% of the run time and the + sign indicates the origin (0,0). These phase plots represent the initially expected behavior of Fourier coefficients as zero-mean random variables.
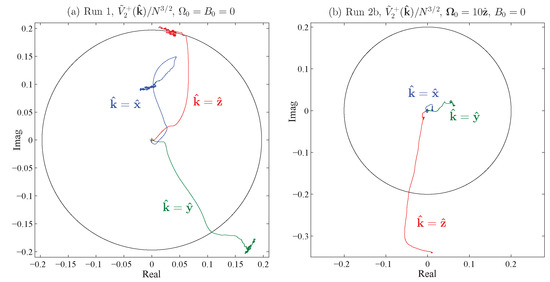
Figure 2.
Broken ergodicity and broken symmetry as evidenced in coefficient trajectories from ideal Runs (a) 1 and (b) 2b; trajectories all begin near the origin (0,0). These are clearly nonzero-mean random variables, a phenomenon that was unexpected but which can be understood theoretically; the black circles indicate the predicted standard deviations of these coefficients; for each trajectory, the expected standard deviation is equal to .
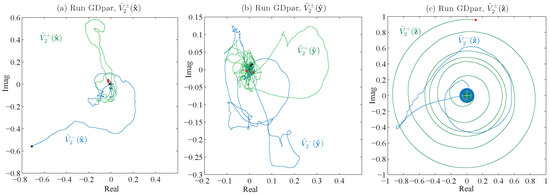
Figure 3.
Phase plots of trajectories of eigenvariables from the parallel helicity Run GDpar for (a) ; (b) ; and . The trajectory of in (c) has become large and circular motion indicates that the coherent structure is in translation across the periodic box with a period of . (Note that these are not normalized by dividing by ). Black circles indicate stanard deviations predicted for these random varibles and the + indicates the origin, i.e., (0,0), for each 2-D plot.
In Figure 1 we show some trajectories for Run 5 of Table 3; these trajectories settle into expected behavior for zero-mean random variables. In Figure 2 we show trajectories for Runs 1 and 2b of Table 3; these trajectories do not exhibit the expected behavior of zero-mean random variables but instead show broken ergodicity and symmetry at the largest length-scale, i.e., they give evidence of the inherent dynamo within MHD turbulence whose existence is explained in Section 4.
In addition to the ideal runs of Table 3, sixteen relatively long-time forced, dissipative runs without parallel helicity were computed. Statistics for six of these Case I and II runs are shown in Table 4 as a representative set; the method of forcing and dissipation is described in Section 8.1. With regard to Case IV of Table 1, we gather together Run 4 of Table 3 with three other Case IV runs: GDpar (), along with P0 and P1, both .
For all the runs in Table 3, Table 4 and Table 5, the values of all the and with were, again, saved every 0.1 units of simulation time t (i.e., every 200 s for the runs and every 100 s for runs). From this numerical data we can calculate a time history of the modal energies:
In Figure 4, Figure 5 and Figure 6, we see how the magnetic energies , , vary with time compared to their expected values.
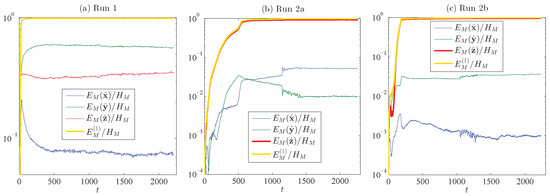
Figure 4.
Numerical verification of in ideal Runs (a) 1; (b) 2a; and (c) 2b; again, in the Fourier case, .
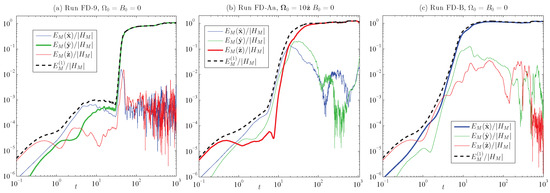
Figure 5.
Numerical verification of in forced, dissipative Runs (a) FD-9; (b) FD-Aa; and (c) FD-B; again, in the Fourier case, . Numerical forcing can affect the evolution of the dynamical system, but the basic law appears independent of any reasonable method of forcing chosen.
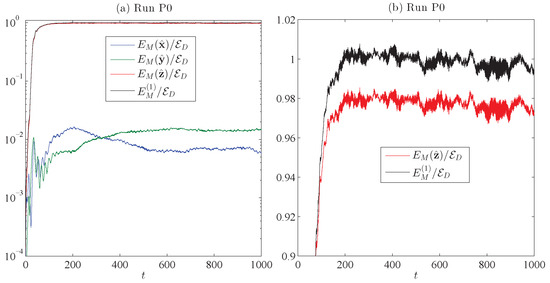
Figure 6.
Here, we see numerical verification of in the ideal parallel helicity Run P0: (a) first, all and ; and (b) second, a close up of and .
In Figure 4, a numerical verification of the essential result (1), i.e., , is presented for ideal Runs 1, 2a and 2b. Figure 5 shows that numerical verification that (1) also applies to forced, dissipative runs, using Runs FD-9 (Case I), FD-Aa (Case II) and FD-B (Case I) as examples. As can be seen in Table 4, these runs differ in the relative values of the forcing magnitudes and , and Figure 5 indicates that either predominantly kinetic or predominantly magnetic forcing, as long as they are helical, produces a large value of ; a coherent structure also arose, similar to that seen in Figure 2. Although the chosen form of numerical forcing can affect the evolution of the dynamical system, the basic law and coherent structure appear, independent of any reasonable method of forcing chosen [27,44,45].
In Table 3, Run 4 is the sole run with parallel helicity . In the case of Run 4, this low value does not satisfy the requirement (117) that by which a coherent structure might be expected. To test the ideal theory for , we added ideal Run P0 and forced, dissipative Run1 P1, along with the forced, dissipative Run GDpar to our collection. Their statistics are, again, given in Table 5, along with ideal Run 4 from Table 3 for comparison. In addition to the ideal Run P0, the statistics of the forced, dissipative Runs P1 () and GDpar () are also given in Table 5. In Figure 6, we see numerical verification from Run P0 of the theoretical prediction (133), i.e., , in the ideal parallel helicity Run P0 for which . A coherent structure also arises in Case IV runs, as long as , as seen, for example, in Figure 3, where phase portraits from Run GDpar are shown.
In Figure 7, we present a numerical verification of (133) in the forced, dissipative, parallel helicity, Run GDpar. In this figure, the values of the magnetic energies , defined in 156, divided by the predicted value (133) of , are given, as well as the sum of these, . Verification of (133) follows because with time, indicating the applicability of ideal results to real MHD turbulence. Figure 7 also indicates that a change of parameters causes a disruption after which the system regains equilibrium.
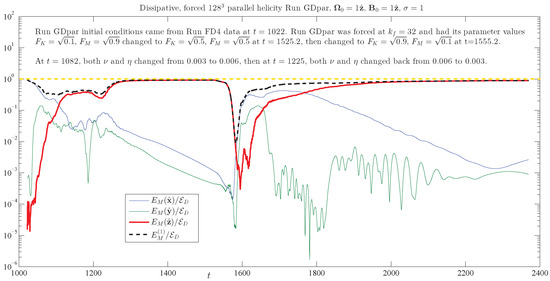
Figure 7.
Numerical verification of Equation (134), i.e., , in the forced, dissipative, parallel helicity Run GDpar. This figure indicates that a change of parameters causes a disruption after which the system regains equilibrium. The yellow dotted line indicates when a given ratio has a value of one.
The dipole angle appearing in Table 3, Table 4 and Table 5 is defined by
In Case II runs (, ), this angle is generally small, as seen in the Tables mentioned, indicating alignment with the rotation axis.
The definitions of averaged MHD turbulent spectra and are
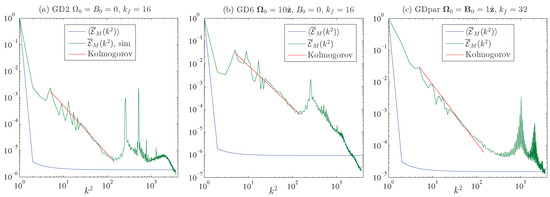
Here, is the number of independent that satisfy . The number jumps around as increases, as shown in (90). The full energy spectra is at each value of and thus jumps wildly as increases because does, which is why we prefer to look at the average energy spectra (156) and (157), as in Figure 8. (However, its running average over near neighbors is well approximated by ).
Using the results in Table 2, we find that the ideal expectation values of and are
Here, and , and are the normalized inverse temperatures related to inverse temperatures appearing in the phase space probability density (44); please see Section 4 for details. Table 3, Table 4 and Table 5 list the average values of E, , and , during a run; using these, as needed in (71) for the ideal values , , and , the normalized inverse temperatures , and are determined by numerically finding the minimum of the entropy functional (71) using a bisection method [76] with the proviso that, for Case II runs, ; for Case III runs, ; for Case IV runs, ; and for Case V runs, . The values of , , and for the runs in Table 3, Table 4 and Table 5 are given in Table 6.

Table 6.
Values of the inverse temperatures , , and for the Runs in Table 3, Table 4 and Table 5, remembering that for Case II runs, ; for Case III, ; and for Case V, and . When needed, , , and took their values from , and , respectively, in the Tables mentioned. [The need for precision here is due to the possible smallness of the denominators in (158) and (159)].
In Figure 8, equilibrium magnetic energy spectra for forced, dissipative Runs (a) GD2 and (b) GD6 of Table 4, along with (c) forced, dissipative, parallel helicity Run GDpar of Table 5 are presented, along with associated ideal prediction (158) and the Kolmogorov prediction. The associated ideal spectra are, again, found using Table 4 average values: , and for GD2; and for GD6; and and for GDpar. The forcing wave number was for GD2 and GD6, while it was for GDpar. The correlation of ‘inertial range’ spectra with the Kolmogorov prediction for spectra integrated over wave number; for the spectra shown in Figure 8, what is plotted is the averaged value at each , for which the Kolmogorov prediction becomes . The results shown in Figure 8 are consistent with what we find in all the forced, dissipative runs we have carried out, so they appear robust and indicate that an inertial range has been resolved in these numerical simulations of real MHD turbulence.
Finally, let us point out the connection between MHD turbulence and the geodynamo. The magnetic field in the Earth’s outer core manifests itself in the latest International Geomagnetic Reference Field (IGRF) [77], which is comprised of the Gauss coefficients of the geomagnetic field, as determined by processing surface and satellite measurements. It has been shown that magnetic energy spectra from forced, dissipative numerical simulations, similar to those presented here, match closely with outer core magnetic spectra derived from IGRF data, as long as the electrical conductivity of the Earth’s mantle is taken into account [78]. This can be viewed as compelling evidence that MHD turbulence exists in the rotating outer core and, as we have reviewed herein, that rotating MHD turbulence, per se, is the dynamo that creates the quasi-stationary, energetically dominant, dipole magnetic field of the Earth. Thus, we have a solution to the ‘dynamo problem’.
10. Conclusions
Five different Cases of MHD turbulence have been defined in Table 1, based on the ideal invariants associated with each Case. The primary result that we wish to emphasize here is that all of the Case II simulations (and to a good approximation, Case I simulations) of ideal and real MHD turbulence in equilibrium that we have presented verify the ‘ideal MHD law’ (1). We have also developed an analogous result for Case IV, i.e., Equation (133), when parallel helicity is an ideal invariant. In these Cases, both ideal and real simulations show the emergence of largest-scale coherent structure.
Case II of Table 1 is perhaps the most pertinent one related to planets and stars. For the Earth, in particular, which possesses an outer core that can be approximated as a rotating, turbulent magnetofluid in equilibrium, the theory described here—verified by numerical results—strongly suggests that we have found a solution to the ‘dynamo problem’ first posed by Joseph Larmor just over a hundred years ago. As there appear to be no other viable extant solutions, this would seem to be an important discovery, and we hope it will be recognized as such.
Concerning ergodicity, some researchers have stated that fluid turbulence is ergodic [79] and others that there are cases of nonergodicity [80]; more recently, it has been said that ‘the as yet unproven general ergodic theorem states that time averages are the same as ensemble averages, assuming the fluctuations are stationary (the ergodic theorem has been proven under certain conditions)’ [81]. With regard to ‘certain conditions’, if the influence of magnetic helicity is not taken into account, and thus assumed to be insignificant, ergodicity may be expected [82]Ḣowever, the discovery that we made long ago [42]—also discussed here—that there is nonergodicity due to nonzero magnetic helicity in a turbulent magnetofluid, implies that there is no general ergodic theorem for all cases of fluid turbulence. This is our essential result here: in MHD turbulence, nonzero magnetic helicity causes nonergodicity, which is expressed as a coherent largest-scale structure.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Conflicts of Interest
The author declares no conflict of interest.
References
- Larmor, J. How could a rotating body such as the sun become a magnet? Rep. Brit. Assoc. Adv. Sci. 1919, 87, 159–160. [Google Scholar]
- Elsässer, W.M. Hydromagnetic dynamo theory. Rev. Mod. Phys. 1956, 28, 135–163. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Roberts, P.H. A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 1995, 377, 203–209. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Roberts, P.H. A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle. Phys. Earth Planet. Int. 1995, 91, 63–75. [Google Scholar] [CrossRef]
- Kuang, W.; Bloxham, J. An Earth-like numerical dynamo model. Nature 1997, 389, 371–374. [Google Scholar] [CrossRef]
- Rice, J.E. Experimental observations of driven and intrinsic rotation in tokamak plasmas. Plasma Phys. Control. Fusion 2016, 58, 083001. [Google Scholar] [CrossRef]
- Le Bars, M.; Barik, A.; Burmann, F.; Lathrop, D.P.; Noir, J.; Schaeffer, N.; Triana, S.A. Fluid Dynamics Experiments for Planetary Interiors. Surv. Geophys. 2022, 43, 229–261. [Google Scholar] [CrossRef] [PubMed]
- Gailitis, A.; Lielausis, O.; Platacis, E.; Demenťev, S.; Cifersons, A.; Gerbeth, G.; Gundrum, T.; Stefani, F.; Christen, M.; Will, G. Magnetic field saturation in the Riga dynamo experiment. Phys. Rev. Lett. 2001, 86, 3024. [Google Scholar] [CrossRef] [PubMed]
- Stieglitz, R.; Müller, U. Experimental demonstration of a homogeneous two-scale dynamo. Phys. Fluids 2002, 13, 561–564. [Google Scholar] [CrossRef]
- Monchaux, R.; Berhanu, M.; Bourgoin, M.; Moulin, M.; Odier, P.; Pinton, J.F.; Volk, R.; Fauve, S.; Mordant, N.; Pétrélis, A.; et al. Generation of a Magnetic Field by Dynamo Action in a Turbulent Flow of Liquid Sodium. Phys. Rev. Lett. 2007, 98, 044502. [Google Scholar] [CrossRef]
- Davidson, P.A. Turbulence in Rotating and Electrically Conducting Fluids; Cambridge U.P.: Cambridge, UK, 2013; p. 532. [Google Scholar]
- Blackett, P.M.S. XI. The magnetic field of massive rotating bodies. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1949, 40, 125–150. [Google Scholar] [CrossRef]
- Bullard, E. The magnetic field within the earth. Phil. Trans. Roy. Soc. Lond. A 1949, 197, 433–453. [Google Scholar]
- Bullard, E.; Gellman, H. Homogeneous Dynamos and Terrestrial Magnetism. Phil. Trans. Roy. Soc. Lond. A 1954, 247, 213–278. [Google Scholar]
- Backus, G. A Class of Self-Sustaining Dissipative Spherical Dynamos. Ann. Phys. 1958, 4, 372–447. [Google Scholar] [CrossRef]
- Roberts, P.H. Kinematic Dynamo Models. Phil. Trans. Roy. Soc. Lond. A 1972, 272, 663–698. [Google Scholar]
- Gubbins, D. Numerical Solutions of the Kinematic Dynamo Problem. Phil. Trans. Roy. Soc. Lond. A 1973, 274, 493–521. [Google Scholar]
- Kumar, S.; Roberts, P.H. A Three-Dimensional Kinematic Dynamo. Phil. Trans. Roy. Soc. Lond. A 1975, 344, 235–258. [Google Scholar]
- Archontis, V.; Dorch, S.B.F.; Nordlund, A. Numerical simulations of kinematic dynamo action. Astron. Astrophys. 2003, 397, 393–399. [Google Scholar] [CrossRef][Green Version]
- Chen, L.; Herreman, W.; Li, K.; Livermore, P.W.; Luo, J.W.; Jackson, A. The optimal kinematic dynamo driven by steady flows in a sphere. J. Fluid Mech. 2018, 839, 1–32. [Google Scholar] [CrossRef]
- Dudley, M.L.; James, R.W. Time-Dependent Kinematic Dynamos with Stationary Flows. Phil. Trans. R. Soc. Lond. A 1989, 425, 407–429. [Google Scholar]
- Schekochihin, A.; Cowley, S.; Maron, J.; Malyshkin, L. Structure of small-scale magnetic fields in the kinematic dynamo theory. Phys. Rev. E 2001, 65, 016305. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Ruzmaikin, A.A.; Molchanov, S.A.; Sokoloff, D.D. Kinematic dynamo problem in a linear velocity field. J. Fluid Mech. 1984, 144, 1–11. [Google Scholar] [CrossRef]
- Hughes, D.W. Mean field electrodynamics: Triumphs and tribulations. J. Plasma Phys. 2018, 84, 735840407. [Google Scholar] [CrossRef]
- Rädler, K.-H. Mean-Field Dynamo Theory: Early Ideas and Today’s Problems. In Magnetohydrodynamics–Historical Evolution and Trends; Molokov, S., Moreau, R., Moffatt, H.K., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 55–72. [Google Scholar]
- Krause, F.; Rädler, K.-H. Mean-Field Magnetohydrodynamics and Dynamo Theory; Oxford U.P.: Oxford, UK, 1980. [Google Scholar]
- Shebalin, J.V. Magnetohydrodynamic turbulence and the geodynamo. Phys. Earth Planet. Inter. 2018, 285, 59–75. [Google Scholar] [CrossRef]
- Batchelor, G.K. On the Spontaneous Magnetic Field in a Conducting Liquid in Turbulent Motion. Proc. Roy. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 201, 405–416. [Google Scholar]
- Loper, D.E. Turbulence and Small-Scale Dynamics in the Core. In Treatise on Geophysics 8: Core Dynamics; Olson, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 187–206. [Google Scholar]
- Nataf, H.-C.; Schaeffer, N. Turbulence in the Core. In Treatise on Geophysics 8: Core Dynamics, 2nd ed.; Olson, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 161–181. [Google Scholar]
- Roberts, P.H. Theory of the Geodynamo. In Treatise on Geophysics 8: Core Dynamics; Olson, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 67–105. [Google Scholar]
- Zhang, K.; Gubbins, D. Is the geodynamo process intrinsically unstable? Geophys. J. Int. 2000, 140, F1–F4. [Google Scholar] [CrossRef]
- Tkalčić, H. Complex inner core of the Earth: The last frontier of global seismology. Rev. Geophys. 2015, 53, 59–94. [Google Scholar] [CrossRef]
- Shebalin, J.V. Broken ergodicity, magnetic helicity, and the MHD dynamo. Geophys. Astrophys. Fluid Dyn. 2013, 107, 353–375. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Kendall, P.C. On Force-Free Magnetic Fields. Astrophys. J. 1957, 12, 457–460. [Google Scholar] [CrossRef]
- Montgomery, D.; Turner, L.; Vahala, G. Three-dimensional magnetohydrodynamic turbulence in a cylindrical geometry. Phys. Fluids 1978, 21, 757–764. [Google Scholar] [CrossRef]
- Mininni, P.D.; Montgomery, D. Magnetohydrodynamic activity inside a sphere. Phys. Fluids 2006, 18, 116602. [Google Scholar] [CrossRef]
- Mininni, P.D.; Montgomery, D.; Turner, L. Hydrodynamic and magnetohydrodynamic computations inside a rotating sphere. New J. Phys. 2007, 9, 303–330. [Google Scholar] [CrossRef]
- Shebalin, J.V. Plasma relaxation and the turbulent dynamo. Phys. Plasmas 2009, 16, 072301. [Google Scholar] [CrossRef]
- Shebalin, J.V. Broken ergodicity in magnetohydrodynamic turbulence. Geophys. Astrophys. Fluid Dyn. 2013, 107, 411–466. [Google Scholar] [CrossRef]
- Frisch, U.; Pouquet, A.; Leorat, J.; Mazure, A. Possibility of an inverse cascade of magnetic helicity in magnetohydrodynamic turbulence. J. Fluid Mech. 1975, 68, 769–778. [Google Scholar] [CrossRef]
- Shebalin, J.V. Anisotropy in MHD Turbulence Due to a Mean Magnetic Field. Ph.D. Thesis, College of William and Mary, Williamsburg, VA, USA, 1982. [Google Scholar]
- Shebalin, J.V. Broken ergodicity and coherent structure in homogeneous turbulence. Phys. D 1989, 37, 173–191. [Google Scholar] [CrossRef]
- Shebalin, J.V. Dynamo action in dissipative, forced, rotating MHD turbulence. Phys. Plasmas 2016, 23, 062318. [Google Scholar] [CrossRef]
- Shebalin, J.V. Magnetic Helicity and the Geodynamo. Fluids 2021, 6, 99. [Google Scholar] [CrossRef]
- Woltjer, L. A theorem on force-free magnetic fields. Proc. Nat. Acad. Sci. USA 1958, 44, 489–491. [Google Scholar] [CrossRef]
- Shebalin, J.V. Ideal homogeneous magnetohydrodynamic turbulence in the presence of rotation and a mean magnetic field. J. Plasma Phys. 2006, 72, 507–524. [Google Scholar] [CrossRef]
- Shebalin, J.V. Transition to Equilibrium and Coherent Structure in Ideal MHD Turbulence. Fluids 2023, 8, 107. [Google Scholar] [CrossRef]
- Shebalin, J.V. Transition to Equilibrium and Coherent Structure in Ideal MHD Turbulence, Part 2. Fluids 2023, 8, 181. [Google Scholar] [CrossRef]
- Taylor, J.B. Relaxation of Toroidal Plasma and Generation of Reverse Magnetic Fields. Phys. Rev. Lett. 1974, 33, 1139–1141. [Google Scholar] [CrossRef]
- Biskamp, D. Magnetohydrodynamic Turbulence; Cambridge U.P.: Cambridge, UK, 2003; Chapter 2. [Google Scholar]
- Polovin, R.V.; Demutskii, V.P. Fundamentals of Magnetohydrodynamics; Consultants Bureau: New York, NY, USA, 1990. [Google Scholar]
- Goedbloed, J.P.; Keppens, R.; Poedts, S. Magnetohydrodynamics of Laboratory and Astrophysical Plasmas; Cambridge U.P.: New York, NY, USA, 2019. [Google Scholar]
- Favier, B.F.N.; Godeferd, F.S.; Cambon, C.; Delache, A.; Bos, W.J.T. Quasi-static magnetohydrodynamic turbulence at high Reynolds number. J. Fluid Mech. 2011, 681, 434–461. [Google Scholar] [CrossRef][Green Version]
- Favier, B.F.N.; Godeferd, F.S.; Cambon, C. On the effect of rotation on magnetohydrodynamic turbulence at high magnetic Reynolds number. Geophys. Astrophys. Fluid Dyn. 2012, 106, 89–111. [Google Scholar] [CrossRef][Green Version]
- Birkhoff, G.D. Dynamical Systems; American Mathematical Soc.: Providence, RI, USA, 1927. [Google Scholar]
- Khinchin, A.I. Mathematical Foundations of Statistical Mechanics; Dover: New York, NY, USA, 1949; pp. 137–145. [Google Scholar]
- Pathria, R.K. Statistical Mechanics, 2nd ed.; Elsevier: Oxford, UK, 1972. [Google Scholar]
- Landau, L.D.; Lishitz, E.M. Statistical Physics, Part 1, 3rd ed.; Pergamon: Oxford, UK, 1980. [Google Scholar]
- Lee, T.D. On some statistical properties of Hydrodynamical and magneto-hydrodynamical fields. Q. Appl. Math. 1952, 10, 69–74. [Google Scholar] [CrossRef]
- Fyfe, D.; Montgomery, D. High beta turbulence in two-dimensional magneto-hydrodynamics. J. Plasma Phys. 1976, 16, 181–191. [Google Scholar] [CrossRef][Green Version]
- Pouquet, A.; Patterson, G.S. Numerical simulation of helical magnetohydrodynamic turbulence. J. Fluid Mech. 1978, 85, 305–323. [Google Scholar] [CrossRef]
- Palmer, R.G. Broken ergodicity. Adv. Phys. 1982, 31, 669–735. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Goldstein, M.L. Stationarity of Magnetohydrodynamic Fluctuations in the Solar Wind. J. Geophys. Res. 1982, 87, 10347–10354. [Google Scholar] [CrossRef]
- Servidio, S.; Matthaeus, W.H.; Carbone, V. Ergodicity of ideal Galerkin three-dimensional magnetohydrodynamics and Hall magnetohydrodynamics models. Phys. Rev. E 2008, 78, 046302. [Google Scholar] [CrossRef]
- Silvester, J.R. Determinants of block matrices. Math. Gaz. 2000, 84, 460–467. [Google Scholar] [CrossRef]
- Andrews, G.E. Number Theory; Dover Pubs.: New York, NY, USA, 1994; p. 148. [Google Scholar]
- Galtier, S. Weak turbulence theory for rotating magnetohydrodynamics and planetary flows. J. Fluid Mech. 2014, 757, 114–154. [Google Scholar] [CrossRef]
- Sauppe, J.P.; Sovinec, C.R. Two-fluid and finite Larmor radius effects on helicity evolution in a plasma pinch. Phys. Plasmas 2016, 23, 032303. [Google Scholar] [CrossRef]
- Menu, M.D.; Galtier, S.; Petitdemange, K. Inverse cascade of hybrid helicity in BΩ-MHD turbulence. Phys. Rev. Fluids 2019, 4, 073701. [Google Scholar] [CrossRef]
- Shebalin, J.V. Broken symmetry in ideal magnetohydrodynamic turbulence. Phys. Plasmas 1994, 1, 541–547. [Google Scholar] [CrossRef][Green Version]
- Orszag, S.A.; Patterson, G.S. Numerical simulation of three-dimensional homogeneous isotropic turbulence. Phys. Rev. Lett. 1972, 28, 76–79. [Google Scholar] [CrossRef]
- Patterson, G.S.; Orszag, S.A. Spectral calculation of isotropic turbulence: Efficient removal of aliasing interaction. Phys. Fluids 1971, 14, 2538–2541. [Google Scholar] [CrossRef]
- Gazdag, J. Time-differencing schemes and transform methods. J. Comp. Phys. 1976, 20, 196–207. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Helical turbulence and absolute equilibrium. J. Fluid Mech. 1973, 59, 745–752. [Google Scholar] [CrossRef]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 4th ed.; Academic Press: New York, NY, USA, 1995; pp. 1005–1008. [Google Scholar]
- Alken, P.; Thébault, E.; Beggan, C.D.; Aubert, J.; Baerenzung, J.; Brown, W.J.; Califf, S.; Chulliat, A.; Cox, G.A.; Finlay, C.C.; et al. International Geomagnetic Reference Field: The 13th generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Shebalin, J.V. Mantle Electrical Conductivity and the Magnetic Field at the Core-Mantle Boundary. Fluids 2021, 6, 403. [Google Scholar] [CrossRef]
- Galanti, B.; Tsinober, A. Is turbulence ergodic? Phys. Lett. A 2004, 330, 173–180. [Google Scholar] [CrossRef]
- Shepherd, T.G. Non-ergodicity of inviscid two-dimensional flow on a beta-plane and on the surface of a rotating sphere. J. Fluid Mech. 1987, 184, 289–302. [Google Scholar] [CrossRef]
- Brown, M.R.; Schaffner, D.A.; Weck, P.J. Magnetohydrodynamic turbulence: Observation and experimental observations. Phys. Plasmas 2015, 22, 055601. [Google Scholar] [CrossRef]
- Yamazaki, K. Ergodicity of A Galerkin Approximation of Three-Dimensional Magnetohydrodynamics System Forced by A Degenerate Noise. Stochastics 2019, 91, 114–142. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).