Experimental Studies on Vortex-Induced Vibration of a Piggyback Pipeline
Abstract
1. Introduction
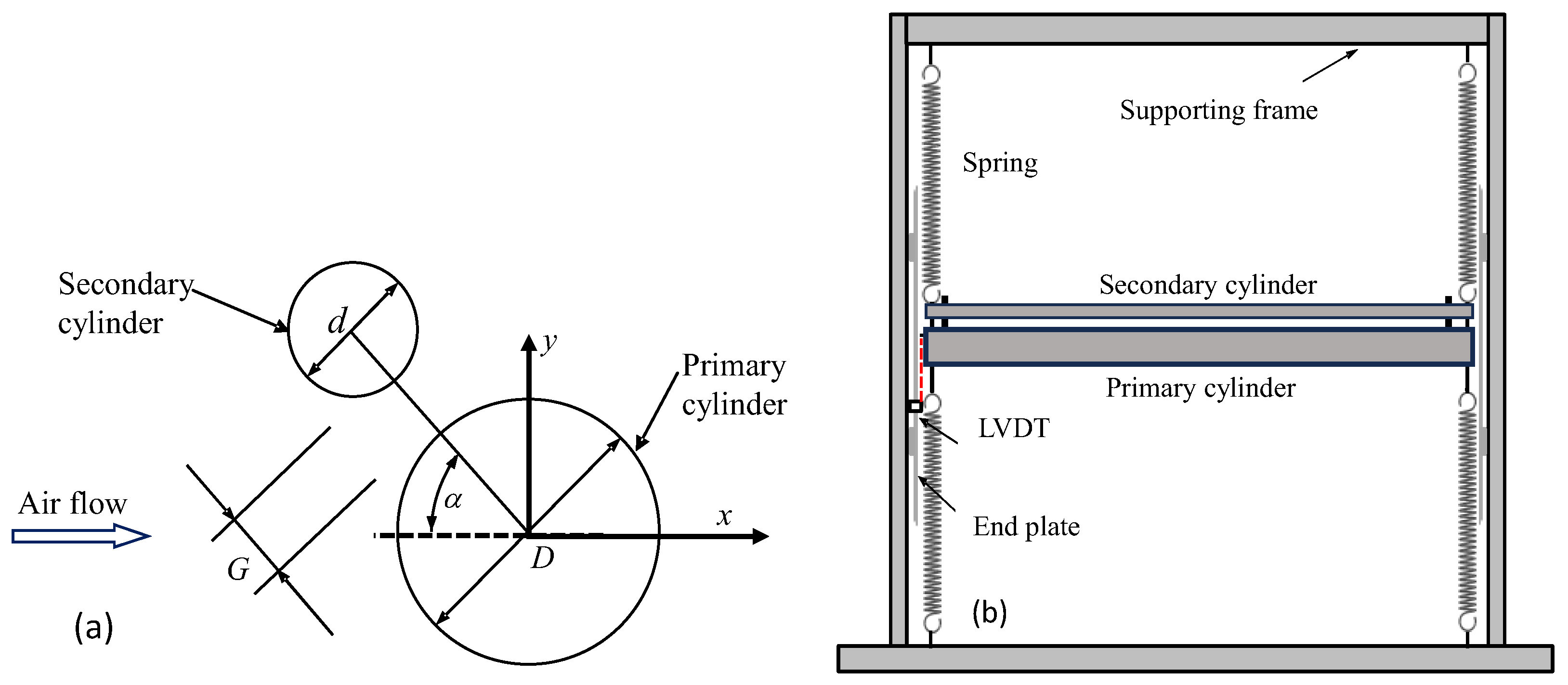
2. Experimental Set Up
3. Results and Discussion
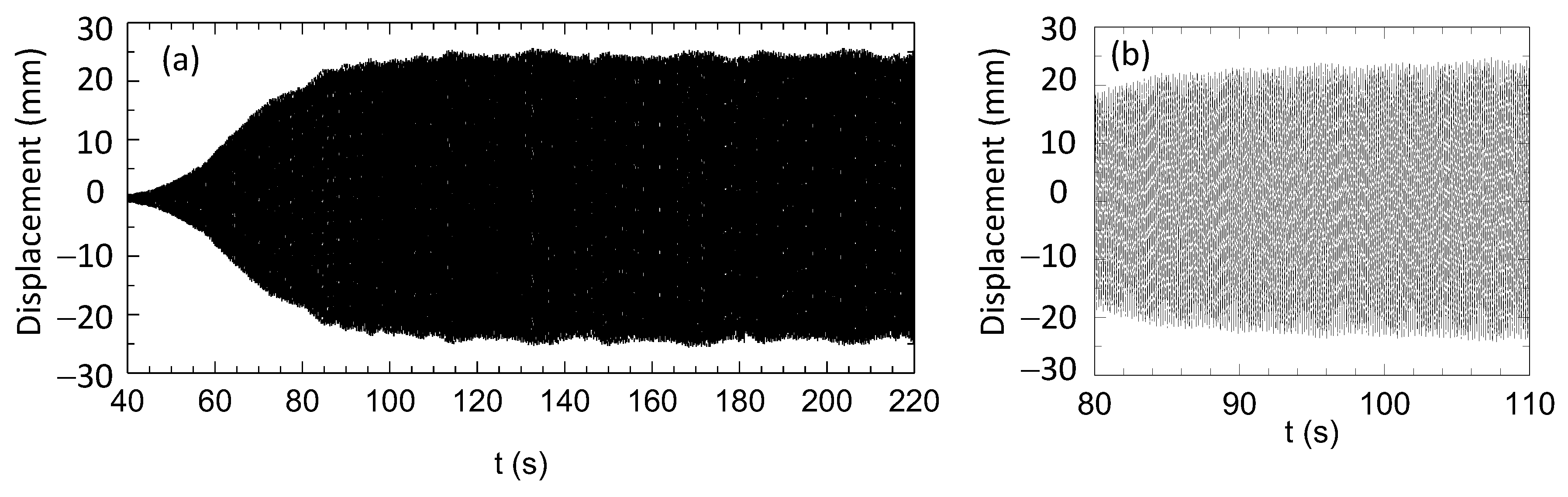
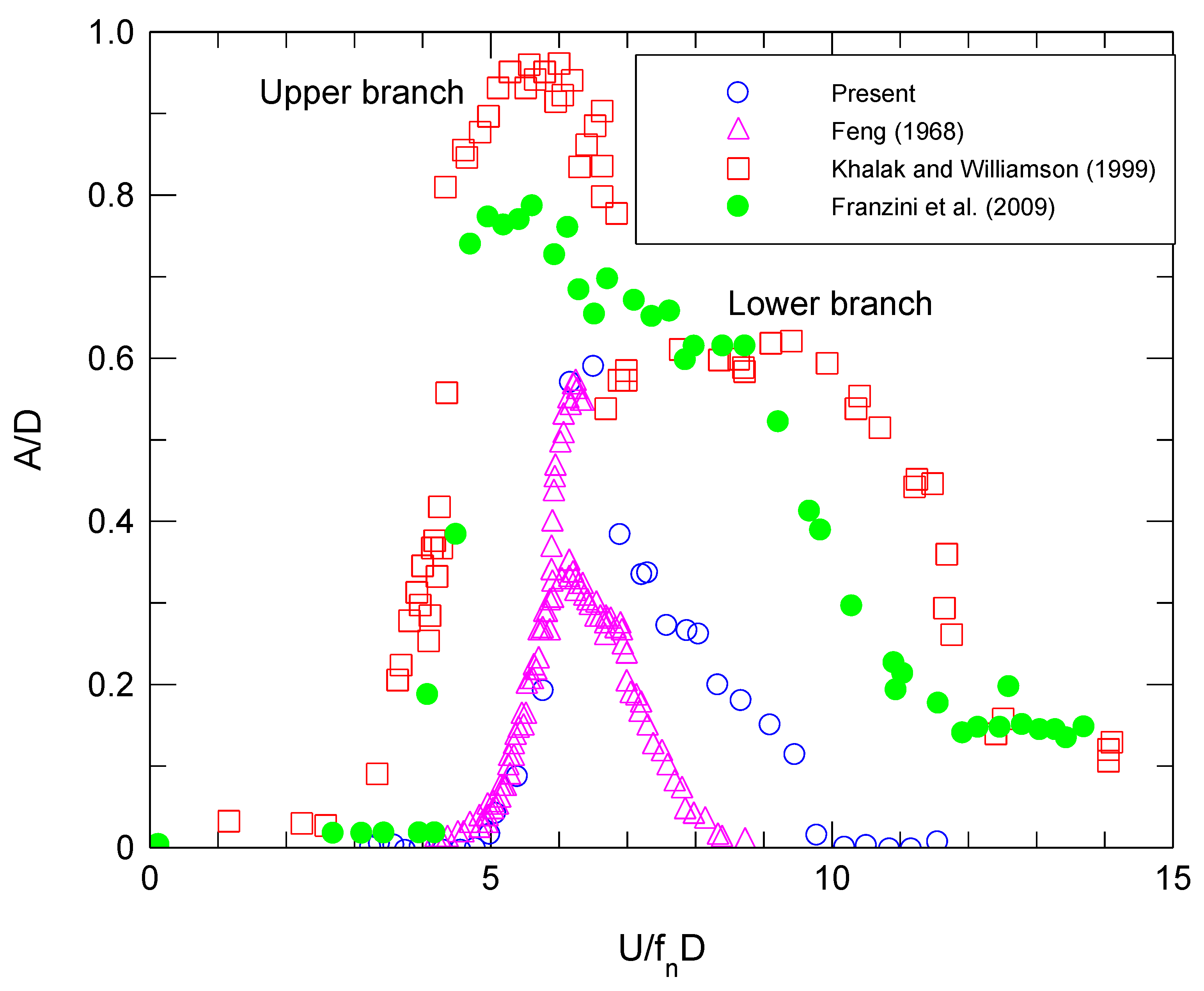
3.1. Single Cylinder with D = 80 mm
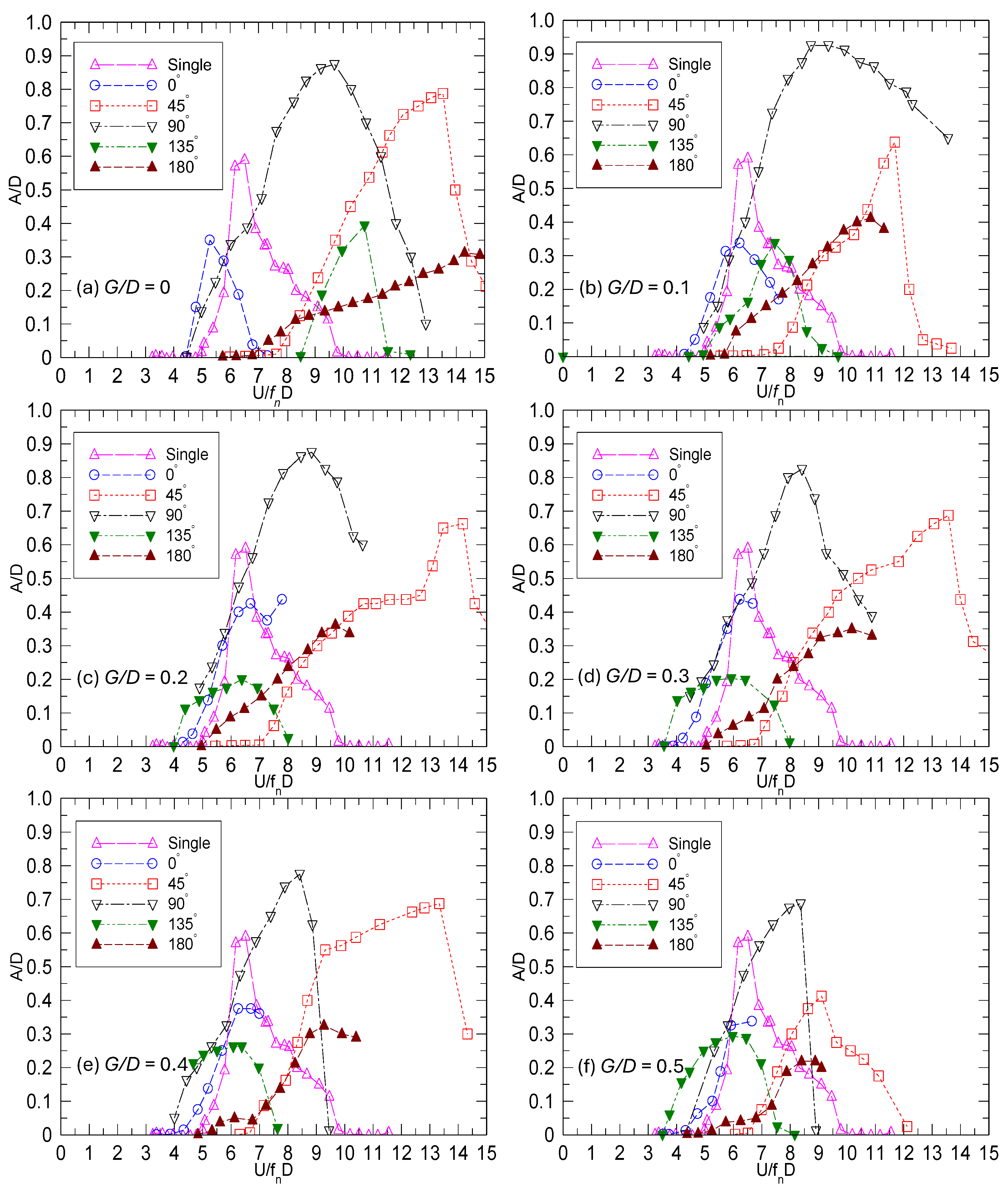
3.2. Vibration Amplitude of the Piggyback Pipeline at Different G/D and α
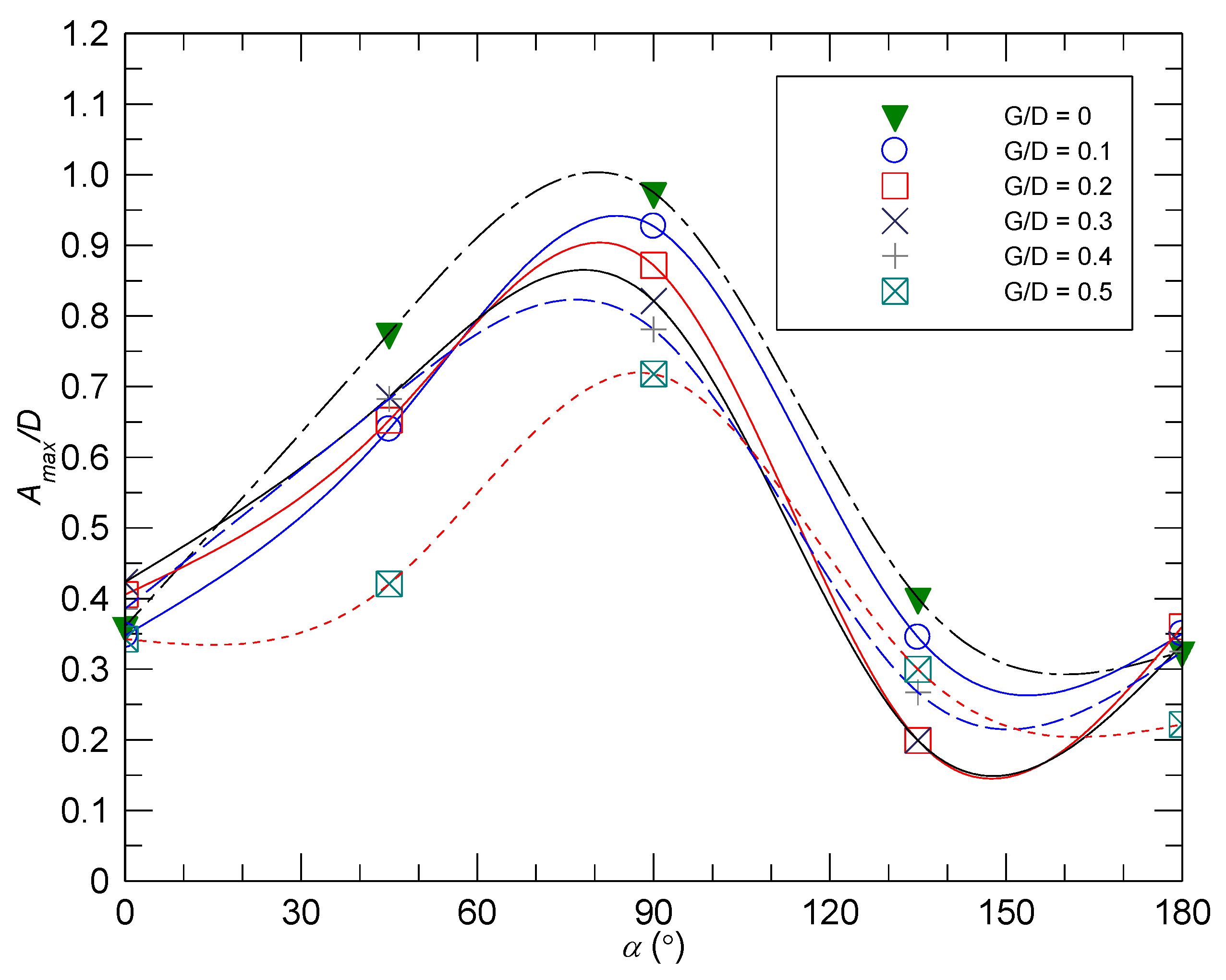
3.3. Effects of α on Amax for Given Values of G/D
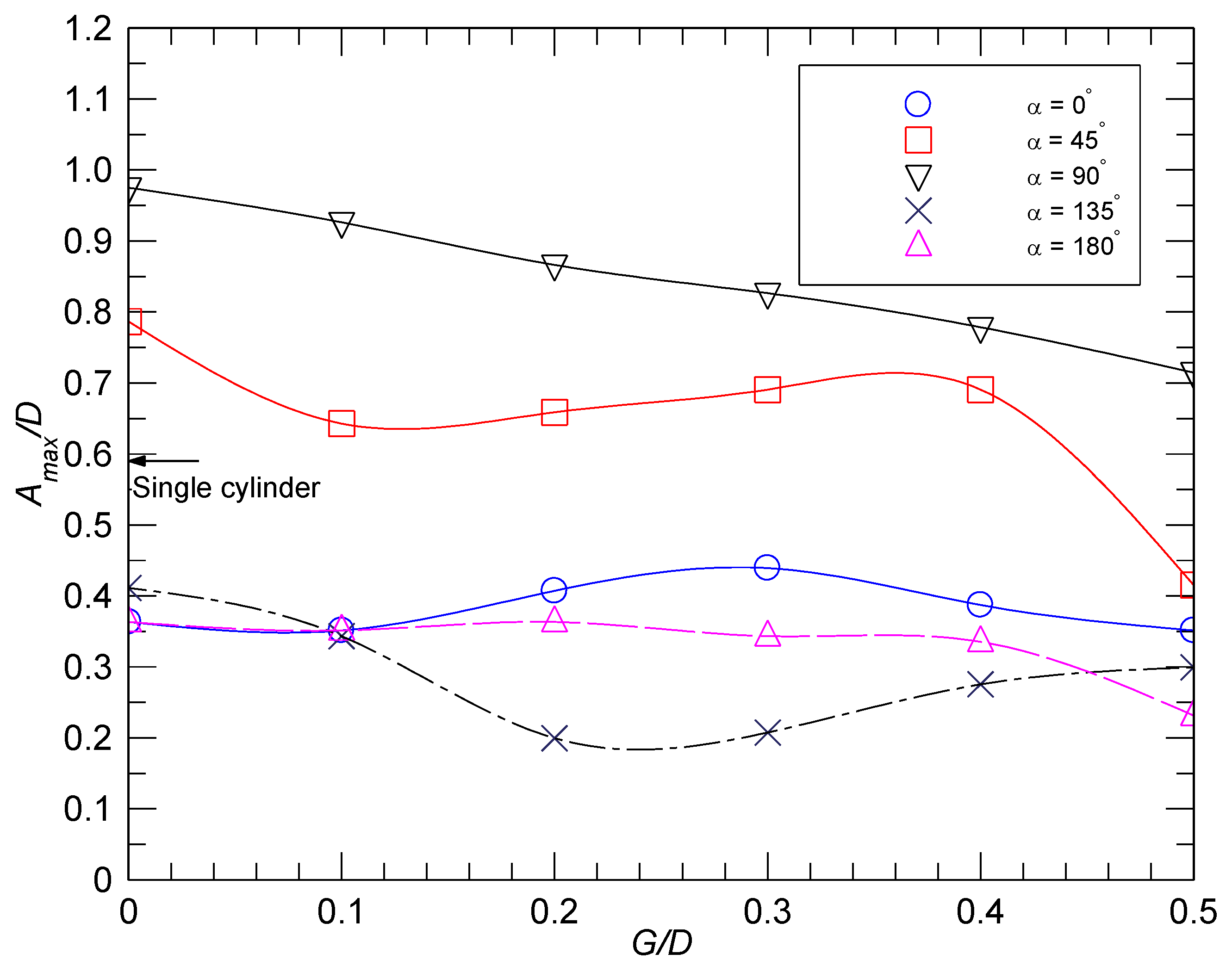
3.4. Effect of G/D on Amax for Given Values of α
4. Conclusions
- The position angle and gap ratio have significant effects on the amplitude of VIV. The maximum vibration amplitudes are higher in some configurations and lower in other configurations than that experienced by a single cylinder.
- The minimum amplitude of vibration occurs around α = 135° for a gap ratio G/D = 0.2–0.3. The maximum amplitude of vibration occurs around α = 90° with G/D = 0 due to the large equivalent diameter.
- The effect of gap ratio on the amplitude of VIV is also dependent on the position angle. Increasing the gap ratio generally reduces the amplitude of vibration, as the two cylinders behave less as one equivalent large cylinder and more as two independent cylinders. This effect is more obvious at α = 45°, 90°, and 135° than at other angles.
- The introduction of a clear vertical gap or opening can significantly disrupt vortex shedding downstream, and, hence, reduce the amplitude of the VIV. This was noticed for α = 45° and 90°.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Igarashi, T. 1982 Characteristics of a flow around two circular cylinders of different diameters arranged in tandem, 1st report. Bull. JSME 1982, 25, 349–357. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Teng, T.; Liang, D. Numerical simulation of viscous flow past two circular cylinders of different diameters. Appl. Ocean Res. 2005, 27, 39–55. [Google Scholar] [CrossRef]
- Alam, M.M.; Zhou, Y. Strouhal numbers, forces and flow structures around two tandem cylinders of different diameters. J. Fluids Struct. 2008, 24, 505–526. [Google Scholar] [CrossRef]
- Gao, Y.Y.; Wang, X.; Tan, D.S.; Keat, S.K. Particle image velocimetry technique measurements of the near wake behind a cylinder-pair of unequal diameters. Fluid Dyn. Res. 2013, 45, 045504. [Google Scholar] [CrossRef]
- Cheng, X.F.; Yang, J.; Xu, T.J.; Xu, Q. Study on Hydrodynamic Coefficients of a Submarine Piggyback Pipeline under the Action of Waves and Current. J. Mar. Sci. Eng. 2021, 9, 1118. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1987, 1, 239–261. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Review of interference-induced oscillation in flow past two parallel circular cylinders in various configurations. J. Wind. Eng. Ind. Aerodyn. 1988, 28, 183–199. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Flow Around Circular Cylinders, Volume 2: Applications; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Medeiros, E.B.; Zdravkovich, M.M. Interference-induced oscillations of two unequal cylinders. J. Wind. Eng. Ind. Aerodyn. 1992, 41, 753–762. [Google Scholar] [CrossRef]
- Zang, Z.; Gao, F. Vortex shedding and vortex-induced vibration of piggyback pipelines in steady currents. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012. [Google Scholar]
- Zang, Z.; Gao, F. Steady current induced vibration of near-bed piggyback pipelines: Configuration effects on VIV suppression. Appl. Ocean Res. 2014, 46, 62–69. [Google Scholar] [CrossRef]
- Zhao, M.; Yan, G. Numerical simulation of vortex-induced vibration of two circular cylinders of different diameters at low Reynolds number. Phys. Fluids 2013, 25, 083601. [Google Scholar] [CrossRef]
- Rahmanian, M.; Zhao, M.; Cheng, L.; Zhou, T. Two-degree-of-freedom vortex-induced vibration of two mechanically coupled cylinders of different diameters in steady current. J. Fluids Struct. 2012, 35, 133–159. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C.H.K. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 1999, 13, 813–851. [Google Scholar] [CrossRef]
- Jauvtis, N.; Williamson, C.H.K. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 2004, 509, 23–62. [Google Scholar] [CrossRef]
- Serta, C.P.V.; Janocha, M.J.; Yin, G.; Ong, M.C. Numerical simulations of flow-induced vibrations of two rigidly coupled cylinders with uneven diameters in the upper transition Reynolds number regime. J. Fluids Struct. 2021, 105, 103332. [Google Scholar] [CrossRef]
- Janocha, M.J.; Ong, M.C. Vortex-induced vibrations of piggyback pipelines near the horizontal plane wall in the upper transition regime. Mar. Struct. 2021, 75, 102872. [Google Scholar] [CrossRef]
- Chen, L.F.; Wu, G.X. Vortex-induced three-degree-of-freedom vibration of a piggyback circular cylinder system. Appl. Ocean. Res. 2022, 123, 103145. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, S.; Wang, L.; Huan, C.; Zhang, J. Numerical Investigation on Vortex-Induced Vibrations of Two Cylinders with Unequal Diameters. J. Mar. Sci. Eng. 2023, 11, 377. [Google Scholar] [CrossRef]
- Yuan, W.; Sun, H.; Li, H.; Bernitsas, M.M. Flow-induced oscillation patterns for two tandem cylinders with turbulence stimulation and variable stiffness and damping. Ocean. Eng. 2020, 218, 108237. [Google Scholar] [CrossRef]
- Sukarnoor, N.I.M.; Quena, L.K.; Abu, A.; Siang, K.H.; Kuwano, N.; Desa, S.M. An investigation of the dynamic behaviour of two rigid cylinders in a tandem arrangement under vortex-induced vibration. J. Ocean Eng. Sci. 2022; in press. [Google Scholar]
- Pal, A.; Soti, A.K. Power harvesting from VIV of rigidly-coupled cylinders in tandem arrangement. In Proceedings of the 48th National Conference on Fluid Mechanics and Fluid Power (FMFP), BITS Pilani, Pilani Campus, Rajasthan, India, 27–29 December 2021. [Google Scholar]
- West, G.S.; Apelt, C.J. The effects of tunnel blockage and aspect ratio on the mean flow past a circular cylinder with Reynolds number between 104 and 105. J. Fluid Mech. 1982, 114, 361–377. [Google Scholar] [CrossRef]
- Xu, G.; Zhou, Y. Strouhal numbers in the wake of two incline cylinders. Expts. Fluids 2004, 37, 248–256. [Google Scholar] [CrossRef]
- Kline, S.J.; McClintock, F.A. Describing uncertainties in single experiments. Mech. Eng. 1953, 75, 3. [Google Scholar]
- Moffat, R.J. Using uncertainty analysis in the planning of an experiment. J. Fluids Eng. 1985, 107, 173. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3. [Google Scholar] [CrossRef]
- Hover, F.S.; Triantafyllou, M.S. Vortex-induced vibrations of a cylinder with tripping wires. J. Fluid Mech. 2001, 448, 175–195. [Google Scholar] [CrossRef]
- Franzini, G.R.; Fujarra, A.L.C.; Meneghini, J.R.; Korkischko, I.; Franciss, R. Experimental investigation of vortex-induced vibration on rigid, smooth and inclined cylinders. J. Fluids Struct. 2009, 25, 742–750. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Hydrodynamics around Cylindrical Structures; World Scientific: Singapore, 2006. [Google Scholar]
- Feng, C.C. The measurement of vortex induced effects in flow past stationary and oscillating circular and D section cylinders. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 1968. [Google Scholar]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluid Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, L. Vortex shedding around two circular cylinders of different diameters. In Proceedings of the Ninth International Offshore and Polar Engineering Conference, Brest, France, 30 May–4 June 1999. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, D.; Hao, Z.; Zhou, T.; Zhu, H. Experimental Studies on Vortex-Induced Vibration of a Piggyback Pipeline. Fluids 2024, 9, 39. https://doi.org/10.3390/fluids9020039
Xiao D, Hao Z, Zhou T, Zhu H. Experimental Studies on Vortex-Induced Vibration of a Piggyback Pipeline. Fluids. 2024; 9(2):39. https://doi.org/10.3390/fluids9020039
Chicago/Turabian StyleXiao, Difei, Zhiyong Hao, Tongming Zhou, and Hongjun Zhu. 2024. "Experimental Studies on Vortex-Induced Vibration of a Piggyback Pipeline" Fluids 9, no. 2: 39. https://doi.org/10.3390/fluids9020039
APA StyleXiao, D., Hao, Z., Zhou, T., & Zhu, H. (2024). Experimental Studies on Vortex-Induced Vibration of a Piggyback Pipeline. Fluids, 9(2), 39. https://doi.org/10.3390/fluids9020039







