A Parametric 3D Model of Human Airways for Particle Drug Delivery and Deposition
Abstract
1. Introduction
2. Materials and Methods
2.1. Baseline Geometry and Centerline Extraction
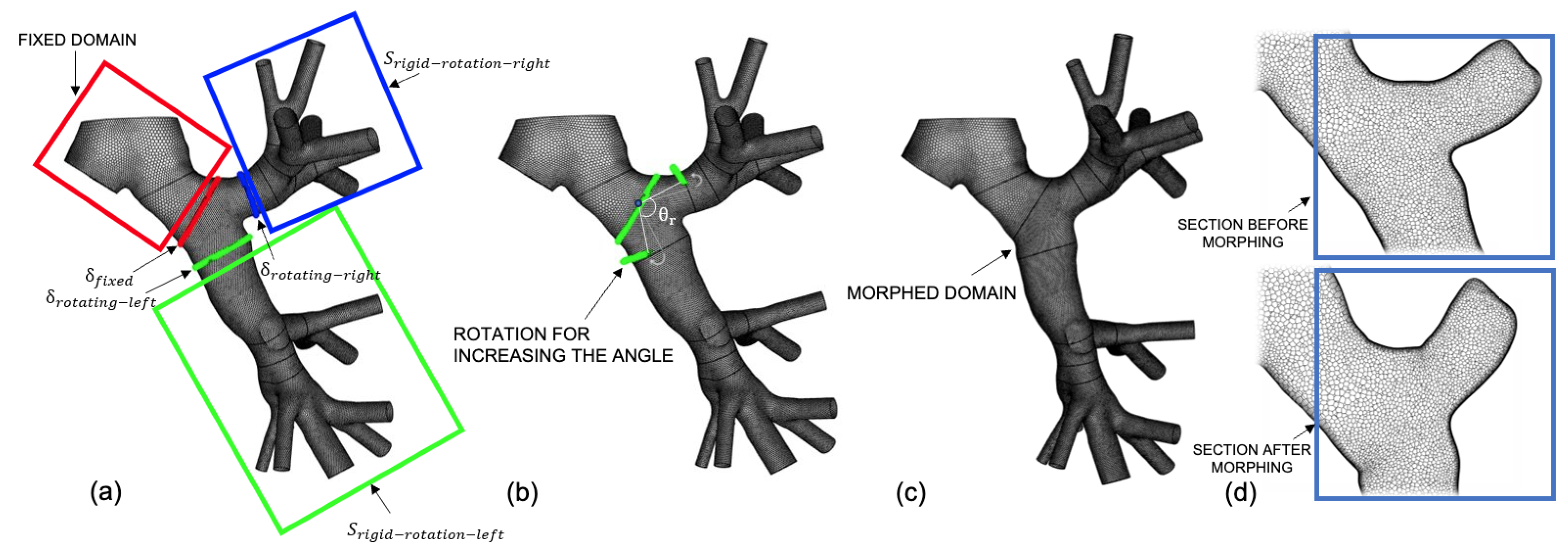
2.2. Mesh Generation and Decomposition
2.3. RBF Mesh Morphing Background
2.4. RBF Mesh Morphing Application
| Algorithm 1: |
|
- The normalized dot product of the area vector of a face (), whose direction is given by the orientation of the face in space, and a vector from the centroid of the cell to the centroid of that face :
- The normalized dot product of the area vector of a face () and a vector from the centroid of the cell to the centroid of the adjacent cell that shares that face ():
2.4.1. Translation
| Algorithm 2: |
|
2.4.2. Rotation
| Algorithm 3: |
|
2.4.3. Offset
| Algorithm 4: |
|
2.5. Synthetic Database Creation
2.6. CFD Settings
2.7. Discrete Phase Model
- (in the 0.1 µm ≤ ≤ 10 µm )
- (in the 15 L/min ≤ ≤ 190 L/min )
- (in the 1 m/s ≤ ≤ 10 m/s )
3. Results
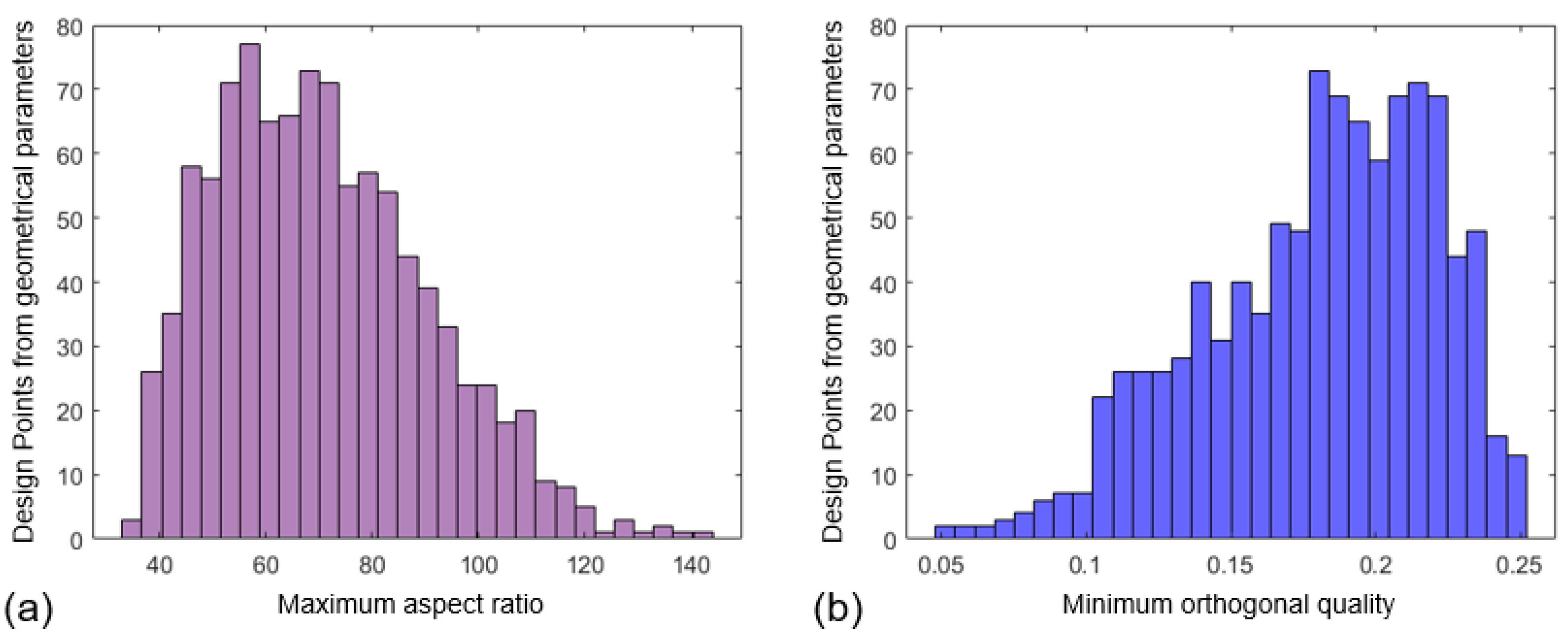
3.1. Mesh Morphing
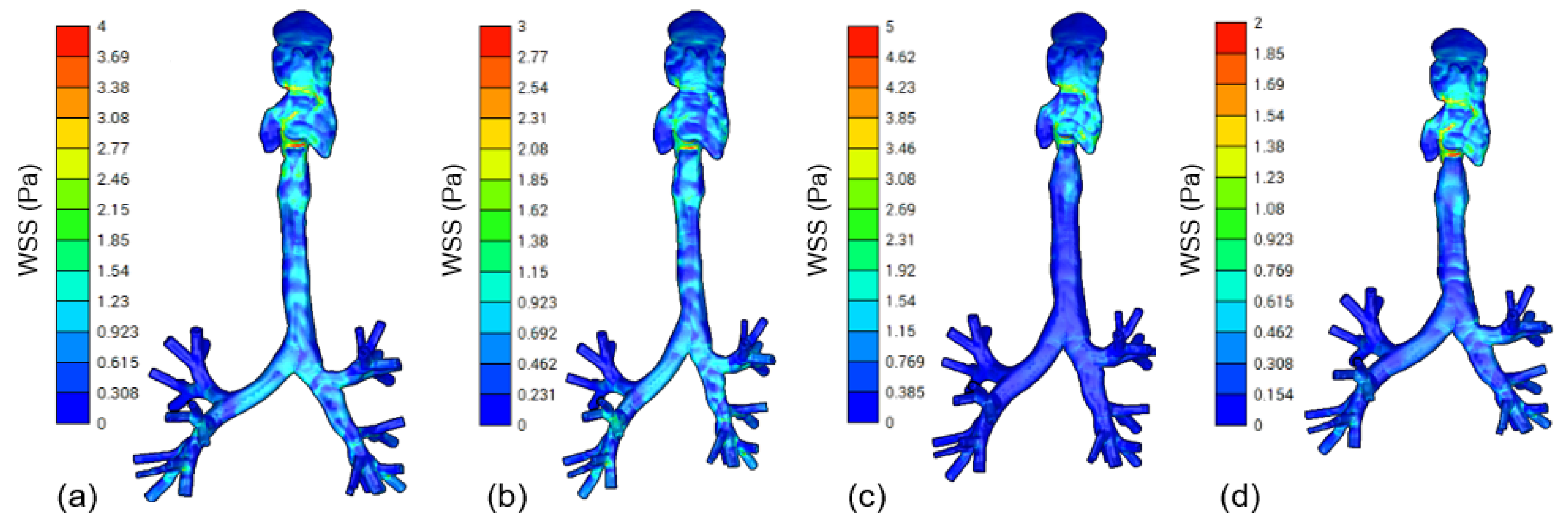
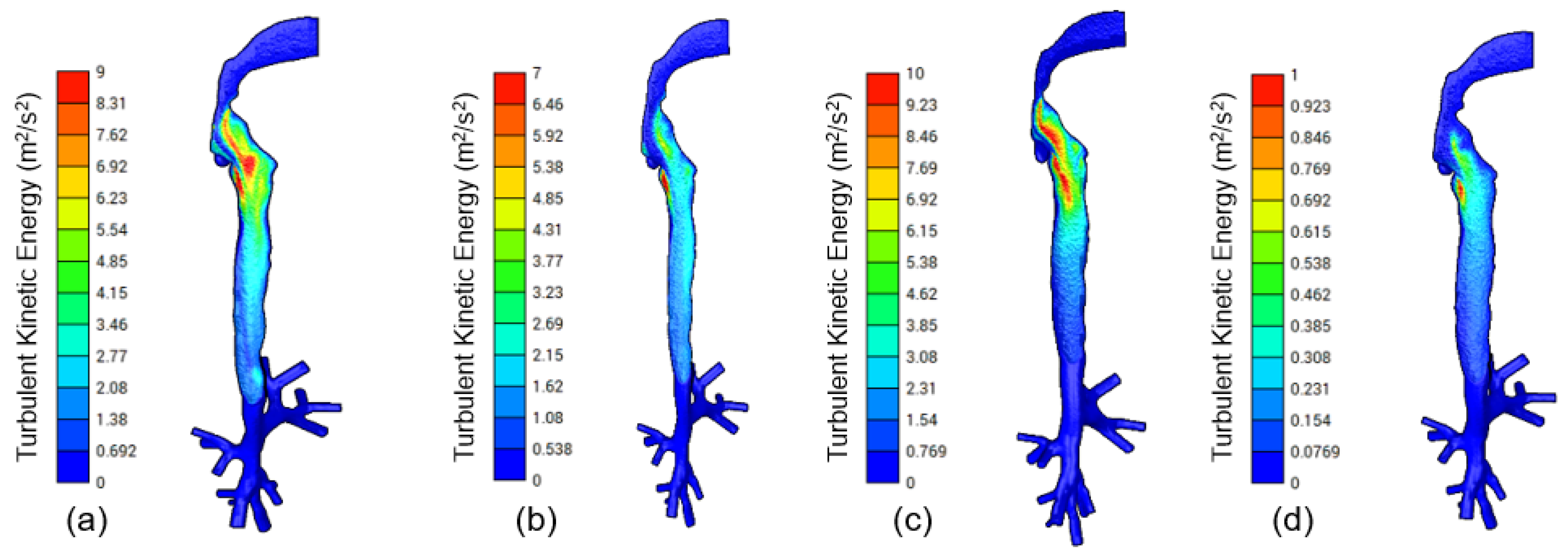
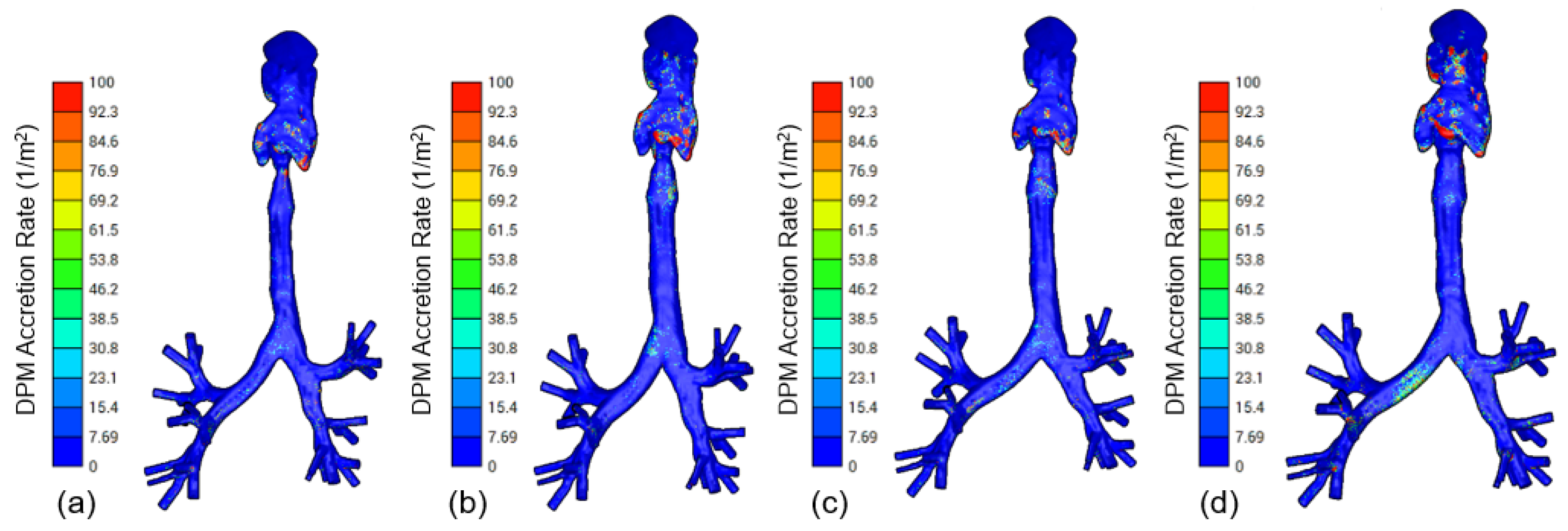
3.2. CFD Modeling
4. Discussion
Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sorino, C.; Negri, S.; Spanevello, A.; Visca, D.; Scichilone, N. Inhalation therapy devices for the treatment of obstructive lung diseases: The history of inhalers towards the ideal inhaler. Eur. J. Intern. Med. 2020, 75, 15–18. [Google Scholar] [CrossRef]
- Reddel, H.K.; Bacharier, L.B.; Bateman, E.D.; Brightling, C.E.; Brusselle, G.G.; Buhl, R.; Cruz, A.A.; Duijts, L.; Drazen, J.M.; FitzGerald, J.M.; et al. Global Initiative for Asthma Strategy 2021: Executive Summary and Rationale for Key Changes. Am. J. Respir. Crit. Care Med. 2022, 205, 17–35. [Google Scholar] [CrossRef]
- Agustí, A.; Celli, B.R.; Criner, G.J.; Halpin, D.; Anzueto, A.; Barnes, P.; Bourbeau, J.; Han, M.K.; Martinez, F.J.; Montes De Oca, M.; et al. Global Initiative for Chronic Obstructive Lung Disease 2023 Report: GOLD Executive Summary. Eur. Respir. J. 2023, 61, 2300239. [Google Scholar] [CrossRef]
- Baldi, S.; Dellaca, R.; Govoni, L.; Torchio, R.; Aliverti, A.; Pompilio, P.; Corda, L.; Tantucci, C.; Gulotta, C.; Brusasco, V.; et al. Airway distensibility and volume recruitment with lung inflation in COPD. J. Appl. Physiol. 2010, 109, 1019–1026. [Google Scholar] [CrossRef][Green Version]
- Donovan, G.M.; Wang, K.C.W.; Shamsuddin, D.; Mann, T.S.; Henry, P.J.; Larcombe, A.N.; Noble, P.B. Pharmacological ablation of the airway smooth muscle layer—Mathematical predictions of functional improvement in asthma. Physiol. Rep. 2020, 8, e14451. [Google Scholar] [CrossRef]
- Thomas, M.L.; Longest, P.W. Evaluation of the polyhedral mesh style for predicting aerosol deposition in representative models of the conducting airways. J. Aerosol Sci. 2022, 159, 105851. [Google Scholar] [CrossRef]
- Rahman, M.; Zhao, M.; Islam, M.S.; Dong, K.; Saha, S.C. Nanoparticle transport and deposition in a heterogeneous human lung airway tree: An efficient one path model for CFD simulations. Eur. J. Pharm. Sci. 2022, 177, 106279. [Google Scholar] [PubMed]
- Longest, P.W.; Tian, G.; Khajeh-Hosseini-Dalasm, N.; Hindle, M. Validating Whole-Airway CFD Predictions of DPI Aerosol Deposition at Multiple Flow Rates. J. Aerosol Med. Pulm. Drug Deliv. 2016, 29, 461–481. [Google Scholar] [CrossRef] [PubMed]
- Bui, V.K.H.; Moon, J.Y.; Chae, M.; Park, D.; Lee, Y.C. Prediction of aerosol deposition in the human respiratory tract via computational models: A review with recent updates. Atmosphere 2020, 11, 137. [Google Scholar] [CrossRef]
- Leclerc, L.; Prévôt, N.; Hodin, S.; Delavenne, X.; Mentzel, H.; Schuschnig, U.; Pourchez, J. Acoustic Aerosol Delivery: Assessing of Various Nasal Delivery Techniques and Medical Devices on Intrasinus Drug Deposition. Pharmaceuticals 2023, 16, 135. [Google Scholar] [CrossRef]
- Hofmann, W. Modelling inhaled particle deposition in the human lung—A review. J. Aerosol Sci. 2011, 42, 693–724. [Google Scholar] [CrossRef]
- Longest, P.W.; Bass, K.; Dutta, R.; Rani, V.; Thomas, M.L.; El-Achwah, A.; Hindle, M. Use of computational fluid dynamics deposition modeling in respiratory drug delivery. Expert Opin. Drug Deliv. 2019, 16, 7–26. [Google Scholar]
- Kharat, S.B.; Deoghare, A.B.; Pandey, K.M. Development of human airways model for CFD analysis. Mater. Today Proc. 2018, 5, 12920–12926. [Google Scholar]
- Leong, S.; Chen, X.; Lee, H.; Wang, D. A review of the implications of computational fluid dynamic studies on nasal airflow and physiology. Rhinology 2010, 48, 139. [Google Scholar] [PubMed]
- James Ayodele, O.; Ebenezer Oluwatosin, A.; Christian Taiwo, O.; Adebukola Dare, A. Computational Fluid Dynamics Modeling in Respiratory Airways Obstruction: Current Applications and Prospects. Int. J. Biomed. Sci. Eng. 2021, 9, 16. [Google Scholar] [CrossRef]
- Faizal, W.; Ghazali, N.N.N.; Khor, C.; Badruddin, I.A.; Zainon, M.; Yazid, A.A.; Ibrahim, N.B.; Razi, R.M. Computational fluid dynamics modelling of human upper airway: A review. Comput. Methods Programs Biomed. 2020, 196, 105627. [Google Scholar]
- Shang, Y.; Dong, J.; Tian, L.; Inthavong, K.; Tu, J. Detailed computational analysis of flow dynamics in an extended respiratory airway model. Clin. Biomech. 2019, 61, 105–111. [Google Scholar]
- Kenjereš, S.; Tjin, J.L. Numerical simulations of targeted delivery of magnetic drug aerosols in the human upper and central respiratory system: A validation study. R. Soc. Open Sci. 2017, 4, 170873. [Google Scholar] [CrossRef]
- Tullio, M.; Aliboni, L.; Pennati, F.; Carrinola, R.; Palleschi, A.; Aliverti, A. Computational fluid dynamics of the airways after left-upper pulmonary lobectomy: A case study. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3462. [Google Scholar] [CrossRef]
- Tanprasert, S.; Kampeewichean, C.; Shiratori, S.; Piemjaiswang, R.; Chalermsinsuwan, B. Non-spherical drug particle deposition in human airway using computational fluid dynamics and discrete element method. Int. J. Pharm. 2023, 639, 122979. [Google Scholar] [CrossRef]
- Inthavong, K.; Zhang, K.; Tu, J. Numerical modelling of nanoparticle deposition in the nasal cavity and the tracheobronchial airway. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 633–643. [Google Scholar]
- Feng, Y.; Zhao, J.; Kleinstreuer, C.; Wang, Q.; Wang, J.; Wu, D.H.; Lin, J. An in silico inter-subject variability study of extra-thoracic morphology effects on inhaled particle transport and deposition. J. Aerosol Sci. 2018, 123, 185–207. [Google Scholar] [CrossRef]
- Zhang, Z.; Kleinstreuer, C.; Hyun, S. Size-change and deposition of conventional and composite cigarette smoke particles during inhalation in a subject-specific airway model. J. Aerosol Sci. 2012, 46, 34–52. [Google Scholar] [CrossRef]
- Geitner, C.M.; Köglmeier, L.J.; Frerichs, I.; Langguth, P.; Lindner, M.; Schädler, D.; Weiler, N.; Becher, T.; Wall, W.A. Pressure-and time-dependent alveolar recruitment/derecruitment in a spatially resolved patient-specific computational model for injured human lungs. arXiv 2023, arXiv:2305.14408. [Google Scholar] [CrossRef] [PubMed]
- Geitner, C.M.; Becher, T.; Frerichs, I.; Weiler, N.; Bates, J.H.T.; Wall, W.A. An approach to study recruitment/derecruitment dynamics in a patient-specific computational model of an injured human lung. Int. J. Numer. Methods Biomed. Eng. 2023, 39, e3745. [Google Scholar] [CrossRef] [PubMed]
- Radulesco, T.; Meister, L.; Bouchet, G.; Varoquaux, A.; Giordano, J.; Mancini, J.; Dessi, P.; Perrier, P.; Michel, J. Correlations between computational fluid dynamics and clinical evaluation of nasal airway obstruction due to septal deviation: An observational study. Clin. Otolaryngol. 2019, 44, 603–611. [Google Scholar] [CrossRef] [PubMed]
- Spasov, G.; Rossi, R.; Vanossi, A.; Cottini, C.; Benassi, A. A critical analysis of the CFD-DEM simulation of pharmaceutical aerosols deposition in extra-thoracic airways. Int. J. Pharm. 2022, 629, 122331. [Google Scholar] [CrossRef]
- Ponzini, R.; Da Vià, R.; Bnà, S.; Cottini, C.; Benassi, A. Coupled CFD-DEM model for dry powder inhalers simulation: Validation and sensitivity analysis for the main model parameters. Powder Technol. 2021, 385, 199–226. [Google Scholar] [CrossRef]
- Grill, M.J.; Biehler, J.; Wichmann, K.R.; Rudlstorfer, D.; Rixner, M.; Brei, M.; Richter, J.; Bügel, J.; Pischke, N.; Wall, W.A.; et al. In silico high-resolution whole lung model to predict the locally delivered dose of inhaled drugs. arXiv 2023, arXiv:2307.04757. [Google Scholar]
- Barrio-Perotti, R.; Martín-Fernández, N.; Vigil-Díaz, C.; Walters, K.; Fernández-Tena, A. Predicting particle deposition using a simplified 8-path in silico human lung prototype. J. Breath Res. 2023, 17, 046002. [Google Scholar]
- Soni, B.; Aliabadi, S. Large-scale CFD simulations of airflow and particle deposition in lung airway. Comput. Fluids 2013, 88, 804–812. [Google Scholar]
- Benassi, A.; Cottini, C. Numerical simulations for inhalation product development: Achievements and current limitations. ONdrugDelivery 2021, 127, 68–75. [Google Scholar]
- Shang, Y.; Tian, L.; Fan, Y.; Dong, J.; Inthavong, K.; Tu, J. Effect of morphology on nanoparticle transport and deposition in human upper tracheobronchial airways. J. Comput. Multiph. Flows 2018, 10, 83–96. [Google Scholar]
- Aghababaie, M.; Suresh, V.; McGlashan, S.; Tawhai, M.; Burrowes, K. In silico prediction of e-cigarette aerosol particle transport and deposition within the airways. In Proceedings of the 2023 45th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Sydney, Australia, 24–27 July 2023; pp. 1–4. [Google Scholar]
- Farghadan, A.; Coletti, F.; Arzani, A. Topological analysis of particle transport in lung airways: Predicting particle source and destination. Comput. Biol. Med. 2019, 115, 103497. [Google Scholar] [CrossRef]
- He, Y.; Bayly, A.E.; Hassanpour, A. Coupling CFD-DEM with dynamic meshing: A new approach for fluid-structure interaction in particle-fluid flows. Powder Technol. 2018, 325, 620–631. [Google Scholar]
- Sigal, I.A.; Yang, H.; Roberts, M.D.; Downs, J.C. Morphing methods to parameterize specimen-specific finite element model geometries. J. Biomech. 2010, 43, 254–262. [Google Scholar] [CrossRef] [PubMed]
- Capellini, K.; Vignali, E.; Costa, E.; Gasparotti, E.; Biancolini, M.E.; Landini, L.; Positano, V.; Celi, S. Computational fluid dynamic study for aTAA hemodynamics: An integrated image-based and radial basis functions mesh morphing approach. J. Biomech. Eng. 2018, 140, 111007. [Google Scholar] [CrossRef]
- Capellini, K.; Gasparotti, E.; Cella, U.; Costa, E.; Fanni, B.M.; Groth, C.; Porziani, S.; Biancolini, M.E.; Celi, S. A novel formulation for the study of the ascending aortic fluid dynamics with in vivo data. Med. Eng. Phys. 2021, 91, 68–78. [Google Scholar] [CrossRef]
- Biancolini, M.E.; Capellini, K.; Costa, E.; Groth, C.; Celi, S. Fast interactive CFD evaluation of hemodynamics assisted by RBF mesh morphing and reduced order models: The case of aTAA modelling. Int. J. Interact. Des. Manuf. (IJIDeM) 2020, 14, 1227–1238. [Google Scholar] [CrossRef]
- Geronzi, L.; Gasparotti, E.; Capellini, K.; Cella, U.; Groth, C.; Porziani, S.; Chiappa, A.; Celi, S.; Biancolini, M.E. High fidelity fluid-structure interaction by radial basis functions mesh adaption of moving walls: A workflow applied to an aortic valve. J. Comput. Sci. 2021, 51, 101327. [Google Scholar] [CrossRef]
- Marin-Castrillon, D.M.; Geronzi, L.; Boucher, A.; Lin, S.; Morgant, M.C.; Cochet, A.; Rochette, M.; Leclerc, S.; Ambarki, K.; Jin, N.; et al. Segmentation of the aorta in systolic phase from 4D flow MRI: Multi-atlas vs. deep learning. Magn. Reson. Mater. Phys. Biol. Med. 2023, 36, 687–700. [Google Scholar] [CrossRef] [PubMed]
- Aykac, D.; Hoffman, E.A.; McLennan, G.; Reinhardt, J.M. Segmentation and analysis of the human airway tree from three-dimensional X-ray CT images. IEEE Trans. Med. Imaging 2003, 22, 940–950. [Google Scholar] [CrossRef] [PubMed]
- Asgari, M.; Lucci, F.; Kuczaj, A.K. Multispecies aerosol evolution and deposition in a human respiratory tract cast model. J. Aerosol Sci. 2021, 153, 105720. [Google Scholar] [CrossRef]
- Antiga, L.; Piccinelli, M.; Botti, L.; Ene-Iordache, B.; Remuzzi, A.; Steinman, D.A. An image-based modeling framework for patient-specific computational hemodynamics. Med. Biol. Eng. Comput. 2008, 46, 1097. [Google Scholar]
- Antiga, L.; Ene-Iordache, B.; Remuzzi, A. Centerline computation and geometric analysis of branching tubular surfaces with application to blood vessel modeling. In Proceedings of the WSCG, Plzen-Bory, Czech Republic, 3–7 February 2003. [Google Scholar]
- Geronzi, L.; Haigron, P.; Martinez, A.; Yan, K.; Rochette, M.; Bel-Brunon, A.; Porterie, J.; Lin, S.; Marin-Castrillon, D.M.; Lalande, A.; et al. Assessment of shape-based features ability to predict the ascending aortic aneurysm growth. Front. Physiol. 2023, 14, 378. [Google Scholar] [CrossRef]
- Yu, H.; Xie, T.; Paszczynski, S.; Wilamowski, B.M. Advantages of radial basis function networks for dynamic system design. IEEE Trans. Ind. Electron. 2011, 58, 5438–5450. [Google Scholar] [CrossRef]
- Biancolini, M.E. Fast Radial Basis Functions for Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Geronzi, L.; Martinez, A.; Rochette, M.; Yan, K.; Bel-Brunon, A.; Haigron, P.; Escrig, P.; Tomasi, J.; Daniel, M.; Lalande, A.; et al. Computer-aided shape features extraction and regression models for predicting the ascending aortic aneurysm growth rate. Comput. Biol. Med. 2023, 162, 107052. [Google Scholar] [CrossRef]
- Sorgente, T.; Biasotti, S.; Manzini, G.; Spagnuolo, M. A Survey of Indicators for Mesh Quality Assessment. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2023; Volume 42, pp. 461–483. [Google Scholar]
- Choi, S.; Yoon, S.; Jeon, J.; Zou, C.; Choi, J.; Tawhai, M.H.; Hoffman, E.A.; Delvadia, R.; Babiskin, A.; Walenga, R.; et al. 1D network simulations for evaluating regional flow and pressure distributions in healthy and asthmatic human lungs. J. Appl. Physiol. 2019, 127, 122–133. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Hoffman, E.A.; Wenzel, S.E.; Castro, M.; Fain, S.B.; Jarjour, N.N.; Schiebler, M.L.; Chen, K.; Lin, C.L. Quantitative assessment of multiscale structural and functional alterations in asthmatic populations. J. Appl. Physiol. 2015, 118, 1286–1298. [Google Scholar] [CrossRef]
- Sauret, V.; Halson, P.M.; Brown, I.W.; Fleming, J.S.; Bailey, A.G. Study of the three-dimensional geometry of the central conducting airways in man using computed tomographic (CT) images. J. Anat. 2002, 200, 123–134. [Google Scholar] [CrossRef]
- Ahookhosh, K.; Pourmehran, O.; Aminfar, H.; Mohammadpourfard, M.; Sarafraz, M.M.; Hamishehkar, H. Development of human respiratory airway models: A review. Eur. J. Pharm. Sci. 2020, 145, 105233. [Google Scholar] [CrossRef] [PubMed]
- Stein, M. Large sample properties of simulations using Latin hypercube sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Islam, M.S.; Saha, S.C.; Sauret, E.; Ong, H.; Young, P.; Gu, Y. Euler–Lagrange approach to investigate respiratory anatomical shape effects on aerosol particle transport and deposition. Toxicol. Res. Appl. 2019, 3, 2397847319894675. [Google Scholar]
- Luo, H.; Liu, Y. Modeling the bifurcating flow in a CT-scanned human lung airway. J. Biomech. 2008, 41, 2681–2688. [Google Scholar] [CrossRef] [PubMed]
- Nithiarasu, P.; Hassan, O.; Morgan, K.; Weatherill, N.; Fielder, C.; Whittet, H.; Ebden, P.; Lewis, K. Steady flow through a realistic human upper airway geometry. Int. J. Numer. Methods Fluids 2008, 57, 631–651. [Google Scholar]
- Tian, G.; Longest, P.W. Development of a CFD boundary condition to model transient vapor absorption in the respiratory airways. J. Biomech. Eng. 2010, 132, 051003. [Google Scholar] [CrossRef]
- Xu, X.; Wu, J.; Weng, W.; Fu, M. Investigation of inhalation and exhalation flow pattern in a realistic human upper airway model by PIV experiments and CFD simulations. Biomech. Model. Mechanobiol. 2020, 19, 1679–1695. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Kleinstreuer, C. Laminar-to-turbulent fluid–nanoparticle dynamics simulations: Model comparisons and nanoparticle-deposition applications. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 1930–1950. [Google Scholar]
- Langtry, R.B.; Menter, F.R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Biancolini, M.E.; Chiappa, A.; Cella, U.; Costa, E.; Groth, C.; Porziani, S. Radial basis functions mesh morphing: A comparison between the bi-harmonic spline and the wendland c2 radial function. In Proceedings of the International Conference on Computational Science, Las Vegas, NV, USA, 16–18 December 2020; pp. 294–308. [Google Scholar]
- Weibel, E. Morphometry of the human lung: The state of the art after two decades. Bull. Eur. Physiopathol. Respir. 1979, 15, 999–1013. [Google Scholar]
- Kenjereš, S. On recent progress in modelling and simulations of multi-scale transfer of mass, momentum and particles in bio-medical applications. Flow Turbul. Combust. 2016, 96, 837–860. [Google Scholar] [CrossRef]
- Islam, M.S.; Saha, S.C.; Sauret, E.; Gemci, T.; Gu, Y. Pulmonary aerosol transport and deposition analysis in upper 17 generations of the human respiratory tract. J. Aerosol Sci. 2017, 108, 29–43. [Google Scholar]
- Rahman, M.M.; Zhao, M.; Islam, M.S.; Dong, K.; Saha, S.C. Aerosol particle transport and deposition in upper and lower airways of infant, child and adult human lungs. Atmosphere 2021, 12, 1402. [Google Scholar] [CrossRef]
- Gaddam, M.G.; Santhanakrishnan, A. Effects of varying inhalation duration and respiratory rate on human airway flow. Fluids 2021, 6, 221. [Google Scholar] [CrossRef]
- Piemjaiswang, R.; Shiratori, S.; Chaiwatanarat, T.; Piumsomboon, P.; Chalermsinsuwan, B. Computational fluid dynamics simulation of full breathing cycle for aerosol deposition in trachea: Effect of breathing frequency. J. Taiwan Inst. Chem. Eng. 2019, 97, 66–79. [Google Scholar] [CrossRef]
- Koullapis, P.; Kassinos, S.C.; Muela, J.; Perez-Segarra, C.; Rigola, J.; Lehmkuhl, O.; Cui, Y.; Sommerfeld, M.; Elcner, J.; Jicha, M.; et al. Regional aerosol deposition in the human airways: The SimInhale benchmark case and a critical assessment of in silico methods. Eur. J. Pharm. Sci. 2018, 113, 77–94. [Google Scholar]
- Collier, G.J.; Kim, M.; Chung, Y.; Wild, J.M. 3D phase contrast MRI in models of human airways: Validation of computational fluid dynamics simulations of steady inspiratory flow. J. Magn. Reson. Imaging 2018, 48, 1400–1409. [Google Scholar] [CrossRef]
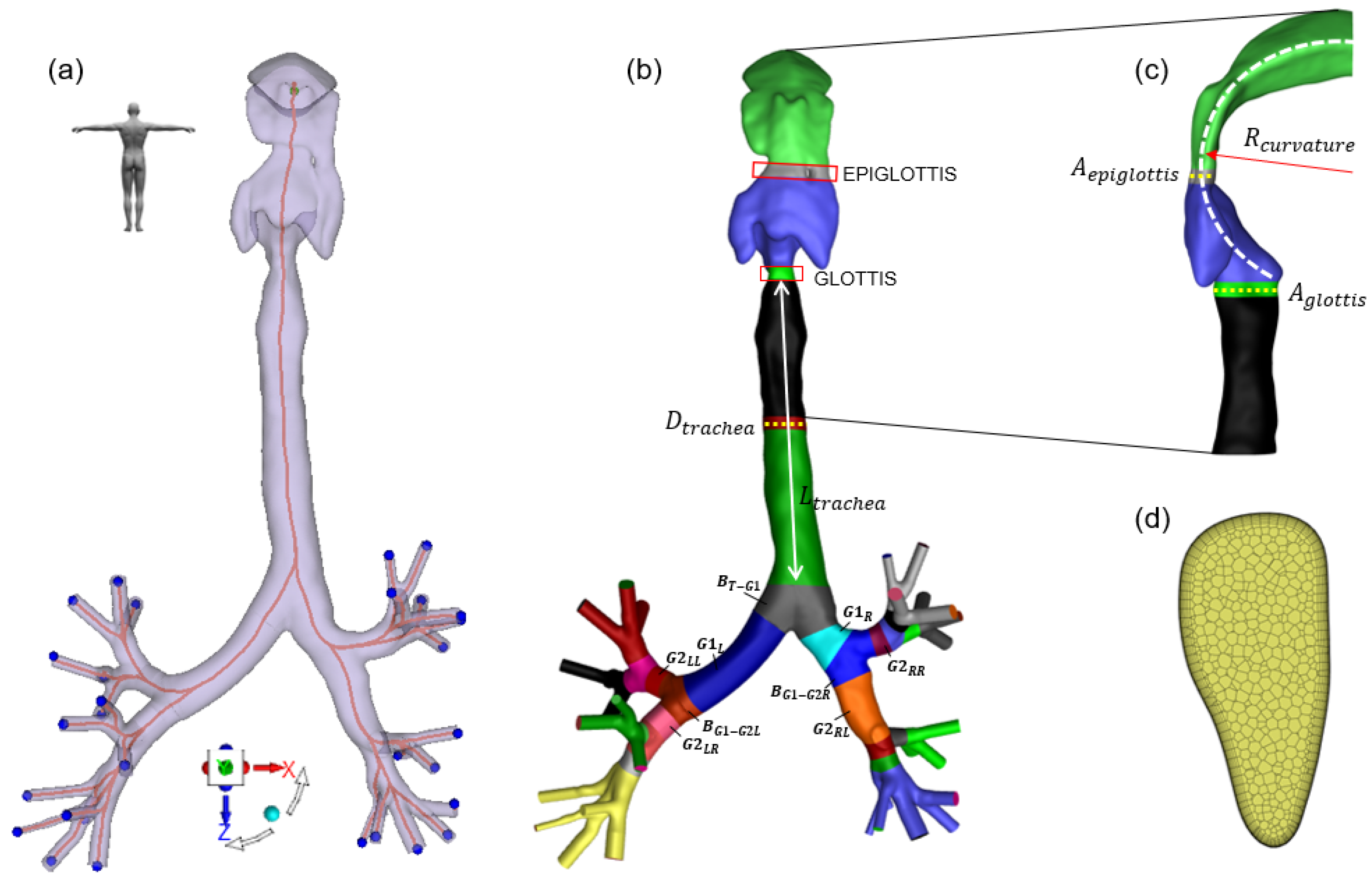


| Full Parameter Name | Parameter Abbreviation | Minimum Value | Maximum Value |
|---|---|---|---|
| Area of the epiglottis | 80 mm | 340 mm | |
| Area of the glottis | 86 mm | 330 mm | |
| Upper airway curvature radius | 45 mm | 55 mm | |
| Trachea diameter | 16.5 mm | 21.5 mm | |
| Trachea length | 103 mm | 132 mm | |
| 1st generation angle | 75 | 105 | |
| 1st generation left branch length | 51 mm | 58 mm | |
| 1st generation right branch length | 23 mm | 29 mm | |
| 2nd generation left branch angle | 70 | 90 | |
| 2nd generation right branch angle | 75 | 95 | |
| 2nd generation left-left branch length | 20 mm | 25 mm | |
| 2nd generation left-right branch length | 19 mm | 25 mm | |
| 2nd generation right-left branch length | 28 mm | 39 mm | |
| 2nd generation right-right branch length | 15 mm | 20 mm | |
| 3rd generation left-left branch angle | 80 | 105 | |
| 3rd generation left-right branch angle | 80 | 105 | |
| 3rd generation right-left branch angle | 75 | 95 | |
| 3rd generation right-right branch angle | 80 | 105 | |
| 3rd generation left-left-left branch length | 7 mm | 13 mm | |
| 3rd generation left-left-right branch length | 6 mm | 10 mm | |
| 3rd generation left-right-left branch length | 7 mm | 11 mm | |
| 3rd generation left-right-right branch length | 7 mm | 11 mm | |
| 3rd generation right-left-left branch length | 15 mm | 19 mm | |
| 3rd generation right-left-right branch length | 8 mm | 13 mm | |
| 3rd generation right-right-left branch length | 7 mm | 10 mm | |
| 3rd generation right-right-right branch length | 7 mm | 10 mm |
| Parameter Name | Model (a) | Model (b) | Model (c) | Model (d) |
|---|---|---|---|---|
| (mm) | 179.16 | 209.90 | 121.05 | 146.02 |
| (mm) | 168.91 | 320.89 | 124.13 | 182.01 |
| (mm) | 47.47 | 52.91 | 50.22 | 48.93 |
| (mm) | 16.52 | 18.33 | 20.98 | 20.75 |
| (mm) | 126.75 | 124.34 | 121.73 | 105.01 |
| () | 99.98 | 80.05 | 82.40 | 98.51 |
| (mm) | 52.13 | 56.24 | 51.69 | 51.64 |
| (mm) | 27.04 | 27.09 | 27.69 | 24.31 |
| () | 82.47 | 82.10 | 78.74 | 86.20 |
| () | 83.33 | 86.25 | 90.05 | 77.39 |
| (mm) | 21.75 | 23.13 | 24.28 | 21.81 |
| (mm) | 19.60 | 22.93 | 21.29 | 23.79 |
| (mm) | 38.14 | 32.53 | 35.38 | 34.65 |
| (mm) | 17.63 | 16.29 | 16.54 | 16.96 |
| () | 89.60 | 93.88 | 87.01 | 96.41 |
| () | 94.24 | 91.68 | 85.83 | 99.93 |
| () | 87.05 | 88.75 | 75.38 | 80.87 |
| () | 95.10 | 101.70 | 98.95 | 93.25 |
| (mm) | 10.79 | 8.64 | 10.63 | 12.14 |
| (mm) | 9.08 | 9.10 | 7.32 | 6.31 |
| (mm) | 8.17 | 10.75 | 8.32 | 7.83 |
| (mm) | 7.33 | 8.41 | 8.78 | 7.04 |
| (mm) | 17.55 | 16.96 | 18.33 | 16.77 |
| (mm) | 11.23 | 10.96 | 9.07 | 11.13 |
| (mm) | 7.35 | 7.69 | 7.45 | 7.34 |
| (mm) | 9.93 | 8.94 | 7.85 | 8.46 |
| (µm) | 2.89 | 5.13 | 5.25 | 7.33 |
| (L/min) | 189.82 | 105.01 | 123.29 | 176.77 |
| (m/s) | 4.36 | 4.54 | 3.39 | 3.09 |
| Parameter Name | Model (a) | Model (b) | Model (c) | Model (d) |
|---|---|---|---|---|
| (mm) | 179.16 | 209.90 | 121.05 | 214.38 |
| (mm) | 168.91 | 320.89 | 124.13 | 274.03 |
| (mm) | 47.47 | 52.91 | 50.22 | 48.70 |
| (mm) | 16.52 | 18.33 | 20.98 | 20.99 |
| (mm) | 126.75 | 124.34 | 121.73 | 114.34 |
| () | 99.98 | 80.05 | 82.40 | 84.09 |
| (mm) | 52.13 | 56.24 | 51.69 | 54.21 |
| (mm) | 27.04 | 27.09 | 27.69 | 26.72 |
| () | 82.47 | 82.10 | 78.74 | 88.76 |
| () | 83.33 | 86.25 | 90.05 | 76.47 |
| (mm) | 21.75 | 23.13 | 24.28 | 21.08 |
| (mm) | 19.60 | 22.93 | 21.29 | 21.87 |
| (mm) | 38.14 | 32.53 | 35.38 | 37.11 |
| (mm) | 17.63 | 16.29 | 16.54 | 15.21 |
| () | 89.60 | 93.88 | 87.01 | 84.60 |
| () | 94.24 | 91.68 | 85.83 | 101.65 |
| () | 87.05 | 88.75 | 75.38 | 81.02 |
| () | 95.10 | 101.70 | 98.95 | 101.25 |
| (mm) | 10.79 | 8.64 | 10.63 | 10.28 |
| (mm) | 9.08 | 9.10 | 7.32 | 9.22 |
| (mm) | 8.17 | 10.75 | 8.32 | 9.53 |
| (mm) | 7.33 | 8.41 | 8.78 | 9.36 |
| (mm) | 17.55 | 16.96 | 18.33 | 17.28 |
| (mm) | 11.23 | 10.96 | 9.07 | 12.57 |
| (mm) | 7.35 | 7.69 | 7.45 | 9.04 |
| (mm) | 9.93 | 8.94 | 7.85 | 7.15 |
| (µm) | 2.89 | 5.13 | 5.25 | 1.84 |
| (L/min) | 189.82 | 105.01 | 123.29 | 42.47 |
| (m/s) | 4.36 | 4.54 | 3.39 | 1.21 |
| Parameter Name | Model (a) | Model (b) | Model (c) | Model (d) |
|---|---|---|---|---|
| (mm) | 90.94 | 121.05 | 175.30 | 207.09 |
| (mm) | 145.64 | 124.13 | 124.81 | 338.24 |
| (mm) | 48.25 | 50.22 | 47.72 | 46.29 |
| (mm) | 16.80 | 20.98 | 18.78 | 18.32 |
| (mm) | 111.38 | 121.73 | 122.64 | 105.05 |
| () | 80.00 | 82.40 | 99.93 | 96.62 |
| (mm) | 51.79 | 51.69 | 53.75 | 56.42 |
| (mm) | 26.56 | 27.69 | 24.52 | 26.34 |
| () | 76.82 | 78.74 | 86.09 | 79.35 |
| () | 86.97 | 90.05 | 85.23 | 86.65 |
| (mm) | 22.35 | 24.28 | 22.76 | 21.70 |
| (mm) | 21.95 | 21.29 | 23.47 | 21.44 |
| (mm) | 33.28 | 35.38 | 31.32 | 36.20 |
| (mm) | 19.56 | 16.54 | 15.33 | 16.77 |
| () | 102.64 | 87.01 | 83.48 | 93.17 |
| () | 87.55 | 85.83 | 100.53 | 96.38 |
| () | 86.36 | 75.38 | 85.49 | 77.47 |
| () | 104.86 | 98.95 | 83.76 | 84.02 |
| (mm) | 11.14 | 10.63 | 10.00 | 12.92 |
| (mm) | 7.67 | 7.32 | 8.33 | 7.96 |
| (mm) | 7.16 | 8.32 | 7.49 | 8.10 |
| (mm) | 10.40 | 8.78 | 10.83 | 9.61 |
| (mm) | 18.70 | 18.33 | 18.89 | 18.12 |
| (mm) | 10.57 | 9.07 | 10.65 | 12.01 |
| (mm) | 9.98 | 7.45 | 8.92 | 9.77 |
| (mm) | 9.17 | 7.85 | 8.83 | 8.67 |
| (µm) | 8.03 | 5.25 | 8.46 | 6.94 |
| (L/min) | 58.43 | 123.29 | 152.89 | 108.11 |
| (m/s) | 1.23 | 3.39 | 1.18 | 4.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geronzi, L.; Fanni, B.M.; De Jong, B.; Roest, G.; Kenjeres, S.; Celi, S.; Biancolini, M.E. A Parametric 3D Model of Human Airways for Particle Drug Delivery and Deposition. Fluids 2024, 9, 27. https://doi.org/10.3390/fluids9010027
Geronzi L, Fanni BM, De Jong B, Roest G, Kenjeres S, Celi S, Biancolini ME. A Parametric 3D Model of Human Airways for Particle Drug Delivery and Deposition. Fluids. 2024; 9(1):27. https://doi.org/10.3390/fluids9010027
Chicago/Turabian StyleGeronzi, Leonardo, Benigno Marco Fanni, Bart De Jong, Gerben Roest, Sasa Kenjeres, Simona Celi, and Marco Evangelos Biancolini. 2024. "A Parametric 3D Model of Human Airways for Particle Drug Delivery and Deposition" Fluids 9, no. 1: 27. https://doi.org/10.3390/fluids9010027
APA StyleGeronzi, L., Fanni, B. M., De Jong, B., Roest, G., Kenjeres, S., Celi, S., & Biancolini, M. E. (2024). A Parametric 3D Model of Human Airways for Particle Drug Delivery and Deposition. Fluids, 9(1), 27. https://doi.org/10.3390/fluids9010027







