Radial Basis Function Surrogates for Uncertainty Quantification and Aerodynamic Shape Optimization under Uncertainties
Abstract
:1. Introduction
2. Methods and Tools
2.1. CFD Tool—Governing Equations
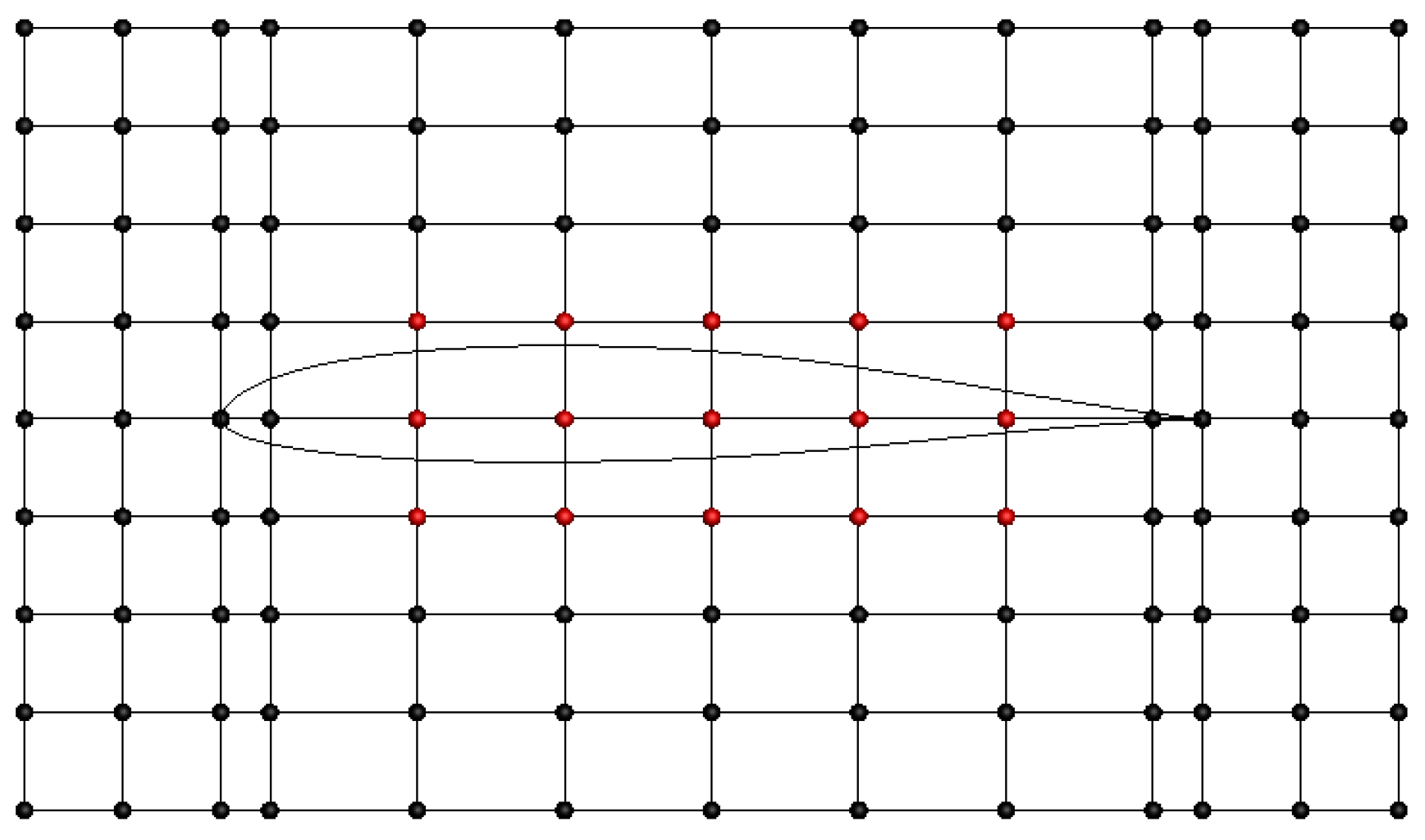
2.2. Shape Parameterization, Mesh Displacement and Geometric Uncertainties
2.3. RBF Networks
2.4. Optimization Method
2.5. Uncertainty Quantification Methods
3. Applications
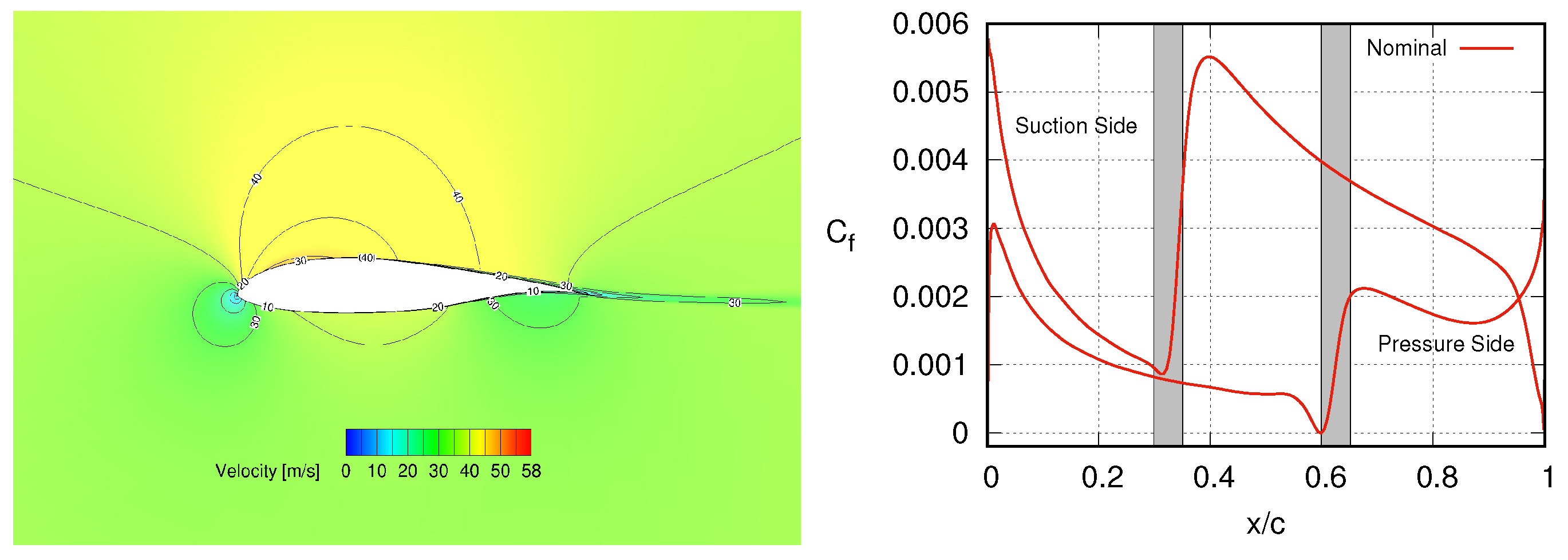
3.1. Case I—The NLF(1)-0416 Airfoil
3.2. Case II—The ONERA M6 Wing
3.3. Case III—The S8052 Airfoil
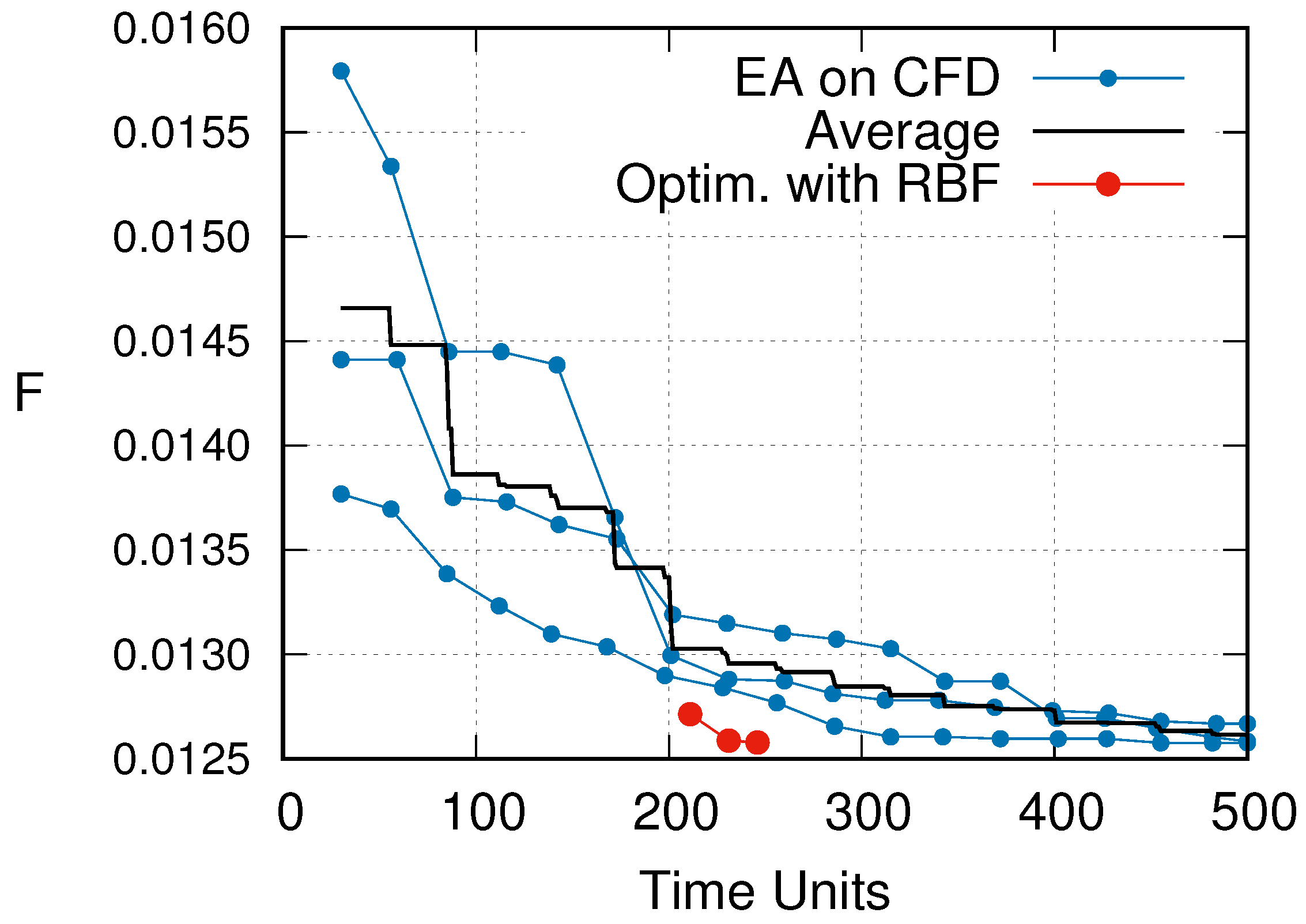
3.3.1. Shape Optimization without Uncertainties
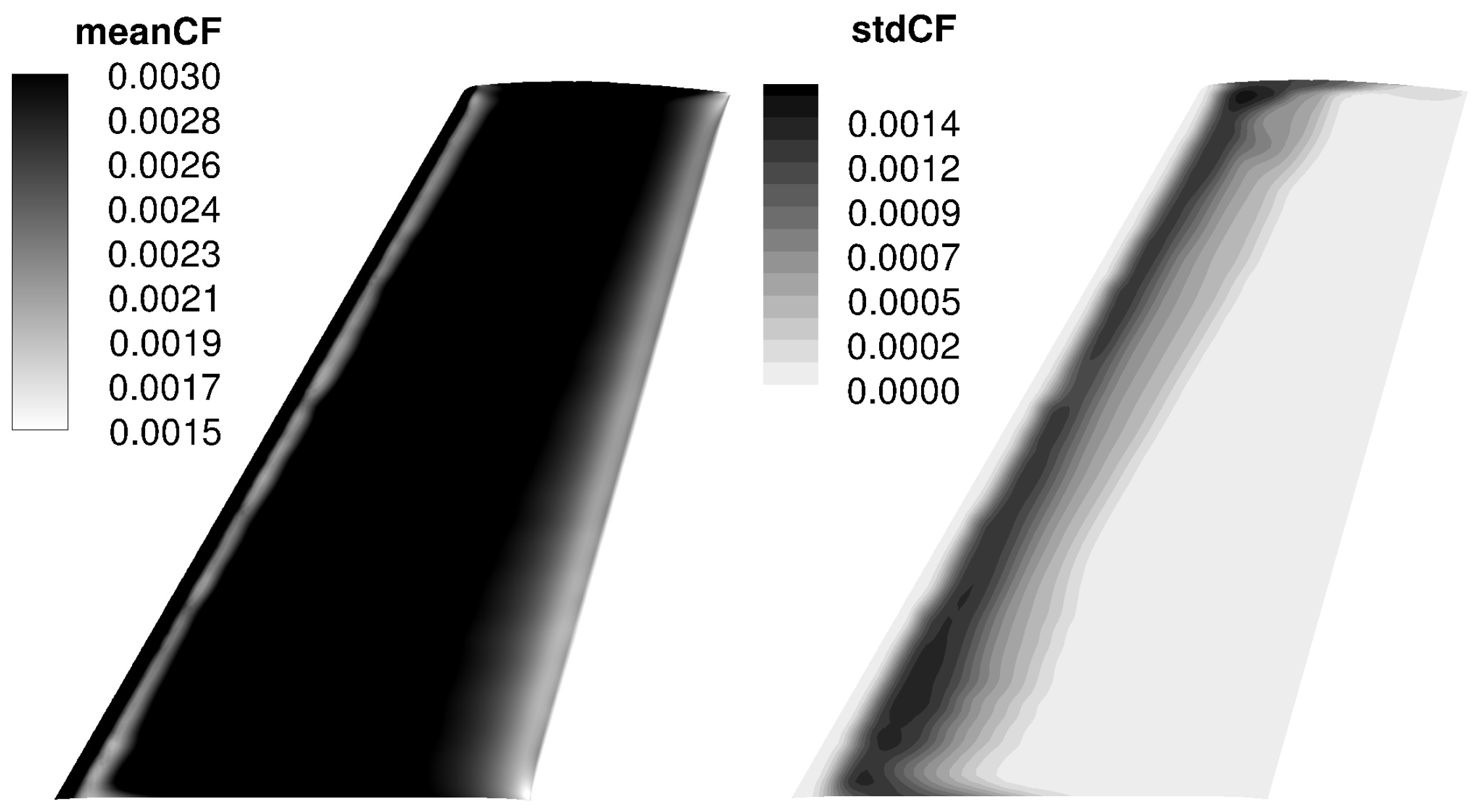
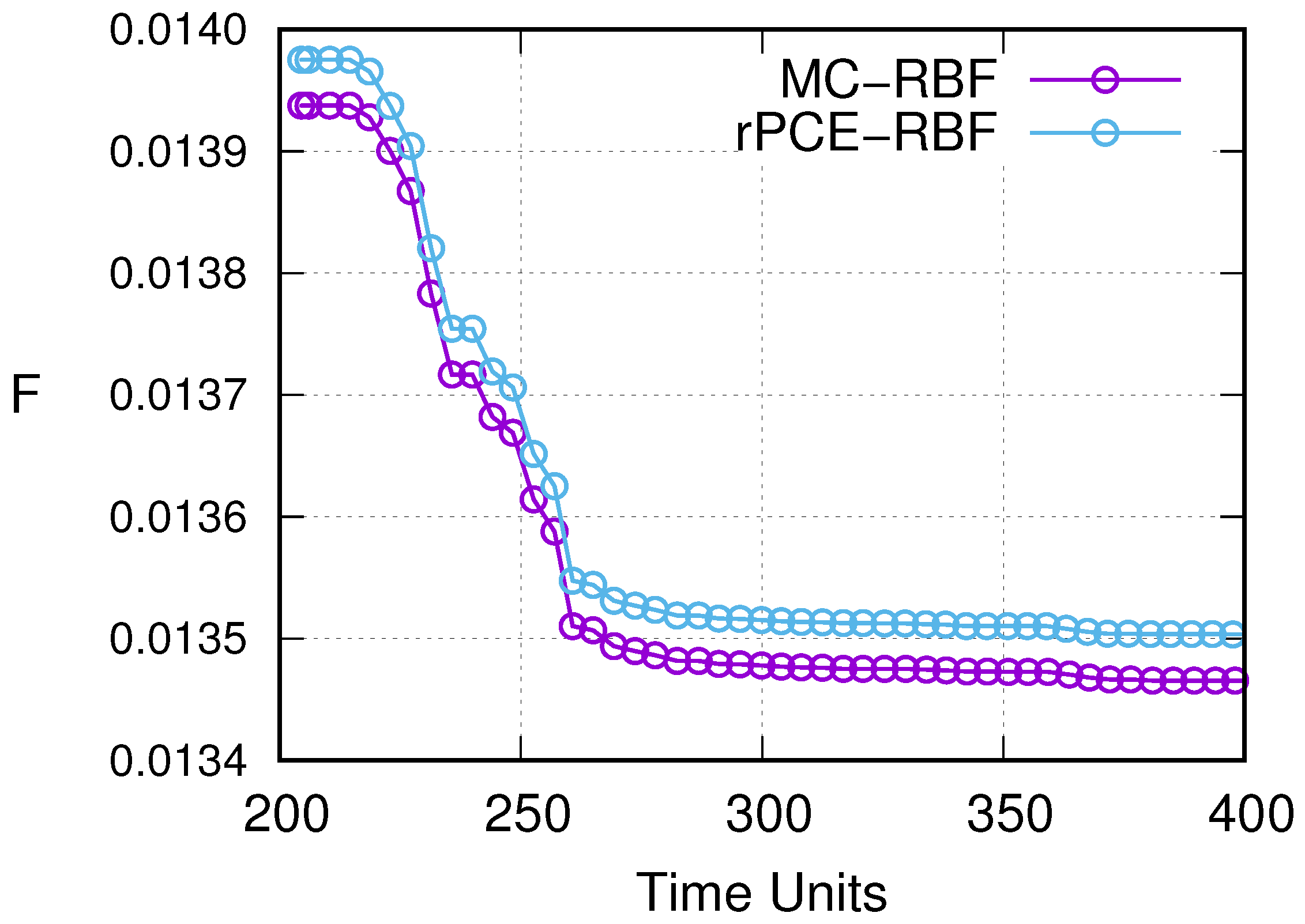
3.3.2. Shape Optimization under Geometric Uncertainties
4. Discussion—Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| CFD | Computational Fluid Dynamics |
| PDE | Partial Differential Equation |
| EA | Evolutionary Algorithm |
| GQ | Gauss Quadrature |
| KL | Karhunen–Loève |
| LHS | Latin Hypercube Sampling |
| MC | Monte Carlo |
| ML | Machine Learning |
| MoM | Method of Moments |
| PCE | Polynomial Chaos Expansion |
| QoI | Quantity of Interest |
| RANS | Reynolds-Averaged Navier–Stokes |
| RMSE | Root Mean Square Error |
| RBF | Radial Basis Function |
| UQ | Uncertainty Quantification |
References
- Xiu, D.; Karniadakis, G. Modeling uncertainty in flow simulations via generalized polynomial chaos. J. Comput. Phys. 2003, 187, 137–167. [Google Scholar]
- Najm, H.N. Uncertainty quantification and polynomial chaos techniques in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar]
- Dinescu, C.; Smirnov, S.; Hirsch, C.; Lacor, C. Assessment of intrusive and non-intrusive non-deterministic CFD methodologies based on polynomial chaos expansions. Int. J. Eng. Syst. Model. Simul. 2010, 2, 87–98. [Google Scholar]
- Schillings, C.; Schmidt, S.; Schulz, V. Efficient shape optimization for certain and uncertain aerodynamic design. Comput. Fluids 2011, 46, 78–87. [Google Scholar]
- Chatzimanolakis, M.; Kantarakias, K.D.; Asouti, V.; Giannakoglou, K. A painless intrusive polynomial chaos method with RANS-based applications. Comput. Methods Appl. Mech. Eng. 2019, 348, 207–221. [Google Scholar]
- Eldred, M.S.; Burkardt, J. Comparison of non-intrusive polynomial chaos and stochastic collocation methods for uncertainty quantification. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Hosder, S.; Walters, R.W. Non-intrusive polynomial chaos methods for uncertainty quantification in fluid dynamics. In Proceedings of the 48th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Walters, R.W.; Huyse, L. Uncertainty analysis for fluid mechanics with applications. In NASA Technical Report 2002-1; NASA: Washington, DC, USA, 2002. [Google Scholar]
- Haldar, A.; Mahadevan, S. Probability, Reliability and Statistical Methods in Engineering Design; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Putko, M.; Taylor, A.; Newman, P.; Green, L. Approach for input uncertainty propagation and robust design in CFD using sensitivity derivatives. J. Fluids Eng. 2002, 124, 60–69. [Google Scholar]
- Skamagkis, T.; Papoutsis-Kiachagias, E.; Giannakoglou, K. CFD-based shape optimization under uncertainties using the Adjoint-assisted polynomial chaos expansion and projected derivatives. Comput. Fluids 2022, 241, 105458. [Google Scholar]
- Liu, Y.; Wang, D.; Sun, X.; Liu, Y.; Dinh, N.; Hu, R. Uncertainty quantification for multiphase-CFD simulations of bubbly flows: A machine learning-based Bayesian approach supported by high-resolution experiments. Reliab. Eng. Syst. Saf. 2021, 212, 107636. [Google Scholar]
- Evangelista, F., Jr.; Almeida, I.F. Machine learning RBF-based surrogate models for uncertainty quantification of age and time-dependent fracture mechanics. Eng. Fract. Mech. 2021, 258, 108037. [Google Scholar]
- Ansari, A.; Mohaghegh, S.D.; Shahnam, M.; Dietiker, J.F. Modeling average pressure and volume fraction of a fluidized bed using data-driven smart proxy. Fluids 2019, 4, 123. [Google Scholar]
- Duraisamy, K.; Zhang, Z.J.; Singh, A.P. New approaches in turbulence and transition modeling using data-driven techniques. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Song, Z.; Liu, Z.; Lu, J.; Yan, C. Quantification of parametric uncertainty in γ − Reθ model for typical flat plate and airfoil transitional flows. Chin. J. Aeronaut. 2023, 36, 237–251. [Google Scholar] [CrossRef]
- Jakobsson, S.; Amoignon, O. Mesh deformation using radial basis functions for gradient-based aerodynamic shape optimization. Comput. Fluids 2007, 36, 1119–1136. [Google Scholar] [CrossRef]
- Biancolini, M.; Viola, I.; Riotte, M. Sails trim optimisation using CFD and RBF mesh morphing. Comput. Fluids 2014, 93, 46–60. [Google Scholar] [CrossRef]
- Gagliardi, F.; Giannakoglou, K. A two-step Radial Basis Function-based CFD mesh displacement tool. Adv. Eng. Softw. 2019, 128, 86–97. [Google Scholar] [CrossRef]
- Kampolis, I.; Trompoukis, X.; Asouti, V.; Giannakoglou, K. CFD-based analysis and two-level aerodynamic optimization on Graphics Processing Units. Comput. Methods Appl. Mech. Eng. 2010, 199, 712–722. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. Rech. Aerosp. 1994, 1, 5–21. [Google Scholar]
- Piotrowski, M.; Zingg, D. Smooth local correlation-based transition model for the Spalart-Allmaras turbulence model. AIAA J. 2020, 59, 474–492. [Google Scholar] [CrossRef]
- Trompoukis, X.; Tsiakas, K.; Asouti, V.; Giannakoglou, K. Continuous adjoint-based optimization of a turbomachinery stage using a 3D volumetric parameterization. Int. J. Numer. Methods Fluids 2023, 6, 20. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Fong, W.; Darve, E. The black-box fast multipole method. J. Comput. Phys. 2009, 228, 8712–8725. [Google Scholar] [CrossRef]
- Karimi, M.S.; Raisee, M.; Farhat, M.; Hendrick, P.; Nourbakhsh, A. On the numerical simulation of a confined cavitating tip leakage vortex under geometrical and operational uncertainties. Comput. Fluids 2021, 220, 104881. [Google Scholar] [CrossRef]
- Ghanem, R.; Spanos, P. Stochastic Finite Elements: A Spectral Approach; Springer: New York, NY, USA, 1991. [Google Scholar]
- Le Maitre, O.P.; Knio, O.M. Spectral Methods for Uncertainty Quantification with Applications to Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 718. [Google Scholar]
- Cho, H.; Venturi, D.; Karniadakis, G. Karhunen–Loève expansion for multi-correlated stochastic processes. Probabilistic Eng. Mech. 2013, 34, 157–167. [Google Scholar] [CrossRef]
- Haykin, S.S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education: London, UK, 2009. [Google Scholar]
- Xiu, D.; Hesthaven, J. High-Order collocation methods for differential equations with random inputs. SIAM J. Sci. Comput. 2005, 27, 1118–1139. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, Z.; Gao, Y.; Wang, C. Effective robust design of high lift NLF airfoil under multi-parameter uncertainty. Aerosp. Sci. Technol. 2017, 68, 530–542. [Google Scholar] [CrossRef]
- Somers, D.M. Design and experimental results for a Natural-Laminar-Flow airfoil for general aviation applications. In NASA Technical Paper 1861; NASA: Washington, DC, USA, 1981. [Google Scholar]
- Coder, J.G. Standard test cases for CFD-based laminar-transition model verification and validation. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Schmitt, V.; Cousteix, J. Etude de la Couche Limite Tridimensionnelle sur une Aile en Fleche; Technical Report No 14/1713 AN; ONERA: Meudon, France, 1975. [Google Scholar]




| Experimental | Tiny | Coarse | Medium | Fine | Extra | Ultra | |
|---|---|---|---|---|---|---|---|
| 0.672 | 0.7166 | 0.7075 | 0.7228 | 0.7230 | 0.7231 | 0.7235 | |
| 0.0051 | 0.006673 | 0.007269 | 0.005984 | 0.005952 | 0.005930 | 0.005905 |
| Method/Tool | Time Units | ||||
|---|---|---|---|---|---|
| MC-RBF () | 40 | 0.7204 | 0.004567 | 0.006195 | 0.0004196 |
| gPCE-RBF (81) | 40 | 0.7204 | 0.004643 | 0.006194 | 0.0004266 |
| rPCE-RBF (81) | 40 | 0.7204 | 0.004548 | 0.006383 | 0.0004203 |
| rPCE-RBF (150) | 40 | 0.7204 | 0.004615 | 0.006446 | 0.0004148 |
| gPCE-CFD (81) | 81 | 0.7210 | 0.004923 | 0.006153 | 0.0004477 |
| rPCE-CFD (81) | 81 | 0.7207 | 0.004584 | 0.006386 | 0.0004198 |
| rPCE-CFD (40) | 40 | 0.7206 | 0.004547 | 0.006421 | 0.0004132 |
| Method/Tool | Time Units | ||
|---|---|---|---|
| MC-RBF () | 80 | 6.8200 | 0.3277 |
| gPCE-RBF (243) | 80 | 6.7946 | 0.3249 |
| rPCE-RBF (243) | 80 | 6.7975 | 0.3127 |
| rPCE-RBF (120) | 80 | 6.8442 | 0.3152 |
| rPCE-RBF (80) | 80 | 6.8603 | 0.3057 |
| rPCE-CFD (120) | 120 | 6.8571 | 0.3277 |
| rPCE-CFD (80) | 80 | 6.8635 | 0.3179 |
| Geometry/Method | F | ||
|---|---|---|---|
| Baseline | 0.0172588 | 0.01694 | 0.0003188 |
| Optimized (using MC-RBF) | 0.0134667 | 0.01317 | 0.0002967 |
| Optimized (using rPCE-RBF) | 0.0134317 | 0.01314 | 0.0002917 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asouti, V.; Kontou, M.; Giannakoglou, K. Radial Basis Function Surrogates for Uncertainty Quantification and Aerodynamic Shape Optimization under Uncertainties. Fluids 2023, 8, 292. https://doi.org/10.3390/fluids8110292
Asouti V, Kontou M, Giannakoglou K. Radial Basis Function Surrogates for Uncertainty Quantification and Aerodynamic Shape Optimization under Uncertainties. Fluids. 2023; 8(11):292. https://doi.org/10.3390/fluids8110292
Chicago/Turabian StyleAsouti, Varvara, Marina Kontou, and Kyriakos Giannakoglou. 2023. "Radial Basis Function Surrogates for Uncertainty Quantification and Aerodynamic Shape Optimization under Uncertainties" Fluids 8, no. 11: 292. https://doi.org/10.3390/fluids8110292
APA StyleAsouti, V., Kontou, M., & Giannakoglou, K. (2023). Radial Basis Function Surrogates for Uncertainty Quantification and Aerodynamic Shape Optimization under Uncertainties. Fluids, 8(11), 292. https://doi.org/10.3390/fluids8110292






