Thermorheological Behavior of κ-Carrageenan Hydrogels Modified with Xanthan Gum
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Rheological Measurements
2.4. Inverse Vial Test
2.5. 3D Printing Process
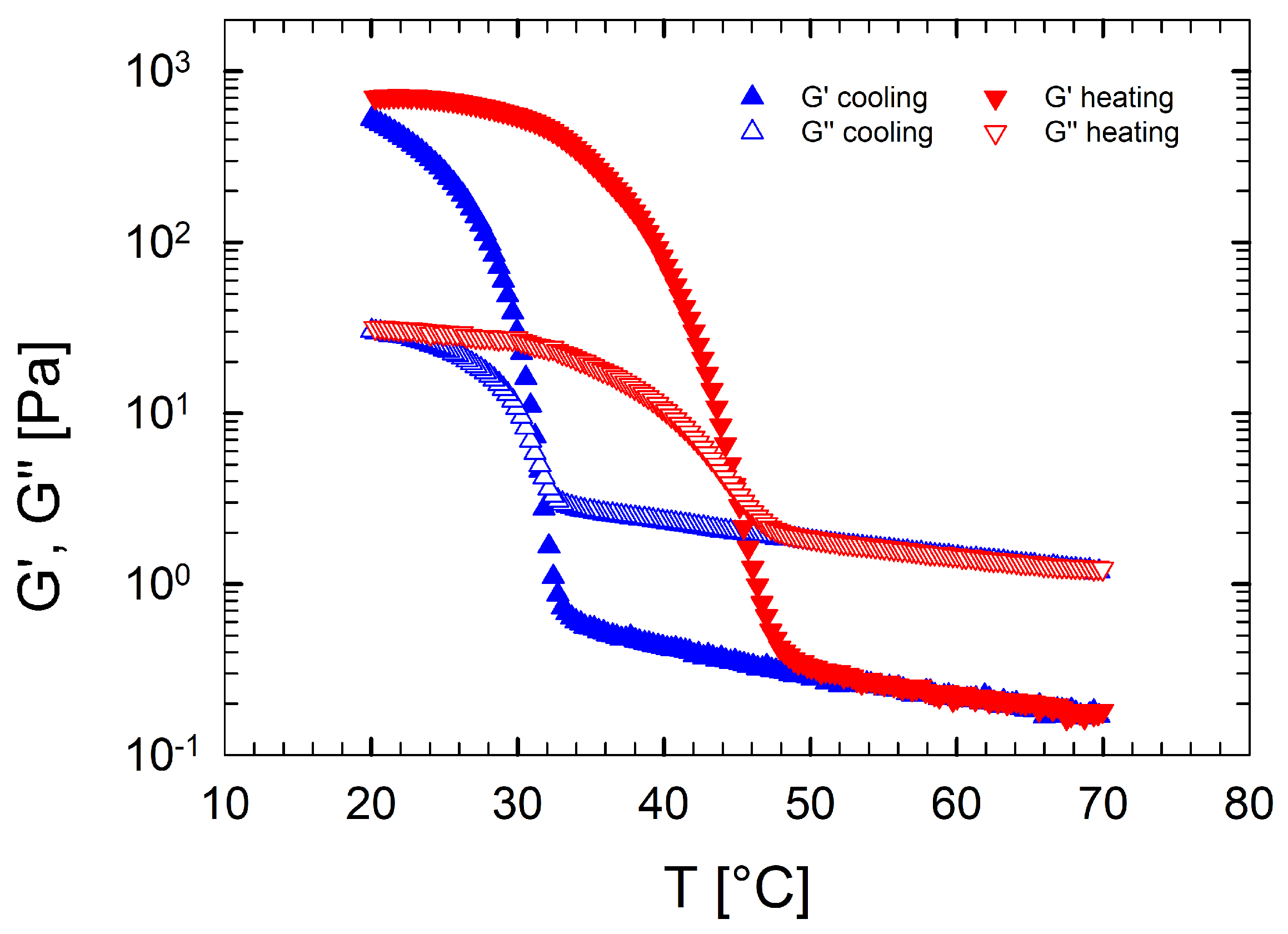
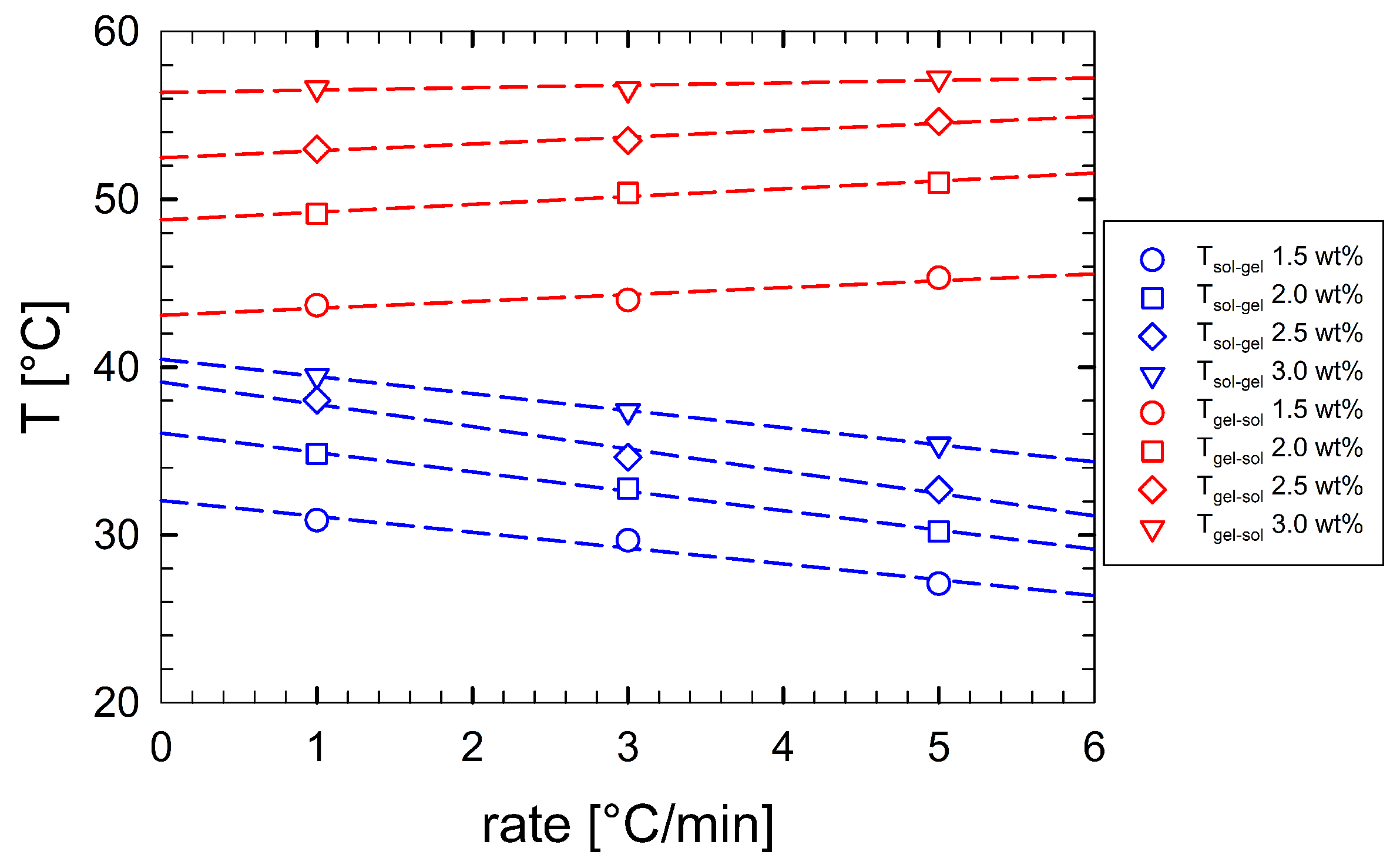
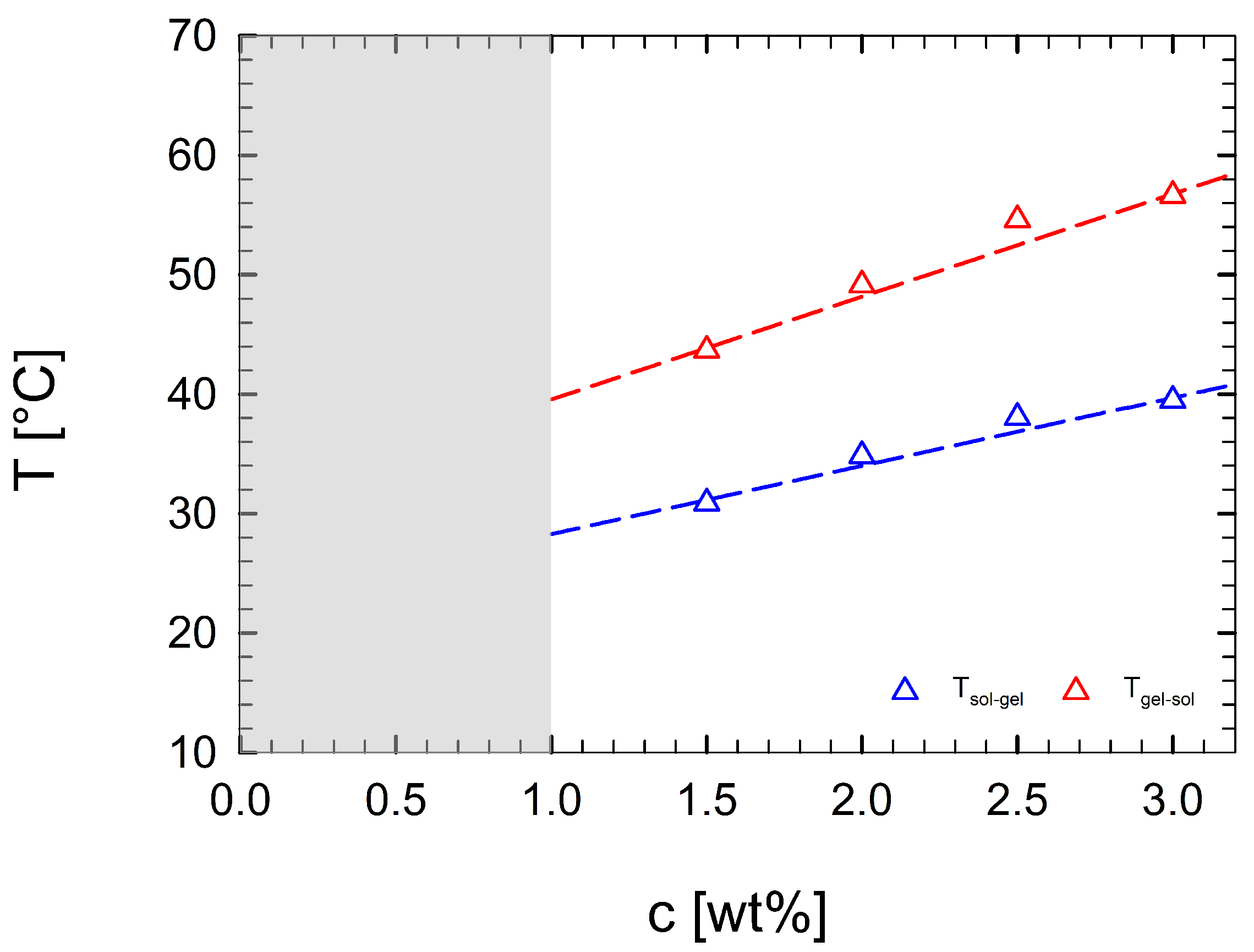
3. Results and Discussion
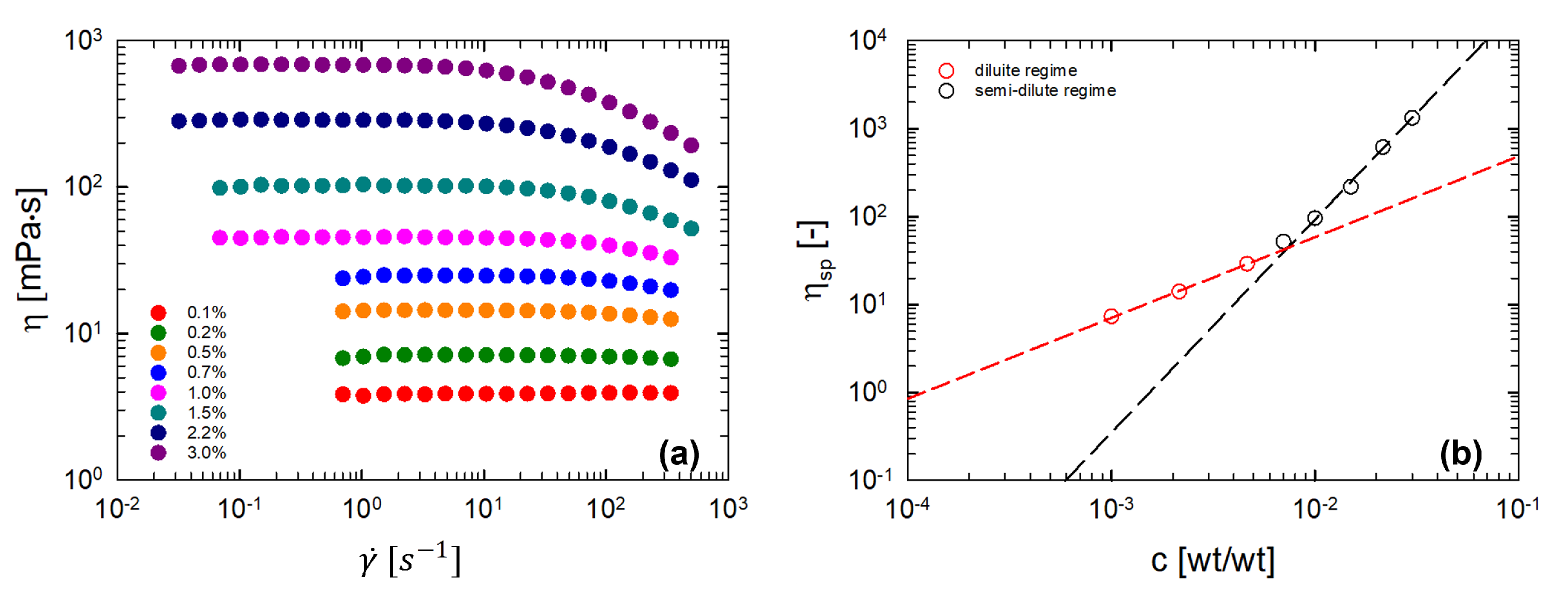
3.1. Rheological Behavior of κ-Carrageenan Solutions
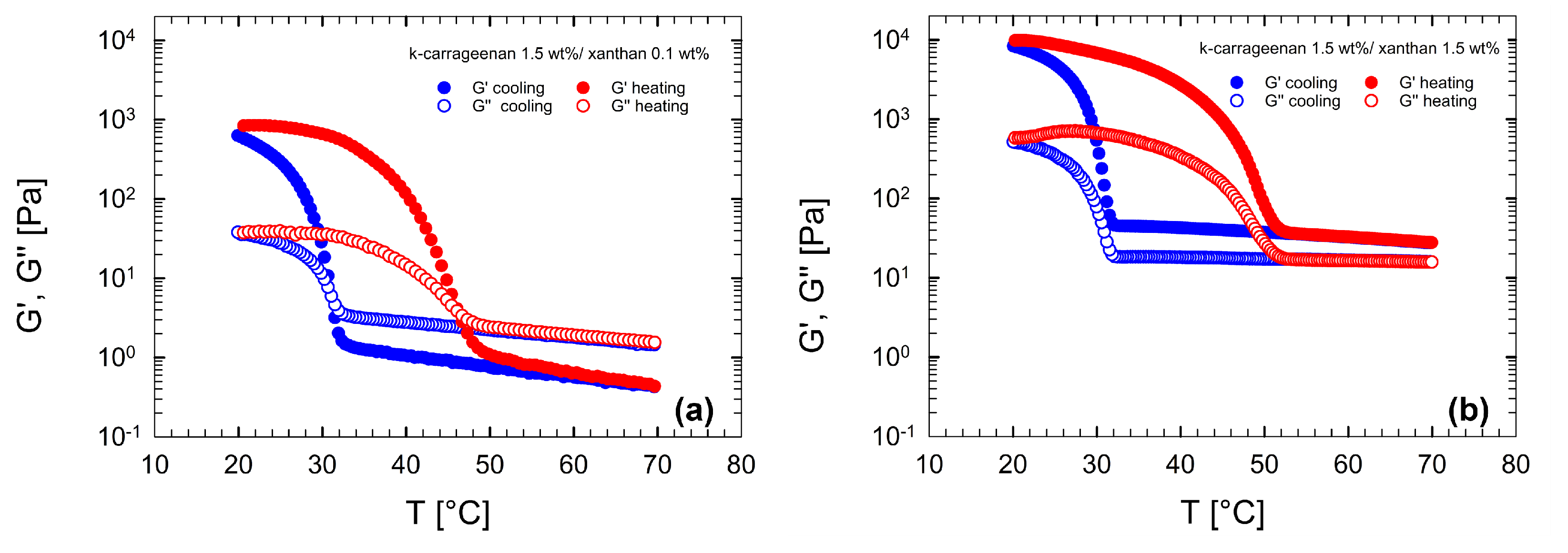
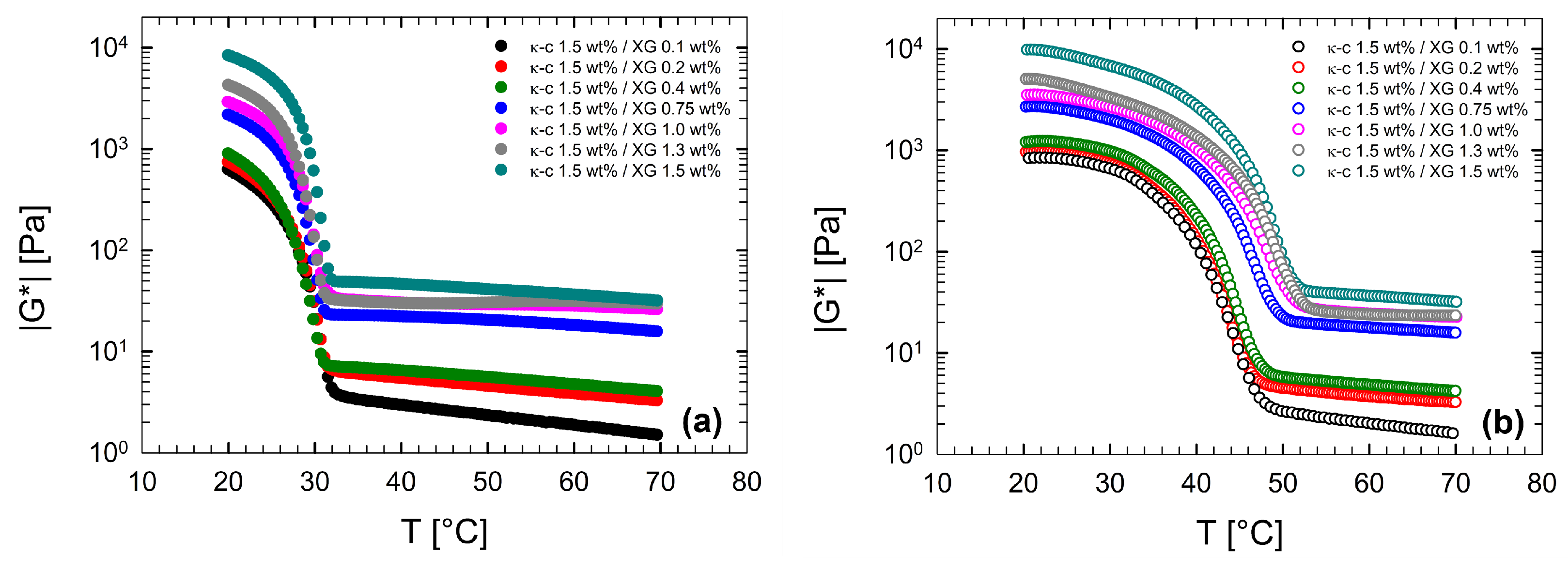
3.2. Rheological Behavior of κ-Carrageenan/Xanthan Gum Solutions
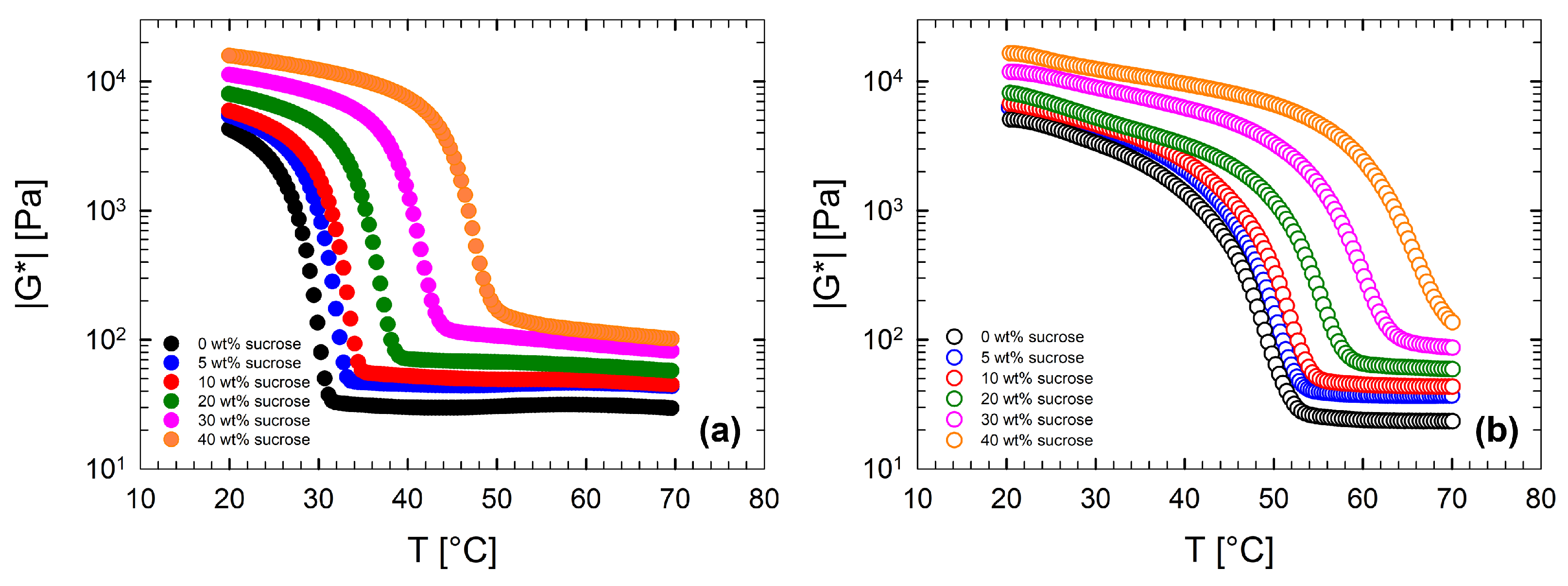
3.3. Rheological Behavior of κ-Carrageenan/Xanthan Gum Solutions with Sucrose
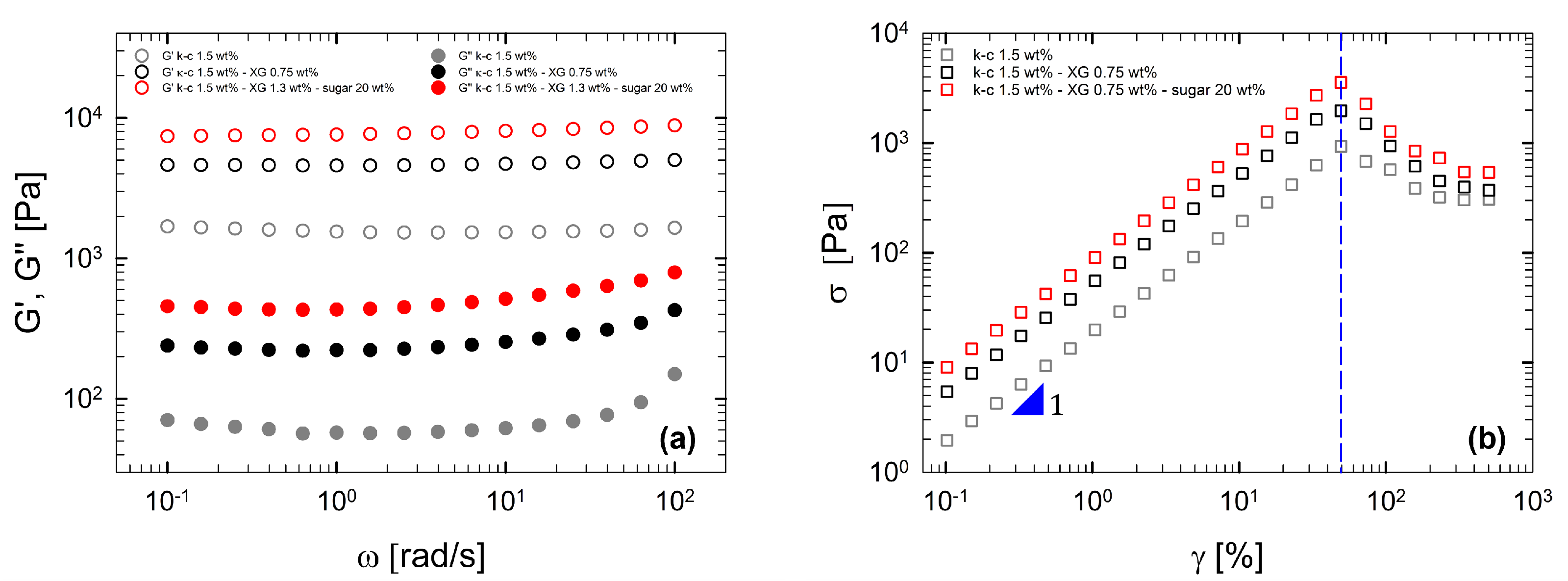
3.4. Yield Stress Evaluation
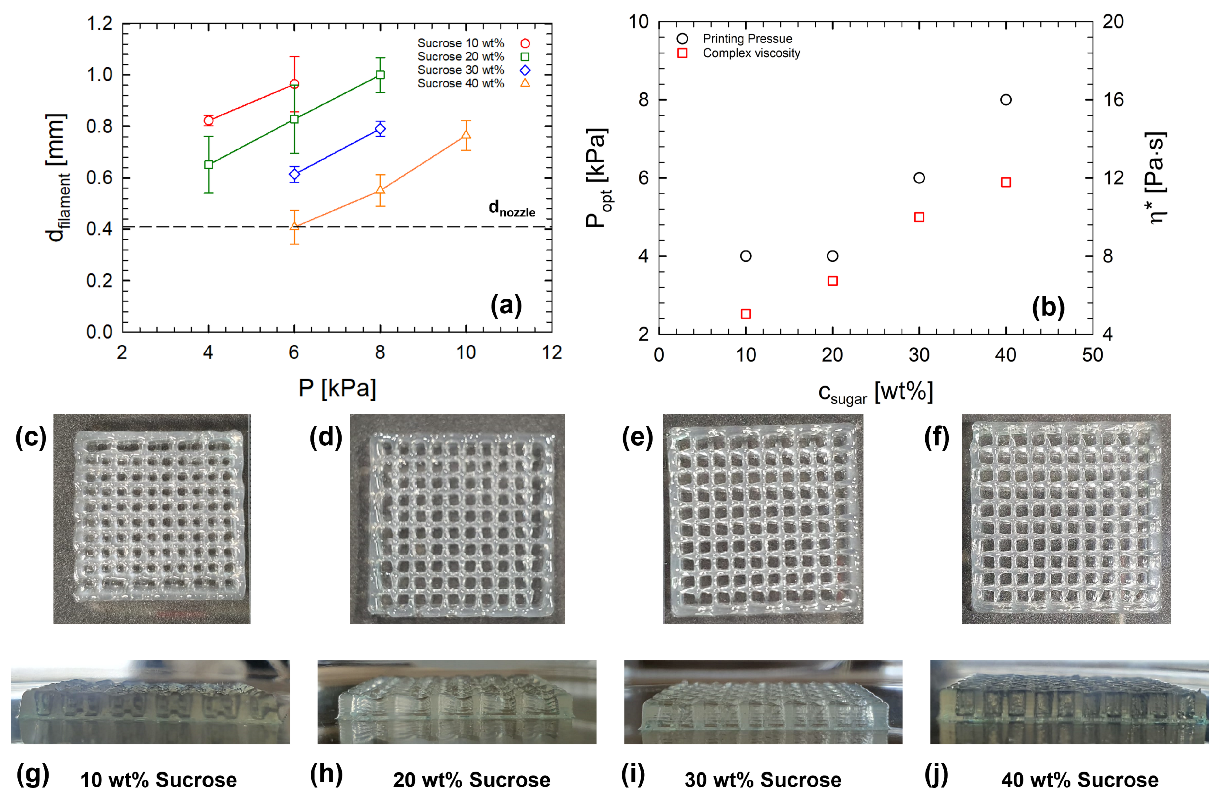
3.5. Printability of Food Hydrogels
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, W.; Li, X.; Fang, Y. Introduction to Food Hydrocolloids. In Food Hydrocolloids: Functionalities and Applications; Springer: Singapore, 2021; pp. 1–28. [Google Scholar]
- Glicksman, M. Food Hydrocolloids; CRC Press: Boca Raton, FL, USA, 2020; Volume 3. [Google Scholar]
- Yemenicioğlu, A.; Farris, S.; Turkyilmaz, M.; Gulec, S. A review of current and future food applications of natural hydrocolloids. Int. J. Food Sci. Technol. 2020, 55, 1389–1406. [Google Scholar] [CrossRef]
- Avallone, P.R.; Romano, M.; Sarrica, A.; Delmonte, M.; Pasquino, R.; Grizzuti, N. Effect of Sugars on Gelation Kinetics of Gelatin Gels. Fluids 2022, 7, 163. [Google Scholar] [CrossRef]
- Xing, G.; Giosafatto, C.V.L.; Carpentieri, A.; Pasquino, R.; Dong, M.; Mariniello, L. Gelling behavior of bio-tofu coagulated by microbial transglutaminase combined with lactic acid bacteria. Food Res. Int. 2020, 134, 109200. [Google Scholar] [CrossRef] [PubMed]
- Nishinari, K. Gelling Properties. In Food Hydrocolloids; Springer: Berlin/Heidelberg, Germany, 2021; pp. 119–170. [Google Scholar]
- Burchard, W.; Ross-Murphy, S. Physical Networks: Polymers and Gels; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Saha, D.; Bhattacharya, S. Hydrocolloids as thickening and gelling agents in food: A critical review. J. Food Sci. Technol. 2010, 47, 587–597. [Google Scholar] [CrossRef]
- Avallone, P.R.; Pasquino, R.; Costanzo, S.; Sarrica, A.; Delmonte, M.; Greco, F.; Grizzuti, N. On the inverse quenching technique applied to gelatin solutions. J. Rheol. 2021, 65, 1081–1088. [Google Scholar] [CrossRef]
- Nordqvist, D.; Vilgis, T.A. Rheological study of the gelation process of agarose-based solutions. Food Biophys. 2011, 6, 450–460. [Google Scholar] [CrossRef]
- Liu, S.; Huang, S.; Li, L. Thermoreversible gelation and viscoelasticity of κ-carrageenan hydrogels. J. Rheol. 2016, 60, 203–214. [Google Scholar] [CrossRef]
- Morrison, N.; Clark, R.; Chen, Y.; Talashek, T.; Sworn, G. Gelatin alternatives for the food industry. In Physical Chemistry and Industrial Application of Gellan Gum; Springer: Berlin/Heidelberg, Germany, 1999; pp. 127–131. [Google Scholar]
- Agoub, A.; Smith, A.M.; Giannouli, P.; Richardson, R.; Morris, E. “Melt-in-the-mouth” gels from mixtures of xanthan and konjac glucomannan under acidic conditions: A rheological and calorimetric study of the mechanism of synergistic gelation. Carbohydr. Polym. 2007, 69, 713–724. [Google Scholar] [CrossRef]
- Karim, A.A.; Bhat, R. Gelatin alternatives for the food industry: Recent developments, challenges and prospects. Trends Food Sci. Technol. 2008, 19, 644–656. [Google Scholar] [CrossRef]
- Gu, Y.S.; Decker, E.A.; McClements, D.J. Influence of pH and carrageenan type on properties of β-lactoglobulin stabilized oil-in-water emulsions. Food Hydrocoll. 2005, 19, 83–91. [Google Scholar] [CrossRef]
- Yuguchi, Y.; Thuy, T.T.T.; Urakawa, H.; Kajiwara, K. Structural characteristics of carrageenan gels: Temperature and concentration dependence. Food Hydrocoll. 2002, 16, 515–522. [Google Scholar] [CrossRef]
- Tziboula, A.; Horne, D. Effect of heat treatment on k-carrageenan gelation in milk. In Gums and Stabilisers for the Food Industry 10; Elsevier: Amsterdam, The Netherlands, 2000; pp. 211–220. [Google Scholar]
- Nguyen, B.T.; Nicolai, T.; Benyahia, L.; Chassenieux, C. Synergistic effects of mixed salt on the gelation of κ-carrageenan. Carbohydr. Polym. 2014, 112, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Chiou, B.S.; Xia, Y.; Chen, M.; Liu, F.; Zhong, F. The improvement of texture properties and storage stability for kappa carrageenan in developing vegan gummy candies. J. Sci. Food Agric. 2022, 102, 3693–3702. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Yu, S.; Liang, H.; Eid, M.; Li, B.; Li, J.; Mao, J. An innovative konjac glucomannan/κ-carrageenan mixed tensile gel. J. Sci. Food Agric. 2021, 101, 5067–5074. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.; Zou, Y.; Cui, B.; Fang, Y.; Lu, L.; Xu, D. Influence of cyclodextrins on the gelation behavior of κ-carrageenan/konjac glucomannan composite gel. Food Hydrocoll. 2021, 120, 106927. [Google Scholar] [CrossRef]
- Normand, V.; Muller, S.; Ravey, J.C.; Parker, A. Gelation kinetics of gelatin: A master curve and network modeling. Macromolecules 2000, 33, 1063–1071. [Google Scholar] [CrossRef]
- Joly-Duhamel, C.; Hellio, D.; Ajdari, A.; Djabourov, M. All gelatin networks: 2. The master curve for elasticity. Langmuir 2002, 18, 7158–7166. [Google Scholar] [CrossRef]
- Avallone, P.R.; Raccone, E.; Costanzo, S.; Delmonte, M.; Sarrica, A.; Pasquino, R.; Grizzuti, N. Gelation kinetics of aqueous gelatin solutions in isothermal conditions via rheological tools. Food Hydrocoll. 2021, 111, 106248. [Google Scholar] [CrossRef]
- Joy, R.; Vigneshkumar, P.; John, F.; George, J. Hydrogels based on carrageenan. In Plant and Algal Hydrogels for Drug Delivery and Regenerative Medicine; Elsevier: Amsterdam, The Netherlands, 2021; pp. 293–325. [Google Scholar]
- Balasubramanian, R.; Kim, S.S.; Lee, J. Novel synergistic transparent k-Carrageenan/Xanthan gum/Gellan gum hydrogel film: Mechanical, thermal and water barrier properties. Int. J. Biol. Macromol. 2018, 118, 561–568. [Google Scholar] [CrossRef]
- Katzbauer, B. Properties and applications of xanthan gum. Polym. Degrad. Stab. 1998, 59, 81–84. [Google Scholar] [CrossRef]
- Whitcomb, P.J.; Macosko, C. Rheology of xanthan gum. J. Rheol. 1978, 22, 493–505. [Google Scholar] [CrossRef]
- Choppe, E.; Puaud, F.; Nicolai, T.; Benyahia, L. Rheology of xanthan solutions as a function of temperature, concentration and ionic strength. Carbohydr. Polym. 2010, 82, 1228–1235. [Google Scholar] [CrossRef]
- Sworn, G. Xanthan gum. In Handbook of Hydrocolloids, 2nd ed.; Phillips, G.O., Williams, P.A., Eds.; Woodhead Publishing Series in Food Science; Technology and Nutrition; Woodhead: Cambridge, UK, 2009; Volume 8, pp. 186–203. [Google Scholar]
- Kasapis, S.; Al-Marhoobi, I.M.; Deszczynski, M.; Mitchell, J.R.; Abeysekera, R. Gelatin vs polysaccharide in mixture with sugar. Biomacromolecules 2003, 4, 1142–1149. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, M.; Bhandari, B.; Wang, Y. 3D printing: Printing precision and application in food sector. Trends Food Sci. Technol. 2017, 69, 83–94. [Google Scholar] [CrossRef]
- Liu, Z.; Bhandari, B.; Prakash, S.; Mantihal, S.; Zhang, M. Linking rheology and printability of a multicomponent gel system of carrageenan-xanthan-starch in extrusion based additive manufacturing. Food Hydrocoll. 2019, 87, 413–424. [Google Scholar] [CrossRef]
- Li, H.; Tan, C.; Li, L. Review of 3D printable hydrogels and constructs. Mater. Des. 2018, 159, 20–38. [Google Scholar] [CrossRef]
- Lin, J.H.; Liang, C.W.; Chang, Y.H. Effect of starch source on gel properties of kappa-carrageenan-starch dispersions. Food Hydrocoll. 2016, 60, 509–515. [Google Scholar] [CrossRef]
- Sweeney, M.; Campbell, L.L.; Hanson, J.; Pantoya, M.L.; Christopher, G.F. Characterizing the feasibility of processing wet granular materials to improve rheology for 3D printing. J. Mater. Sci. 2017, 52, 13040–13053. [Google Scholar] [CrossRef]
- Estevez, J.M.; Ciancia, M.; Cerezo, A.S. The system of galactans of the red seaweed, Kappaphycus alvarezii, with emphasis on its minor constituents. Carbohydr. Res. 2004, 339, 2575–2592. [Google Scholar] [CrossRef]
- Thrimawithana, T.R.; Young, S.; Dunstan, D.; Alany, R.G. Texture and rheological characterization of kappa and iota carrageenan in the presence of counter ions. Carbohydr. Polym. 2010, 82, 69–77. [Google Scholar] [CrossRef]
- Wei, Y.; Li, R.; Zhang, H. Measures of the yield stress fluids oriented for dysphagia management using steady-state shear, transient shear, and large-amplitude oscillatory shear (LAOS). Phys. Fluids 2022, 34, 123107. [Google Scholar] [CrossRef]
- Venezia, V.; Avallone, P.R.; Vitiello, G.; Silvestri, B.; Grizzuti, N.; Pasquino, R.; Luciani, G. Adding humic acids to gelatin hydrogels: A way to tune gelation. Biomacromolecules 2021, 23, 443–453. [Google Scholar] [CrossRef] [PubMed]
- Acierno, S.; Pasquino, R.; Grizzuti, N. Rheological techniques for the determination of the crystallization kinetics of a polypropylene–EPR copolymer. J. Therm. Anal. Calorim. 2009, 98, 639–644. [Google Scholar] [CrossRef]
- Wang, C.S.; Virgilio, N.; Wood-Adams, P.; Heuzey, M.C. A mechanism for the synergistic gelation properties of gelatin B and xanthan gum aqueous mixtures. Carbohydr. Polym. 2017, 175, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Russo Spena, S.; Grizzuti, N.; Tammaro, D. Linking Processing Parameters and Rheology to Optimize Additive Manufacturing of k-Carrageenan Gel Systems. Gels 2022, 8, 493. [Google Scholar] [CrossRef] [PubMed]
- Morris, E.R.; Cutler, A.; Ross-Murphy, S.; Rees, D.; Price, J. Concentration and shear rate dependence of viscosity in random coil polysaccharide solutions. Carbohydr. Polym. 1981, 1, 5–21. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Shahbazi, M.; Rajabzadeh, G.; Ettelaie, R.; Rafe, A. Kinetic study of κ-carrageenan degradation and its impact on mechanical and structural properties of chitosan/κ-carrageenan film. Carbohydr. Polym. 2016, 142, 167–176. [Google Scholar] [CrossRef]
- Vadillo, D.C.; Mathues, W.; Clasen, C. Microsecond relaxation processes in shear and extensional flows of weakly elastic polymer solutions. Rheol. Acta 2012, 51, 755–769. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: New York, NY, USA, 2003; Volume 23. [Google Scholar]
- Lai, V.M.F.; Li, C.Y.; Hung, W.L.; Lu, T.J. Kinetic compensation effect in depolymerisation of food polysaccharides. Food Chem. 2000, 68, 319–325. [Google Scholar] [CrossRef]
- Clark, A.H. Structural and mechanical properties of biopolymer gels. In Food Polymers, Gels and Colloids; Woodhead Publishing: Sawston, UK, 1991; pp. 322–338. [Google Scholar]
- Ross-Murphy, S. Incipient behaviour of gelatin gels. Rheol. Acta 1991, 30, 401–411. [Google Scholar] [CrossRef]
- Han, C.K.; Bae, Y.H. Inverse thermally-reversible gelation of aqueous N-isopropylacrylamide copolymer solutions. Polymer 1998, 39, 2809–2814. [Google Scholar] [CrossRef]
- Liu, Y.; Pandey, R. Sol–gel phase transitions in thermoreversible gels: Onset of gelation and melting. J. Chem. Phys. 1996, 105, 825–836. [Google Scholar] [CrossRef]
- Liu, S.; Li, L. Thermoreversible gelation and scaling behavior of Ca2+-induced κ-carrageenan hydrogels. Food Hydrocoll. 2016, 61, 793–800. [Google Scholar] [CrossRef]
- Rochas, C.; Rinaudo, M. Mechanism of gel formation in κ-carrageenan. Biopolym. Orig. Res. Biomol. 1984, 23, 735–745. [Google Scholar] [CrossRef]
- Rochas, C.; Rinaudo, M. Activity coefficients of counterions and conformation in kappa-carrageenan systems. Biopolym. Orig. Res. Biomol. 1980, 19, 1675–1687. [Google Scholar] [CrossRef]
- Liu, S.; Chan, W.L.; Li, L. Rheological properties and scaling laws of κ-carrageenan in aqueous solution. Macromolecules 2015, 48, 7649–7657. [Google Scholar] [CrossRef]
- Lu, L.; Liu, X.; Tong, Z.; Gao, Q. Critical exponents and self-similarity for sol-gel transition in aqueous alginate systems induced by in situ release of calcium cations. J. Phys. Chem. B 2006, 110, 25013–25020. [Google Scholar] [CrossRef]
- Bertasa, M.; Dodero, A.; Alloisio, M.; Vicini, S.; Riedo, C.; Sansonetti, A.; Scalarone, D.; Castellano, M. Agar gel strength: A correlation study between chemical composition and rheological properties. Eur. Polym. J. 2020, 123, 109442. [Google Scholar] [CrossRef]
- Draget, K.; Bræk, G.S.; Smidsrød, O. Alginic acid gels: The effect of alginate chemical composition and molecular weight. Carbohydr. Polym. 1994, 25, 31–38. [Google Scholar] [CrossRef]
- Wyatt, N.B.; Liberatore, M.W. Rheology and viscosity scaling of the polyelectrolyte xanthan gum. J. Appl. Polym. Sci. 2009, 114, 4076–4084. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W.; Duan, F.; Tang, Q.; Li, X.; Zeng, L.; Zhang, J.; Xing, Z.; Dong, Y.; Jia, L.; et al. The synergistic gelation of okra polysaccharides with kappa-carrageenan and its influence on gel rheology, texture behaviour and microstructures. Food Hydrocoll. 2019, 87, 425–435. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, W.; He, Q. The gelation properties of tara gum blended with κ-carrageenan or xanthan. Food Hydrocoll. 2018, 77, 764–771. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, H.; Yang, H. Effects of sucrose addition on the rheology and microstructure of κ-carrageenan gel. Food Hydrocoll. 2018, 75, 164–173. [Google Scholar] [CrossRef]
- Dinkgreve, M.; Paredes, J.; Denn, M.M.; Bonn, D. On different ways of measuring “the” yield stress. J. Non-Newton. Fluid Mech. 2016, 238, 233–241. [Google Scholar] [CrossRef]
- He, Y.; Yang, F.; Zhao, H.; Gao, Q.; Xia, B.; Fu, J. Research on the printability of hydrogels in 3D bioprinting. Sci. Rep. 2016, 6, 29977. [Google Scholar] [CrossRef]




| κ-c Concentration | |||
|---|---|---|---|
| 1.5 wt% | |||
| 2 wt% | |||
| 2.5 wt% | |||
| 3 wt% | |||
| 1.5 wt% | |||
| 2 wt% | |||
| 2.5 wt% | |||
| 3 wt% |
| Samples | Yield Stress [Pa] | Yield Strain [%] |
|---|---|---|
| 933 | ||
| 1758 | ||
| 3042 | ||
| 4390 | ||
| — | 1368 | |
| — | 1965 | |
| — | 2400 | |
| ——sucrose | 2450 | |
| ——sucrose | 3580 | |
| ——sucrose | 5072 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avallone, P.R.; Russo Spena, S.; Acierno, S.; Esposito, M.G.; Sarrica, A.; Delmonte, M.; Pasquino, R.; Grizzuti, N. Thermorheological Behavior of κ-Carrageenan Hydrogels Modified with Xanthan Gum. Fluids 2023, 8, 119. https://doi.org/10.3390/fluids8040119
Avallone PR, Russo Spena S, Acierno S, Esposito MG, Sarrica A, Delmonte M, Pasquino R, Grizzuti N. Thermorheological Behavior of κ-Carrageenan Hydrogels Modified with Xanthan Gum. Fluids. 2023; 8(4):119. https://doi.org/10.3390/fluids8040119
Chicago/Turabian StyleAvallone, Pietro Renato, Simona Russo Spena, Stefano Acierno, Maria Giovanna Esposito, Andrea Sarrica, Marco Delmonte, Rossana Pasquino, and Nino Grizzuti. 2023. "Thermorheological Behavior of κ-Carrageenan Hydrogels Modified with Xanthan Gum" Fluids 8, no. 4: 119. https://doi.org/10.3390/fluids8040119
APA StyleAvallone, P. R., Russo Spena, S., Acierno, S., Esposito, M. G., Sarrica, A., Delmonte, M., Pasquino, R., & Grizzuti, N. (2023). Thermorheological Behavior of κ-Carrageenan Hydrogels Modified with Xanthan Gum. Fluids, 8(4), 119. https://doi.org/10.3390/fluids8040119







