Dynamics of Magnetic Fluids and Bidisperse Magnetic Systems under Oscillatory Shear
Abstract
1. Introduction
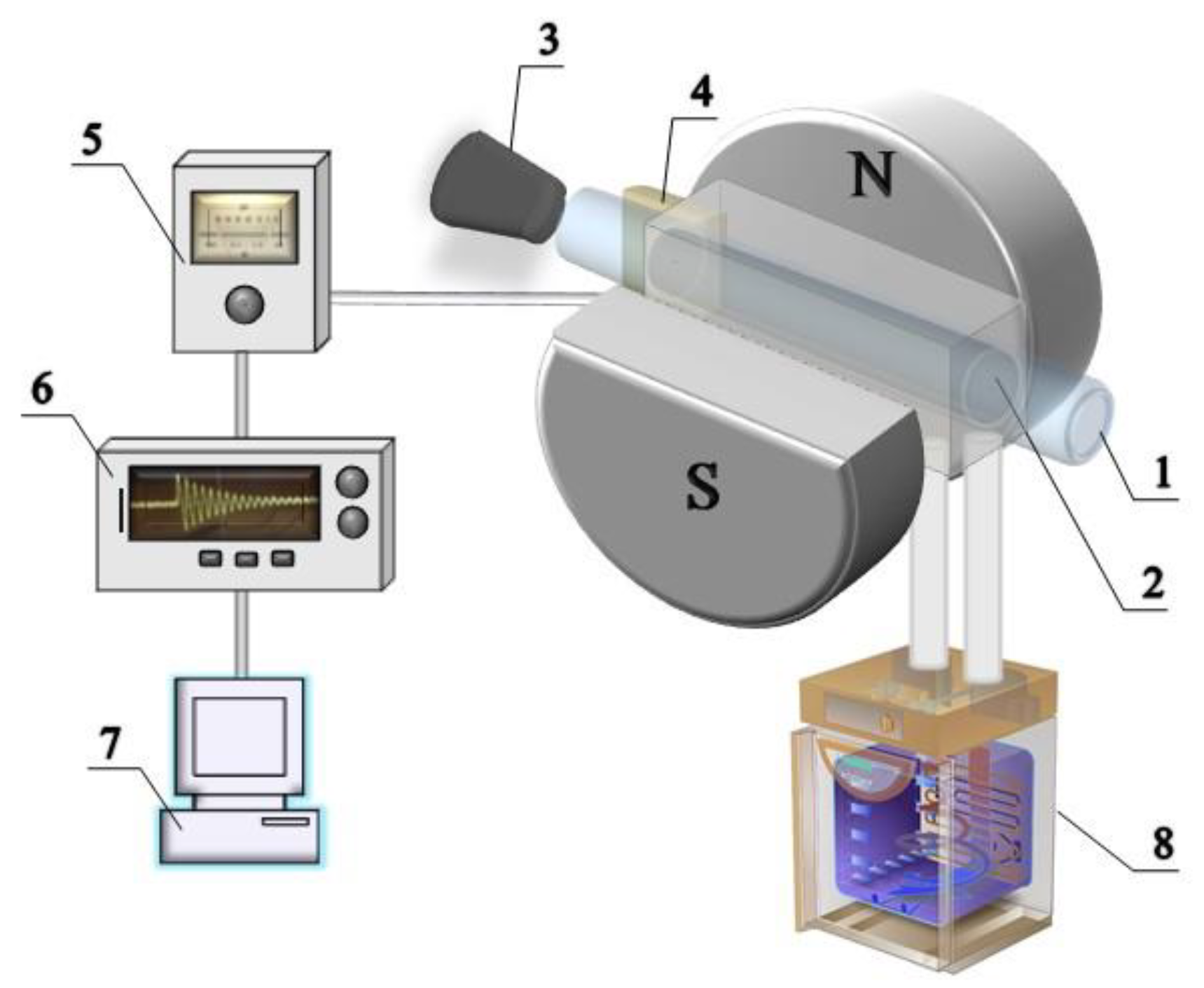
2. Materials and Methods
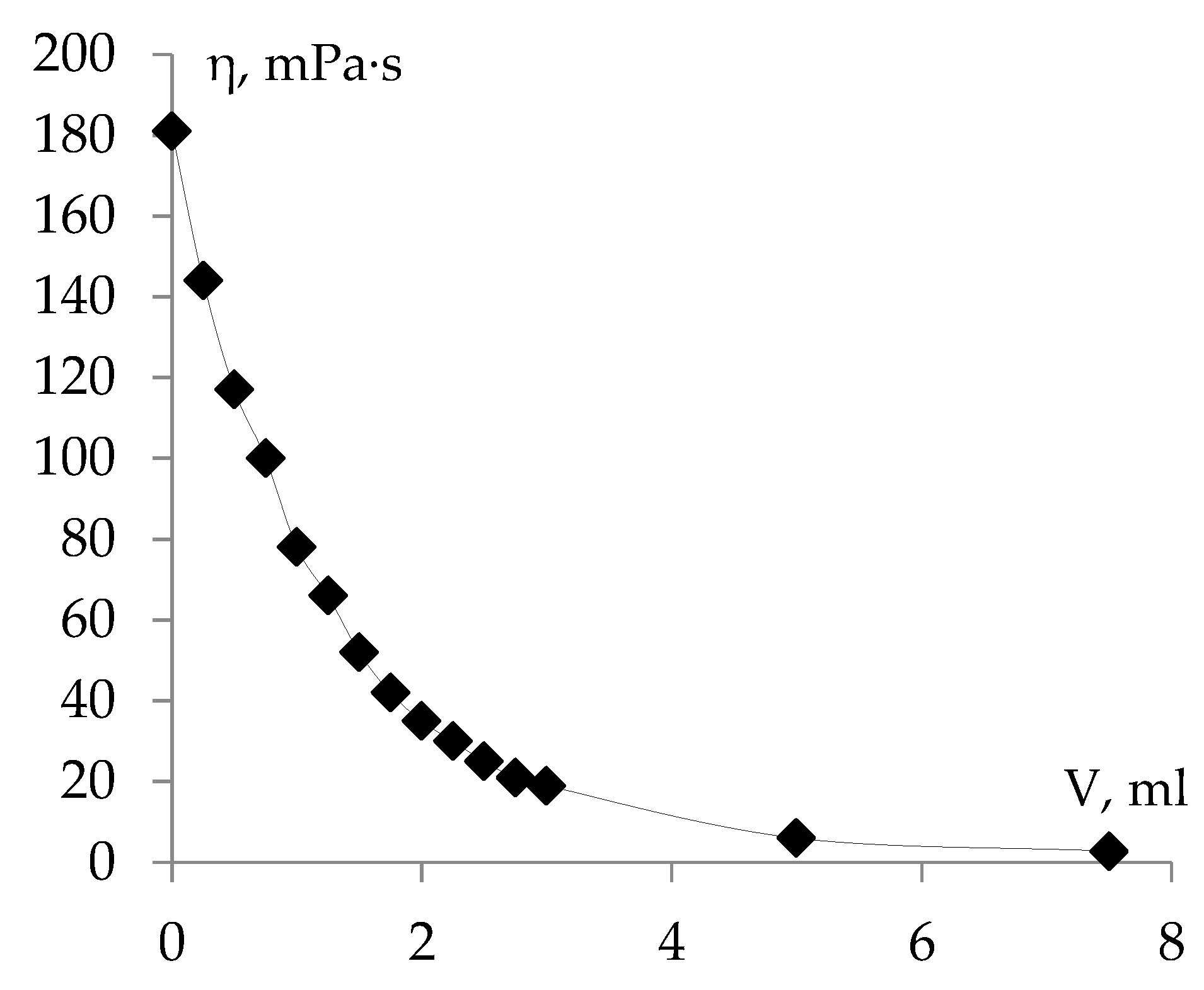
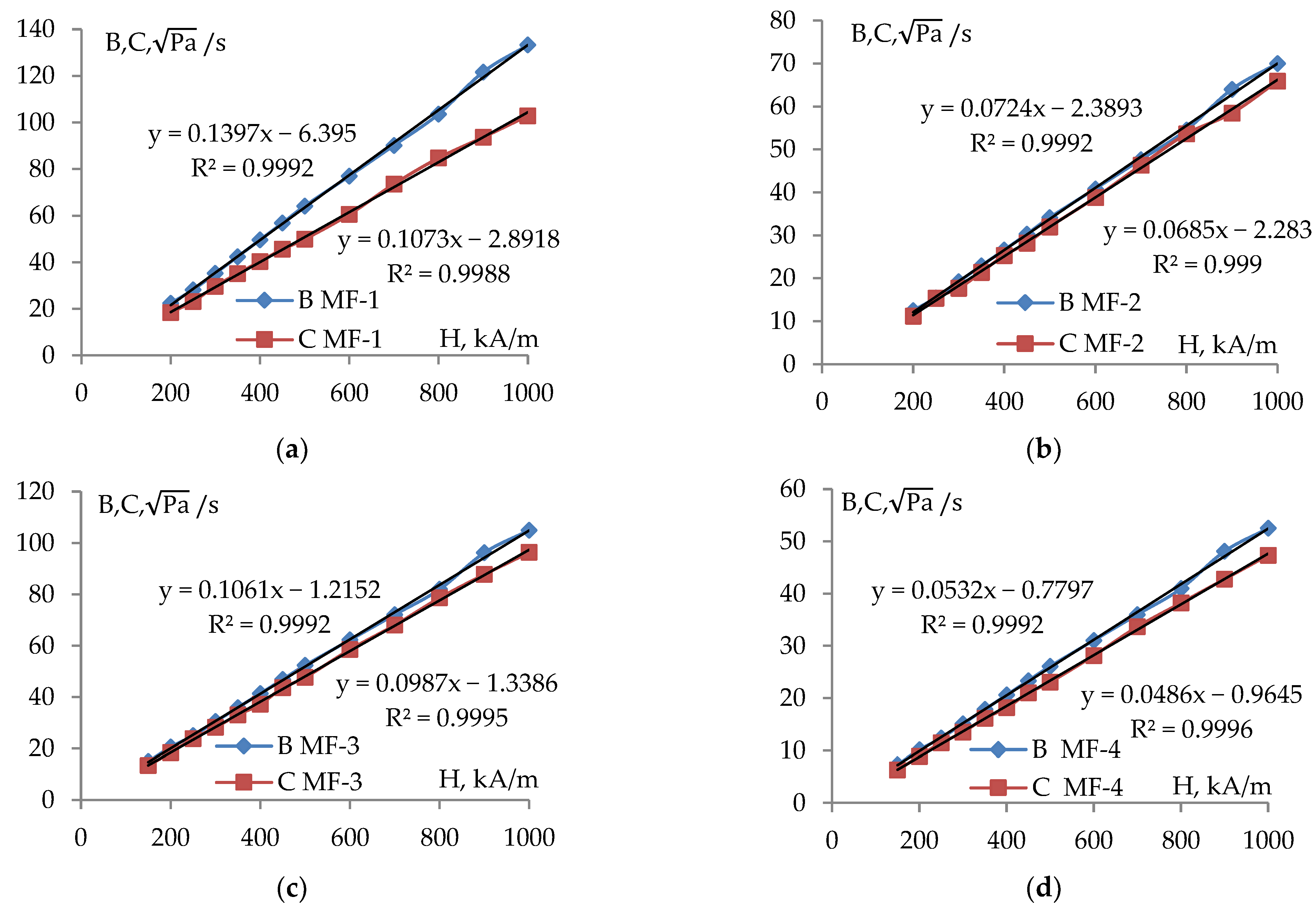
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rosensweig, R.E. Ferrohydrodynamics; Courier Corporation: Chelmsford, MA, USA, 2013; 368p. [Google Scholar]
- Socoliuc, V.; Avdeev, M.V.; Kuncser, V.; Turcu, R.; Tombácz, E.; Vekas, L. Ferrofluids and bio-ferrofluids: Looking back and stepping forward. Nanoscale 2022, 14, 4786–4886. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Yu, Y.; Zhao, Y. Flexible ferrofluids: Design and applications. Adv. Mater. 2019, 31, 1903497. [Google Scholar] [CrossRef] [PubMed]
- Odenbach, S. Colloidal Magnetic Fluids: Basics, Development and Application of Ferrofluids; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 763, 429p. [Google Scholar] [CrossRef]
- Philip, J. Magnetic nanofluids: Recent advances, applications, challenges, and future directions. Adv. Colloid Interface Sci. 2022, 311, 102810. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Yao, J.; Zhang, T.; Chen, Y.; Jiang, H.; Li, D. Damping applications of ferrofluids: A review. J. Magn. 2017, 22, 109–121. [Google Scholar] [CrossRef]
- Lebedev, A.V.; Kantorovich, S.S.; Ivanov, A.O.; Arefyev, I.M.; Pshenichnikov, A.F. Weakening of magnetic response experimentally observed for ferrofluids with strongly interacting magnetic nanoparticles. J. Mol. Liq. 2019, 277, 762–768. [Google Scholar] [CrossRef]
- Bashtovoi, V.; Reks, A.; Kuzhir, P.; Zubarev, A.; Volkova, O.; Moroz, V. Effect of magnetophoresis and Brownian diffusion on mechanical processes in magnetic fluids: The role of a condensation phase transition. J. Magn. Magn. Mater. 2020, 498, 166148. [Google Scholar] [CrossRef]
- Polunin, V.M.; Tantsyura, A.O.; Storozhenko, A.M.; Ryapolov, P.A. Study of demagnetizing field induced by a sound wave. Acoust. Phys. 2013, 59, 662–666. [Google Scholar] [CrossRef]
- Zakinyan, A.A.; Belykh, S.S.; Zakinyan, A.R.; Yerin, K.V. Structured media based on magnetic colloids as a promising material for magnetically controllable optical elements. J. Opt. Technol. 2021, 88, 158–165. [Google Scholar] [CrossRef]
- Ivanov, A.S.; Pshenichnikov, A.F. Magnetostatic buoyancy force acting on a non-magnetic sphere immersed in a ferrofluid magnetized by a gradient field. J. Magn. Magn. Mater. 2022, 565, 170294. [Google Scholar] [CrossRef]
- Ivanov, A.S.; Solovyova, A.Y.; Zverev, V.S.; Elfimova, E.A. Distribution functions of magnetic moments and relaxation times for magnetic fluids exhibiting controllable microstructure evolution. J. Mol. Liq. 2022, 367, 120550. [Google Scholar] [CrossRef]
- Lacava, L.M.; Lacava, B.M.; Azevedo, R.B.; Lacava, Z.G.M.; Buske, N.; Tronconi, A.L.; Morais, P.C. Nanoparticle sizing: A comparative study using atomic force microscopy, transmission electron microscopy, and ferromagnetic resonance. J. Magn. Magn. Mater. 2001, 225, 79–83. [Google Scholar] [CrossRef]
- Passeri, D.; Angeloni, L.; Rossi, M. Magnetic Force Microscopy and Magnetic Nanoparticles: Perspectives and Challenges; In New Trends in Nanoparticle Magnetism; Springer: Cham, Switzerland, 2021; Volume 308, pp. 285–300. [Google Scholar] [CrossRef]
- Raşa, M.; Kuipers, B.W.M.; Philipse, A.P. Atomic force microscopy and magnetic force microscopy study of model colloids. J. Colloid Interface Sci. 2002, 250, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Butter, K.; Bomans, P.H.H.; Frederik, P.M.; Vroege, G.J.; Philipse, A.P. Direct observation of dipolar chains in iron ferrofluids by cryogenic electron microscopy. Nat. Mater. 2003, 2, 88–91. [Google Scholar] [CrossRef] [PubMed]
- Butter, K.; Bomans, P.H.; Frederik, P.M.; Vroege, G.J.; Philipse, A.P. Direct observation of dipolar chains in ferrofluids in zero field using cryogenic electron microscopy. J. Phys. Condens. Matter 2003, 15, S1451. [Google Scholar] [CrossRef]
- Morillas, J.R.; de Vicente, J. Magnetorheology: A review. Soft Matter 2020, 16, 9614–9642. [Google Scholar] [CrossRef]
- Damdinov, B.B.; Mitypov, C.M.; Ershov, A.A.; An, V.V. Bulk Viscosity in Liquids and Liquid Disperse Systems. Russ. Phys. J. 2022, 65, 840–846. [Google Scholar] [CrossRef]
- Odenbach, S. Magnetic fluids-suspensions of magnetic dipoles and their magnetic control. J. Phys. Condens. Matter 2003, 15, S1497. [Google Scholar] [CrossRef]
- El-Sapa, S. The force on a magneto-spherical particle oscillating in a viscous fluid perpendicular to an impermeable planar wall with slippage. European J. Pure Appl. Math. 2022, 15, 1376–1401. [Google Scholar] [CrossRef]
- Afifah, A.N.; Syahrullail, S.; Sidik, N.A.C. Magnetoviscous effect and thermomagnetic convection of magnetic fluid: A review. Renew. Sustain. Energy Rev. 2016, 55, 1030–1040. [Google Scholar] [CrossRef]
- Nam-Trung, N. Micro-magnetofluidics: Interactions between magnetism and fluid flow on the microscale. Microfluid. Nanofluid 2012, 12, 1–16. [Google Scholar] [CrossRef]
- Ivanov, A.O.; Zubarev, A. Chain formation and phase separation in ferrofluids: The influence on viscous properties. Materials 2020, 13, 3956. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.; Pathak, S.; Kumar, P.; Singh, A.; Jain, K.; Chaturvedi, R.; Pant, R.P. Measurement of static and dynamic magneto-viscoelasticity in facile varying pH synthesized CoFe2O4-based magnetic fluid. IEEE Trans. Magn. 2019, 55, 1–7. [Google Scholar] [CrossRef]
- Pathak, S.; Verma, R.; Kumar, P.; Singh, A.; Singhal, S.; Sharma, P.; Wang, X. Facile synthesis, static, and dynamic magnetic characteristics of varying size double-surfactant-coated mesoscopic magnetic nanoparticles dispersed stable aqueous magnetic fluids. Nanomaterials 2021, 11, 3009. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Pathak, S.; Singh, A.; Khanduri, H.; Wang, X.; Basheed, G.A.; Pant, R.P. Optimization of cobalt concentration for improved magnetic characteristics and stability of CoxFe3−xO4 mixed ferrite nanomagnetic fluids. Mater. Chem. Phys. 2021, 265, 124476. [Google Scholar] [CrossRef]
- Shahrivar, K.; Morillas, J.R.; Luengo, Y.; Gavilan, H.; Morales, P.; Bierwisch, C.; de Vicente, J. Rheological behavior of magnetic colloids in the borderline between ferrofluids and magnetorheological fluids. J. Rheol. 2019, 63, 547–558. [Google Scholar] [CrossRef]
- Shah, K.; Choi, S.B. The influence of particle size on the rheological properties of plate-like iron particle based magnetorheological fluids. Smart Mater. Struct. 2014, 24, 015004. [Google Scholar] [CrossRef]
- Liu, X.; Li, D. Tuning the magneto-rheological properties of magnetic fluid using hydrophilic fumed silica nanoparticles. Soft Matter 2021, 17, 8175–8184. [Google Scholar] [CrossRef]
- Jain, K.; Kumar, P.; Pant, R.P.; Basheed, G.A. Tunning of rheological and magnetic properties of Ni doped magnetite based magnetic nanofluid. Phys. B Condens. Matter 2022, 643, 414136. [Google Scholar] [CrossRef]
- López-López, M.T.; De Vicente, J.; Bossis, G.; González-Caballero, F.; Durán, J.D.G. Preparation of stable magnetorheological fluids based on extremely bimodal iron–magnetite suspensions. J. Mater. Res. 2005, 20, 874–881. [Google Scholar] [CrossRef]
- Cvek, M.; Jamatia, T.; Suly, P.; Urbanek, M.; Torres-Mendieta, R. Stable Magnetorheological Fluids Containing Bidisperse Fillers with Compact/Mesoporous Silica Coatings. Int. J. Mol. Sci. 2022, 23, 11044. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Magnetorheological particle clouds. J. Magn. Magn. Mater. 2019, 479, 301–306. [Google Scholar] [CrossRef]
- Susan-Resiga, D.; Socoliuc, V.; Bunge, A.; Turcu, R.; Vékás, L. From high colloidal stability ferrofluids to magnetorheological fluids: Tuning the flow behavior by magnetite nanoclusters. Smart Mater. Struct. 2019, 28, 115014. [Google Scholar] [CrossRef]
- Siebert, E.; Dupuis, V.; Neveu, S.; Odenbach, S. Rheological investigations on the theoretical predicted “Poisoning” effect in bidisperse ferrofluids. J. Magn. Magn. Mater. 2015, 374, 44–49. [Google Scholar] [CrossRef]
- Susan-Resiga, D.; Vékás, L. Yield stress and flow behavior of concentrated ferrofluid-based magnetorheological fluids: The influence of composition. Rheol. Acta 2014, 53, 645–653. [Google Scholar] [CrossRef]
- Doganay, S.; Alsangur, R.; Turgut, A. Effect of external magnetic field on thermal conductivity and viscosity of magnetic nanofluids: A review. Mater. Res. Express 2019, 6, 112003. [Google Scholar] [CrossRef]
- Pathak, S.; Jain, K.; Kumar, P.; Wang, X.; Pant, R.P. Improved thermal performance of annular fin-shell tube storage system using magnetic fluid. Appl. Energy 2019, 239, 1524–1535. [Google Scholar] [CrossRef]
- Iwamoto, Y.; Kondoh, S.; Ido, Y.; Yamamoto, H.; Nishida, H.; Yamasaki, H.; Jeyadevan, B. Influence of size on anisotropic thermophysical properties of magnetic suspensions. Int. J. Appl. Electromagn. Mech. 2018, 58, 371–385. [Google Scholar] [CrossRef]
- Lei, J.; Luo, Z.; Qing, S.; Huang, X.; Li, F. Effect of surfactants on the stability, rheological properties, and thermal conductivity of Fe3O4 nanofluids. Powder Technol. 2022, 399, 117197. [Google Scholar] [CrossRef]
- Li, Y.; Han, P.; Li, D.; Chen, S.; Wang, Y. Typical dampers and energy harvesters based on characteristics of ferrofluids. Friction 2022, 11, 165–186. [Google Scholar] [CrossRef]
- Purnomo, E.D.; Ubaidillah, U.; Imaduddin, F.; Yahya, I.; Mazlan, S.A. Preliminary experimental evaluation of a novel loud-speaker featuring magnetorheological fluid surround absorber. Indones. J. Electr. Eng. Comput. Sci. 2020, 17, 922–928. [Google Scholar] [CrossRef]
- Li, Z.; Li, D. A comparative study of magnetic seals by ferrofluids, magnetorheological fluids and magnetic powders. Front. Mater. 2022, 9, 984761. [Google Scholar] [CrossRef]
- Yao, J.; Liu, J.; Hu, Y.; Li, Z.; Li, D. The Theoretical and Experimental Study of a Ferrofluid Inertial Sensor. IEEE Sens. J. 2021, 22, 107–114. [Google Scholar] [CrossRef]
- Nowak, J.; Borin, D.; Haefner, S.; Richter, A.; Odenbach, S. Magnetoviscous effect in ferrofluids diluted with sheep blood. J. Magn. Magn. Mater. 2017, 442, 383–390. [Google Scholar] [CrossRef]
- Huang, H.; Li, H.; Wang, W.; Peng, X. Analysis on the enhancement mechanism of bidisperse magnetorheological fluid based on the local microstructural models. Rheol. Acta 2022, 61, 87–98. [Google Scholar] [CrossRef]
- Polunin, V.M.; Ryapolov, P.A.; Zhakin, A.I.; Ivanov, A.M.; Shel’deshova, E.V. Magnetoviscous effect in case of magnetic fluid oscillations in strong magnetic field. Magnetohydrodynamics 2018, 54, 353–360. [Google Scholar]
- Karpova, G.V.; Kutuev, A.N.; Ryapolov, P.A.; Polunin, V.M.; Zubarev, E.K.; Kovarda, V.V. On the dissipation processes in the oscillating system with a magneto-liquid element. Magnetohydrodynamics 2009, 45, 85–93. [Google Scholar]
- Polunin, V.M.; Ryapolov, P.A.; Platonov, V.B.; Kuz’ko, A.E. Free oscillations of magnetic fluid in strong magnetic field. Acoust. Phys. 2016, 62, 313–318. [Google Scholar] [CrossRef]
- Polunin, V.M.; Ryapolov, P.A.; Shel’deshova, E.V.; Kuz’ko, A.E.; Aref’ev, I.M. Dynamic Elasticity of a magnetic fluid column in a strong magnetic field. Russ. Phys. J. 2017, 60, 381–388. [Google Scholar] [CrossRef]
- Ryapolov, P.A.; Polunin, V.M.; Shel’deshova, E.V. An alternative way to study magnetic fluid magnetization and viscosity. J. Magn. Magn. Mater. 2020, 496, 165924. [Google Scholar] [CrossRef]
- Polunin, V.M.; Ryapolov, P.A.; Zhakin, A.I.; Sheldeshova, E.V. Viscosity of a Magnetic Fluid in a Strong Magnetic Field. Acoust. Phys. 2019, 65, 379–384. [Google Scholar] [CrossRef]
- Polunin, V.M.; Ryapolov, P.A.; Platonov, V.B.; Sheldeshova, E.V.; Karpova, G.V.; Aref’ev, I.M. Elasticity of a magnetic fluid in a strong magnetic field. Acoust. Phys. 2017, 63, 416–423. [Google Scholar] [CrossRef]
- Leupold, H.A.; Tilak, A.S.; Potenziani, E. Multi-Tesla permanent magnet field sources. J. Appl. Phys. 1993, 73, 6861–6863. [Google Scholar] [CrossRef]
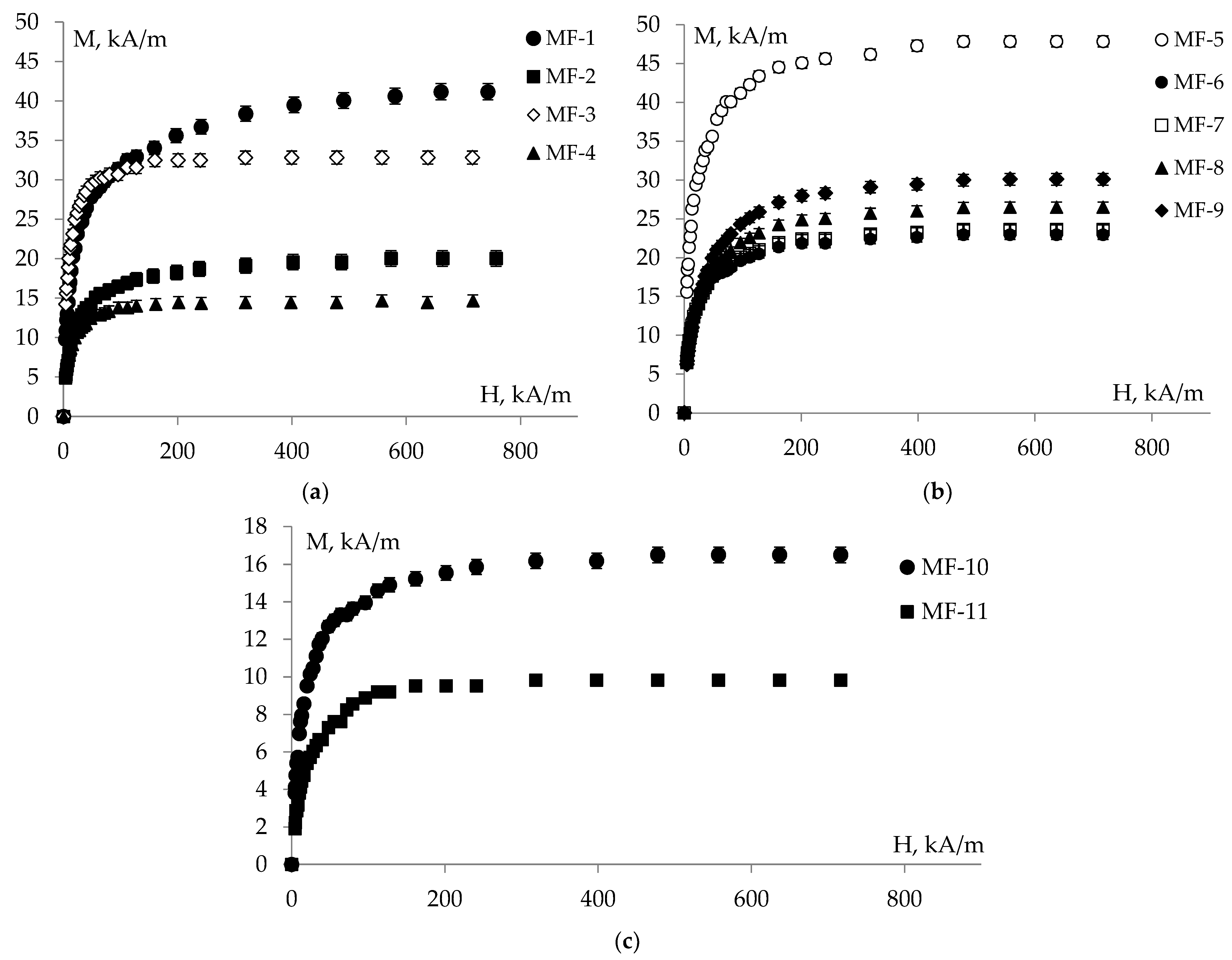

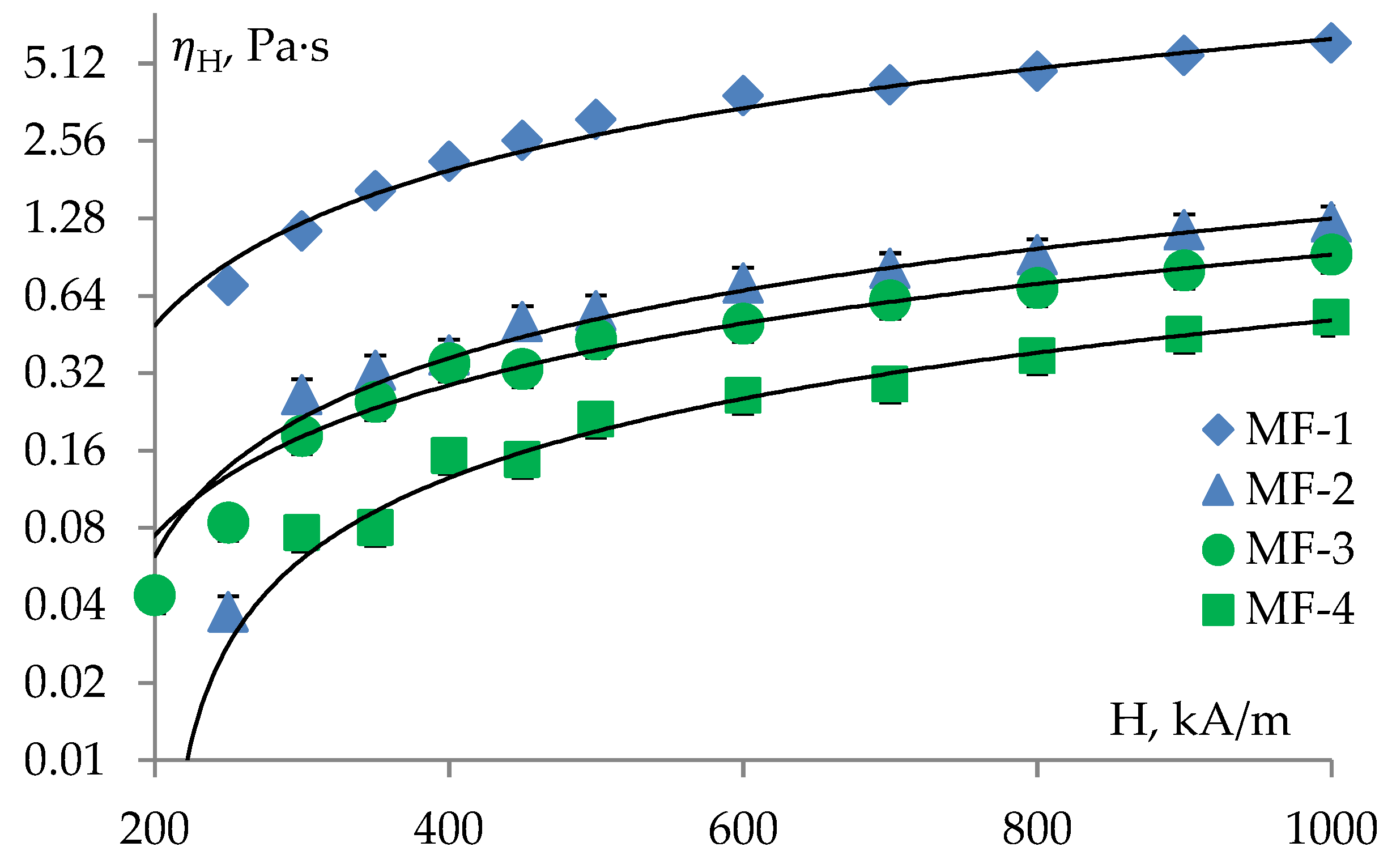
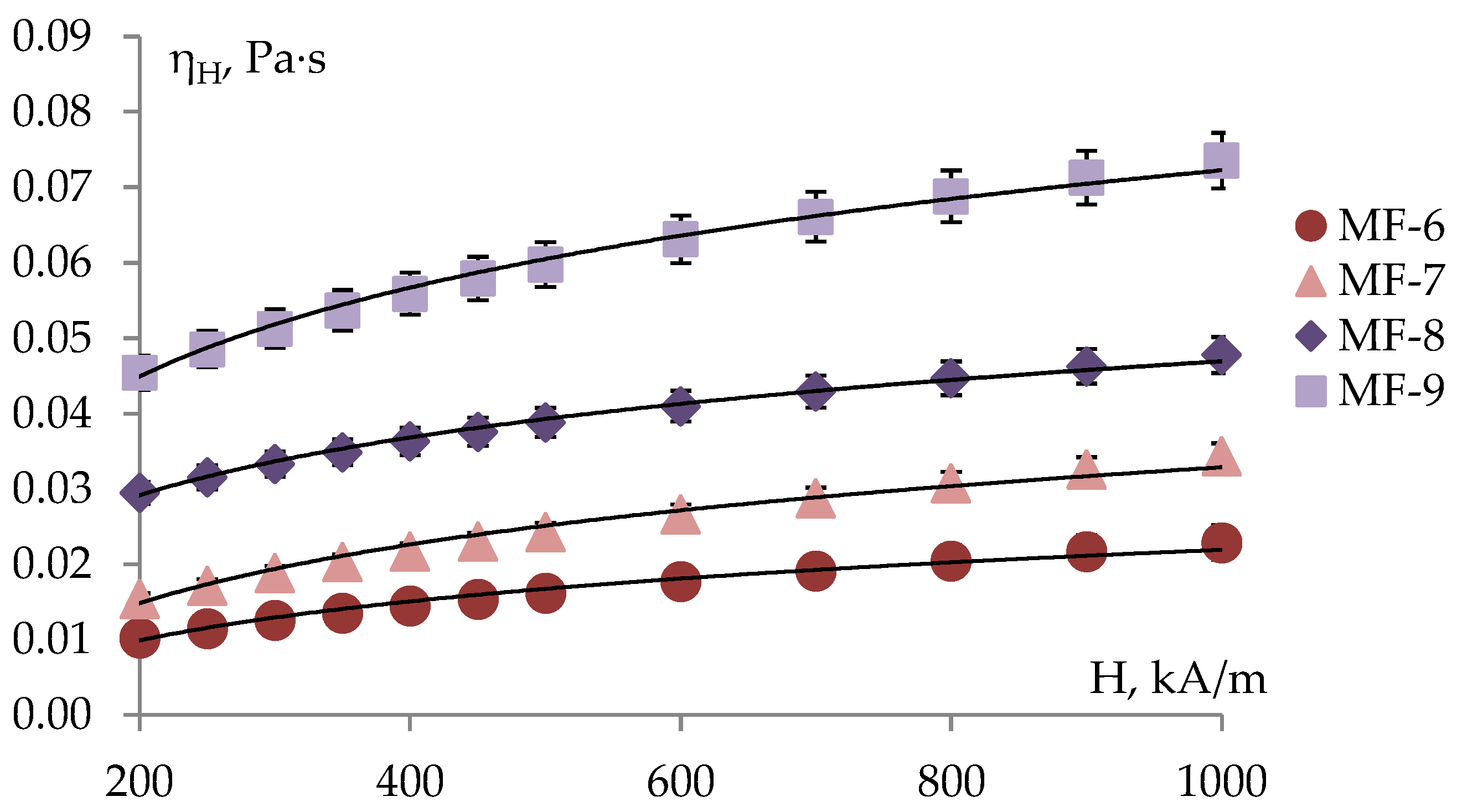
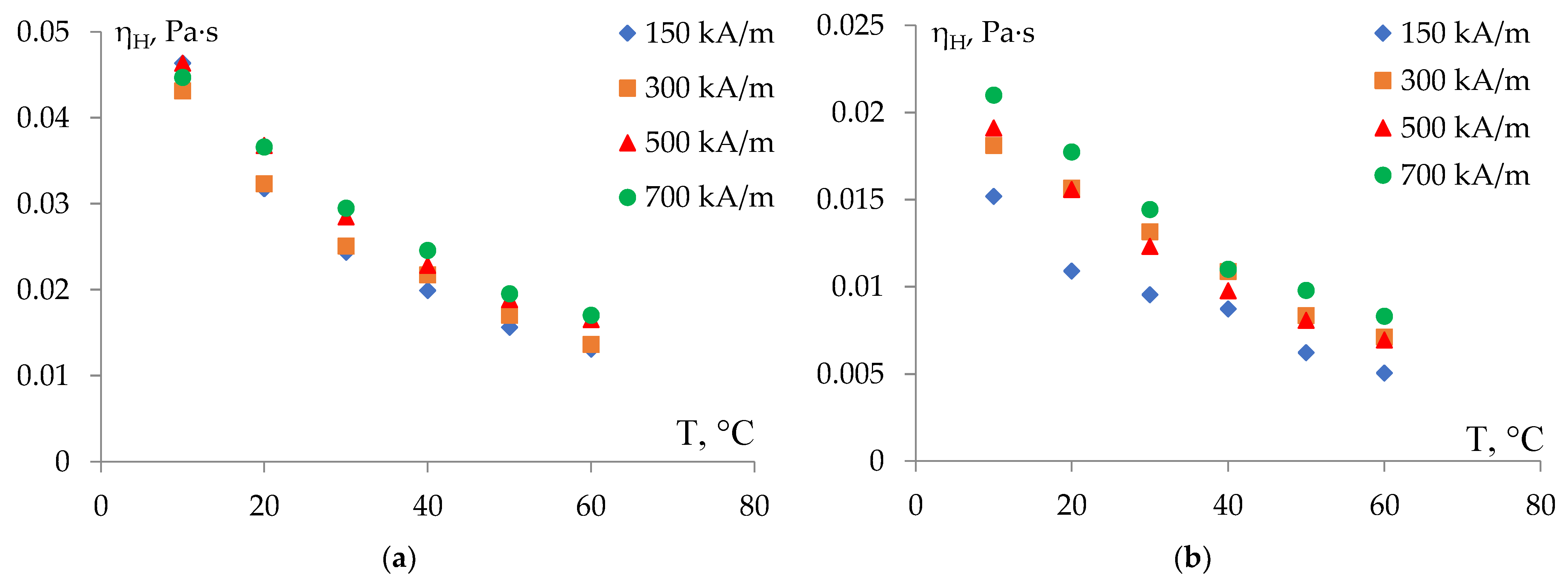
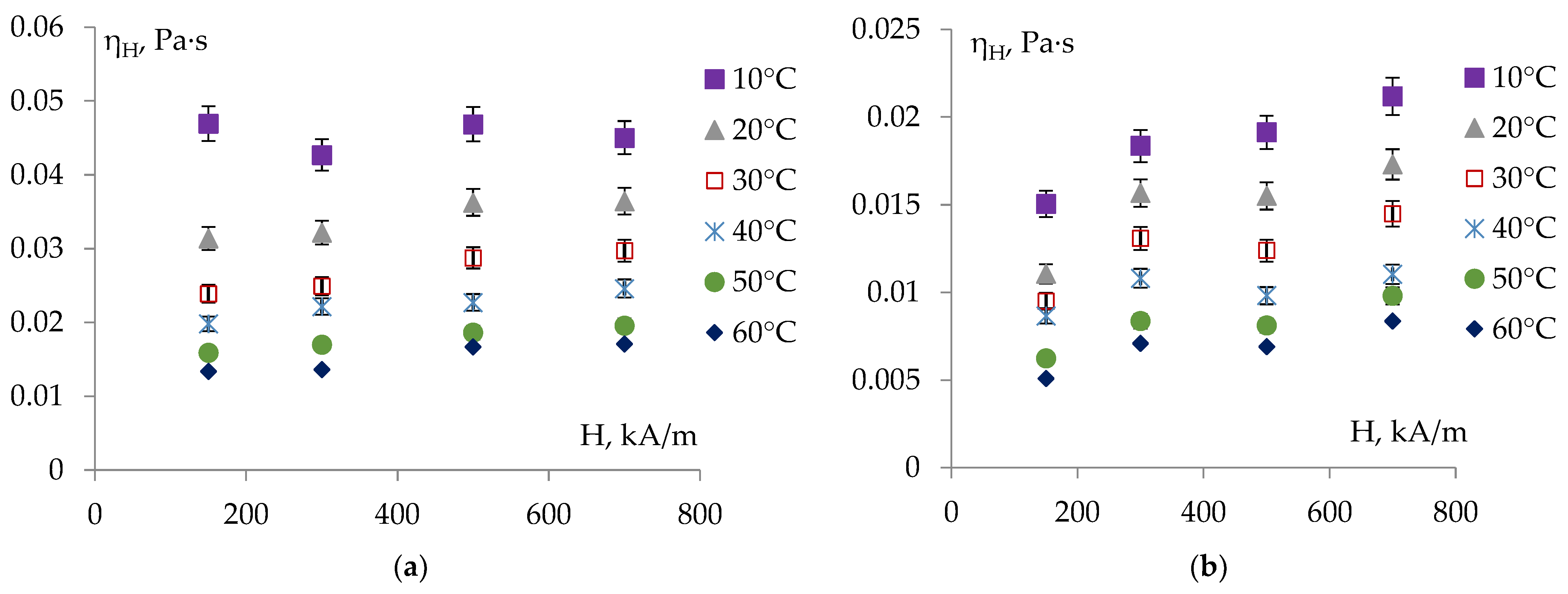
| Sample | MF Density ρ, kg/m3 | Volume Concentration φ, % | Saturation Magnetization Ms, kA/m | MF Viscosity η, mPa∙s |
|---|---|---|---|---|
| MF-1 | 1245 | 11.02 | 43.3 | 31.8 |
| MF-2 | 1058 | 6.62 | 20.7 | 4.15 |
| MF-3 | 1245 | 11.06 | 33 | 4.05 |
| MF-4 | 985 | 4.9 | 14.7 | 2.45 |
| MF-5 | 1382 | 14.2 | 49.4 | 180 |
| MF-6 | 1080 | 7.04 | 23.6 | 6.3 |
| MF-7 | 1087 | 7.22 | 24.4 | 5.7 |
| MF-8 | 1089 | 7.25 | 27.4 | 5.95 |
| MF-9 | 1091 | 7.29 | 31.2 | 5.5 |
| MF-10 | 1074 | 4.78 | 17 | 9.45 |
| MF-11 | 981 | 2.52 | 10.03 | 4.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shel’deshova, E.; Churaev, A.; Ryapolov, P. Dynamics of Magnetic Fluids and Bidisperse Magnetic Systems under Oscillatory Shear. Fluids 2023, 8, 47. https://doi.org/10.3390/fluids8020047
Shel’deshova E, Churaev A, Ryapolov P. Dynamics of Magnetic Fluids and Bidisperse Magnetic Systems under Oscillatory Shear. Fluids. 2023; 8(2):47. https://doi.org/10.3390/fluids8020047
Chicago/Turabian StyleShel’deshova, Elena, Alexander Churaev, and Petr Ryapolov. 2023. "Dynamics of Magnetic Fluids and Bidisperse Magnetic Systems under Oscillatory Shear" Fluids 8, no. 2: 47. https://doi.org/10.3390/fluids8020047
APA StyleShel’deshova, E., Churaev, A., & Ryapolov, P. (2023). Dynamics of Magnetic Fluids and Bidisperse Magnetic Systems under Oscillatory Shear. Fluids, 8(2), 47. https://doi.org/10.3390/fluids8020047







