Portable Air Purifiers’ Predicted Efficacy in Mitigating Airborne Pathogen Transmission in an Office Room Featuring Mixing Ventilation
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Office Model
2.2. The Algebraic-Slip Mixture Model for Dilute Air-Particle Flows
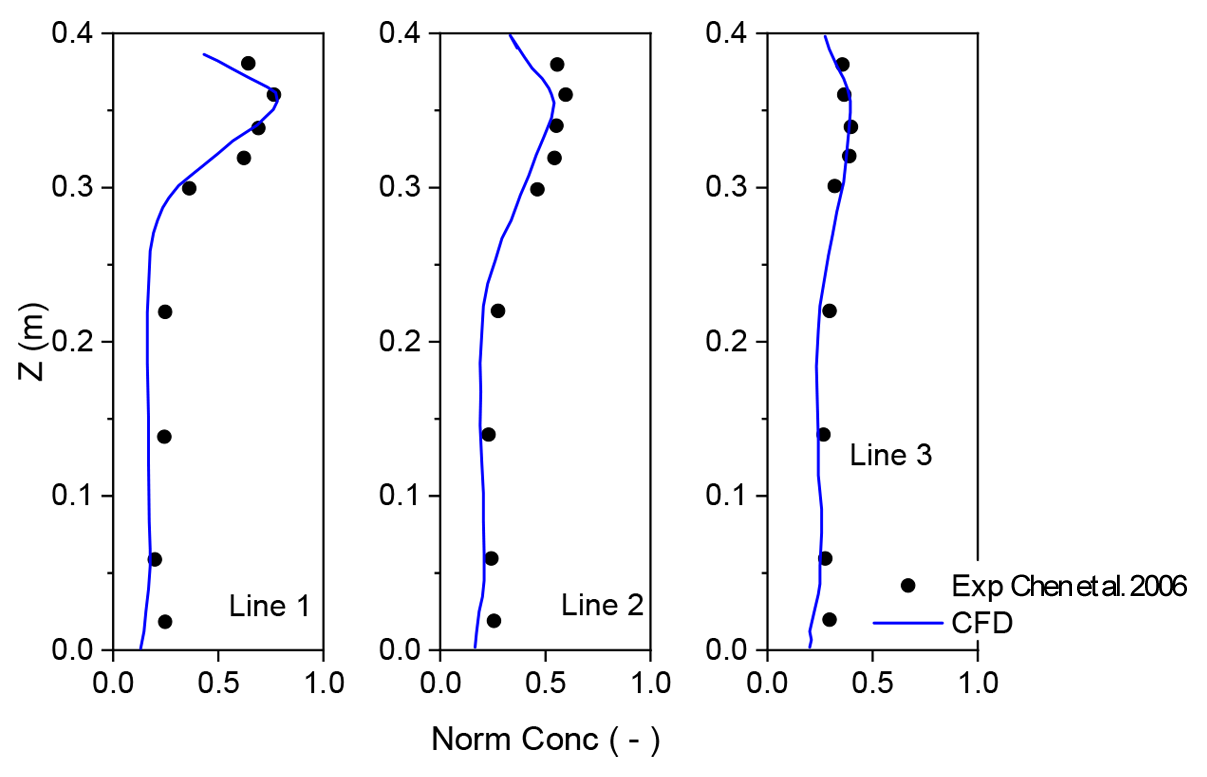
2.3. The Numerical Procedures
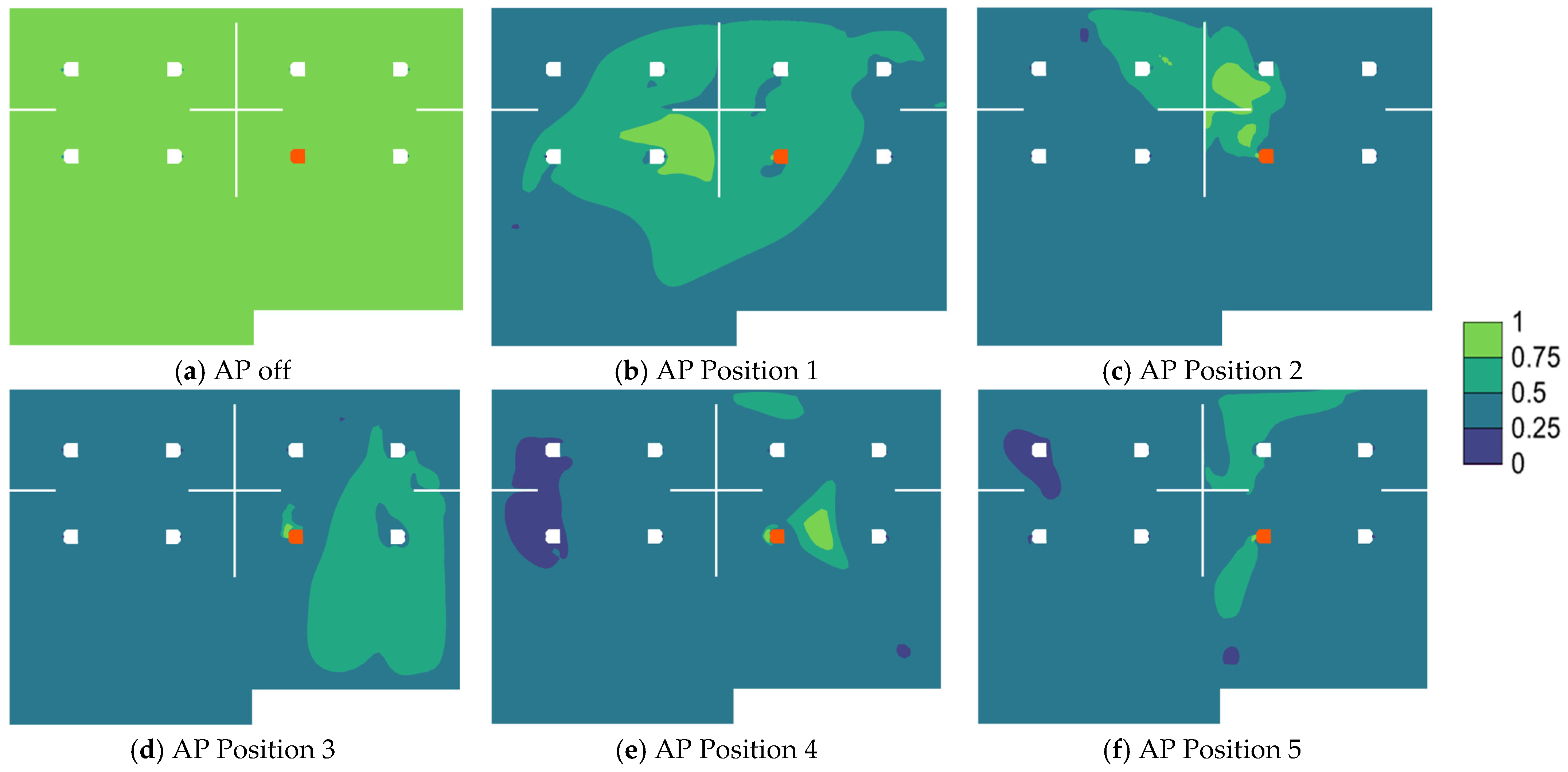
2.4. Analysis Tools
3. Results
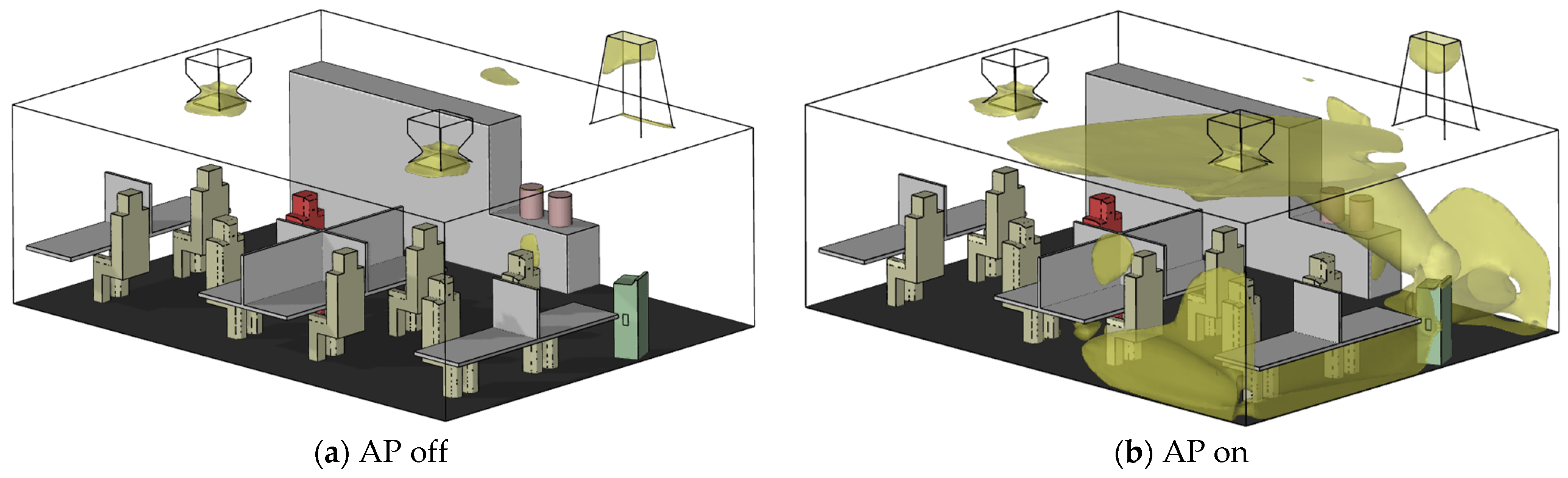
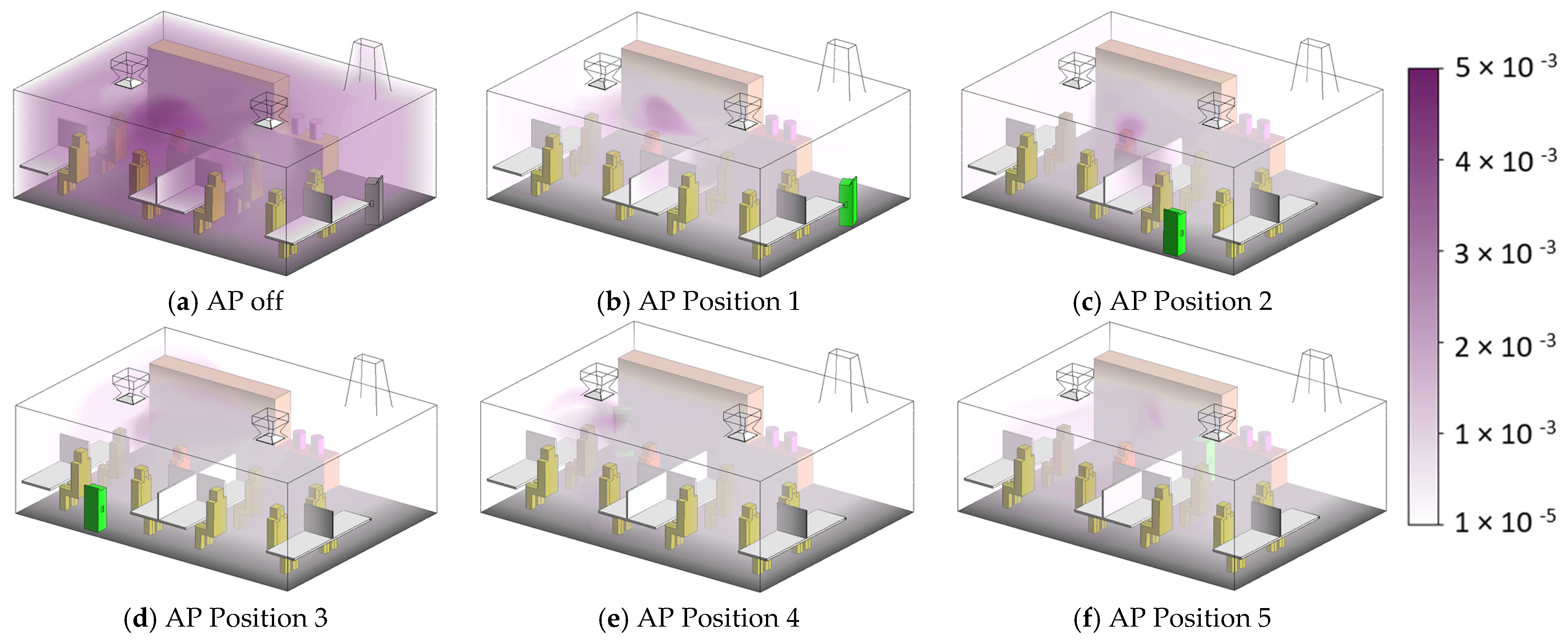
3.1. Effect of Air Purifiers on the Airflow Field
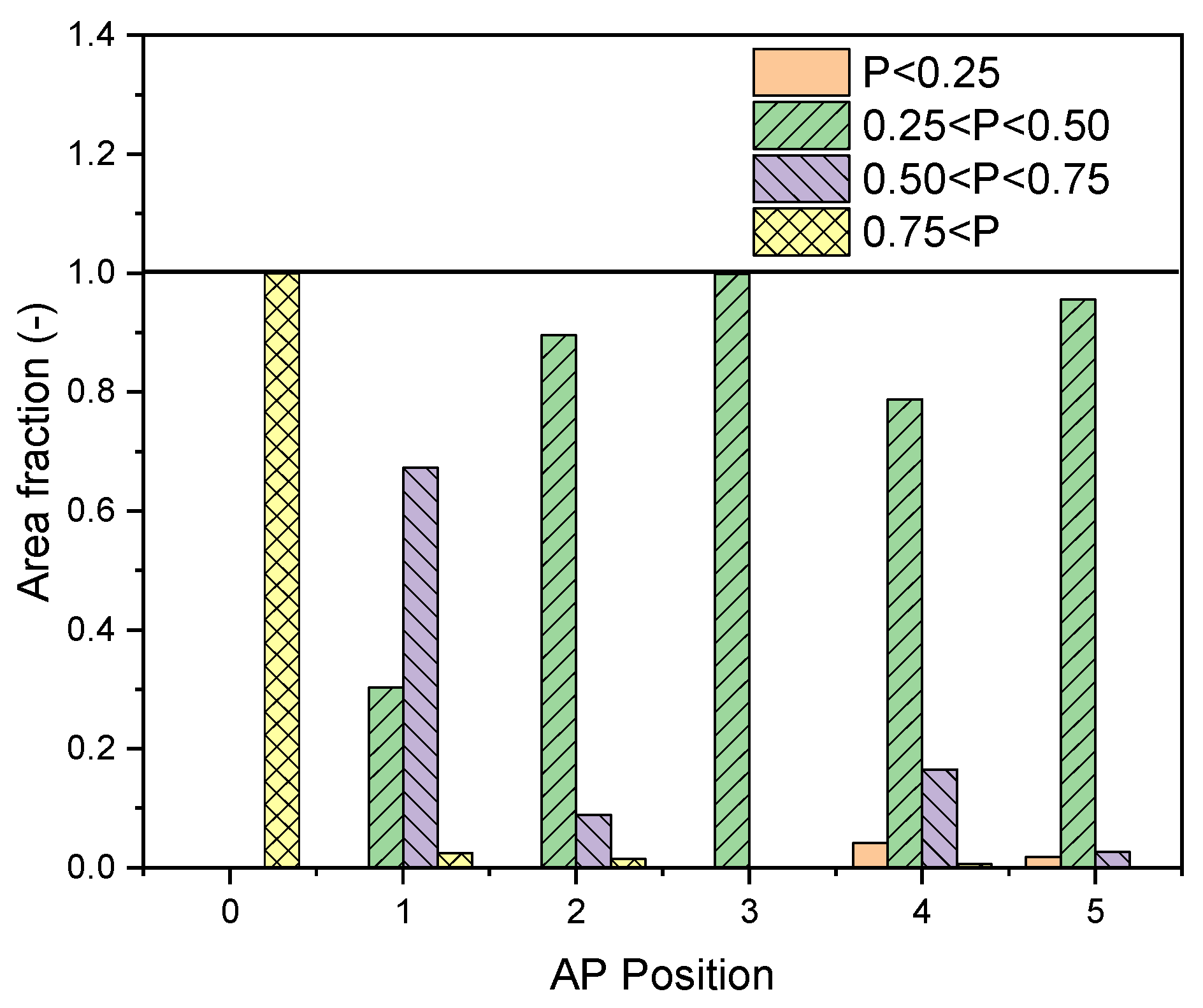
3.2. Effects of Air Purifier Locations
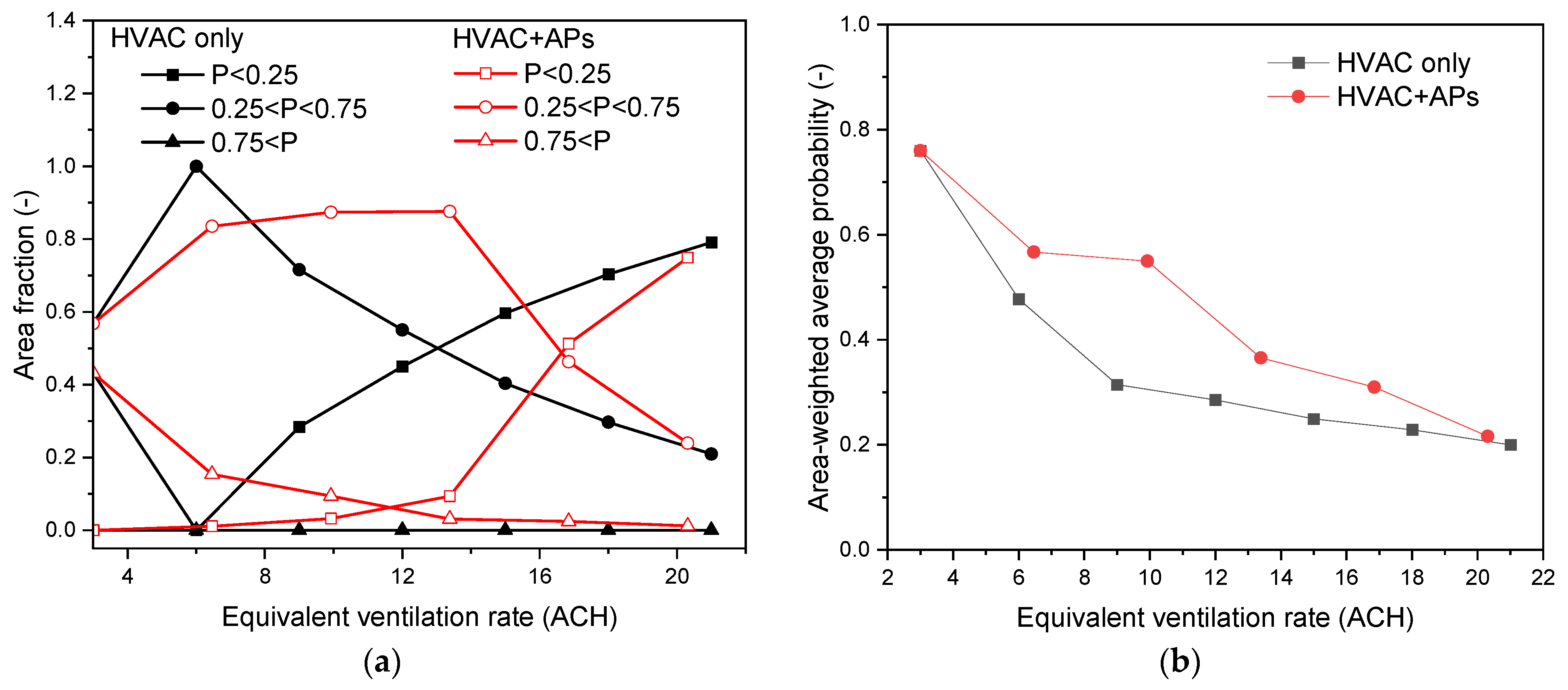
3.3. Air Purifiers vs. Central HVAC System
4. Conclusions
- (1)
- Air purifiers can effectively remove particulate matter and thus mitigate the infection risk of airborne diseases in the room. The efficiency of particle removal is proportional to the capacity of air processing by air purifiers.
- (2)
- Due to the complex interactions between the air jets from air purifiers and background ventilation airflow, the efficiency of particle removal is strongly affected by the position of the air purifier.
- (3)
- With the same ventilation rate measured by air changes per hour (ACH), the central HVAC system is more efficient than air purifiers for particle removal and infection control.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Energy Department. Doe Technical Standard—Specification for HEPA Filters Used by DOE Contractors; Energy Department: Washington, DC, USA, 2015.
- Srikrishna, D. Can 10× cheaper, lower-efficiency particulate air filters and box fans complement High-Efficiency Particulate Air (HEPA) purifiers to help control the COVID-19 pandemic? Sci. Total Environ. 2022, 838 Pt 1, 155884. [Google Scholar] [CrossRef]
- Cheek, E.; Guercio, V.; Shrubsole, C.; Dimitroulopoulou, S. Portable air purification: Review of impacts on indoor air quality and health. Sci. Total Environ. 2021, 766, 142585. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www2.education.vic.gov.au/pal/ventilation-air-purification/guidance/operation-placement-air-purifiers (accessed on 11 August 2023).
- Na, H.; Kim, H.; Kim, T. Dispersion of droplets due to the use of air purifiers during summer: Focus on the spread of COVID-19. Build. Environ. 2023, 234, 110136. [Google Scholar] [CrossRef]
- Kim, C.; Yu, J.; Lee, Y.G.; Kim, J.; Bae, S. Identifying behavior of long-distance virus transmission and mitigation performance from a COVID-19 outbreak of a daycare center. Environ. Res. 2022, 212 Pt B, 113318. [Google Scholar] [CrossRef] [PubMed]
- Bertolín, L.S.; Oro, J.M.F.; Díaz, K.A.; Vega, M.G.; Velarde-Suárez, S.; Del Valle, M.E.; Fernández, L.J. Optimal position of air purifiers in elevator cabins for the improvement of their ventilation effectiveness. J. Build. Eng. 2023, 63, 105466. [Google Scholar] [CrossRef]
- Ham, S. Prevention of exposure to and spread of COVID-19 using air purifiers: Challenges and concerns. Epidemiol. Health 2020, 42, e2020027. [Google Scholar] [CrossRef]
- Cooper, E.; Wang, Y.; Stamp, S.; Burman, E.; Mumovic, D. Use of portable air purifiers in homes: Operating behaviour, effect on indoor PM2.5 and perceived indoor air quality. Build. Environ. 2021, 191, 107621. [Google Scholar] [CrossRef]
- Moghadam, T.T.; Morales, C.E.O.; Zambrano, M.J.L.; Bruton, K.; O’Sullivan, D.T. Energy efficient ventilation and indoor air quality in the context of COVID-19—A systematic review. Renew. Sustain. Energy Rev. 2023, 182, 113356. [Google Scholar] [CrossRef]
- Li, X.; Lester, D.; Rosengarten, G.; Aboltins, C.; Patel, M.; Cole, I. A spatiotemporally resolved infection risk model for airborne transmission of COVID-19 variants in indoor spaces. Sci. Total Environ. 2021, 812, 152592. [Google Scholar] [CrossRef]
- Li, X.; Restrepo, J.P.; Dalaney, J.; Cheng, C.T.; Gunasekera, S.; Langhorne, M.; Patel, M.J.; Lester, D.; Qin, K.; Pang, T.Y.; et al. Digitisation for Safe Workplaces—Victorian Higher Educaton State Investment Fund; RMIT University: Melbourne, Australia, 2023. [Google Scholar]
- de Dear, R.J.; Arens, E.; Hui, Z.; Oguro, M. Convective and radiative heat transfer coefficients for individual human body segments. Int. J. Biometeorol. 1997, 40, 141–156. [Google Scholar] [CrossRef]
- Hawkins, G. Rules of Thumb—Guidelines for Building Services, 5th ed.; BSRIA: Bracknell, UK, 2011. [Google Scholar]
- Li, X.; Shang, Y.; Yan, Y.; Yang, L.; Tu, J. Modelling of evaporation of cough droplets in inhomogeneous humidity fields using the multi-component Eulerian-Lagrangian approach. Build. Environ. 2018, 128, 68–76. [Google Scholar] [CrossRef] [PubMed]
- Chao, C.Y.H.; Wan, M.P.; Morawska, L.; Johnson, G.R.; Ristovski, Z.D.; Hargreaves, M.; Mengersen, K.; Corbett, S.; Li, Y.; Xie, X.; et al. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J. Aerosol Sci. 2009, 40, 122–133. [Google Scholar] [CrossRef] [PubMed]
- Ansys, I. Ansys Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Schiller, L.; Naumann, Z. A drag coefficient correlation. VDI Ztg. 1935, 77, 318–320. [Google Scholar]
- Chen, F.; Yu, S.C.M.; Lai, A.C.K. Modeling particle distribution and deposition in indoor environments with a new drift–flux model. Atmos. Environ. 2006, 40, 357–367. [Google Scholar] [CrossRef]
- Li, X.; Yan, Y.; Shang, Y.; Tu, J. An Eulerian–Eulerian model for particulate matter transport in indoor spaces. Build. Environ. 2015, 86, 191–202. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng.-Trans. ASME 2008, 130, 078001. [Google Scholar]
- Haller, G. An objective definition of a vortex. J. Fluid Mech. 2005, 525, 1–26. [Google Scholar] [CrossRef]
- Wells, W.F. Airborne Contagion and Air Hygiene: An Ecological Study of Droplet Infections. J. Am. Med. Assoc. 1955, 159, 90. [Google Scholar]
- Riley, E.C.; Murphy, G.; Riley, R.L. Airborne spread of measles in a suburban elementary school. Am. J. Epidemiol. 1978, 107, 421–432. [Google Scholar] [CrossRef]
- Lei, C.; Yang, J.; Hu, J.; Sun, X. On the Calculation of TCID(50) for Quantitation of Virus Infectivity. Virol. Sin. 2021, 36, 141–144. [Google Scholar] [CrossRef] [PubMed]
- Nikitin, N.; Petrova, E.; Trifonova, E.; Karpova, O. Influenza virus aerosols in the air and their infectiousness. Adv. Virol. 2014, 2014, 859090. [Google Scholar] [CrossRef] [PubMed]
- Boucau, J.; Marino, C.; Regan, J.; Uddin, R.; Choudhary, M.C.; Flynn, J.P.; Chen, G.; Stuckwisch, A.M.; Mathews, J.; Liew, M.Y.; et al. Duration of viable virus shedding in SARS-CoV-2 omicron variant infection. medRxiv 2022. [Google Scholar] [CrossRef]
- Shang, W.; Liu, J.; Wang, C.; Li, J.; Dai, X. Developing smart air purifier control strategies for better IAQ and energy efficiency using reinforcement learning. Build. Environ. 2023, 242, 110556. [Google Scholar] [CrossRef]
- Wang, Y.; Cooper, E.; Tahmasebi, F.; Taylor, J.; Stamp, S.; Symonds, P.; Burman, E.; Mumovic, D. Improving indoor air quality and occupant health through smart control of windows and portable air purifiers in residential buildings. Build. Serv. Eng. Res. Technol. 2022, 43, 571–588. [Google Scholar] [CrossRef]
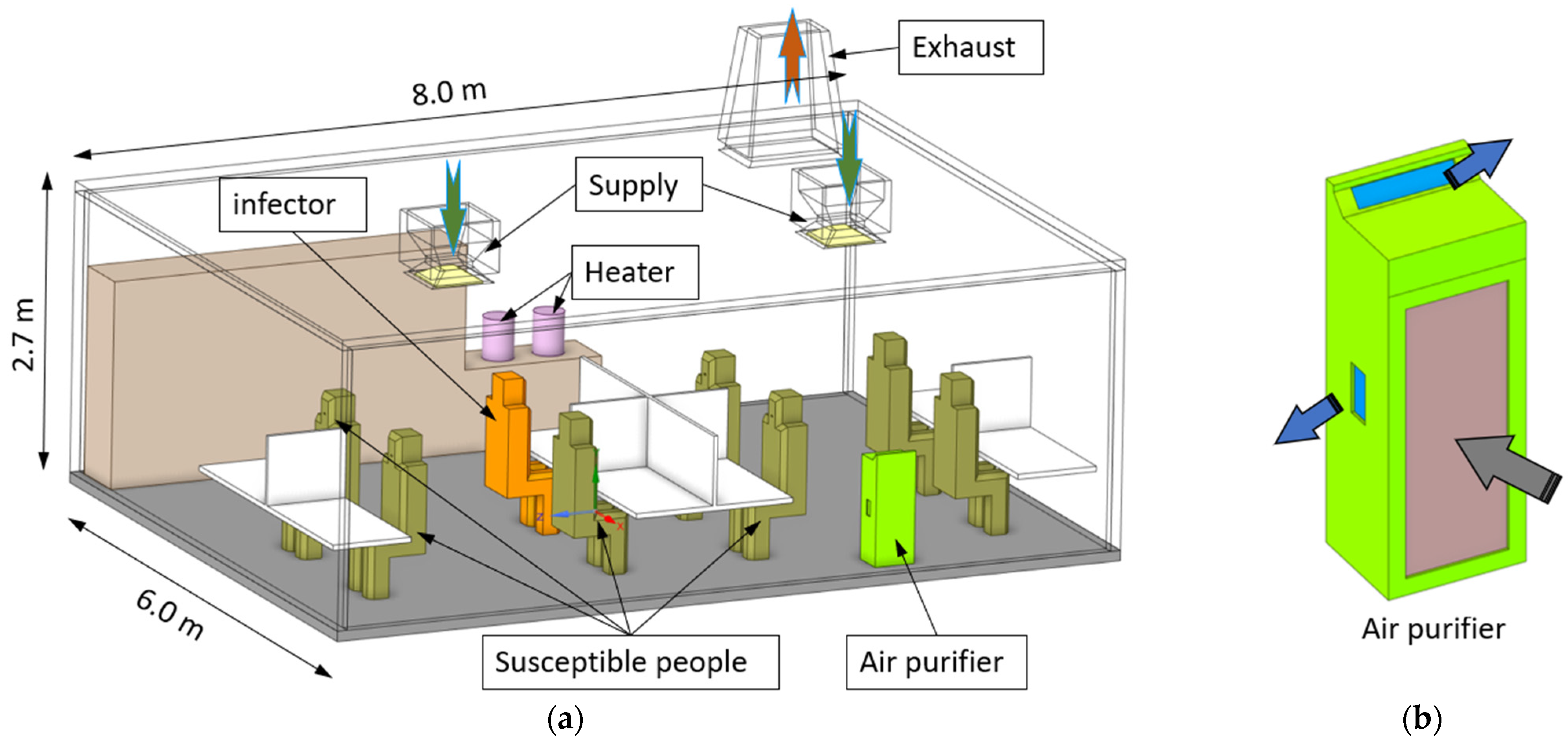


| Air supply rate per inlet (m3/s) | 0.051 (ACH 3)–0.354 (ACH 21) |
| Air processing rate per air purifier (m3/s) | 0 (off)–0.195 (full capacity) |
| Human exhalation rate (L/min) | 9.0 |
| Human heat flux (W/m2) | 22.4 |
| Heater heat flux (W/m2) | 4000 |
| Variable | Value | Variable | Value |
|---|---|---|---|
| β | 0.0 | TCIF50 | 4000 virons |
| dp,0 | 25 μm | dp | 6.6 μm |
| cpth | 1.0 × 109 virons/mL | v | 9.0 L/min |
| te | 6 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Patel, M.J.; Cole, I.S. Portable Air Purifiers’ Predicted Efficacy in Mitigating Airborne Pathogen Transmission in an Office Room Featuring Mixing Ventilation. Fluids 2023, 8, 307. https://doi.org/10.3390/fluids8120307
Li X, Patel MJ, Cole IS. Portable Air Purifiers’ Predicted Efficacy in Mitigating Airborne Pathogen Transmission in an Office Room Featuring Mixing Ventilation. Fluids. 2023; 8(12):307. https://doi.org/10.3390/fluids8120307
Chicago/Turabian StyleLi, Xiangdong, Milan J. Patel, and Ivan S. Cole. 2023. "Portable Air Purifiers’ Predicted Efficacy in Mitigating Airborne Pathogen Transmission in an Office Room Featuring Mixing Ventilation" Fluids 8, no. 12: 307. https://doi.org/10.3390/fluids8120307
APA StyleLi, X., Patel, M. J., & Cole, I. S. (2023). Portable Air Purifiers’ Predicted Efficacy in Mitigating Airborne Pathogen Transmission in an Office Room Featuring Mixing Ventilation. Fluids, 8(12), 307. https://doi.org/10.3390/fluids8120307






