Prediction of Self-Sustained Oscillations of an Isothermal Impinging Slot Jet
Abstract
1. Introduction
- (1)
- Studying a plane-impinging jet laminar fluid flow in detail by means of DNS and the turbulent flow with LES;
- (2)
- Assessing the ability in terms of accuracy of different RANS models in the description of plane-impinging jets and presenting a detailed evaluation of them according to their capability to predict impinging jet flows;
- (3)
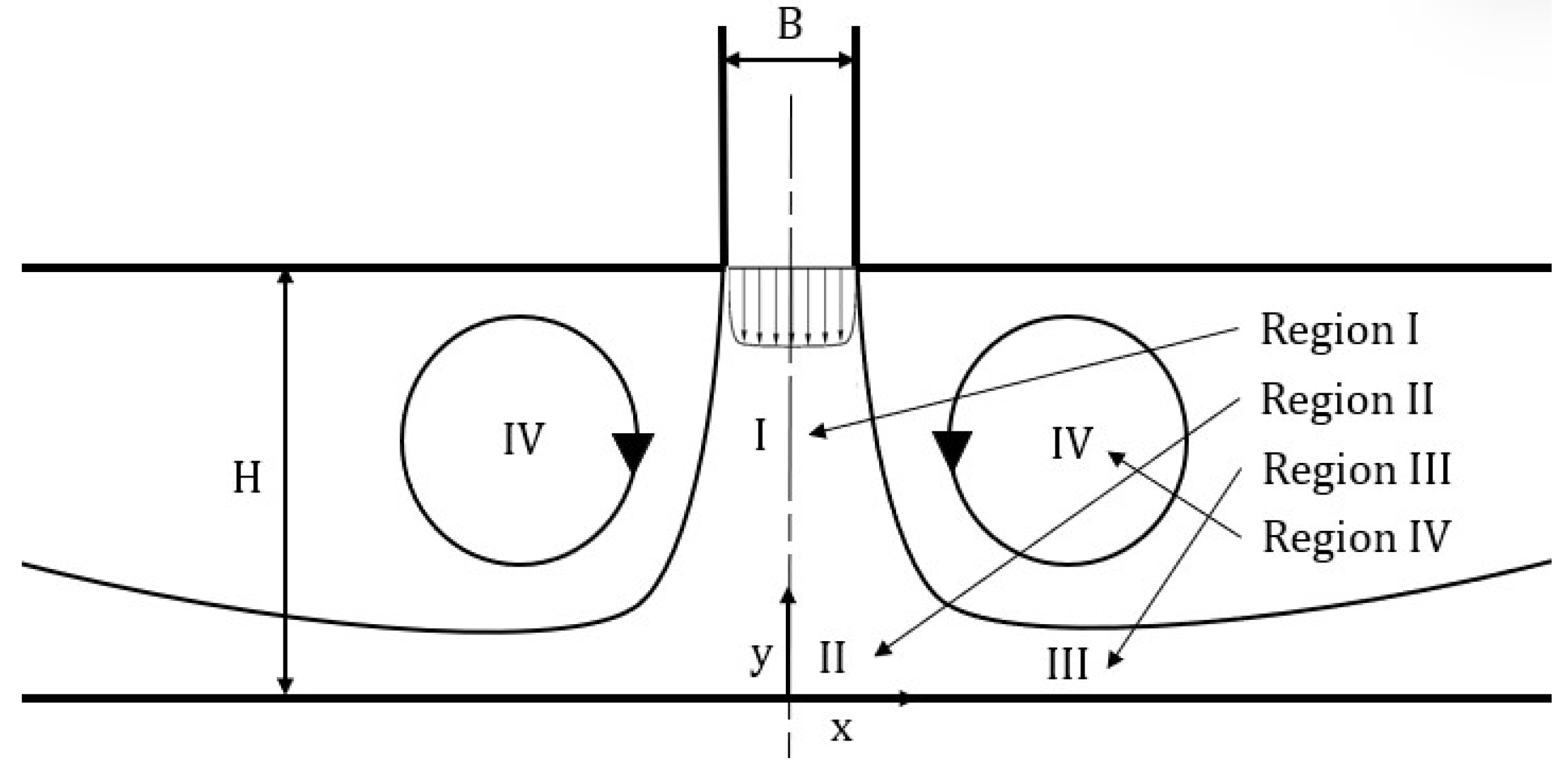
- Analyzing the self-sustained oscillations in laminar and turbulent isothermal impinging slot jets, relating their role in the complex flow characteristics mentioned above.
2. Mathematical Modeling
2.1. Direct Numerical Simulation
2.2. Large-Eddy Simulation
2.2.1. Smagorinsky–Lilly Model
2.2.2. Dynamic Smagorinsky–Lilly Model
2.3. RANS Turbulence Modeling
2.3.1. Realizable k- Model
2.3.2. Shear Stress Transport (SST) k- Model
2.3.3. Reynolds Stress Model
3. Numerical Method
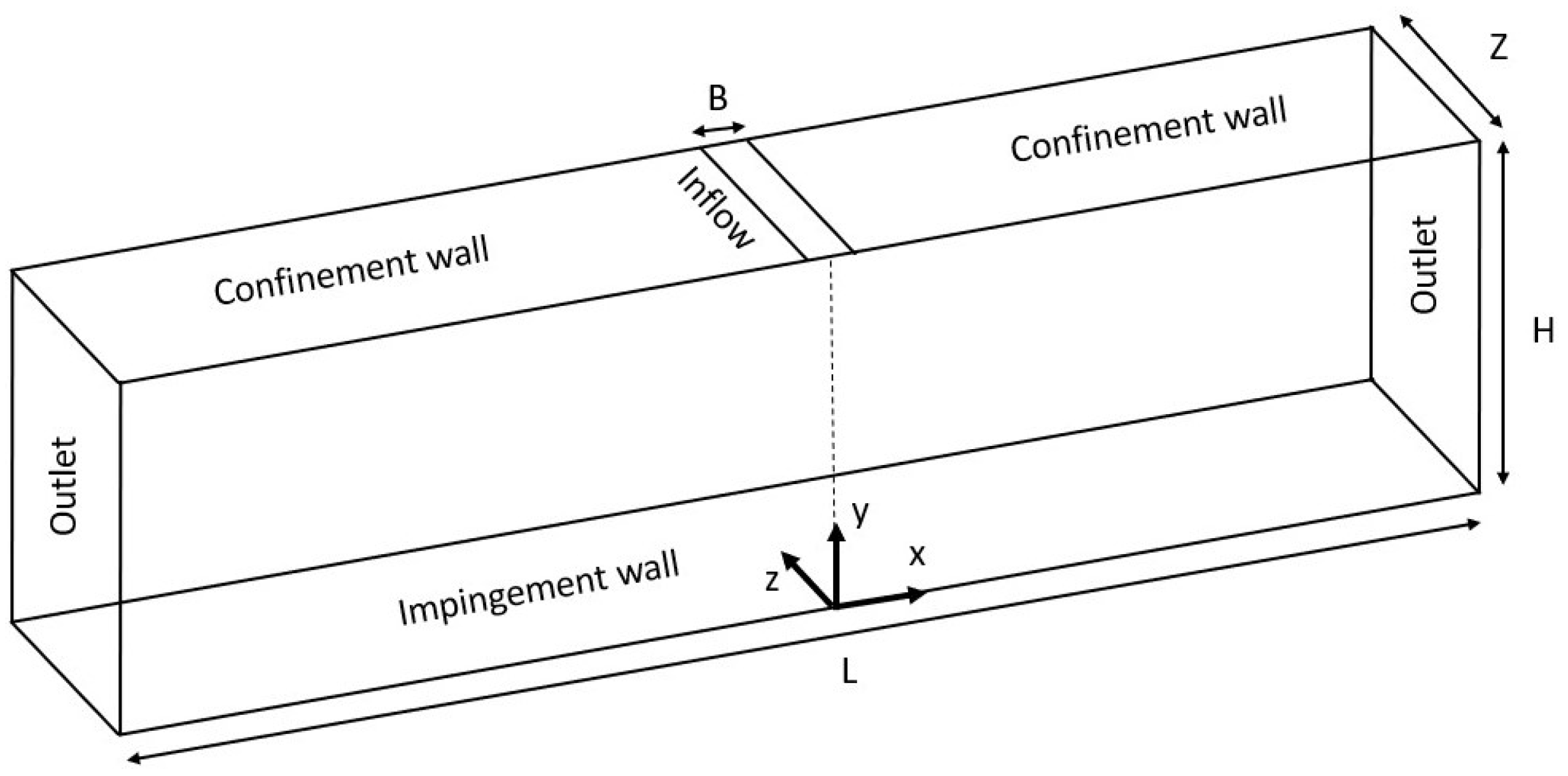
3.1. Unsteady 3D Models
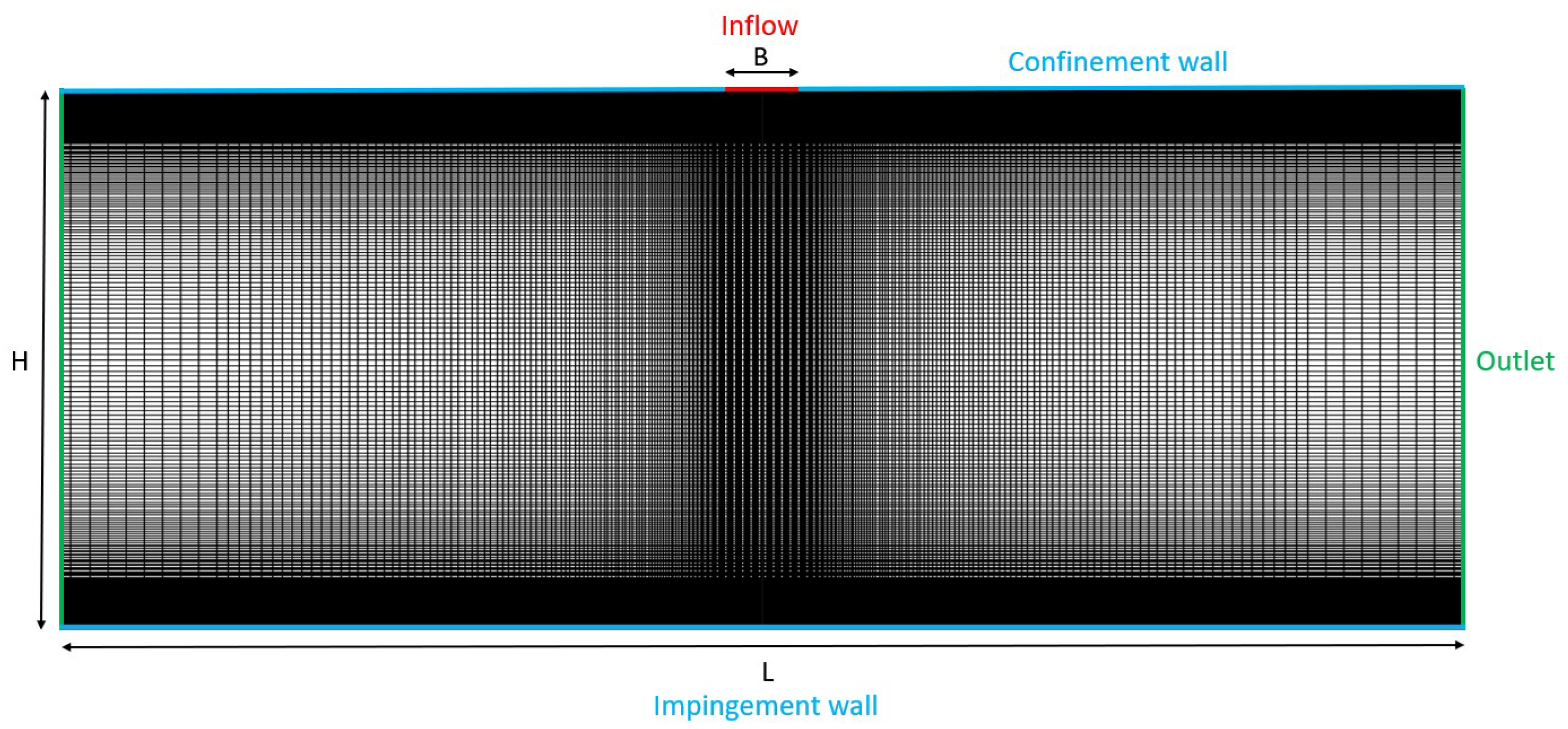
3.2. Steady 2D Model
4. Results and Discussion
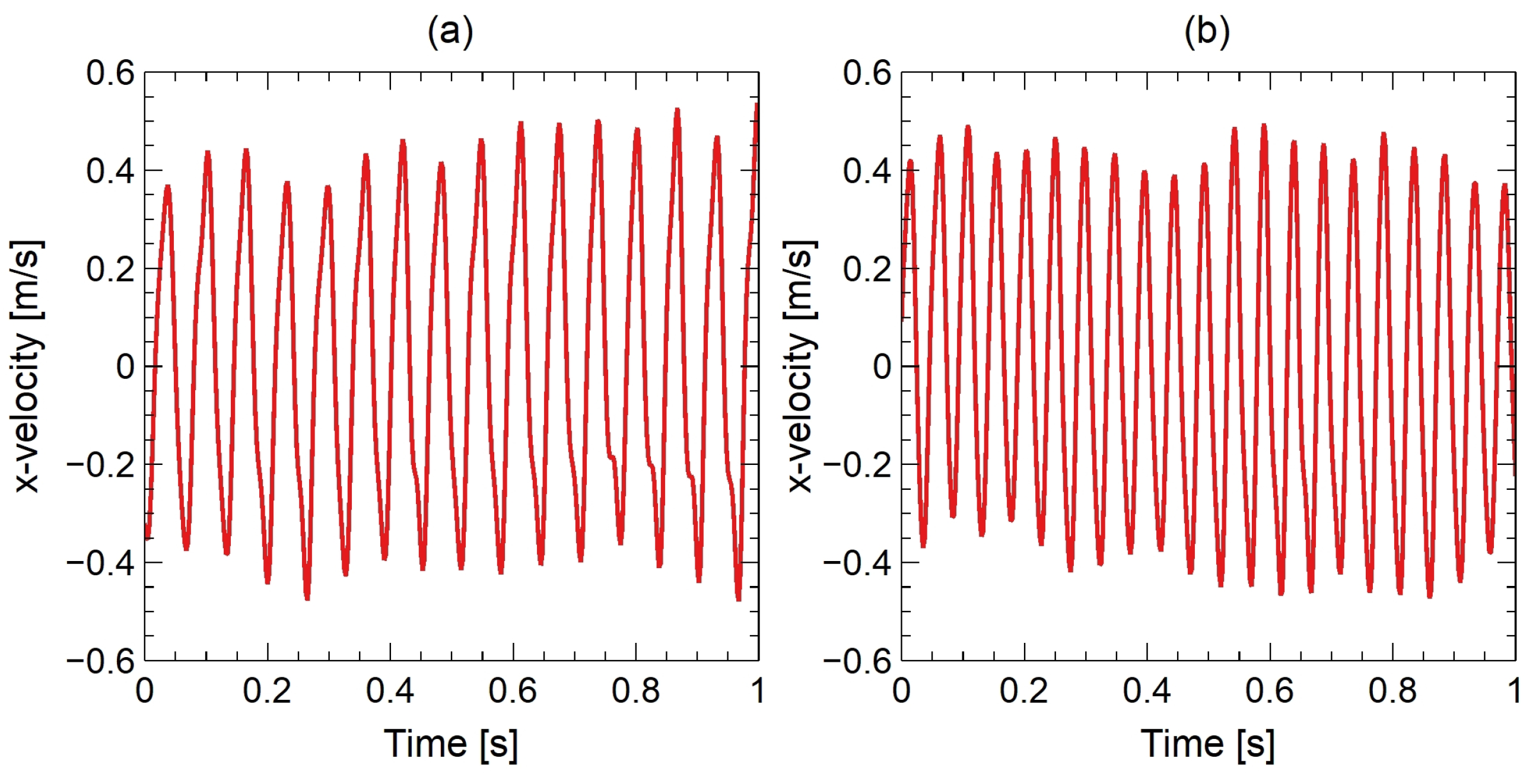
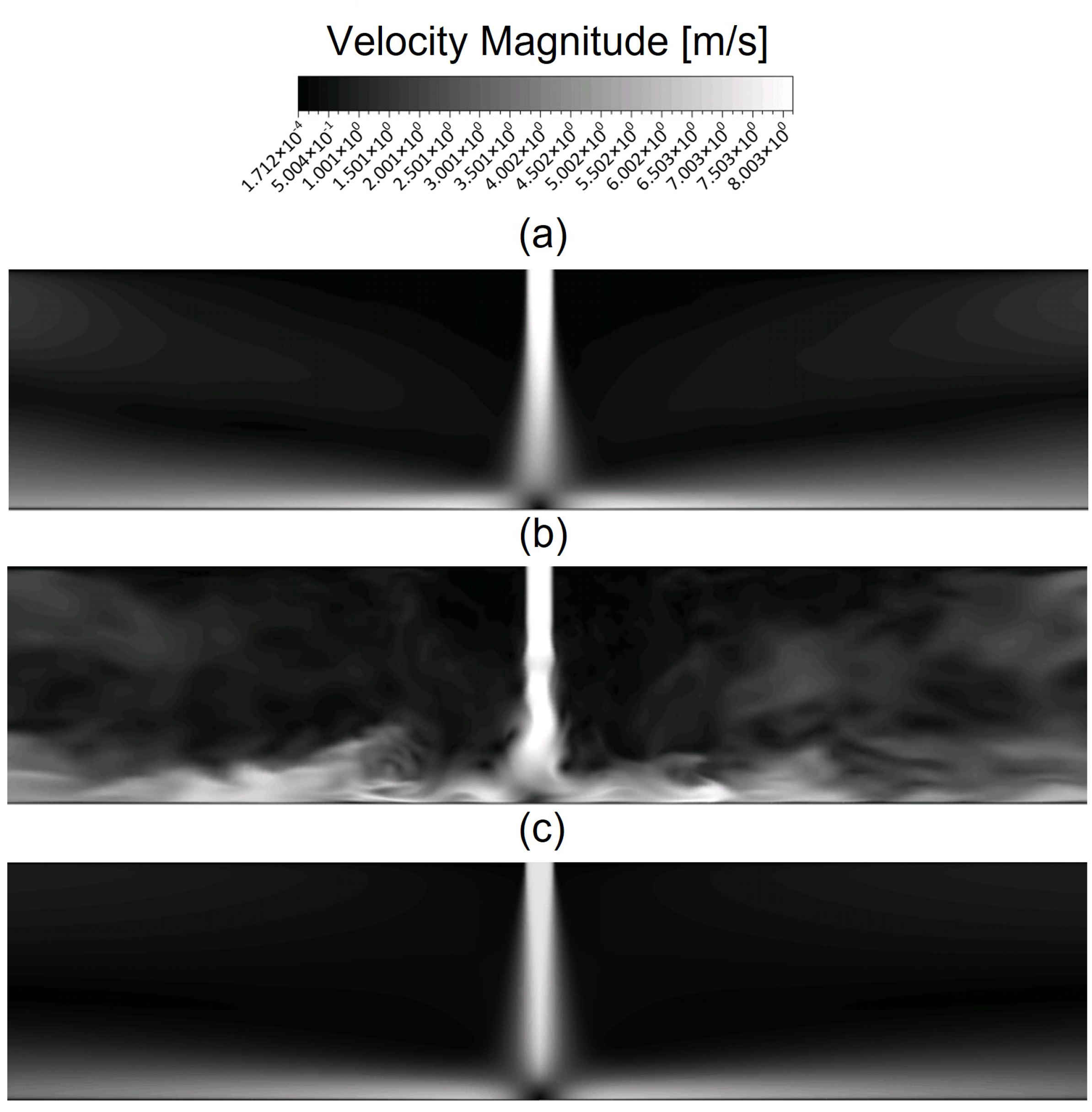
4.1. DNS Results
4.2. RANS Results
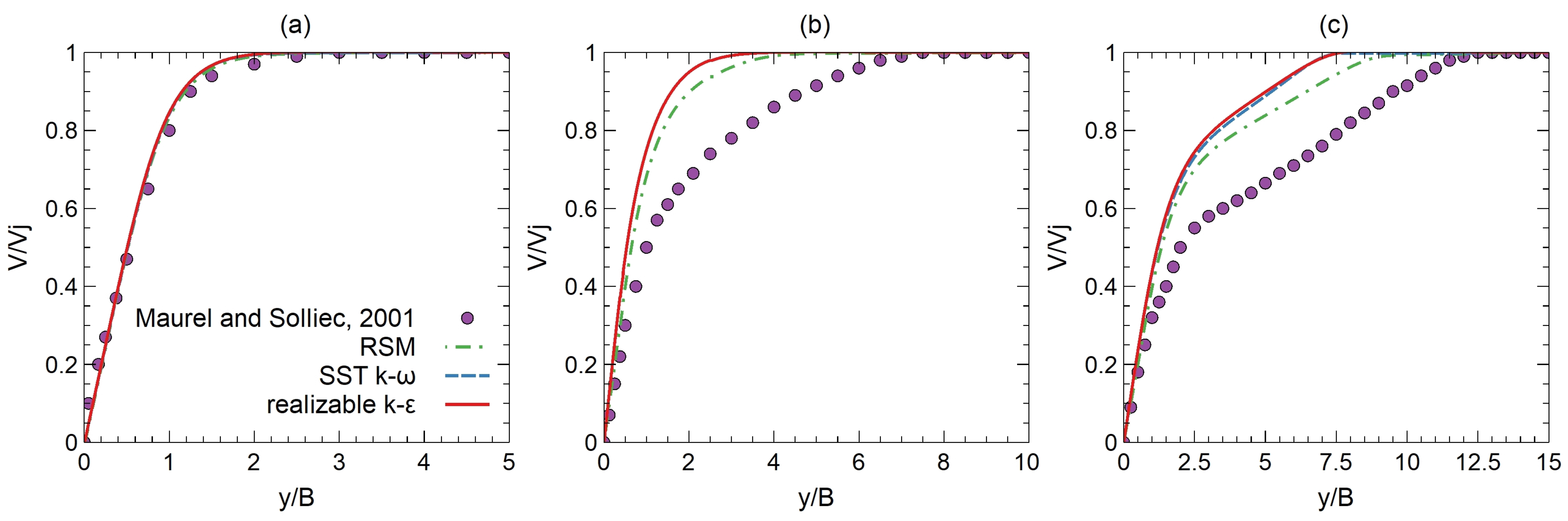
4.2.1. Centerline y Velocity Component
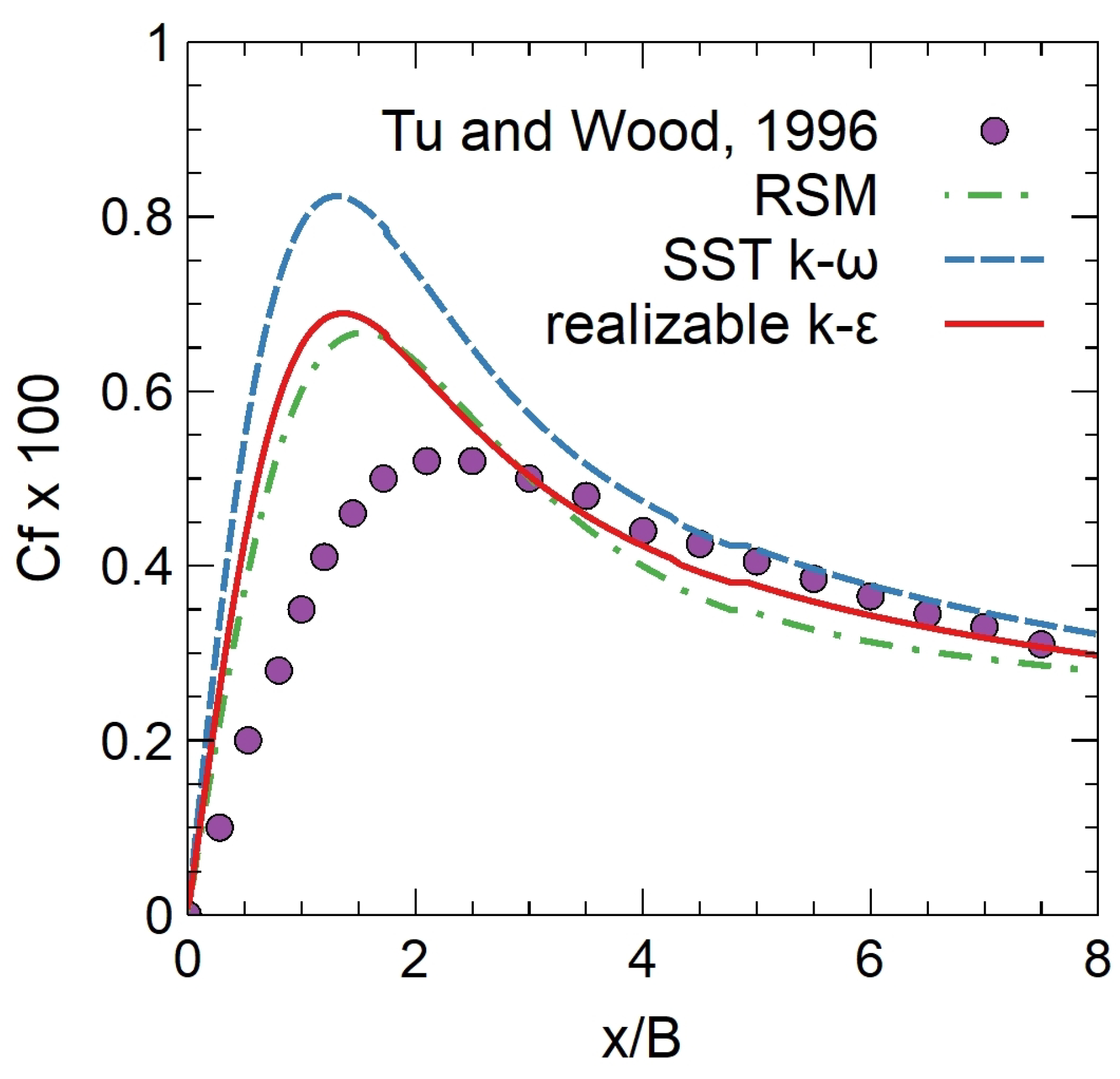
4.2.2. and Surface Pressure
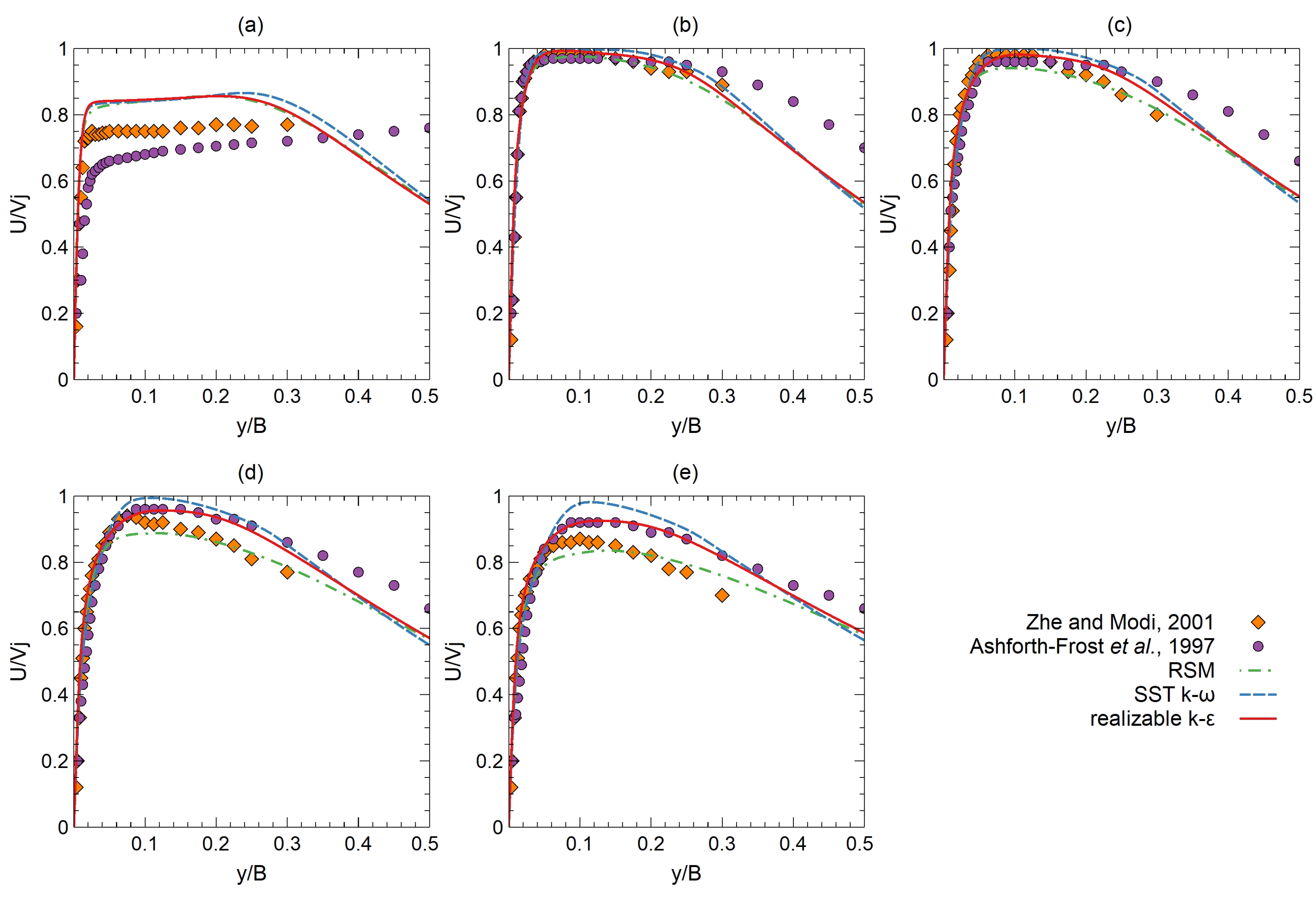
4.2.3. Velocity Magnitude in the x Direction
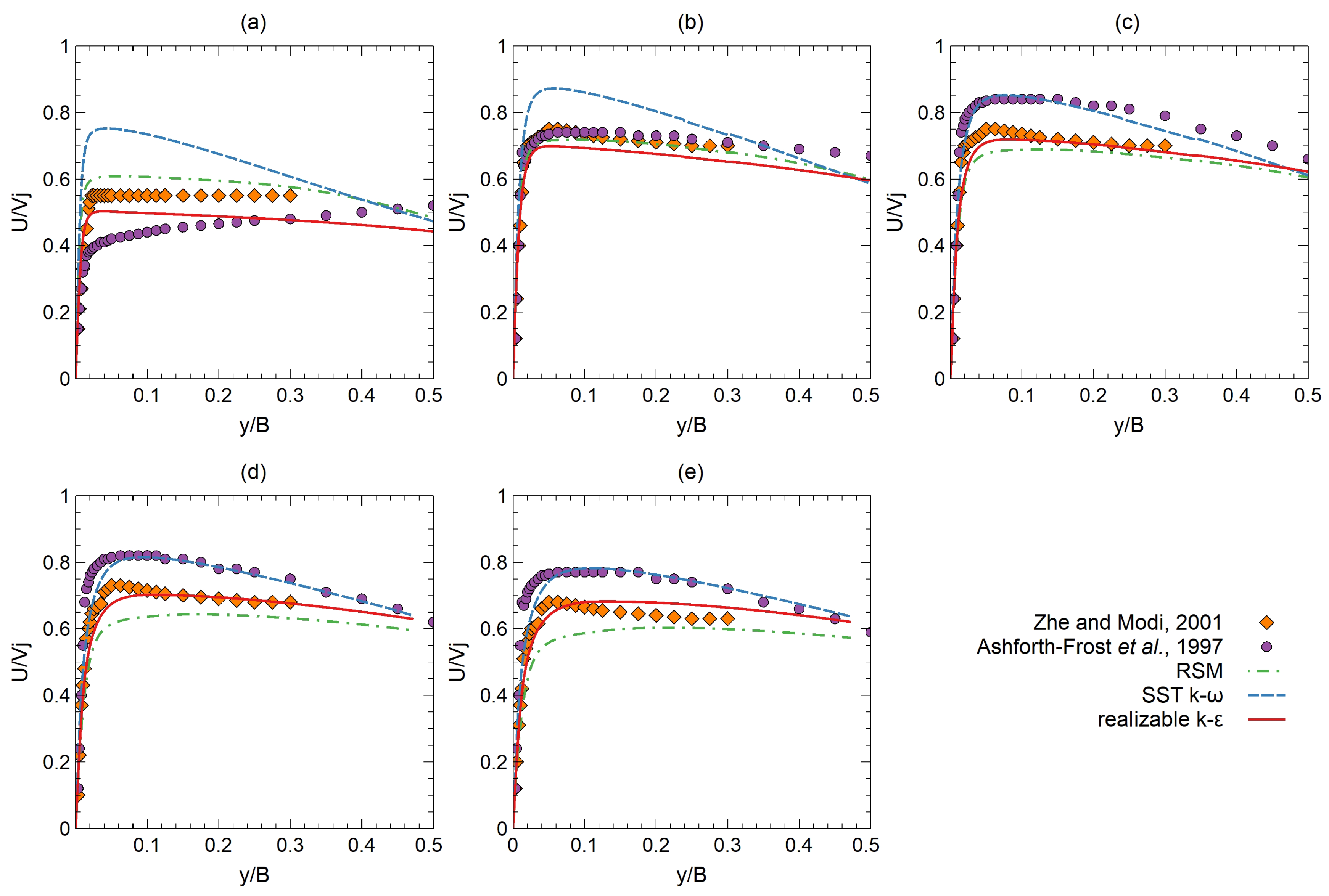
4.2.4. Spanwise Velocity Profiles
4.3. LES Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, B.; Goldstein, R. Jet-Impingement Heat Transfer in Gas Turbine Systems. Ann. N. Y. Acad. Sci. 2001, 934, 147–161. [Google Scholar] [CrossRef]
- Pavlova, A.; Amitay, M. Electronic Cooling Using Synthetic Jets. J. Heat Transf.-Trans. ASME 2006, 128, 493–501. [Google Scholar] [CrossRef]
- Polat, S. Heat and Mass Transfer in Impingement Drying. Dry. Technol. 1993, 11, 1147–1176. [Google Scholar] [CrossRef]
- Martin, H. Heat and Mass Transfer Between Impinging Gas Jets and Solid Surfaces. Adv. Heat Transf. 1977, 13, 1–60. [Google Scholar] [CrossRef]
- Jambunathan, K.; Lai, E.; Moss, M.; Button, B. A Review of Heat Transfer Data for Single Circular Jet Impingement. Int. J. Heat Fluid Flow 1992, 13, 106–115. [Google Scholar] [CrossRef]
- Viskanta, R. Heat Transfer to Isothermal Gas and Flame Jets. Exp. Therm. Fluid Sci. 1993, 6, 111–134. [Google Scholar] [CrossRef]
- van Hout, R.; Murugan, S.; Mitra, A.; Cukurel, B. Coaxial Circular Jets-A Review. Fluids 2021, 6, 147. [Google Scholar] [CrossRef]
- Viegas, J.; Carrasco, L.; Pinto, L.; Morais, J.; Morais, P.; Aelenei, D. Full-Size Experimental Assessment of the Aerodynamic Sealing of Low Velocity Air Curtains. Fluids 2021, 6, 359. [Google Scholar] [CrossRef]
- Foster, A.; Swain, M.; Barrett, R.; D’Agaro, P.; Ketteringham, L.; James, S. Three-dimensional effects of an air curtain used to restrict cold room infiltration. Appl. Math. Model. 2007, 31, 1109–1123. [Google Scholar] [CrossRef]
- Viegas, J. Saltwater experiments with air curtains for smoke control in the event of fire. J. Build. Eng. 2016, 8, 243–248. [Google Scholar] [CrossRef]
- Khayrullina, A.; Hooff, T.; Blocken, B.; van Heijst, G. PIV measurements of isothermal plane turbulent impinging jets at moderate Reynolds numbers. Exp. Fluids 2017, 58, 31. [Google Scholar] [CrossRef]
- Thysen, J.H.; Hooff, T.; Blocken, B.; Heijst, G. PIV measurements of opposing-jet ventilation flow in a reduced-scale simplified empty airplane cabin. Eur. J. Mech.-B/Fluids 2022, 94, 212–227. [Google Scholar] [CrossRef]
- Tu, C.; Wood, D. Wall pressure and shear stress measurements beneath an impinging jet. Exp. Therm. Fluid Sci. 1996, 13, 364–373. [Google Scholar] [CrossRef]
- Zhe, J.; Modi, V. Near wall measurements for a turbulent impinging slot jet. J. Fluids Eng. Trans. ASME 2001, 123, 112–120. [Google Scholar] [CrossRef]
- Ashforth-Frost, S.; Jambunathan, K.; Whitney, C. Velocity and turbulence characteristics of a semiconfined orthogonally impinging slot jet. Exp. Therm. Fluid Sci. 1997, 14, 60–67. [Google Scholar] [CrossRef]
- Sangsom, W.; Inprasit, C. Design Parameters on Impingement Steam Jet Heat Transfer of Continuous Liquid Food Sterilization. Fluids 2022, 7, 185. [Google Scholar] [CrossRef]
- Zhang, X.; Agarwal, R. Numerical Simulation of Fountain Formation due to Normal and Inclined Twin-Jet Impingement on Ground. Fluids 2020, 5, 132. [Google Scholar] [CrossRef]
- Dutta, R.; Dewan, A. Comparison of various integration to wall (ITW) RANS models for predicting turbulent slot jet impingement heat transfer. Int. J. Heat Mass Transf. 2013, 65, 750–764. [Google Scholar] [CrossRef]
- Achari, A.; Das, M. Application of various RANS based models towards predicting turbulent slot jet impingement. Int. J. Therm. Sci. 2015, 98, 332–351. [Google Scholar] [CrossRef]
- Craft, T.; Graham, L.; Launder, B. Impinging Jet Studies for Turbulence Model Assessment—II. An Examination of the Performance of Four Turbulence Models. Int. J. Heat Mass Transf. 1993, 36, 2685–2697. [Google Scholar] [CrossRef]
- Fernández, J.; Elicer-Cortés, J.; Valencia, A.; Pavageau, M.; Gupta, S. Comparison of low-cost two-equation turbulence models for prediction flow dynamics in twin-jets devices. Int. Commun. Heat Mass Transf. 2007, 34, 570–578. [Google Scholar] [CrossRef]
- Jaramillo, J.; Perez Segarra, C.D.; Rodriguez, I.; Oliva, A. Numerical Study of Plane and Round Impinging Jets using RANS Models. Numer. Heat Transf. Part B Fundam. 2008, 54, 213–237. [Google Scholar] [CrossRef]
- Tahsini, A.M.; Mousavi, S.T. Parametric Study of Confined Turbulent Impinging Slot Jets upon a Flat Plate. Int. J. Aerosp. Mech. Eng. 2012, 6, 2794–2798. [Google Scholar]
- Hofmann, H.; Kaiser, R.; Kind, M.; Martin, H. Calculations of Steady and Pulsating Impinging Jets—An Assessment of 13 Widely used Turbulence Models. Numer. Heat Transf. Part B-Fundam. 2007, 51, 565–583. [Google Scholar] [CrossRef]
- Schweikert, J.; Riedelsheimer, A.; Weigand, B. Numerical study of a turbulent impinging jet for different jet-to-plate distances using two-equation turbulence models. Eur. J. Mech.-B/Fluids 2016, 61, 210–217. [Google Scholar] [CrossRef]
- Ramezanpour, A.; Mirzaee, I.; Firth, D.; Shirvani, H. A numerical heat transfer study of slot jet impinging on an inclined plate. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 661–676. [Google Scholar] [CrossRef]
- Dewan, A.; Dutta, R. Recent Trends in Computation of Turbulent Jet Impingement Heat Transfer. Heat Transf. Eng. 2012, 33, 447–460. [Google Scholar] [CrossRef]
- Popiel, C.; Trass, O. Visualization of a Free and Impinging Round Jet. Exp. Therm. Fluid Sci. 1991, 4, 253–264. [Google Scholar] [CrossRef]
- Olsson, M.; Fuchs, L. Large Eddy Simulation of a Forced Semiconfined Circular Impinging Jet. Phys. Fluids 1998, 10, 476–486. [Google Scholar] [CrossRef]
- Ozdemir, B.; Whitelaw, J. Impingement of an axisymmetric jet on unheated and heated flat plates. J. Fluid Mech. 1992, 240, 503–532. [Google Scholar] [CrossRef]
- Liu, T.; Sullivan, J. Heat Transfer and Flow Structures in an Excited Circular Impinging Jet. Int. J. Heat Mass Transf. 1996, 39, 3695–3706. [Google Scholar] [CrossRef]
- Goldschmidt, V.; Bradshaw, P. Flapping of a Plane Jet. Phys. Fluids 1973, 16, 354–355. [Google Scholar] [CrossRef]
- Silva, C.; Metais, O. On the influence of coherent structures upon interactions in turbulent plane jet. J. Fluid Mech. 2002, 473. [Google Scholar] [CrossRef]
- Ho, C.; Huerre, P. Perturbed Free Shear Layers. Annu. Rev. Fluid Mech. 2003, 16, 365–422. [Google Scholar] [CrossRef]
- Varieras, D.; Brancher, P.; Giovannini, A. Self-sustained oscillations of confined impinging jet. Flow Turbul. Combust. 2007, 78, 1. [Google Scholar] [CrossRef]
- Ho, C.M.; Nosseir, N. Dynamics of an Impinging Jet. Part 1. The Feedback Phenomenon. J. Fluid Mech. 1981, 105, 119–142. [Google Scholar] [CrossRef]
- Didden, N.; Ho, C.M. Unsteady separation in a boundary layer produced by an impinging jet. J. Fluid Mech. 1985, 160, 235–256. [Google Scholar] [CrossRef]
- Sakakibara, J.; Hishida, K.; Phillips, W. On the vortical structure in a plane impinging jet. J. Fluid Mech. 2001, 434, 273–300. [Google Scholar] [CrossRef][Green Version]
- El Hassan, M.; Nobes, D. Experimental Investigation of the Vortex Dynamics in Circular Jet Impinging on Rotating Disk. Fluids 2022, 7, 223. [Google Scholar] [CrossRef]
- Chung, Y.; Luo, K. Unsteady Heat Transfer Analysis of an Impinging Jet. J. Heat Transf. 2002, 124, 1039–1048. [Google Scholar] [CrossRef]
- Hadžiabdić, M.; Hanjalic, K. Vortical structures and heat transfer in a round impinging jet. J. Fluid Mech. 2008, 596, 221–260. [Google Scholar] [CrossRef]
- Rohlfs, W.; Haustein, H.; Garbrecht, O.; Kneer, R. Insights into the local heat transfer of a submerged impinging jet: Influence of local flow acceleration and vortex-wall interaction. Int. J. Heat Mass Transf. 2012, 55, 7728–7736. [Google Scholar] [CrossRef]
- Dairay, T.; Fortuné, V.; Lamballais, E.; Brizzi, L. Direct numerical simulation of a turbulent jet impinging on a heated wall. J. Fluid Mech. 2015, 764, 362–394. [Google Scholar] [CrossRef]
- Aillaud, P.; Duchaine, F.; Gicquel, L.Y.M.; Didorally, S. Secondary peak in the Nusselt number distribution of impinging jet flows: A phenomenological analysis. Phys. Fluids 2016, 28, 095110. [Google Scholar] [CrossRef]
- Hattori, H.; Nagano, Y. Direct numerical simulation of turbulent heat transfer in plane impinging jet. Int. J. Heat Fluid Flow 2004, 25, 749–758. [Google Scholar] [CrossRef]
- Beaubert, F.; Viazzo, S. Large Eddy Simulations of plane turbulent impinging jets at moderate Reynolds numbers. Int. J. Heat Fluid Flow 2003, 24, 512–519. [Google Scholar] [CrossRef]
- Bisoi, M.; Das, M.; Roy, S.; Patel, D. Large eddy simulation of three-dimensional plane turbulent free jet flow. Eur. J. Mech.-B/Fluids 2017, 65, 423–439. [Google Scholar] [CrossRef]
- Shukla, A.; Dewan, A. OpenFOAM based LES of slot jet impingement heat transfer at low nozzle to plate spacing using four SGS models. Heat Mass Transf. 2019, 55, 911–931. [Google Scholar] [CrossRef]
- Kubacki, S.; Dick, E. Simulation of plane impinging jets with k-ω based hybrid RANS/LES models. Int. J. Heat Fluid Flow 2010, 31, 862–878. [Google Scholar] [CrossRef]
- Kubacki, S.; Rokicki, J.; Dick, E. Hybrid RANS/LES computations of plane impinging jets with DES and PANS models. Int. J. Heat Fluid Flow 2013, 44, 596–609. [Google Scholar] [CrossRef]
- Wu, W.; Piomelli, U. Reynolds-averaged and wall-modelled large-eddy simulations of impinging jets with embedded azimuthal vortices. Eur. J. Mech.-B/Fluids 2015, 55, 348–359. [Google Scholar] [CrossRef]
- So, H.; Yoon, H.; Chung, M. Large eddy simulation of flow characteristics in an unconfined slot impinging jet with various nozzle-to-plate distances. J. Mech. Sci. Technol. 2011, 25, 721–729. [Google Scholar] [CrossRef]
- Dairay, T.; Fortuné, V.; Lamballais, E.; Brizzi, L. LES of a turbulent jet impinging on a heated wall using high-order numerical schemes. Int. J. Heat Fluid Flow 2014, 50, 177–187. [Google Scholar] [CrossRef]
- Ghadi, S.; Esmailpour, K.; Hosseinalipour, S.; Mujumdar, A. Experimental Study of formation and development of Coherent Vortical Structures in Pulsed turbulent Impinging jet. Exp. Therm. Fluid Sci. 2015, 74, 382–389. [Google Scholar] [CrossRef]
- Xu, B.; Wen, J.; Volkov, K. Large-eddy simulation of vortical structures in a forced plane impinging jet. Eur. J. Mech.-B/Fluids 2013, 42, 104–120. [Google Scholar] [CrossRef]
- Esmailpour, K.; Bozorgmehr, B.; Hosseinalipour, S.; Mujumdar, A. Entropy generation and second law analysis of pulsed impinging jet. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1089–1106. [Google Scholar] [CrossRef]
- Jaramillo, J.; Trias, F.; Gorobets, A.; Perez Segarra, C.D.; Oliva, A. DNS and RANS modelling of a turbulent plane impinging jet. Int. J. Heat Mass Transf. 2012, 55, 789–801. [Google Scholar] [CrossRef]
- Kim, K.; Min, Y.; Oh, S.; An, N.H.; Seoudi, B.; Chun, H.; Lee, I. Time-resolved PIV investigation on the unsteadiness of a low Reynolds number confined impinging jet. J. Vis. 2007, 10, 367–379. [Google Scholar] [CrossRef]
- Chatterjee, A.; Tarbell, J. Laminar stability and heat transport in high aspect ratio planar confined impinging flows. Int. J. Heat Mass Transf. 2019, 137, 534–544. [Google Scholar] [CrossRef]
- Chiriac, V.; Ortega, A. A numerical study of the unsteady flow and heat tranfer in a transitional confined slot jet impinging on an isothermal surface. Int. J. Heat Mass Transf. 2002, 45, 1237–1248. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with Primitive Equations. J. Fluid Mech. 1963, 104, 99–165. [Google Scholar] [CrossRef]
- Lilly, D. A proposed modification of the Germano subgrid-scale closure. Phys. Fluids A 1994, 4, 633–635. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W. A dynamic subgrid scale eddy viscosity model. Phys. Fluids A 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Ansys. Ansys Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Hinze, J.; Hinze, J. Turbulence; McGraw-Hill Classic Textbook Reissue Series; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Shih, T.H.; Liou, W.; Shabbir, A.; Yang, Z.; Zhu, J. A New k-ε Eddy Viscosity Model for High Reynolds Number Turbulent Flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Menter, F. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Launder, B.; Reece, G.; Rodi, W. Progress in the Development of a Reynolds Stress Turbulence Closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Daly, B.; Harlow, F. Transport Equations in Turbulence. Phys. Fluids 1970, 13, 2634–2649. [Google Scholar] [CrossRef]
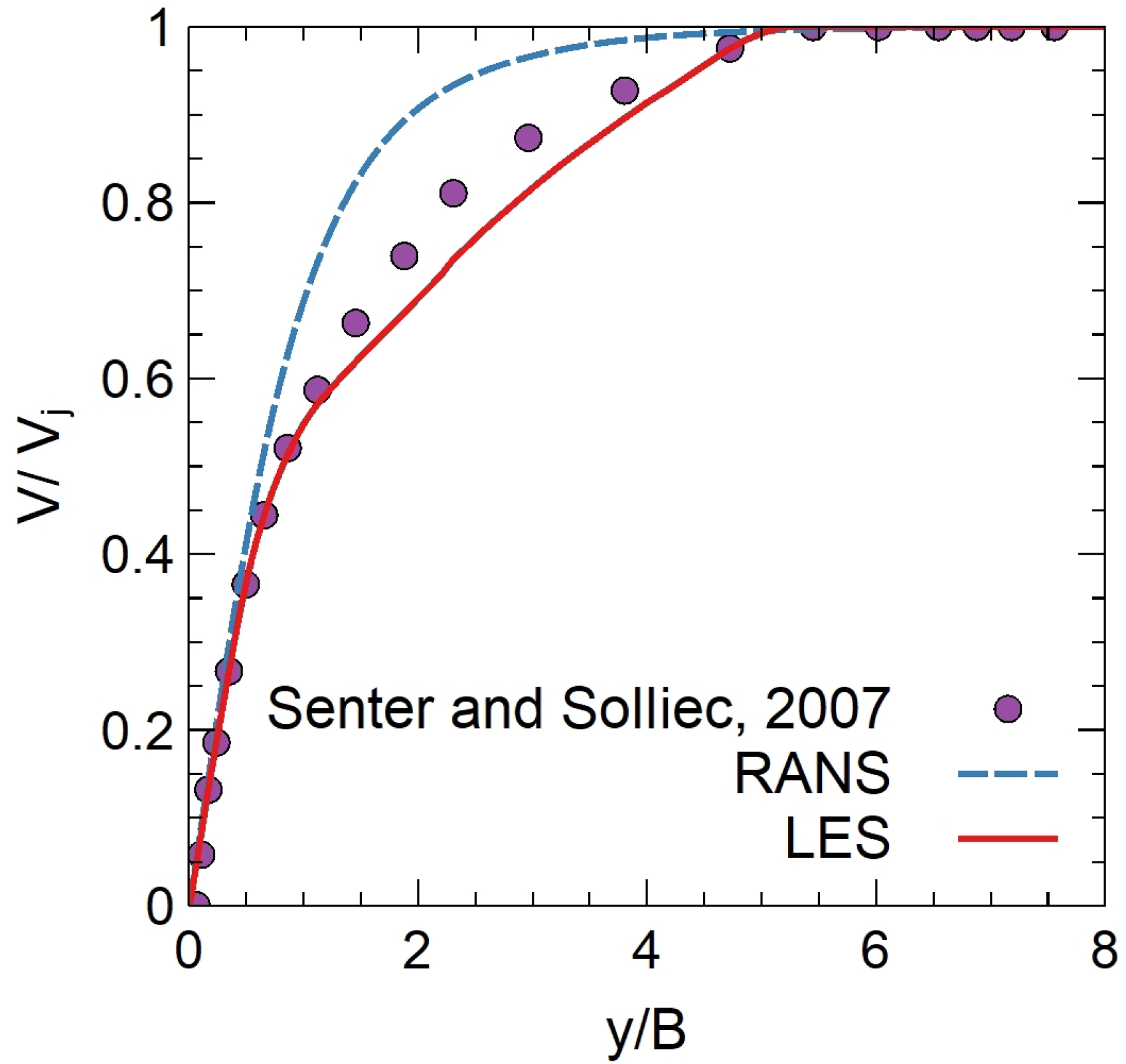
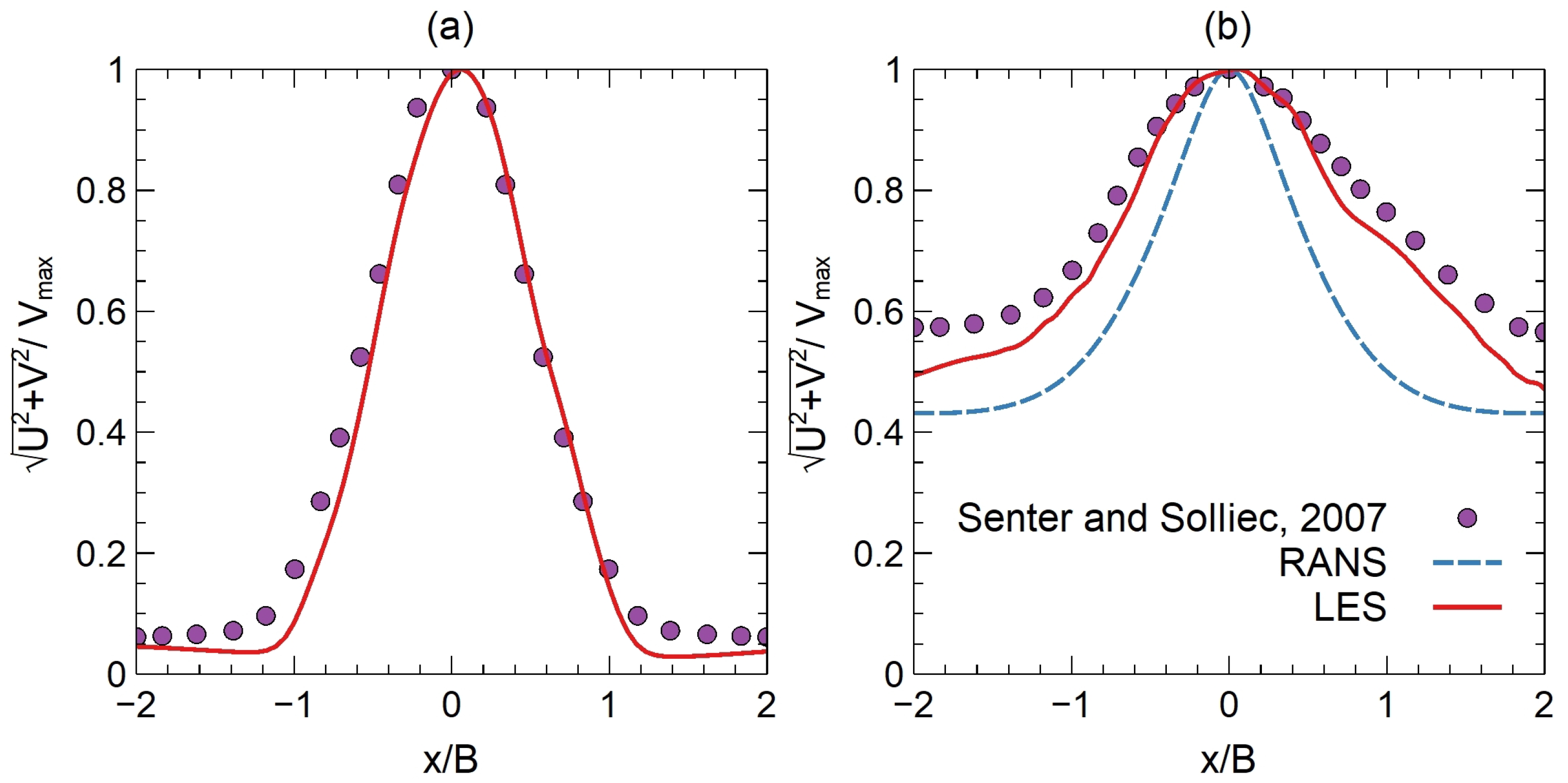
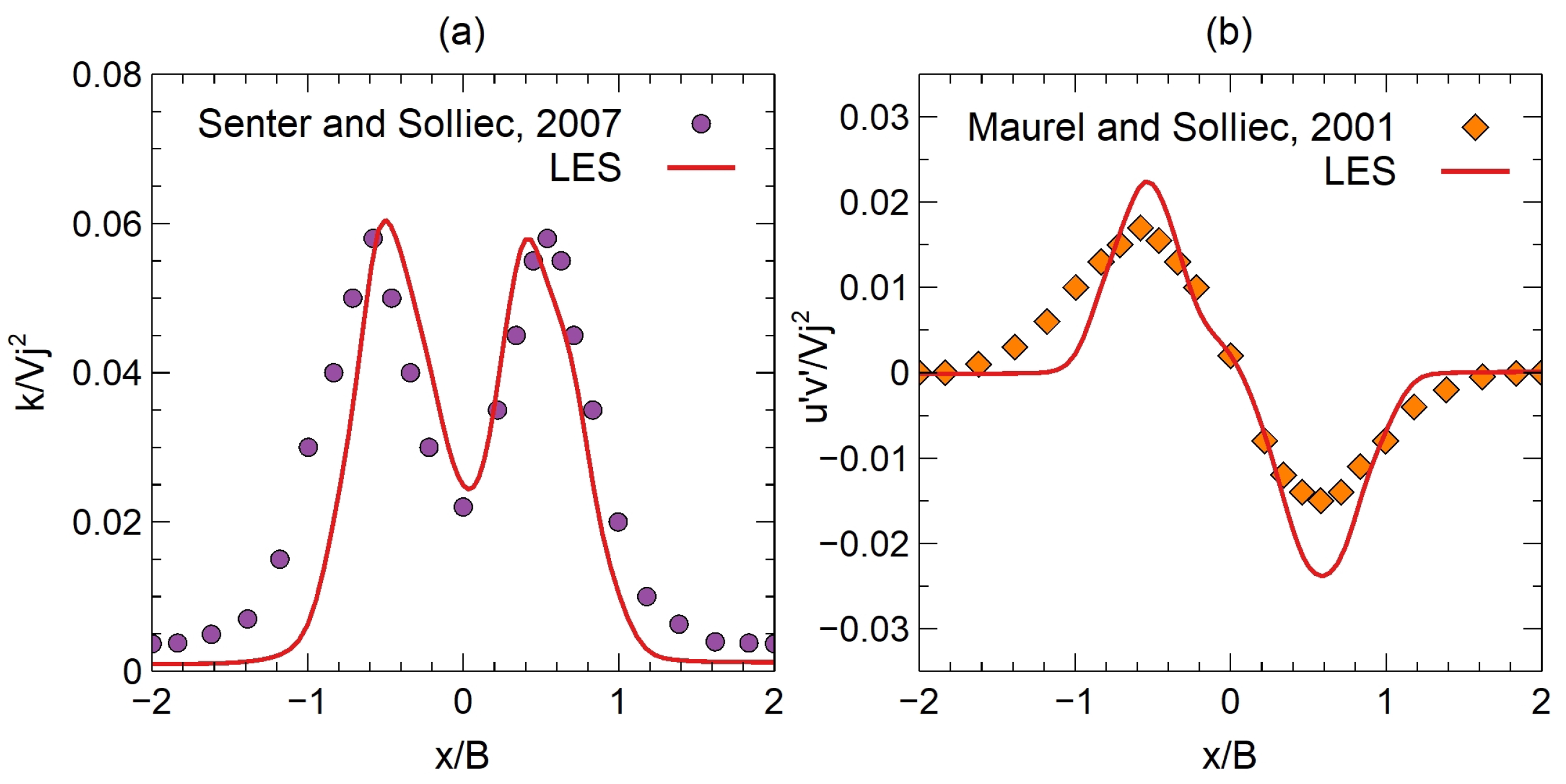
- Senter, J.; Solliec, C. Flow field analysis of a turbulent slot air jet impinging on a moving flat surface. Int. J. Heat Fluid Flow 2007, 28, 708–719. [Google Scholar] [CrossRef]
- Kraichnan, R. Diffusion by a Random Velocity Field. Phys. Fluids 1970, 13, 22–31. [Google Scholar] [CrossRef]
- Smirnov, A.; Shi, S.; Celik, I. Random Flow Generation Technique for Large Eddy Simulations and Particle-Dynamics Modeling. J. Fluids Eng. 2001, 123, 359–371. [Google Scholar] [CrossRef]
- Voke, P.; Gao, S.; Leslie, D. Large-eddy simulations of plane impinging jets. Int. J. Numer. Methods Eng. 1995, 38, 489–507. [Google Scholar] [CrossRef]
- Voke, P.R.; Gao, S. Numerical study of heat transfer from an impinging jet. Int. J. Heat Mass Transf. 1998, 41, 671–680. [Google Scholar] [CrossRef]
- Tsubokura, M.; Kobayashi, T.; Taniguchi, N.; Jones, W. A numerical study on the eddy structures of impinging jets excited at the inlet. Int. J. Heat Fluid Flow 2003, 24, 500–511. [Google Scholar] [CrossRef]
- Hoffmann, G.; Benocci, C. Numerical simulation of spatially-developing planar jets. In Proceedings of the 74th Fluid Dynamics Symposium on Application of Direct and Large Eddy Simulation of Transition and Turbulence, Adelaide, Australia, 10–14 December 1994; Volume 26. [Google Scholar]
- Cziesla, T.; Biswas, G.; Chattopadhyay, H.; Mitra, N. Large-eddy simulation of flow and heat transfer in an impinging slot jet. Int. J. Heat Fluid Flow 2001, 22, 500–508. [Google Scholar] [CrossRef]
- Rhea, S.; Bini, M.; Fairweather, M.; Jones, W. RANS modelling and LES of a single-phase, impinging plane jet. Comput. Chem. Eng. 2009, 33, 1344–1353. [Google Scholar] [CrossRef]
- Yu, M.; Chen, L.; Jin, H.; Fan, J. Large eddy simulation of coherent structure of impinging jet. J. Therm. Sci. 2005, 14, 150–155. [Google Scholar] [CrossRef]
- Piomelli, U.; Chasnov, J.R. Large-Eddy Simulations: Theory and Applications. In Turbulence and Transition Modelling: Lecture Notes from the ERCOFTAC/IUTAM Summerschool Held in Stockholm, 12–20 June 1995; Springer: Dordrecht, The Netherlands, 1996; pp. 269–336. [Google Scholar] [CrossRef]
- Maurel, S.; Solliec, C. A turbulent plane jet impinging nearby and far from a flat plate. Exp. Fluids 2001, 31, 687–696. [Google Scholar] [CrossRef]
- Dutta, R.; Dewan, A. LES of a Turbulent Slot Impinging Jet to Predict Fluid Flow and Heat Transfer. Numer. Heat Transf. Part A Appl. 2013, 64, 759–776. [Google Scholar] [CrossRef]
- Kubacki, S.; Dick, E. Convective heat transfer prediction for an axisymmetric jet impinging onto a flat plate with an improved k-ω model. Int. J. Numer. Methods Heat Fluid Flow 2009, 19, 960–981. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barata, B.A.C.; Navalho, J.E.P.; Pereira, J.C.F. Prediction of Self-Sustained Oscillations of an Isothermal Impinging Slot Jet. Fluids 2023, 8, 15. https://doi.org/10.3390/fluids8010015
Barata BAC, Navalho JEP, Pereira JCF. Prediction of Self-Sustained Oscillations of an Isothermal Impinging Slot Jet. Fluids. 2023; 8(1):15. https://doi.org/10.3390/fluids8010015
Chicago/Turabian StyleBarata, Bruno A. C., Jorge E. P. Navalho, and José C. F. Pereira. 2023. "Prediction of Self-Sustained Oscillations of an Isothermal Impinging Slot Jet" Fluids 8, no. 1: 15. https://doi.org/10.3390/fluids8010015
APA StyleBarata, B. A. C., Navalho, J. E. P., & Pereira, J. C. F. (2023). Prediction of Self-Sustained Oscillations of an Isothermal Impinging Slot Jet. Fluids, 8(1), 15. https://doi.org/10.3390/fluids8010015







