Abstract
The decay of the kinetic energy of a turbulent flow with time is not necessarily monotonic. This is revealed by simulations performed in the framework of discrete mechanics, where the kinetic energy can be transformed into pressure energy or vice versa; this persistent phenomenon is also observed for inviscid fluids. Different types of viscous vortex filaments generated by initial velocity conditions show that vortex stretching phenomena precede an abrupt onset of vortex bursting in high-shear regions. In all cases, the kinetic energy starts to grow by borrowing energy from the pressure before the transfer phase to the small turbulent structures. The result observed on the vortex filament is also found for the Taylor–Green vortex, which significantly differs from the previous results on this same case simulated from the Navier–Stokes equations. This disagreement is attributed to the physical model used, that of discrete mechanics, where the formulation is based on the conservation of acceleration. The reasons for this divergence are analyzed in depth; however, a spectral analysis allows finding the established laws on the decay of kinetic energy as a function of the wave number.
1. Introduction
The phenomena of vortex stretching and bursting are the main mechanisms for the appearance of turbulence and interactions between the different scales of energy transfer: [1,2,3,4]. From the physical point of view, these phenomena are related to the balance of the different actions associated with the terms of the equations of motion, inertia, compression, diffusion, and dissipation. The production of turbulence, the transfer of energy, and energy decay are described by the different contributions of the law of motion. The progress on the physical understanding of turbulence analyzed on experiments has been corroborated by simulations produced from the Navier–Stokes equation.
An alternative to the Navier–Stokes equation was recently implemented to search for solutions related to fluid flows or two-phase flows. The corresponding equation of motion [5] was also used to represent fluid–structure interactions or heat transfer on small time scales. The solutions of the discrete formulation and the Navier–Stokes equation for fluids or the Navier–Lamé equation for solids are the same despite important differences in the physical models.
The discrete formulation is here implemented in the framework of turbulent vortex flows. Indeed, the discrete formulation includes a different modeling of the physical effects; this is the case, in particular, for the inertia that is formulated in two terms of a Helmholtz–Hodge decomposition [6]. These terms play a very important role in the energy transfer mechanism of vortices on different spatial scales. The form of the equation of motion causes inertial effects to be intertwined with compressive effects. In a turbulent flow, pressure plays a regulating role, allowing local energy storage and energy redistribution in the form of kinetic energy; this phenomenon is present in all turbulent flows, including incompressible ones. The analysis of a rotating flow of a solid body clearly shows that the discrete formulation satisfies the rotational invariance of the equation of motion. In this sense, it extends the Galilean invariance of translational motion to the rotations of the solid body.
Several cases of inviscid or viscous vortex filament are analyzed in a first step to understand and verify that energy exchanges between turbulent structures are due to both vortex stretching and, occasionally, vortex bursting. The evolution of the mean kinetic energy and pressure fields shows inverse variations even for inviscid flows. The last part is devoted to the simulation of a Taylor–Green vortex at a Reynolds number of . The result is consistent with the previous long-term validations but shows a different behavior of the variation in the mean kinetic energy in the first instants of the flow. Contrary to the simulations performed with the Navier–Stokes equation, the kinetic energy increases by transforming the potential energy. As in a vortex filament, the velocity increases in the core at the expense of the pressure energy, while maintaining its angular momentum. A thorough analysis is provided to explain the observations and to give the reasons for the disagreements with the Navier–Stokes equation.
2. Discrete Mechanics Framework
2.1. Physical Principles
The fundamental principles of discrete mechanics have already been described Cal19a, Cal21b. Its presentation is developed here in a more synthetic way by specifying the most essential aspects related to the described phenomena. Some concepts of classical mechanics are abandoned, such as the existence of a global inertial reference frame, which forces us to abandon the principles of one-point derivation, integration, and analysis in general. At the same time, the notion of continuous medium is disregarded, it is the very reason for the creation of a global reference frame. Similarly, mass is an abstraction that is not necessary for the description of the laws of physics, as is momentum; in fact, the physical quantities that are expressed using mass are all of the first order, which allows the same quantities to be defined per unit of mass.
The main concepts introduced by discrete mechanics can be summarized by:
- A primary one-dimensional view of mechanical equilibrium governed by acceleration, thus preserving the notion of relativity of velocity. The one-dimensional geometrical description is fixed by the existence of a rectilinear segment delimited by two extremities and a length , called a discrete horizon. The extension of the physical model to several dimensions of space is realized by cause and effect, with the interactions being established through the extremities common to several segments.
- A translation invariance in time that, according to Noether’s theorem, ensures the conservation of energy. The discrete equation of motion is therefore the same at all times. With the exception of acceleration, which is an absolute quantity, the other quantities of physics are subject to the principle of invariance, which allows us to evaluate the value of a quantity at time t from its knowledge at an earlier time . This incremental process allows building a continuous memory model where velocity, energy, and other quantities are updated by a time integration.
- A local reference frame linked to a segment, which inhibits any change in reference frame, allows building an equation of motion on a geometrical structure, where the spatial dependencies from one segment to another are ensured by the principle of causality. The dynamics of a material medium or a particle in a one-dimensional space is limited by the velocity of the medium (the propagation of the swell, the acoustic signal, and the light). To use the concept of change in reference frame, the velocity must be constant, which is not guaranteed. Therefore, any interaction is limited by a horizon defined by the velocity of the medium.
- Classical notions of scalar, vector, pseudo-vector, and tensor are replaced by a unique concept of amplitude parameter defining the value of the intensity of the quantity attached to a point, segment, surface, etc. If this parameter is attached to a point, it is a scalar; if it is attached to a segment, it is a vector, etc. For example, kinetic energy is a scalar when it is defined at a point and becomes a vector when it is associated with a segment.
- Conservation of the total energy per unit of mass: mass and energy are two homologous forms of the equivalence principle of relativity. The laws of classical mechanics require several equations to translate the conservation of mass, momentum, and energy; they are redundant. The conservation of discrete energy also conserves acceleration as well as angular momentum, so it is not necessary to explicitly conserve mass.
- The association to the principles of equivalence and relativity of an additional concept, the Helmholtz–Hodge decomposition, which consists of writing that any acceleration is the sum of a solenoidal contribution and an irrotational one. The intrinsic acceleration of the particle or of the material medium is thus the sum of the gradient of a scalar potential and of the curl of a vector potential. This decomposition gives very valuable properties to the conservation laws written in this form.
- A principle included in Maxwell’s analysis to synthesize the laws of electrostatics and magnetism by introducing the time dependence of the fields. Direct and induced unsteady currents are the two possible alternatives for the creation of fields in electromagnetism. These two forms are associated with the two components of the Helmholtz–Hodge decomposition. The extension of these concepts to mechanics leads to consider compressive effects as direct actions and viscous effects as induced actions.
2.2. One-Dimensional Model
Discrete mechanics is developed from a one-dimensional view of dynamic equilibrium. Figure 1 represents a rectilinear segment oriented by the vector bounded by the two vertices a and b; its length is named a discrete horizon in reference to the maximum distance perceived by an observer located on one of the ends. This distance is related to the wave velocity c (swell, acoustic, and light) and to a duration corresponding to the observation time of the phenomenon by the relationship .
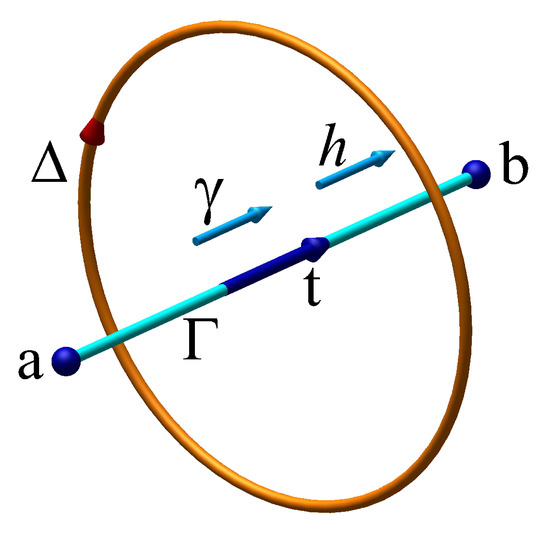
Figure 1.
Local frame of reference of discrete mechanics; the rectilinear segment oriented by is the constitutive element of the primal structure and the support of the intrinsic acceleration or imposed by the exterior . This segment, limited by its extremities a and b, is of length and called the discrete horizon. The dual structure is schematized by the contour , which defines the induced actions then projected on .
The intrinsic acceleration of the material medium or of a particle on the segment is denoted ; it is both a scalar defined on the oriented segment and a vector , but also the component of the acceleration vector of a space for which knowledge is not necessary. In the same way, the velocity is the component of a vector of space projected on . While the velocity is relative and is given only at a constant, the acceleration is considered absolute. The derivation of the equation of motion in discrete mechanics is based on the equality of the accelerations: those due to the external actions and the intrinsic acceleration of the material medium or of a particle. This law expresses the conservation of acceleration, it is written as:
where is the sum of the accelerations: those of the effects of compression and shear but also all the other potential source terms: gravitation, capillary acceleration, etc.
The law (1) does not disagree with the fundamental principle of dynamics ; in the case where the force is associated with gravity, we have , where m is the moving mass, or . Galileo’s principle of equivalence expresses that the effects of inertia and gravitation are of the same nature. However, the presence of mass poses two problems: (i) its generalization to any acceleration other than gravity; (ii) the association of a necessarily volumetric quantity, mass, and another essentially vectorial one, acceleration. Paradoxically, the force seen as a vector in the context of classical mechanics is the product of two disjoint quantities. The law (1) restricts the principle of equivalence to accelerations only by expressing that the intrinsic acceleration of a medium is equal to the sum of the accelerations applied to it.
Mass is at the center of Copernican and Galilean mechanics, which is attributed to the understanding of planetary motion. This importance continues today even if the theory of special relativity introduces the equivalence between mass and energy; moreover, mass is still present in the expression of energy . In the same way, the actual law of fluid mechanics is a conservation of momentum, , the product of mass and velocity. Discrete mechanics abandons the notion of momentum to define an equivalent quantity per unit of mass, the acceleration.
The principle of relativity must be respected; the velocity is a relative quantity that has no absolute reference, not even the velocity that is a strictly independent physical quantity. Velocity at time is calculated from the acceleration in the form , where is the velocity at time . In the same way, the displacement is calculated from the velocity in the form . These two quantities are thus updated from their values at time . Many other quantities are relative, in particular energy, which is defined only to a constant. If we define the total energy per unit mass , then its variation along the segment takes the form:
The intrinsic acceleration is that of an isolated particle that follows the trajectory or that of the material medium, and the acceleration of the law (1) is the sum of the external accelerations on . In one dimension of space, the intrinsic acceleration is written as . The quantity is the kinetic energy; it is also written as . It is both a scalar assigned to the oriented segment and the vector . This quantity can also be defined on the extremities a and b of the segment, where represents an acceleration opposing the increase or decrease in the velocity over time. This is the principle of inertia, which tends to establish a uniform motion in the absence of any external acceleration .
2.3. Extension of Physical Model to Other Dimensions
The discrete physical model is one-dimensional, represented by the segment on which all direct and induced accelerations are projected, whether intrinsic or applied. The extension to a higher dimension is immediate; it is realized by assembling the segments by their extremities. These extremities become the vertices of the primal structure formed of planar polygons delimited by the collection of the sides of the triangle in Figure 2. This primal structure is thus composed of vertices, segments, and polygonal facets; contrary to other approaches coming from differential geometry, mimetic methods, discrete exterior calculus, or the cell method, discrete mechanics does not address volumes even if the assembly of facets forms polyhedra with planar faces.
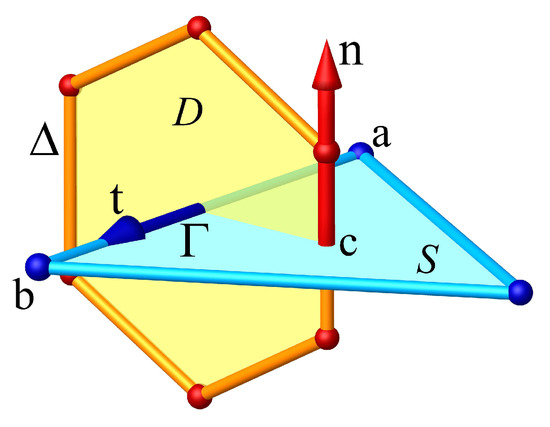
Figure 2.
Geometric structures of discrete mechanics: the primal structure (in blue) is composed of a collection of segments oriented by a unit vector bounded by the ends a or b; these segments form a polygonal planar surface , whose barycenter, denoted c, defines the normal that is positively oriented according to Maxwell’s rule. The dual structure (in red) has a flat polygonal surface bounded by segments . The unit vectors are orthogonal by construction, .
The absence of a global reference frame is both a disadvantage and an advantage. It is no longer possible to express the invariance of the system of equations in a change of reference frame, for example, or to project each term on axes in an inertial reference frame to ensure mechanical equilibrium, as in continuum mechanics. The advantage is the ability to extend the principle of inertia to uniform rotational motions. The interactions from one local reference frame to another are realized by cause and effect. The celerity c of the waves is defined locally including for the celerity of light , which can vary according to the medium.
Energies per unit volume of compression carried by and of rotation, represented by , are defined at time and are named the retarded potentials in reference to the electromagnetic potentials of Liénard [7].
where and are the longitudinal and transverse celerities.
They express the accumulation of the respective energies over time from an initial state, where all quantities satisfy the equation of motion. From this point of view, the discrete equation of motion is a physical model with continuous memory.
2.4. Discrete Equation of Motion
The conservation of the total energy corresponds to the integration of the acceleration on the segment , but and the velocity are average values on this segment. It is then possible to derive an equation of motion whose unknowns are the velocities on the basis of discrete operators, the divergence , gradient of a scalar , primal curl , and dual curl . The law of discrete mechanics (1) expresses that the intrinsic acceleration of an isolated particle or of the material medium is equal to the sum of the accelerations imposed by the exterior, mainly the compressive and rotational accelerations. Intrinsic acceleration is simply the material derivative .
Discrete mechanical equilibrium corresponds to the equality on the accelerations , which becomes in the framework of a Helmholtz–Hodge decomposition where is the scalar potential, and is the potential vector of the intrinsic acceleration; and are named the retarded potentials in reference to the electromagnetic potentials [7,8]. Physical modeling of the increases in potentials, and , can be found in the references associated with discrete mechanics [9,10]. The relative increase in compression is a function of the divergence of the velocity, and that of the rotation is obtained by the primal curl of the latter. The equation of motion becomes:
where represents the acceleration due to sources, gravitation, capillary effects, etc.; and are the attenuation factors for longitudinal and transverse waves, respectively. For a Newtonian fluid, and the factor is equal to zero for characteristic times lower than s; transverse waves are dissipated very quickly.
The discrete equation of motion is accompanied by two updates of the scalar and vector potentials computed from the divergence and the primal curl of the velocity. Symbol ⟼ means that the potentials are updated from the retarded potentials. The discrete equation is self-contained: it does not require any additional mass conservation law or constitutive laws. The variable is the velocity on each of the segments of the primal structure. The quantity is the time lapse between two observations of the physical system. It is closely related to the physical phenomenon studied, and its value can be very large for the simulation of stationary phenomena, at s to translate the propagation of light, where . In all unsteady cases, it is necessary to choose a time span . Even if the velocity of the medium is very large, the compression energy is not zero. Indeed, the grouping is the energy increase between two observations of the evolution of the physical system; remains constant because . Thus, a medium considered rather incompressible can propagate sound waves, for example, in water. The discrete equation of motion applies to any incompressible or compressible flow.
The system (4) is an alternative to the Navier-Stokes equation and the conservation of mass. It is primarily a law of conservation of total energy per unit mass, i.e., acceleration. As mass is a form of energy, it is not necessary to keep the mass or density in the equation of motion; it would be an overabundant quantity. Moreover, all the quantities of physics that are currently functions of mass make this one appear at the order one, which allows the definition of equivalent quantities per unit of mass. The length and time are the only two fundamental quantities to define any law of mechanics and, more generally, of physics.
Finally, the acceleration or the material derivative [6] in one or more space dimensions is written as:
This discrete form significantly differs from that of continuum mechanics. In particular, the last term is here a dual curl with zero divergence, whereas the corresponding term in continuum mechanics, the Lamb vector, , is the gradient of another potential. The two terms of inertia or the equivalent form have projections on each of the three axes of a global reference frame. In discrete mechanics, the two terms of inertia (5) have as support the same segment of the local reference frame.
The cornerstone of the discrete model is precisely the formulation of the inertia; Figure 1 well schematizes the competition between the compression term and the rotation term of the relation (5). The first contribution is fixed by the gradient of the inertial potential defined on the vertices a and b,and the second contribution is represented by the dual curl of the vector potential . Within a turbulent flow, the energy exchange between these two forms of inertial acceleration is most likely the force driving the transfer between the different spatial scales.
2.5. Discrete Kinetic Energy Theorem
It is important to specify the differences in the kinetic energy theorem between continuum mechanics and discrete mechanics. These differences are not so much related to the presence or absence of mass as to the fact that we consider the integration on an elementary volume specific to the notion of continuous medium. Let us take the Navier-Stokes equation multiplied by the velocity vector of space and, to simplify the matter, let us consider the only contribution of the pressure and an incompressible flow. Let us consider an elementary volume limited by an impermeable surface ; the conservation of kinetic energy is written as follows:
The term can be transformed into the form ; the last term in (6) vanishes when incompressibility is taken into account, and the equation becomes:
and, as the surface is impermeable, , we obtain:
This observation translated by (8) is perfectly legitimate if we stick to the equilibrium on the volume . For a material point , the kinetic energy remains constant when we follow the medium in its motion; this local form is, however, questionable. In the presence of viscous forces, the form adopted by many authors Bra84, Van11, Wan13 only takes into account the latter terms, and the energy decay becomes:
considered as the evolution of the only dissipation , where denotes the deviating part of the rate-of-strain tensor. The problem remains for compressible flows where the divergence is not zero.
The major objection to this conclusion lies in the notion of the continuous medium itself; the use of a transformation of a weak integral formulation leads to a loss of information: it amounts to asserting that locally one imposes but these two vectors are not necessarily orthogonal. In continuum mechanics, the kinetic energy theorem specifies that the sum of the forces applied to a material medium is equal to the variation in its kinetic energy.
Its transposition into discrete mechanics is immediate: the sum of the accelerations applied to a material medium is equal to the variation in the kinetic energy per unit of mass; this is noted . It is both a scalar attached to the vertices of the primal structure and a vector related to the segment, because the vector is associated with the segment . This is not a new law; it is deduced from the equation of motion. In discrete mechanics, the equation of motion (4) is multiplied by and integrated over the length of the segment:
The potential is the compression or translational kinetic energy and is the rotational energy or angular kinetic energy. The form (4) of the equation of motion includes from the start the balance of the sum of the forces but also the moments. The acceleration is not only related to the translational motion but also translates the conservation of angular momentum.
Contrary to classical mechanics, where the vector is not necessarily collinear with the pressure gradient vector and similar to viscous forces, the discrete formulation removes any interpretation on the orientation of the terms in the kinetic energy equation. is well collinear to and to ; the results of the scalar product allow us to consider that and are, at the same time, scalars on the oriented segment and vectors. With the unknown of the equation of motion being , the local kinetic energy is simply obtained by a scalar product . The quantity considered as an average on a segment allows the definition of the discrete theorem of the local kinetic energy:
It is possible to define an average value on the whole physical domain of the kinetic energy per unit of mass from its value on each segment of the primal structure :
where is the length measure of all segments. Similarly, the global compression energy is represented by an integral over the primal volume :
Returning to the local form (11), the velocity is aligned not only with but also with . This last term corresponds to the rotation of the medium but only reflects dissipation in the case of a viscous fluid for which the potential vector is of the form . In this situation, the transverse waves are completely attenuated over very small time constants . The local variation in the kinetic energy of a material medium during its motion can thus be positive or negative, but the most important aspect is that the integration to the whole volume of the considered flow cannot be limited a priori to a monotonous decay. Indeed, the discrete law of motion (4) expresses the conservation of the total energy , where is the compression energy per unit of mass, and is the rotation energy. The kinetic energy is only a part of the total energy. In the absence of viscous friction for a fluid, there remain two energies, and , the sum of which is indefinitely conserved over time from an Eulerian view. For a given flow, the velocity and the potential are nonzero and fixed by the initial condition. The evolution in time of the system is governed by only the equation of motion (4). Equation (11) is only a consequence of it. Like any mechanical system, the kinetic energy and the potential energy evolves in such a way as to preserve the total energy. The following form of the equation of motion allows us to be convinced of this:
The two terms of the right-hand side are two Lagrangians associated, respectively, with the conservation of the compression and rotation accelerations. Noether’s theorem applied to laws of physics in the form of Lagrangians or Hamiltonians allows us to invoke the invariances of a mechanical system. In particular, the pressure energy defined by and the kinetic energy can change over the course of time while keeping the total energy. In particular, the total kinetic energy can increase while the pressure decreases.
In the case of a vortex filament where the angular velocity is and the potential depend only on the distance to the axis of rotation, these two quantities are orthogonal and , and the flow remains axial. When a modulation of the velocity along the axial direction is introduced, this condition is no longer met and axial currents are generated to try to re-establish the axisymmetric equilibrium; this is the phenomenon of vortex stretching.
2.6. Conservation of Angular Momentum
The equation of motion (4) is a law of conservation of total energy per unit mass, but it also conserves angular momentum along with momentum. In continuum mechanics, the angular momentum theorem is a separate law from the equation of motion expressing the conservation of the quantity , where is the momentum, and is the distance from the axis of rotation.
Let us consider an incompressible rotational motion without longitudinal effects; in these conditions, the discrete equation of motion becomes:
The first term of the parenthesis is the potential , which would represent a possible mechanical action that would be associated with a storage of the mechanical energy of rotation, for example, a balance spring of a watch or a pendulum. The second term is a kinetic energy per unit of mass; it is the rotational inertia and is the inertial acceleration related to the rotation. The term is the instantaneous energy that is redistributed to the other components of the equation over time. In an unsteady rotational motion, all these terms are related, but the total rotational energy is conserved. The dual curl of the sum of these is the rotational acceleration, i.e., the angular momentum per unit mass. In the absence of viscous dissipation, the angular momentum is conserved.
For example, the application of Equation (15) to a simple pendulum oscillating under the effect of the acceleration of gravity allows us to find the result of Newtonian or Lagrangian mechanics, including in the nonlinear regime. In the linear domain, the solution is then , and the period , where is the initial angle of the pendulum, and r is its length.
In the case of a purely viscous flow, the term is replaced by the kinematic viscosity , and the attenuation factor is equal to unity, the transverse waves are attenuated in a very short time. The retarded vector potential at time is equal to , but the exchanges between the rotational inertia and the other terms of the equation, including pressure terms, persist. In classical mechanics, the formulation of the inertia is not at all the same as in discrete mechanics, and the Navier–Stokes equation does not preserve a priori the angular momentum. In turbulence, this discrepancy can be of the first order in the representation of the interactions between vortices.
3. Turbulent Flows in Vortex Filaments
Examples of vortex filaments for a perfect or viscous fluid are analyzed in order to highlight the phenomena of vortex stretching and bursting in configurations simpler than a developed turbulent flow. The objective is to show that the kinetic energy can increase, even in cases of decreasing turbulence. Finally, the reference case of the Taylor–Green vortex at a Reynolds number of is taken again to highlight these same phenomena and to demonstrate to a disagreement with the previous results and to attribute it to the chosen physical model.
3.1. Inviscid Vortex-Filament
The appearance of turbulence is first analyzed on a cylindrical vortex of an inviscid fluid in the first moments of the flow before the creation of small structures leads to its divergence. The physical domain corresponds to a cylinder of dimensions , . In cylindrical coordinates , the initial velocity field is given by the vector:
where is a modulation factor of the velocity perturbation along the z direction. The initial scalar potential (pressure) is directly deduced from the equation of motion and the imposed velocity (16).
If , the initial streamlines are circles, , and the potential field is purely radial. Under these conditions, the vector quantities and are orthogonal, and the evolution of the kinetic energy per unit mass during its motion given by:
is zero. We notice that the components and are carried by the same segment ; they are thus collinear. This is not a paradox because they are components of the velocity and not of the velocity vector itself. Moreover, when and are oriented along the radius, the velocity component is indeed null and vice versa for the orthoradial direction. The simulation of this case with the system (4) leads to a strictly angular motion with constant velocity and a kinetic energy constant in time. Contrary to a common idea, the nonexistence of a 2D turbulent motion is not due to a 2D restriction of the physical space. By applying the curl operator to the Navier–Stokes equation, we find the form on :
where represents the advection of the vortex, and a term , which cancels out in the two dimensions of space because the velocity is defined in this planar surface whereas is orthogonal to it. The result obtained in discrete mechanics shows that a vortex without longitudinal modulation leads to an invariance of the kinetic energy, even in three dimensions.
In the case where there is a velocity modulation along the z direction with , the problem is different. Indeed, and are no longer orthogonal, and a longitudinal motion is superimposed on the rotational motion of the vortex. As the flow is incompressible and the boundary conditions are such that , the motion generates positive and negative longitudinal velocities, which in turn generate pressure variations along the axis of the vortex. This phenomenon of stretching and compression of the vortex can be observed in Figure 3 from an initial condition fixed by the velocity field (16). This vortex stretching shows that the axial velocities in the core of the vortex are higher than on the periphery. In the image of the center, we can see that the kinetic energy is more important in the central core.
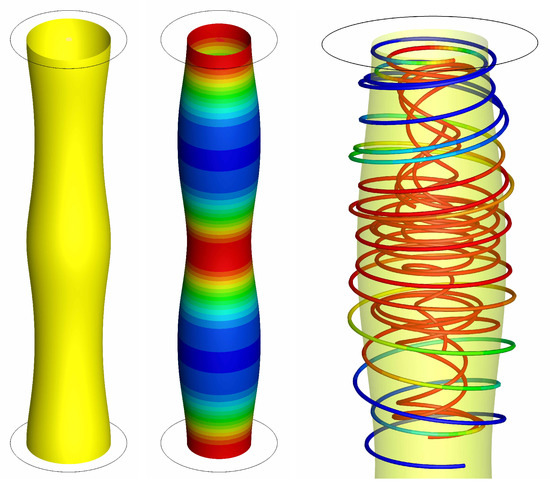
Figure 3.
Inviscid vortex filament initiated by the velocity field (16); initial potential field (left), potential field at decorated by the local kinetic energy (center), and a snapshot of streamlines (right).
Figure 4 shows the evolution over time of the kinetic energy defined by the average over all segments of the local energy on each segment . We observe that the variations in the kinetic energy and potential are in phase opposition even if the definitions of these quantities are different. They reflect the periodic movements of the vortex stretching phenomenon. To understand these oscillations, we return to the equation of motion for an inviscid flow:
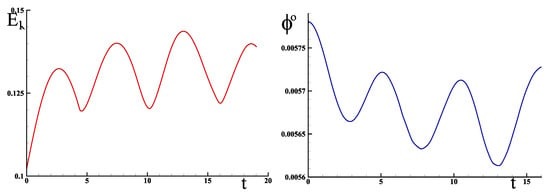
Figure 4.
Evolutions of the mean kinetic energy and the scalar potential where and are given in and t in s.
First, it is necessary to recall that the incompressibility of the flow is not fixed a priori but established by the term , which becomes constant for a lapse of time because the divergence of the velocity is of the order of magnitude of the inverse of . This term corresponds to the update of the scalar potential linked to a modification of the equilibrium between the compression energy characterized by the retarded potential and the kinetic energy. Equation (19) is solved for an inviscid flow () for several spatial approximations and the solution well converges, but, in all cases, the numerical solution diverges for a time . It is not possible to obtain a very long-term solution without viscosity. However, a stable flow can be maintained by introducing a very low viscosity in order to find the behavior obtained for .
The exchange between kinetic energy and pressure energy is a major element for the understanding of turbulent flows, including for incompressible flows. The discrete equation of motion (4) has the essential characteristic of interweaving the compression and rotation accelerations with the two components of inertia within the same law. Any splitting aiming at separating the conservation of the total energy from the conservation of the mass can lead to unpredictable artifacts.
3.2. Vortex Filament at
The case treated now is of another nature: the modulation of the initial velocity of the previous problem is replaced by a very important shear generated by the inversion of the direction of rotation of the flow along the longitudinal direction. It is close to the Taylor–Green vortex benchmark discussed later. For a physical domain defined by , the initial condition of the vortex is fixed by the velocity in Cartesian coordinates:
The potential field , the pressure in the presence of a density , is defined unilaterally as the quantity which translates the mechanical equilibrium by the equation of motion for the velocity field (21). Indeed, in the case of an incompressible flow, it is useless to specify the pressure field corresponding to this equilibrium. From this, simulations were carried out for three configurations representing a vortex filament: (i) a cylinder of radius and height tessellated by curvilinear hexahedra in cylindrical coordinates, (ii) a prism circumscribed to the previous cylinder represented by a mesh based on prisms with triangular sections, and (iii) a parallel channel with square section whose meshes are Cartesian hexahedra. The approximations used have approximately the same number of cells, about , which corresponds to a number of unknowns , the number of edges of geometric structure. The Reynolds number adopted in the three cases is , where . Details of the numerical methodology are provided in several cited papers including [10]. The objective of this section is to show that although the geometries of the three configurations are different, the turbulence appears in the same way; however, the turbulent structures generated are impacted by the shape of the vortex filament considered.
Figure 5 shows three snapshots corresponding to time s. The Bernoulli scalar potential field is colored by the local kinetic energy.
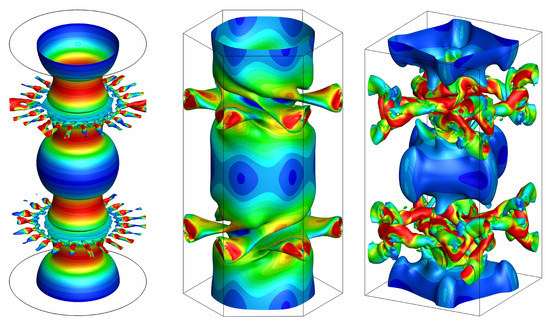
Figure 5.
Snapshots of potential fields decorated by kinetic energy for three vortex filaments with circular, hexagonal, and square bases.
In all three cases, we observe that the turbulent structures are animated by an important velocity in the zones of important shear. The number of structures resulting from vortex busting closely depends on the geometry of the chosen physical domain. Figure 6 shows the evolution of the mean kinetic energy over time for the cases of the cylindrical and square-based filaments; the evolution corresponding to the prismatic structure is roughly the same as for the cylinder. In the cases, we observe a rapid increase in the mean kinetic energy over time for a time , which is accompanied, as for the inviscid filament, by a decrease in the scalar potential .
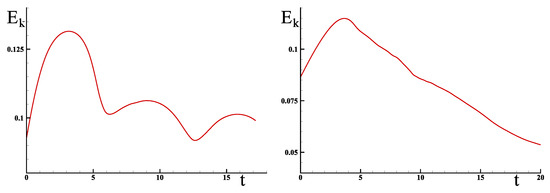
Figure 6.
Evolution of the kinetic energy with time in the case of a cylinder (left) and for the geometry with square base (righ).
The potential energy characterized by is transformed from the first instants into kinetic energy, while the impact of viscosity is negligible. In the case of the cylinder, we observe the effect of the vortex stretching phenomenon similar to that of inviscid vortex-filament. Beyond a time , the vortex bursting creates finer and finer structures, which are then dissipated by viscosity; for the hexahedral geometry, the evolution of the kinetic energy presents three phases: (i) an increase until the appearance of the vortex bursting at , (ii) a decrease characterizing the transfers between the large and small structures, and (iii) a decreasing exponential evolution for characterizing the viscous dissipation.
The mechanisms leading to the appearance of vortex bursting turbulence in viscous and nonviscous cases having now been described, it is necessary to confront the discrete physical model with a reference case that has been the subject of numerous theoretical studies and numerical simulations: the Taylor–Green vortex at .
3.3. Taylor–Green Vortex at
The Taylor–Green vortex test case is emblematic of the turbulence decay of a three-dimensional velocity field, initially introduced into a cubic cavity of dimensions , where the boundary conditions are periodic for velocity and pressure. This test case is widely used to verify the convergence properties of numerical methods; the results are broadly reported in the literature, for example, [11]. The Reynolds number chosen is the one whose results are most often found, namely , a value adopted for the benchmark corresponding to [12]. The Reynolds number is defined by , where , , and is the kinematic viscosity, assumed constant. The initial condition is defined in Cartesian coordinates by the components of the vector :
The potential field is obtained from the conservation of acceleration Equation (4), consistent with the constraint , where is the discrete velocity. The simulation from this initial condition allows us to obtain at each instant the solution . The associated instantaneous quantities, the kinetic energy per unit of mass , the dissipation , and the enstrophy per unit of mass are saved in time. The time evolutions of the global kinetic energy and the compression energy as a function of time are shown in Figure 7.
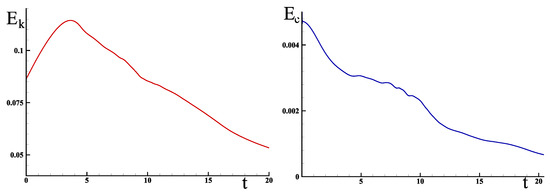
Figure 7.
Global kinetic energy and compression energy at Reynolds number for cells and unknowns.
As for the vortex filament cases, the kinetic energy increases until a time , where the first turbulent structures appear in the form of vortex bursting, mainly in the shear zones generated by the initial conditions (21).
In correlation with the growth of the kinetic energy, the compression energy decreases; the mechanical equilibrium defined by the invariance of the total energy imposed by the Equation (4) allows the exchanges between the two terms of inertia, pressure, and effect of the limited viscosity in this phase. From a time begins the energy cascade phase toward the small structures, which is marked by a quasilinear decrease in the kinetic energy in time and irregular variations in the pressure energy. Beyond a time begins the dissipation phase, marked by a decay toward zero of the kinetic and compression energies.
The observation of the velocity and pressure fields shows that the energy cascade where the kinetic energy is globally decreasing is due to the phenomena of vortex stretching and vortex bursting at different scales. Instantaneous variations in the fields, in particular of the pressure, reveal very sudden increasing variations of the pressure, which can reach local values several times higher than , the initial maximum kinetic energy. Figure 8 shows the Bernoulli potential field decorated by the local kinetic energy for time .
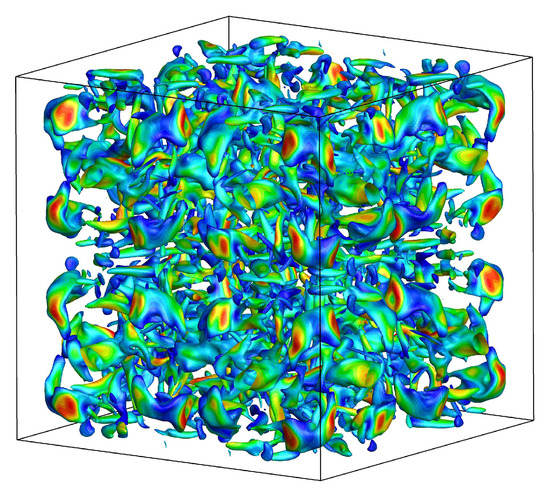
Figure 8.
Snapshot of the potential field decorated by the kinetic energy for , et unknowns.
This representation of the turbulent field is quite consistent with the fields given by the many authors who have simulated this benchmark.
The energy cascade in the inertial zone is very comparable to the evolutions previously obtained by different authors. More precisely, the spectral analysis in wavelengths k for Reynolds number and time allows us to show the spectrum in Figure 9. The Kolmogorov law is approximately satisfied by discrete mechanics.
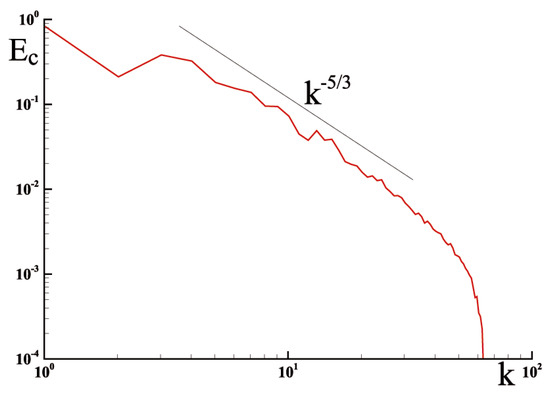
Figure 9.
Energy spectrum as a function of the wave number for on one-quarter of the domain.
However, if the energy decay phase in the domain seems to qualitatively be the same, the first phase of increase in presented in Figure 7 is radically different from the results obtained by the many authors who have studied this configuration since 1983. The following section provides an analysis of the underlying reasons for this disagreement.
3.4. Behavior as a Function of Reynolds Number
Like other simulations performed with the proposed model, the numerical solutions obtained are convergent to order two in space and time. The specificity of turbulent flow simulations lies in the ability to capture the smallest spatial and temporal scales of turbulence by using adapted meshes and time steps. The decrease in the scales to capture those related to viscosity is all the more important as the Reynolds number increases; the range of Reynolds numbers studied is therefore necessarily limited. Considering the available means, the Reynolds number of 1600 has been chosen in most of the simulations on this test case. In order to verify that this value corresponds to a case of developed turbulence, other values of Reynolds number have been used for the numerical simulations: , , and a case of flow for an inviscid fluid. For , the flow is clearly laminar, while the one corresponding to is transient but presents strong similarities on the turbulence decay to the case.
Figure 10 presents the evolutions of kinetic energy for these values () as a function of the time limited to s; indeed, the solution for the inviscid case explodes beyond this time, whereas it is perfectly represented for the lower times. The structure of the flows is the same in all three cases at this time; the shearing of the fluid filaments generates a vortex bursting similar to those observed on the individual filaments simulated before. These results at different Reynolds numbers show very similar behaviors even though, just after the vortex bursting, the decay shows limited differences.
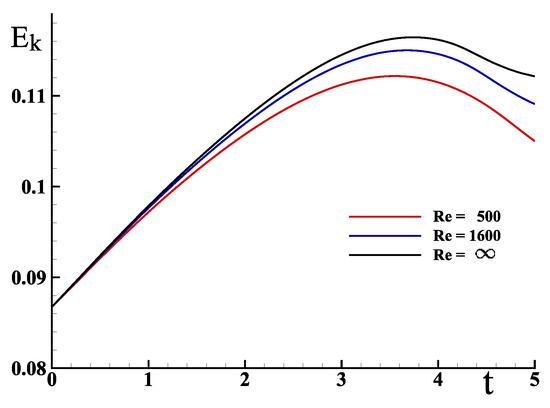
Figure 10.
The evolution of the kinetic energy corresponding to the Taylor–Green vortex case shows a similar behavior at Reynolds numbers of and for an inviscid fluid.
4. Analysis
Let us take the incompressible Navier–Stokes equation with constant density used for many decades for the Taylor–Green vortex and especially in reference [12]:
where is the curl of the velocity vector. The inertia is here split into a part with zero rotation to form the Bernoulli pressure and the Lamb vector , which is a priori not a curl. The incompressibility constraint is taken into account in a different way according to the authors, whereas others have used a compressible formulation at low Mach numbers. In all cases, among which include [12,13,14,15,16,17], the results obtained with the model (22) are very close. This problem is now considered as a benchmark to present new physical models or innovative numerical methodologies of high accuracy. Direct simulations of the TGV case at Reynolds number can be summarized by the time variations in the kinetic energy and dissipation ; they are represented in Figure 11,where the values are borrowed from W. van Rees [11].
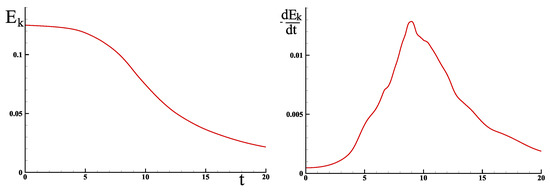
Figure 11.
Taylor–Green vortex at ; the spectral simulation provides the evolution of and dissipation rate for the Navier–Stokes model after W. van Rees [11], file Re-1600-512.gdiag.
The kinetic energy on the volume decreases toward zero in a monotonic way over time with a very slight decrease for times lower than due to the viscosity of the fluid. For times , the inertial zone is characterized by a fast decrease in . The dissipation , calculated from the expression or directly from , shows a maximum of this quantity around .
The comparison between the discrete kinetic energy in Figure 7 and the Navier–Stokes one (Figure 11) reveals profound discrepancies in the behavior of the flow at . These differences are not due to the method of performing the statistics or to the form of the kinetic energy theorem because it is directly derived from the physical model used. The numerous simulation results from discrete mechanics on reference flows all show a very good agreement with those of continuum mechanics [5,6,18,19]. For the first time, for the TGV flow, the results diverge.
In discrete mechanics, the unknowns of the equation of motion are the velocities on the segment , and the velocity vector is not necessary to model the flow. The kinetic energy per unit mass is a quantity attached to but is also defined on the vertices of the primal structure, a or b, and on the barycenters of the facets. The global kinetic energy computed on the segments, on the dual volumes or on the facets has an identical behavior over time; increases in the preinertial phase, whereas it remains almost constant in continuum mechanics.
The growth of the kinetic energy can only be possible at the expense of the potential energy represented by the Bernoulli scalar potential . Indeed, in the region , the viscous effects are not perceptible. Numerous simulations at different Reynolds numbers all show the same phenomenon, including for an inviscid flow; in this last case, the vortex bursting phenomenon for logically leads to a divergence in the simulation. The conservation of the total energy given by the discrete Equation (4) associates the two inertia terms, the compression term, and the viscous term. The energy exchanges due to inertia and compression effects are reciprocal because compression does not lead to dissipation of acoustic waves on these spatial scales. Thus, a decrease in compression energy can be transformed into an increase in kinetic energy and vice versa. This is the phenomenon observed in the first phase where the potential pressure energy is converted into kinetic energy. Let’s take the inertia term from the Navier-Stokes equation:
The two equivalent formulations are established within the concept of a continuous medium and therefore valid at a point of it. To be able to calculate explicitly each term it becomes necessary to project the equation on a global reference frame.
In discrete mechanics the mechanical equilibrium is realized within a local reference frame. Solving the discrete equation of motion (4) implicitly entangle all the terms of this nonlinear equation over time and it is difficult to predict the behavior of the solution. Observation of the simulation results shows that the roles of the Bernoulli scalar potential are related to compression and that they correspond to the rotational inertia . The inertial potentials and also exchange their energy; the longitudinal compression generates a modification of the rotation and vice versa. The inertial acceleration, , is written as:
This quantity, , is globally conserved in the absence of external accelerations, notably viscous effects. The physical meaning of the inertial vector is illustrated by the vortex schematized in Figure 12.
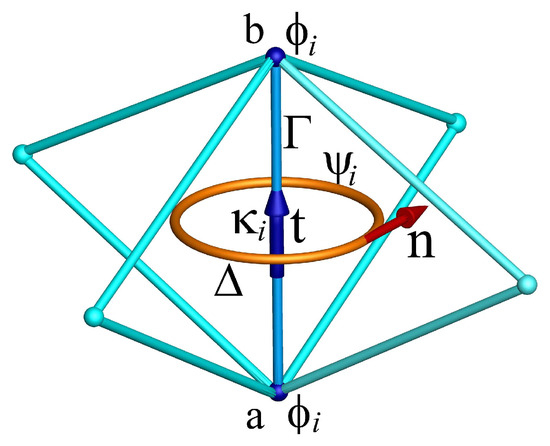
Figure 12.
Scheme of the inertia vector on the oriented segment and the respective representations of its two components such that .
A change in the compression energy represented by generates a variation in the velocity on and, consequently, of the velocities on the other segments of the four primal structures. The circulation of the velocities on these lead us to define a potential vector carried by the unit vector . The dual curl of this vector, , is in turn carried by the segment . Thus, the compression energy is compensated by an equivalent variation in the rotational kinetic energy, i.e., a variation in the velocity on the dual contour . More precisely, a stretching in the direction associated with a decrease in leads to an increase in the rotational inertial term . The vortex stretching mechanism is closely related to the energy exchange between the two components of the vector; while the angular momentum is conserved in the rotation of a vortex filament, the kinetic energy increases.
This expression of the inertia in the form of a Helmholtz–Hodge decomposition gives the physical model particular properties, for example, when the divergence or curl operators are applied to , which allows the suppression of one of its components. Let us consider the velocity field corresponding to a solid body rotation . In the framework of continuum mechanics, the inertia would be written as , which does not conform to the classical view of a mechanical equilibrium defined by component. In discrete mechanics, each component has a direct acceleration and an induced acceleration, both associated with the same segment. The assembly of the segments in a geometrical structure such as the one represented in Figure 2 leads to an entanglement of the inertia terms. In turbulence, rotation and inertia play major roles in the production of kinetic energy, in the exchange between vortices, and in the decay of energy at small scales. The classical (23) and discrete (24) forms are very different and lead to divergences in the specific cases of turbulence in rotating flows.
The law of motion of discrete mechanics represents the conservation of total energy per unit mass, i.e., acceleration. It has the particularity of strongly entangling the terms of pressure and inertia; this dynamic entanglement is a strict coupling of the scalar potential and the divergence of the velocity. There is no adjoint equation; mass, or density, is absent from the discrete equation of motion also for flows with variable density [10]. The scalar and vector potentials are completely subject to acceleration. There are also no constitutive laws to take into account. Whether the flows are compressible or incompressible, the energy increase associated with compression is always and that of rotation at ; only the velocities and must be known. From a fixed velocity field, we derive the scalar potential field satisfying the initial mechanical equilibrium. Then, all the terms of the equation come into action and exchange energy in the course of time. It is very difficult to predict the behavior of each term, but we know that the energy initially introduced in the form of kinetic and potential energy decreases towards zero through viscous dissipation. Thus, the TGV case solved in discrete mechanics shows an increasing evolution of the kinetic energy in the first instants, in contradiction with the phenomenon observed in continuum mechanics. The dynamic entanglement of inertia and compression effects represents the essence of the creation of turbulence and its evolution in time.
5. Conclusions
The proposed formulation is essentially based on (i) the conservation of the total energy, the sum of the compressive energy, and the rotational energy; and (ii) the form of the inertia, which is decomposed into a curl-free part and a divergence-free part:
- The observation of the solutions on the turbulent vortex filament cases and on the Taylor–Green vortex case shows a nonmonotonic decay in the kinetic energy. This observation is consistent with the principle of conservation of angular momentum for a vortex-like flow for an inviscid fluid where the potential and kinetic energies can be mutually exchanged over time. However, the Taylor–Green vortex at , considered as a reference for the study of turbulence decay and as a benchmark for numerical methods, approached with the Navier–Stokes equation, shows a monotonic decay over time of the kinetic energy. The reasons for this disagreement are attributed to the essential discrepancies between discrete and continuum mechanics, and the derivation of the equation of motion on a segment instead of a volume model. Discrete mechanics leads us to consider the conservation of the total energy on the segment as an equality between the intrinsic acceleration of the material medium and the accelerations imposed on it.
- In the particular cases of turbulence in vortices, inertia plays a very important role in the energy exchange; the very different form adopted in discrete mechanics helps to explain the discrepancy in behavior in the inertial zone, even though the decay in the kinetic energy in the transfer zone is very similar to the observations made from the Navier–Stokes equation. The numerous simulations carried out from this equation are not questioned: only the choice of the physical model can explain the differences observed. Discrete mechanics develops another point of view that remains consistent with the fundamental principles of mechanics; it has particular properties whose effects should be specified in the future.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Buaria, D.; Bodenschatz, E.; Pumir, A. Vortex stretching and enstrophy production in high Reynolds number turbulence. Phys. Rev. Fluids 2020, 5, 104602. [Google Scholar] [CrossRef]
- Carbone, M.; Bragg, A.D. Is vortex stretching the main cause of the turbulent energy cascade? J. Fluid Mech. 2020, 883. [Google Scholar] [CrossRef]
- Spalart, P.R. Airplane Trailing Vortices. Annu. Rev. Fluid Mech. 1998, 30, 107–138. [Google Scholar] [CrossRef]
- Moet, H.; Laporte, F.; Chevalier, G.; Poinsot, T. Wave propagation in vortices and vortex bursting. Phys. Fluids 2005, 17, 054109. [Google Scholar] [CrossRef]
- Caltagirone, J.P.; Vincent, S. On primitive formulation in fluid mechanics and fluid-structure interaction with constant piecewise properties in velocity-potentials of acceleration. Acta Mech. 2020, 231, 2155–2171. [Google Scholar] [CrossRef]
- Caltagirone, J.P. On Helmholtz-Hodge decomposition of inertia on a discrete local frame of reference. Phys. Fluids 2020, 32, 083604. [Google Scholar] [CrossRef]
- Liénard, A. Champ électrique et Magnétique Produit par une Charge électrique Concentrée en un Point et Animée d’un Mouvement Quelconque; G. Carré et C. Naud: Paris, France, 1898. [Google Scholar]
- Heras, R. Alternative routes to the retarded potentials. Eur. J. Phys. 2017, 38, 055203. [Google Scholar] [CrossRef][Green Version]
- Caltagirone, J.P. Discrete Mechanics, Concepts and Applications; ISTE, John Wiley & Sons: London, UK, 2019. [Google Scholar] [CrossRef]
- Caltagirone, J.P. Application of discrete mechanics model to jump conditions in two-phase flows. J. Comput. Phys. 2021, 432, 110151. [Google Scholar] [CrossRef]
- van Rees, W.M. Vortex bursting. Phys. Rev. Fluids 2020, 5, 110504. [Google Scholar] [CrossRef]
- Brachet, M.E.; Meiron, D.I.; Orszag, S.A.; Nickel, B.G.; Morf, R.H. Small-scale structure of the Taylor-Green vortex. J. Fluid Mech. 1983, 130, 411–452. [Google Scholar] [CrossRef]
- Brachet, M.; Meiron, D.; Orszag, S.; Nickel, B.; Morf, R.; Frish, U. The Taylor-Green vortex and fully developed turbulence. J. Stat. Phys. 1984, 34, 1049–1063. [Google Scholar] [CrossRef]
- van Rees, W.M.; Leonard, A.; Pullin, D.; Koumoutsakos, P. A comparison of vortex and pseudo-spectral methods for the simulation of periodic vortical fows at high Reynolds numbers. J. Comput. Phys. 2011, 230, 2794–2805. [Google Scholar] [CrossRef]
- Wang, Z.; Fidkowski, K.; Abgrall, R.; Bassi, F.; Caraeni, D.; Cary, A.; Deconinck, H.; Hartmann, R.; Hillewaert, K.; Huynh, H.; et al. High-Order CFD Methods: Current Status and Perspective. Int. J. Numer. Methods Fluids 2013, 72, 811–845. [Google Scholar] [CrossRef]
- Diosady, L.; Murman, S. Case 3.3: Taylor-Green Vortex Evolution. In Proceedings of the Case Summary for 3rd International Workshop on Higher-Order CFD Methods, Kissimmee, FL, USA, 3–4 January 2015. [Google Scholar]
- de la Llave Plata, M.; Lamballais, E.; Naddei, F. On the performance of a high-order multiscale DG approach to LES at increasing Reynolds number. Comput. Fluids 2019, 194, 104306. [Google Scholar] [CrossRef]
- Caltagirone, J.P. On a reformulation of Navier-Stokes equations based on Helmholtz-Hodge decomposition. Phyics Fluids 2021, 33, 063605. [Google Scholar] [CrossRef]
- Caltagirone, J.P. An alternative to the concept of continuous medium. Acta Mech. 2021, 232, 4691–4703. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).