Wall-Modeled and Hybrid Large-Eddy Simulations of the Flow over Roughness Strips
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations
2.2. Turbulence Models
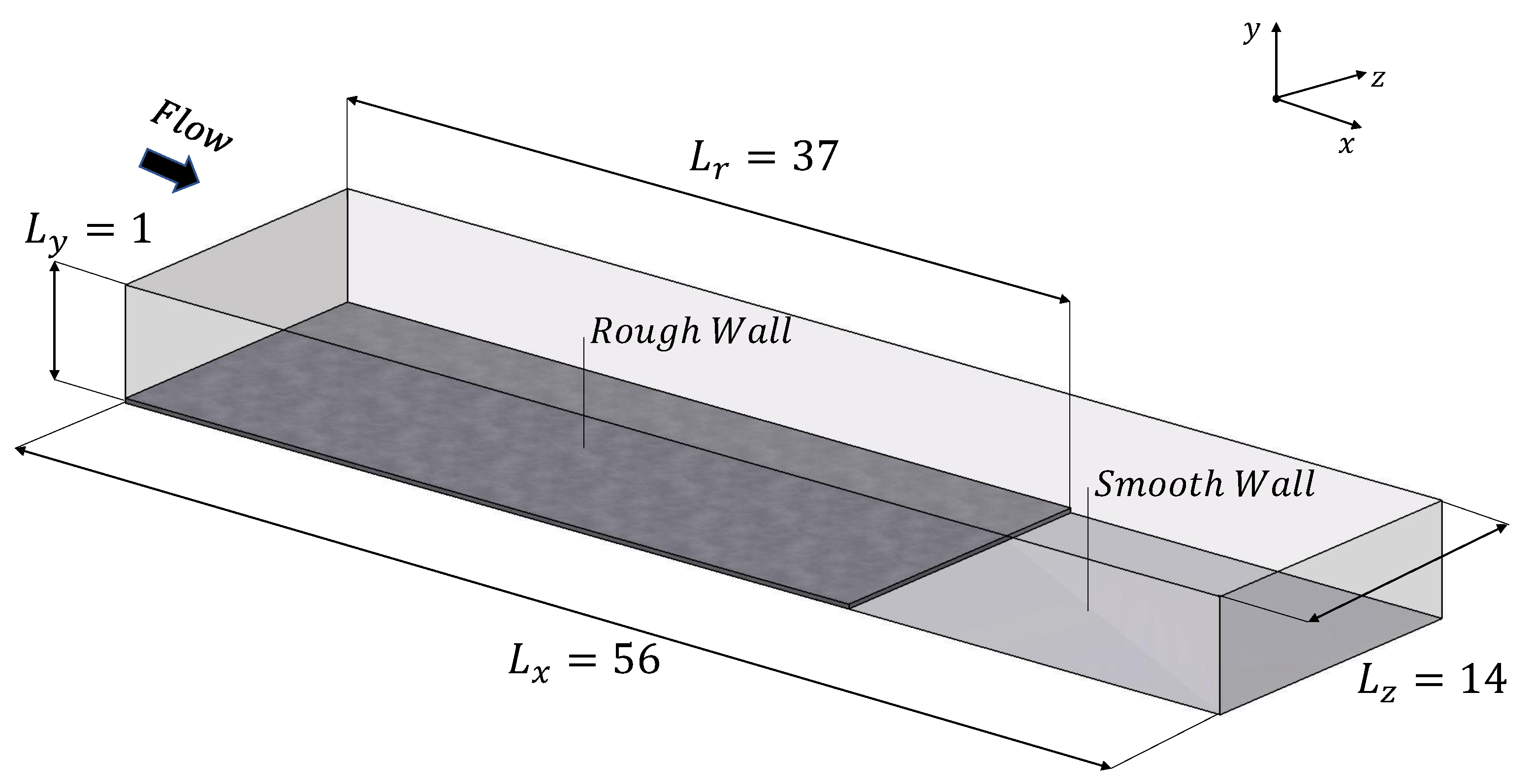
2.3. Numerical Model
2.4. Roughness Modeling
3. Results
3.1. Grid Convergence Study
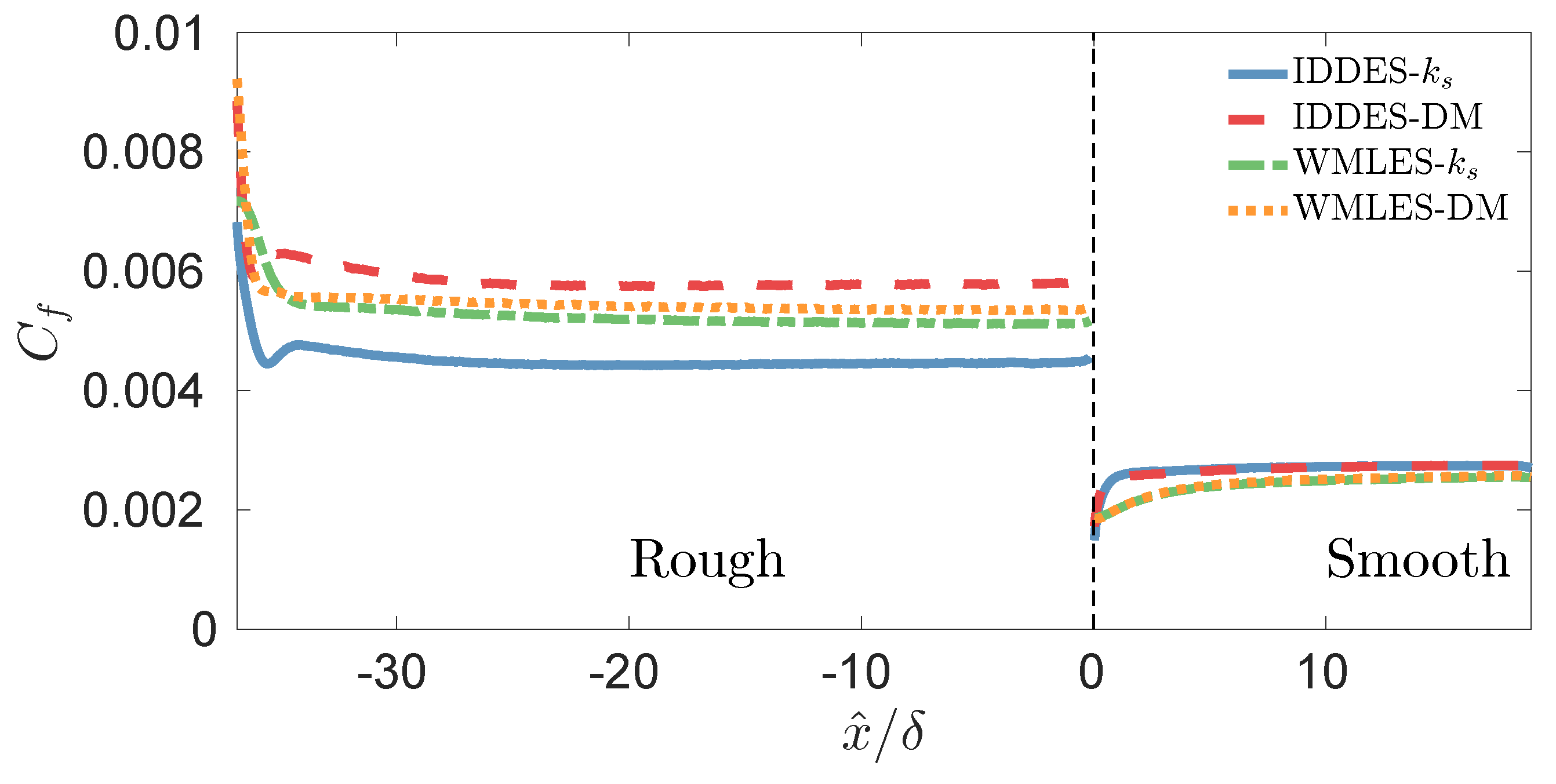
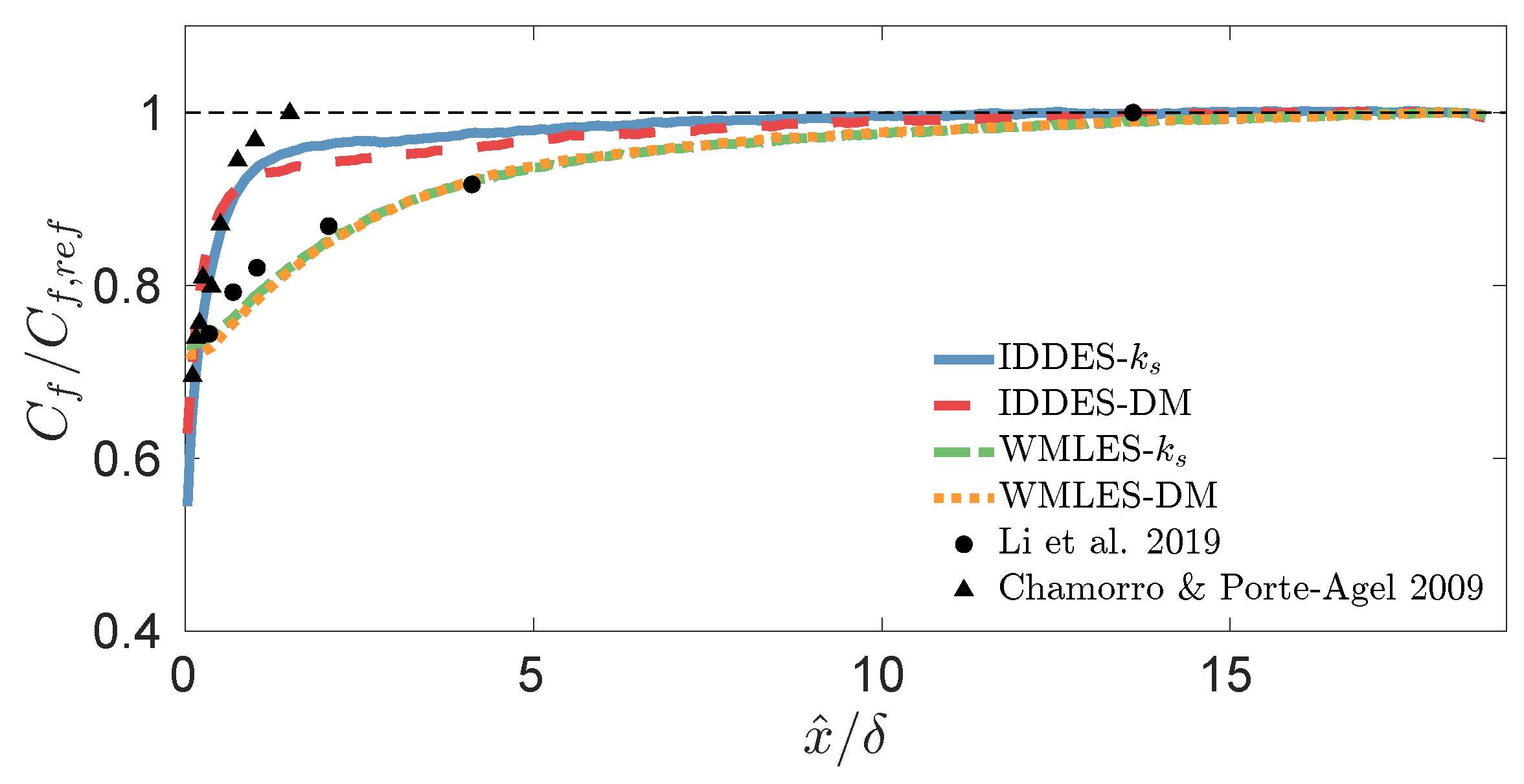
3.2. Skin Friction
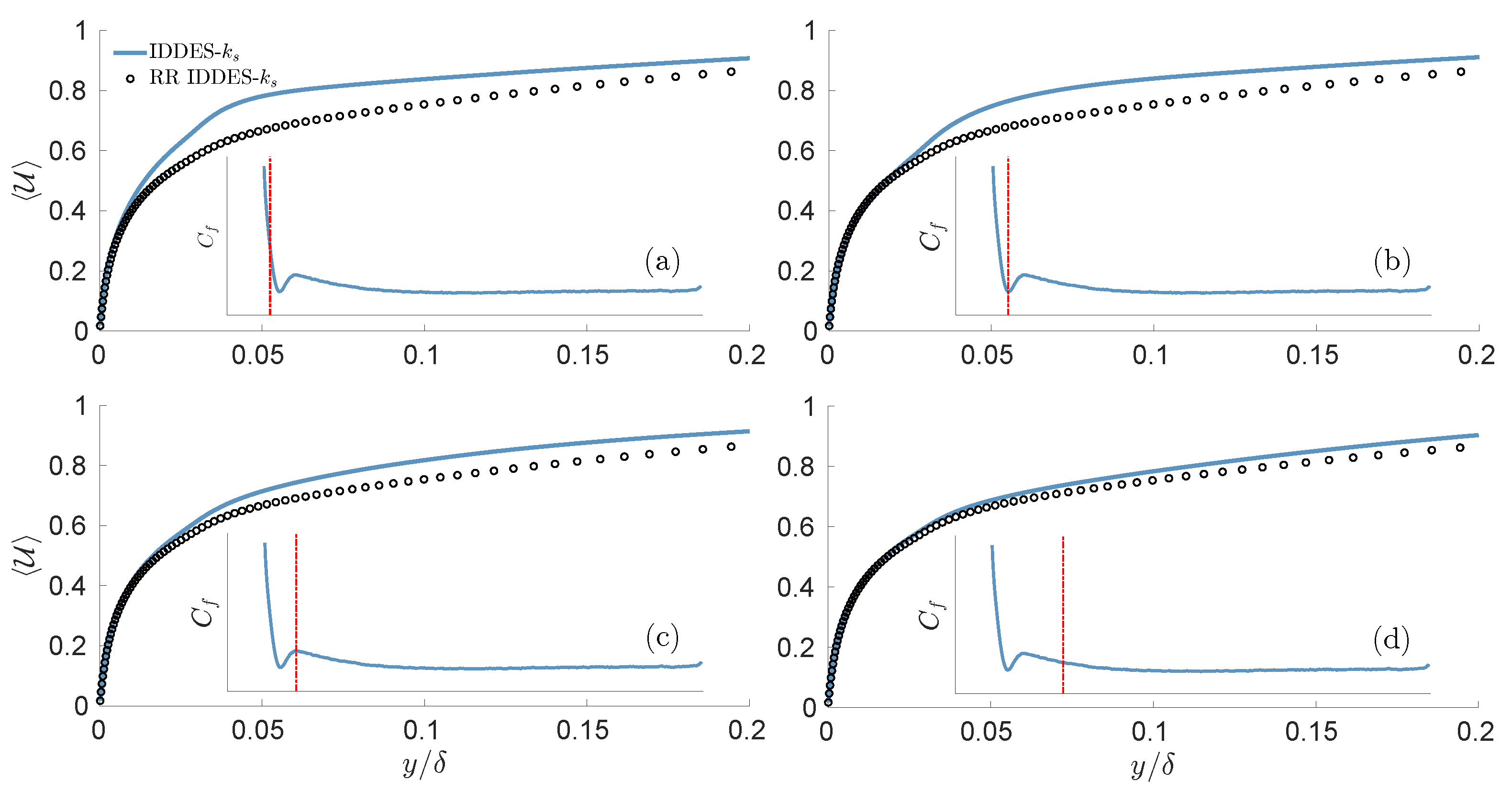
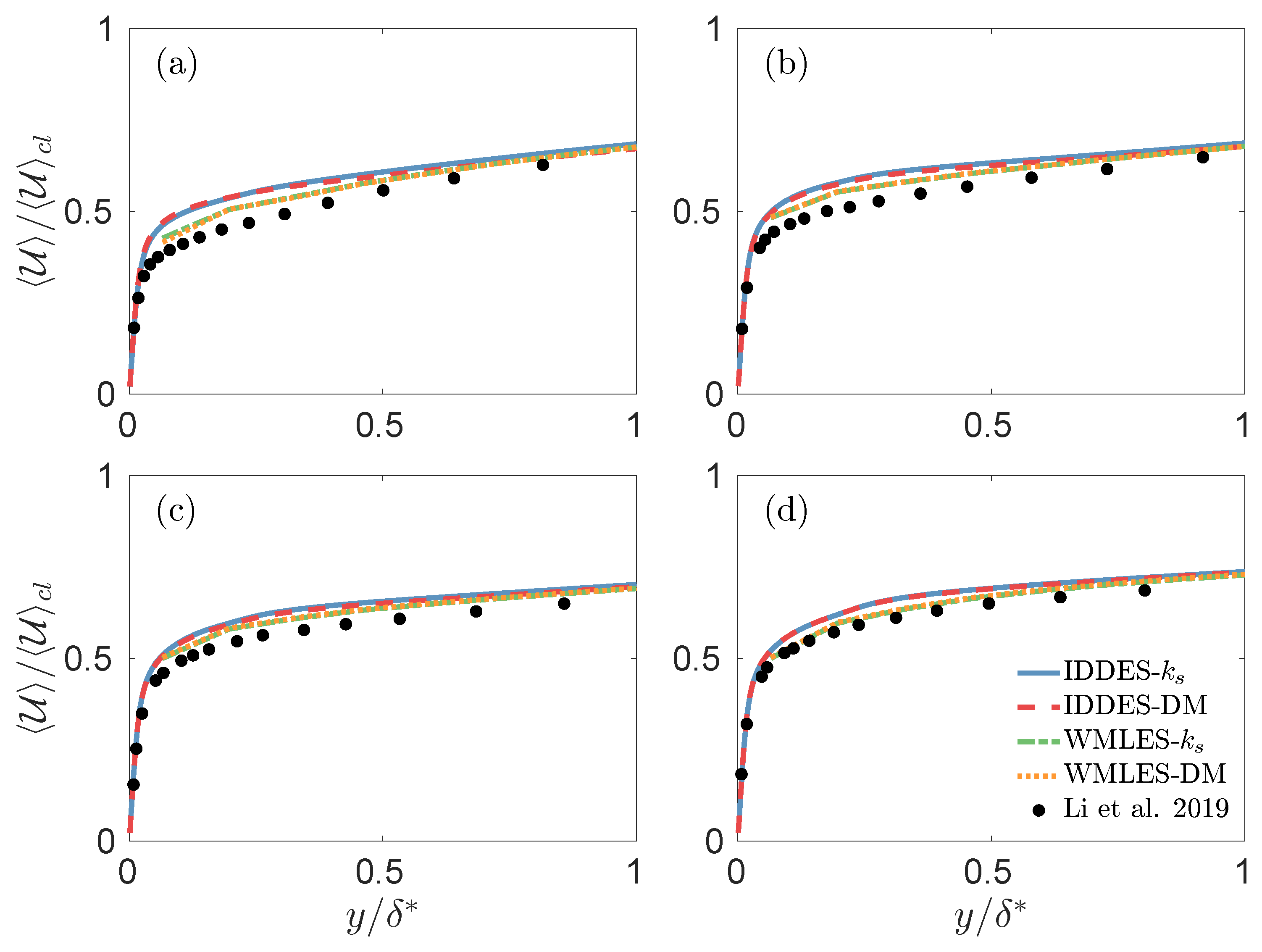
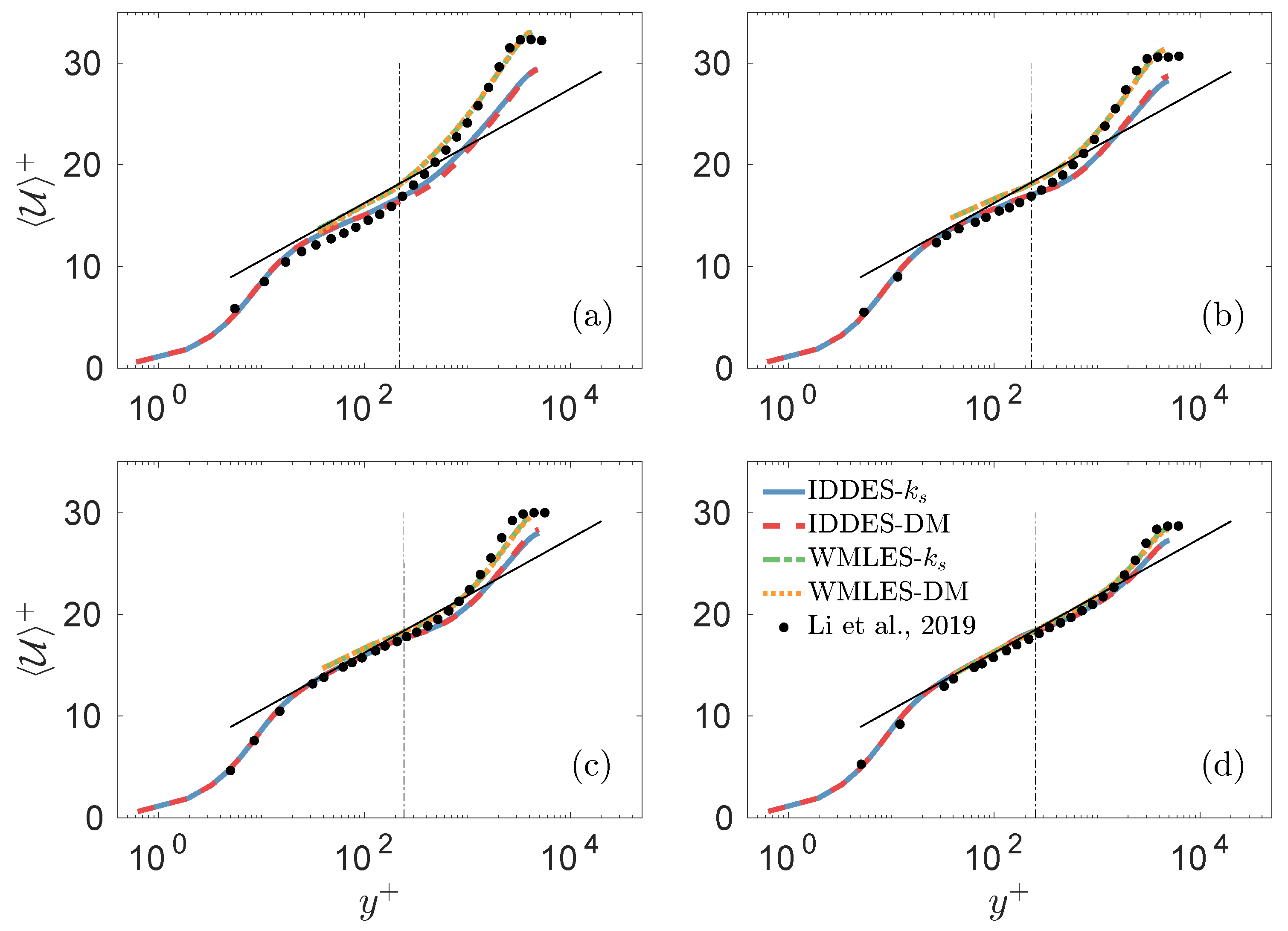
3.3. Mean Velocity
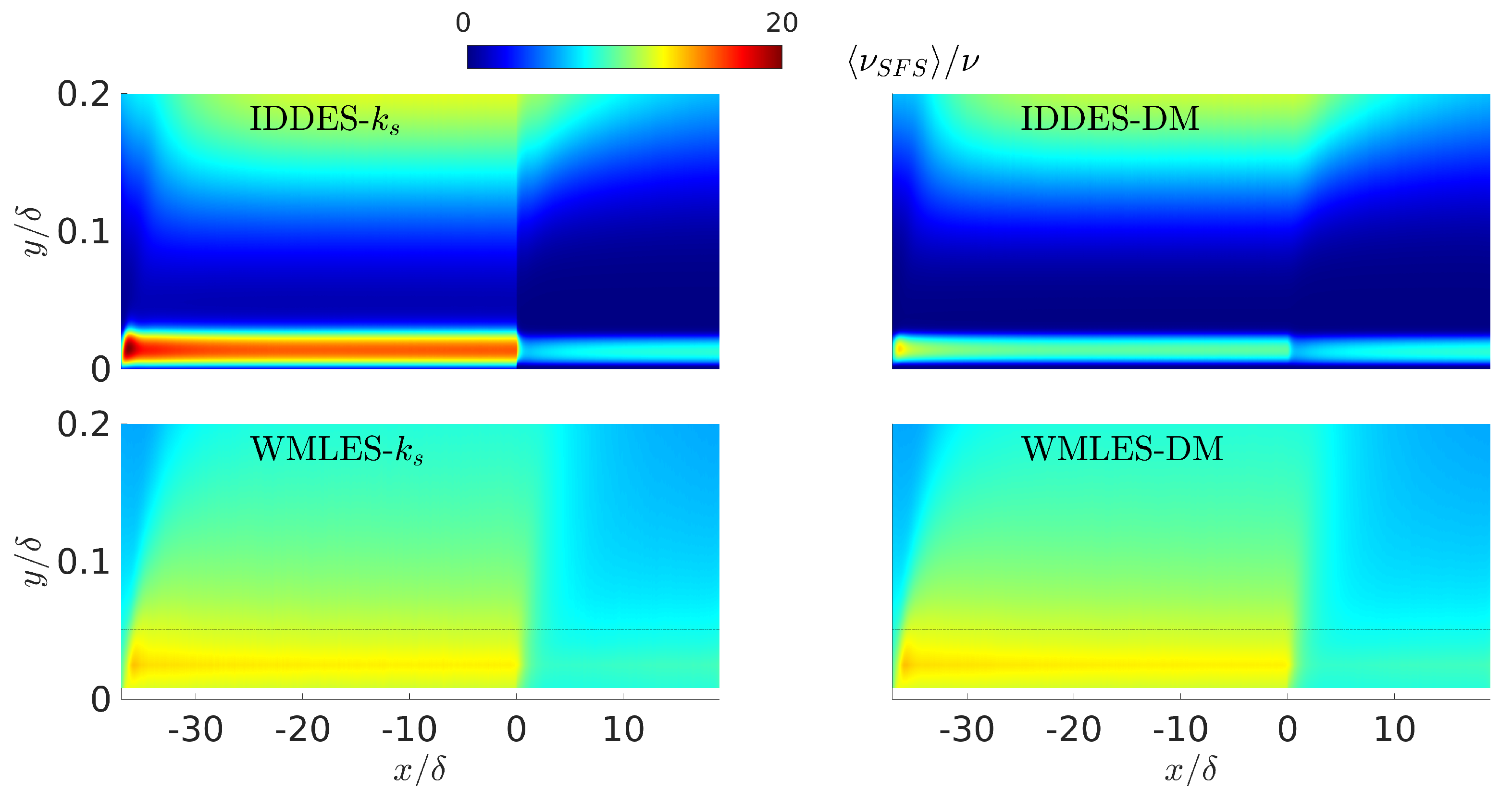
3.4. Eddy Viscosity and Reynolds Stresses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BC | boundary condition |
| DNS | direct numerical simulation |
| IDDES | improved delayed detached-eddy simulation |
| LES | large-eddy simulation |
| RANS | Reynolds-averaged Navier–Stokes |
| SA | Spalart–Allmaras |
| SFS | subfilter scale |
| WMLES | wall-modeled large-eddy simulation |
| WRLES | wall-resolved large-eddy simulation |
References
- Nikuradse, J. Strömungsgesetze in Rauhen Rohren. VDI-Forschungsheft 1933, 361, 1–64. [Google Scholar]
- Raupach, M.R.; Antonia, R.A.; Rajagopalan, S. Rough-wall boundary layers. Appl. Mech. Rev. 1991, 44, 1–25. [Google Scholar] [CrossRef]
- Jiménez, J. Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 2004, 36, 173–196. [Google Scholar] [CrossRef]
- Colebrook, C.F. Turbulent flow in pipes, with particular reference to the transition region between smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Shafi, H.S.; Antonia, R.A. Anisotropy of the Reynolds stresses in a turbulent boundary layer on a rough wall. Exp. Fluids 1995, 18, 213–215. [Google Scholar] [CrossRef]
- Finnigan, J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Cheng, H.; Castro, I.P. Near-wall flow development after a step change in surface roughness. Bound. Layer Meteorol. 2002, 105, 411–432. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Porté-Agel, F. Velocity and surface shear stress distributions behind a rough-to-smooth surface transition: A simple new model. Bound. Layer Meteorol. 2009, 130, 29–41. [Google Scholar] [CrossRef]
- Garratt, J.R. The internal boundary layer—A review. Bound. Layer Meteorol. 1990, 50, 171–203. [Google Scholar] [CrossRef]
- Bradley, E.F. A micrometeorological study of velocity profiles and surface drag in the region modified by a change in surface roughness. Q. J. R. Meteorol. Soc. 1968, 94, 361–379. [Google Scholar] [CrossRef]
- Antonia, R.A.; Luxton, R.E. The response of a turbulent boundary layer to a step change in surface roughness. Part 1. Smooth to rough. J. Fluid Mech. 1971, 48, 721–761. [Google Scholar] [CrossRef]
- Antonia, R.A.; Luxton, R.E. The response of a turbulent boundary layer to a step change in surface roughness. Part 2. Rough to smooth. J. Fluid Mech. 1972, 53, 737–757. [Google Scholar] [CrossRef]
- Hanson, R.E.; Ganapathisubramani, B. Development of turbulent boundary layers past a step change in wall roughness. J. Fluid Mech. 2016, 795, 494–523. [Google Scholar] [CrossRef]
- Li, M.; de Silva, C.M.; Rouhi, A.; Baidya, R.; Chung, D.; Marusic, I.; Hutchins, N. Recovery of wall-shear stress to equilibrium flow conditions after a rough-to-smooth step change in turbulent boundary layers. J. Fluid Mech. 2019, 872, 472–491. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; Meneveau, C.; Parlange, M.B. Large-eddy simulation of neutral atmospheric boundary layer flow over heterogeneous surfaces: Blending height and effective surface roughness. Water Resour. Res. 2004, 40, W02505. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. A new boundary condition for large-eddy simulation of boundary-layer flow over surface roughness transitions. J. Turbul. 2012, 13, N23. [Google Scholar] [CrossRef]
- Saito, N.; Pullin, D.I. Large eddy simulation of smooth–rough–smooth transitions in turbulent channel flows. Int. J. Heat Mass Trans. 2014, 78, 707–720. [Google Scholar] [CrossRef]
- Ismail, U.; Zaki, T.A.; Durbin, P.A. The effect of cube-roughened walls on the response of rough-to-smooth (RTS) turbulent channel flows. Int. J. Heat Fluid Flow 2018, 72, 174–185. [Google Scholar] [CrossRef]
- Ismail, U.; Zaki, T.A.; Durbin, P.A. Simulations of rib-roughened rough-to-smooth turbulent channel flows. J. Fluid Mech. 2018, 843, 419–449. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Hellsten, A.; Laine, S. Extension of the k-omega-SST turbulence model for flows over rough surfaces. In Proceedings of the 22nd AIAA Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–13 August 1997. [Google Scholar]
- Knopp, T.; Eisfeld, B.; Calvo, J.B. A new extension for k-ω turbulence models to account for wall roughness. Int. J. Heat Fluid Flow 2009, 30, 54–65. [Google Scholar] [CrossRef]
- Aupoix, B.; Spalart, P.R. Extensions of the Spalart–Allmaras turbulence model to account for wall roughness. Int. J. Heat Fluid Flow 2003, 24, 454–462. [Google Scholar] [CrossRef]
- Aupoix, B. Roughness corrections for the k-ω shear stress transport model: Status and proposals. ASME J. Fluids Eng. 2015, 137, 021202. [Google Scholar] [CrossRef]
- Dutta, R.; Nicolle, J.; Giroux, A.M.; Piomelli, U. Evaluation of turbulence models in rough-wall boundary layers for hydroelectric application. Int. J. Fluid Mach. Sys. 2017, 10, 228–239. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Piomelli, U. Wall-layer models for large-eddy simulations. Prog. Aerosp. Sci. 2008, 44, 437–446. [Google Scholar] [CrossRef]
- Larsson, J.; Kawai, S.; Bodart, J.; Bermejo-Moreno, I. Large eddy simulation with modeled wall-stress: Recent progress and future directions. Mech. Eng. Rev. 2016, 3, 1–23. [Google Scholar] [CrossRef]
- Bose, S.T.; Park, G.I. Wall-modeled large-eddy simulation for complex turbulent flows. Annu. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Heinz, S. A review of hybrid RANS-LES methods for turbulent flows: Concepts and applications. Prog. Aerosp. Sci. 2020, 114, 100597. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; Parlange, M.B.; Meneveau, C. On the parameterization of surface roughness at regional scales. J. Atmos. Sci. 2007, 64, 216–227. [Google Scholar] [CrossRef]
- Varghese, J.; Durbin, P.A. Representing surface roughness in eddy resolving simulation. J. Fluid Mech. 2020, 897, A10. [Google Scholar] [CrossRef]
- Vreman, A.W. An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications. Phys. Fluids 2004, 16, 3670–3681. [Google Scholar] [CrossRef]
- Travin, A.K.; Shur, M.L.; Spalart, P.R.; Strelets, M.K. Improvement of delayed detached-eddy simulation for LES with wall modelling. In Proceedings of the European Conference on Computational Fluid Dynamics ECCOMAS CFD 2006, Bergen, The Netherlands, 5–8 September 2006; Wesseling, P., Oñate, E., Pèriaux, J., Eds.; TU Delft: Delft, The Netherlands, 2006; pp. 410–432. [Google Scholar]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. Rech. Aerosp. 1994, 1, 5–21. [Google Scholar]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS/LES model with delayed DES and wall-modeled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Schumann, U. Subgrid-scale model for finite difference simulation of turbulent flows in plane channels and annuli. J. Comput. Phys. 1975, 18, 376–404. [Google Scholar] [CrossRef]
- Kawai, S.; Larsson, J. Wall-modeling in large eddy simulation: Length scales, grid resolution, and accuracy. Phys. Fluids 2012, 24, 015105. [Google Scholar] [CrossRef]
- Fowler, M.; Zaki, T.A.; Meneveau, C. A Lagrangian relaxation towards equilibrium wall model for large eddy simulation. J. Fluid Mech. 2022, 934, 1–37. [Google Scholar] [CrossRef]



| Resolution | Grid Points | 1 | 1 | |
|---|---|---|---|---|
| Coarse | 0.055 | 400 | 279 | |
| Medium | 0.031 | 219 | 155 | |
| Fine | 0.025 | 175 | 124 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salomone, T.; Piomelli, U.; De Stefano, G. Wall-Modeled and Hybrid Large-Eddy Simulations of the Flow over Roughness Strips. Fluids 2023, 8, 10. https://doi.org/10.3390/fluids8010010
Salomone T, Piomelli U, De Stefano G. Wall-Modeled and Hybrid Large-Eddy Simulations of the Flow over Roughness Strips. Fluids. 2023; 8(1):10. https://doi.org/10.3390/fluids8010010
Chicago/Turabian StyleSalomone, Teresa, Ugo Piomelli, and Giuliano De Stefano. 2023. "Wall-Modeled and Hybrid Large-Eddy Simulations of the Flow over Roughness Strips" Fluids 8, no. 1: 10. https://doi.org/10.3390/fluids8010010
APA StyleSalomone, T., Piomelli, U., & De Stefano, G. (2023). Wall-Modeled and Hybrid Large-Eddy Simulations of the Flow over Roughness Strips. Fluids, 8(1), 10. https://doi.org/10.3390/fluids8010010







