Study on the Sensitivity of the Streamwise Location of MVG on SWBLI in MVG-Based Supersonic Flow Control
Abstract
1. Introduction
2. Numerical Methods
3. Case Setup
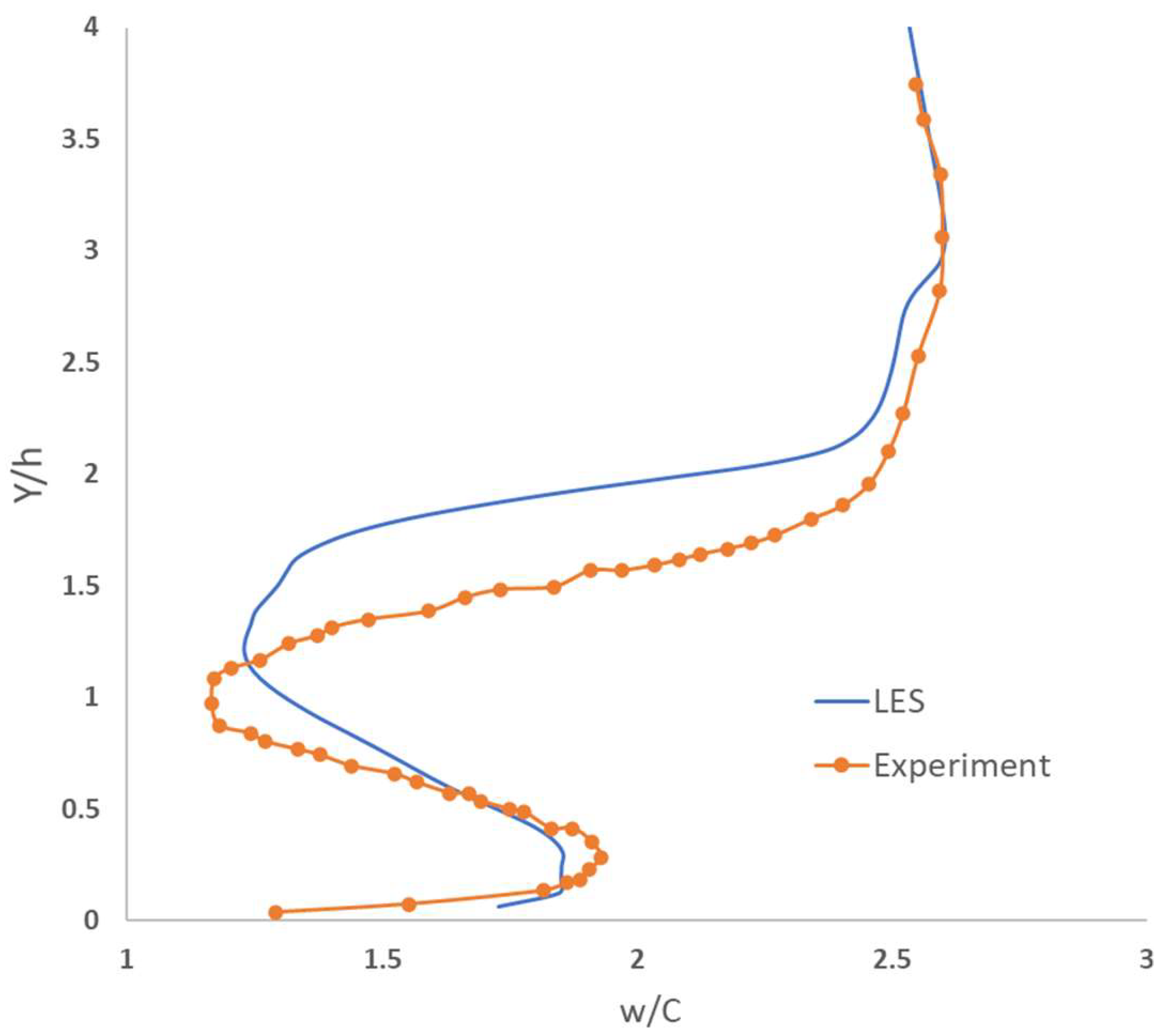
4. Numerical Results and Discussion
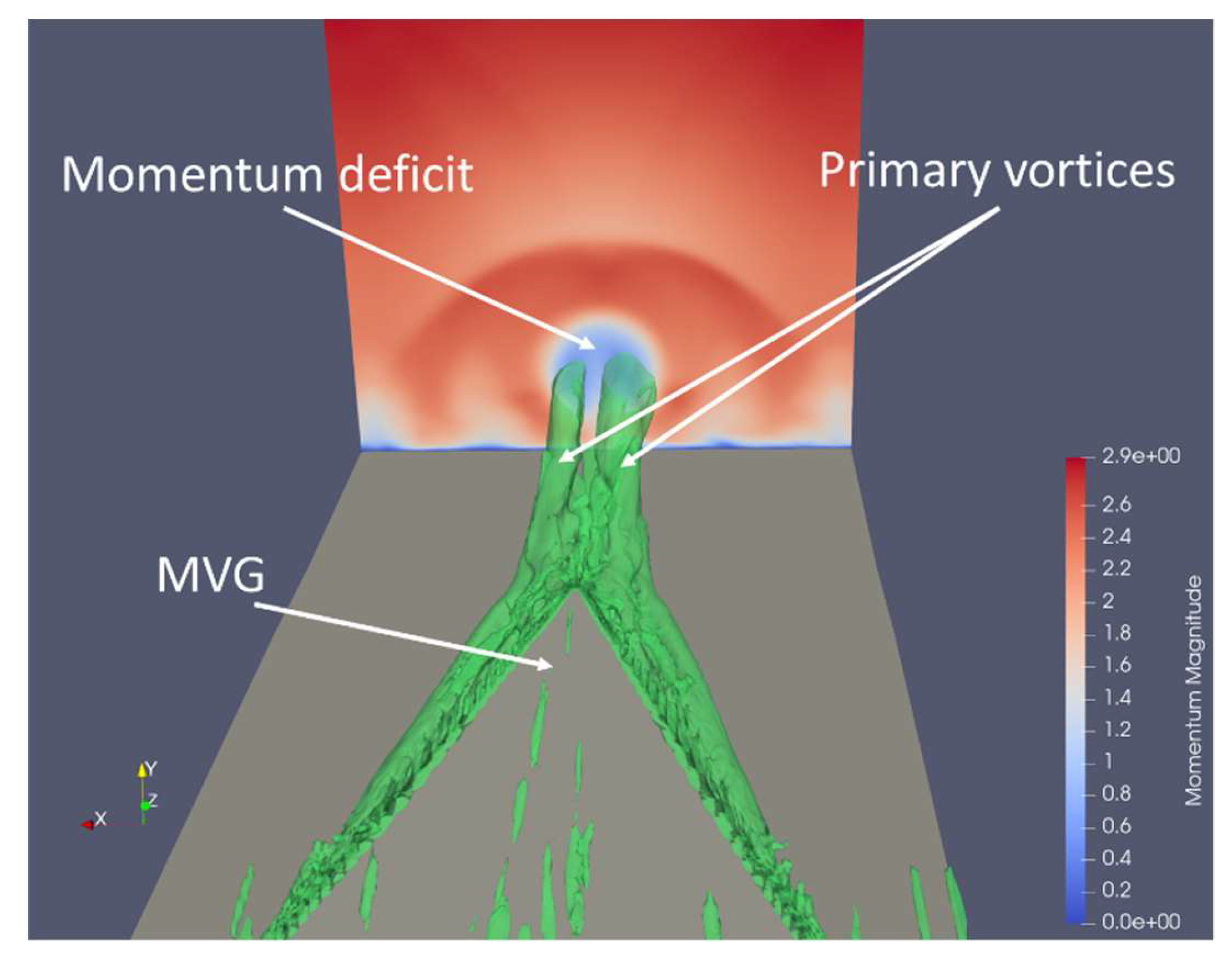
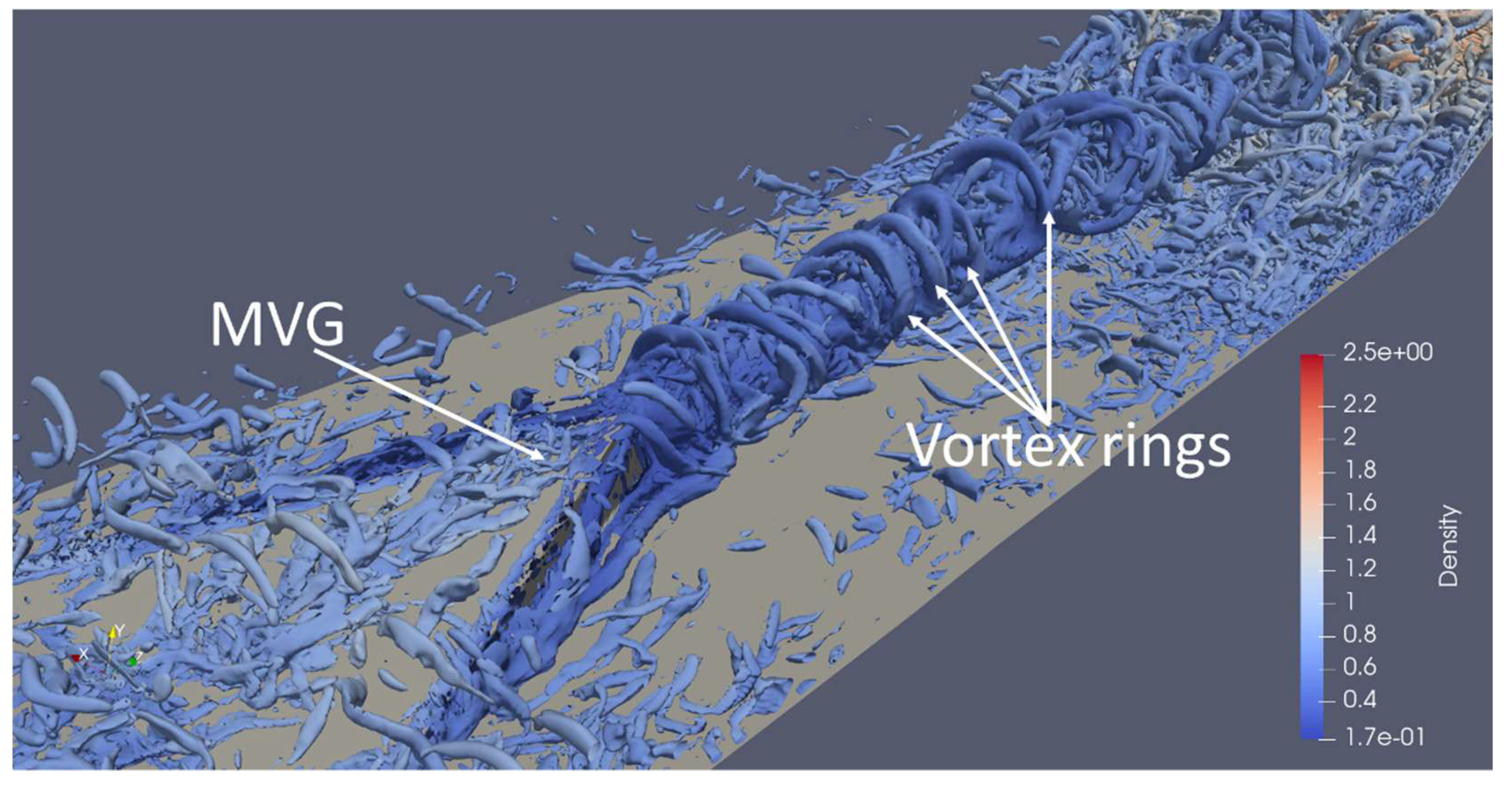
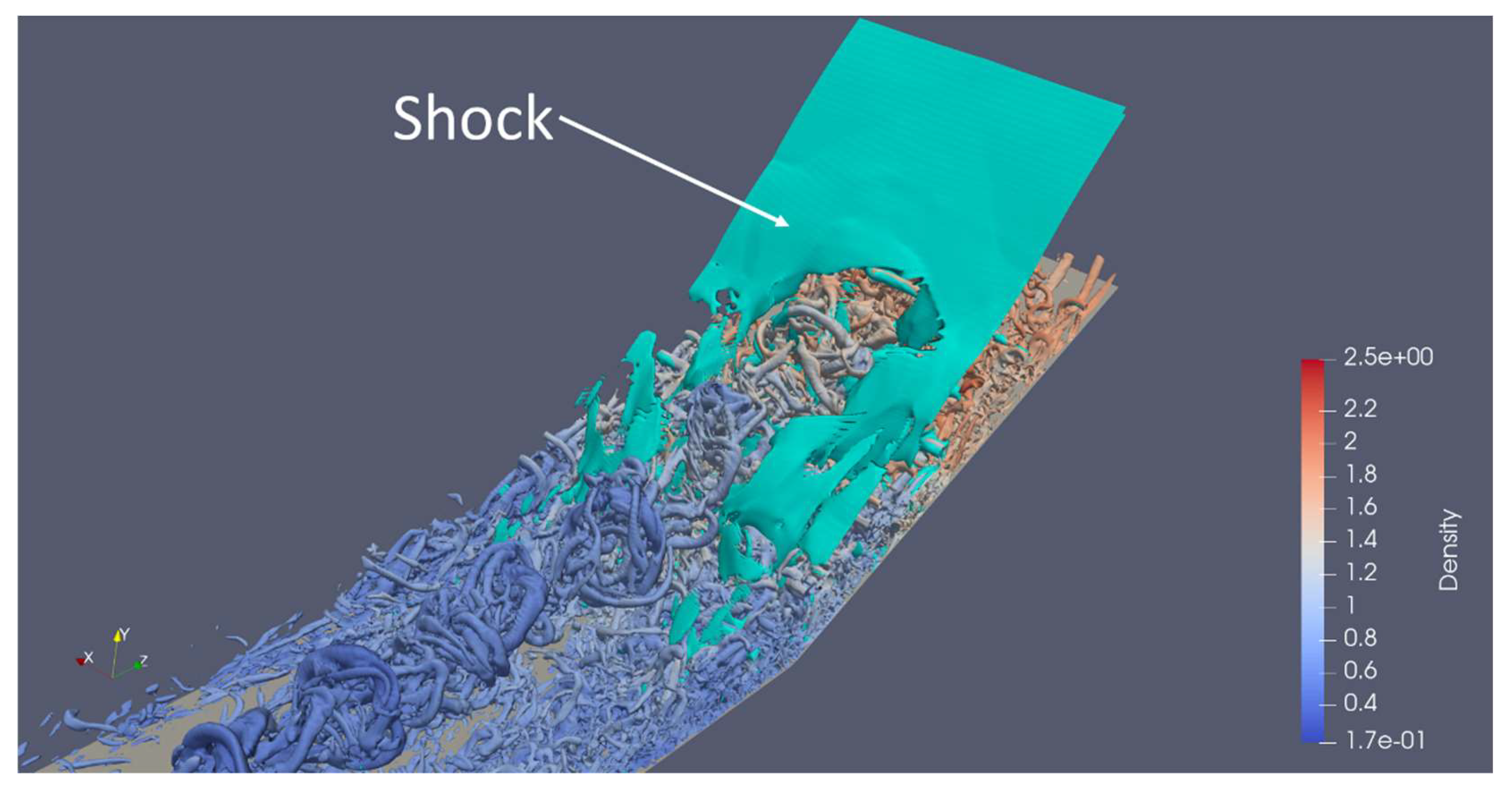
4.1. Revisit the Mechanism How MVG Reduce the Flow Separation
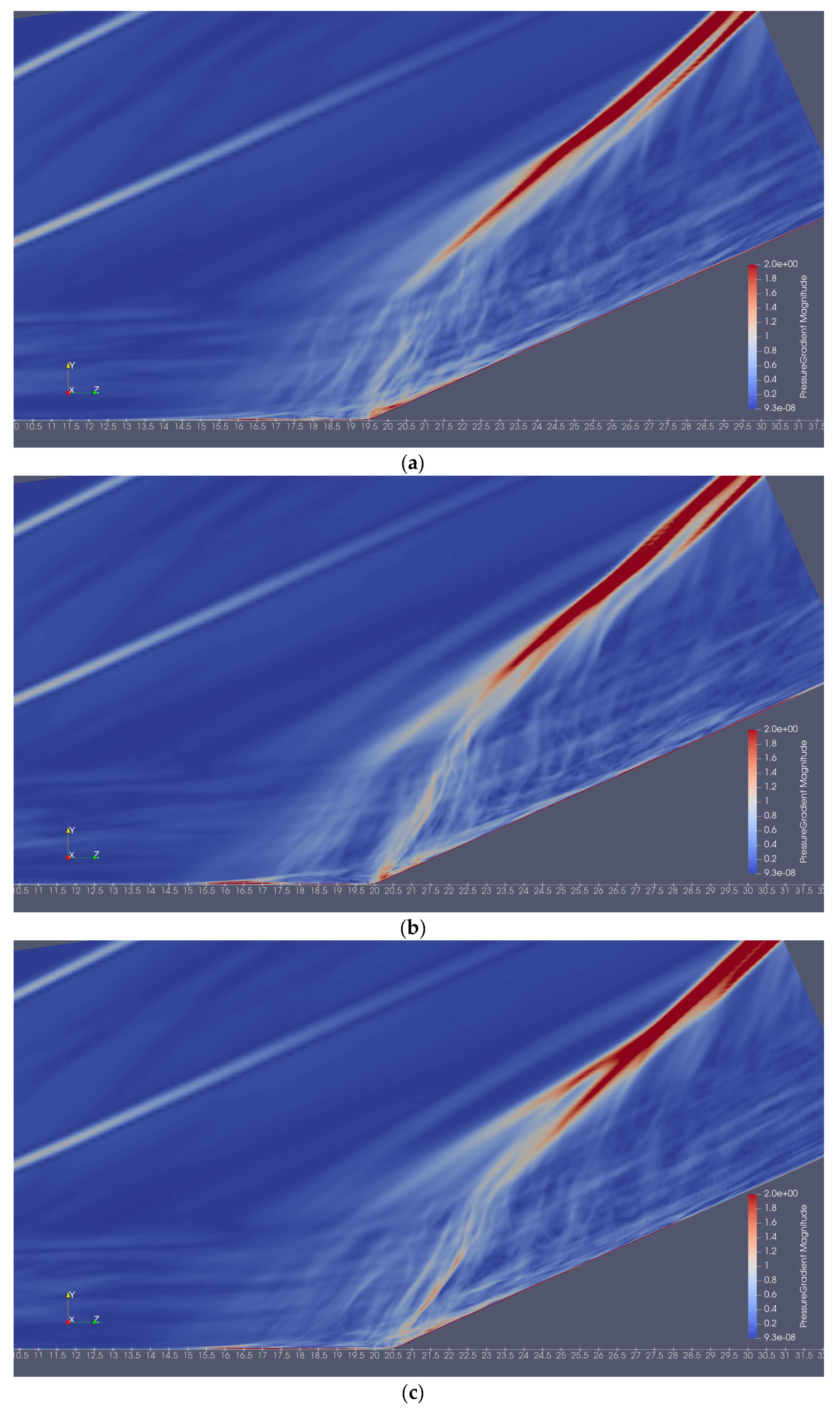
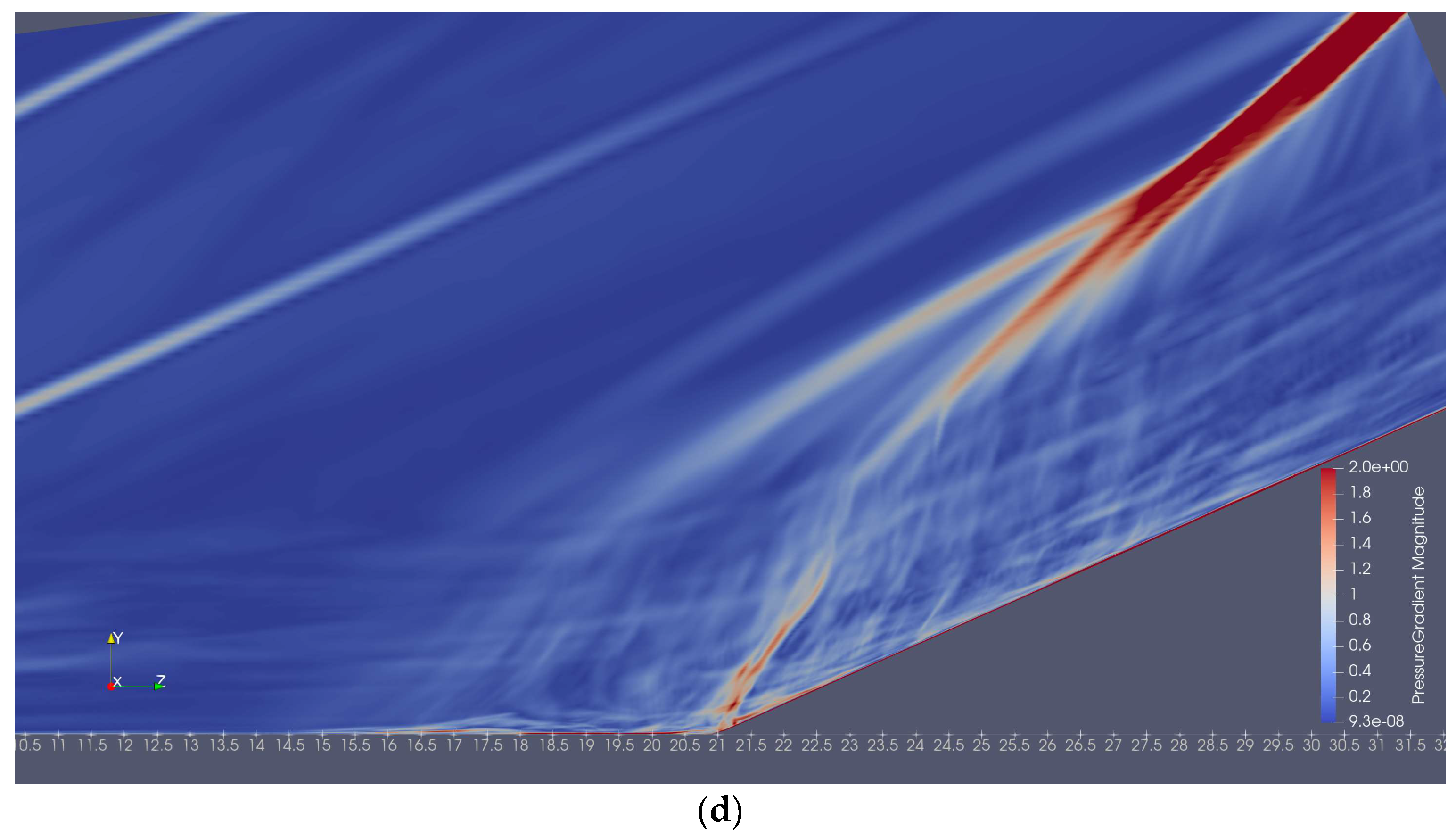
4.2. Impact of the Minor Changes of Distance between MVG and Ramp Corner on SWBLI Separation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| MVG | Micro vortex generator |
| SWBLI | Shock wave-boundary layer interaction |
| DNS | Direct numerical simulation |
| LES | Large eddy simulation |
| RANS | Reynolds-averaged Navier–Stokes |
| PIV | Particle Image Velocimetry |
| Density of the fluids | |
| Velocity vector | |
| Total energy | |
| Internal shear stress | |
| Internal energy per unit mass | |
| Pressure | |
| Temperature | |
| Thermal conductivity | |
| Dynamic viscosity | |
| Gas constant | |
| Specific heat capacity | |
| Ma | Mach |
| Reynolds number based on momentum thickness | |
| Micro ramp height | |
| Incompressible boundary layer nominal thickness | |
| Distance between apex of MVG and ramp corner | |
| Characteristics time | |
| Sound speed | |
| Frequency | |
| Strouhal number | |
| Spanwise, normal and streamwise coordinate axes | |
| Spanwise, normal and streamwise velocity | |
| Subscript | |
| w | wall |
| free stream | |
References
- Ashill, P.R.; Fulker, J.L.; Hackett, K.C. A review of recent developments in flow control. Aeronaut. J. 2005, 109, 205–232. [Google Scholar] [CrossRef]
- Lin, J.C. Review of research on low-profile vortex generators to control boundary-layer separation. Prog. Aerosp. Sci. 2002, 38, 389–420. [Google Scholar] [CrossRef]
- Anderson, B.; Tinapple, J.; Surber, L. Optimal Control of Shock Wave Turbulent Boundary Layer Interactions Using Micro-Array Actuation. In Proceedings of the 3rd AIAA Flow Control Conference, American Institute of Aeronautics and Astronautics, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Babinsky, H.; Li, Y.; Pitt Ford, C.W. Microramp Control of Supersonic Oblique Shock-Wave/Boundary-Layer Interactions. AIAA J. 2009, 47, 668–675. [Google Scholar] [CrossRef]
- Sun, Z.; Scarano, F.; van Oudheusden, B.W.; Schrijer, F.F.J.; Yan, Y.; Liu, C. Numerical and Experimental Investigations of the Supersonic Microramp Wake. AIAA J. 2014, 52, 1518–1527. [Google Scholar] [CrossRef][Green Version]
- Syahin, A.A.T.; Zinnyrah, M.; Azfar, N.A.; Said, I.; Idris, A.C.; Rahman, M.R.A.; Saad, M.R. Effect of micro-ramp vortex generator in improving aerodynamics performance of wing-in-gound craft fuselage. PERINTIS Ejournal 2021, 11, 61–69. [Google Scholar]
- Rizzetta, D.P.; Visbal, M.R. Application of Large-Eddy Simulation to Supersonic Compression Ramps. AIAA J. 2002, 40, 1574–1581. [Google Scholar] [CrossRef]
- Kaenel, R.V.; Kleiser, L.; Adams, N.A.; Vos, J.B. Large-Eddy Simulation of Shock-Turbulence Interaction. AIAA J. 2004, 42, 2516–2528. [Google Scholar] [CrossRef]
- Ghosh, S.; Choi, J.-I.; Edwards, J.R. Numerical Simulations of Effects of Micro Vortex Generators Using Immersed-Boundary Methods. AIAA J. 2010, 48, 92–103. [Google Scholar] [CrossRef]
- Lee, S.; Loth, E. Supersonic Boundary Layer Interactions with Various Micro-Vortex Generator Geometries. Aeronaut. J. 2009, 113, 683–697. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, Q.; Xiang, X.; Xu, J. An improved micro-vortex generator in supersonic flows. Aerosp. Sci. Technol. 2015, 47, 210–215. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, Y.; Liu, C. ILES for mechanism of ramp-type MVG reducing shock induced flow separation. Sci. China Phys. Mech. Astron. 2016, 59, 124711. [Google Scholar] [CrossRef]
- Yan, Y.; Chen, L.; Li, Q.; Liu, C. Numerical study of micro-ramp vortex generator for supersonic ramp flow control at Mach 2.5. Shock. Waves 2017, 27, 79–96. [Google Scholar] [CrossRef]
- Yan, Y.; Yang, Y.; Chen, C.; Cotton, H.A.; Serrano, A. Numerical study on the ring-like vortex structure generated by MVG in high-speed flows with different Mach numbers. Jpn. J. Indust. Appl. Math. 2022, 39, 3–18. [Google Scholar] [CrossRef]
- Martín, M.P.; Taylor, E.M.; Wu, M.; Weirs, V.G. A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence. J. Comput. Phys. 2006, 220, 270–289. [Google Scholar] [CrossRef]
- Yan, Y.; Tang, J.; Liu, C.; Yang, F. DNS study on the formation of Lambda rotational core and the role of TS wave in boundary layer transition. J. Turbul. 2016, 17, 572–601. [Google Scholar] [CrossRef]
- Jiang, G.-S.; Shu, C.-W. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- LarKermani, E.; Roohi, E.; Porté-Agel, F. Evaluating the modulated gradient model in large eddy simulation of channel flow with OpenFOAM. J. Turbul. 2018, 19, 600–620. [Google Scholar] [CrossRef]
- Zahiri, A.-P.; Roohi, E. Anisotropic minimum-dissipation (AMD) subgrid-scale model implemented in OpenFOAM: Verification and assessment in single-phase and multi-phase flows. Comput. Fluids 2019, 180, 190–205. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.; Tian, S.; Dong, X. Rortex—A new vortex vector definition and vorticity tensor and vector decompositions. Phys. Fluids 2018, 30, 035103. [Google Scholar] [CrossRef]
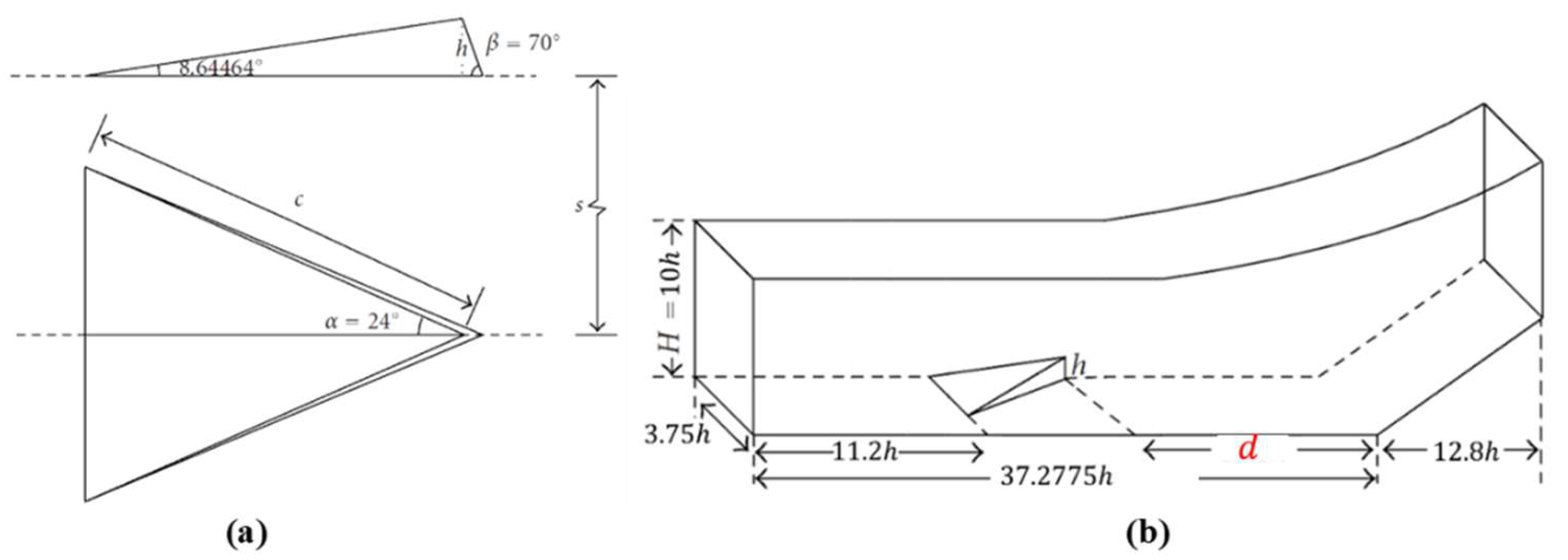


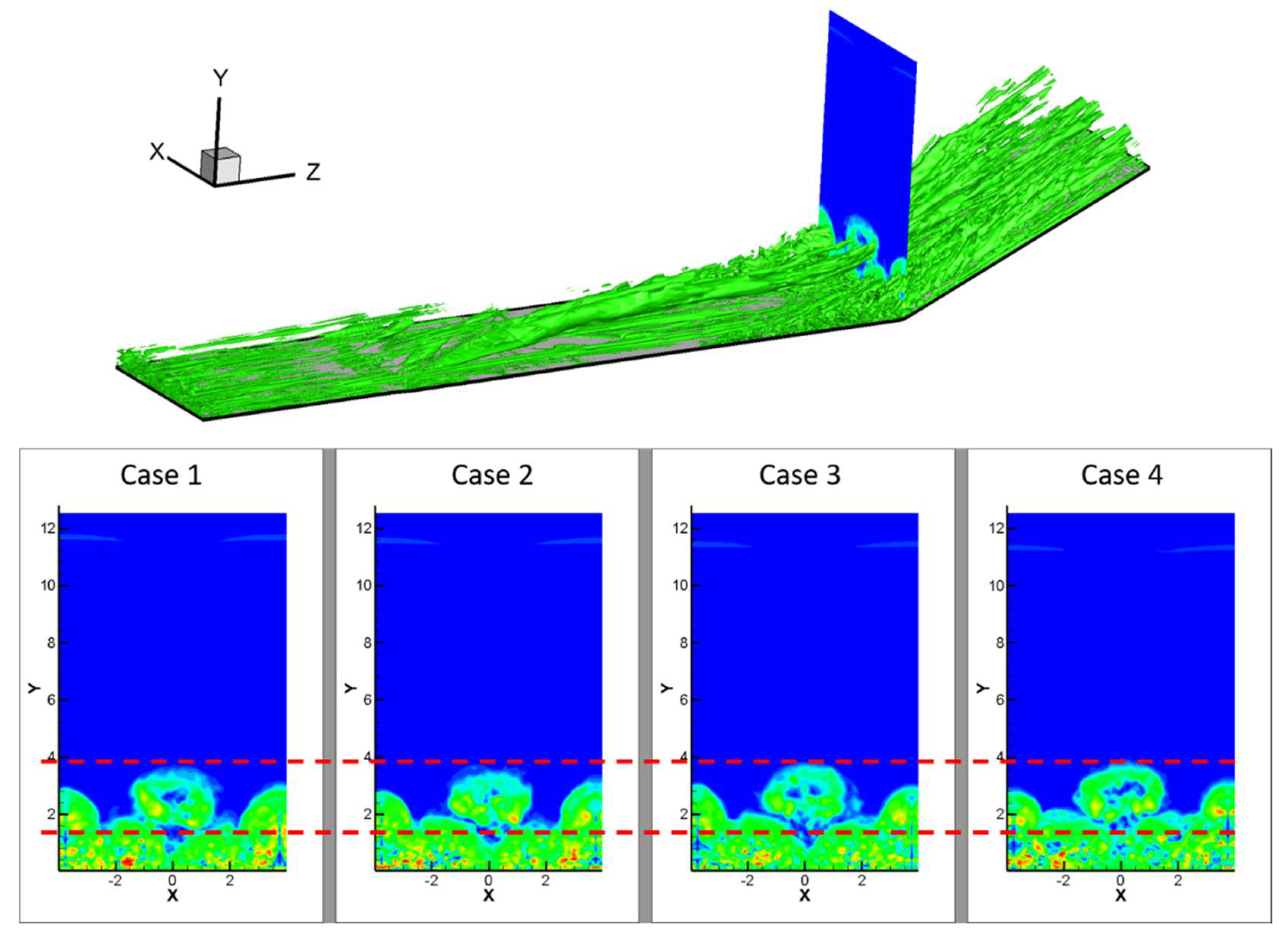

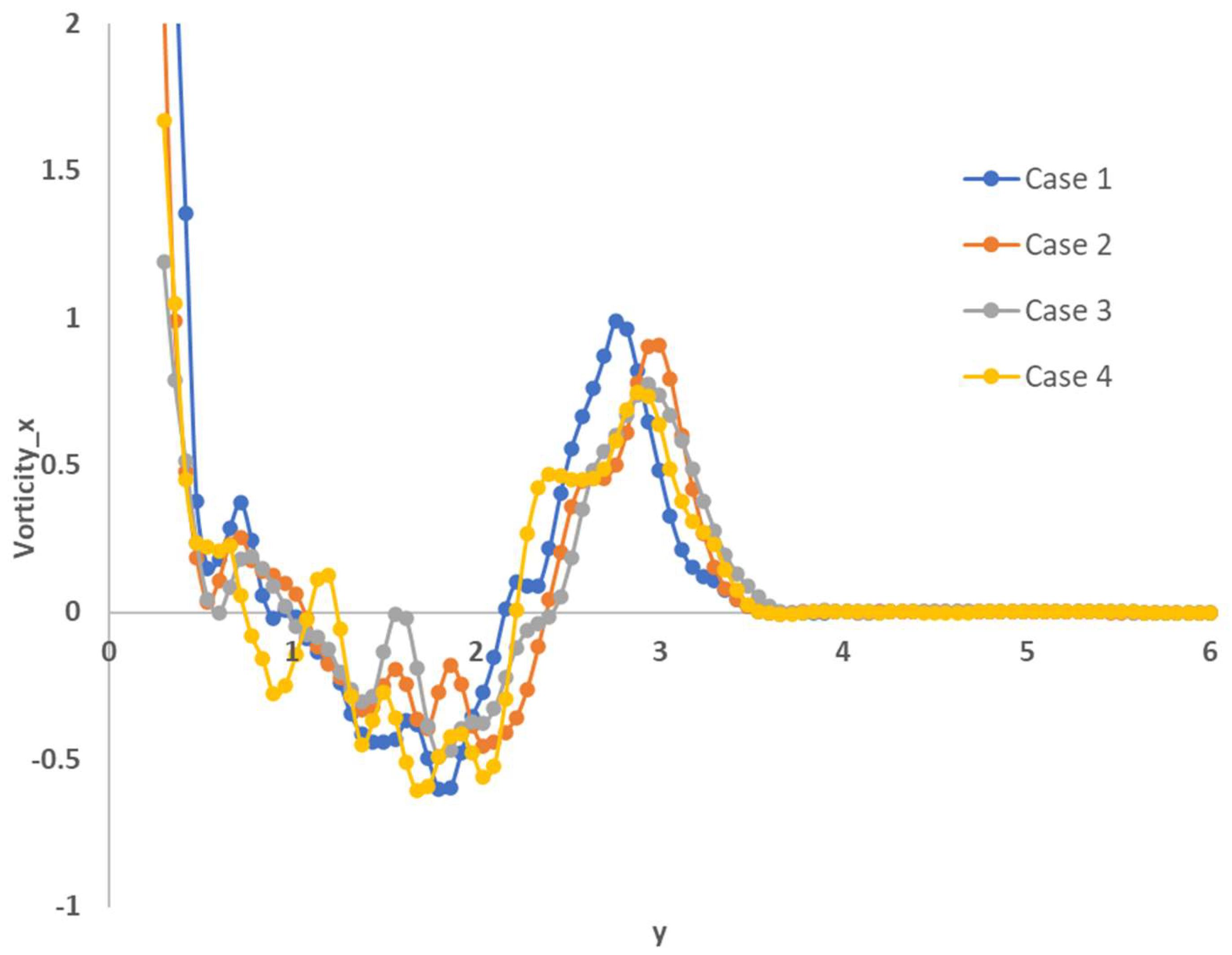



| Case | ||||||||
| 1 | 2.5 | 5760 | 288.15 K | 300 K | 4 mm | 340 m/s | s | |
| 2 | ||||||||
| 3 | ||||||||
| 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Baines, D.L.; Yang, Y.; Chen, C.; Kwembe, T.A. Study on the Sensitivity of the Streamwise Location of MVG on SWBLI in MVG-Based Supersonic Flow Control. Fluids 2022, 7, 285. https://doi.org/10.3390/fluids7090285
Yan Y, Baines DL, Yang Y, Chen C, Kwembe TA. Study on the Sensitivity of the Streamwise Location of MVG on SWBLI in MVG-Based Supersonic Flow Control. Fluids. 2022; 7(9):285. https://doi.org/10.3390/fluids7090285
Chicago/Turabian StyleYan, Yonghua, Demetric L. Baines, Yong Yang, Caixia Chen, and Tor A. Kwembe. 2022. "Study on the Sensitivity of the Streamwise Location of MVG on SWBLI in MVG-Based Supersonic Flow Control" Fluids 7, no. 9: 285. https://doi.org/10.3390/fluids7090285
APA StyleYan, Y., Baines, D. L., Yang, Y., Chen, C., & Kwembe, T. A. (2022). Study on the Sensitivity of the Streamwise Location of MVG on SWBLI in MVG-Based Supersonic Flow Control. Fluids, 7(9), 285. https://doi.org/10.3390/fluids7090285









