Field Study of Three–Parameter Flow Resistance Model in Rivers with Vegetation Patch
Abstract
:1. Introduction
- Emadzadeh et al. (2010) and Fazlollahi et al. (2007) showed that the Von Kármán constant is less than 0.4 in the conditions of sediment transfer and more than 0.4 in the presence of the bed form; and in the absence of these cases, it is equal to 0.4. In this study, the value of 0.4 has been used [26,27]. Naderi et al. (2021) found a value of 0.4 for reaches with vegetation cover when there is no sediment transport, and the effect of bedforms is insignificant [28].
- Different researchers have found different values for ks; For example, Song and Chiew (2001) presented the value of and Alonso et al. (2009) presented the value of . The amount suggested by Alonso et al. (2009) has been used in this study [29,30]. In this study, to show the effect of larger particles on surface roughness in coarse rivers, ks = 2.4 d90 was considered.
- In coarse–bed rivers, there may be a flow between the coarse–grained particles and below the measured points; therefore, the flow has a velocity at zero depth and cannot be considered zero. Therefore, to solve this problem, a concept called hypothetical line is used. A hypothetical line is a line on which the velocity is zero. This line is defined as follows:
- The selected reaches have a direct path without the presence of obstacles such as boulders.
- The transfer of sediment from the bed is insignificant.
- The wind velocity in the area does not affect the velocity profiles.
- There is no flexibility in vegetation patches and deformation during data collection.
2. Materials and Methods
2.1. Reaches Location
2.2. Vegetation Patches in Selected Reaches
2.3. Measured Data
2.3.1. Velocity Measurement
2.3.2. Surveying Operations
2.3.3. Sampling of Bed Sediments
2.4. Calculation of Darcy–Weisbach Friction Factor
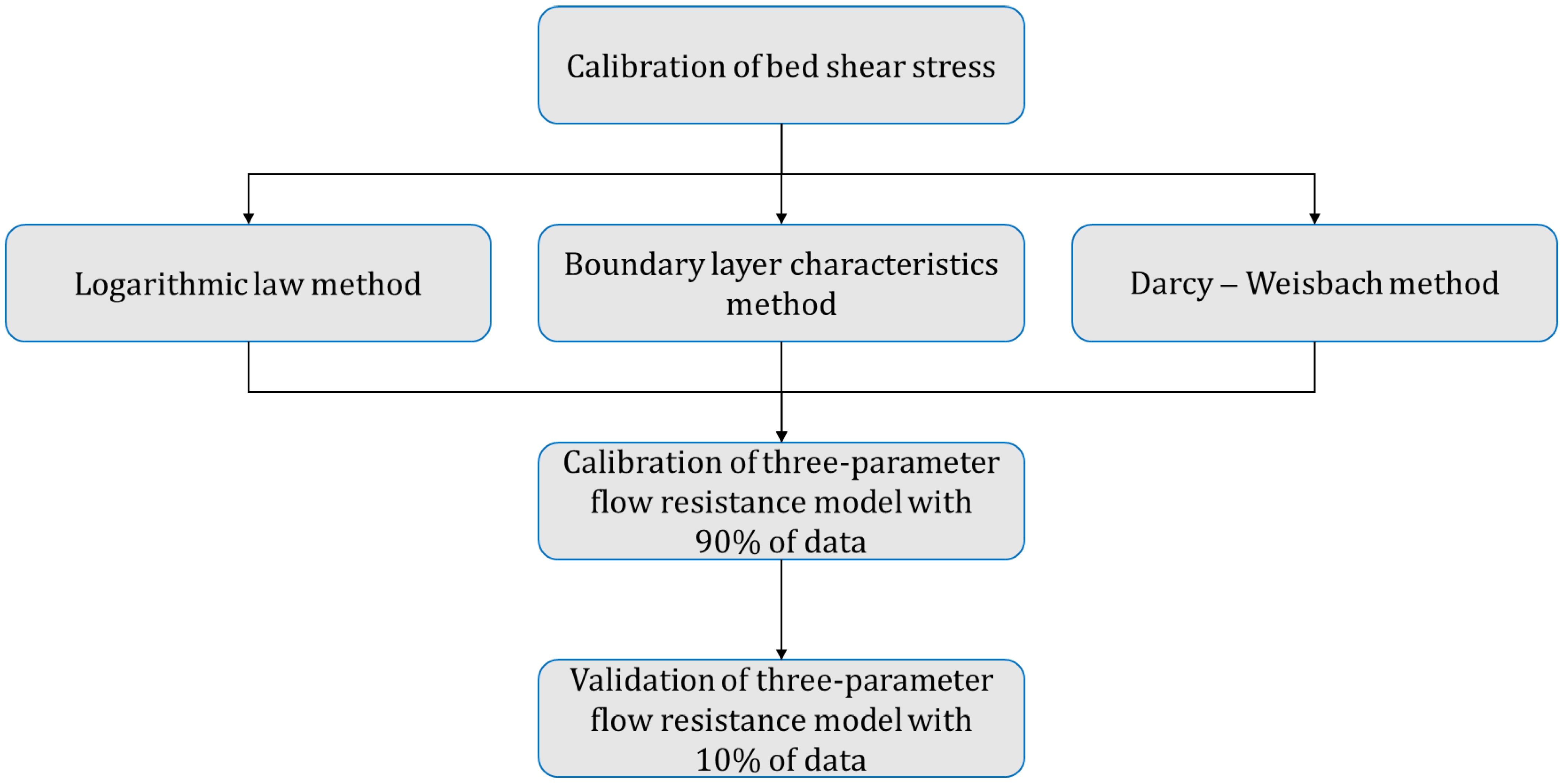
2.5. The General Framework of This Research
3. Results and Discussion
3.1. Sediment and Hydraulic Parameters
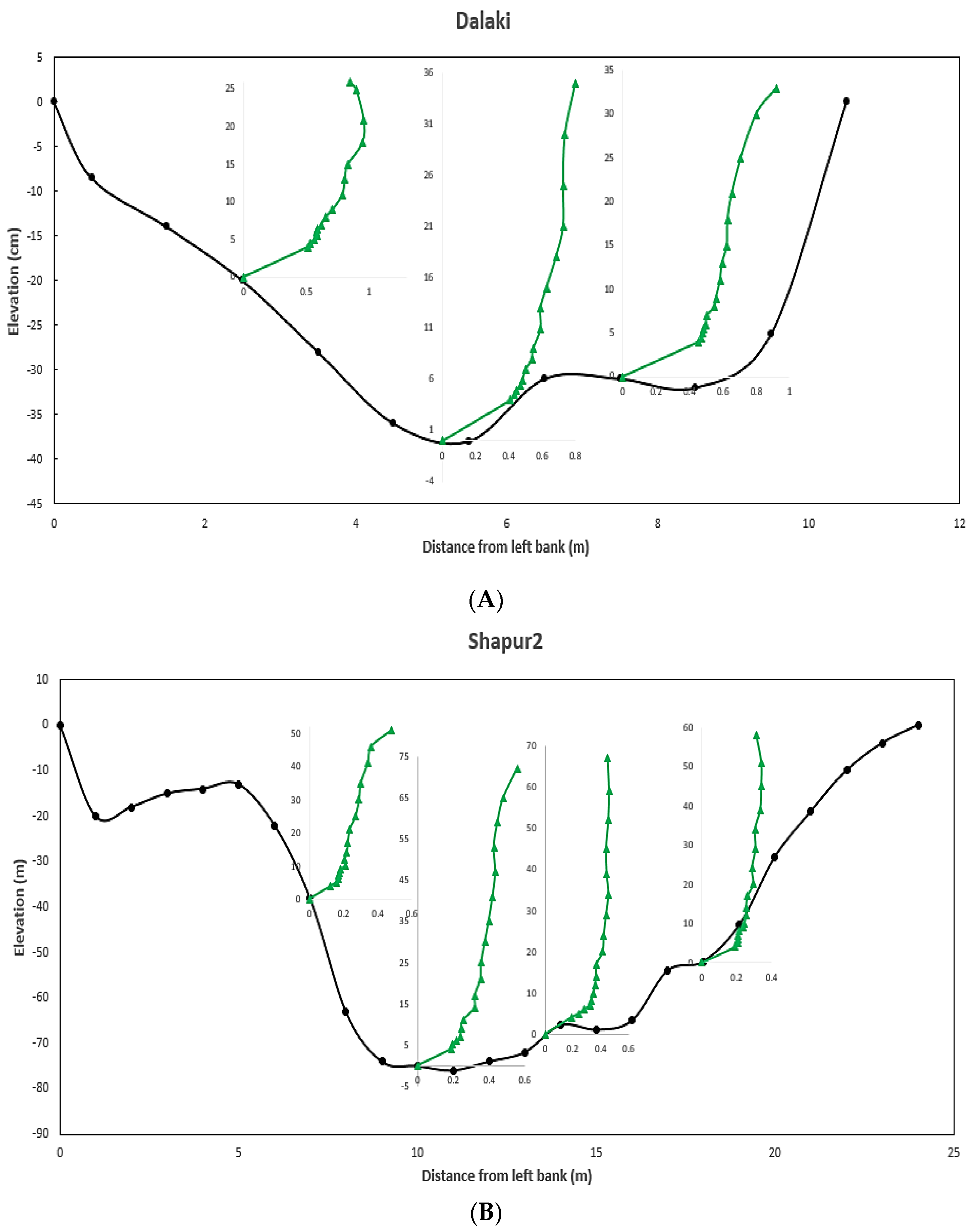
3.2. Velocity Profiles
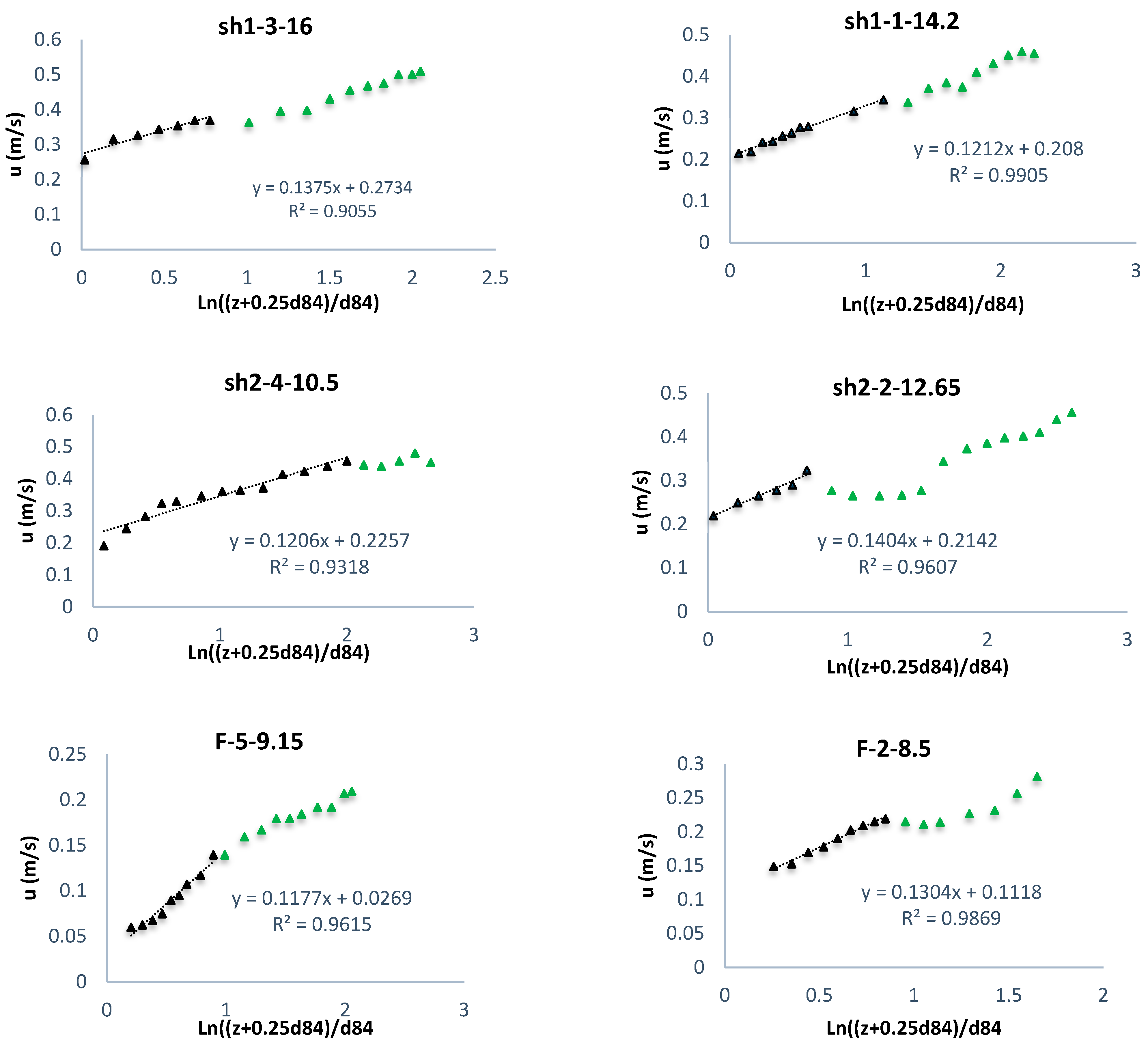
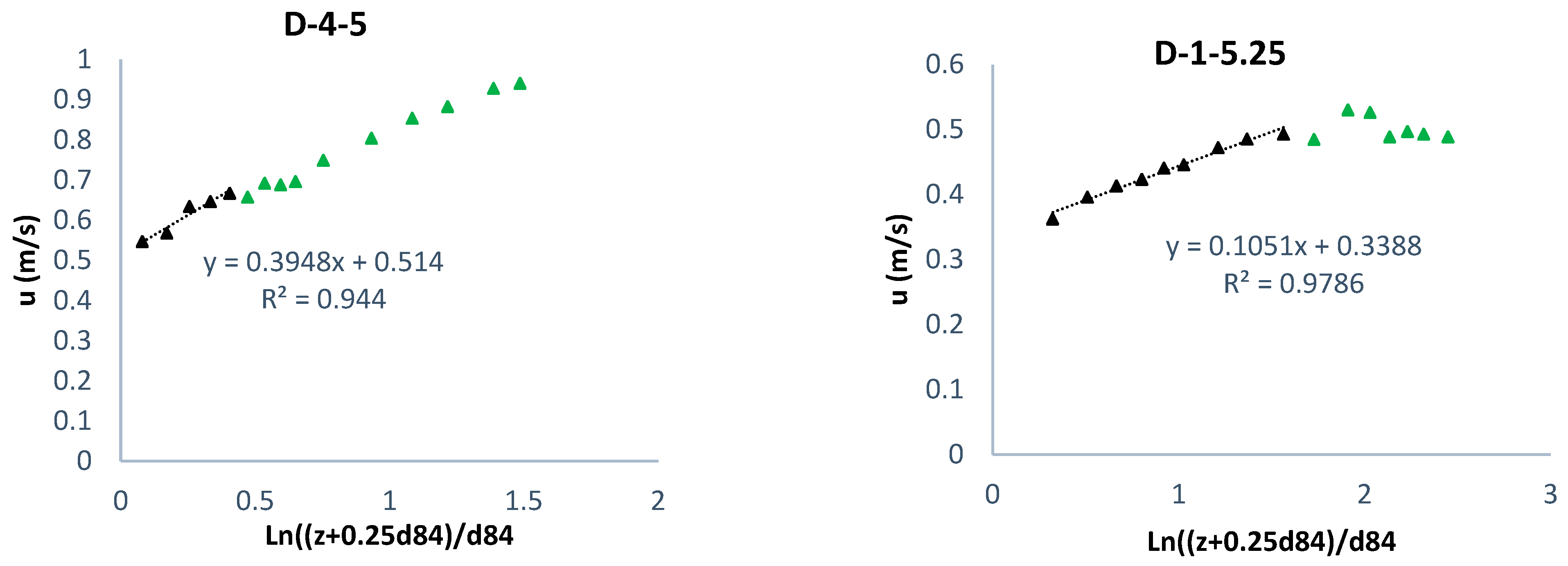
3.3. Validity of Logarithmic Law
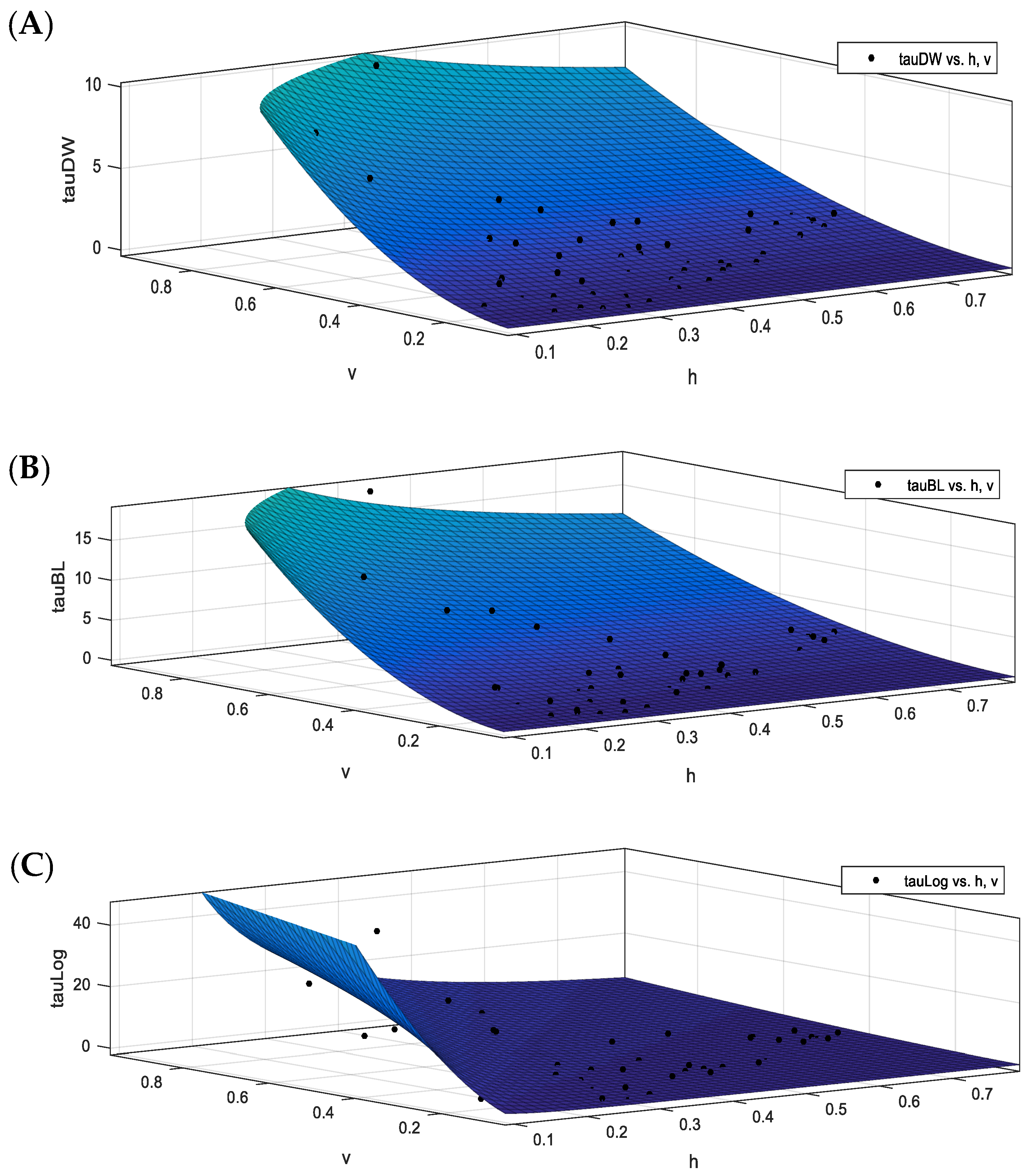
3.4. Calculation of Shear Velocity
- The logarithmic law method reveals the highest range of changes in estimating the shear velocity due to the sensitivity of this method to adjusting the reference level and using the velocity variation near the bed. However, the Darcy–Weisbach method shows the lowest range of changes in shear velocity estimation because it uses all data measured in a velocity profile.
- The boundary layer characteristics method is reliable in coarse–grained rivers for calculating shear velocity [23] because it considers all velocity data in each profile. It was found that the relative differences between the logarithmic law and Darcy–Weisbach methods compared to the boundary layer characteristics method are equal to 87% and 39%, respectively, which indicates more reasonable agreement between Darcy–Weisbach method and the boundary layer characteristics method.
3.5. Calibration of Three–Parameter Flow Resistance Model
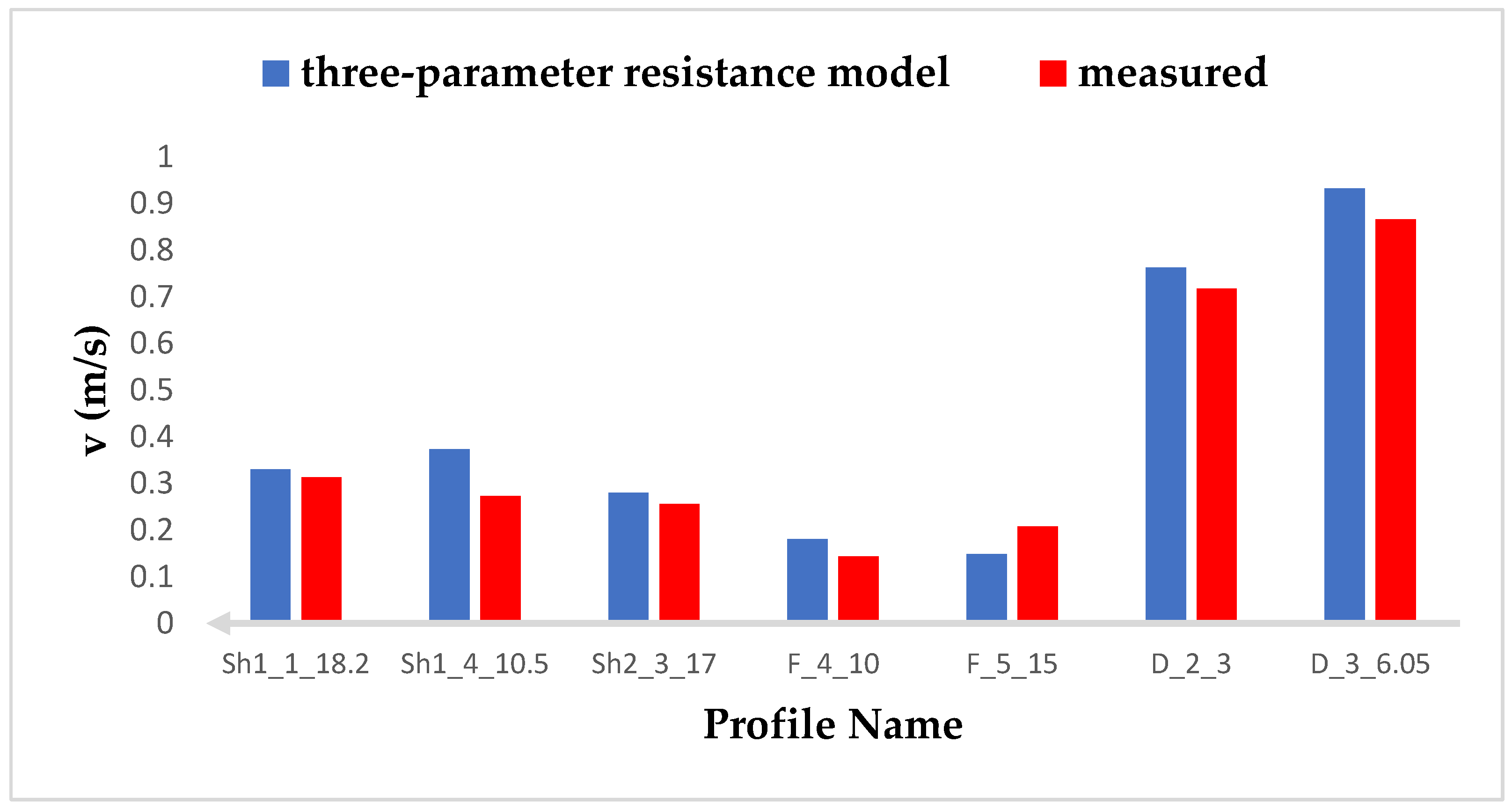
3.6. Validation of Three–Parameter Flow Resistance Model
- Difficulty working in the river with rough bed and non–uniform flow;
- Difficulty working with high–precision measuring instruments in field research;
- Not recognizing all the factors affecting error production;
- Assumptions and simplifications performed that generate errors.
4. Conclusions
- The three–parameter flow resistance model shows that the average error percentage of the model is 17%, indicating the accuracy of the model.
- The logarithmic law method has the highest range of changes in estimating the bed shear stress compared to the methods of Darcy–Weisbach and the boundary layer characteristics method. This is due to the sensitivity of the logarithmic law method to adjusting the reference surface and using the near bed data of the velocity profile. The Darcy–Weisbach method reveals the lowest range of changes.
- The relative difference percentages between the logarithmic law and the Darcy–Weisbach methods compared to the boundary layer characteristics method were equal to 87% and 39%, respectively. This indicated a more reasonable agreement between the Darcy–Weisbach method and the boundary layer characteristics method.
- By investigating 71 measured velocity profiles, it was found that the logarithmic law was well applicable in reaches with vegetation patches. A high coefficient of determination () in fitting the velocity profile data to the logarithmic law indicated their reasonable agreement with this law.
- The investigation of measured velocity profiles shows the occurrence of the Dip phenomenon in the velocity profiles near the vegetation patches. However, by moving away from the vegetation patches, the effect of this phenomenon is decreased, and the profiles illustrate an S–shaped distribution. The Dip location plays a significant role in the boundary layer thickness and estimation of key hydraulic parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Shi, F.-Y.; Chen, P.-P.; Wu, P.; Sui, J. Impact of bridge pier on the stability of ice jam. J. Hydrodyn. 2015, 27, 865–871. [Google Scholar] [CrossRef]
- Folkard, A.M. Vegetated flows in their environmental context: A review. Proc. Inst. Civ. Eng. Eng. Comput. Mech. 2011, 164, 3–24. [Google Scholar] [CrossRef]
- Marion, A.; Nikora, V.; Puijalon, S.; Bouma, T.; Koll, K.; Ballio, F.; Tait, S.; Zaramella, M.; Sukhodolov, A.; O’Hare, M. Aquatic interfaces: A hydrodynamic and ecological perspective. J. Hydraul. Res. 2014, 52, 744–758. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hayashi, K.; Hashimoto, H. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows. J. Hydraul. Res. 2009, 47, 691–699. [Google Scholar] [CrossRef]
- Palmer, M.R.; Nepf, H.M.; Pettersson, T.J.; Ackerman, J.D. Observations of particle capture on a cylindrical collector: Implications for particle accumulation and removal in aquatic systems. Limnol. Oceanogr. 2004, 49, 76–85. [Google Scholar] [CrossRef] [Green Version]
- López, F.; García, M. Open-channel flow through simulated vegetation: Suspended sediment transport modeling. Water Resour. Res. 1998, 34, 2341–2352. [Google Scholar] [CrossRef]
- Cotton, J.; Wharton, G.; Bass, J.; Heppell, C.; Wotton, R. The effects of seasonal changes to in-stream vegetation cover on patterns of flow and accumulation of sediment. Geomorphology 2006, 77, 320–334. [Google Scholar] [CrossRef]
- Setayesh, P.; Afzalimehr, H. Effect of Reedy Emergent Side-Vegetation in Gravel-Bed Streams on Bed Shear Stress: Patch Scale Analysis. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 46, 1375–1392. [Google Scholar] [CrossRef]
- Shahmohammadi, R.; Afzalimehr, H.; Sui, J. Impacts of turbulent flow over a channel bed with a vegetation patch on the incipient motion of sediment. Can. J. Civ. Eng. 2018, 45, 803–816. [Google Scholar] [CrossRef]
- Liu, X.-D.; Tang, L.-C.; Han, Y.; Chen, J.; Yang, S.-Q. Experimental study on flow resistance over rigid vegetated channel. IEEE Access 2019, 7, 93974–93985. [Google Scholar] [CrossRef]
- Kazem, M.; Afzalimehr, H.; Sui, J. Formation of Coherent Flow Structures beyond Vegetation Patches in Channel. Water 2021, 13, 2812. [Google Scholar] [CrossRef]
- Green, J.C. Comparison of blockage factors in modelling the resistance of channels containing submerged macrophytes. River Res. Appl. 2005, 21, 671–686. [Google Scholar] [CrossRef]
- Thoman, R.W.; Niezgoda, S.L. Determining erodibility, critical shear stress, and allowable discharge estimates for cohesive channels: Case study in the Powder River basin of Wyoming. J. Hydraul. Eng. 2008, 134, 1677–1687. [Google Scholar] [CrossRef]
- Box, W.; Järvelä, J.; Västilä, K. Flow resistance of floodplain vegetation mixtures for modelling river flows. J. Hydrol. 2021, 601, 126593. [Google Scholar] [CrossRef]
- Van Dijk, W.; Teske, R.; Van de Lageweg, W.; Kleinhans, M. Effects of vegetation distribution on experimental river channel dynamics. Water Resour. Res. 2013, 49, 7558–7574. [Google Scholar] [CrossRef] [Green Version]
- Shields, F.D.; Coulton, K.G.; Nepf, H. Representation of Vegetation in Two-Dimensional Hydrodynamic Models. J. Hydraul. Eng. 2017, 143, 8. [Google Scholar] [CrossRef] [Green Version]
- Nosrati, K.; Afzalimehr, H.; Sui, J. Drag Coefficient of Submerged Flexible Vegetation Patches in Gravel Bed Rivers. Water 2022, 14, 743. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Barahimi, M.; Sui, J. Non-uniform flow over cobble bed with submerged vegetation strip. Proc. Inst. Civ. Eng. Water Manag. 2019, 172, 86–101. [Google Scholar] [CrossRef] [Green Version]
- Ferguson, R. Time to abandon the Manning equation? Earth Surf. Processes Landf. 2010, 35, 1873–1876. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Levesque, B.; Molls, T.; Zhao, G.; Molls, F. Friction Slope in Depth-Averaged Flow. J. Hydraul. Eng. 1999, 125, 549. [Google Scholar] [CrossRef]
- Bellos, V.; Nalbantis, I.; Tsakiris, G. Friction modeling of flood flow simulations. J. Hydraul. Eng. 2018, 144, 04018073. [Google Scholar] [CrossRef] [Green Version]
- Afzalimehr, H.; Anctil, F. Accelerating shear velocity in gravel-bed channels. Hydrol. Sci. J. 2000, 45, 113–124. [Google Scholar] [CrossRef] [Green Version]
- Afzalimehr, H.; Rennie, C.D. Determination of bed shear stress in gravel-bed rivers using boundary-layer parameters. Hydrol. Sci. J. 2009, 54, 147–159. [Google Scholar] [CrossRef] [Green Version]
- Afzalimehr, H.; Maddahi, M.R.; Naziri, D.; Sui, J. Effects of non-submerged boulder on flow characteristics—A field investigation. Int. J. Sediment Res. 2019, 34, 136–143. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Maddahi, M.R.; Sui, J.; Rahimpour, M. Impacts of vegetation over bedforms on flow characteristics in gravel-bed rivers. J. Hydrodyn. 2019, 31, 986–998. [Google Scholar] [CrossRef]
- Emadzadeh, A.; Chiew, Y.M.; Afzalimehr, H. Effect of accelerating and decelerating flows on incipient motion in sand bed streams. Adv. Water Resour. 2010, 33, 1094–1104. [Google Scholar] [CrossRef]
- Fazlollahi, A.; Afzalimehr, H.; Haghighi, A.; Barati, R.; Neyshabouri, S.A.A.S.; Ahmadi, G.; Omidvar, P.; Kheirkhahan, M.; Hosseini, K.; Kabiri-Samani, A. 101. Validation of Spatially Averaging Method for Using the Law of the Wall over Concave Bed Form (pool). SMR 2007, 2, 27–42. [Google Scholar]
- Naderi, M.; Afzalimehr, H.; Sohrabi, S. Investigation of three-parameter flow resistance model in coarse-bed rivers (Case study: Deryuk River). Iran. J. Soil Water Res. 2021, 52, 1423–1435. [Google Scholar]
- Song, T.; Chiew, Y. Turbulence measurement in nonuniform open-channel flow using acoustic Doppler velocimeter (ADV). J. Eng. Mech. 2001, 127, 219–232. [Google Scholar] [CrossRef]
- Alonso, R.L.; Fernández, J.B.; Cugat, M.C. Flow resistance equations for mountain rivers. For. Syst. 2009, 18, 81–91. [Google Scholar]
- Brierley, G.J.; Fryirs, K.A. Geomorphology and River Management: Applications of the River Styles Framework; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wolman, M.G. A method of sampling coarse river-bed material. EOS Trans. Am. Geophys. Union 1954, 35, 951–956. [Google Scholar] [CrossRef]
- Okhravi, S.; Gohari, S. Form friction factor of armored riverbeds. Can. J. Civ. Eng. 2020, 47, 1238–1248. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Ramazany, R. Validation of Double-Averaged Velocity Method for Decelerating Flow in Coarse-Bed Rivers. J. Hydraul. 2019, 2, 47–67. [Google Scholar]
- Afzalimehr, H.; Subhasish, D. Influence of bank vegetation and gravel bed on velocity and Reynolds stress distributions. Int. J. Sediment Res. 2009, 24, 236–246. [Google Scholar] [CrossRef]
- Maddahi, M.R.; Afzalimehr, H.; Rowinski, P.M. Flow characteristics over a gravel bedform: Kaj River case study. Acta Geophys. 2016, 64, 1779–1796. [Google Scholar] [CrossRef] [Green Version]
- Houra, T.; Tsuji, T.; Nagano, Y. Effects of adverse pressure gradient on quasi-coherent structures in turbulent boundary layer. Int. J. Heat Fluid Flow 2000, 21, 304–311. [Google Scholar] [CrossRef]
- Wu, B.; Molinas, A.; Julien, P.Y. Bed-material load computations for nonuniform sediments. J. Hydraul. Eng. 2004, 130, 1002–1012. [Google Scholar] [CrossRef]







| Q (m3/s) | S0 (%) | D (m) | W (m) | Lr (m) | Latitude | Longitude | Reach Name |
|---|---|---|---|---|---|---|---|
| 3.25 | 0.25 | 0.34 | 30.74 | 43 | Shapour1 | ||
| 3.00 | 0.21 | 0.40 | 24.58 | 30 | Shapour2 | ||
| 0.86 | 0.16 | 0.30 | 17.56 | 35 | Fahlyan | ||
| 1.39 | 0.25 | 0.24 | 10.15 | 28 | Dalaki |
| Reach Name | ||||
|---|---|---|---|---|
| 0.062 | 0.118 | 0.089 | 0.59 | Shapur1 |
| 0.035 | 0.088 | 0.108 | 0.37 | Shapur2 |
| 0.054 | 0.039 | 0.082 | 0.48 | Fahlyan |
| 0.083 | 0.145 | 0.135 | 0.39 | Dalaki |
| Fr | NP + NPT | NTP | NP | Profiles Measured Number | Cross–Section Number | Reach Name |
|---|---|---|---|---|---|---|
| 2630 | 698 | 303 | 395 | 20 | 5 | Shapur1 |
| 1902 | 516 | 194 | 322 | 16 | 4 | Shapur2 |
| 1992 | 560 | 175 | 385 | 20 | 5 | Fahlyan |
| 1660 | 400 | 98 | 302 | 15 | 5 | Dalaki |
| 8184 | 2174 | 770 | 1404 | 71 | 19 | Sum |
| DV (Point/m2) | DB (Point/m2) | NV | NB | Reach Name |
|---|---|---|---|---|
| 12 | 2 | 358 | 2745 | Shapur1 |
| 12 | 2 | 286 | 1554 | Shapur2 |
| 12 | 2 | 195 | 1302 | Fahlyan |
| 12 | 2 | 228 | 604 | Dalaki |
| - | - | 1067 | 6205 | Sum |
| d84 (mm) | d16 (mm) | Fr | Re | A (m2) | D (m) | Q (m3/s) | Section Number | Reach | |
|---|---|---|---|---|---|---|---|---|---|
| 1.59 | 49.00 | 19.33 | 0.15 | 484,524 | 11.53 | 0.406 | 3.44 | 1 | Shpur1 |
| 1.44 | 47.00 | 22.67 | 0.14 | 425,096 | 11.10 | 0.383 | 3.08 | 2 | |
| 1.67 | 52.00 | 18.67 | 0.17 | 405,308 | 10.52 | 0.329 | 3.24 | 3 | |
| 1.73 | 46.67 | 15.67 | 0.24 | 456,342 | 9.36 | 0.284 | 3.76 | 4 | |
| 1.76 | 42.33 | 13.67 | 0.20 | 370,611 | 8.67 | 0.277 | 2.90 | 5 | |
| 1.66 | 53.33 | 19.33 | 0.16 | 431,846 | 9.37 | 0.360 | 2.81 | 1 | Shpur2 |
| 1.58 | 50.67 | 20.33 | 0.17 | 512,777 | 9.68 | 0.383 | 3.24 | 2 | |
| 1.59 | 43.00 | 17.00 | 0.15 | 486,667 | 9.84 | 0.410 | 3.92 | 3 | |
| 1.45 | 47.67 | 22.67 | 0.15 | 542,123 | 10.06 | 0.437 | 3.12 | 4 | |
| 1.41 | 46.67 | 23.33 | 0.13 | 225,339 | 4.87 | 0.295 | 0.93 | 1 | Fahlyan |
| 1.42 | 38.33 | 19.00 | 0.12 | 204,318 | 5.28 | 0.310 | 0.87 | 2 | |
| 1.39 | 37.33 | 19.33 | 0.14 | 176,823 | 5.54 | 0.310 | 0.79 | 3 | |
| 1.54 | 44.00 | 18.67 | 0.12 | 186,734 | 5.56 | 0.309 | 0.84 | 4 | |
| 1.52 | 41.00 | 17.67 | 0.13 | 192,184 | 5.22 | 0.285 | 0.88 | 5 | |
| 1.47 | 35.33 | 16.33 | 0.26 | 525,546 | 3.13 | 0.298 | 1.38 | 1 | Dalaki |
| 1.72 | 43.33 | 14.67 | 0.36 | 568,702 | 2.62 | 0.250 | 1.49 | 2 | |
| 1.59 | 42.00 | 16.67 | 0.48 | 576,104 | 1.93 | 0.209 | 1.33 | 3 | |
| 1.57 | 42.00 | 17.00 | 0.29 | 444,000 | 2.49 | 0.249 | 1.37 | 4 | |
| 1.68 | 46.00 | 16.33 | 0.47 | 529,397 | 2.09 | 0.199 | 1.39 | 5 |
| U | Profile Name | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.029 | 0.84 | 0.122 | 0.235 | 1.14 | 0.034 | 4.61 | 8.47 | 2.61 | 0.051 | 0.1278 | Sh1_1_4.5 |
| 0.039 | 1.52 | 0.097 | 0.355 | 2.01 | 0.045 | 5.86 | 10.26 | 2.35 | 0.048 | 0.1212 | Sh1_1_14.2 |
| 0.031 | 0.99 | 0.081 | 0.313 | 1.19 | 0.035 | 6.47 | 10.84 | 2.19 | 0.047 | 0.1169 | Sh1_1_18.2 |
| 0.039 | 1.51 | 0.082 | 0.384 | 1.59 | 0.040 | 3.99 | 6.74 | 4.76 | 0.069 | 0.1724 | Sh1_1_24.9 |
| 0.025 | 0.63 | 0.088 | 0.240 | 1.37 | 0.037 | 4.69 | 9.12 | 1.18 | 0.034 | 0.0859 | Sh1_2_10 |
| 0.035 | 1.22 | 0.088 | 0.334 | 1.74 | 0.042 | 6.58 | 11.51 | 1.51 | 0.039 | 0.0971 | Sh1_2_15 |
| 0.038 | 1.46 | 0.093 | 0.355 | 2.74 | 0.052 | 5.79 | 11.50 | 9.96 | 0.032 | 0.0789 | Sh1_2_19.5 |
| 0.050 | 2.51 | 0.111 | 0.426 | 2.18 | 0.047 | 3.44 | 5.96 | 2.02 | 0.045 | 0.1124 | Sh1_2_26 |
| 0.035 | 1.22 | 0.0128 | 0.276 | 1.57 | 0.040 | 3.66 | 7.00 | 3.65 | 0.061 | 0.1511 | Sh1_3_11 |
| 0.046 | 2.07 | 0.107 | 0.393 | 2.33 | 0.048 | 5.22 | 8.94 | 3.03 | 0.055 | 0.1375 | Sh1_3_16 |
| 0.041 | 1.71 | 0.118 | 0.340 | 2.27 | 0.048 | 4.45 | 8.27 | 4.17 | 0.065 | 0.1615 | Sh1_3_18.4 |
| 0.049 | 2.40 | 0.095 | 0.451 | 3.97 | 0.063 | 5.12 | 9.94 | 5.56 | 0.074 | 0.1848 | Sh1_3_26 |
| 0.037 | 1.35 | 0.145 | 0.273 | 3.44 | 0.059 | 3.06 | 7.00 | 9.9 | 0.099 | 0.2488 | Sh1_4_10.5 |
| 0.035 | 1.23 | 0.165 | 0.244 | 2.76 | 0.053 | 3.53 | 7.90 | 0.82 | 0.029 | 0.0714 | Sh1_4_14.5 |
| 0.049 | 2.35 | 0.123 | 0.392 | 2.53 | 0.050 | 2.99 | 5.55 | 4.50 | 0.067 | 0.1681 | Sh1_4_16.5 |
| 0.057 | 3.28 | 0.104 | 0.503 | 5.71 | 0.076 | 5.45 | 10.59 | 3.10 | 0.056 | 0.1392 | Sh1_4_25 |
| 0.036 | 1.30 | 0.141 | 0.272 | 2.20 | 0.047 | 3.50 | 7.06 | 2.66 | 0.052 | 0.1290 | Sh1_5_9.3 |
| 0.051 | 2.60 | 0.118 | 0.420 | 3.21 | 0.057 | 3.56 | 6.54 | 5.20 | 0.072 | 0.1804 | Sh1_5_15.65 |
| 0.062 | 3.81 | 0.100 | 0.551 | 5.70 | 0.076 | 4.37 | 8.23 | 8.73 | 0.093 | 0.2336 | Sh1_5_22.3 |
| 0.021 | 0.45 | 0.118 | 0.175 | 0.71 | 0.026 | 5.55 | 9.82 | 1.47 | 0.038 | 0.0959 | Sh1_5_27.3 |
| 0.024 | 0.57 | 0.091 | 0.224 | 2.84 | 0.053 | 7.95 | 20.42 | 0.225 | 0.015 | 0.0375 | Sh2_1_8 |
| 0.044 | 1.95 | 0.078 | 0.447 | 2.10 | 0.046 | 7.63 | 12.08 | 2.36 | 0.049 | 0.1217 | Sh2_1_13 |
| 0.040 | 1.60 | 0.073 | 0.419 | 2.33 | 0.048 | 9.92 | 16.47 | 2.04 | 0.045 | 0.1130 | Sh2_1_15 |
| 0.024 | 0.56 | 0.091 | 0.223 | 2.81 | 0.053 | 8.07 | 20.57 | 0.28 | 0.017 | 0.0419 | Sh2_1_18 |
| 0.025 | 0.63 | 0.083 | 0.246 | 1.09 | 0.033 | 6.09 | 11.44 | 1.89 | 0.043 | 0.1087 | Sh2_2_8 |
| 0.034 | 1.13 | 0.076 | 0.346 | 1.64 | 0.041 | 9.85 | 16.18 | 3.15 | 0.056 | 0.1404 | Sh2_2_12.65 |
| 0.038 | 1.46 | 0.073 | 0.400 | 2.34 | 0.048 | 10.26 | 17.23 | 1.32 | 0.036 | 0.0909 | Sh2_2_15.4 |
| 0.018 | 0.315 | 0.100 | 0.159 | 1.01 | 0.032 | 5.46 | 13.11 | 0.33 | 0.018 | 0.0459 | Sh2_2_18.4 |
| 0.024 | 0.59 | 0.080 | 0.243 | 1.08 | 0.033 | 6.25 | 11.57 | 0.42 | 0.020 | 0.0510 | Sh2_3_7 |
| 0.040 | 1.61 | 0.068 | 0.435 | 2.93 | 0.054 | 7.93 | 14.14 | 3.52 | 0.059 | 0.1484 | Sh2_3_12 |
| 0.038 | 1.44 | 0.068 | 0.412 | 2.19 | 0.047 | 8.25 | 13.84 | 1.82 | 0.043 | 0.1067 | Sh2_3_14 |
| 0.025 | 0.60 | 0.074 | 0.256 | 1.34 | 0.037 | 8.60 | 16.00 | 0.46 | 0.021 | 0.0535 | Sh2_3_17 |
| 0.028 | 0.78 | 0.079 | 0.281 | 0.81 | 0.028 | 6.75 | 10.61 | 0.68 | 0.026 | 0.0654 | Sh2_4_6 |
| 0.039 | 1.49 | 0.074 | 0.403 | 1.84 | 0.043 | 6.61 | 10.88 | 2.32 | 0.048 | 0.1206 | Sh2_4_10.5 |
| 0.035 | 1.24 | 0.071 | 0.374 | 2.15 | 0.046 | 10.17 | 17.36 | 2.25 | 0.047 | 0.1185 | Sh2_4_14 |
| 0.027 | 0.72 | 0.084 | 0.262 | 1.60 | 0.040 | 7.56 | 14.54 | 1.06 | 0.033 | 0.0814 | Sh2_4_17 |
| 0.012 | 0.15 | 0.123 | 0.100 | 0.28 | 0.017 | 3.77 | 7.75 | 1.26 | 0.036 | 0.0889 | F_1_4.5 |
| 0.023 | 0.54 | 0.129 | 0.183 | 1.26 | 0.036 | 3.75 | 8.28 | 1.22 | 0.035 | 0.0874 | F_1_8.25 |
| 0.035 | 1.26 | 0.093 | 0.329 | 2.06 | 0.045 | 5.81 | 10.57 | 1.37 | 0.037 | 0.0925 | F_1_11.5 |
| 0.028 | 0.79 | 0.087 | 0.272 | 1.47 | 0.038 | 8.57 | 14.89 | 2.39 | 0.049 | 0.1222 | F_1_13.5 |
| 0.014 | 0.21 | 0.129 | 0.113 | 0.49 | 0.022 | 2.95 | 6.69 | 0.81 | 0.028 | 0.0710 | F_2_6 |
| 0.024 | 0.58 | 0.129 | 0.190 | 0.98 | 0.031 | 3.14 | 6.15 | 2.72 | 0.052 | 0.1304 | F_2_8.5 |
| 0.029 | 0.81 | 0.087 | 0.273 | 2.17 | 0.047 | 6.55 | 12.96 | 3.24 | 0.057 | 0.1423 | F_2_11 |
| 0.026 | 0.65 | 0.081 | 0.254 | 0.98 | 0.031 | 5.08 | 8.93 | 1.05 | 0.032 | 0.0811 | F_2_14 |
| 0.010 | 0.11 | 0.103 | 0.092 | 0.25 | 0.016 | 3.46 | 7.56 | 0.12 | 0.011 | 0.0271 | F_3_5 |
| 0.014 | 0.20 | 0.113 | 0.120 | 0.74 | 0.027 | 3.15 | 8.54 | 0.34 | 0.018 | 0.0460 | F_3_9 |
| 0.025 | 0.62 | 0.077 | 0.255 | 1.50 | 0.039 | 8.94 | 14.73 | 1.40 | 0.037 | 0.0934 | F_3_13 |
| 0.019 | 0.035 | 0.079 | 0.188 | 0.58 | 0.024 | 7.48 | 12.63 | 2.65 | 0.052 | 0.1288 | F_3_15 |
| 0.012 | 0.15 | 0.103 | 0.109 | 0.31 | 0.018 | 4.06 | 8.50 | 0.67 | 0.026 | 0.0646 | F_4_8 |
| 0.016 | 0.26 | 0.099 | 0.144 | 0.44 | 0.021 | 4.64 | 8.83 | 2.27 | 0.048 | 0.1190 | F_4_10 |
| 0.026 | 0.65 | 0.080 | 0.247 | 1.20 | 0.035 | 5.87 | 11.02 | 1.53 | 0.039 | 0.0979 | F_4_13 |
| 0.022 | 0.49 | 0.090 | 0.209 | 0.72 | 0.027 | 5.84 | 10.19 | 1.83 | 0.043 | 0.1069 | F_4_15 |
| 0.015 | 0.21 | 0.121 | 0.119 | 0.52 | 0.022 | 3.13 | 7.36 | 0.76 | 0.027 | 0.0687 | F_5_5 |
| 0.017 | 0.28 | 0.102 | 0.148 | 0.70 | 0.026 | 4.04 | 9.09 | 2.22 | 0.047 | 0.1177 | F_5_9.15 |
| 0.028 | 0.78 | 0.091 | 0.261 | 1.09 | 0.033 | 4.00 | 7.27 | 1.47 | 0.038 | 0.0959 | F_5_12 |
| 0.022 | 0.48 | 0.089 | 0.208 | 0.80 | 0.028 | 4.59 | 8.65 | 2.25 | 0.048 | 0.1188 | F_5_15 |
| 0.071 | 4.99 | 0.077 | 0.720 | 5.91 | 0.077 | 4.90 | 7.99 | 8.61 | 0.093 | 0.2320 | D_1_3 |
| 0.046 | 2.10 | 0.082 | 0.454 | 2.01 | 0.045 | 3.60 | 5.74 | 1.76 | 0.042 | 0.1051 | D_1_5.25 |
| 0.031 | 0.96 | 0.087 | 0.296 | 2.49 | 0.050 | 7.15 | 13.28 | 3.28 | 0.057 | 0.1432 | D_1_6 |
| 0.086 | 7.37 | 0.115 | 0.717 | 10.72 | 0.104 | 2.72 | 5.54 | 18.00 | 0.134 | 0.3362 | D_2_3 |
| 0.068 | 4.60 | 0.097 | 0.616 | 6.54 | 0.081 | 3.88 | 7.17 | 7.00 | 0.084 | 0.2093 | D_2_5.25 |
| 0.062 | 3.84 | 0.100 | 0.554 | 4.04 | 0.064 | 3.28 | 5.64 | 3.56 | 0.060 | 0.1492 | D_2_7.5 |
| 0.069 | 4.73 | 0.118 | 0.566 | 7.97 | 0.089 | 3.57 | 7.02 | 12.34 | 0.111 | 0.2778 | D_3_1.55 |
| 0.070 | 4.94 | 0.128 | 0.556 | 6.56 | 0.081 | 3.04 | 5.70 | 45.27 | 0.213 | 0.5319 | D_3_4.6 |
| 0.110 | 11.99 | 0.128 | 0.866 | 15.59 | 0.125 | 2.81 | 5.34 | 9.10 | 0.095 | 0.2385 | D_3_6.05 |
| 0.061 | 3.76 | 0.091 | 0.574 | 7.22 | 0.085 | 7.11 | 12.59 | 8.47 | 0.092 | 0.2301 | D_4_1.5 |
| 0.090 | 8.01 | 0.132 | 0.697 | 11.24 | 0.106 | 2.62 | 5.19 | 24.94 | 0.158 | 0.3948 | D_4_5 |
| 0.051 | 2.57 | 0.124 | 0.407 | 10.49 | 0.102 | 3.59 | 9.58 | 26.18 | 0.162 | 0.4045 | D_4_8 |
| 0.099 | 9.77 | 0.091 | 0.927 | 18.26 | 0.135 | 4.48 | 9.04 | 16.01 | 0.127 | 0.3163 | D_5_2 |
| 0.133 | 17.61 | 0.211 | 0.818 | 20.15 | 0.142 | 1.51 | 3.36 | 71.18 | 0.267 | 0.6670 | D_5_5.25 |
| 0.076 | 5.79 | 0.136 | 0.585 | 13.01 | 0.114 | 3.24 | 7.34 | 10.44 | 0.102 | 0.2554 | D_5_9.5 |
| Model | C | B | A | Method | ||
|---|---|---|---|---|---|---|
| 0.1608 | 0.9929 | 0.5131 | 141.80 | 1.937 | Darcy–Weisbach | |
| 1.3110 | 0.8461 | 0.5977 | 94.33 | 1.955 | boundary layer characteristics | |
| 4.587 | 0.5938 | 1.638 | 251.50 | 1.625 | logarithmic law |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naderi, M.; Afzalimehr, H.; Dehghan, A.; Darban, N.; Nazari-Sharabian, M.; Karakouzian, M. Field Study of Three–Parameter Flow Resistance Model in Rivers with Vegetation Patch. Fluids 2022, 7, 284. https://doi.org/10.3390/fluids7080284
Naderi M, Afzalimehr H, Dehghan A, Darban N, Nazari-Sharabian M, Karakouzian M. Field Study of Three–Parameter Flow Resistance Model in Rivers with Vegetation Patch. Fluids. 2022; 7(8):284. https://doi.org/10.3390/fluids7080284
Chicago/Turabian StyleNaderi, Masoud, Hossein Afzalimehr, Ayoub Dehghan, Nader Darban, Mohammad Nazari-Sharabian, and Moses Karakouzian. 2022. "Field Study of Three–Parameter Flow Resistance Model in Rivers with Vegetation Patch" Fluids 7, no. 8: 284. https://doi.org/10.3390/fluids7080284
APA StyleNaderi, M., Afzalimehr, H., Dehghan, A., Darban, N., Nazari-Sharabian, M., & Karakouzian, M. (2022). Field Study of Three–Parameter Flow Resistance Model in Rivers with Vegetation Patch. Fluids, 7(8), 284. https://doi.org/10.3390/fluids7080284








