Free-Decay Heave Motion of a Spherical Buoy
Abstract
:1. Introduction
2. Experimental Measurements
3. Numerical Simulations
3.1. High-Fidelity Model Based on Solution of Navier–Stokes Equations
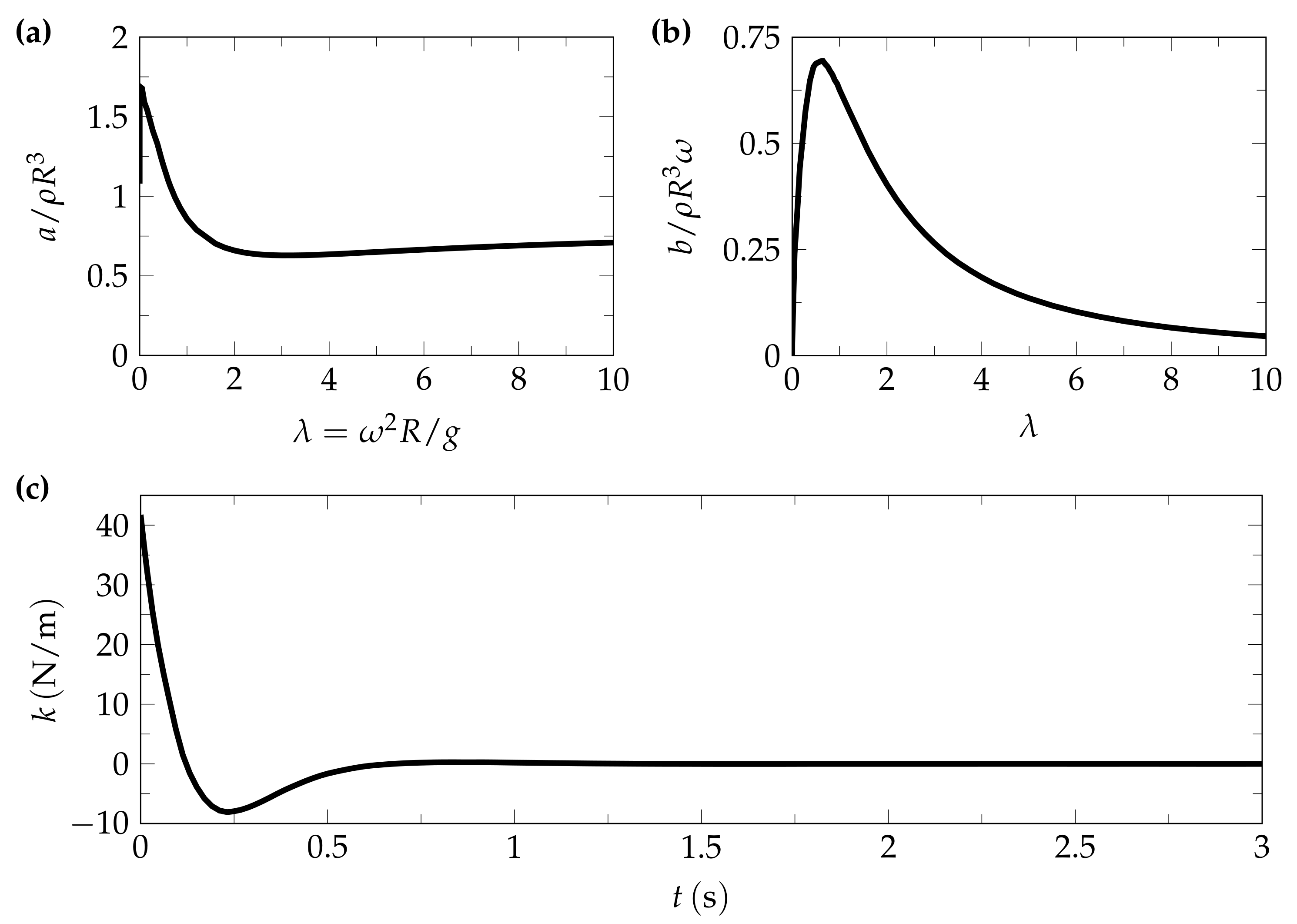
3.2. Reduced-Order Models Based on Linear Potential Flow Theory
3.2.1. Cummins Model
3.2.2. Mass-Spring-Damper Model
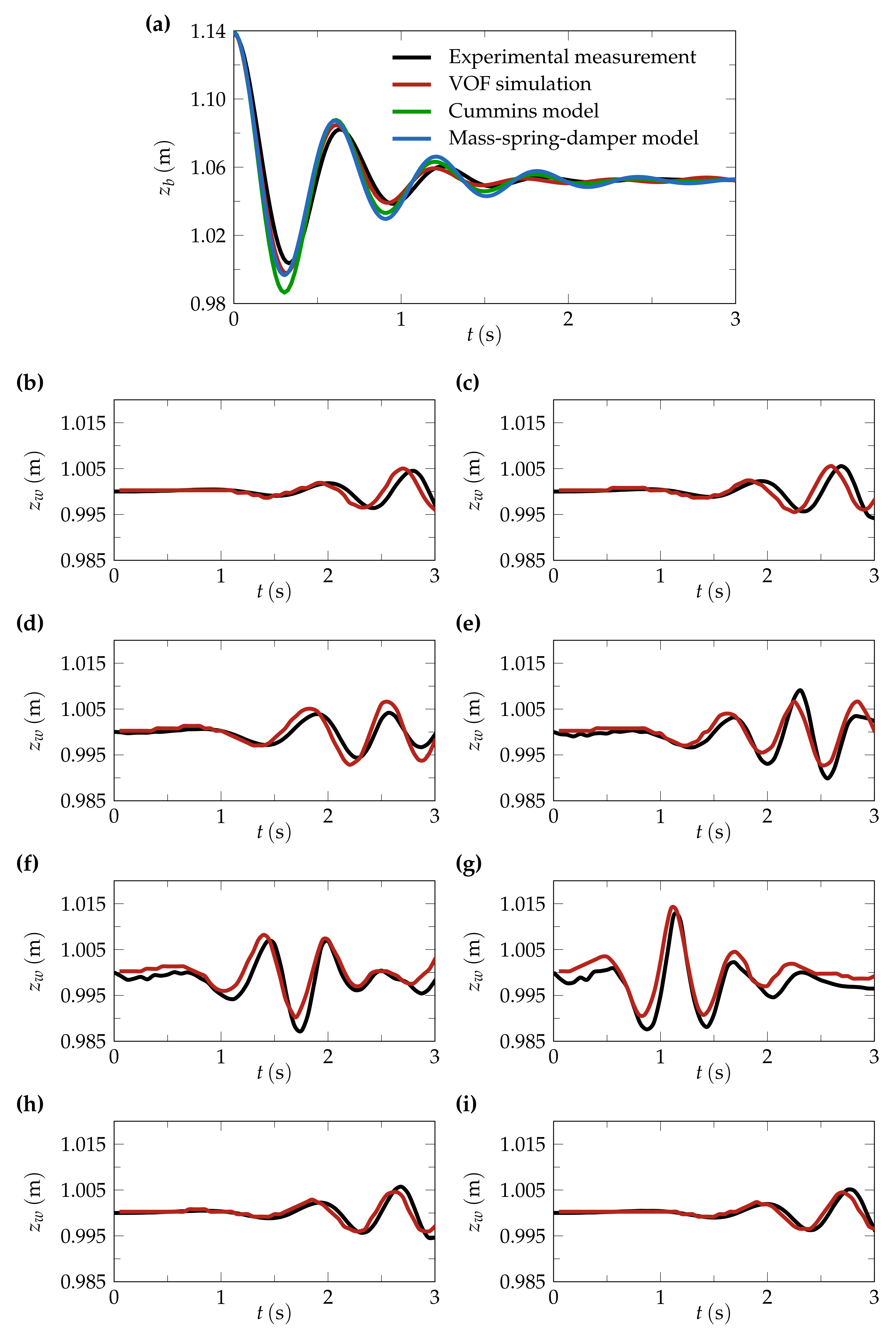
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korde, U.A.; Ringwood, J. Hydrodynamic Control of Wave Energy Devices; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Forehand, D.I.M.; Kiprakis, A.E.; Nambiar, A.J.; Wallace, A.R. A fully coupled wave-to-wire model of an array of wave energy converters. IEEE Trans. Sustain. Energy 2015, 7, 118–128. [Google Scholar] [CrossRef] [Green Version]
- Husain, S.; Parker, G.G. Effects of Hydrodynamic Coupling on Energy Extraction Performance of Wave Energy Converter Arrays. In Proceedings of the OCEANS MTS/IEEE, Charleston, SC, USA, 22–25 October 2018; pp. 1–8. [Google Scholar]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef] [Green Version]
- Hansen, R.H.; Kramer, M.M.; Vidal, E. Discrete displacement hydraulic power take-off system for the wavestar wave energy converter. Energies 2013, 6, 4001–4044. [Google Scholar] [CrossRef]
- Wang, L.; Isberg, J. Nonlinear passive control of a wave energy converter subject to constraints in irregular waves. Energies 2015, 8, 6528–6542. [Google Scholar] [CrossRef] [Green Version]
- Mei, C.C. Power extraction from water waves. J. Sh. Res. 1976, 20, 63–66. [Google Scholar] [CrossRef]
- Demonte Gonzalez, T.; Parker, G.G.; Anderlini, E.; Weaver, W.W. Sliding mode control of a nonlinear wave energy converter model. J. Mar. Sci. Eng. 2021, 9, 951. [Google Scholar] [CrossRef]
- Richter, M.; Magana, M.E.; Sawodny, O.; Brekken, T.K. Nonlinear model predictive control of a point absorber wave energy converter. IEEE Trans. Sustain. Energy 2012, 4, 118–126. [Google Scholar] [CrossRef]
- Wilson, D.G.; Robinett, R.D.; Bacelli, G.; Abdelkhalik, O.; Coe, R.G. Extending Complex Conjugate Control to Nonlinear Wave Energy Converters. J. Mar. Sci. Eng. 2020, 8, 84. [Google Scholar] [CrossRef] [Green Version]
- Havelock, T.H. Waves due to a floating sphere making periodic heaving oscillations. Proc. Royal Soc. Lond. A 1955, 231, 1–7. [Google Scholar]
- Mei, C.C. Numerical methods in water-wave diffraction and radiation. Annu. Rev. Fluid Mech. 1978, 10, 393–416. [Google Scholar] [CrossRef]
- Hulme, A. The wave forces acting on a floating hemisphere undergoing forced periodic oscillations. J. Fluid Mech. 1982, 121, 443–463. [Google Scholar] [CrossRef]
- Evans, D.V.; McIver, P. Added mass and damping of a sphere section in heave. Appl. Ocean Res. 1984, 6, 45–53. [Google Scholar] [CrossRef]
- Wolgamot, H.A.; Fitzgerald, C.J. Nonlinear hydrodynamic and real fluid effects on wave energy converters. Proc. Inst. Mech. Eng. A J. Power Energy 2015, 229, 772–794. [Google Scholar] [CrossRef]
- Mercadé Ruiz, P.; Ferri, F.; Kofoed, J.P. Experimental validation of a wave energy converter array hydrodynamics tool. Sustainability 2017, 9, 115. [Google Scholar] [CrossRef]
- Penalba, M.; Giorgi, G.; Ringwood, J.V. Mathematical modelling of wave energy converters: A review of nonlinear approaches. Renew. Sustain. Energy Rev. 2017, 78, 1188–1207. [Google Scholar] [CrossRef] [Green Version]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-fidelity numerical modelling of ocean wave energy systems: A review of computational fluid dynamics-based numerical wave tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef] [Green Version]
- Sheng, W. Wave energy conversion and hydrodynamics modelling technologies: A review. Renew. Sustain. Energy Rev. 2019, 109, 482–498. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A.; Katsaounis, G.M. Theoretical evaluation of the hydrodynamic characteristics of arrays of vertical axisymmetric floaters of arbitrary shape in front of a vertical breakwater. J. Mar. Sci. Eng. 2020, 8, 62. [Google Scholar] [CrossRef] [Green Version]
- Ransley, E.; Yan, S.; Brown, S.; Hann, M.; Graham, D.; Windt, C.; Schmitt, P.; Davidson, J.; Ringwood, J.; Musiedlak, P.H.; et al. A blind comparative study of focused wave interactions with floating structures (CCP-WSI Blind Test Series 3). Int. J. Offshore Polar Eng. 2020, 30, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Windt, C.; Davidson, J.; Ransley, E.J.; Greaves, D.; Jakobsen, M.; Kramer, M.; Ringwood, J.V. Validation of a CFD-based numerical wave tank model for the power production assessment of the wavestar ocean wave energy converter. Renew. Energy 2020, 146, 2499–2516. [Google Scholar] [CrossRef]
- Ransley, E.J.; Brown, S.A.; Hann, M.; Greaves, D.M.; Windt, C.; Ringwood, J.; Davidson, J.; Schmitt, P.; Yan, S.; Wang, J.X.; et al. Focused wave interactions with floating structures: A blind comparative study. Proc. Inst. Civ.-Eng.-Eng. Comput. Mech. 2021, 174, 46–61. [Google Scholar] [CrossRef]
- Zurkinden, A.S.; Ferri, F.; Beatty, S.; Kofoed, J.P.; Kramer, M. Non-linear numerical modeling and experimental testing of a point absorber wave energy converter. Ocean Eng. 2014, 78, 11–21. [Google Scholar] [CrossRef]
- Tampier, G.; Grueter, L. Hydrodynamic analysis of a heaving wave energy converter. Int. J. Mar. Energy 2017, 19, 304–318. [Google Scholar] [CrossRef]
- Têtu, A.; Ferri, F.; Kramer, M.B.; Todalshaug, J.H. Physical and mathematical modeling of a wave energy converter equipped with a negative spring mechanism for phase control. Energies 2018, 11, 2362. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Li, Y.; Yu, Y.H.; Ding, B.; Jiang, Z.; Lin, Z.; Cazzolato, B. Experimental and numerical investigations of a two-body floating-point absorber wave energy converter in regular waves. J. Fluids Struct. 2019, 91, 102613. [Google Scholar] [CrossRef]
- Beatty, S.J.; Bocking, B.; Bubbar, K.; Buckham, B.J.; Wild, P. Experimental and numerical comparisons of self-reacting point absorber wave energy converters in irregular waves. Ocean Eng. 2019, 173, 716–731. [Google Scholar] [CrossRef]
- Kramer, M.B.; Andersen, J.; Thomas, S.; Bendixen, F.B.; Bingham, H.; Read, R.; Holk, N.; Ransley, E.; Brown, S.; Yu, Y.H.; et al. Highly accurate experimental heave decay tests with a floating sphere: A public benchmark dataset for model validation of fluid–structure interaction. Energies 2021, 14, 269. [Google Scholar] [CrossRef]
- Edinburgh Designs Ltd. The Edinburgh Designs WG8USB Wave Gauge Controller. Available online: http://www4.edesign.co.uk/product/wavegauges (accessed on 11 September 2021).
- Vicon. Vicon Study of Dynamic Object Tracking Accuracy. Available online: https://www.vicon.com/cms/wp-content/uploads/2021/01/PS4933_Standard-Individual-Case-Study_16_Vicon-Dynamic-Object-Tracking-Accuracy.pdf (accessed on 11 September 2021).
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab®; Springer: Berlin/Heidelberg, Germany, 2015; Volume 113. [Google Scholar]
- Griffith, B.E.; Patankar, N.A. Immersed Methods for Fluid–Structure Interaction. Annu. Rev. Fluid Mech. 2020, 52, 421–448. [Google Scholar] [CrossRef] [Green Version]
- Freitas, C.J.; Runnels, S.R. Simulation of fluid–structure interaction using patched-overset grids. J. Fluid. Struct. 1999, 13, 191–207. [Google Scholar] [CrossRef]
- Chan, W.M. Overset grid technology development at NASA Ames Research Center. Comput. Fluids 2009, 38, 496–503. [Google Scholar] [CrossRef]
- Tang, H.S.; Jones, S.C.; Sotiropoulos, F. An overset-grid method for 3D unsteady incompressible flows. J. Comput. Phys. 2003, 191, 567–600. [Google Scholar] [CrossRef]
- Deng, H.B.; Xu, Y.Q.; Chen, D.D.; Dai, H.; Wu, J.; Tian, F.B. On numerical modeling of animal swimming and flight. Comput. Mech. 2013, 52, 1221–1242. [Google Scholar] [CrossRef]
- Shen, Z.; Wan, D.; Carrica, P.M. Dynamic overset grids in OpenFOAM with application to KCS self-propulsion and maneuvering. Ocean Eng. 2015, 108, 287–306. [Google Scholar] [CrossRef]
- Meakin, R. Moving body overset grid methods for complete aircraft tiltrotor simulations. In Proceedings of the 11th Computational Fluid Dynamics Conference, Orlando, FL, USA, 6–9 July 1993; p. 3350. [Google Scholar]
- Steger, J.L.; Dougherty, F.C.; Benek, J.A. A chimera grid scheme. Multiple overset body-conforming mesh system for finite difference adaptation to complex aircraft configurations. Adv. Grid Gener. 1983, 59–69. [Google Scholar]
- Hubbard, B.; Chen, H.C. A Chimera scheme for incompressible viscous flows with application to submarine hydrodynamics. In Proceedings of the Fluid Dynamics Conference, Colorado Springs, CO, USA, 20–23 June 1994; p. 2210. [Google Scholar]
- Chesshire, G.; Henshaw, W.D. Composite overlapping meshes for the solution of partial differential equations. J. Comput. Phys. 1990, 90, 1–64. [Google Scholar] [CrossRef]
- Henshaw, W.D.; Schwendeman, D.W. Parallel computation of three-dimensional flows using overlapping grids with adaptive mesh refinement. J. Comput. Phys. 2008, 227, 7469–7502. [Google Scholar] [CrossRef] [Green Version]
- Henshaw, W.D. Adaptive Mesh and Overlapping Grid Methods. In Encyclopedia of Aerospace Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Sherer, S.E.; Scott, J.N. High-order compact finite-difference methods on general overset grids. J. Comput. Phys. 2005, 210, 459–496. [Google Scholar] [CrossRef]
- Cummins, W.E. The impulse response function and ship motions. Schiffstechnik 1962, 47, 101–109. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Zimmerman, W.B.J. Multiphysics Modeling with Finite Element Methods; World Scientific Publishing Company: Singapore, 2006. [Google Scholar]
- Pepper, D.W.; Heinrich, J.C. The Finite Element Method: Basic Concepts and Applications with MATLAB, MAPLE, and COMSOL; CRC Press: New York, NY, USA, 2017. [Google Scholar]
- Zou, S.; Abdelkhalik, O. A numerical simulation of a variable-shape buoy wave energy converter. J. Mar. Sci. Eng. 2021, 9, 625. [Google Scholar] [CrossRef]



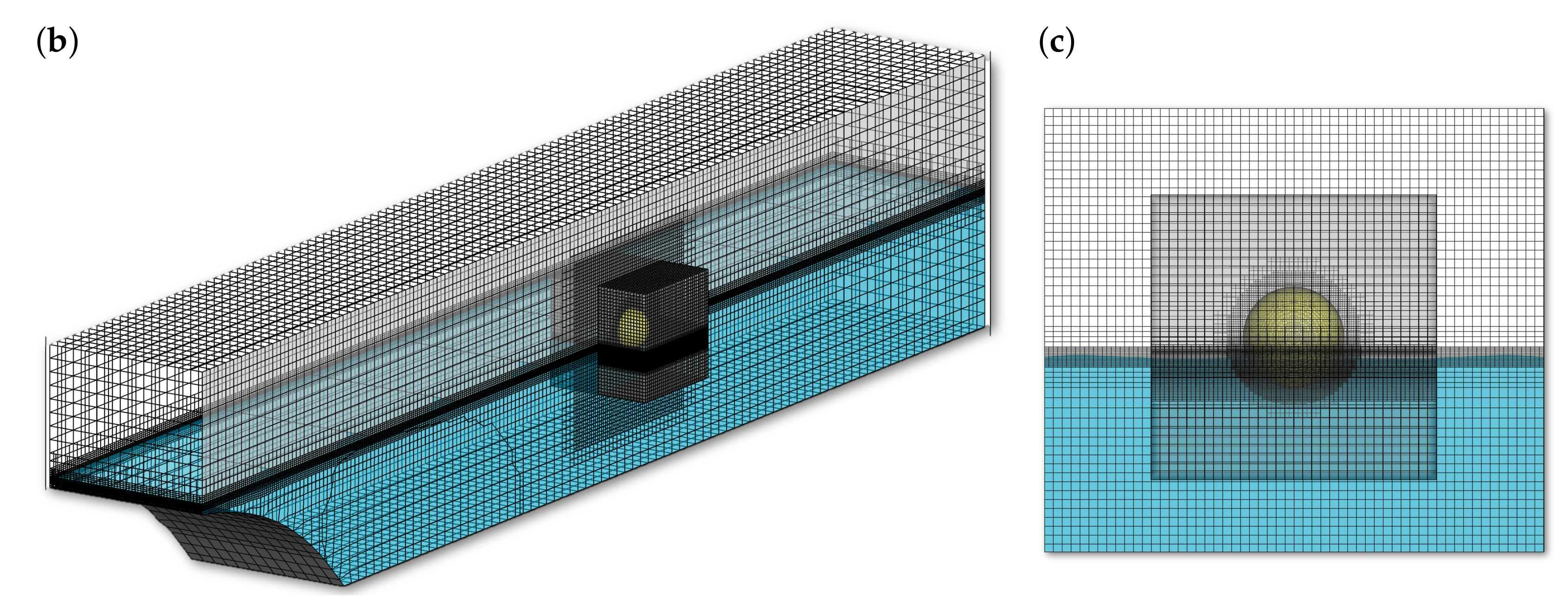
| Item | Purpose |
|---|---|
| Edinburgh Designs wave tank () | Pool for experiments |
| Eight resistive wave gauges | Water height measurement |
| Eleven-camera Qualisys motion tracking system | Buoy motion measurement |
| Spherical buoy | Test article |
| Twelve 19 mm reflective markers | Motion tracking |
| Wave Gauge Index | X Position (m) | Y Position (m) | |
|---|---|---|---|
| 1 | 1.393 | 0.004 | 1.393 |
| 2 | 1.292 | 0.004 | 1.292 |
| 3 | 0.027 | 1.159 | 1.159 |
| 4 | 0.025 | 0.950 | 0.950 |
| 5 | 0.023 | 0.705 | 0.705 |
| 6 | 0.017 | 0.458 | 0.458 |
| 7 | −1.293 | 0.019 | 1.293 |
| 8 | −1.394 | 0.021 | 1.394 |
| aexp-vof | aexp-Cumm | aexp-msd | b | c | d | e | f | g | h | i |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0028 | 0.0041 | 0.0045 | 0.0008 | 0.0010 | 0.0012 | 0.0015 | 0.0018 | 0.0023 | 0.0007 | 0.0006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colling, J.K.; Jafari Kang, S.; Dehdashti, E.; Husain, S.; Masoud, H.; Parker, G.G. Free-Decay Heave Motion of a Spherical Buoy. Fluids 2022, 7, 188. https://doi.org/10.3390/fluids7060188
Colling JK, Jafari Kang S, Dehdashti E, Husain S, Masoud H, Parker GG. Free-Decay Heave Motion of a Spherical Buoy. Fluids. 2022; 7(6):188. https://doi.org/10.3390/fluids7060188
Chicago/Turabian StyleColling, Jacob K., Saeed Jafari Kang, Esmaeil Dehdashti, Salman Husain, Hassan Masoud, and Gordon G. Parker. 2022. "Free-Decay Heave Motion of a Spherical Buoy" Fluids 7, no. 6: 188. https://doi.org/10.3390/fluids7060188
APA StyleColling, J. K., Jafari Kang, S., Dehdashti, E., Husain, S., Masoud, H., & Parker, G. G. (2022). Free-Decay Heave Motion of a Spherical Buoy. Fluids, 7(6), 188. https://doi.org/10.3390/fluids7060188








