Computational Investigation of the Aerodynamics of a Wheel Installed on a Race Car with a Multi-Element Front Wing
Abstract
1. Introduction
2. CFD Analysis of the Flow Structures around an Isolated Wheel
2.1. Governing Equations
2.2. CFD Model
2.3. Validation and Flow Structure Analysis
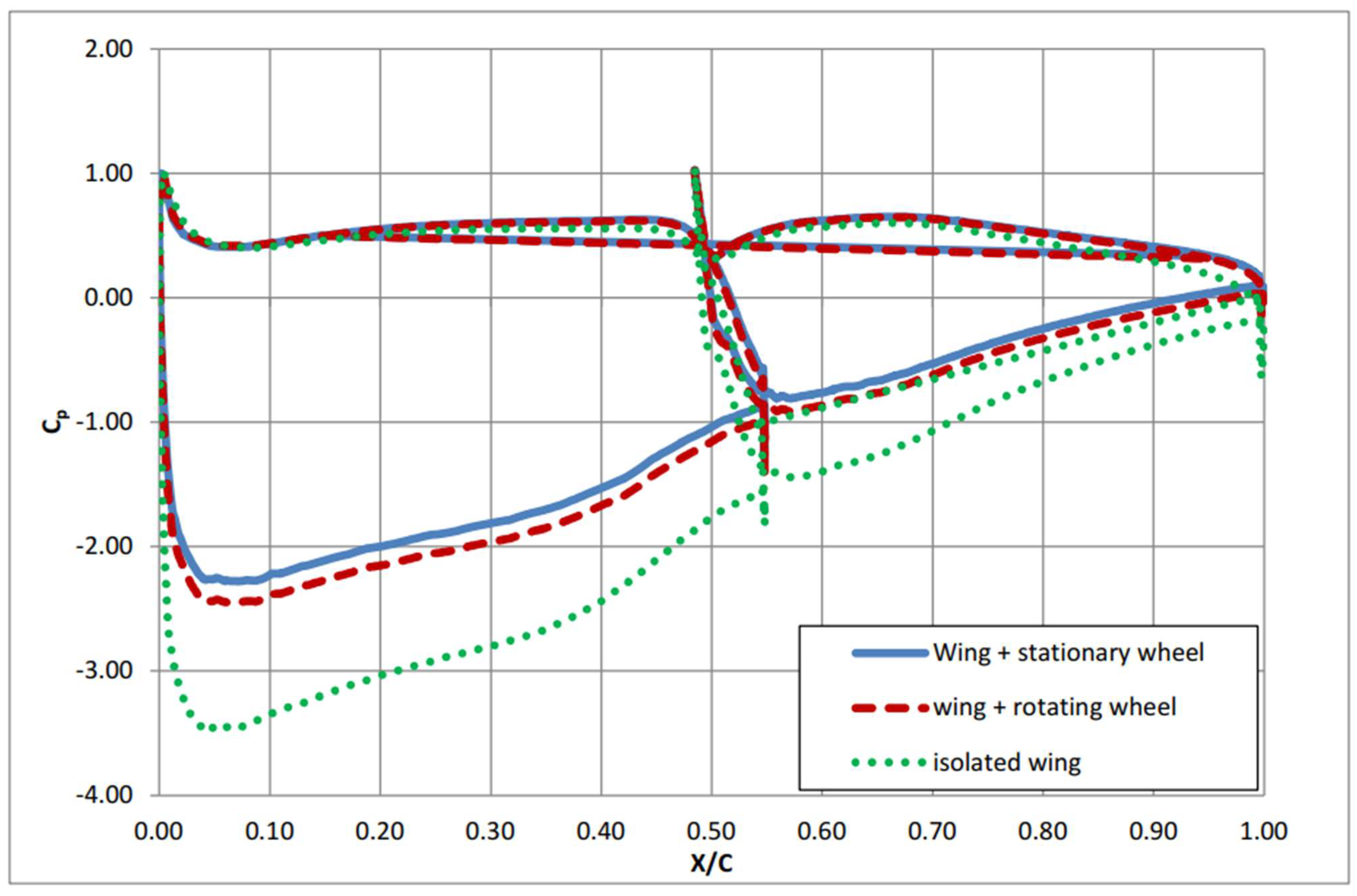
3. Front Wing and Wheel CFD Model
4. Flow Structure around an Open Wheel on Race Car with Front Wing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Wheel frontal area: d × b |
| b | Wheel breadth |
| C | Chord |
| Cd | Drag coefficient: L/(q∞A) |
| Cl | Lift coefficient: D/(q∞A) |
| Cp | Pressure coefficient: p − p∞/q∞ |
| d | Wheel diameter |
| D | Drag force |
| k | Turbulent kinetic energy |
| lv | Vehicle length |
| L | Lift force |
| p∞ | Freestream static pressure |
| P | Static pressure |
| q∞ | Freestream dynamic pressure: (r∞U2∞)/2 |
| u | velocity |
| Free stream velocity | |
| W | Width |
| y+ | Non dimensional boundary layer distance from wall |
| µ | Dynamic viscosity |
| ρ | Density |
| ρ∞ | Freestream density |
| τ | Tensor of tangential and normal stress |
| ω | Specific rate of dissipation |
References
- Cogotti, A. Aerodynamic characteristics of car wheel. In Proceedings of the International Conference Held at the Café Royal, London, UK, 16–18 June 1982. [Google Scholar]
- Wickern, G.; Zwicker, K.; Pfadenhauer, M. Rotating Wheels–Their Impact on Wind Tunnel Test Techniques and on Vehicle Drag Results; SAE Technical Paper No. 970133; SAE: Warrendale, PA, USA, 1997. [Google Scholar]
- Katz, J. Race Car Aerodynamics: Designing for Speed; Bentley Publishers: Philadelphia, PA, USA, 1995. [Google Scholar]
- Katz, J. Aerodynamic model for wing-generated down force on open-wheel-racing-car configurations. SAE paper 860218. SAE Trans. 1986, 95, 129–137. [Google Scholar]
- Dominy, R.G. Aerodynamics of Grand Prix cars. Proc. Inst. Mech. Eng. Part D 1992, 206, 267. [Google Scholar] [CrossRef]
- Agathangelou, B.; Gascoyne, M. Aerodynamic Design Considerations of a Formula 1 Racing Car; SAE Technical Paper No. 980399; SAE: Warrendale, PA, USA, 1998. [Google Scholar]
- Wright, P. Ferrari Formula 1: Under the Skin of the Championship Winning F1-2000; David Bull Publishing: Phoenix, AZ, USA, 2003. [Google Scholar]
- Axon, L. The Aerodynamic Characteristics of Automobile Wheels–CFD Prediction and Wind Tunnel Experiment. Ph.D. Thesis, Cranfield University, Cranfield, UK, 1999. [Google Scholar]
- Mears, A.P. The Aerodynamic Characteristics of an Exposed Racing Car Wheel. Ph.D. Thesis, Durham University, Durham, UK, 2004. [Google Scholar]
- Fackrell, J.E. The Aerodynamic Characteristics of an Isolated Wheel Rotating in Contact with the Ground. Ph.D. Thesis, University of London, London, UK, 1974. [Google Scholar]
- McManus, J.; Zhang, X. A computational study of the flow around an isolated wheel in contact with the ground. ASME J. Fluids Eng. 2006, 128, 520–530. [Google Scholar] [CrossRef]
- Issakhanian, E.; Chris, J.E.; Kin, P.L.; John, K.E. An experimental study of the flow around a formula one racing car tire. ASME J. Fluids Eng. 2010, 132, 071103.1–071103.8. [Google Scholar] [CrossRef]
- Axerio-Cilies, J.; Gianluca, I. An aerodynamic investigation of an isolated rotating formula 1 wheel assembly. ASME J. Fluids Eng. 2012, 134, 121101.1–121101.16. [Google Scholar] [CrossRef]
- Cilies, J.; Issakhanian, E.; Jimenez, J.; Gianluca, I. An aerodynamic investigation of an isolated stationary formula 1 wheel assembly. ASME J. Fluids Eng. 2012, 134, 021101.1–021101.17. [Google Scholar] [CrossRef]
- Kang, S.O.; Jun, S.O.; Park, H.I.; Song, K.S.; Kee, J.D.; Kim, K.H.; Lee, D.H. Actively translating a rear diffuser device for the aerodynamic drag reduction of a passenger car. Int. J. Automot. Technol. 2012, 13, 583–592. [Google Scholar] [CrossRef]
- Ting, L.; Qing, J.; Zhi, G.Y. The influence of rotating wheels on vehicle aerodynamics. Appl. Mech. Mater. 2012, 246–247, 543–547. [Google Scholar]
- Waschle, A.; Cyr, S.; Kuthada, T.; Wiedemann, J. Flow Around an Isolated Wheel–Experimental and Numerical Comparison of Two CFD Codes; SAE Technical Paper No. 2004-01-0445; SAE: Warrendale, PA, USA, 2004. [Google Scholar]
- Waschle, A. The Influence of Rotating Wheels on Vehicle Aerodynamics–Numerical and Experimental Investigations; SAE Technical Paper No. 2007-01-0107; SAE: Warrendale, PA, USA, 2007. [Google Scholar]
- Regert, T.; Lajos, T. Description of flow field in the wheelhouses of cars. Int. J. Heat Fluid Flow 2007, 28, 616–629. [Google Scholar] [CrossRef]
- Rajaratnam, E.; Walker, D. Investigation of wheelhouse flow interaction and the influence of lateral wheel displacement. Energies 2019, 12, 3340. [Google Scholar] [CrossRef]
- Pavia, G.; Passmore, M. Characterisation of wake bi-stability for a square-back geometry with rotating wheels. In Proceedings of the 11th FKFS Conference, Sttutgart, Germany, 26–27 September 2017; Springer: Cham, Switzerland, 2017; pp. 93–109. [Google Scholar]
- Bonitz, S.; Larsson, L.; Sebben, S. Unsteady pressure analysis of the near wall flow downstream of the front wheel of a passenger car under yaw conditions. Int. J. Heat Fluid Flow. 2018, 73, 188–198. [Google Scholar] [CrossRef]
- Wang, S.; Avadiar, T.; Thompson, M.C.; Burton, D. Effect of moving ground on the aerodynamics of a generic automotive model: The DrivAer-Estate. J. Wind. Eng. Ind. Aerodyn. 2019, 195, 104000. [Google Scholar] [CrossRef]
- Wang, Y.; Sicot, C.; Borée, J.; Grandemange, M. Experimental study of wheel-vehicle aerodynamic interactions. J. Wind. Eng. Ind. Aerodyn. 2020, 198, 104062. [Google Scholar] [CrossRef]
- Yu, X.; Jia, Q.; Yang, Z. Comprehensive study of the aerodynamic influence of ground and wheel states on the notchback DrivAer. Energies 2022, 15, 1124. [Google Scholar] [CrossRef]
- Zhou, H.; Jiang, Z.; Wang, G.; Zhang, S. Aerodynamic Characteristics of isolated loaded tires with different tread patterns: Experiment and simulation. Chin. J. Mech. Eng. 2021, 34, 6. [Google Scholar] [CrossRef]
- Bolzon, M.D.P.; Sebben, S.; Broniewicz, A. Effects of wheel configuration on the flow field and the drag coefficient of a passaenger vehicle. Int. J. Automot. Technol. 2019, 20, 763–777. [Google Scholar] [CrossRef]
- Hobeika, T.; Sebben, S. CFD investigation on wheel rotation modelling. J. Wind Eng. Ind. Aerodyn. 2018, 174, 241–251. [Google Scholar] [CrossRef]
- Broniszewski, J.; Piechna, J.R. Fluid-structure interaction analysis of a competitive car during brake-in-turn manoeuvre. Energies 2022, 15, 2917. [Google Scholar] [CrossRef]
- Piechna, J.R.; Kurec, K.; Broniszewski, J.; Remer, M.; Piechna, A.; Kamieniecki, K.; Bibik, P. Influence of the car movable aerodynamic elements on fast road car cornering. Energies 2022, 15, 689. [Google Scholar] [CrossRef]
- Yu, X.; Jia, Q.; Bao, D.; Yang, Z. A Comparative Study of Different Wheel Rotating Simulation Methods in Automotive Aerodynamics; SAE Technical Paper 2018-01-0728; SAE: Warrendale, PA, USA, 2018. [Google Scholar]
- Yu, X.; Jia, Q.; Rashidi, M.M.; Yang, Z. Comprehensive investigation on the aerodynamic influences of the wheel contact patch. J. Appl. Comput. Mech. 2020, 6, 934–955. [Google Scholar]
- Huminic, A.; Chiru, A. On CFD Investigations of Vehicle Aerodynamics with Rotating Wheels’ Simulation; Technical Paper 2006-01-08-04; SAE: Detroit, MI, USA, 2006. [Google Scholar]
- Wang, Y.N.; Tseng, C.Y.; Huang, Y.L.; Leong, J.C. Investigation of 2004 ferrari formula one race car wing effects. In Proceedings of the 2010 International Symposium on Computer, Communication, Control and Automation (3CA), Tainan, Taiwan, 5–7 May 2010; pp. 85–88. [Google Scholar]
- Kieffer, W.; Moujares, S.; Armbya, N. CFD study of section characteristics of Formula Mazda race car wings. Math. Comput. Model. 2006, 43, 1275–1287. [Google Scholar] [CrossRef]
- Huminic, A.; Huminic, G. CFD investigations of an open-wheel race car. In Proceedings of the 4th European Automotive Simulation Conference, Munich, Germany, 6–7 July 2009. [Google Scholar]
- Soso, M.D.; Wilson, P.A. Aerodynamic of a wing in ground effect in generic racing car wake flows. Proc. Inst. Mech. Eng. Part D 2006, 220, 1–13. [Google Scholar] [CrossRef]
- Newbon, J.; Dominy, R.; Sims-Williams, D. CFD investigation of the effect of the salient flow features in the wake of a generic open-wheel race car. SAE Int. J. Passeng. Cars-Mech. Syst. 2015, 8, 217–232. [Google Scholar] [CrossRef][Green Version]
- Bradford, J.; Montomoli, F.; D’Ammaro, A. Uncertainty quantification and race car aerodynamics. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2014, 228, 403–411. [Google Scholar] [CrossRef]
- Ahlfeld, R.; Ciampoli, F.; Pietropaoli, M.; Pepper, N.; Montomoli, F. Data-driven uncertainty quantification for Formula 1: Diffuser, wing tip and front wing variations. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 1495–1506. [Google Scholar] [CrossRef]
- Basso, M.; Cravero, C.; Marsano, D. Aerodynamic effect of the gurney flap on the front wing of a F1 car and flow interactions with car components. Energies 2021, 14, 2059. [Google Scholar] [CrossRef]
- Cravero, C. Aerodynamic performance prediction of a profile in ground effect with and without a Gurney flap. ASME J. Fluids Eng. 2017, 139, 031105-1–031105-15. [Google Scholar] [CrossRef]
- Cravero, C.; Marogna, N.; Marsano, D. A Numerical study of correlation between recirculation length and shedding frequency in vortex shedding phenomena. WSEAS Trans. Fluid Mech. 2021, 16, 48–62. [Google Scholar] [CrossRef]
- Cravero, C.; Marsano, D. Numerical prediction of tonal noise in centrifugal blowers. In Proceedings of the Turbo Expo 2018: Turbomachinery Technical Conference & Exposition, Oslo, Norway, 11–15 June 2018. ASME Paper GT2018-75243. [Google Scholar]
- Niccolini Marmont Du Haut Champ, C.A.; Silvestri, P. Experimental and numerical vibro-acoustic investigation on a trimmed car door to analyze slamming event. Appl. Acoust. 2020, 166, 107380. [Google Scholar] [CrossRef]
- Guerrero, J.E.; Pacioselli, C.; Pralits, J.O.; Negrello, F.; Silvestri, P.; Lucifredi, A.; Bottaro, A. Preliminary design of a small-sized flapping UAV: I. Aerodynamic performance and static longitudinal stability. Meccanica 2016, 51, 1343–1367. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys CFX Theory Guide v.17; ANSYS Inc.: Canonsburg, PA, USA.
- Bardina, J.E.; Huang, P.G.; Coakley, T.J. Turbulence Modeling Validation Testing and Development; NASA Technical Memorandum; Create Space Independent Publishing Platform: Scotts Valley, CA, USA, 1997; p. 110446. [Google Scholar]
- Zerihan, J.; Zhang, X. Aerodynamics of a single element wing in ground effect. J. Aircr. 2000, 37, 1058. [Google Scholar] [CrossRef]
- Cravero, C.; Marsano, D. Flow and thermal analysis of a racing car braking system. Energies 2022, 15, 2934. [Google Scholar] [CrossRef]
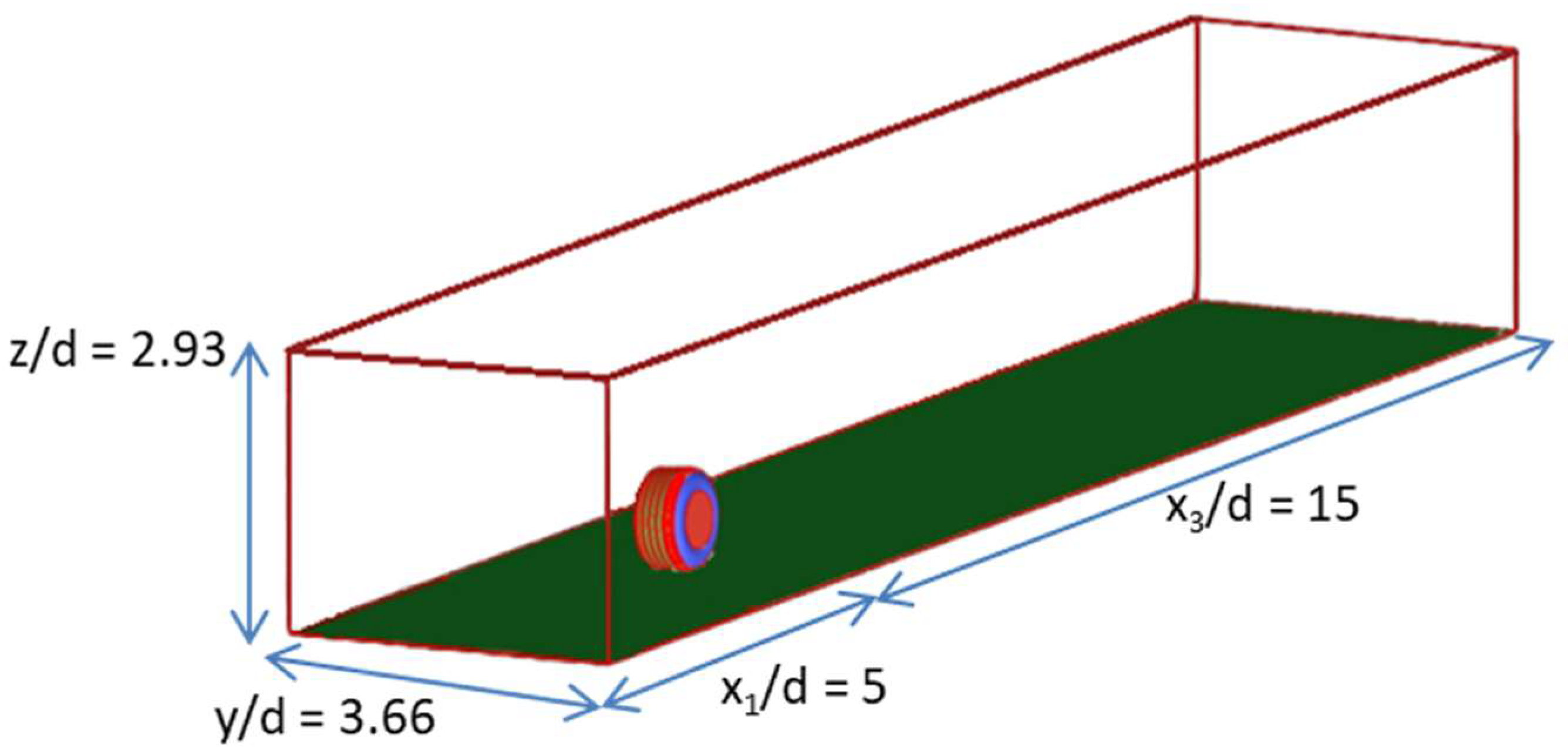

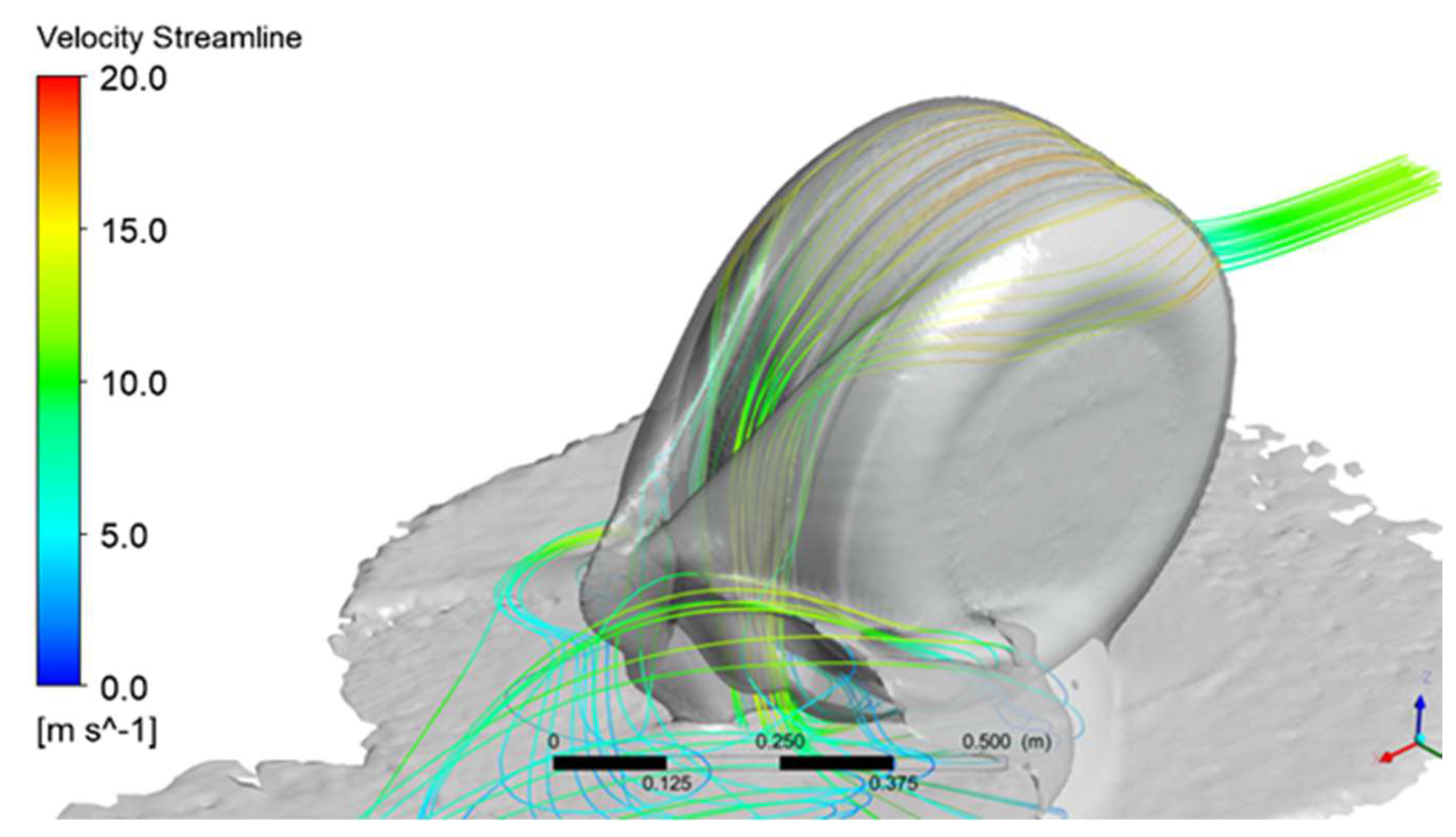


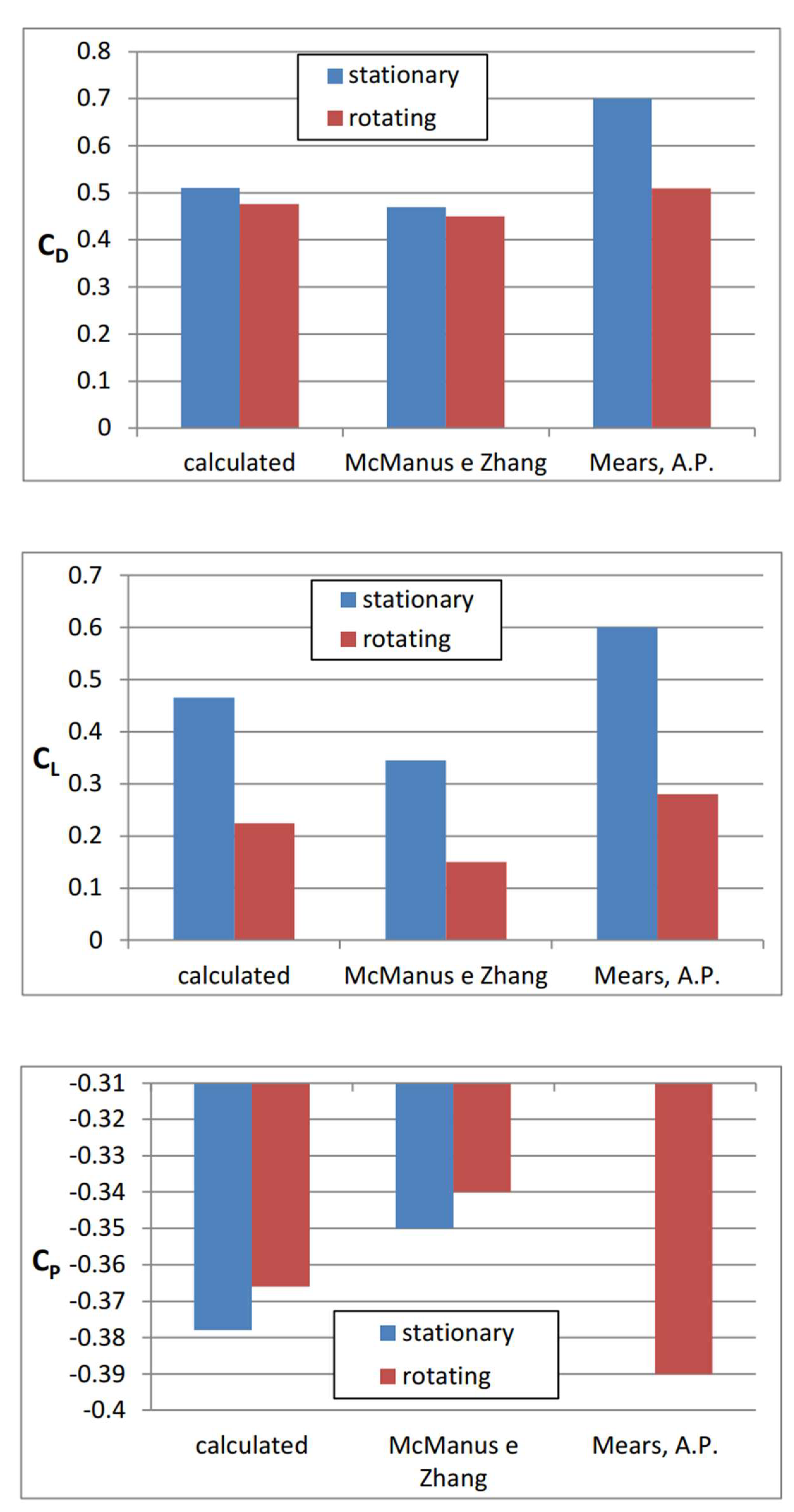
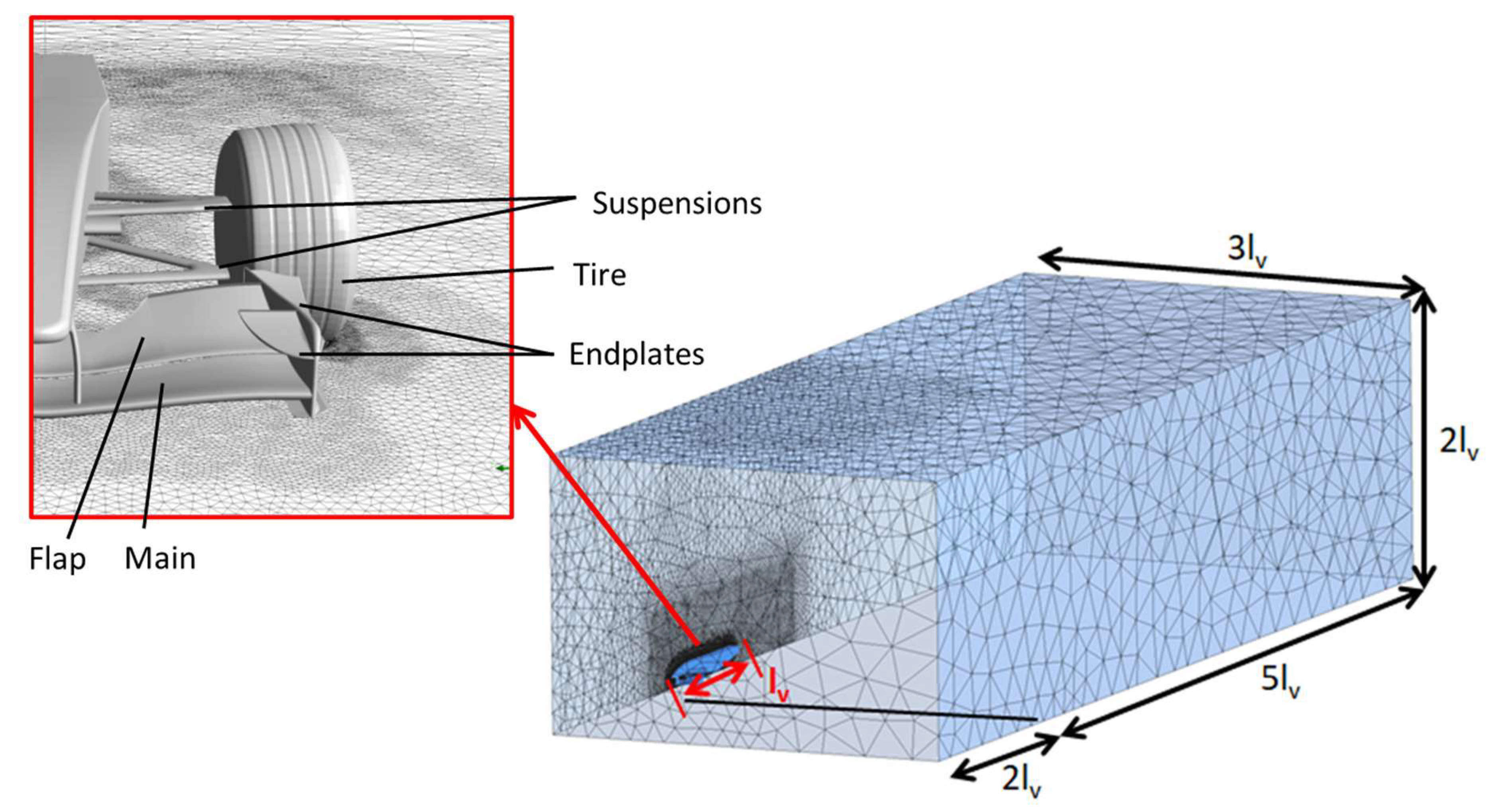

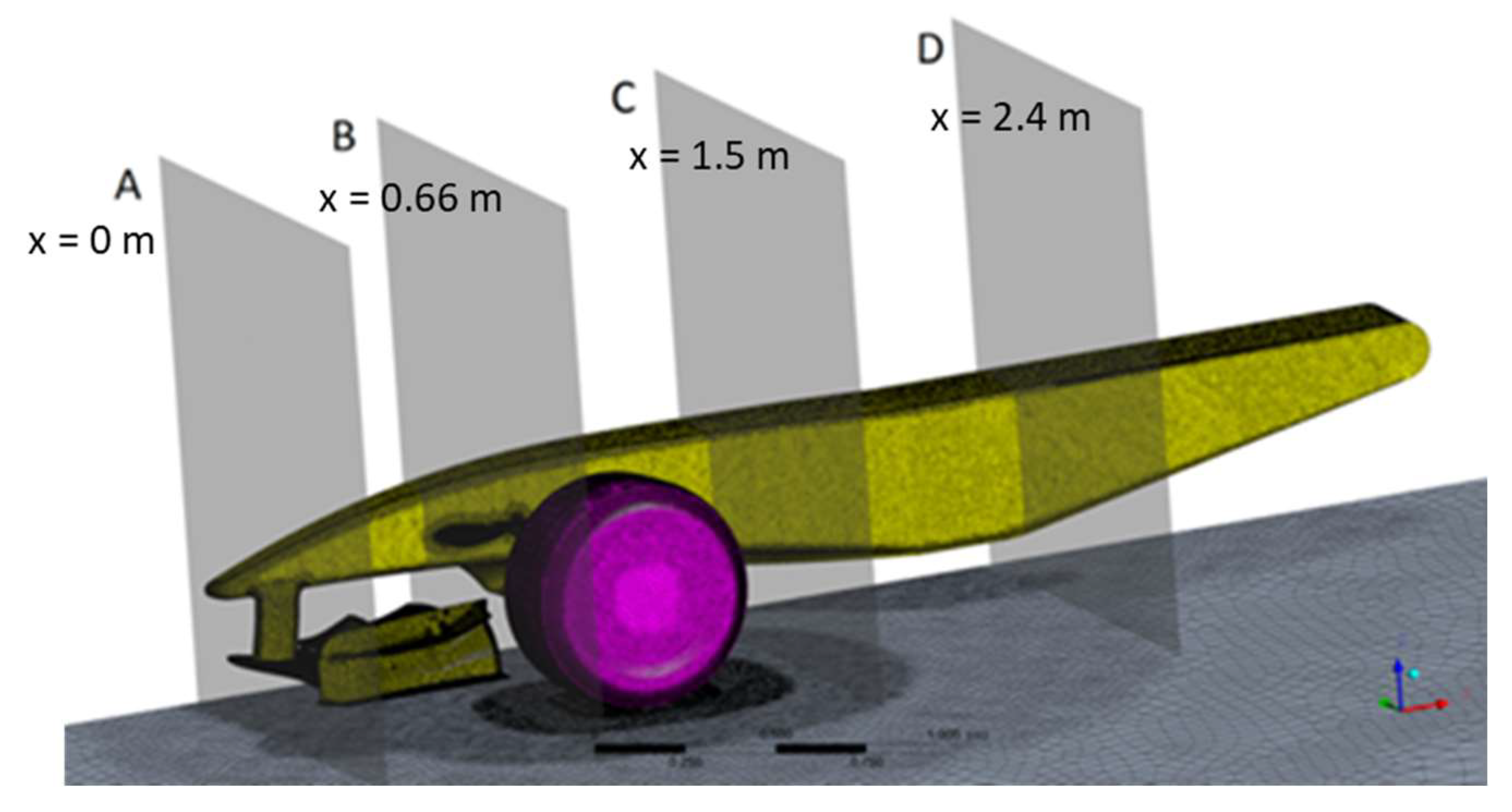

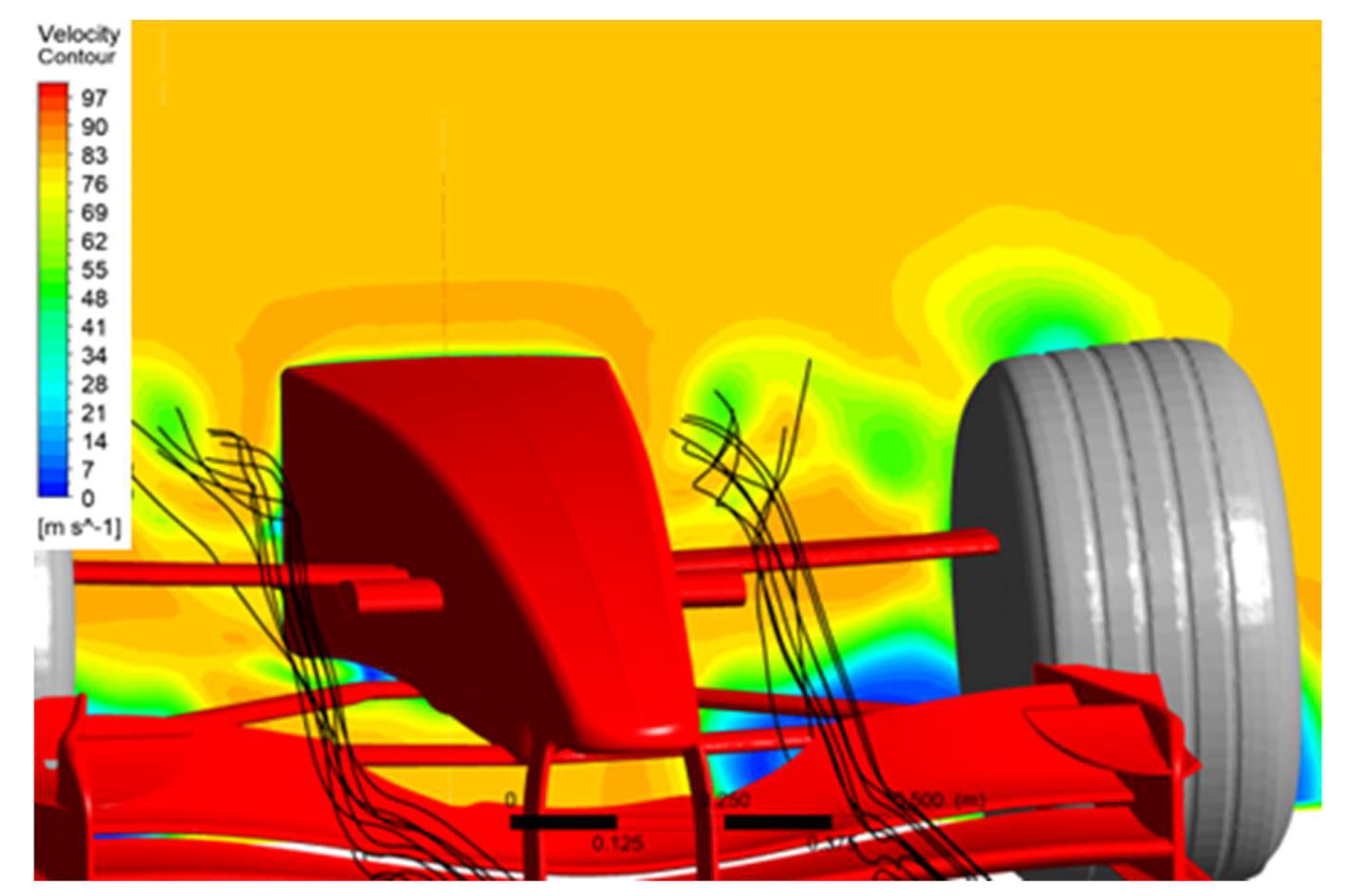
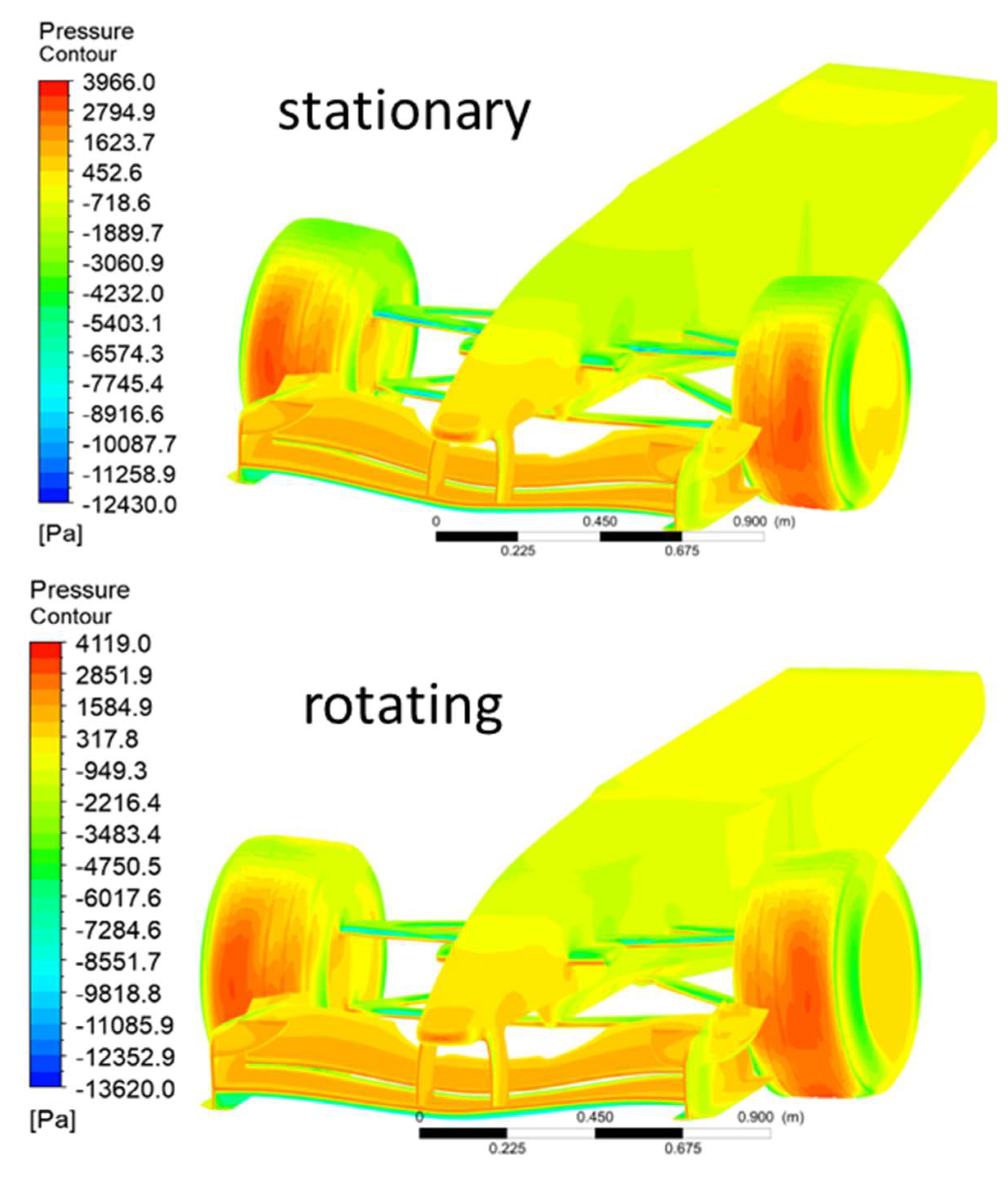
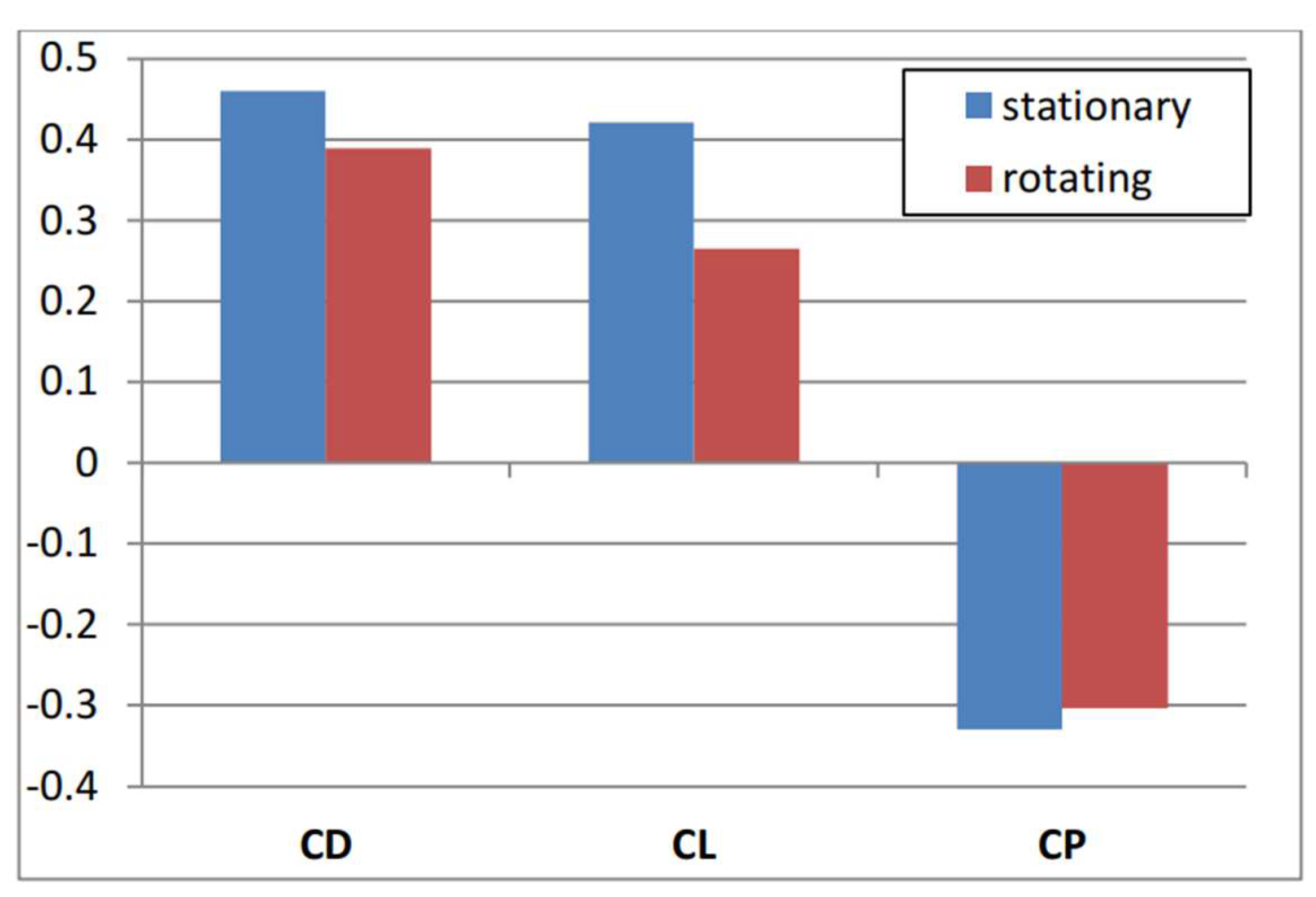
| # | Case |
|---|---|
| Case 1 | Geometry without suspension and wheel |
| Case 2 | Complete model with stationary wheel |
| Case 3 | Complete model with rotating wheel |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cravero, C.; Marsano, D. Computational Investigation of the Aerodynamics of a Wheel Installed on a Race Car with a Multi-Element Front Wing. Fluids 2022, 7, 182. https://doi.org/10.3390/fluids7060182
Cravero C, Marsano D. Computational Investigation of the Aerodynamics of a Wheel Installed on a Race Car with a Multi-Element Front Wing. Fluids. 2022; 7(6):182. https://doi.org/10.3390/fluids7060182
Chicago/Turabian StyleCravero, Carlo, and Davide Marsano. 2022. "Computational Investigation of the Aerodynamics of a Wheel Installed on a Race Car with a Multi-Element Front Wing" Fluids 7, no. 6: 182. https://doi.org/10.3390/fluids7060182
APA StyleCravero, C., & Marsano, D. (2022). Computational Investigation of the Aerodynamics of a Wheel Installed on a Race Car with a Multi-Element Front Wing. Fluids, 7(6), 182. https://doi.org/10.3390/fluids7060182







