Advances in CFD Modeling of Urban Wind Applied to Aerial Mobility

Abstract

The feasibility, safety, and efficiency of a drone mission in an urban environment are heavily influenced by atmospheric conditions. However, numerical meteorological models cannot cope with fine-grained grids capturing urban geometries; they are typically tuned for best resolutions ranging from 1 to 10 km. To enable urban air mobility, new now-casting techniques are being developed based on different techniques, such as data assimilation, variational analysis, machine-learning algorithms, and time series analysis. Most of these methods require generating an urban wind field database using CFD codes coupled with the mesoscale models. The quality and accuracy of that database determines the accuracy of the now-casting techniques. This review describes the latest advances in CFD simulations applied to urban wind and the alternatives that exist for the coupling with the mesoscale model. First, the distinct turbulence models are introduced, analyzing their advantages and limitations. Secondly, a study of the meshing is introduced, exploring how it has to be adapted to the characteristics of the urban environment. Then, the several alternatives for the definition of the boundary conditions and the interpolation methods for the initial conditions are described. As a key step, the available order reduction methods applicable to the models are presented, so the size and operability of the wind database can be reduced as much as possible. Finally, the data assimilation techniques and the model validation are presented.

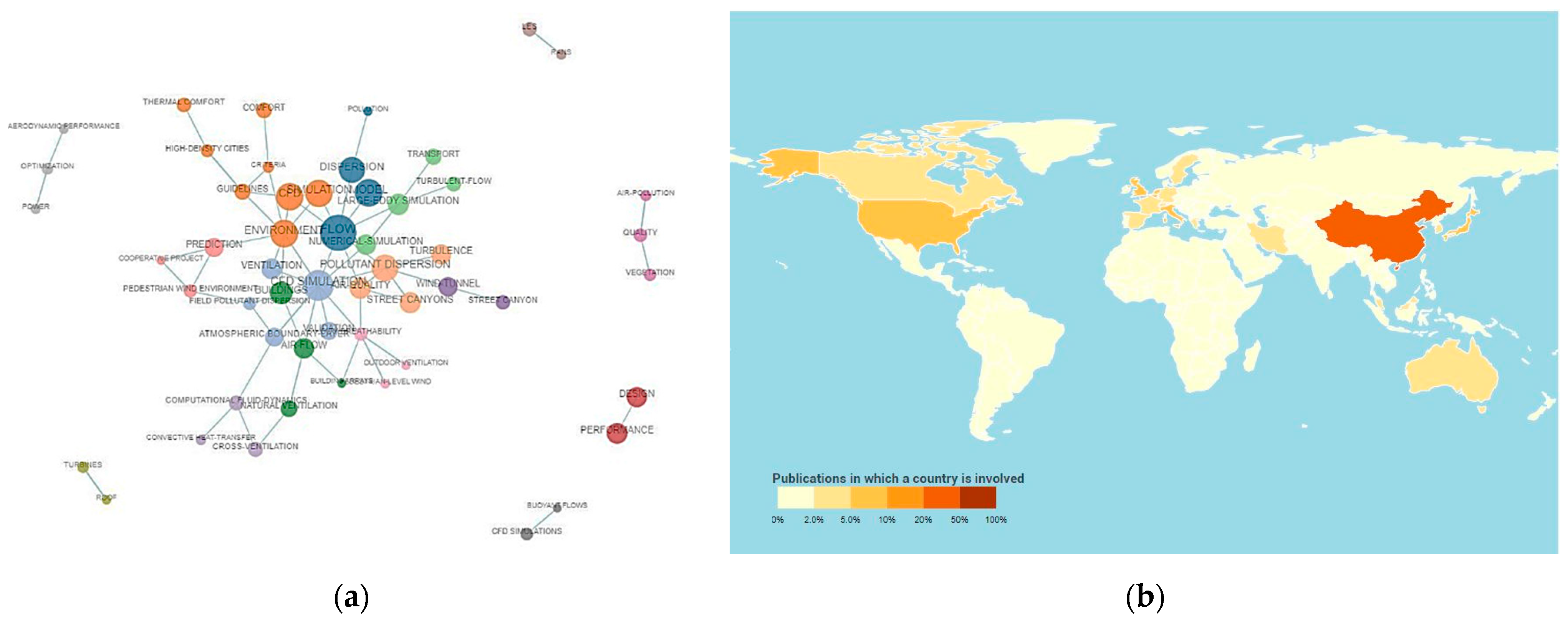
1. Introduction

The use of UAVs in urban areas is becoming a growing trend [1]. This is due to numerous applications varying from civil security to parcel delivery. In spite of this considerable interest, the flight of drones in cities is a genuine challenge due to the high turbulence levels and the drastic changes in wind patterns experienced by the aircraft [2]. This is further aggravated given that the small size of the aircraft increases its vulnerability to weather.

To guarantee the safety of these missions, it is essential to know, as precisely as possible, the wind and turbulence conditions that the aircraft are likely to undergo [3]. Traditionally, mesoscale models have been the tools used to numerically predict the weather [4]. These algorithms implement full-physical models, including long- and shortwave radiation, surface interaction, planetary boundary layer and, of course, water vapor and rain behavior. Nevertheless, these models have best resolutions in the range of 1–1.5 km at best, which is insufficient to accurately represent the relevant scales for the operation of UAVs [5].

CFD simulations are typically used to obtain the required resolution of this application [6]. Usually, the initial and boundary conditions are interpolated from the results produced by a coarser mesoscale prediction, making it necessary to have a proper procedure for the coupling of both models. Though reliable results are obtained, the high cost, both in time and resources, makes this technique unfeasible for real-time now-casting as per today.

Given the previous, current studies are focused on refining the predictions (mainly wind fields) made with mesoscale models using other auxiliary numerical techniques, such as neural networks and sparse regression techniques [7,8], in order to enhance the spatial and temporal resolution. Most of these algorithms, however, require training with huge datasets of real wind fields. In order to generate these wind fields, CFD simulations are again necessary.

A brief bibliometric analysis was undertaken for this review, along with detailed a continuation. The following databases were analyzed for searching scientific articles: Scopus, Web of Science, and Google Scholar. Web of Science was selected because it generates the largest number of results. The following search criteria (query string) were adopted and applied to the fields for title, keywords, or abstract: “CFD urban winds” or “CFD city wind” or “RANS city wind” or “RANS urban winds”. After filtering, using the tool Biblio ToolBox [9], 1266 scientific papers directly related to the topic were identified in the period from January 1990 to the present. Figure 1 shows the number of publications per year. The total number of publications for each of the five countries with the largest number of papers were China (421), USA (123), UK (114), Italy (83), and Japan (82). The relevance of each country is shown in Figure 2 together with the most relevant keywords that appear in the abstracts.

This paper presents the recent advancements in CFD simulation of urban wind to examine how these advancements can be applied to obtain the datasets required to train the now-casting algorithms (see Figure 3). Section 2 describes the different turbulence models available, as well as the modifications to be applied to the closure coefficients. In Section 3, the emphasis is on the preparation of the digital terrain model and the meshing necessary for the simulations. Subsequently, the way that the mesoscale model forecasts have to be interpolated to obtain the initial and boundary conditions of the CFD simulations is discussed. Finally, as the goal was to generate a wind database of a substantial size, different model order reduction techniques are explored. To validate the CFD simulations and increase the reliability of the results, experimental measurements can also be considered, as detailed in Section 5.

2. Turbulence Models

The first question is related to the CFD engine and, more specifically, to which turbulence model is optimal to solve the CFD simulations. In fact, it is possible to directly solve the following Navier-Stokes equations without using any modeling assumptions:

$$\mathsf{\rho }\left[\frac{\partial {\tilde{u}}_i}{\partial \mathrm{t}}+{\tilde{u}}_i\frac{\partial {\tilde{u}}_i}{\partial x_j}\right]=-\frac{\partial \tilde{p}}{\partial x_i}+\frac{\partial T_{ij}}{\partial x_j},$$

(1)

$$\left[\frac{\partial \tilde{\mathsf{\rho }}}{\partial t}+{\tilde{u}}_i\frac{\partial \tilde{\mathsf{\rho }}}{\partial x_j}\right]+\tilde{\mathsf{\rho }}\frac{\partial \widetilde{u_i}}{\partial x_j}=0,$$

(2)

where ${\tilde{u}}_i$ represents the ith component of the fluid velocity at a point in space and time, $\tilde{p}$ represents the static pressure, $T_{ij}$ represents the viscous stresses, and $\tilde{\rho }$ represents the fluid density.

This approach is called direct numerical simulation, or DNS, and requires solving the extensive range of temporal and spatial scales of a turbulent flow from the integral scale up to the Kolmogorov length scale. The mesh resolution and time steps required to correctly resolve the complexity of the fluid structure scale with the 9/4 power of the Reynolds number makes the DNS approach practically unaffordable for engineering applications [10].

The next option is to use LES models. In these models, the smaller scales of the turbulence are spatially filtered:

$${\overline{u}}_i(\overrightarrow{x})={\displaystyle \int }G(\overrightarrow{x}-\overrightarrow{\mathsf{\xi }}){\tilde{u}}_i(\overrightarrow{\mathsf{\xi }})d\overrightarrow{\mathsf{\xi }},$$

(3)

Meanwhile the larger, more energy-containing scales are solved directly. The symbol $G$ denotes the filtering kernel. Given the inherent nature of turbulence, at a very small scale, the flow structures tend to be quite similar to each other, even in different applications [11]. This allows the use of simpler turbulence models for these particular scales.

Finally, in RANS models, the flow is decomposed in two parts: a mean (capital letter) component and a fluctuating component:

$$\begin{array}{c}{\tilde{\mathrm{u}}}_{\mathrm{i}}={\mathrm{U}}_{\mathrm{i}}+{\mathrm{u}}_{\mathrm{i}},\\ \tilde{\mathrm{p}}=\mathrm{P}+\mathrm{p},\\ {\tilde{T}}_{ij}=T_{ij}^{ }+{\mathsf{\tau }}_{ij}^{ }.\end{array}$$

(4)

This way, the equations for the conservation of momentum can be written as:

$$\mathsf{\rho }\left[\frac{\partial U_i}{\partial t}+U_j\frac{\partial U_i}{\partial x_j}\right]=-\frac{\partial P}{\partial x_i}+\frac{\partial T_{ij}^{ }}{\partial x_j}-\frac{\partial }{\partial x_j}\left(\mathsf{\rho }\langle u_i{u}_j\rangle \right),$$

(5)

where $\langle \rangle$ is the averaging operator and the terms $\langle u_i{u}_j\rangle$ are known as the Reynolds stresses. The RANS models are characterized by the fact that the Reynolds stresses are fully modeled.

Turbulence models are typically classified according to the number of additional equations required to model the effect of turbulence on the flow. Models range from simple to complex algebraic relationships and improve their fidelity as the number of equations used increases [12].

It is worth noting that Toparlar et al. [13] investigated 176 studies, reported until 2015, on CFD modeling of urban microclimate, out of which 96% used RANS, 2.8% used LES, and the rest used both. It seems clear, therefore, that there is a predominance for the use of RANS models in this particular application, with an outstanding level of maturity.

As it has been mentioned, DNS is not currently a viable option for these studies, so the decision is between a RANS or a LES model.

LES models are capable of solving the finer scales while modeling the scales in the inertial range. They have been used in several previous works [14], their main drawback being the considerable amount of computational power and time they require. One of the key concerns when simulating urban flows is the large variability and uncertainty of the initial and boundary conditions [15]. Despite using a very accurate turbulence model, which has been successfully validated with experimental results, the errors are not eliminated when comparing predictions against full-scale measurements [16]. This was demonstrated, for example, in simulations of wind flow in the center of various cities [17]. When compared to RANS results, a more expensive and detailed LES did not systematically improve the mean velocity prediction.

Alternatively, RANS models can significantly reduce computing time. A large number of RANS models are available depending on the type of application. The vast majority of the studies carried out to date have used RANS models, with the standard $k-ϵ$ and realizable $k-ϵ$ models standing out [18,19,20,21,22].

The standard $k-ϵ$ model is inefficient when solving complex three-dimensional flows, such as the one arising in urban environments, due to the onset of strong pressure gradients and flow separation [23]. As an alternative, many authors prefer the realizable $k-ϵ$ model [24], which makes some of the closure coefficients become functions of strain rate and rotation rate. In this way, it allows for a consideration of the impact of the flow rate of deformation; thus, it is more flexible.

Other studies have shown that the RNG $k-ϵ$ [25] model presents better results in most cases examined. Another solution is the Reynolds-stress model, although its accuracy is not significantly better than the other models and it presents convergence problems [25].

Previous studies [26,27,28] have shown that standard eddy viscosity closures are not able to fully capture the physics of the atmospheric boundary layer. The underlying cause of this inadequacy is that the wall functions were developed for the boundary layers attached to the wall, assuming equilibrium conditions, i.e., small pressure gradients, local balance between turbulent energy generation and dissipation, and a constant shear stress in the near-wall region. This is far from conditions analogous to those encountered in urban environments. Therefore, it is necessary to modify the coefficients for a realistic coupling between the mesoscale model and the RANS models. New closure coefficients for the $k-ϵ$ model with the proper near-wall treatment for non-neutral and transient simulation have already been tested by Temel and van Beeck [20].

To model the effect of vegetation zones, the most commonly used method is known as the Darcy–Forchheimer (DF) model [29]. In this model, plants are considered to be a momentum sink, which constitutes a simple and robust tool to depict the flow of air through vegetation, regardless of what its morphology is [30]. Two parameters are necessary to model green areas: the Forchheimer drag and the permeability of the vegetation. The permeability parameter is sensitive to variation between species, while Forchheimer drag is not [30]. Thus, the main limitation of these methods is that it depends on the plant morphologies and it should be adapted to the particular situation of study.

Another alternative is to use the model of Shaw and Schumann [31,32], assuming that turbulent kinetic energy is dissipated by the canopy due to the rapid dissipation of wake turbulence in the lee of plant elements. Thus, the plant canopy acts as a sink for momentum due to pressure and viscous drag forces. More details about the model can be found in [31,32]. Several studies apply similar roughness setting methods for the ground surface to approximate building structures [33].

It is worth highlighting several specific implementations of the CFD models:

• MITRAS [34], defined by authors as a “microscale obstacle-resolving model”, computes the wind components, temperature, humidity, and precipitation fields, explicitly resolving obstacles, such as buildings, which are represented by impermeable grid cells at the building positions so that the wind speed vanishes in these grid cells.
• PALM [35], which is an abbreviation for “Parallelized Large-Eddy Simulation Model”, has been widely used to model the atmospheric layer both in the ocean and on land. It uses an LES turbulence model and is especially focused on parallelization. PALM has been used to study ventilation at the pedestrian level, to study wind in street canyons, and even to simulate entire cities. In this regard, the simulation of the city of Macau stands out [36]. The simulation domain has an extension of 30 km² and a spatial resolution of 1 m. The simulation time was about one hour, while the results required 128 CPUs in parallel, running for 1.5 h.
• ASMUS [37] has been specifically designed to simulate wind and temperature distribution in cities. The turbulence model is RANS and employs the Prandtl–Kolmogorov relation to fulfill the kinetic energy of turbulence modeling. They achieved mesh resolutions of 2 m and were able to simulate more than 44 h. However, the total CPU time is not included in the original paper and it appears that no other studies since 2014 have used this software.
• ENVI-met [38] is built on RANS equations using a 1.5 order turbulence closure model. Some studies [39] mentioned that this closure model tends to overestimate the turbulent production in areas with high acceleration or deceleration, such as the flow around a building. ENVI-met is the detailed vegetation model, in which plants are not only symbolized as a porous media to solar insolation and wind flow, but could actually interact with the surrounding environment by evapotranspiration [40] It has been used to study the wind pattern in cities such as Bilbao [39]. Unlike the other options, it is a paid software.
• MISKAM [41] incorporates a Reynolds-averaged Navier–Stokes solver that adopts the Boussinesq approximations with a modified k—ε turbulence closure. This code has been used to simulate city centers such as Budapest [42] and Stuttgard [43].

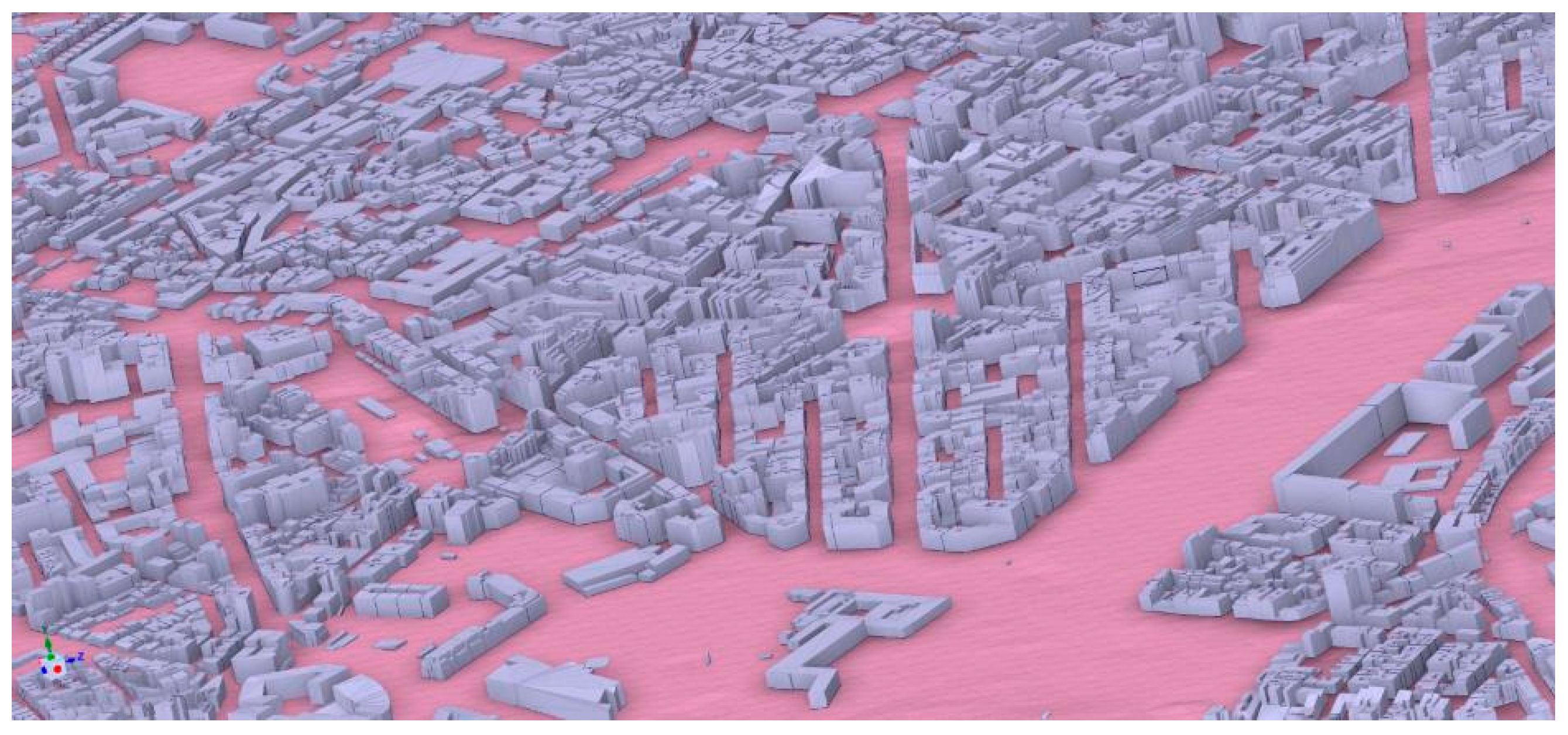
3. Meshing

Meshing is one of the most important stages of any CFD simulation. In principle, meshing can be achieved with any of the several available software packages (open or paid). Often, the selection of this software depends on the chosen simulation software. Among the various options available, blockMesh/snappyhexMesh (Openfoam) [44], Gambit [45], and ICEM [21] stand out.

One of the most challenging parts of meshing is the generation of the digital terrain model that forms one of the boundaries of the simulation domain. Many studies utilize existing digital terrain models (DTMs) of large or major cities [46]. Other projects with more financial resources create their own maps using LIDAR instruments or satellite products [47]. However, it is currently feasible to build digital models of many cities around the world at almost no cost. The digital models can be built through geographic information system (GIS) data, such as the model given by the AW3D Satellite [48] or European national geographic institutes [49]. These institutes, following the European Directive Inspire (Directive 2007/2/EC, Infrastructure for Spatial Information in Europe), provides web services that allow the download of predefined geographic datasets using ATOM technology [50].

However, with this information, the buildings can be reconstructed in a horizontal plane because the ATOM models do not consider the contribution of the terrain to the difference in the heights of the ground itself and, consequently, the heights of the roofs of the buildings.

To solve this problem, the data of the city map has to be fused with the geographic properties of the terrain. In many countries, the DTM of the region of interest can be downloaded from the different national centers for geographic information [50]. Joining the data from both sources, a complete model can be obtained. For example, Figure 4 shows how the proposed methodology allows the creation of a 3D model of a medium-sized Spanish city.

Experiments have found that in the simulation of large-scale urban wind fields, low-rise buildings and buildings with too small an area have little impact on the wind field of the whole city [42]. Thus, the urban building models can be simplified to reduce the amount of data and calculations in urban-scale CFD wind field simulations. Li et al. [46] proposed an algorithm to perform this simplification based on ArcGIS 10.2 (ESRI, California, EEUU) to complete the building data generalization program. However, it is unclear how these simplifications could potentially impact the operation of UAVs.

Typically, the vertical extension of the simulation domain is determined by the lockage ratio. That number is defined as the ratio of the projected area of the obstacles to the cross-section of the computational domain, and it is generally required to be less than 3%. Further studies may focus on dynamically adjusting the vertical extent of the domain based on calculations from the mesoscale meteorological models [51].

Due to some instability problems in numerical solutions, in many studies, simulation domains are artificially extended to include fetch zones (typically 10% of the domain length). These regions are added to allow the development of the boundary layer before the flow reaches the modeling region of interest and can be used to avoid pressure field anomalies at the inlet [52].

The use of hexahedral meshes is recommended, since the use of tetrahedral meshes often implies the use of low-order numerical discretization methods. This way, the poor grid quality is compensated with numerical diffusion errors caused by first-order schemes. Although these errors cause a stabilizing effect, the quality of the simulation is reduced [28].

The resolution of the mesh must be sufficient to capture the behavior of the smallest scales. In general, for urban winds, at least a 10 cell per cube root of the building volume is recommended as well as 10 cells in between every two buildings. It should not be forgotten that the overall resolution must be analyzed by means of a mesh convergence study for which at least three different meshes must be used, with a refinement factor of about 1.5 in each direction. This study must be accompanied by an evaluation of errors by what is known as Richardson extrapolation [53].

4. Boundary Conditions

Once the turbulence model has been selected and the meshing process has been successfully completed, it is time to set up the boundary conditions.

In general, the simulation domain is a prism with six boundary faces (see Figure 5). On the bottom face, the ground, the no-slip condition is set, using the appropriate wall functions for the turbulence model variables. For the remaining five faces, different strategies have been used:

• One of the most common options is known as extrapolation [54]. In this method, only one of the mesoscale model profiles is imposed on an entire inlet face of the CFD domain, while the mesoscale wind data are extrapolated in the grid points outside that profile. This method is the easiest to implement; however, the distributions of the wind velocity on the boundary is uniform in the horizontal direction and, as a consequence, extrapolation is not capable of appropriately coupling the mesoscale and CDF solvers over complex terrains.
• Imposing the zero-gradient boundary conditions at the outflow boundaries and a space-varying inlet condition is another solution [55]. The problem with this solution is in determining which boundary is an inlet and which one is outlet, and how that configuration can change from one day to another.
• The side and top surfaces are modeled as spatially and time-varying velocity inflow and outflow conditions, and the data are extracted from the mesoscale model solutions using interpolation [56]. This solution is the most robust while it comes at the price of implementation complexity.

As it has been seen, in all methods it is required to interpolate the value from the mesoscale mesh to the CFD mesh. Different difficulties can be found when conducting that interpolation. First of all, the horizontal and vertical spacing of each model are very different from each other. In addition, the topography of the boundaries in the CFD domain can also be very different from those of the mesoscale domain. Usually, the interpolation scheme selected is the trilinear interpolation [57]. However, as an alternative, the Cressman interpolation [58] or the inverse distance weighting (IDW) [59] method can be used instead. This way, a great improvement of the models can be achieved [60].

Near the ground (i.e., the first cell of the mesoscale model), all the interpolation schemes may increase the errors, so the velocity is computed following the wall law [61]:

$$U\left(h\right)=\frac{u_{*}}{\kappa }\ln \left(\frac{h}{z_0}\right),$$

(6)

in which $u_{*}$ is the shear velocity, $\kappa$ is the von Kárman constant, $U\left(h\right)$ is the wind speed, and $z_0$ is the distance from the boundary at which the idealized velocity given by the law of the wall goes to zero. Since the mesh of the CFD model has a higher resolution than that of the mesoscale model, it is possible that the ground does not match in both models. In that case, the mesoscale model profiles are shifted until the origin coincides with the CFD model terrain.

When the atmosphere is non-neutral, the Monin–Obukhov similarity theory should be used instead of Equation (6):

$$U\left(h\right)=\frac{u_{*}}{\kappa }\left\{\ln \left(\frac{h}{z_0}\right)-{\psi }_m\left(\frac{h}{L}\right)\right\},$$

(7)

in which the non-neutral condition is modelled by the stability function ${\psi }_m\left(\frac{h}{L}\right)$. $L$ is known as the Obukhov length and determines the stability of the atmospheric boundary layer [62]. In a neutral boundary layer, the effects of buoyancy are neglectable, as the temperature of an air parcel decreases at the same rate as that of the surroundings. The neutral condition is the characteristic regime of windy and cloudy conditions so that there is neither a strong heating nor cooling over the surface. The boundary layer tends to be unstable during sunny days when the surface is warmer than the air. Conversely, the atmosphere tends to be stable at night when the surface is cooler than the air.

Apart from the interpolation scheme, it is also important to determine how to compute the variables of the turbulence closure of the CFD, i.e., the kinetic turbulence energy and the viscous dissipation. As it is subsequently shown, TKE values for CFD simulations can be directly obtained from the mesoscale grids if the proper physics model has been selected, which are nearer to the building scale domain. However, certain variables, such as the momentum diffusion coefficient and TKE dissipation rate are estimated using parameterized expressions.

Relative to the turbulent kinetic energy, following the methodology of different studies, such as [63,64,65], it is better to use a boundary layer model for the mesoscale solver which explicitly computes the turbulent kinetic energy. In WRF, there are four different options: MYJ, QNSE, MYNN, and BouLac [66]. However, data from several studies suggest that the MYNN scheme is the best option, offering the lowest root mean square error [63,67].

In order to estimate the viscous dissipation, different approaches can be found in literature:

• Baik, Park, and Kim [64], using the turbulence model RNG $k-ϵ$, estimated the viscosity dissipation using following the equation:

  $$ϵ\left(z\right)=\frac{C_{\mu }^{\frac{3}{4}}{k}^{\frac{3}{2}}}{\kappa z},$$

  (8)

  in which $C_{\mu }$ is a constant fixed to 0.09, $k$ is the turbulent kinetic energy, and $\kappa$ is the von Kárman constant.
• Mochida et al. [65] calculated the viscous dissipation based on the length scale of the precedent mesoscale domain. In order to do it, they used the following equation:

  $$ϵ\left(z\right)=2\sqrt{\frac{2k^{3/2}}{B_{1}l}},$$

  (9)

  in which $l$ is the ration between the spatial scales and $B_1=24.0$. is the closure constant.
• Another method is considered by Tewari et al. [63]. They used the definition of the viscous dissipation:

  $$ϵ\left(z\right)=\frac{\rho C_{\mu }{k}^2}{{\mu }_t},$$

  (10)

  in which the density is computed from the state equation, ${\mu }_t$ is a product of the mesoscale model, and $C_{\mu }$ is a constant that is usually fixed to 0.09. However, this method seems to produce too high values of viscous dissipation.

5. Dimensionality Reduction Methods

Following the discussion of the introduction, a large number of wind fields are needed to train the numerical now-casting algorithms in such a way that all plausible wind conditions can be collected (see, for example, Figure 6). Due to the considerable size of the files generated in the simulations, it is advisable to use some reduction method in order to minimize the file size. The task is not easy, since the degrees of freedom of the system must be reduced as much as possible while the main characteristics of the system are maintained [68].

The reduction methods are based on the existence of so-called coherent structures, regions containing the most significant features of the flows [69]. Figure 7, for example, shows how the presence of the buildings causes specific and well-defined wind patterns. By capturing the behavior of these structures, one would be able to reproduce the behavior of the entire wind field with excellent accuracy.

Reduction techniques are classified into two types: linear and nonlinear. An extensive review of both types of methods as applied to urban winds can be found in [70]. Among the linear techniques, the most common is the proper orthogonal decomposition, also known as POD [8,71], in which the most energetic modes in the system can be extracted using the singular value decomposition. To give an idea of its capabilities, Masoumi-Verki et al. [72] reported that, within the wake region of an isolated high-rise building, the contribution of the first 30 POD modes to the total turbulent kinetic energy was about 80.89% and 81.39%, respectively. The total number of wind fields used to calculate the PODs was 4500. Considering that their simulation had approximately 2 million cells, this implies that, instead of storing the 108 Gb of their initial data, they could reconstruct 80% of the kinetic energy using just 1Gb of data. The compression rate improves as the size of the simulations and the number of snapshots increase.

Contrary to the POD, the dynamic mode decomposition computed the modes based on the dynamics of the system rather than the energy content [73]. A POD mode may contain a continuous frequency spectrum, while each DMD mode is characterized by a single frequency. This is a major difference between the two methods, innately. Sometimes, if a flow structure contains relatively small energy but is strongly connected to other structures sharing the same frequency, this structure is likely to be ignored by POD analysis but would be captured by the DMD. However, up to this day, PODs are still the most widely used linear technique [74,75,76,77,78].

Of course, the major drawback of both the POD and the DMD is their linear nature. They project the wind field snapshots in an optimal linear subspace. However, the non-linear nature of the Navier-Stokes equations and the dynamic boundary conditions [79,80] can penalize the performance of these algorithms. It is for these reasons that many authors argue that using linear dimensionality reduction techniques is not the most suitable choice for urban wind now-casting [70].

This hypothesis has been supported by several studies comparing POD techniques with nonlinear methods based on encoders [80]. The nonlinear approaches performed better in obtaining a low-dimensional model of the original data. Other investigations based on nonlinear reduction may be found in [79,80,81]. At the present time, research is also being conducted on deep learning methods [82] with promising results.

6. Data Assimilation and Validation

Finally, to check the performance and to improve the reliability of the CFD simulations, it is necessary to validate the results. This can be done using wind tunnel experiments [83]. This approach faces the challenge of actually being able to produce realistic wind conditions, in spite of the cost of building the test models and of the wind tunnel operation. The second option is to deploy multiple wind sensors throughout the city under study and to compare the measurements recorded by the instruments to the results of the simulations for specific wind conditions. As sensors, one may find a wide range of solutions from meteorological stations [84] to LIDAR instruments [61,85], such as in Figure 8, satellites [86], and/or other more innovative methods [87].

Despite all previous efforts, it is unlikely that the predictions made are completely accurate, i.e., they must be adjusted according to the measurements made by a network of sensors distributed throughout the city. In this manner, data assimilation using wind sensors located within the urban canopy offers promising possibilities to enhance the reliability of the predictions.

Considerable studies have discussed how to accomplish this data assimilation. The different algorithms rely mainly on either variational principles [88], nonlinear Kalman filters [89], and/or Bayesian techniques [90].

Under that premise, there are currently several ongoing studies that have addressed the use of real wind measurements from UAVs to solve the inverse problem of predicting wind conditions as it flies over the city [91]. The most common method to do it is the use of a particle filter in combination with a surrogate model [92,93].

Although the results are encouraging, it should be noted that, due to the large size of cities and the high variability of winds around buildings, the number of sensors required is expected to be relatively high. For this reason, and also due to the cost of acquisition and maintenance of wind sensors, it is essential to optimize their distribution. This optimization has been studied in several studies, such as [94,95].

7. Conclusions

Currently, the implementation of U-space in urban environments requires now-casting techniques that can accurately estimate wind fields and turbulence levels. Since the resolution of mesoscale models is not sufficient and CFD models require too much simulation time, the most suitable solution is to use a machine-learning algorithm trained with a large dataset of wind field data. In this review, we have collected the key steps for the elaboration of this database: choice of the turbulence model, creation of the mesh, interpolation of the boundary conditions from the mesoscale fields, and the necessary order reduction methods.

Due to the high number of wind field required to train the prediction algorithms, the use of RANS-type turbulence models is preferable. The $k-ϵ$ models are currently a standard for this type of study, although it is necessary to modify the closure turbulence.

Concerning the meshing, obtaining the digital model of the terrain and the buildings is one of the most difficult steps. Other recommendations are: to use hexahedral cells to reduce numerical diffusion, to adequately refine the high gradient zones, and to perform the corresponding sensitivity analysis of the mesh.

The initial and boundary conditions are to be interpolated from the mesoscale model results. The Cressman interpolation is outstanding for this purpose, except for the cells closest to the ground, where the logarithmic law must be considered. For determining the viscous dissipation, there are several alternatives, which have been described in this document.

In the post-processing phase, the result is to reduce the size of the wind fields as much as possible while preserving their most relevant characteristics. With more conventional techniques, such as POD or DMD, compression ratios of up to 100 can be achieved. This rate can be increased even further by means of nonlinear methods, the study of which is currently on the rise.

Finally, it is important to highlight the relevance of making these databases publicly accessible. In this way, the different now-casting algorithms could be tested, trained, and validated using the same data, encouraging their continuous evolution.