Two Methods to Improve the Efficiency of Supersonic Flow Simulation on Unstructured Grids
Abstract
:1. Introduction
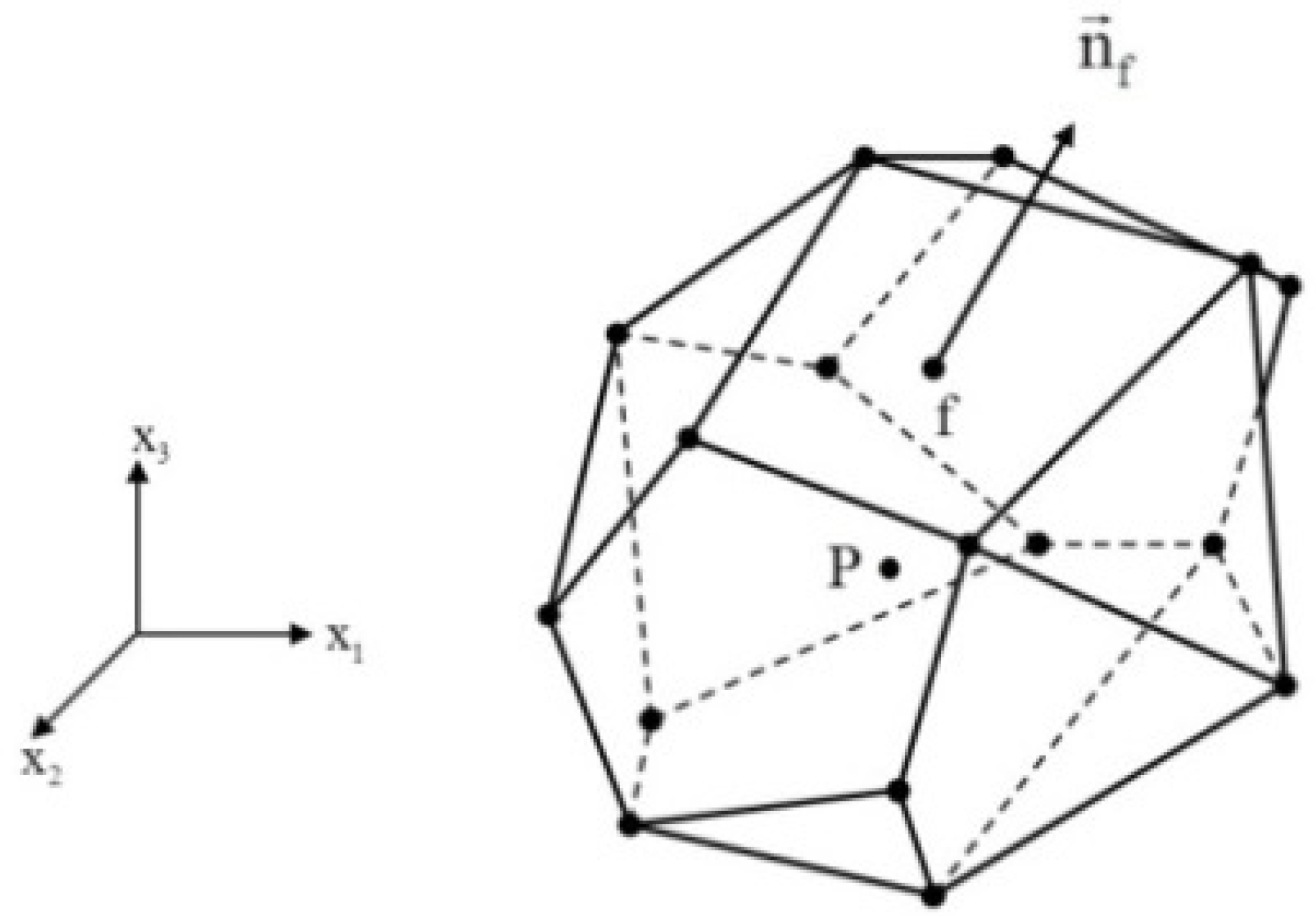
2. Basic Equations
3. The Multigrid Method for Starting Initialization
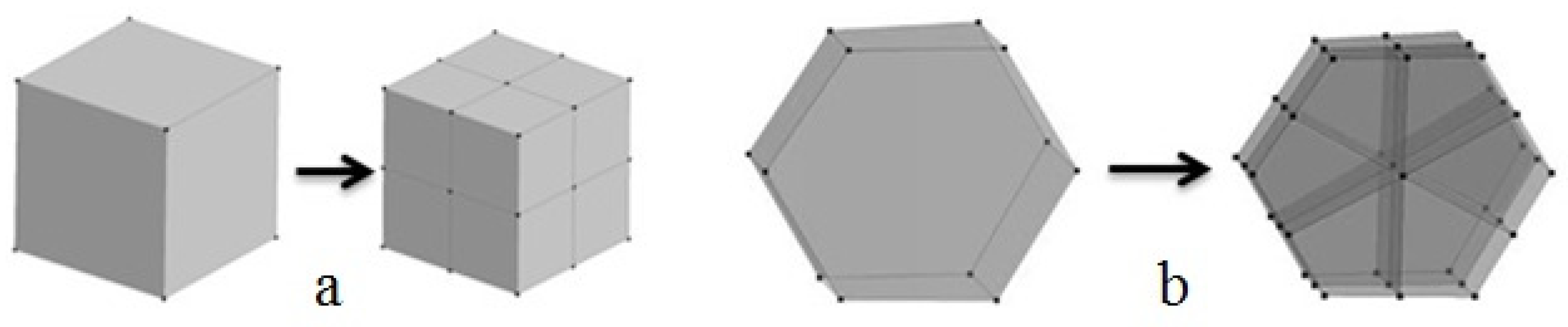
3.1. Generation of Coarse Grids
3.2. An Algorithm of Solving a Problem on a Series of Coarse Grids
- Grids of the current level are built according to the given size of cells.
- To build a coarse-level grid, a list of cell faces of the original grid, which are faces of macro cells of the current grid level, is generated.
- On each external face of original grid’s cells, flows are calculated according to the imposed boundary condition.
- Interprocessor communications are performed.
- The computation termination criterion is verified at the given level of coarsening.
- The termination criterion is verified for the multigrid initialization procedure. With the maximum 7th grid coarsening achieved, or with a minimum number of cells of the original grid less than 50, the basic loop with respect to grid levels is terminated.
- Then, the iterative process of solving the problem on the original grid runs.
4. The Static Adaptation Method
4.1. An Algorithm of Refining Cells
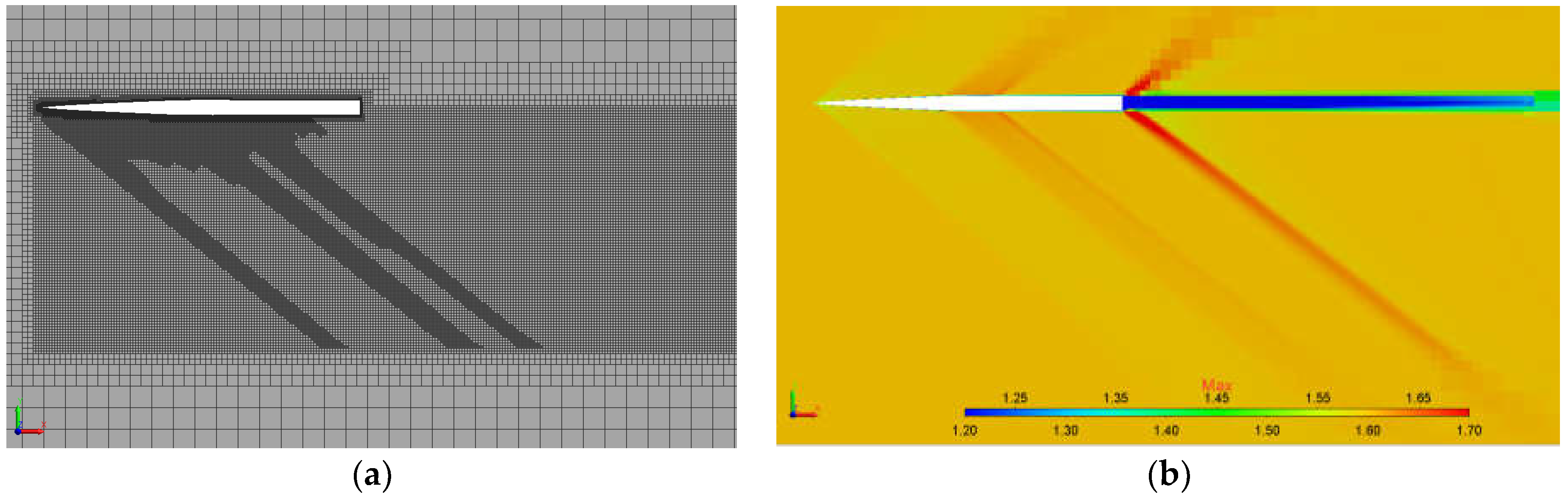
4.2. Computational Grid Adaptation Criteria
5. Numerical Tests
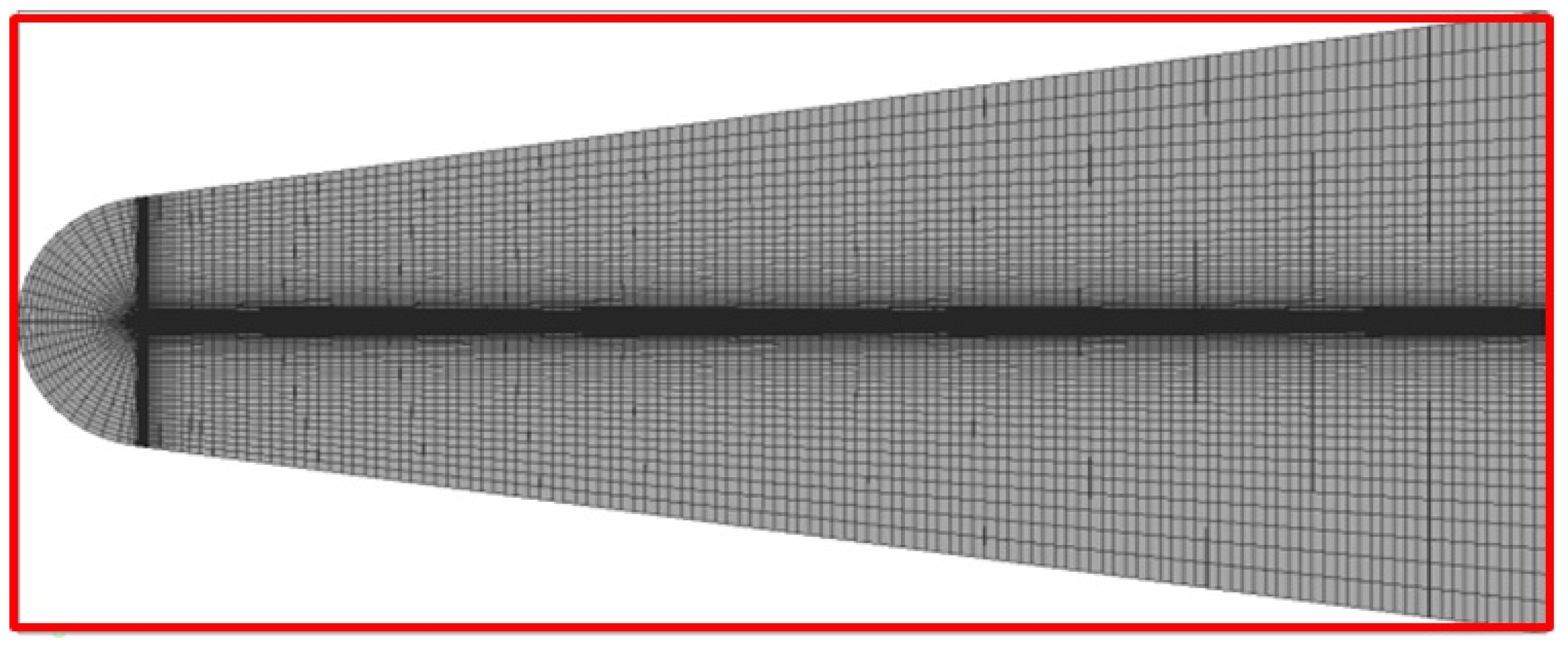
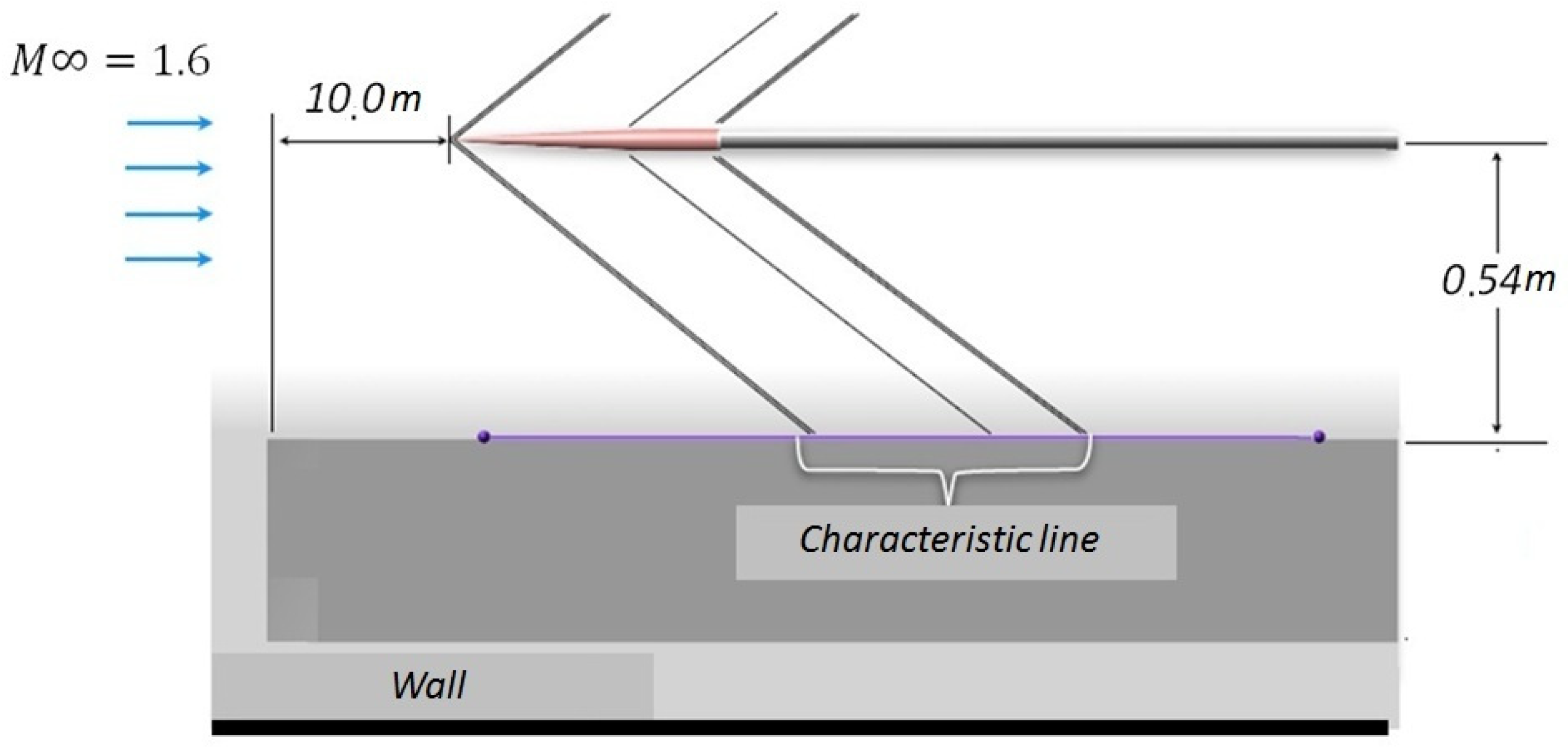
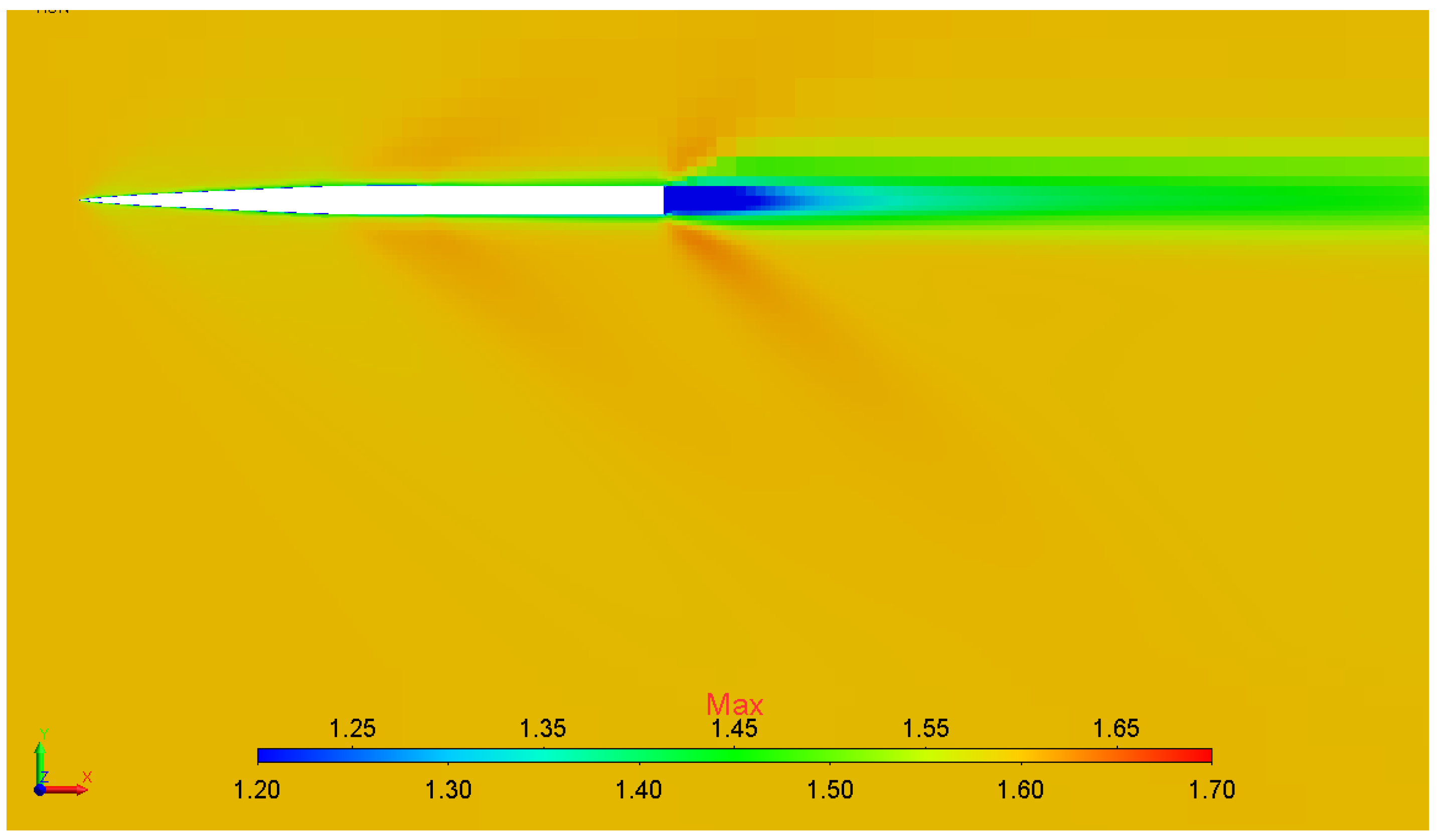
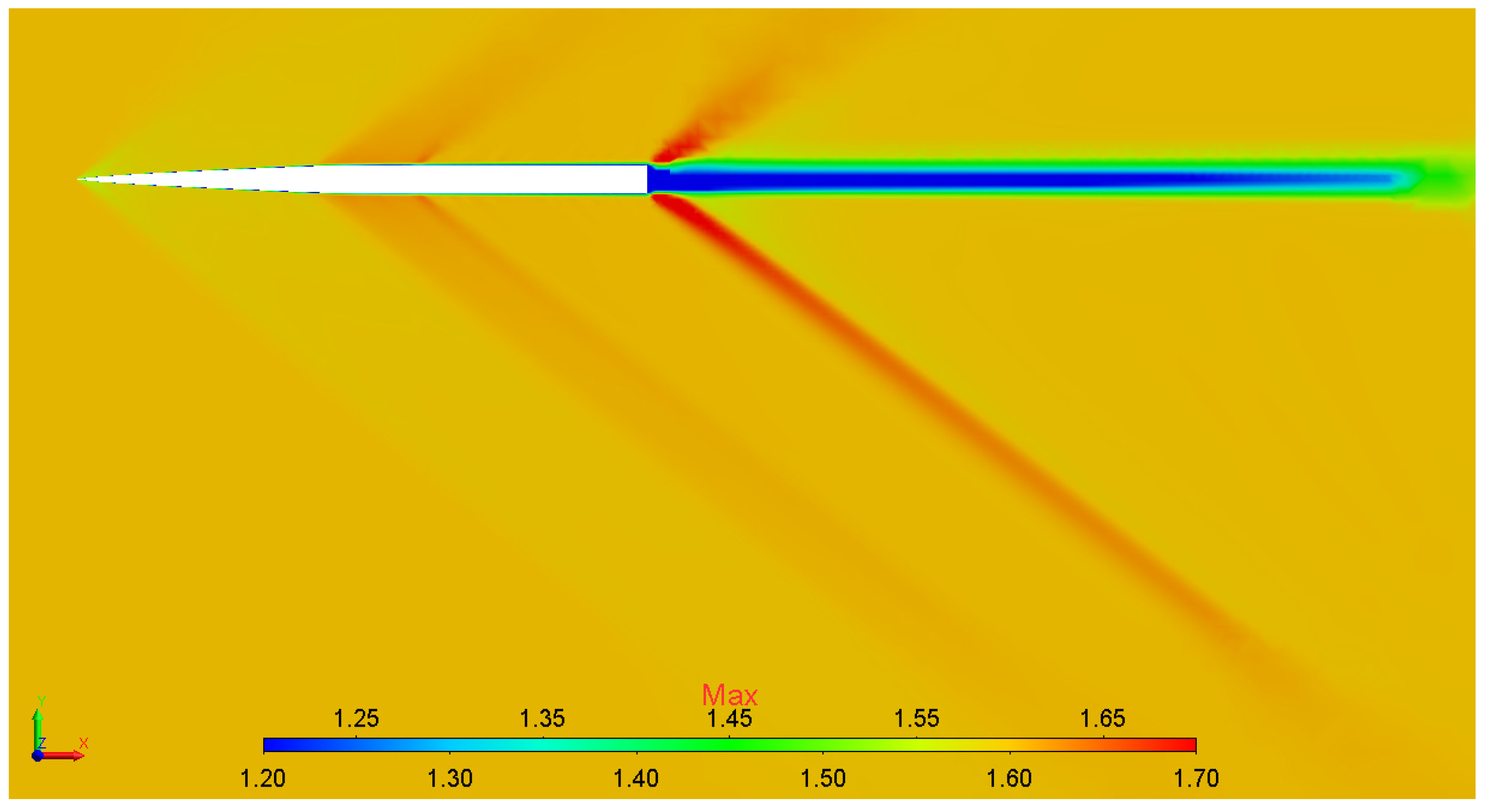
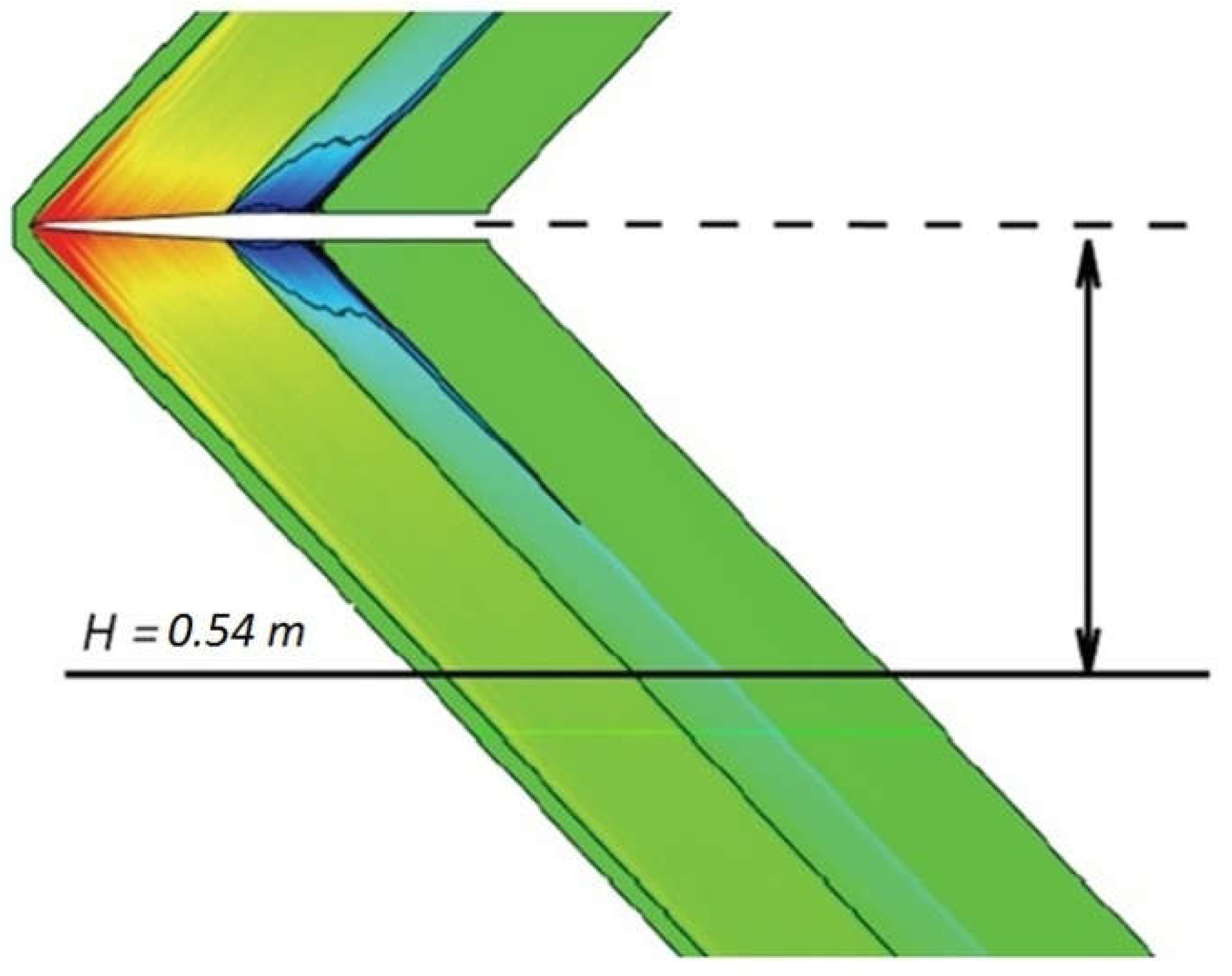
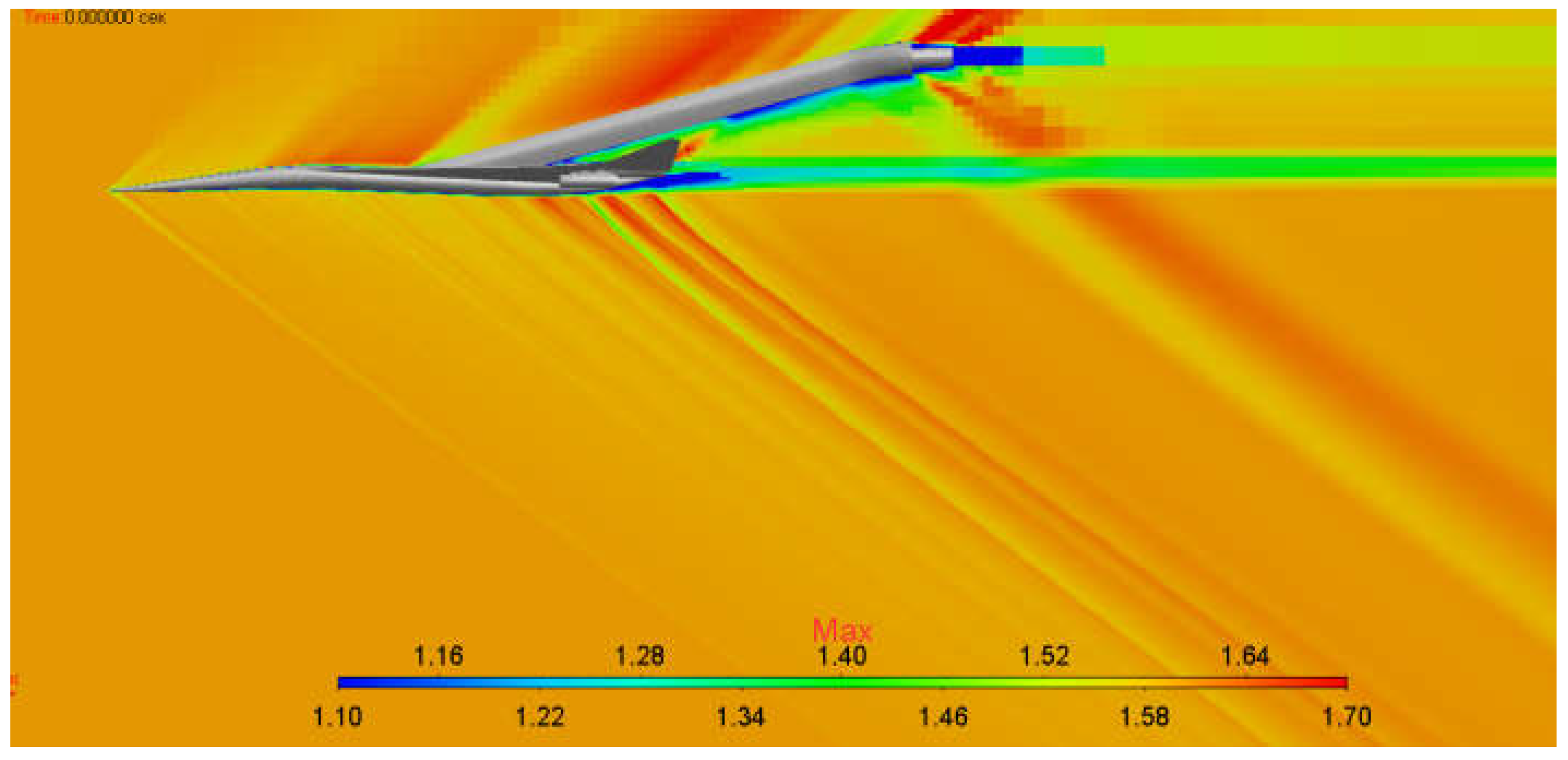
5.1. Simulation of a Supersonic Flow around an Axially Symmetric Body (Seeb-ALR)
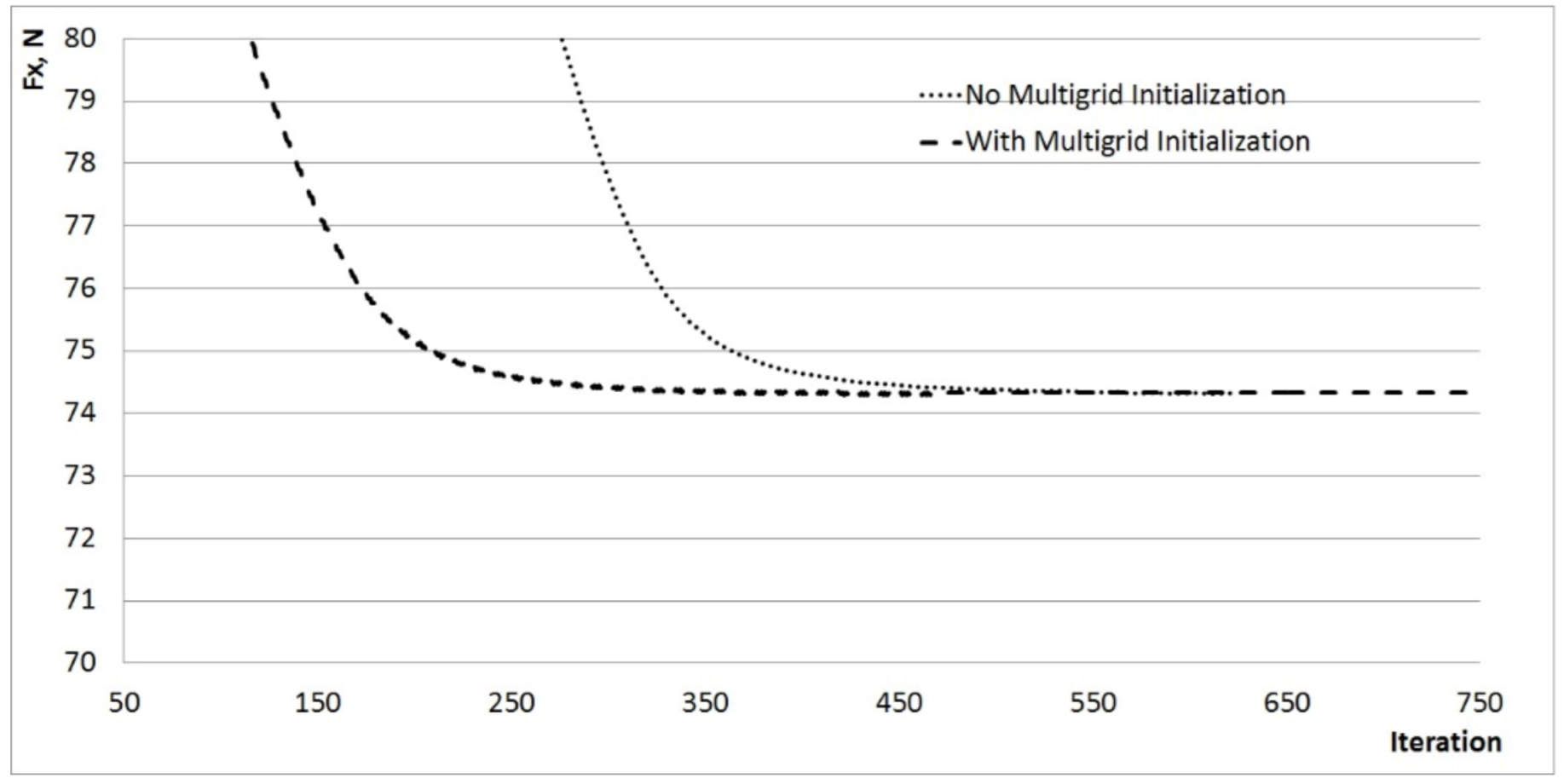
- The method of preliminary multigrid initialization provides up to a 20% increase in the solution convergence rate.
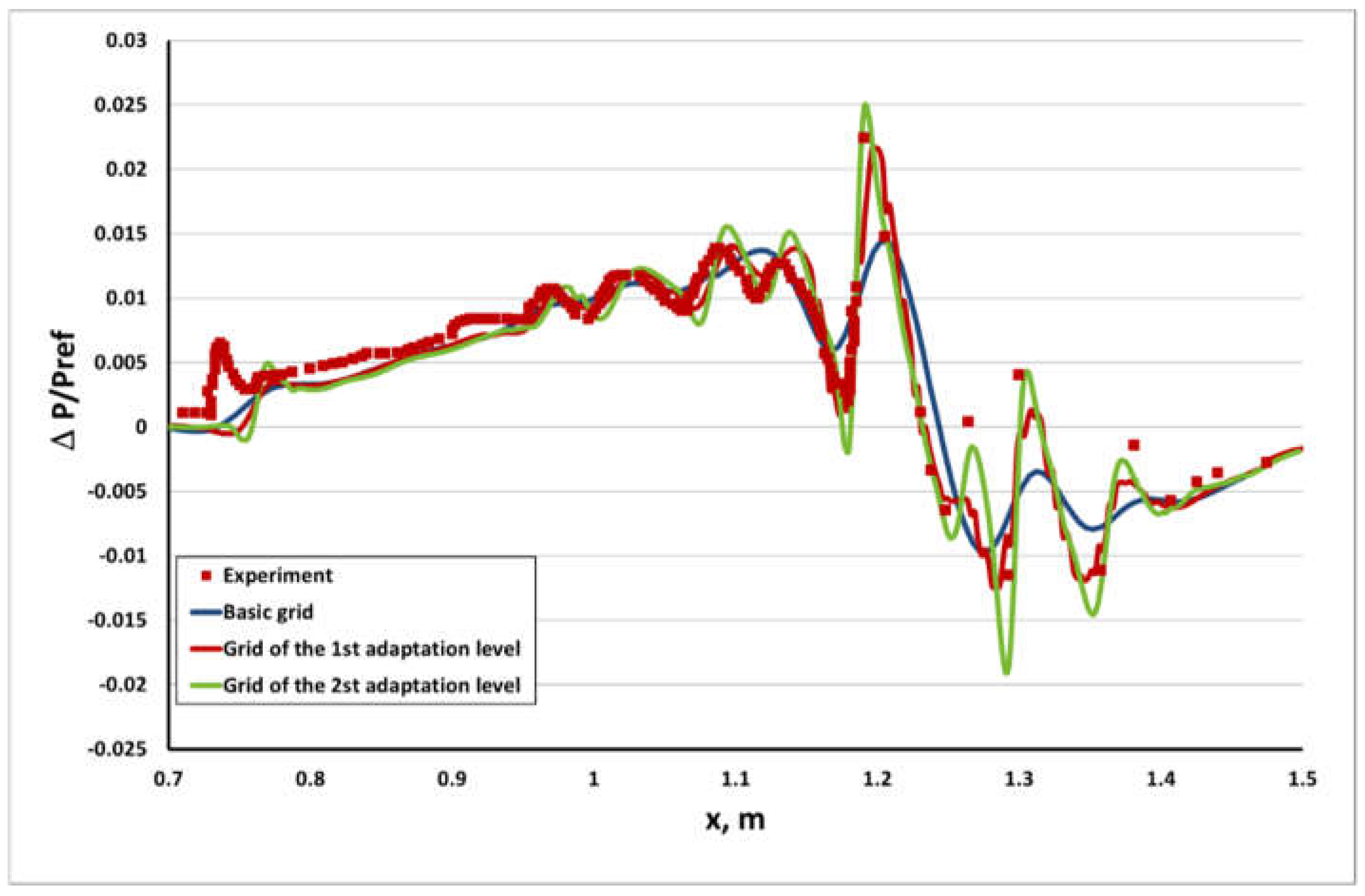
- The static adaptation algorithm provides efficient automatic generation of a computational model and allows the grid convergence of solution to be gained.
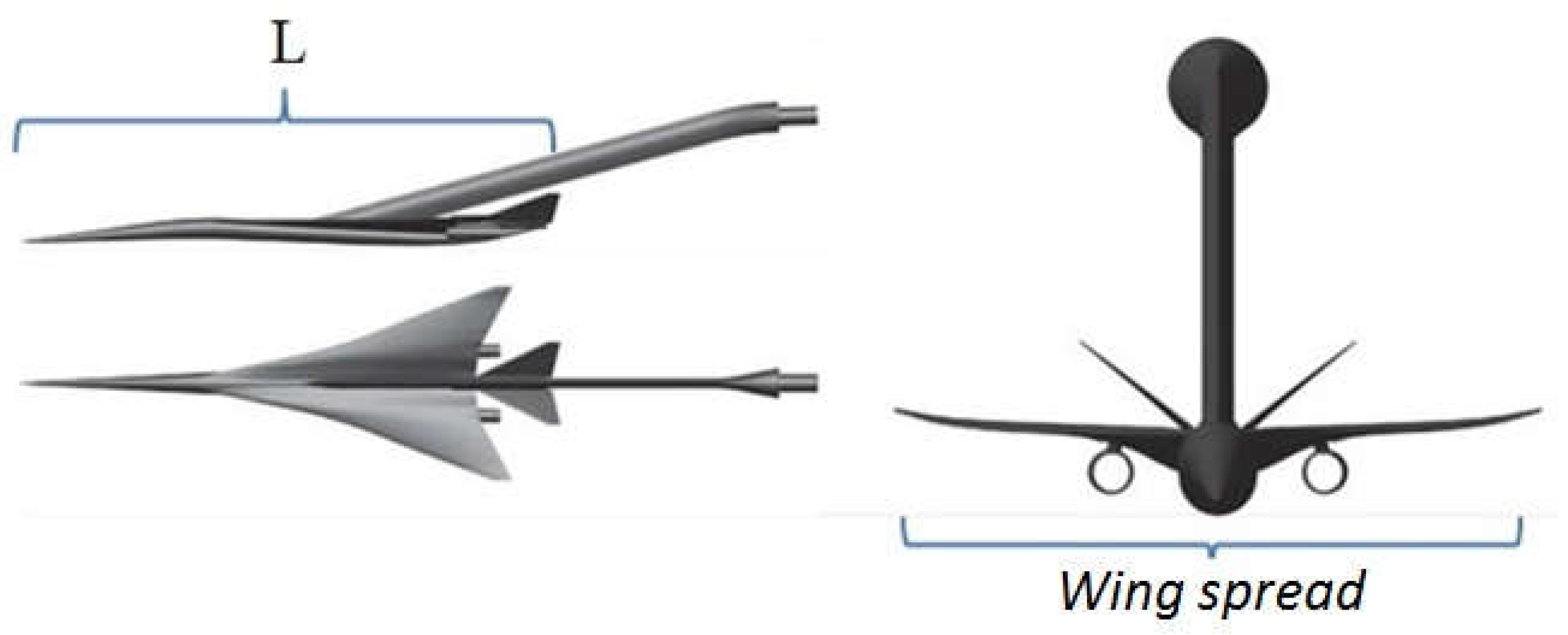
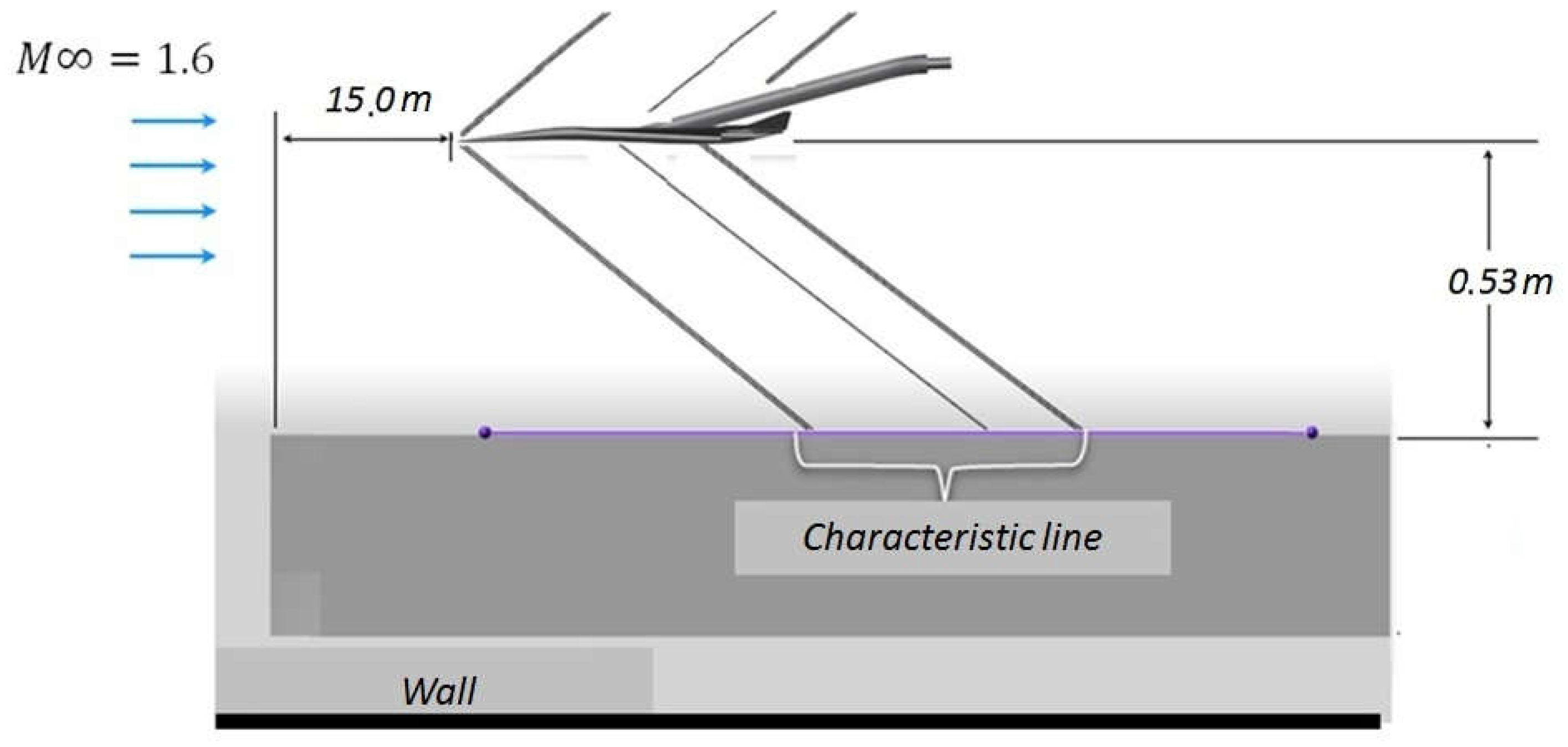
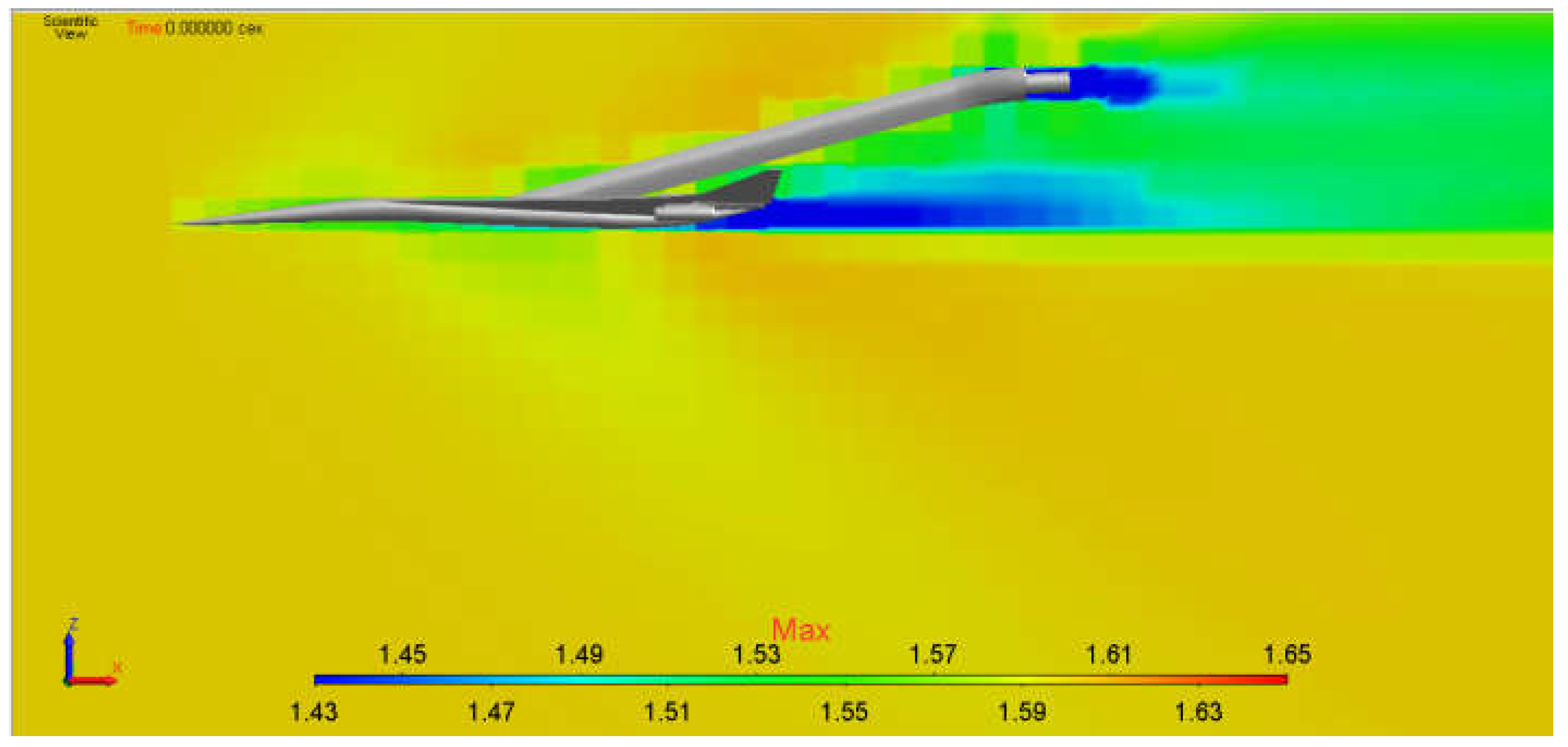
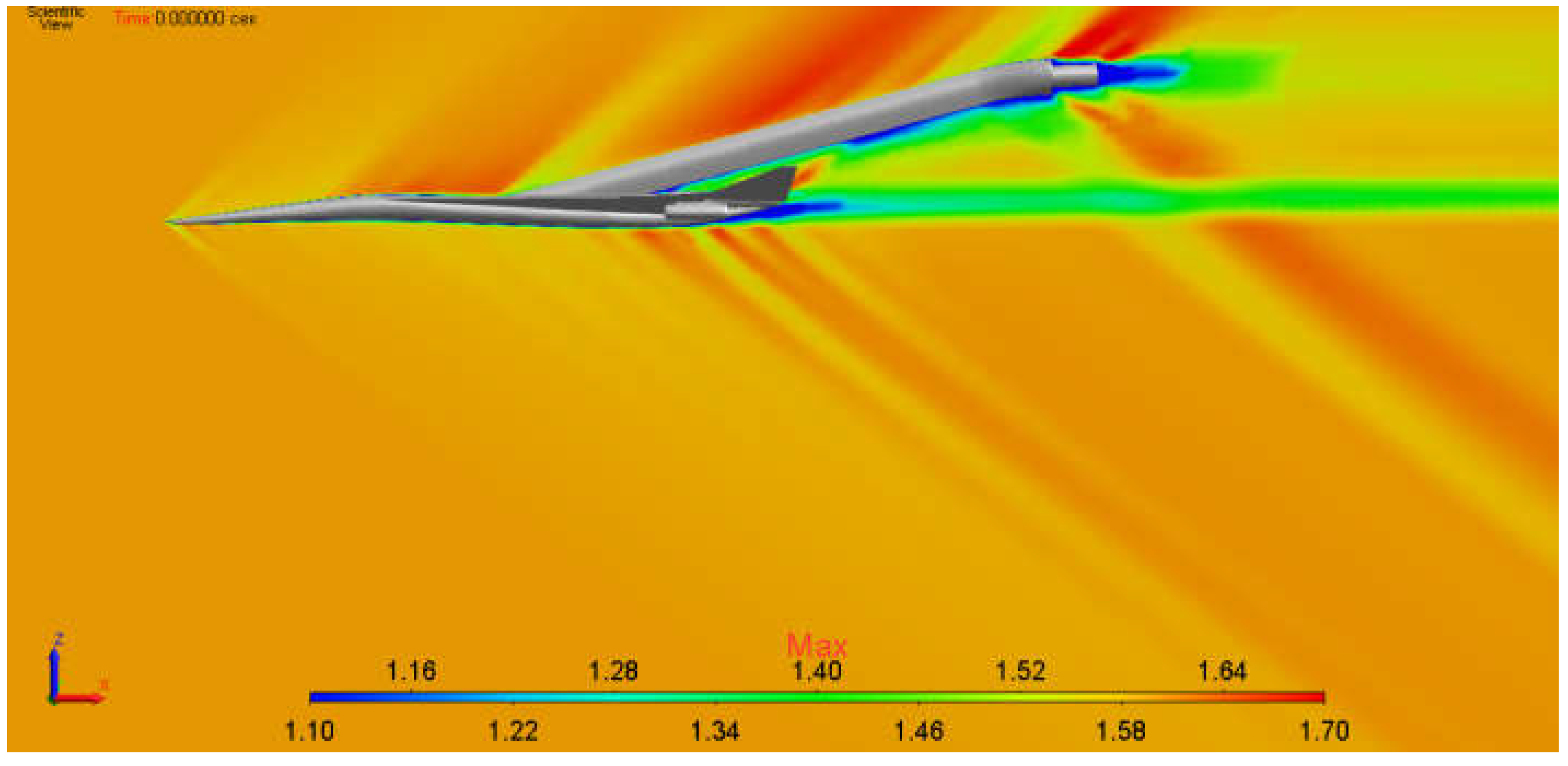
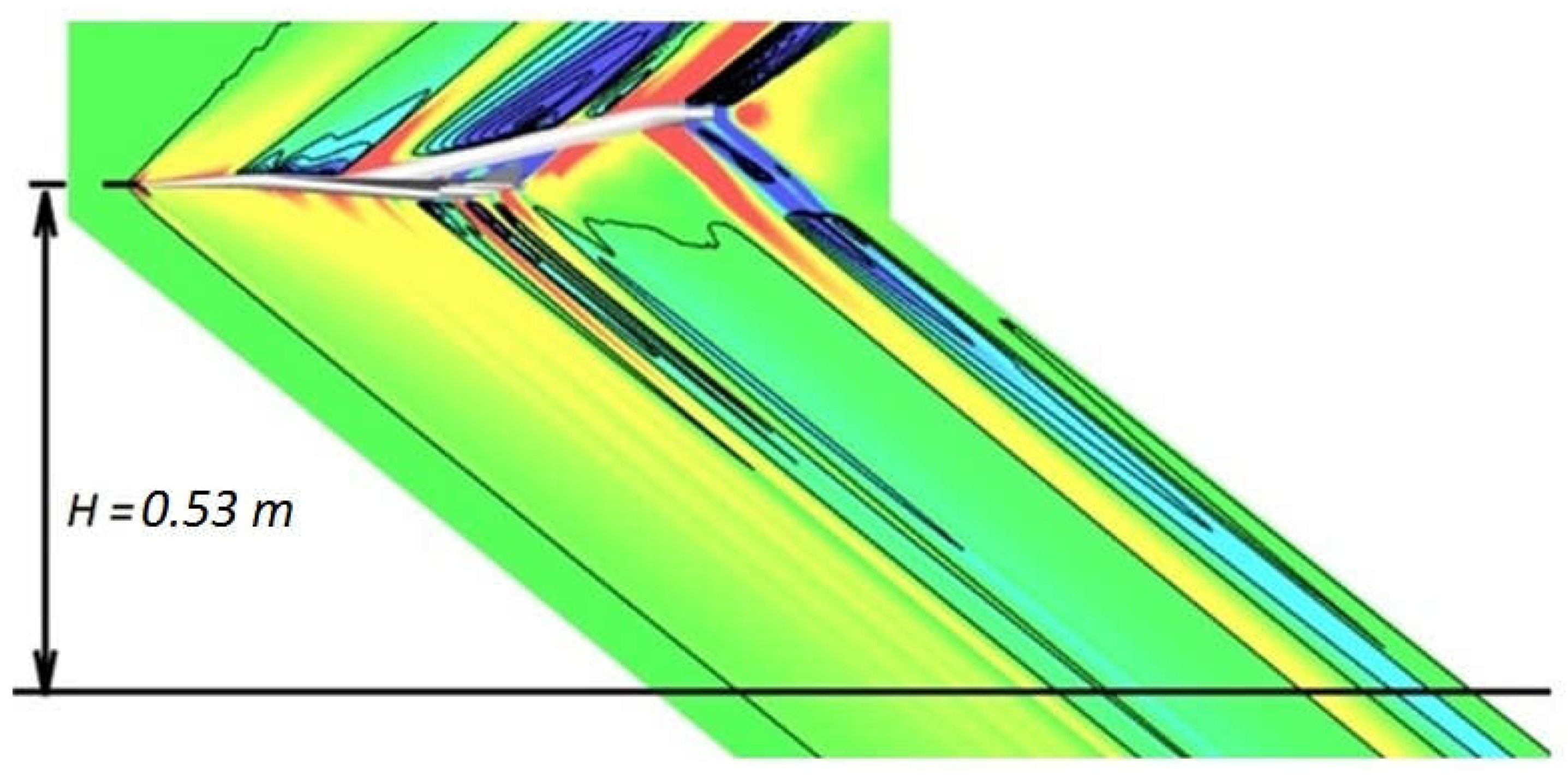
5.2. Simulation of Supersonic Flow around a Model of Aircraft Lockheed Martin 1021 (LM1021)
- The method of preliminary multigrid initialization allows increasing the solution convergence rate up to almost 20%;
- The static adaptation algorithm provides efficient generation of a computational model that allows obtaining a more accurate solution owing to the local grid refinement in the shock-wave region and gaining the grid convergence of solution.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dmitriev, S.M.; Kozelkov, A.S.; Kurkin, A.A.; Legchanov, M.A.; Tarasova, N.V.; Kurulin, V.V.; Efremov, V.R.; Shamin, R. Simulation of turbulent convection at high Rayleigh numbers. In Modeling and Simulation in Engineering; Hindawi Publishing Corporation: London, UK, 2018; Volume 5781602. [Google Scholar]
- Kozelkov, A.S.; Krutyakova, O.L.; Kurulin, V.V.; Lashkin, S.V.; Tyatyushkina, E.S. Application of numerical schemes with singling out the boundary layer for the computation of turbulent flows using eddy-resolving approaches on unstructured grids. Comput. Math. Math. Phys. 2017, 57, 1036–1047. [Google Scholar] [CrossRef]
- Kozelkov, A.S.; Kurulin, V.V.; Lashkin, S.V.; Shagaliev, R.M.; Yalozo, A.V. Investigation of Supercomputer Capabilities for the Scalable Numerical Simulation of Computational Fluid Dynamics Problems in Industrial Applications. Comput. Math. Math. Phys. 2016, 56, 1506–1516. [Google Scholar] [CrossRef]
- Volkov, K.N.; Kozelkov, A.S.; Lashkin, S.V.; Tarasova, N.V.; Yalozo, A.V. A Parallel Implementation of the Algebraic Multigrid Method for Solving Problems in Dynamics of Viscous Incompressible Fluid. Comput. Math. Math. Phys. 2017, 57, 2030–2046. [Google Scholar] [CrossRef]
- Kozelkov, A.S. The Numerical Technique for the Landslide Tsunami Simulations Based on Navier-Stokes Equations. J. Appl. Mech. Tech. Phys. 2017, 58, 1192–1210. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Cham, Switzerland, 2002; 431p. [Google Scholar]
- Wesseling, P.; Oosterlee, C.W. Geometric multigrid with applications to computational of fluid dynamics. J. Comput. Appl. Math. 2001, 128, 311–334. [Google Scholar] [CrossRef]
- Kozelkov, A.S.; Kurulin, V.V. Eddy resolving numerical scheme for simulation of turbulent incompressible flows. Comput. Math. Math. Phys. 2015, 55, 1255–1266. [Google Scholar] [CrossRef]
- Caraeni, D.; Weiss, J.; Smith, W.; Snyder, D.; Halliday, N.; Clement, J. Continuity Convergence Acceleration of a Density-Based Coupled Algorithm. In Fluid Dynamics and Co-Located Conferences, Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; AIAA: Reston, VA, USA, 2013; pp. 2013–2962. [Google Scholar]
- Tsoutsanis, P.; Titarev, V.A.; Drikakis, D. WENO schemes on arbitrary mixed-element unstructured meshes in three space dimensions. J. Comput. Phys. 2010, 230, 1585–1601. [Google Scholar] [CrossRef] [Green Version]
- Weizhang, H.; Russell, R.D. Adaptive Moving Mesh Methods; Springer: New York, NY, USA, 2011; 434p. [Google Scholar]
- Plewa, T.; Linde, T.; Weirs, V. (Eds.) Adaptive mesh refinement—Theory and applications. In Proceedings of the Chicago Workshop on Adaptive Mesh Refinement Methods, Chicago, IL, USA, 3–5 September 2003; Springer: Cham, Switzerland, 2005. [Google Scholar]
- Zegeling, A. Theory and application of adaptive moving grid methods. In Adaptive Computations: Theory and Algorithms; Tang, T., Xu, J., Eds.; Mathematics Monograph Series 6; Science Press: Beijing, China, 2007; pp. 279–332. [Google Scholar]
- Arslanbekov, R.R.; Kolobov, V.I.; Frolova, A.A. Kinetic solvers with adaptive mesh in phase space. Phys. Rev. E 2013, 88, 063301. [Google Scholar] [CrossRef] [Green Version]
- Baranger, C.; Claudel, J.; Herouard, N.; Mieussens, L. Locally refined discrete velocity grids for stationary rarefied flow simulations. J. Comput. Phys. 2014, 257, 572–593. [Google Scholar] [CrossRef] [Green Version]
- Struchkov, A.V.; Kozelkov, A.S.; Volkov, K.; Kurkin, A.A.; Zhuchkov, R.N.; Sarazov, A.V. Numerical simulation of aerodynamic problems based on adaptive mesh refinement method. Acta Astronaut. 2020, 172, 7–15. [Google Scholar] [CrossRef]
- Efremov, V.; Kozelkov, A.; Dmitriev, S.; Kurkin, A.; Kurulin, V.; Utkin, D. Technology of 3D Simulation of High-Speed Damping Processes in the Hydraulic Brake Device. In Modeling and Simulation in Engineering; Volkov, K., Ed.; Kingston University: London, UK, 2018. [Google Scholar]
- Tyatyushkina, E.S.; Kozelkov, A.S.; Kurkin, A.A.; Pelinovsky, E.N.; Kurulin, V.V.; Plygunova, K.S.; Utkin, D.A. Verification of the LOGOS Software Package for Tsunami Simulations. Geosciences 2020, 10, 385. [Google Scholar] [CrossRef]
- Waithe, K. Introduction of First Low Boom Prediction Workshop. In Proceedings of the 51st AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 7–10 January 2013; AIAA: Reston, VA, USA, 2013; Volume 650. [Google Scholar]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows; Department of Mechanical Engineering Imperial College of Science, Technology and Medicine: London, UK, 1996; 394p. [Google Scholar]
- Spalart, P.R.; Allmaras, S.R. A one equation turbulence model for aerodynamic flows. AIAA Pap. 1992, 92–0439. [Google Scholar] [CrossRef]
- Shur, M.L.; Strelets, M.K.; Travin, A.K.; Spalart, P.R. Turbulence Modeling in Rotating and Curved Channels: Assessing the Spalart-Shur Correction. AIAAJ 2000, 38, 784–792. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence modeling for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Chakravarthy, S.R.; Osher, S. A new class of high-accuracy TVD schemes for hyperbolic conservation laws. AIAA Pap. 1985, 85–0363. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Rieman problem solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar]
- Cliff, S.E. Computational and Experimental Assessment of Models for the First IAA Sonic Boom Prediction Workshop. In Proceedings of the 52st AIAA Aerospace Sciences Meeting, National Harbor, Maryland, 13–17 January 2014. [Google Scholar]











| Calculation Method | Initialization | Calculation Time before Convergence | Total Time |
|---|---|---|---|
| With multigrid initialization | 40 s | 400 s (1 iteration—1 s) | 440 s |
| Without multigrid initialization | – | 550 s (1 iteration—1 s) | 550 s |
| Grid | Number of Cells |
|---|---|
| Basic grid | 2.5 million |
| Grid of the 1st adaptation level | 4.9 million |
| Grid of the 2nd adaptation level | 21.4 million |
| Grid of the 3rd adaptation level | 67.5 million |
| Calculation Method | Initialization | Calculation Time before Convergence | Total Time |
|---|---|---|---|
| With multigrid initialization | 46.44 s | 366.36 s (1 iteration—1.032 s) | 412.8 s |
| Without multigrid initialization | – | 516 s (1 iteration—1.032 s) | 516 s |
| Grid | Number of Cells |
|---|---|
| Basic grid | 4.5 million |
| Grid of the 1st adaptation level | 10 million |
| Grid of the 2nd adaptation level | 52.2 million |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozelkov, A.S.; Struchkov, A.V.; Strelets, D.Y. Two Methods to Improve the Efficiency of Supersonic Flow Simulation on Unstructured Grids. Fluids 2022, 7, 136. https://doi.org/10.3390/fluids7040136
Kozelkov AS, Struchkov AV, Strelets DY. Two Methods to Improve the Efficiency of Supersonic Flow Simulation on Unstructured Grids. Fluids. 2022; 7(4):136. https://doi.org/10.3390/fluids7040136
Chicago/Turabian StyleKozelkov, Andrei S., Andrei V. Struchkov, and Dmitry Y. Strelets. 2022. "Two Methods to Improve the Efficiency of Supersonic Flow Simulation on Unstructured Grids" Fluids 7, no. 4: 136. https://doi.org/10.3390/fluids7040136
APA StyleKozelkov, A. S., Struchkov, A. V., & Strelets, D. Y. (2022). Two Methods to Improve the Efficiency of Supersonic Flow Simulation on Unstructured Grids. Fluids, 7(4), 136. https://doi.org/10.3390/fluids7040136






