From Darcy Equation to Darcy Paradox

Abstract

This theoretical paper focuses on the single-phase fluid flow through a granular porous medium. The emphasis is on the Darcy flow regime (without free boundary) of a linear viscous fluid in a saturated, deformable, homogeneous porous medium. The approach is developed at the Darcy scale (also referred to as macroscale or phenomenological scale). Within this framework, some discrete aspects of the flow model are highlighted, the governing equations are revisited, the thermodynamic state functions are reconsidered, and the Darcy paradox is presented. The Darcy paradox is illustrated for the isoshoric-isothermal flow of a viscous fluid in the liquid state, in a homogenous porous medium. After some remarks about the intrinsic assumption of this kind of flow, the governing equations are reduced to a well-known parabolic equation. According to this equation, infinitesimal pressure disturbances diffuse at an infinite speed. To remove this paradox, a mathematical model, based on the elementary scales method, is employed.

1. Introduction

The phenomenological description of the fluid flow through porous media, which is very attractive (e.g., [1,2,3,4,5,6,7]), can give rise to a variety of paradoxes. For instance, the viscous-capillary paradox [8], which emerges in the context of multi-phase flow, or the paradox involving viscous dissipation in non-Darcy flow regime [9]. Focusing on the single-phase flow through a granular porous medium, a new paradox, called the Darcy paradox, is presented. Taking a cue from this paradox, this paper examines some fundamental topics of the fluid flow through porous media. The emphasis is on the Darcy flow regime (without free boundary) of a linear viscous fluid in a saturated, deformable, homogeneous porous medium. The porous medium deformation, which is regarded as a reversible quasi-static process, is linked to the rigid grains rearrangement (the ratio between the bulk elastic moduli of the fluid and the grains is assumed so small that the grains are modeled as rigid). The theoretical approach is developed at the Darcy scale (also referred to as macroscale or phenomenological scale): using the continuum approach [10], the heterogeneous medium (the linear viscous fluid plus the porous medium) is replaced by a continuum medium, the apparent fluid, consisting of apparent fluid particles. The apparent fluid flow is described in terms of apparent field functions (e.g., density $\rho$, pressure p, velocity $\mathit{v}$, temperature T, ⋯). In agreement with spatio-temporal continuity of the motion [11,12], the method of homogenization assumes that all the field functions are regular functions of both space $\mathit{r}$ and time t. The continuity in space involves the continuum hypothesis: the apparent fluid particles are, virtually, in one-to-one correspondence with the points of the Euclidean space. The size of the apparent fluid particles coincides with the Representative Elementary Volume (REV) $dV$. The REV, which is required for any continuous macroscopic representation of the material systems, is large compared to the grains size and small compared to the size of the flow domain [13]. According to this, the continuity in the space implies that $\frac{l}{\left|d\mathit{r}\right|}\ll 1$, where l is a characteristic length of the material system, $\left|d\mathit{r}\right|$ the elementary spatial scale (the REV scale). Within the framework of the Classical Continuum Thermomechanics (CCT), the continuity in the time requires that $\frac{t_r}{\left|dt\right|}\ll 1$, where $t_r$ is the relaxation time (the interval time required to restore a Local Thermodynamic Equilibrium (LTE) condition in place of a local thermodynamic non-equilibrium condition), $\left|dt\right|$ the elementary time scale. Within the framework of CCT:

• $b(\mathit{r}\pm \delta \mathit{r})=b\left(\mathit{r}\right)$ for $\left|\delta \mathit{r}\right|<\left|d\mathit{r}\right|$ and $b(t\pm \delta t)=b\left(t\right)$ for $\left|\delta t\right|<\left|dt\right|$, where $b=b(\mathit{r},t)$ is the generic (scalar, vector or tensor) apparent field function;
• if $\left|db\right|$ is the elementary scale of b, then $b\pm \delta b=b$ for $\left|\delta b\right|<\left|db\right|$;
• the field functions are well defined in both $\mathit{r}$ and t;
• the apparent fluid is in LTE condition.

From a thermomechanic point of view, the Darcy flow regime corresponds to the Linear Non-Equilibrium Regime (LNER). The LNER, which is characterized by small values of $\parallel \nabla \mathit{v}\parallel$ and $|\nabla T|$, is stable and regular: a perturbation of the mechanical and thermodynamic state regresses during the evolution of the motion. In Fluid Mechanics, the LNER is referred to as viscous flow regime. Within the framework of CCT, the thermomechanics description of the Darcy flow regime is formulated using classical irreversible thermodynamics, in addition to Newtonian mechanics. On this topic, in Section 2, the conservation equations of mass, momentum, mechanical energy, internal energy, entropy are given, the thermodynamics relationships are formalized, and the transport theorem and the Reynolds theorem are illustrated. In Section 3, the general flow problem is reformulated for the isochoric-isothermal flow of a viscous fluid, in the liquid state, in a homogenous porous medium. Within this framework, the constitutive equations are examined, the momentum equation is reduced to Darcy equation, and some intrinsic approximations and intrinsic characteristics of the proposed model are discussed. After reducing the governing flow equations to a well-known parabolic [10], Section 4 is devoted to illustrating and elucidating the Darcy paradox: the parabolic equation shows infinitesimal pressure disturbances that diffuse at an infinite speed. To remove this paradox, a mathematical model based on the elementary scales method [14] is employed. According to this method, which is founded on the introduction of other elementary scales next to $\left|d\mathit{r}\right|$ and $\left|dt\right|$, the Darcy paradox is only apparent. Finally, the conclusions are presented in Section 5.

2. General Conservation Equations

In this section, the general conservation equations for the Darcy flow regime (without free boundary) of a linear viscous fluid in a saturated, deformable, homogeneous, anisotropic porous medium are deduced. The porous medium deformation is linked to rigid grains rearrangement which occurs during a reversible quasi-static process. Using the method of homogenization, the linear viscous fluid and the porous medium are replaced by a continuum medium, referred to as the apparent fluid. At the Darcy scale, the mass and the momentum conservation equations which govern the apparent fluid flow are given as [15]:

$$\frac{D}{Dt}\left(\eta \rho \right)+\eta \rho \nabla ·\left(\frac{\mathit{v}}{\eta }\right)=0$$

(1)

$$\eta \rho \frac{D}{Dt}\left(\frac{\mathit{v}}{\eta }\right)=-\eta \rho \mathit{f}-\nabla \left(\eta p\right)-\nabla ·{\underline{\mathit{T}}}_{vis}$$

(2)

where $\eta$ is the porosity; $\rho$ the density; $\mathit{v}$ the Darcy velocity; $\mathit{f}=-\mathit{g}=-g{\widehat{\mathit{e}}}_{\mathit{z}}=-g\nabla z$, with $\mathit{g}$ the vector of gravitational acceleration, $g=\left|\mathit{g}\right|$, ${\widehat{\mathit{e}}}_{\mathit{z}}$ the unit vector in the vertical direction, z the elevation; p the pressure; ${\underline{\mathit{T}}}_{vis}$ the viscous stress tensor. The apparent field functions $\eta ,\rho ,\mathit{v},\mathit{f},p,$ and ${\underline{\mathit{T}}}_{vis}$, which refer to the apparent fluid, are regular functions of both space $\mathit{r}$ and time t. It should be stressed that $\eta$ is linked to the granular porous medium, $\rho$ is the viscous fluid density, p is the viscous fluid pressure. The material derivative $D/Dt$ is given as:

$$\frac{Db}{Dt}=\frac{\partial b}{\partial t}+\nabla b·\frac{\mathit{v}}{\eta }$$

(3)

The continuity Equation (1) can be deduced by putting:

$$\eta \rho dV={\eta }^{\prime }{\rho }^{\prime }d{V}^{\prime }$$

(4)

where $\eta \rho dV$ is the constant fluid mass in the material REV $dV$ and:

$$\eta =\eta (\mathit{r},t);\rho =\rho (\mathit{r},t);dV=dV(\mathit{r},t)$$

(5)

$$\begin{array}{cc}\hfill {\eta }^{\prime }& ={\eta }^{\prime }({\mathit{r}}^{\prime },t^{\prime })=\eta (\mathit{r}+d\mathit{r},t+dt)\hfill \\ \hfill & =\eta (\mathit{r},t)+\frac{\partial }{\partial t}\eta (\mathit{r},t)dt+\frac{\partial }{\partial \mathit{r}}\eta (\mathit{r},t)·d\mathit{r}\hfill \\ \hfill & =\eta (\mathit{r},t)+\frac{\partial }{\partial t}\eta (\mathit{r},t)dt+\nabla \eta (\mathit{r},t)·d\mathit{r}\hfill \\ \hfill & =\eta (\mathit{r},t)+\frac{\partial }{\partial t}\eta (\mathit{r},t)dt+\nabla \eta (\mathit{r},t)·\frac{\mathit{v}}{\eta }dt\hfill \end{array}$$

(6)

$${\rho }^{\prime }={\rho }^{\prime }({\mathit{r}}^{\prime },t^{\prime })=\rho (\mathit{r},t)+\frac{\partial }{\partial t}\rho (\mathit{r},t)dt+\nabla \rho (\mathit{r},t)·\frac{\mathit{v}}{\eta }dt$$

(7)

$$d{V}^{\prime }=d{V}^{\prime }({\mathit{r}}^{\prime },t^{\prime })=dV(\mathit{r}+d\mathit{r},t+dt)$$

(8)

$${\mathit{r}}^{\prime }=\mathit{r}+d\mathit{r}=\mathit{r}+\frac{\mathit{v}}{\eta }dt$$

(9)

With this setting, the following relationship holds:

$$db=\frac{Db}{Dt}dt=\frac{\partial b}{\partial t}dt+\nabla b·\frac{\mathit{v}}{\eta }dt=\frac{\partial b}{\partial t}dt+\frac{\partial b}{\partial \mathit{r}}·d\mathit{r}$$

(10)

The connection between $dV$ and $d{V}^{\prime }$ is expressed as:

$$d{V}^{\prime }=\left(det\underline{\mathit{J}}\right)dV=JdV$$

(11)

where $\underline{\mathit{J}}$ is the jacobian matrix:

$$\underline{\mathit{J}}=\frac{\partial {\mathit{r}}^{\prime }}{\partial \mathit{r}}=\nabla {\mathit{r}}^{\prime }=\underline{\mathit{I}}+\left(\nabla \frac{\mathit{v}}{\eta }\right)dt$$

(12)

and J the jacobian determinant:

$$J=det\underline{\mathit{J}}=det\left[\underline{\mathit{I}}+\left(\nabla {\displaystyle \frac{\mathit{v}}{\eta }}\right)dt\right]$$

(13)

If $\left|\left|\left(\nabla \frac{\mathit{v}}{\eta }\right)dt\right|\right|\ll 1$, Equation (13) is well approximated as [16]:

$$J=1+\left(\nabla ·\frac{\mathit{v}}{\eta }\right)dt$$

(14)

According to Equation (14) and by neglecting the higher-order infinitesimal, Equation (4) reads as:

$$\eta \rho =\eta \rho +\left[\frac{\partial }{\partial t}\left(\eta \rho \right)+\nabla \left(\eta \rho \right)·\frac{\mathit{v}}{\eta }+\left(\nabla ·\frac{\mathit{v}}{\eta }\right)\eta \rho \right]$$

(15)

Equation (15), with Equation (3), leads to the continuity Equation (1):

$$\frac{\partial }{\partial t}\left(\eta \rho \right)+\nabla \left(\eta \rho \right)·\frac{\mathit{v}}{\eta }+\left(\nabla ·\frac{\mathit{v}}{\eta }\right)\eta \rho =\frac{D}{Dt}\left(\eta \rho \right)+\eta \rho \nabla ·\left(\frac{\mathit{v}}{\eta }\right)=\frac{\partial }{\partial t}\left(\eta \rho \right)+\nabla ·\left(\rho \mathit{v}\right)=0$$

(16)

Formally, this line of reasoning assures that: $\forall \nabla \frac{\mathit{v}}{\eta }\exists dt:\frac{t_r}{\left|dt\right|}\ll 1$ and $\left|\left|\left(\nabla \frac{\mathit{v}}{\eta }\right)dt\right|\right|\ll 1$.

In an alternative way, the continuity equation can be deduced by putting:

$$\frac{D}{Dt}\left(\eta \rho dV\right)=dV\frac{D}{Dt}\left(\eta \rho \right)+\eta \rho \frac{D}{Dt}\left(dV\right)=0$$

(17)

Equation (17) reduces to Equation (1) setting:

$$\frac{1}{dV}\frac{D}{Dt}\left(dV\right)=\nabla ·\left(\frac{\mathit{v}}{\eta }\right)$$

(18)

Equation (2) can be deduced writing the integral momentum conservation equation as:

$$\frac{D}{Dt}{\int }_V\eta \rho \left(\frac{\mathit{v}}{\eta }\right)dV={\int }_V\eta \rho \mathit{f}dV-{\int }_V\nabla \left(\eta p\right)dV-{\int }_V\nabla ·{\underline{\mathit{T}}}_{vis}dV$$

(19)

where ${\int }_V\eta \rho \left(\frac{\mathit{v}}{\eta }\right)dV$ is the momentum of the fluid in the material volume V; ${\int }_V\eta \rho \mathit{f}dV$ the external body force; $-{\int }_V\nabla \left(\eta p\right)dV-{\int }_V\nabla ·{\underline{\mathit{T}}}_{vis}dV$ the external surface forces. Using the following identity:

$$\begin{array}{cc}\hfill \frac{D}{Dt}{\int }_V\eta \rho \left(\frac{\mathit{v}}{\eta }\right)dV& ={\int }_V\frac{D}{Dt}\left[\eta \rho \left(\frac{\mathit{v}}{\eta }\right)dV\right]=\hfill \\ & ={\int }_V\eta \rho \frac{D}{Dt}\left(\frac{\mathit{v}}{\eta }\right)dV+{\int }_V\frac{\mathit{v}}{\eta }\frac{D}{Dt}\left(\eta \rho dV\right)={\int }_V\eta \rho \frac{D}{Dt}\left(\frac{\mathit{v}}{\eta }\right)dV\hfill \end{array}$$

(20)

being:

$${\int }_V\frac{\mathit{v}}{\eta }\frac{D}{Dt}\left(\eta \rho dV\right)=0$$

(21)

the integral momentum conservation Equation (19) becomes:

$${\int }_V\eta \rho \frac{D}{Dt}\left(\frac{\mathit{v}}{\eta }\right)dV={\int }_V\rho \eta \mathit{f}dV-{\int }_V\nabla \left(\eta p\right)dV-{\int }_V\nabla ·{\underline{\mathit{T}}}_{vis}dV$$

(22)

According to Equation (22), the (differential) momentum conservation equation is given by Equation (2).

In line with these results, the transport theorem is expressed as:

$$\frac{D}{Dt}{\int }_V\eta \rho bdV={\int }_V\eta \rho \frac{Db}{Dt}dV$$

(23)

while the Reynolds theorem is given as:

$$\begin{array}{cc}\hfill \frac{D}{Dt}{\int }_V\eta \rho bdV& ={\int }_V\frac{\partial }{\partial t}\left(\eta \rho b\right)dV+{\int }_V\nabla ·\left(\eta \rho b\frac{\mathit{v}}{\eta }\right)dV=\hfill \\ \hfill & ={\int }_V\frac{\partial }{\partial t}\left(\eta \rho b\right)dV+{\int }_V\nabla ·\left(\rho b\mathit{v}\right)dV\hfill \end{array}$$

(24)

In the Darcy flow regime, Equation (2) can be well approximated as:

$$\eta \rho \mathit{f}-\nabla \left(\eta p\right)-\nabla ·{\underline{\mathit{T}}}_{vis}=0$$

(25)

being $\eta \rho \frac{D}{Dt}\left(\frac{\mathit{v}}{\eta }\right)\ll 1$ [17]. Under this hypothesis, the friction forces per unit volume, $-\nabla ·{\underline{\mathit{T}}}_{vis}$, can be expressed as (e.g., [15,18]):

$$-\nabla ·{\underline{\mathit{T}}}_{vis}=-\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}$$

(26)

where, according to the method of homogenization, the tensor $\underline{\mathit{Z}}$ depends on both the viscous fluid and the porous medium. It should be stressed that, in agreement with the constitutive Equation (26), the term $-\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}$ represents the friction forces per unit volume related to the shape variation of the fluid particles:

$$-\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}=-{\left(\nabla ·{\underline{\mathit{T}}}_{vis}\right)}_{shape}$$

(27)

while the friction forces related to the volume variation of the fluid particle vanish:

$$-{\left(\nabla ·{\underline{\mathit{T}}}_{vis}\right)}_{volume}=0$$

(28)

In line with this, the momentum equation is given as:

$$\eta \rho \mathit{f}-\nabla \left(\eta p\right)-\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}=0$$

(29)

In agreement with Equation (29), the mechanical energy equation reads as follows:

$$\eta \rho \frac{D{e}_m}{Dt}=\eta \rho \frac{D}{Dt}\left[\frac{1}{2}{\left(\frac{v}{\eta }\right)}^2+u_e\right]=\eta \rho \frac{D{u}_e}{Dt}=-\nabla \left(\eta p\right)·\frac{\mathit{v}}{\eta }-\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }$$

(30)

where $e_m=\frac{1}{2}{\left(\frac{v}{\eta }\right)}^2+u_e$ is the mechanical energy per unit of mass; $\eta \rho \frac{D}{Dt}\left[\frac{1}{2}{\left(\frac{v}{\eta }\right)}^2+u_e\right]=\eta \rho \frac{D{u}_e}{Dt}$, being $\frac{1}{2}\eta \rho \frac{D}{Dt}{\left(\frac{v}{\eta }\right)}^2\ll 1$; $\eta \rho \frac{D{u}_e}{Dt}=\eta \rho \mathit{f}·\frac{\mathit{v}}{\eta }$. Equation (30) is deduced from the inner product of the momentum Equation (29) with $\frac{\mathit{v}}{\eta }$. To not overburden the discussion, only the adiabatic flow is treated. With this setting, the basic conservation equations are gives as:

$$\eta \rho \frac{D{u}_i}{Dt}=-\eta p\nabla ·\left(\frac{\mathit{v}}{\eta }\right)+\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }$$

(31)

$$\eta \rho T\frac{D{e}_s}{Dt}=\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }$$

(32)

$$\eta \rho c_{\widehat{v}}\frac{DT}{Dt}=\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}·\frac{v}{\eta }-\alpha T\epsilon \nabla ·\left(\frac{\mathit{v}}{\eta }\right)$$

(33)

$$\eta \rho c_p\frac{DT}{Dt}=\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }+\alpha T\frac{D}{Dt}\left(\eta p\right)$$

(34)

$$\alpha \frac{DT}{Dt}=\nabla ·\left(\frac{\mathit{v}}{\eta }\right)+\frac{1}{\epsilon }\frac{D}{Dt}\left(\eta p\right)$$

(35)

where $u_i$ is the internal energy per unit of mass; $e_s$ the entropy per unit of mass; $\alpha =-\frac{1}{\eta \rho }{\left[\frac{\partial }{\partial T}\left(\eta \rho \right)\right]}_{\left(\eta p\right)}$ is the homolog of the thermal expansion coefficient; $\epsilon =\frac{1}{\beta }$ the homolog of the bulk modulus, with $\beta =\frac{1}{\eta \rho }{\left[\frac{\partial }{\partial \left(\eta p\right)}\left(\eta \rho \right)\right]}_T$ the homolog of the isothermal compressibility coefficient; $c_{\widehat{v}}={\left(\frac{\partial u_i}{\partial T}\right)}_{\left(\rho \eta \right)}$ the homolog of the constant volume specific heat; $c_p={\left(\frac{\partial e_h}{\partial T}\right)}_{\left(\eta p\right)}$ the homolog of the constant pressure specific heat. The relationship between $c_{\widehat{v}}$ and $c_p$ is given as:

$$c_p-c_{\widehat{v}}=\frac{\alpha T\tilde{k}\eta \rho }{\eta \rho }=\frac{T{\alpha }^2\epsilon }{\eta \rho }$$

(36)

where $\tilde{k}=\frac{1}{\eta \rho }{\left[\frac{\partial }{\partial T}\left(\eta \rho \right)\right]}_{\left(\eta \rho \right)}=\frac{\alpha \epsilon }{\eta \rho }$ is the homolog of the thermal pressure coefficient. From a thermodynamics point of view, the term $\eta \rho$ and $\eta p$ assume the meaning of the apparent fluid state functions.

Equation (35) can be deduced expressing the state equation in the form:

$$\eta \rho =\eta \rho (\eta p,T)$$

(37)

The comparison between the differential form of Equation (37):

$$d\left(\eta \rho \right)={\left(\frac{\partial \left(\eta \rho \right)}{\partial \left(\eta p\right)}\right)}_{T}d\left(\eta p\right)+{\left(\frac{\partial \left(\eta \rho \right)}{\partial T}\right)}_{\left(\eta p\right)}dT=\frac{\eta \rho }{\epsilon }d\left(\eta p\right)-\eta \rho \alpha dT$$

(38)

and the following Equation (obtained from Equations (1) and (10)):

$$d\left(\eta \rho \right)=-\eta \rho \nabla ·\left(\frac{\mathit{v}}{\eta }\right)dt$$

(39)

provides:

$$\eta \rho \alpha dT=\frac{\eta \rho }{\epsilon }d\left(\eta p\right)+\eta \rho \nabla ·\left(\frac{\mathit{v}}{\eta }\right)dt$$

(40)

By simplifying and rearranging, Equation (40) reduces to Equation (35). Equations (33) and (34) are the homologs of the energy equations with temperature as the dependent variable [19].

The proposed line of reasoning allows expressing the classical thermodynamics relationships in the form:

$$d{u}_i=Td{e}_s+\frac{\eta p}{{\left(\eta \rho \right)}^2}d\left(\eta \rho \right)$$

(41)

$$d{e}_h=Td{e}_s+\frac{1}{\eta \rho }d\left(\eta p\right)$$

(42)

$$d{e}_f=-e_{s}dT+\frac{\eta p}{{\left(\eta \rho \right)}^2}d\left(\eta \rho \right)$$

(43)

$$d{e}_g=-e_{s}dT+\frac{1}{\eta \rho }d\left(\eta p\right)$$

(44)

where $e_h$ is the enthalpy per unit of mass, $e_f$ the Helmholtz free energy per unit of mass, $e_g$ the Gibbs free energy per unit of mass. In agreement with the entropy Equation (32), the term $\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }$ is the quadratic form that represents the irreversible transformation of mechanical energy into internal energy. The Clausius-Duhem inequality assures that $\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }\ge 0$; consequently, $\underline{\mathit{Z}}$ is a symmetric, positive semi definite tensor [18,20]. According to the proposed formulation, the flow problem is governed by the following equations:

$$\frac{D}{Dt}\left(\eta \rho \right)+\eta \rho \nabla ·\left(\frac{\mathit{v}}{\eta }\right)=0$$

(45)

$$\eta \rho \mathit{f}-\nabla \left(\eta p\right)-\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }=0$$

(46)

$$\eta \rho c_p\frac{DT}{Dt}=\frac{\mathit{v}}{\eta }·\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }+\alpha T\frac{D}{Dt}\left(\eta p\right)$$

(47)

$$\alpha \frac{DT}{Dt}=\nabla ·\left(\frac{\mathit{v}}{\eta }\right)+\frac{1}{\epsilon }\frac{D}{Dt}\left(\eta p\right)$$

(48)

where $\eta \rho$, $\frac{\mathit{v}}{\eta }$, $\eta p$ and T are unknown. The system equations are completed by the constitutive Equation (which describes the relationship between the tensor $\underline{\mathit{Z}}$, the viscous fluid and the porous medium), by the auxiliary thermodynamics relationships $\alpha =\alpha (\eta p,T)$, $\epsilon =\epsilon (\eta p,T)$, $c_p=c_p(\eta p,T)$, and by the appropriate initial and boundary conditions, which depend on the problem under consideration.

3. Darcy Equation

In this section, the general flow problem is reformulated for the isochoric-isothermal flow of a viscous fluid, in the liquid state, in a homogenous porous medium.

For isothermal flow, the comparison between the continuity Equations (45) and (48), rewritten as:

$$\nabla ·\left(\frac{\mathit{v}}{\eta }\right)=-\frac{1}{\epsilon }\frac{D}{Dt}\left(\eta p\right)$$

(49)

provides:

$$\frac{1}{\eta \rho }\frac{D}{Dt}\left(\eta \rho \right)=\frac{1}{\epsilon }\frac{D}{Dt}\left(\eta p\right)$$

(50)

According to Equation (10), Equation (50) reduced to the barotropic equation:

$$\frac{d\left(\rho \eta \right)}{\rho \eta }=\frac{d\left(\eta p\right)}{\epsilon }$$

(51)

For viscous fluid in the liquid state, the density $\rho$ and the bulk modulus $\epsilon$ can be assumed constant, $\rho =constant$, $\epsilon =constant$, with $\epsilon \gg 1$. With this setting, the continuity Equation (45) and the barotropic Equation (51) are given as:

$$\frac{D\eta }{Dt}+\eta \nabla ·\left(\frac{\mathit{v}}{\eta }\right)=0$$

(52)

$$\frac{d\eta }{\eta }=\frac{d\left(\eta \rho \right)}{\epsilon }$$

(53)

Using Equation (3), Equation (52) reduces to the well-known continuity [10]:

$$\frac{\partial \eta }{\partial t}+\nabla ·\mathit{v}=0$$

(54)

As $\epsilon \gg 1$, $d\eta \ll 1$, then:

$$d\left(\eta p\right)=\eta dp+pd\eta \simeq \eta dp$$

(55)

and Equation (53) can be approximated as:

$$\frac{d\eta }{\eta }=\eta \frac{dp}{\epsilon }$$

(56)

Equation (55) must be considered to be intrinsic to the proposed model. About this, in the static condition, the momentum Equation (46) reduces to:

$$\eta \rho \mathit{f}-\nabla \left(\eta p\right)=\eta \rho \nabla \left(gz\right)-\nabla \left(\eta p\right)=0$$

(57)

Equation (57) provides the classic Stevin equation if and only if Equation (55) holds.

The adopted line of reasoning leads to reduce the momentum equation:

$$\eta \rho \mathit{f}-\nabla \left(\eta p\right)-\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }=\eta \rho \mathit{f}-\eta \nabla p-\underline{\mathit{Z}}·\frac{\mathit{v}}{\eta }=0$$

(58)

to the Darcy Equation (for anisotropic porous medium):

$$\mathit{v}=-\underline{\mathit{K}}\nabla \phi$$

(59)

where $\underline{\mathit{K}}=\rho g{\eta }^2{\underline{\mathit{Z}}}^{-1}$ is the permeability tensor, $\phi =z+p/\left(\rho g\right)$ the apparent piezometric head. As $\underline{\mathit{Z}}$ is symmetric, also $\underline{\mathit{K}}$ is symmetric, hence $K_{ij}=K_{ji}$, where $K_{ij}$, which is the generic component of $\underline{\mathit{K}}$, depends on both the viscous fluid and the porous medium. According to the proposed model, a correlation between the $K_{ij}$ variations and the $\eta$ variations exists: as $d\eta \ll 1$ also $d{K}_{ij}\ll 1$, and $K_{ij}$ can be assumed constant, $K_{ij}=constant$. For a homogenous isotropic porous medium, Equation (59) reduces to the Darcy Equation (for isotropic porous medium):

$$\mathit{v}=-k\nabla \phi$$

(60)

where k is the permeability coefficient, with $k=constant$. According to the proposed formulation, the problem under consideration is governed by the following equations:

$$\frac{\partial \eta }{\partial t}+\nabla ·\mathit{v}=0$$

(61)

$$\mathit{v}=-k\nabla \phi$$

(62)

$$\frac{d\eta }{\eta }=\eta \frac{dp}{\epsilon }$$

(63)

where $\eta$, $\mathit{v}$ and p are unknown. The equations system is completed by the auxiliary equation $\phi =z+p/\left(\rho g\right)$; by the relationship which express k and $\epsilon$ as functions of the viscous fluid and of the porous medium; and by the appropriate initial and boundary conditions.

According to the barotropic Equation (63), it follows that:

$$\frac{\partial \eta }{\partial t}=\frac{\rho g{\eta }^2}{\epsilon }\frac{\partial \phi }{\partial t}$$

(64)

being $\frac{\partial p}{\partial t}=\rho g\frac{\partial \phi }{\partial t}$ and $\frac{\partial z}{\partial t}=0$. The combination of Equations (61), (62) and (64) yields to the well-known parabolic [10]:

$$\frac{S}{\tilde{T}}\frac{\partial \phi }{\partial t}={\nabla }^2\phi$$

(65)

where S is the storativity, $\tilde{T}$ the trasmissivity, $\frac{S}{\tilde{T}}=\frac{\rho g{\eta }^2}{k\epsilon }$

4. Darcy Paradox

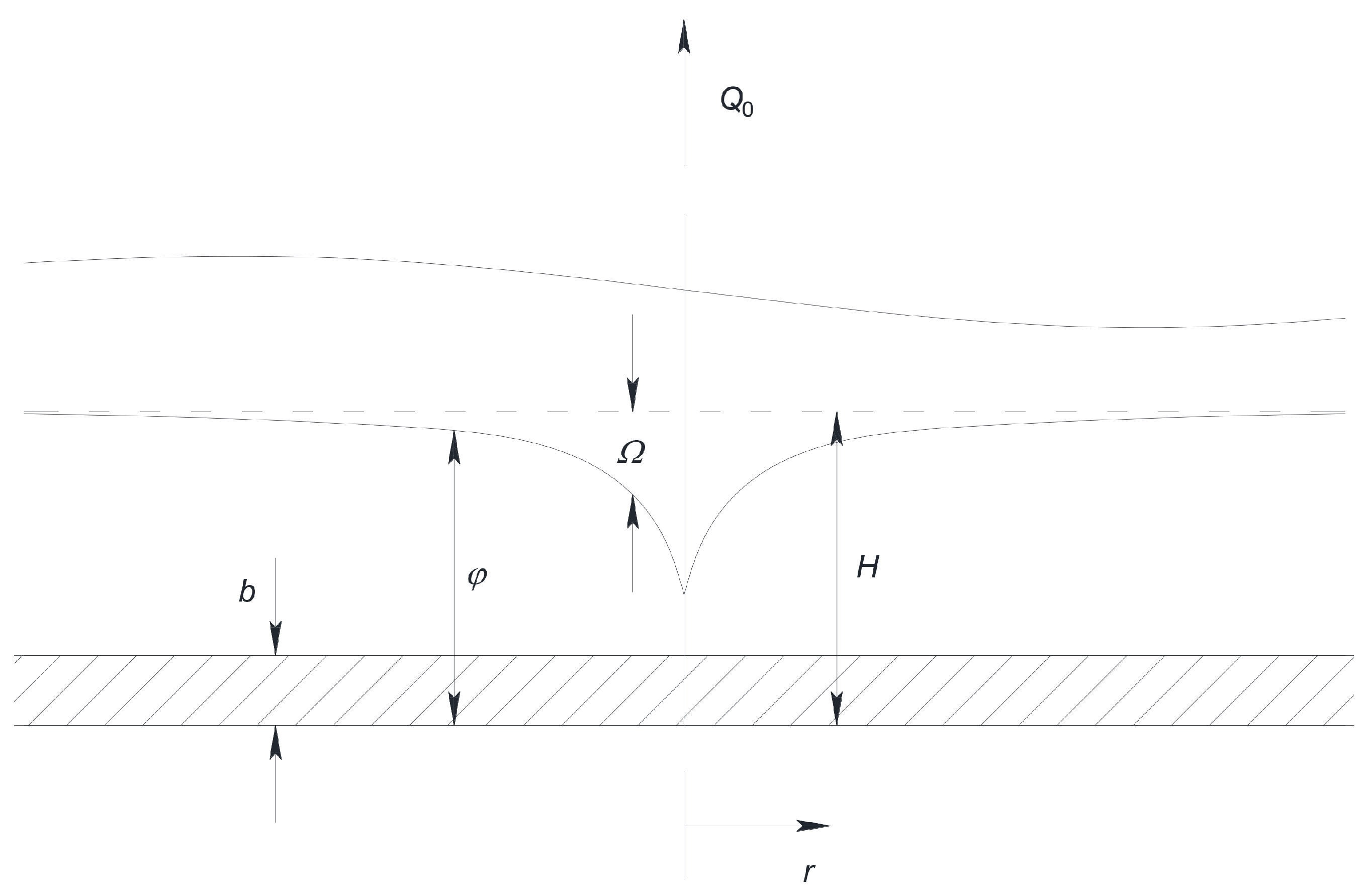
For the sake of clarity, the Darcy paradox is highlighted with a focus on the unsteady axisymmetric flow toward a fully penetrating well in a horizontal aquifer (Figure 1). The following notation is used: r is the radial distance from the well center; $H=\phi (r,0)$ the initial piezometric head, $\Omega (r,t)=H-\phi (r,t)$ the drawdown of the piezometric head; $b=constant$ the porous layer thickness; $Q_0=constant$ the imposed well flow rate; $Q=Q(r,t)$ the porous flow rate. For the problem under consideration, Equation (65) becomes:

$$\frac{S}{\tilde{T}}\frac{\partial \phi }{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial \phi }{\partial r}\right)$$

(66)

while the Darcy equation can be rewritten as:

$$Q=2\pi Tr\frac{\partial \phi }{\partial r}$$

(67)

where $\tilde{T}=constant$ is expressed as:

$$\tilde{T}=bk$$

(68)

and the continuity equation reads as:

$$\frac{\partial Q}{\partial r}=2\pi Sr\frac{\partial \phi }{\partial t}$$

(69)

where $S=constant$ is takes as:

$$S=b{\eta }^2\frac{\rho g}{\epsilon }$$

(70)

The initial condition is given as:

$$\Omega (r,0)=0$$

(71)

while, according to Equation (67), the boundary condition of Equation (66) is given as:

$$\underset{r\to 0}{lim}r\frac{\partial \phi }{\partial r}=\frac{Q_0}{2\pi \tilde{T}}$$

(72)

Using the Boltzmann transformation:

$$u=\frac{S{r}^2}{4\tilde{T}t}$$

(73)

and following the Theis procedure [21], the drawdown $\Omega$ is expressed as:

$$\Omega =\frac{Q_0}{4\pi \tilde{T}}Ei\left(u\right)$$

(74)

where $Ei\left(u\right)$ is the integral exponential function:

$$Ei\left(u\right)={\int }_u^{\infty }\frac{exp(-u)}{u}du=-\lambda -logu+u-\frac{u^2}{2·2!}+\frac{u^3}{3·3!}-\cdots$$

(75)

being:

$$\lambda =\underset{m\to \infty }{lim}\left(\sum _{n=1}^m\frac{1}{n}-logm\right)\simeq 0.577215$$

(76)

the Euler–Mascheroni constant.

According to Equation (74), for $t>0$, and for any $r\ne 0,\Omega >0$. This leads to the conclusion that the speed of diffusion of an infinitesimal drawdown signal is infinite (Darcy paradox). To overcome the Darcy paradox, the elementary scales method is employed. Along with $\left|d\mathit{r}\right|$ and $\left|dt\right|$, the elementary drawdown $|d\Omega |$ is introduced. To define $|d\Omega |$ the following procedure can be adopted. The continuity Equation (52), which can be rewritten in the form:

$$d\eta +\eta \nabla ·\left(\frac{\mathit{v}}{\eta }\right)dt=0$$

(77)

allows defining the elementary porosity scale $\left|d\eta \right|$ as:

$$\left|d\eta \right|=\left|\eta \nabla ·\left(\frac{\mathit{v}}{\eta }\right)\right|$$

(78)

On the other hand, the barotropic Equation (63), which can be rewritten in the form:

$$\frac{d\eta }{\eta }=\eta \frac{dp}{\epsilon }=\frac{\eta \rho g}{\epsilon }d\phi -\frac{\eta \rho g}{\epsilon }dz$$

(79)

allows defining the elementary scale of the piezometric head $\left|d\phi \right|$ as:

$$\left|d\phi \right|=\left|dz+\frac{\epsilon }{\rho g{\eta }^2}d\eta \right|$$

(80)

The elementary scale $\left|dz\right|$ is, in turn, proportional to the REV scale $\left|d\mathit{r}\right|$. Due to the link between $\Omega$ and $\phi$, the elementary scale $\left|d\phi \right|$ coincides to the elementary scale $|d\Omega |$. In line with the method of elementary scales, if $|\delta \Omega |<|d\Omega |$, $\Omega \pm \delta \Omega =\Omega$ and, consequently, the Darcy paradox is only apparent: for $t<dt$, $\Omega =0$; for $t\ge dt$, $\exists \overline{r}$: for $r>\overline{r}$, $\Omega <d\Omega (\Omega =0)$.

5. Conclusions

This theoretical paper focuses on the single-phase fluid flow through a granular porous medium. The emphasis is on the Darcy flow regime (without free boundary) of a linear viscous fluid in a saturated, deformable, homogeneous porous medium. The approach is developed at the Darcy scale. Within this framework:

• the governing equations are revisited;
• new apparent fluid state functions are introduced;
• the elementary scales method and the discrete aspects of the flow model are highlighted;
• the constrain imposed on the elementary temporal scale $\left|dt\right|$ is defined (it is shown that the dimensionless number $\left|\left|\left(\nabla {\displaystyle \frac{\mathit{v}}{\eta }}\right)dt\right|\right|$ is always evanescent);
• the Darcy paradox is presented.

The Darcy paradox is illustrated for the isoshoric-isothermal flow of a viscous fluid in the liquid state, in a homogenous porous medium. In this context: an intrinsic assumption of the proposed model, expressed by Equation (55), is highlighted; the basic equations are reduced to the well-known parabolic Equation (65). According to this parabolic equation, infinitesimal pressure disturbances diffuse at an infinite speed. To overcome this paradox, a mathematical model based on the elementary scales method is employed. In agreement with the obtained results, the Darcy paradox is only apparent. The theoretical analysis proposed in this paper allows overcoming some intrinsic difficulties of the phenomenological model of the fluid flow through porous media. The theoretical refutation of the Darcy paradox avoids the use of physical justifications which are similar to those proposed by [22,23] to remove the Fourier paradox. Following [22,23], the Darcy law can be viewed as a result of experimental observations; these observations are affected by the degree of refinement of the measurement, and, consequently, the infinitesimal pressure disturbances cannot be experimentally observed; the bulk of the pressure disturbance, which is physically significant, diffuses at a finite speed.