Numerical Investigation of the Influence of Tire Deformation and Vehicle Ride Height on the Aerodynamics of Passenger Cars
Abstract
:1. Introduction
2. Case Study
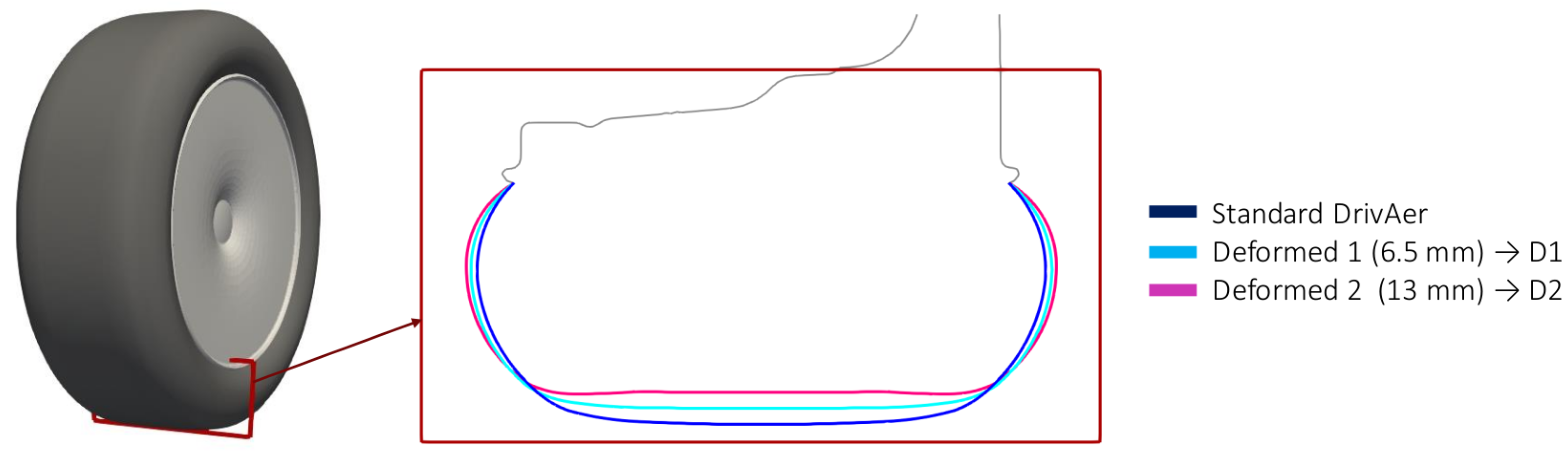
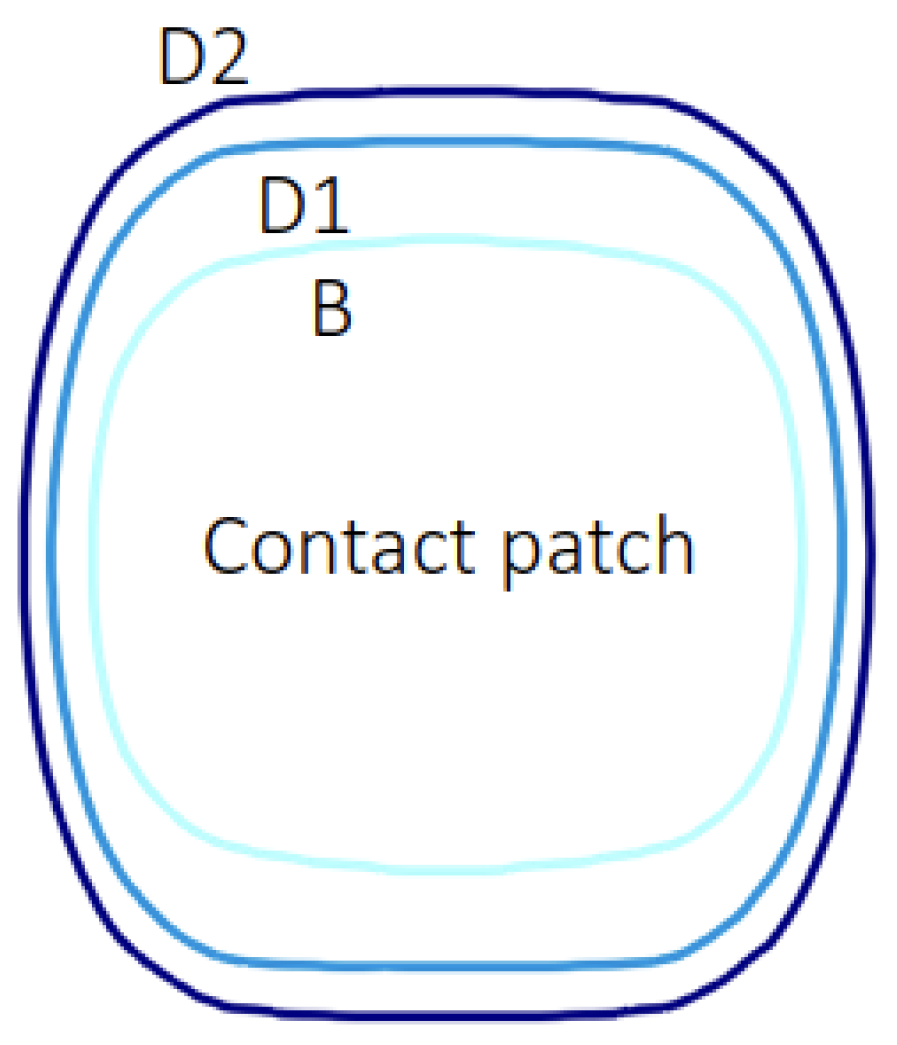
2.1. Tire Deformation
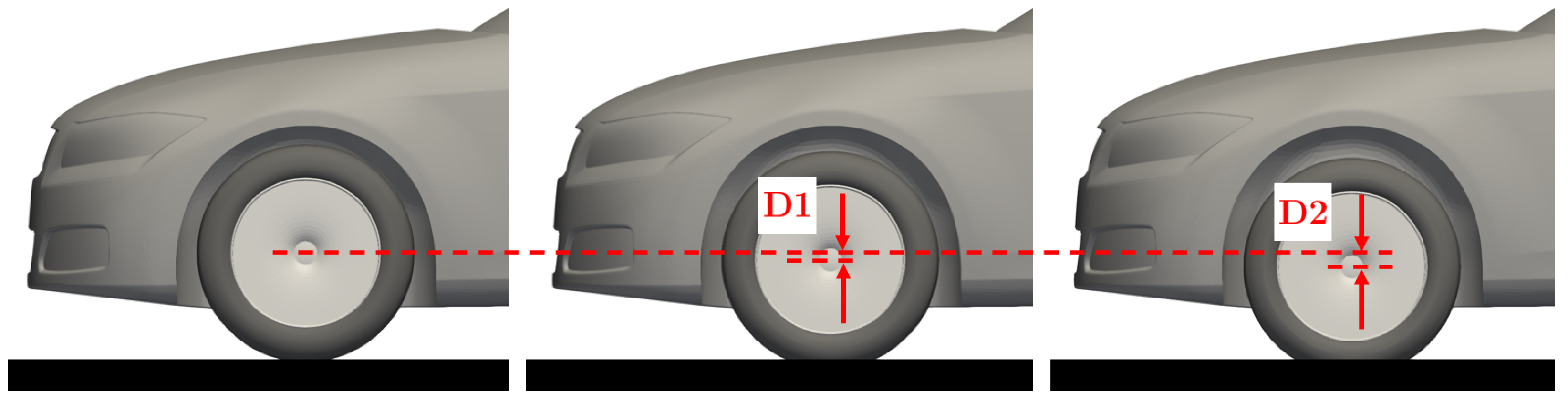
2.2. Vehicle Ride Height
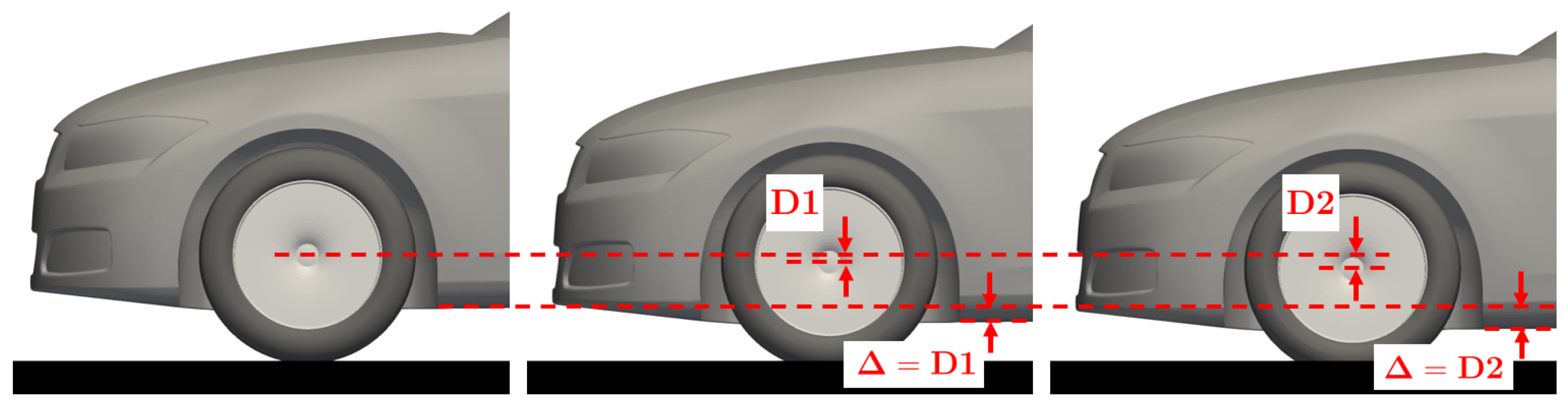
2.3. Combined Effect
3. Numerical Setup
3.1. Governing Equations
3.2. Grid and Boundary Conditions
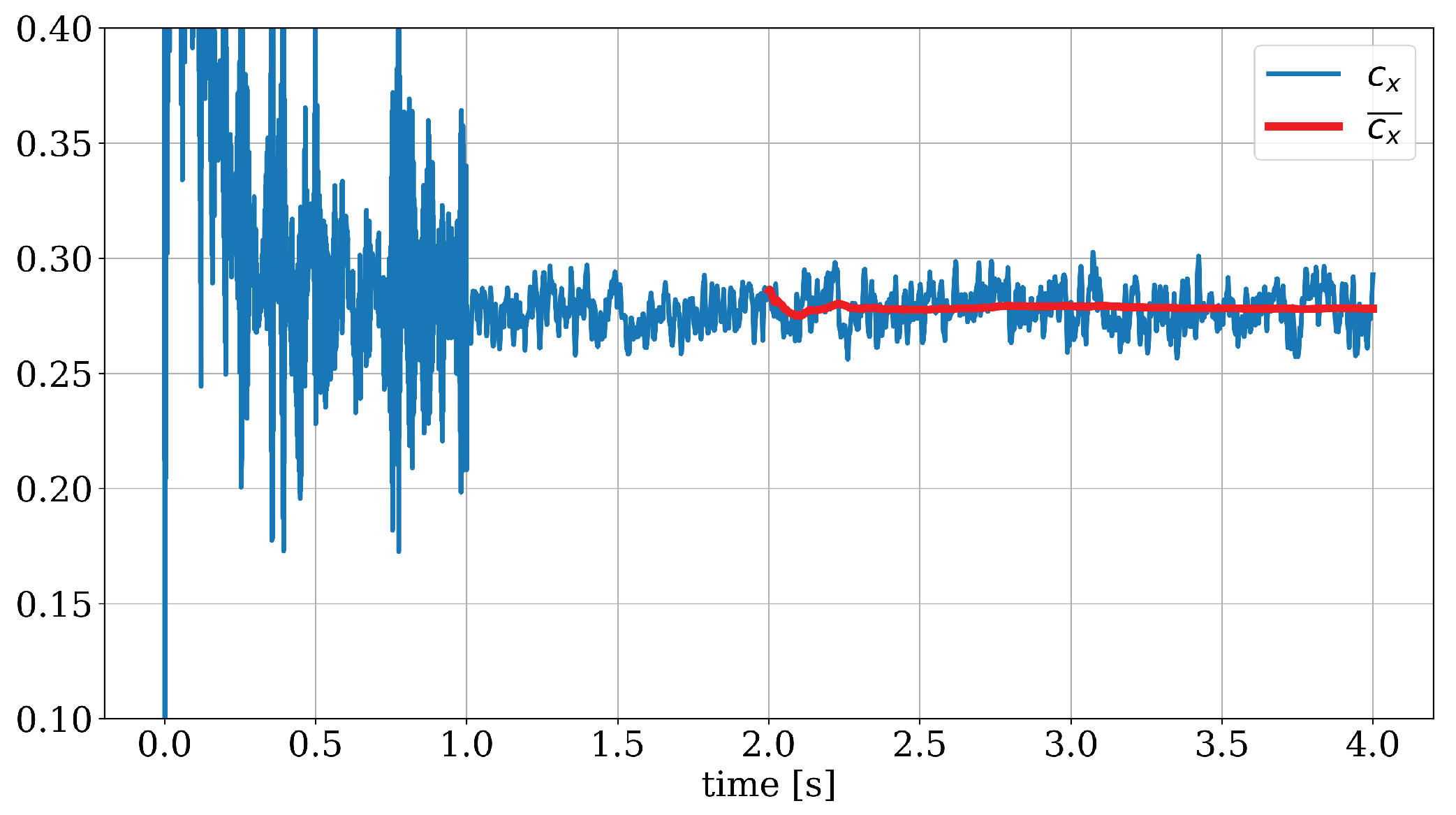
3.3. Data Extraction and Validation
4. Results
4.1. Vehicle Ride Height
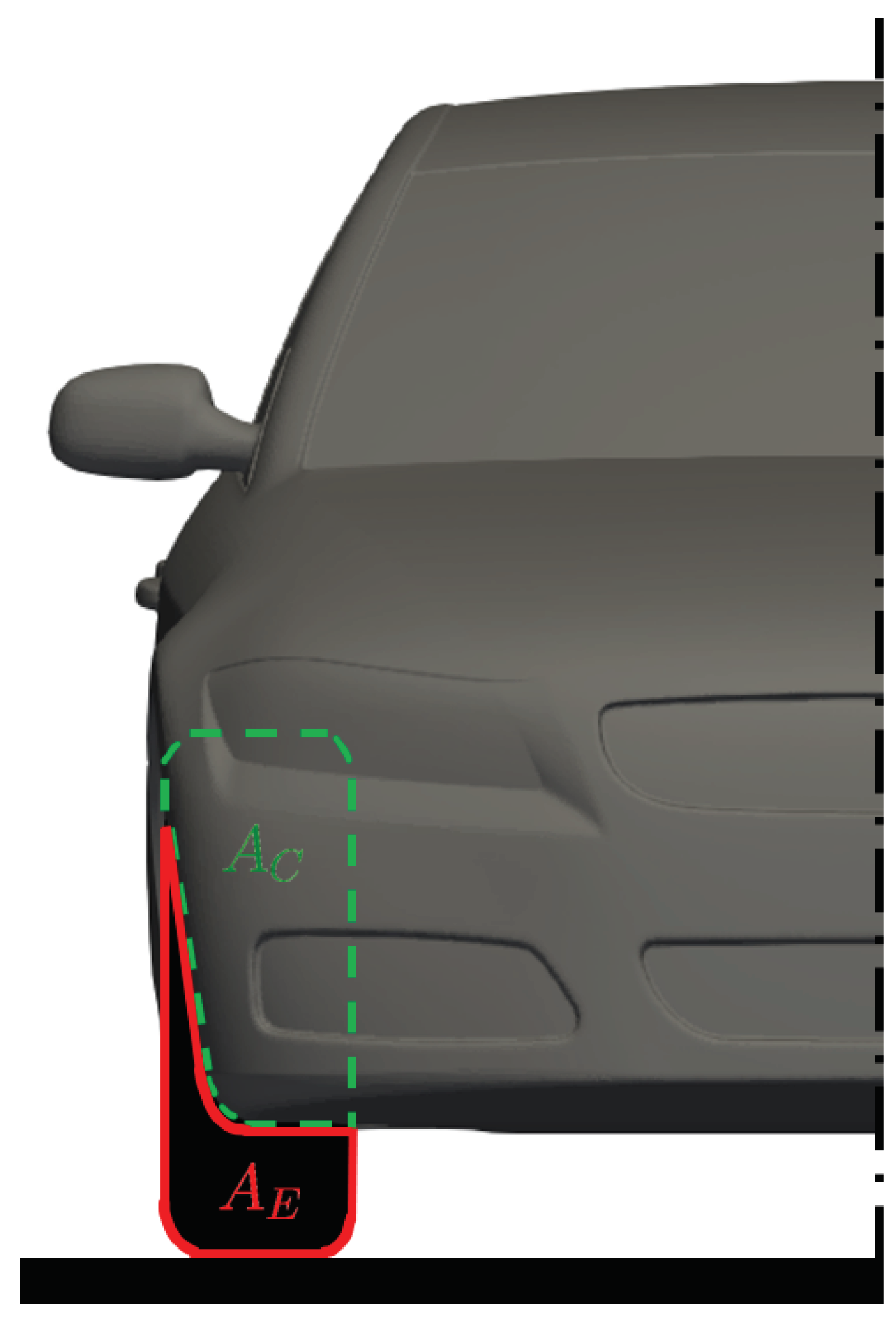
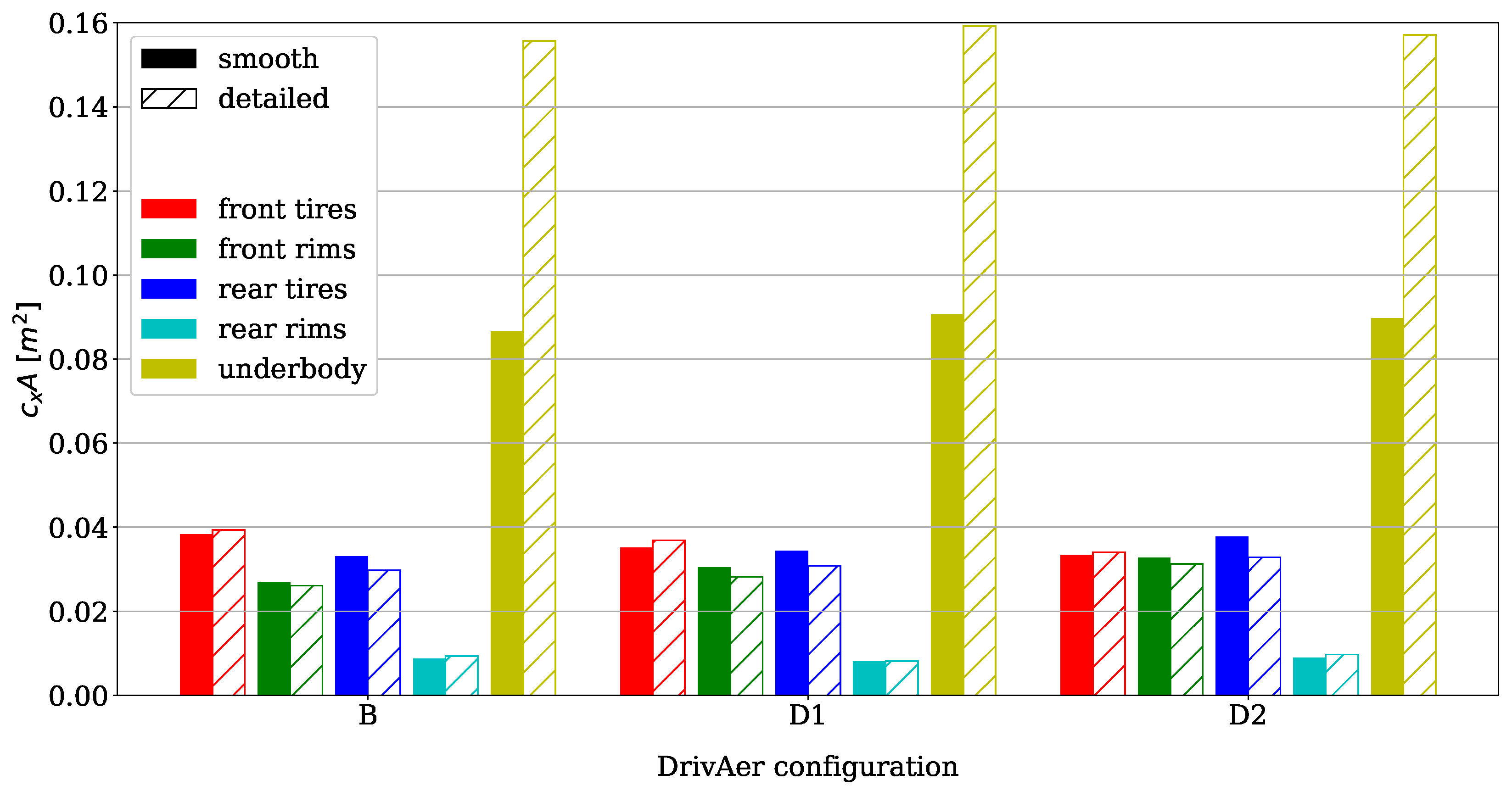
4.1.1. Tire Exposed Area
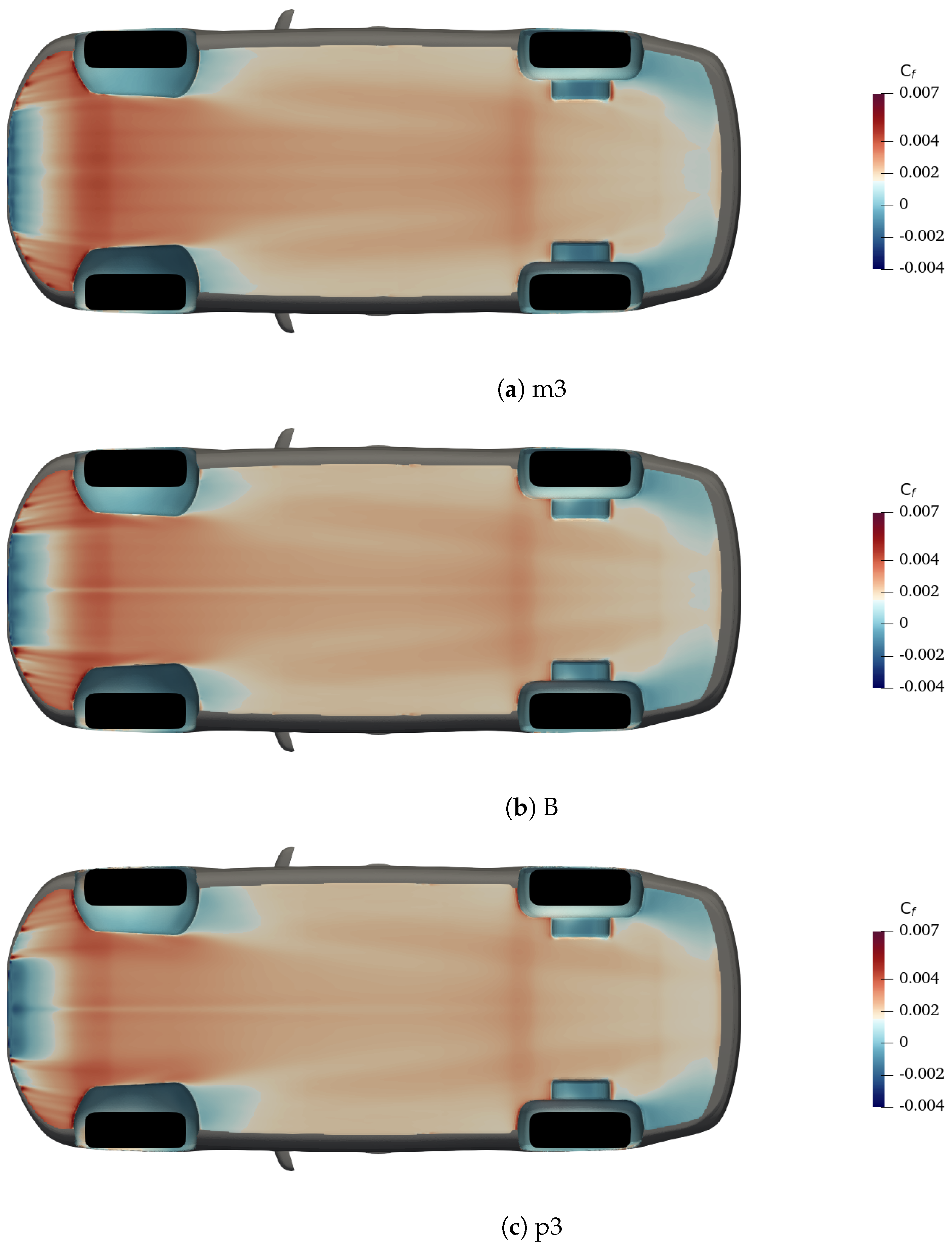
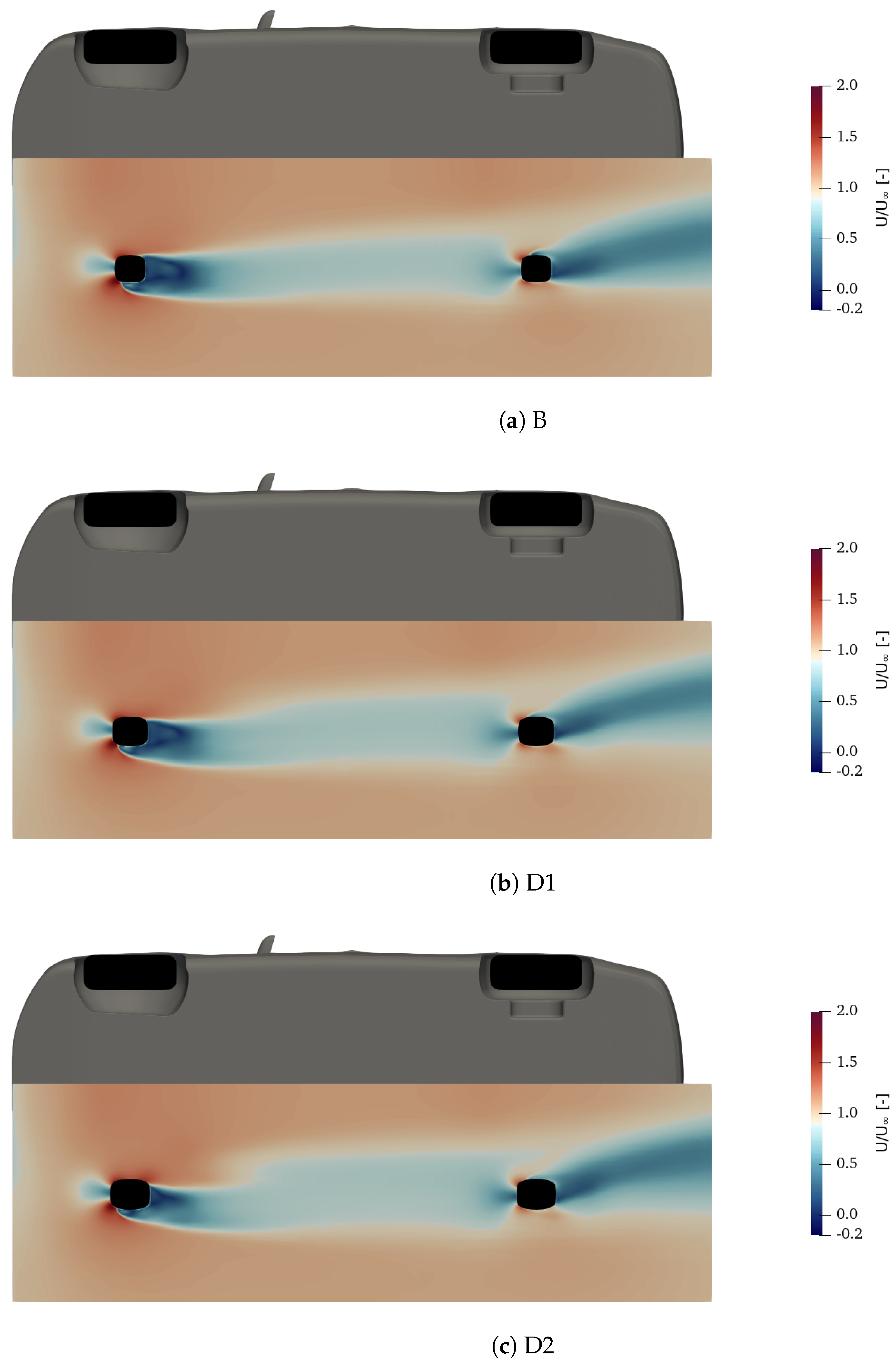
4.1.2. Interaction between Underbody and Ground
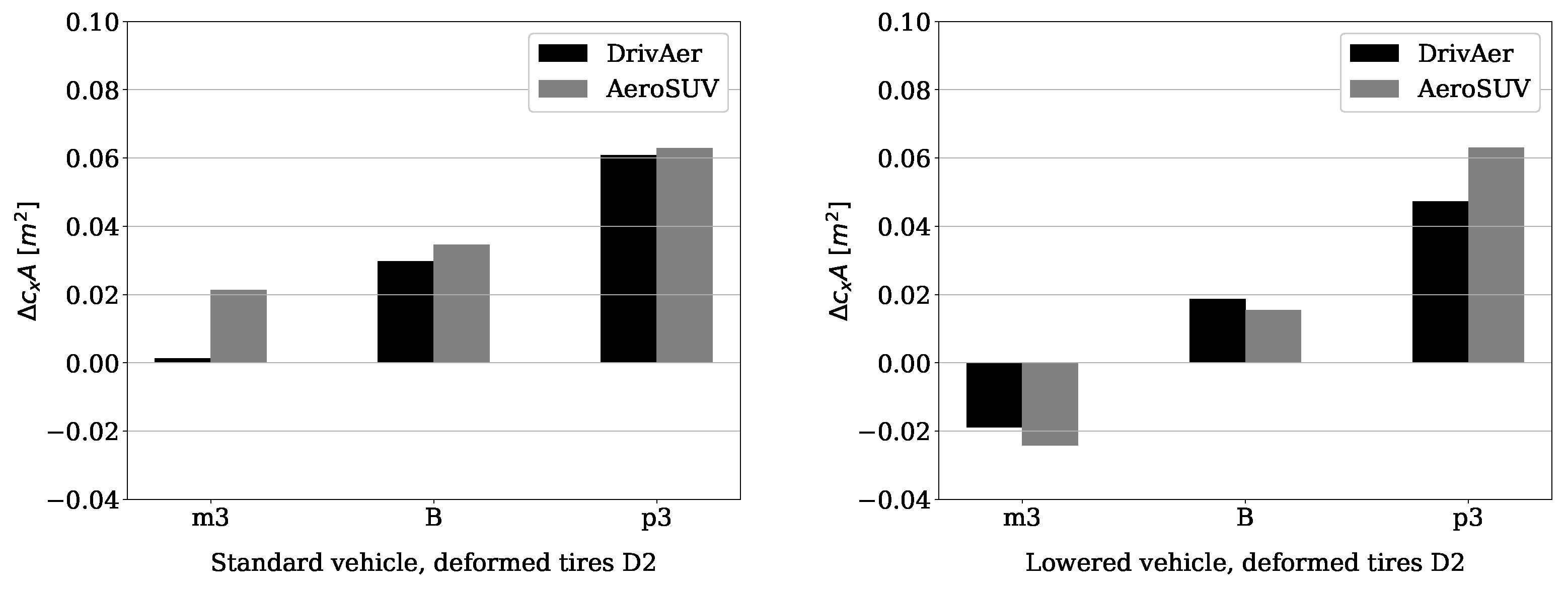
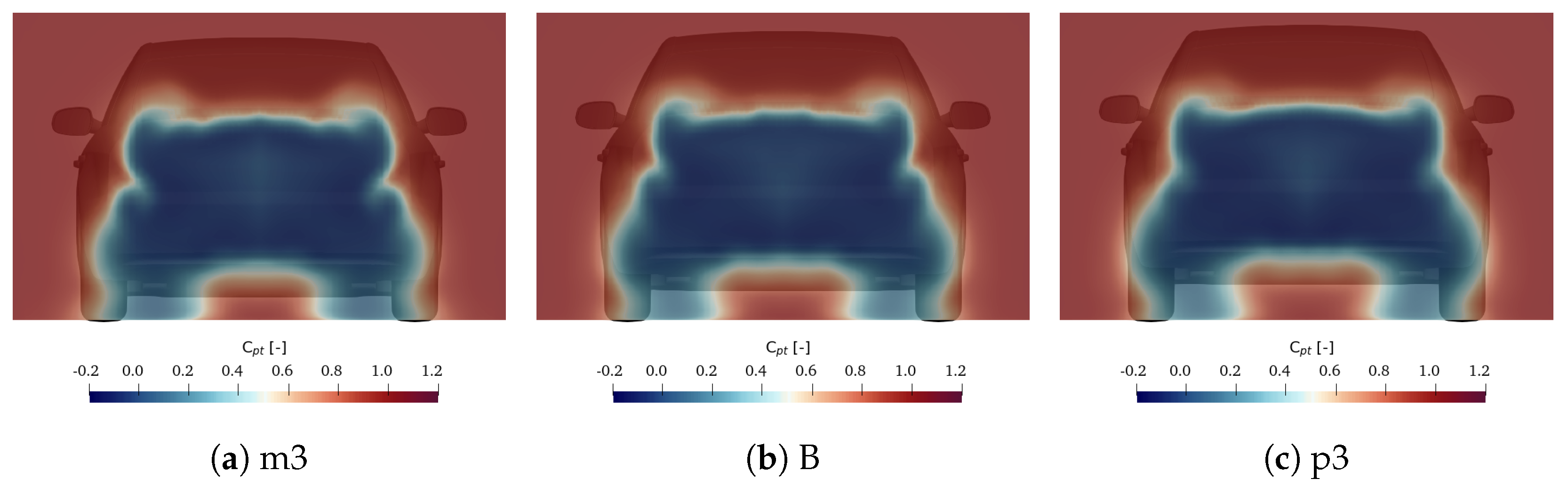
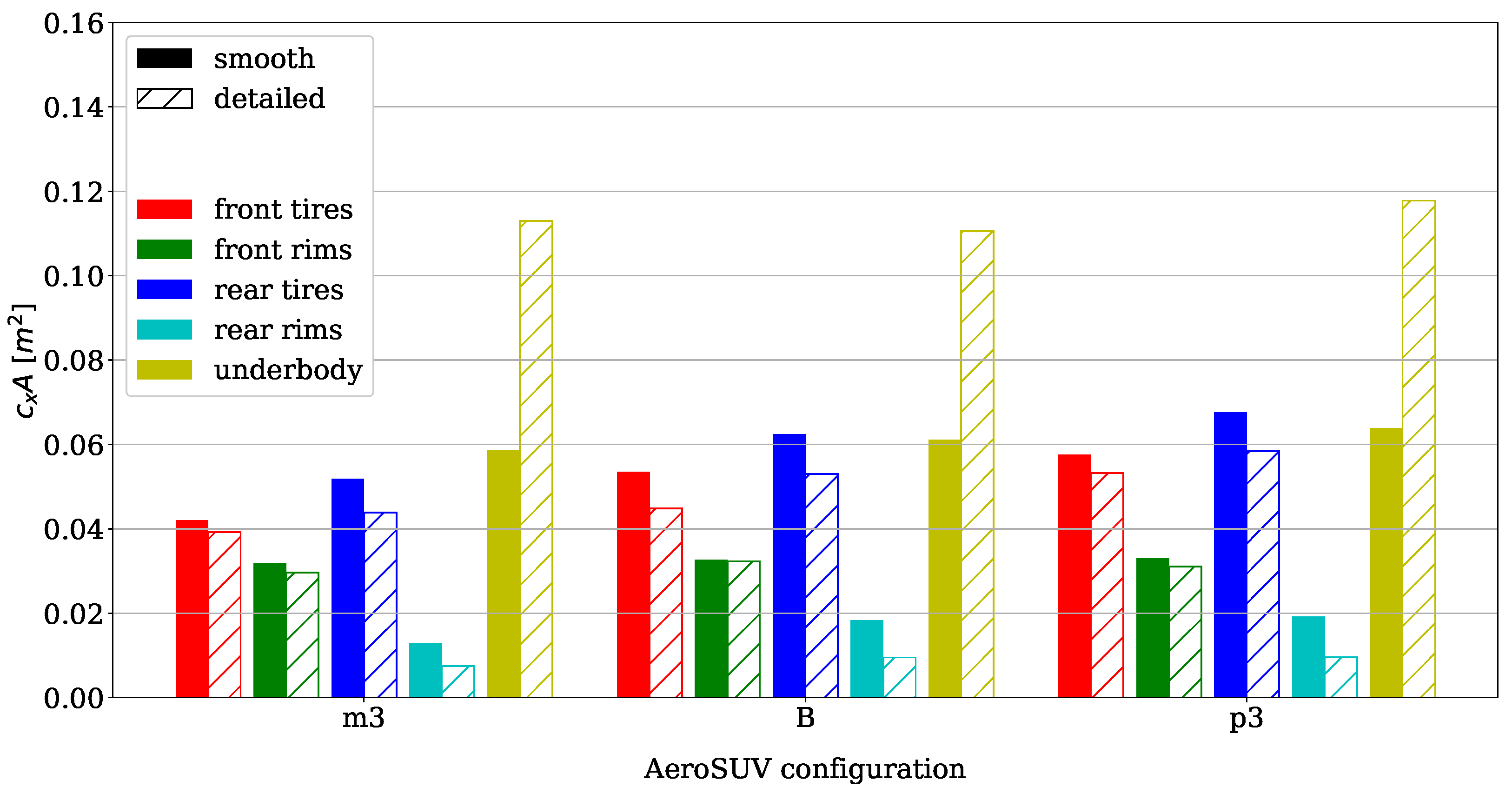
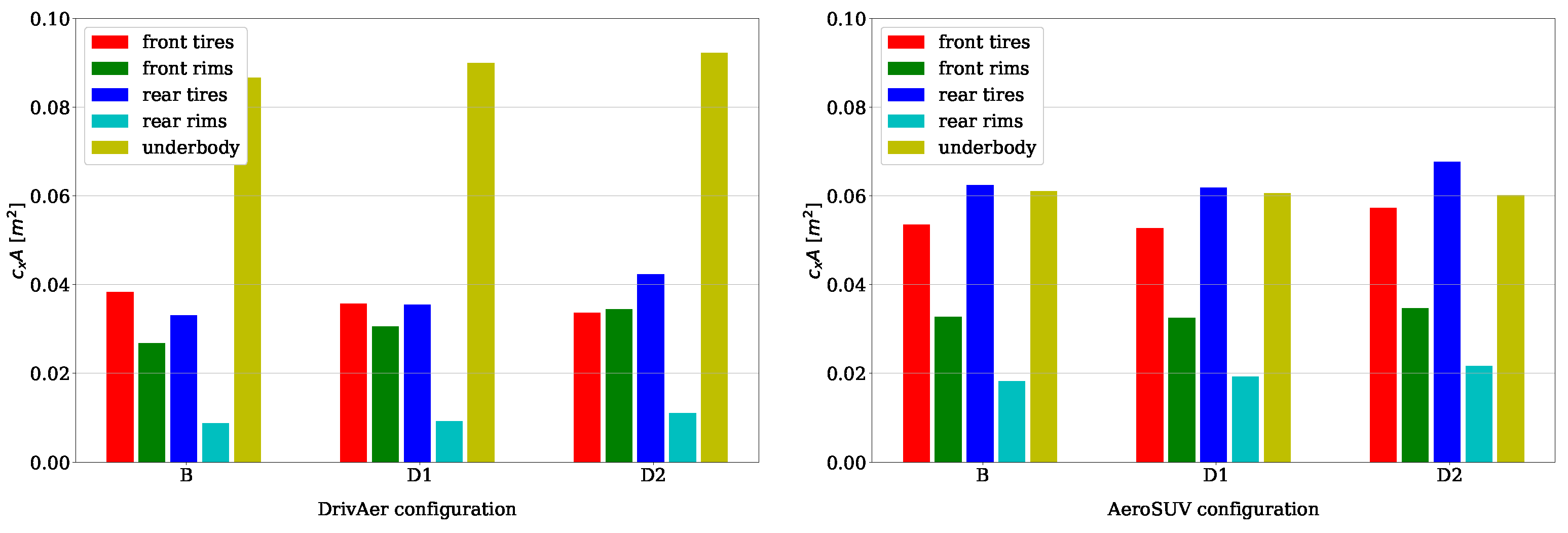
4.2. Tire Deformation Effect
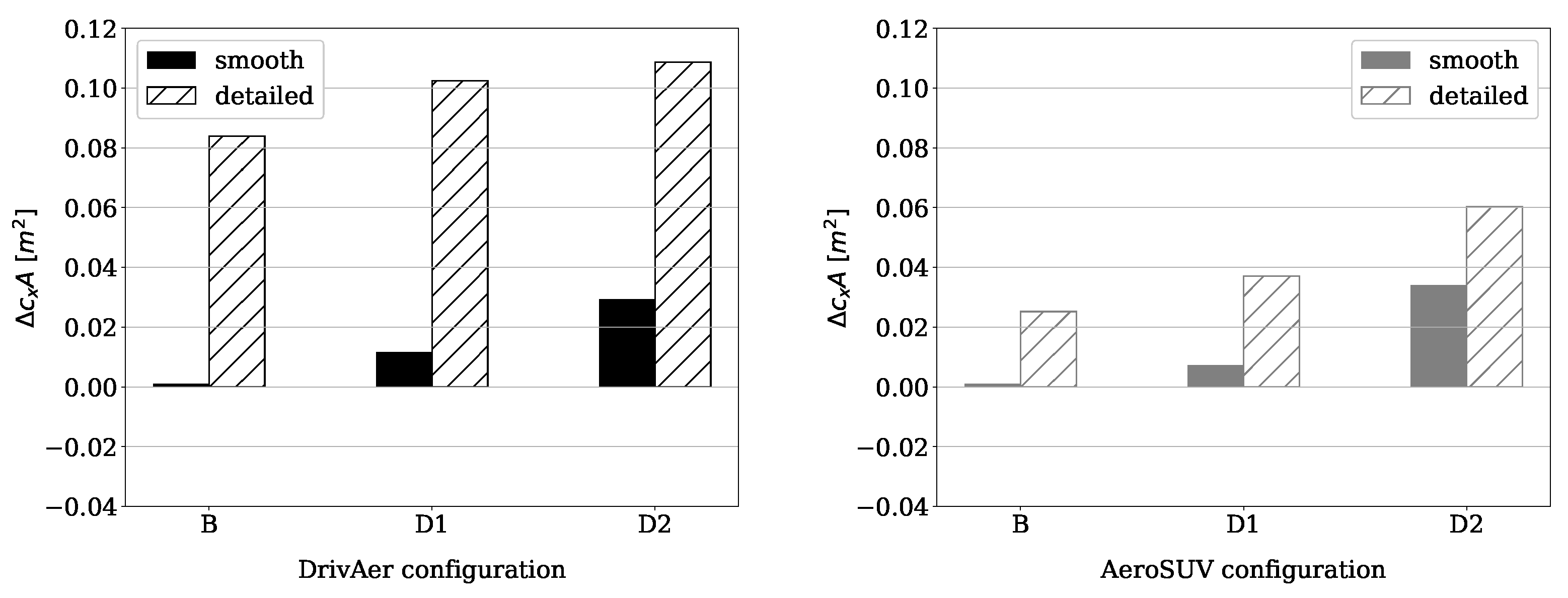
4.3. Tire Deformation and Vehicle Ride Height Combined
5. Conclusions
Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| WLTP | Worldwide Harmonised Light Vehicle Test Procedure |
| NEDC | New European Driving Cycle |
| SM | Sliding Mesh |
| MRF | Moving Reference Frame |
| RWBC | Rotating Wall Boundary Condition |
| DDES | Delayed-Detached Eddy Simulation |
| RANS | Reynolds Averaged Navier Stokes |
| LES | Large Eddy Simulation |
| Re | Reynolds number |
| BEV | Battery Electric Vehicle |
| Drag coefficient | |
| Side force coefficient | |
| Lift coefficient | |
| Pitch moment coefficient | |
| Drag Area | |
| e | Blockage ratio |
| Coefficient of exposure | |
| Wheel exposed area | |
| Wheel covered area | |
| CDL | Micro-drag |
| Static pressure coefficient | |
| Total pressure coefficient | |
| Friction Coefficient |
References
- Mock, P.; Kühlwein, J.; Tietge, U.; Franco, V.; Bandivadekar, A.; German, J. The WLTP: How a new test procedure for cars will affect fuel consumption values in the EU. Int. Counc. Clean Transp. 2014. Available online: https://theicct.org/publication/the-wltp-how-a-new-test-procedure-for-cars-will-affect-fuel-consumption-values-in-the-eu/ (accessed on 1 December 2021).
- Lee, H.; Lee, K. Comparative Evaluation of the Effect of Vehicle Parameters on Fuel Consumption under NEDC and WLTP. Energies 2020, 13, 4245. [Google Scholar] [CrossRef]
- Wickern, G.; Zwicker, K.; Pfadenhauer, M. Rotating wheels-their impact on wind tunnel test techniques and on vehicle drag results. SAE Trans. 1997, 106, 254–270. [Google Scholar]
- Morelli, A. Aerodynamic Effects on an Automobile Wheel. ATA Rev. 1969, 22, 281–288. [Google Scholar]
- Fackrell, J.E. The Aerodynamics of an Isolated Wheel Rotating in Contact with the Ground. Ph.D. Thesis, Faculty of Engineering, University of London, London, UK, 1974. [Google Scholar]
- Cogotti, A. Aerodynamic characteristics of car wheel. Int. J. Veh. Des. 1983, 3, 173–196. [Google Scholar]
- Wäschle, A.; Cyr, S.; Kuthada, T.; Wiedemann, J. Flow around an Isolated Wheel-Experimental and Numerical Comparison of Two CFD Codes; No. 2004-01-0445; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2004. [Google Scholar]
- Hobeika, T.; Sebben, S.; Lofdahl, L. Study of different tyre simulation methods and effects on passenger car aerodynamics. In Proceedings of the International Vehicle Aerodynamics Conference, Holywell Park, Loughborough, UK, 14–15 October 2014; pp. 187–195. Available online: https://www.semanticscholar.org/paper/Study-of-different-tyre-simulation-methods-and-on-Hobeika-Sebben/976af046013ca7425fbbbea5a4c4f4bc9525c267 (accessed on 1 December 2021).
- Haag, L.; Kiewat, M.; Indinger, T.; Blacha, T. Numerical and experimental investigations of rotating wheel aerodynamics on the DrivAer model with engine bay flow. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York, NY, USA, 2017; p. V01BT12A005. [Google Scholar]
- Hobeika, T.; Sebben, S. CFD investigation on wheel rotation modelling. J. Wind Eng. Ind. Aerodyn. 2018, 174, 241–251. [Google Scholar] [CrossRef] [Green Version]
- Ashton, N.; Revell, A. Comparison of RANS and DES Methods for the DrivAer Automotive Body; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2015. [Google Scholar]
- Ashton, N.; West, A.; Lardeau, S.; Revell, A. Assessment of RANS and DES methods for realistic automotive models. Comput. Fluids 2016, 128, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Schuetz, T. Aerodynamics of Road Vehicles; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Heft, A.I.; Indinger, T.; Adams, N.A. Introduction of a New Realistic Generic Car Model for Aerodynamic Investigations; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2012. [Google Scholar]
- Zhang, C.; Tanneberger, M.; Kuthada, T.; Wittmeier, F.; Wiedemann, J.; Nies, J. Introduction of the AeroSUV—A New Generic SUV Model for Aerodynamic Research; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Ahmed, S.R.; Ramm, G.; Faltin, G. Some salient features of the time-averaged ground vehicle wake. SAE Trans. 1984, 93, 473–503. [Google Scholar]
- Cogotti, A. A parametric study on the ground effect of a simplified car model. SAE Trans. 1998, 107, 180–204. [Google Scholar]
- Littlewood, R.; Passmore, M. The Optimization of Roof Trailing Edge Geometry of a Simple Square-Back; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Acea. Available online: https://www.acea.auto/figure/fuel-types-of-new-passenger-cars-in-eu/ (accessed on 1 December 2021).
- Spalart, P. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; p. 439. [Google Scholar]
- Guilmineau, E.; Deng, G.B.; Leroyer, A.; Queutey, P.; Visonneau, M.; Wackers, J. Assessment of hybrid RANS-LES formulations for flow simulation around the Ahmed body. Comput. Fluids 2018, 176, 302–319. [Google Scholar] [CrossRef]
- Ekman, P.; Wieser, D.; Virdung, T.; Karlsson, M. Assessment of hybrid RANS-LES methods for accurate automotive aerodynamic simulations. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104301. [Google Scholar] [CrossRef]
- Cogotti, A. Flow-Field Surveys behind Three Squareback Car Models Using a New “Fourteen-Hole” Probe; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1987. [Google Scholar]

















| DrivAer-Notchback | AeroSUV-Estateback | |
|---|---|---|
| Length/Width/Height (mm) | 4613/2029/1418 | 4619/2044/1608 |
| Wheelbase (mm) | 2786 | 2786 |
| Front/Rear track (mm) | 1524 | 1552 |
| Wheels (in) | 16 | 19 |
| Front/Rear ride height (mm) | 148/166 | 196/215 |
| Frontal Area (m) | 2.17 | 2.47 |
| Quantity | ||||
|---|---|---|---|---|
| Boundary | U | p | nut | nuTilda |
| inlet | fixedValue | zeroGradient | calculated | fixedValue |
| outlet | zeroGradient | fixedValue | calculated | zeroGradient |
| sides | symmetry | symmetry | symmetry | symmetry |
| ground | translatingWall | zeroGradient | nutUSpaldingWF | fixedValue |
| car | noSlip | zeroGradient | nutUSpaldingWF | fixedValue |
| wheels | rotatingWall | zeroGradient | nutUSpaldingWF | fixedValue |
| DrivAer notchback, exp., moving ground [14] | 0.2460 |
| Current study, smooth underbody | 0.2488 |
| DrivAer notchback, exp., detailed UB, moving ground [14] | 0.2770 |
| Current study, detailed underbody | 0.2886 |
| AeroSUV estateback, exp., moving ground [15] | 0.3050 |
| AeroSUV estateback, CFD, moving ground [15] | 0.3280 |
| Current study | 0.3206 |
| DrivAer | AeroSUV | |||||
|---|---|---|---|---|---|---|
| Configuration | −30 | B | +30 | −30 | B | +30 |
| CE | 0.25 | 0.30 | 0.35 | 0.30 | 0.33 | 0.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semeraro, F.F.; Schito, P. Numerical Investigation of the Influence of Tire Deformation and Vehicle Ride Height on the Aerodynamics of Passenger Cars. Fluids 2022, 7, 47. https://doi.org/10.3390/fluids7020047
Semeraro FF, Schito P. Numerical Investigation of the Influence of Tire Deformation and Vehicle Ride Height on the Aerodynamics of Passenger Cars. Fluids. 2022; 7(2):47. https://doi.org/10.3390/fluids7020047
Chicago/Turabian StyleSemeraro, Francesco Fabio, and Paolo Schito. 2022. "Numerical Investigation of the Influence of Tire Deformation and Vehicle Ride Height on the Aerodynamics of Passenger Cars" Fluids 7, no. 2: 47. https://doi.org/10.3390/fluids7020047
APA StyleSemeraro, F. F., & Schito, P. (2022). Numerical Investigation of the Influence of Tire Deformation and Vehicle Ride Height on the Aerodynamics of Passenger Cars. Fluids, 7(2), 47. https://doi.org/10.3390/fluids7020047







