Experience of Patient-Specific CFD Simulation of Blood Flow in Proximal Anastomosis for Femoral-Popliteal Bypass
Abstract
1. Introduction
2. Materials and Methods
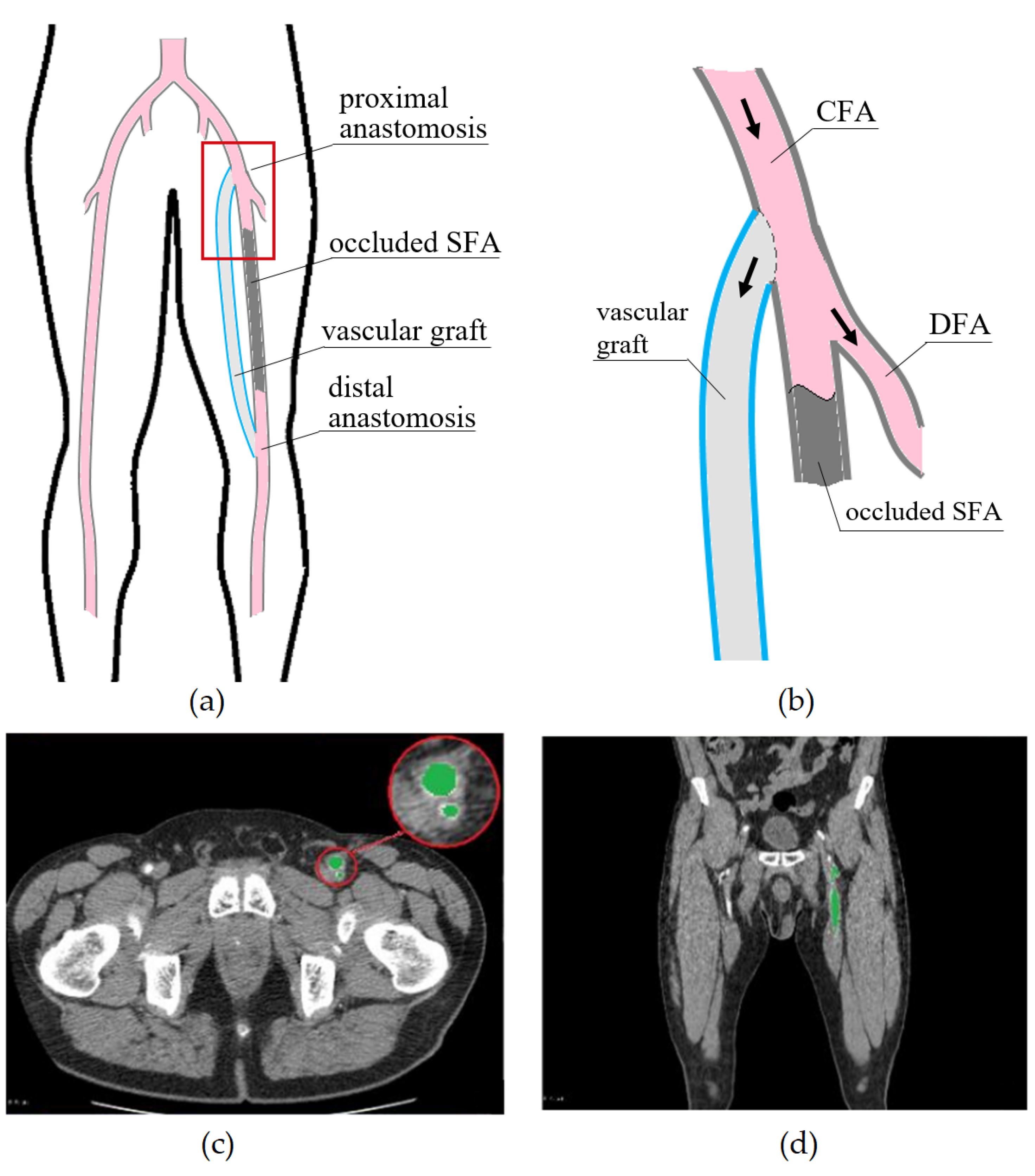
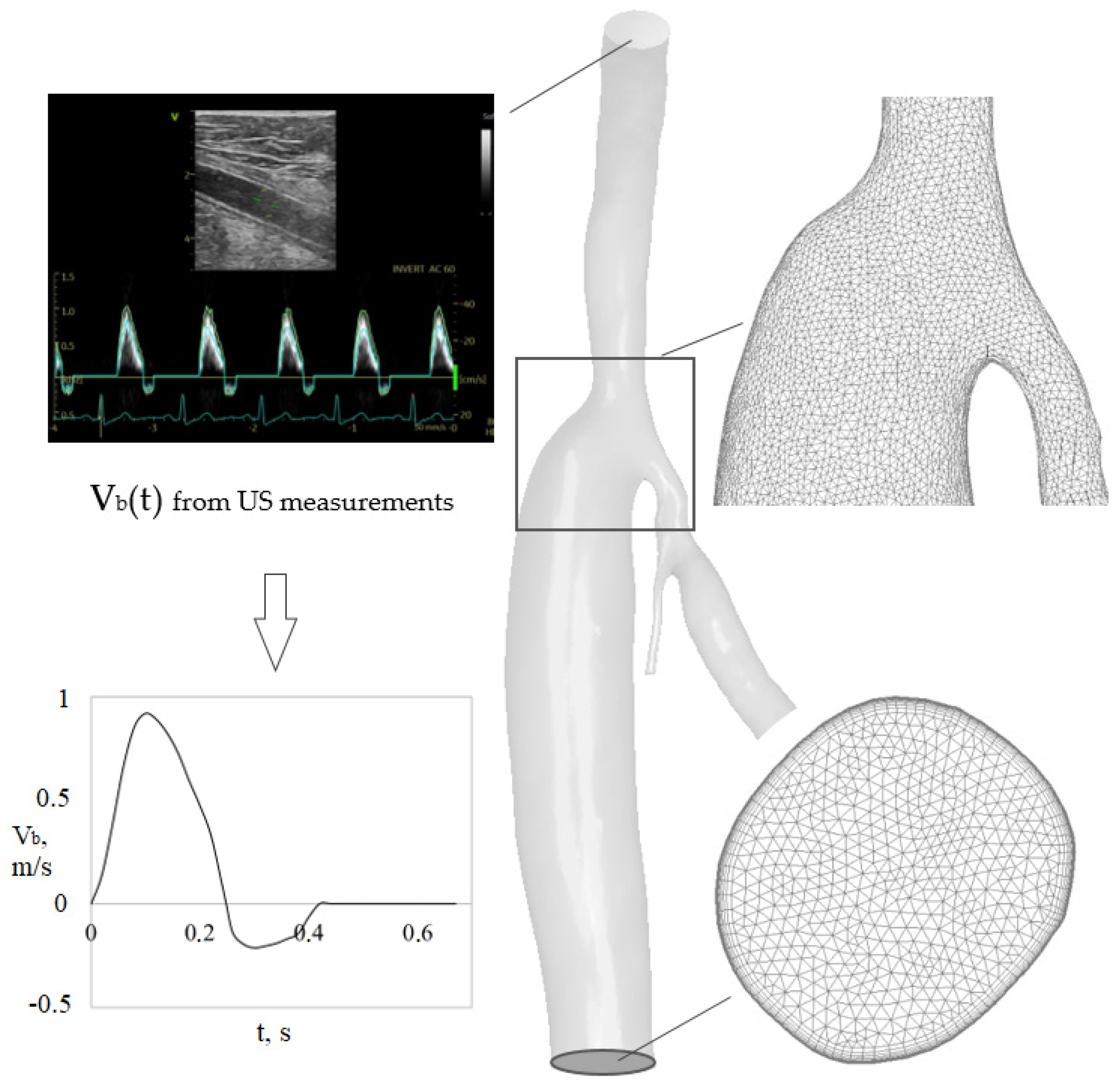
2.1. Geometric Models and Blood Flow Parameters
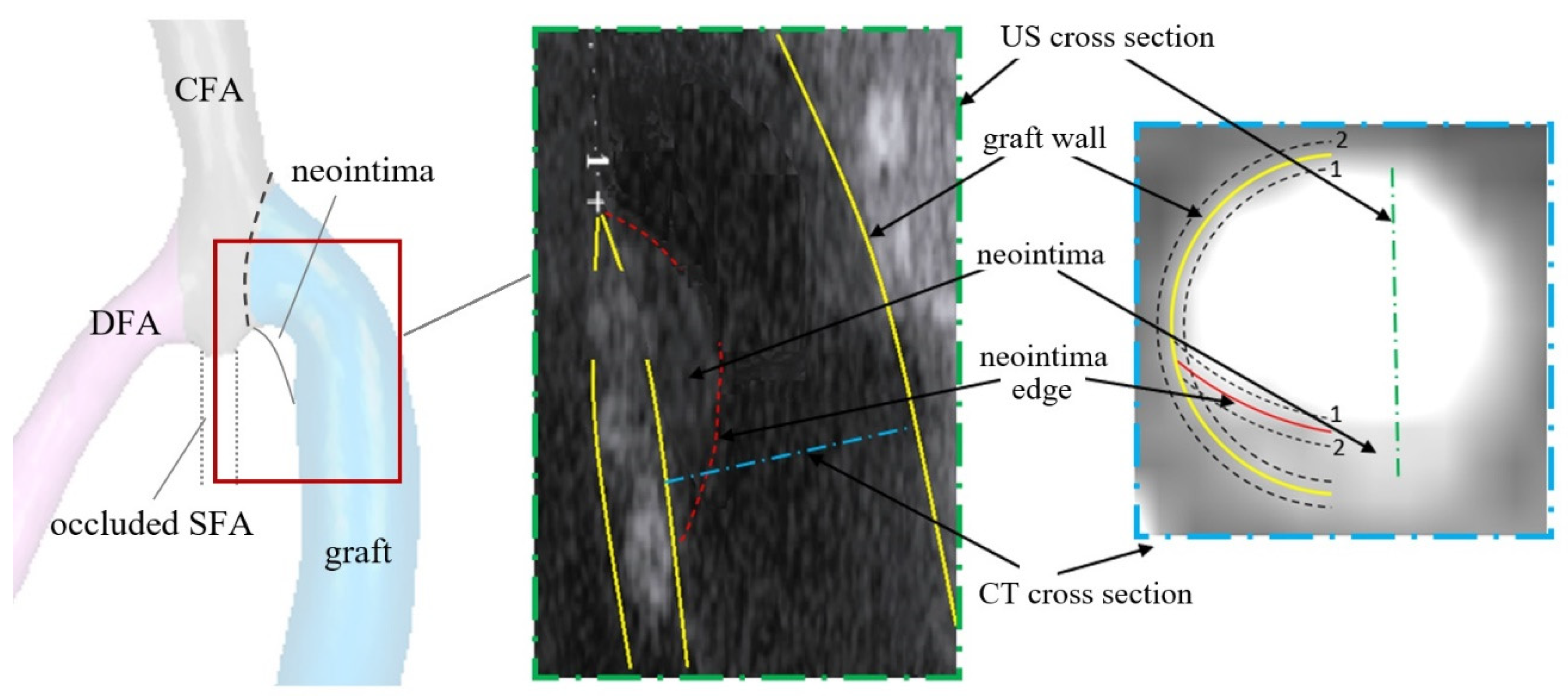
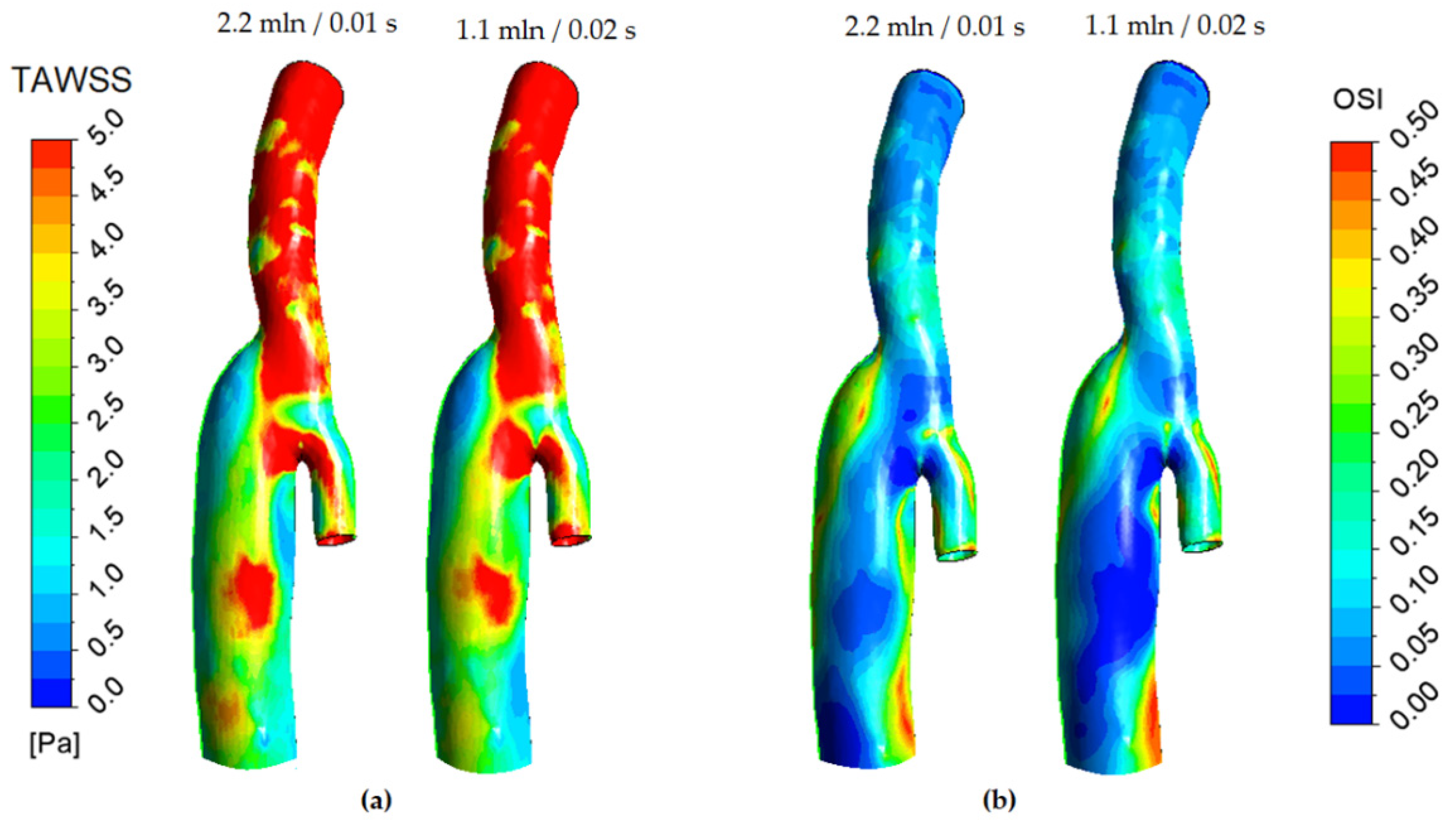
2.2. Numerical Simulation Aspect
3. Results and Discussion
3.1. Flow Features
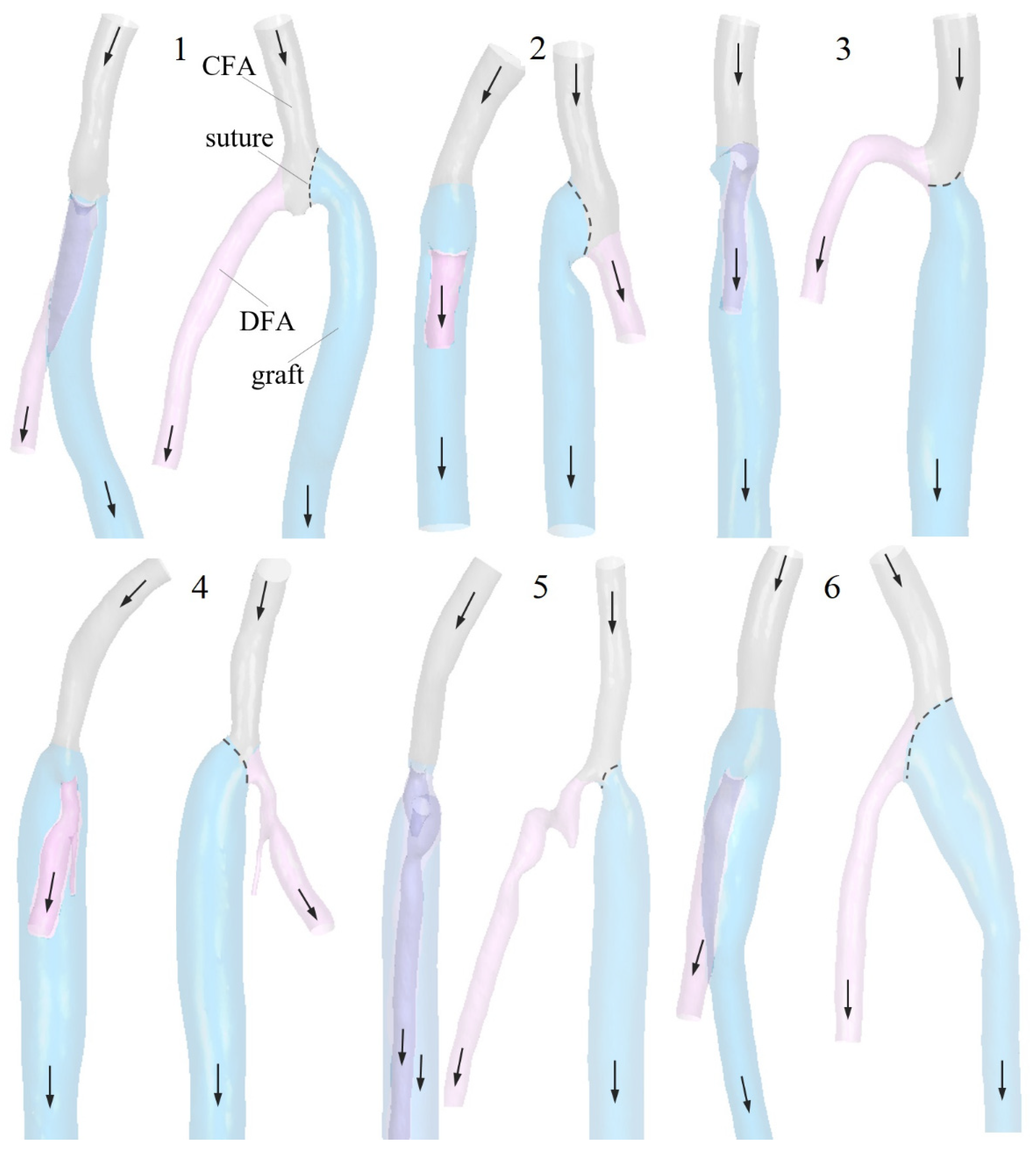
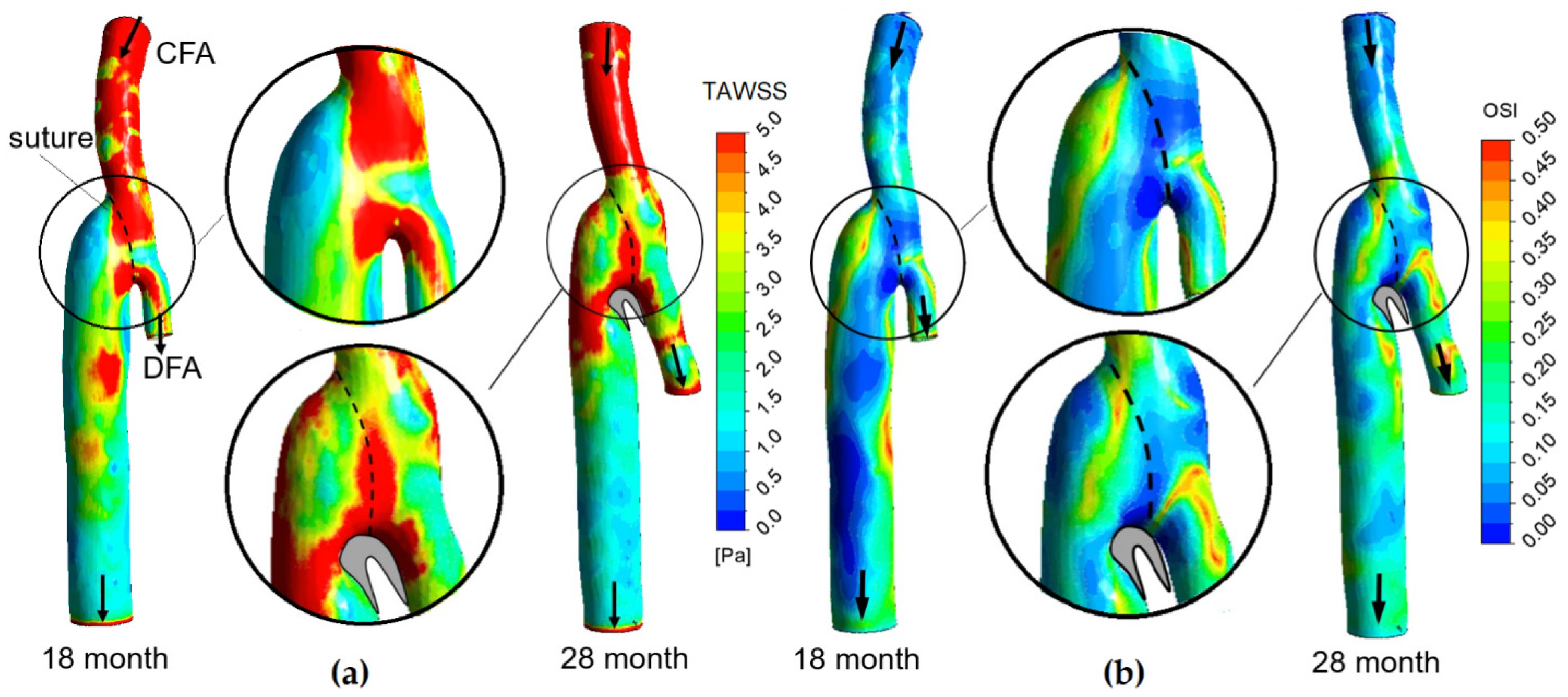
3.2. The Impact of the Geometry Changes on the Blood Flow
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herrington, W.; Lacey, B.; Sherliker, P.; Armitage, J.; Lewington, S. Epidemiology of atherosclerosis and the potential to reduce the global burden of atherothrombotic disease. Circ. Res. 2016, 118, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Timmis, A.; Townsend, N.; Gale, C.P.; Torbica, A.; Lettino, M.; Petersen, S.E.; Mossialos, E.A.; Maggioni, A.P.; Kazakiewicz, D.; May, H.T.; et al. European society of cardiology: Cardiovascular disease statistics 2019. Eur. Heart J. 2020, 41, 12–85. [Google Scholar] [CrossRef]
- Bozkurt, A.K.; Tasci, I.; Tabak, O.; Gumus, M.; Kaplan, Y. Peripheral artery disease assessed by anklebrachial index in patients with established cardiovascular disease or at least one risk factor for atherothrombosis—CAREFUL Study: A national, multi-center, cross-sectional observational study. BMC Cardiovasc. Disord. 2011, 11, 4. [Google Scholar] [CrossRef]
- Dieter, R.S.; Chu, W.W.; John, P.; Pacanowski, J.P., Jr.; McBride, P.E.; Tanke, T.E. The significance of lower extremity peripheral arterial disease. Clin. Cardiol. 2002, 25, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Shu, J.; Santulli, G. Update on peripheral artery disease: Epidemiology and evidence-based facts. Atherosclerosis 2018, 275, 379–381. [Google Scholar] [CrossRef] [PubMed]
- Poredos, P.; Poredos, P.; Jezovnik, M.K. Structure of atherosclerotic plaques in different vascular territories: Clinical relevance. Curr. Vasc. Pharmacol. 2018, 16, 125–129. [Google Scholar] [CrossRef] [PubMed]
- Poredos, P.; Cevc, M.; Blinc, A. Characteristics of atherosclerosis in femoropopliteal artery and its clinical relevance. Atherosclerosis 2021, 335, 31–40. [Google Scholar] [CrossRef]
- So, B.J.; Byun, S.J. Usefulness of PTFE graft in above-knee femoropopliteal artery bypass. J. Korean Surg. Soc. 2009, 77, 410–416. [Google Scholar] [CrossRef]
- Ambler, G.K.; Twine, C.P. Graft type for femoro-popliteal bypass surgery. Cochrane Database Syst. Rev. 2018, 2, 86. [Google Scholar] [CrossRef]
- Lemson, M.S.; Tordoir, J.H.M.; Daemen, M.J.A.P.; Kitslaar, P.J.E.H.M. Intimal hyperplasia in vascular grafts. Eur. J. Vasc Endovasc Surg 2000, 19, 336–350. [Google Scholar] [CrossRef]
- Subbotin, V.M. Analysis of arterial intimal hyperplasia: Review and hypothesis. Theor. Biol. Med. Model. 2007, 4, 41. [Google Scholar] [CrossRef] [PubMed]
- Li, l.; Terry, C.M.; Shiu, Y.-T.; Cheung, A.K. Neointimal hyperplasia associated with synthetic hemodialysis grafts. Kidney Int. 2008, 74, 1247–1261. [Google Scholar] [CrossRef]
- Krepkogorskiy, N.V.; Bulatov, D.G. Results of in situ femoropopliteal (tibial) bypass in patients with extended lower limbs arterial bed lesion and critical ischemia. Kazan. Meditsinskiy Zhurnal 2015, 96, 942–949. [Google Scholar] [CrossRef]
- Loth, F.; Jones, S.A.; Zarins, C.K.; Giddens, D.P.; Nassar, R.F.; Glagov, S.; Bassiouny, H.S. Relative contribution of wall shear stress and injury in experimental intimal thickening at PTFE end-to-side arterial anastomoses. J. Biomech. Eng. 2002, 124, 44–51. [Google Scholar] [CrossRef]
- Jackson, M.; Wood, N.B.; Zhao, S.; Augst, A.; Wolfe, J.H.; Gedroyc, W.M.W.; Hughes, A.D.; Thom, S.A.M.G.; Xu, X.Y. Low wall shear stress predicts subsequent development of wall hypertrophy in lower limb bypass grafts. Artery Res. 2009, 3, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Himburg, H.A.; Grzybowski, D.M.; Hazel, A.L.; LaMack, J.A.; Li, X.-M.; Friedman, M.H. Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. Am. J. Physiol Heart Circ. Physiol 2003, 286, 1916–1922. [Google Scholar] [CrossRef] [PubMed]
- Hoogendoorn, A.; Kok, A.M.; Hartman, E.M.J.; de Nisco, G.; Casadonte, L.; Chiastra, C.; Coenen, A.; Korteland, S.-A.; Van der Heiden, K.; Gijsen, F.J.H.; et al. Multidirectional wall shear stress promotes advanced coronary plaque development: Comparing five shear stress metrics. Cardiovasc. Res. 2020, 116, 1136–1146. [Google Scholar] [CrossRef]
- Schlager, O.; Giurgea, A.; Margeta, C.; Seidinger, D.; Steiner-Boeker, S.; van der Loo, B.; Koppensteiner, R. Wall shear stress in the superficial femoral artery of healthy adults and its response to postural changes and exercise. Eur. J. Vasc Endovasc. Surg. 2011, 41, 821–827. [Google Scholar] [CrossRef]
- Desyatova, A.; MacTaggart, J.; Romarowski, R.; Poulson, W.; Conti, M.; Kamenskiy, A. Effect of aging on mechanical stresses, deformations, and hemodynamics in human femoropopliteal artery due to limb flexion. Biomech. Model. Mechanobiol. 2017, 17, 181–189. [Google Scholar] [CrossRef]
- Dolan, J.M.; Kolega, J.; Meng, H. High wall shear stress and spatial gradients in vascular pathology: A review. Ann. Biomed. Eng. 2012, 41, 1411–1427. [Google Scholar] [CrossRef]
- Colombo, M.; He, Y.; Corti, A.; Gallo, D.; Casarin, S.; Rozowsky, J.M.; Migliavacca, F.; Berceli, S.; Chiastra, C. Baseline local hemodynamics as predictor of lumen remodeling at 1-year follow-up in stented superficial femoral arteries. Sci. Rep. 2021, 11, 1613. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, X.; Li, X.; Xu, L.; Chen, X.; Liang, F. Tortuosity of the superficial femoral artery and its influence on blood flow patterns and risk of atherosclerosis. Biomech. Model. Mechanobiol. 2019, 18, 883–896. [Google Scholar] [CrossRef] [PubMed]
- Gökgöl, C.; Diehm, N.; Räber, L.; Büchler, P. Prediction of restenosis based on hemodynamical markers in revascularized femoro-popliteal arteries during leg flexion. Biomech. Model. Mechanobiol. 2019, 18, 1883–1893. [Google Scholar] [CrossRef] [PubMed]
- Singh, J.; Brunner, G.; Morrisett, J.D.; Ballantyne, C.M.; Lumsden, A.B.; Shah, D.J.; Decuzzi, P. Patient-specific flow descriptors and normalised wall index in peripheral artery disease: A preliminary study. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2016, 6, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Liu, X.; Song, Q.; Chen, G.; Wang, D.; Zhang, H.; Yan, L.; Liu, D.; Huang, W. Patient-specific structural effects on hemodynamics in the ischemic lower limb artery. Sci. Rep. 2016, 6, 39225. [Google Scholar] [CrossRef]
- Donadoni, F.; Pichardo-Almarza, C.; Bartlett, M.; Dardik, A.; Homer-Vanniasinkam, S.; Díaz-Zuccarini, V. Patient-specific, multi-scale modeling of neointimal hyperplasia in vein grafts. Front. Physiol. 2017, 8, 226. [Google Scholar] [CrossRef]
- Donadoni, F.; Bonfanti, M.; Pichardo-Almarza, C.; Homer-Vanniasinkam, S.; Dardik, A.; Díaz-Zuccarini, V. An in silico study of the influence of vessel wall deformation on neointimal hyperplasia progression in peripheral bypass grafts. Med. Eng. Phys. 2019, 74, 137–145. [Google Scholar] [CrossRef]
- Donadoni, F.; Pichardo-Almarza, C.; Homer-Vanniasinkam, S.; Dardik, A.; Díaz-Zuccarini, V. Multiscale, patient-specific computational fluid dynamics models predict formation of neointimal hyperplasia in saphenous vein grafts. J. Vasc. Surg. Cases Innov. Tech. 2020, 6, 292–306. [Google Scholar] [CrossRef]
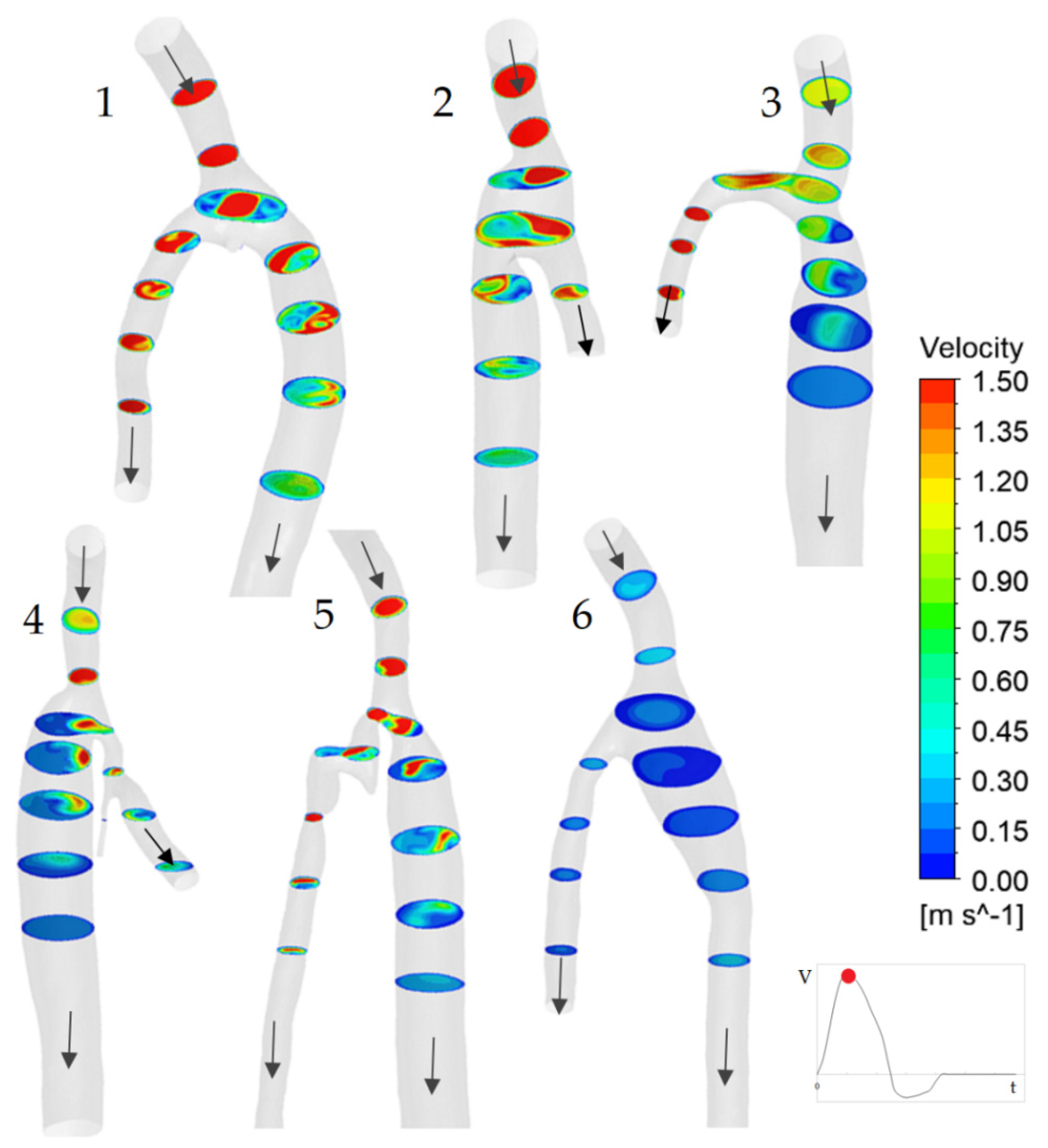
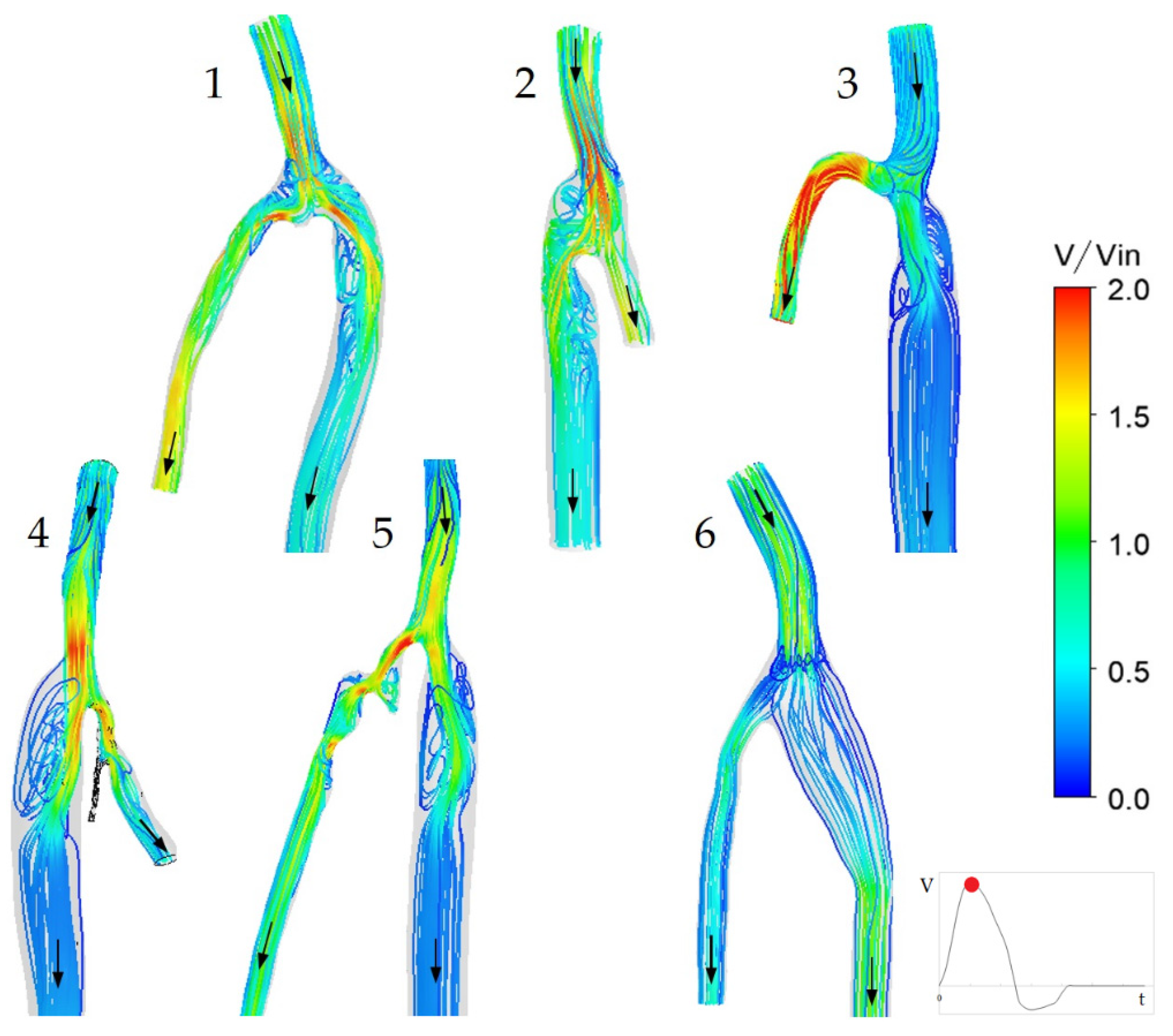

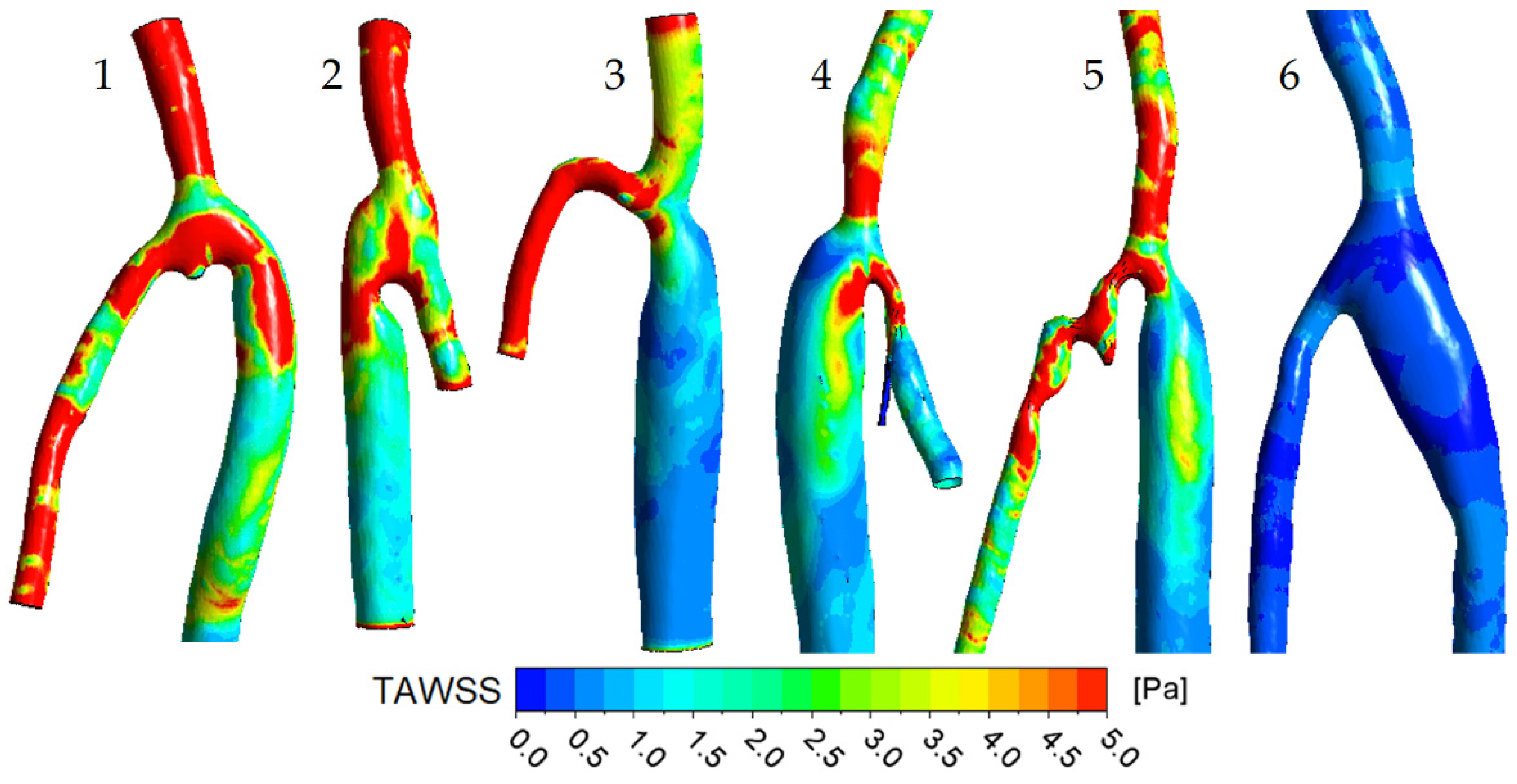
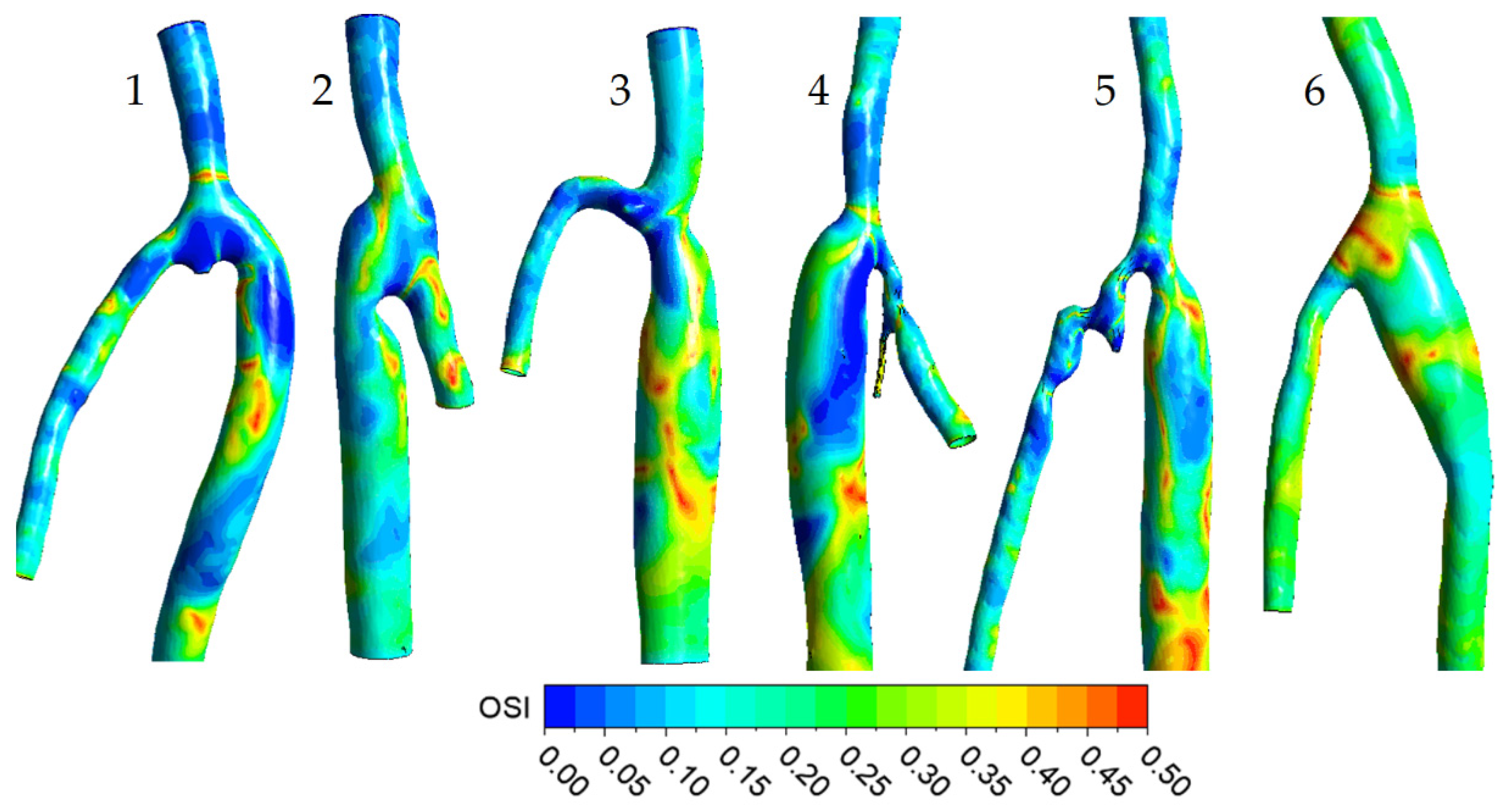
| № | ∆t, month | DCFA, mm | Dgraft/DCFA | α, ° | QCFA, mL/min | Qgraft/QCFA | ReCFAmax | WoCFA |
|---|---|---|---|---|---|---|---|---|
| 1 | 12 | 8.2 | 1.0 | 45 | 823 | 0.5 | 2920 | 12.6 |
| 2 | 28 | 7.4 | 1.2 | 35 | 516 | 0.7 | 2030 | 11.4 |
| 3 | 30 | 6.8 | 1.3 | 85 | 370 | 0.5 | 1580 | 10.4 |
| 4 | 18 | 6.4 | 1.7 | 55 | 328 | 0.9 | 1490 | 9.8 |
| 5 | 14 | 5.5 | 1.7 | 45 | 313 | 0.6 | 1650 | 8.4 |
| 6 | 4 | 6.8 | 1.0 | 150 | 109 | 0.9 | 470 | 10.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanova, Y.; Yukhnev, A.; Tikhomolova, L.; Smirnov, E.; Vrabiy, A.; Suprunovich, A.; Morozov, A.; Khubulava, G.; Vavilov, V. Experience of Patient-Specific CFD Simulation of Blood Flow in Proximal Anastomosis for Femoral-Popliteal Bypass. Fluids 2022, 7, 314. https://doi.org/10.3390/fluids7100314
Ivanova Y, Yukhnev A, Tikhomolova L, Smirnov E, Vrabiy A, Suprunovich A, Morozov A, Khubulava G, Vavilov V. Experience of Patient-Specific CFD Simulation of Blood Flow in Proximal Anastomosis for Femoral-Popliteal Bypass. Fluids. 2022; 7(10):314. https://doi.org/10.3390/fluids7100314
Chicago/Turabian StyleIvanova, Yana, Andrey Yukhnev, Ludmila Tikhomolova, Evgueni Smirnov, Andrey Vrabiy, Andrey Suprunovich, Alexey Morozov, Gennady Khubulava, and Valery Vavilov. 2022. "Experience of Patient-Specific CFD Simulation of Blood Flow in Proximal Anastomosis for Femoral-Popliteal Bypass" Fluids 7, no. 10: 314. https://doi.org/10.3390/fluids7100314
APA StyleIvanova, Y., Yukhnev, A., Tikhomolova, L., Smirnov, E., Vrabiy, A., Suprunovich, A., Morozov, A., Khubulava, G., & Vavilov, V. (2022). Experience of Patient-Specific CFD Simulation of Blood Flow in Proximal Anastomosis for Femoral-Popliteal Bypass. Fluids, 7(10), 314. https://doi.org/10.3390/fluids7100314






