High-Efficiency Can Be Achieved for Non-Uniformly Flexible Pitching Hydrofoils via Tailored Collective Interactions
Abstract
:1. Introduction
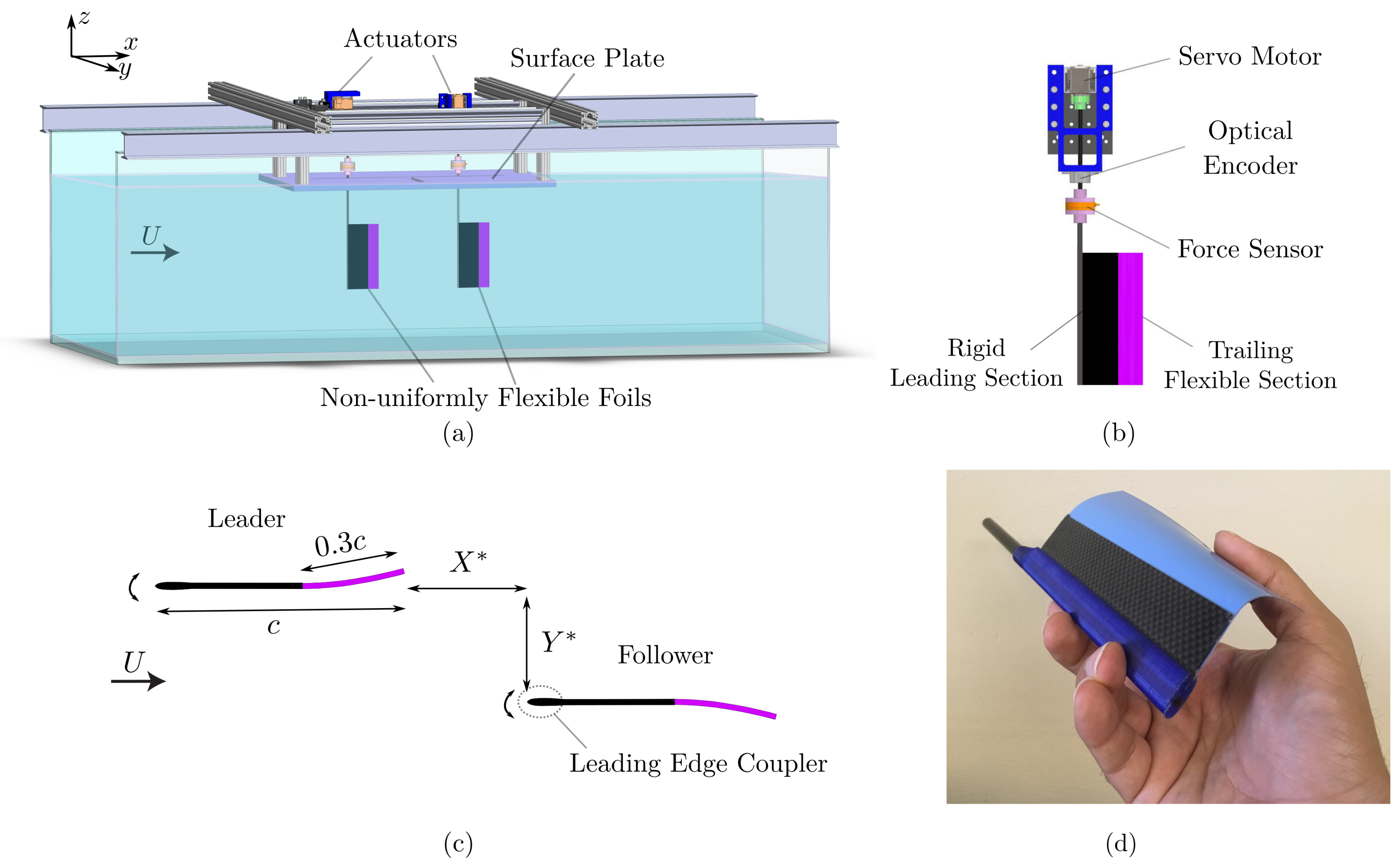
2. Experimental Methods
3. Results
3.1. Isolated Flexible Foil Performance
3.2. Case I: Flexible Foils in In-Line Arrangements
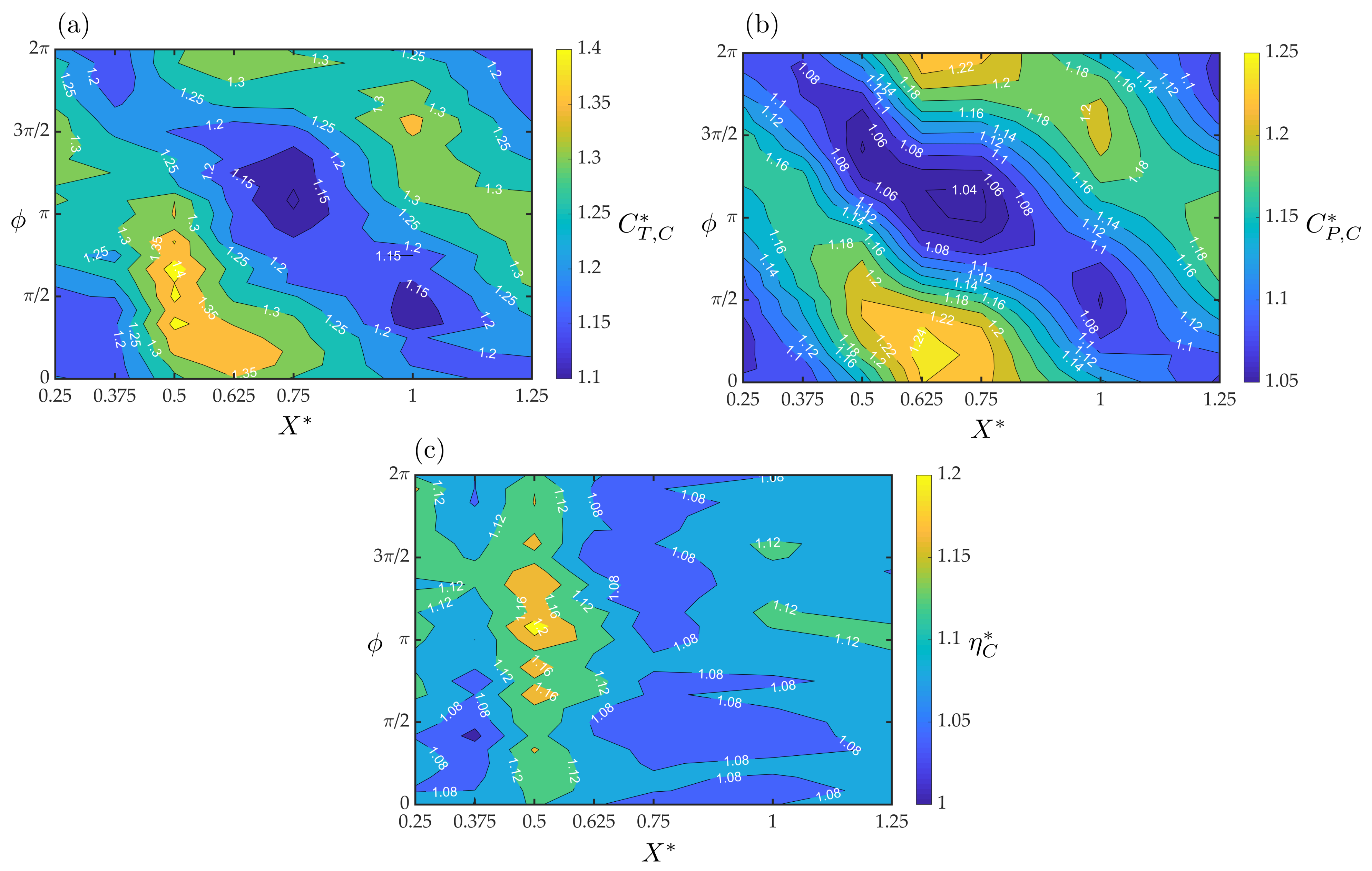
3.3. Case II: Flexible Foils in Staggered Arrangements
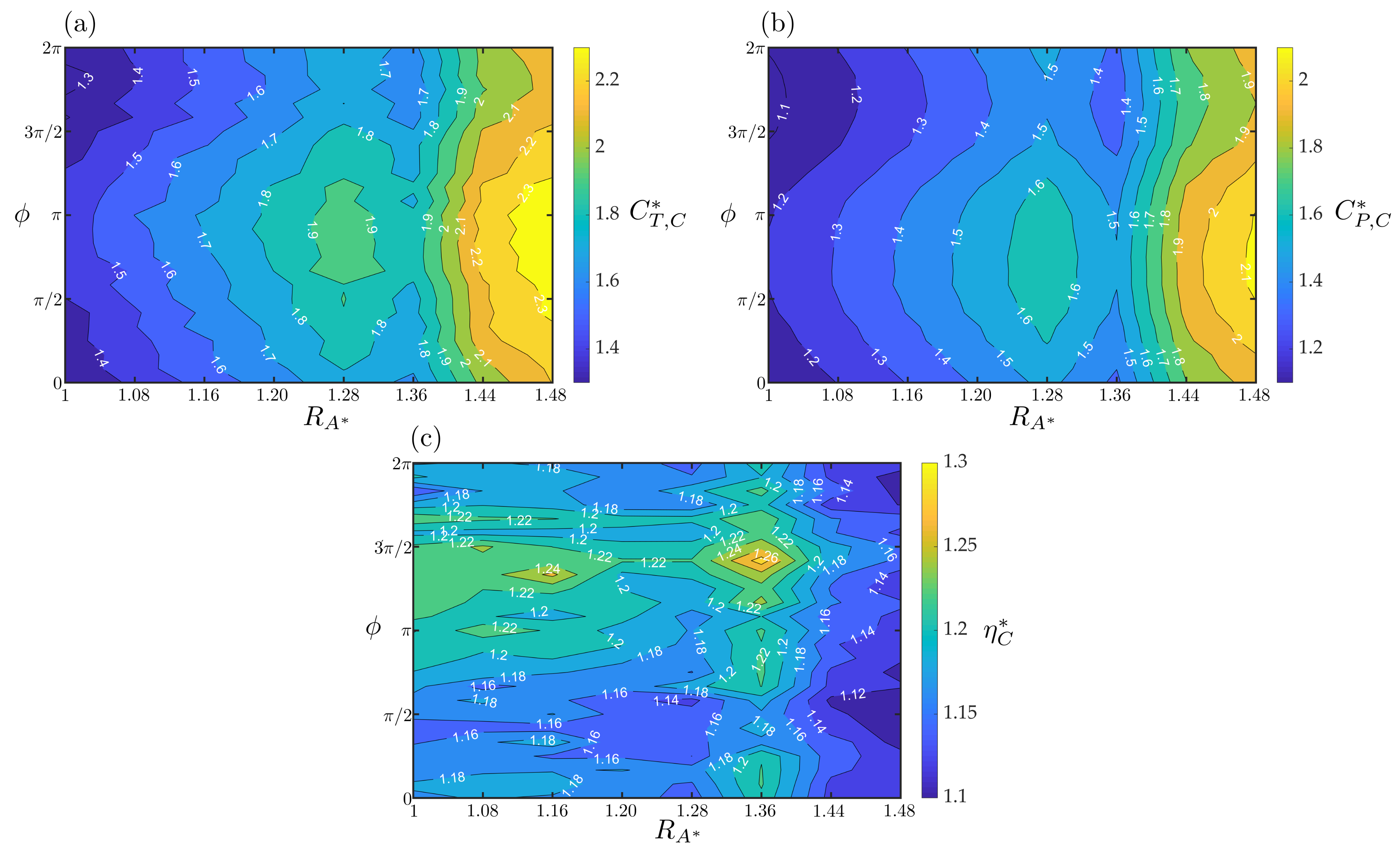
3.4. Case III: Flexible Foils Pitching at Different Amplitudes
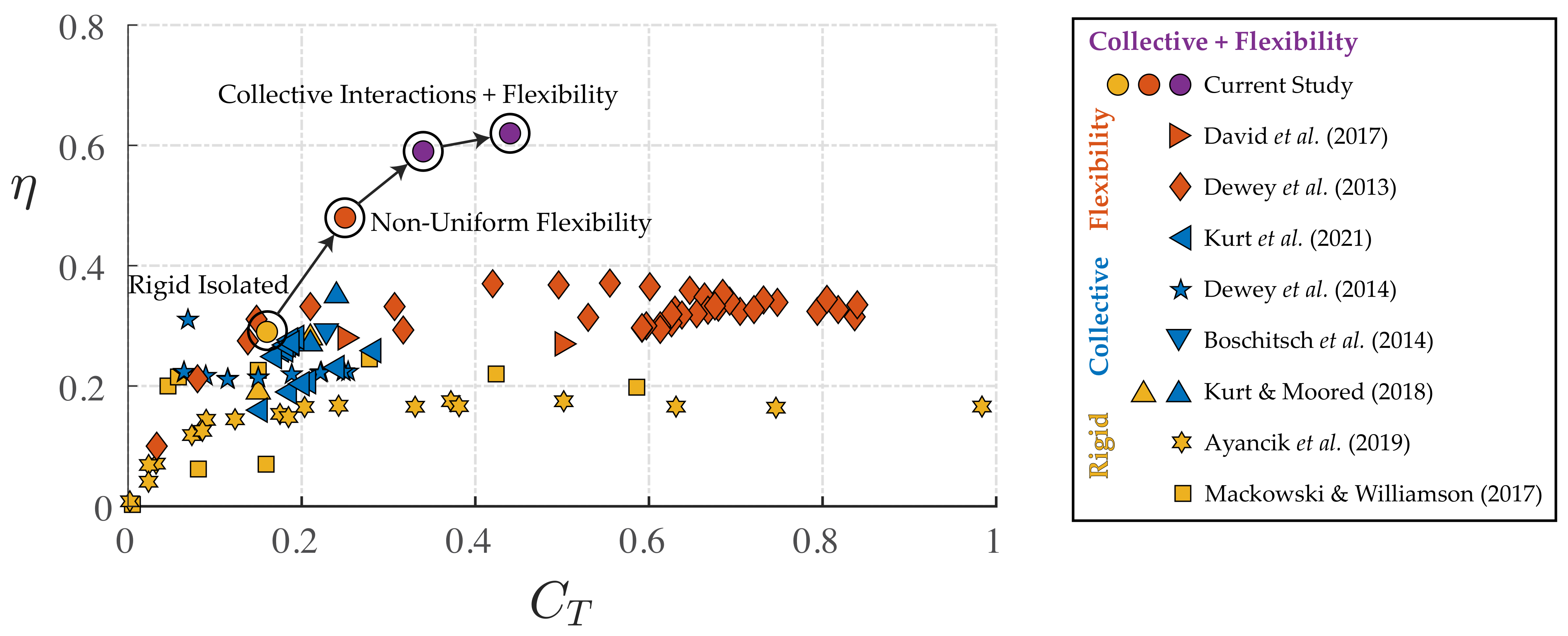
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Fully Rigid Foil Isolated Thrust and Efficiency
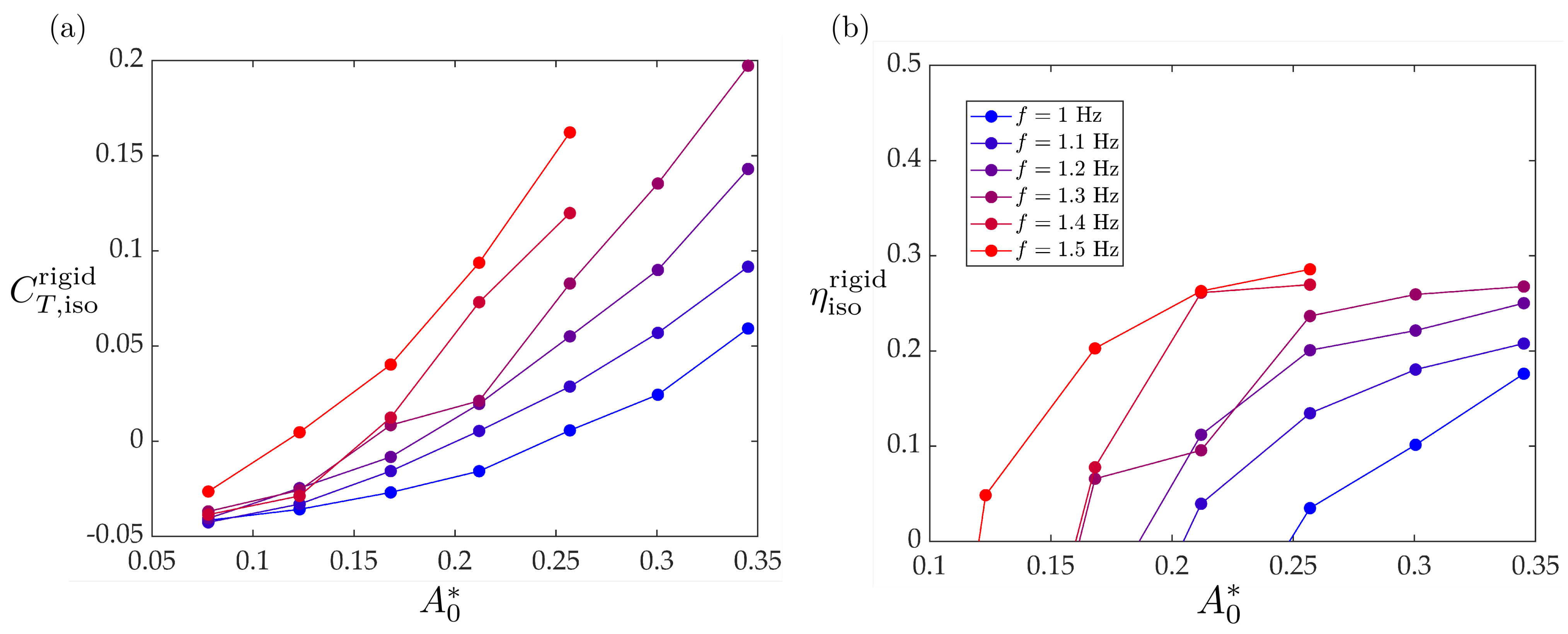
Appendix B. Weighted Average
Appendix C. Normalized Collective Performance Metrics
Appendix D. Leader and Follower Foil Performance
Appendix D.1. Flexible Foils in In-Line Arrangements
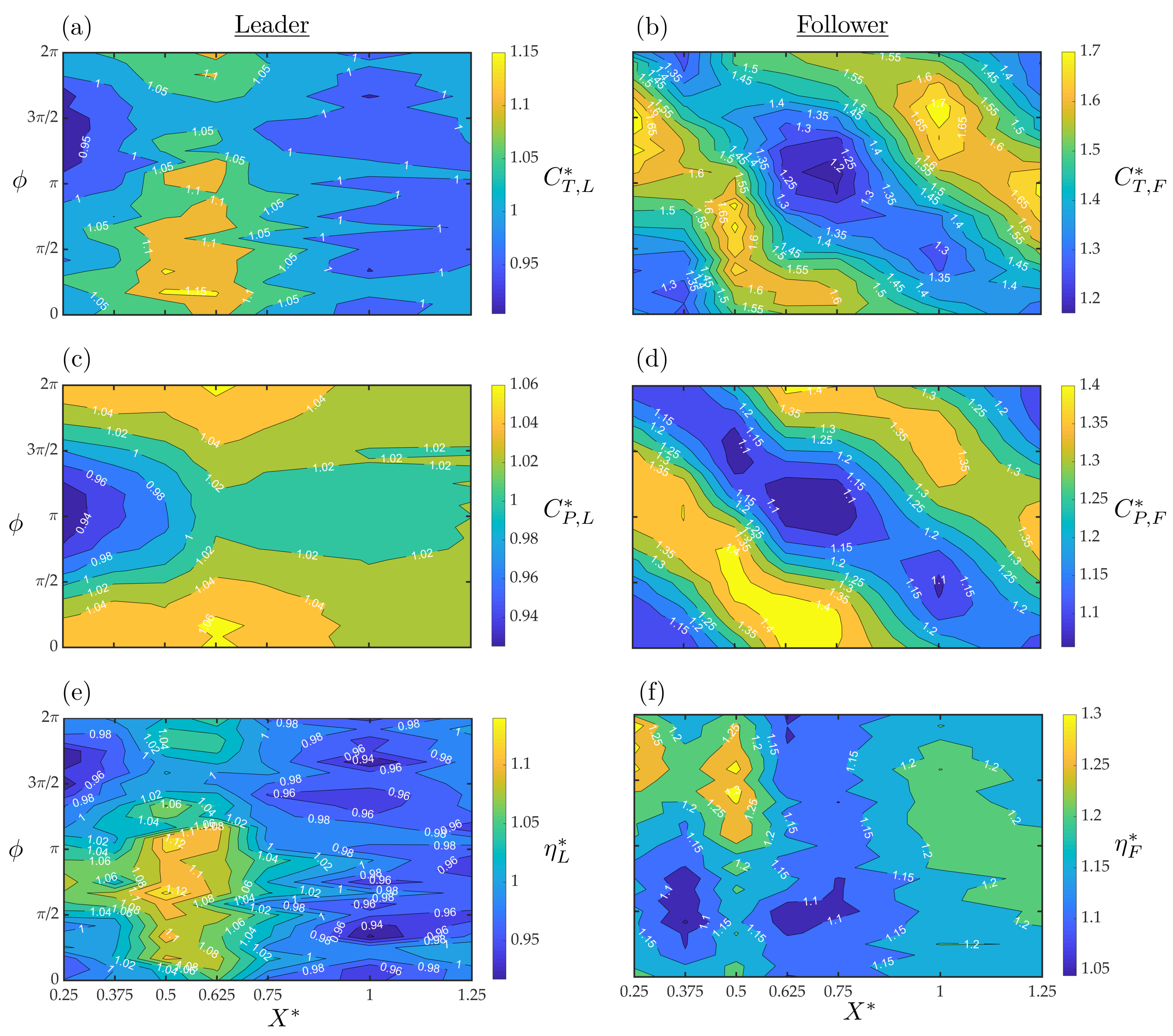
Appendix D.2. Flexible Foils in Staggered Arrangements
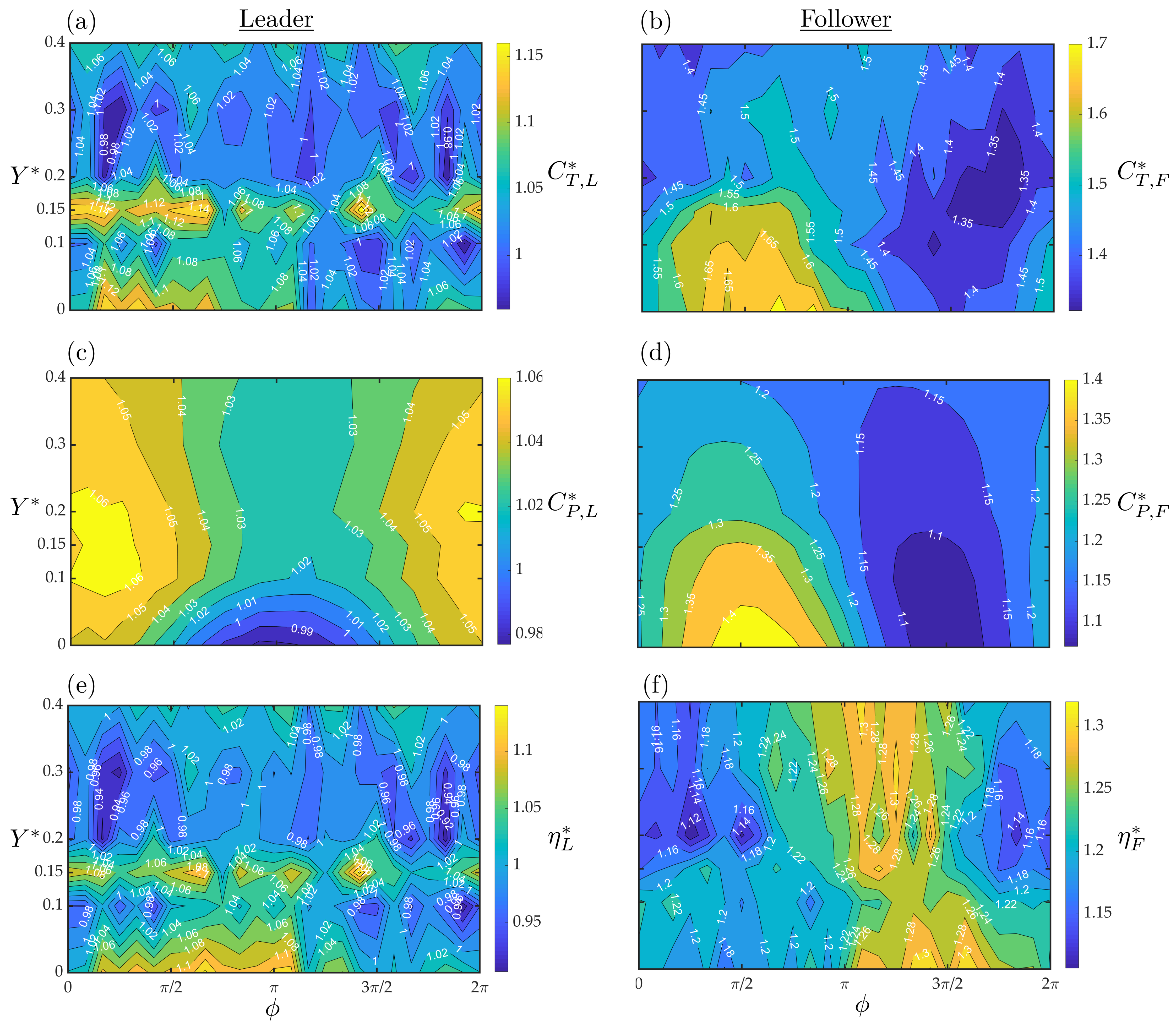
Appendix D.3. Flexible Foils Pitching at Different Amplitudes

References
- Lucas, K.N.; Lauder, G.V.; Tytell, E.D. Airfoil-like mechanics generate thrust on the anterior body of swimming fishes. Proc. Natl. Acad. Sci. USA 2020, 117, 10585–10592. [Google Scholar] [CrossRef]
- Drucker, E.G.; Lauder, G.V. Locomotor function of the dorsal fin in teleost fishes: Experimental analysis of wake forces in sunfish. J. Exp. Biol. 2001, 204, 2943–2958. [Google Scholar] [CrossRef] [PubMed]
- Standen, E.; Lauder, G.V. Hydrodynamic function of dorsal and anal fins in brook trout (Salvelinus fontinalis). J. Exp. Biol. 2007, 210, 325–339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fish, F.; Lauder, G. Passive and Active Flow Control By Swimming Fishes and Mammals. Annu. Rev. Fluid Mech. 2006, 38, 193–224. [Google Scholar] [CrossRef] [Green Version]
- Lauder, G.V.; Tytell, E.D. Hydrodynamics of undulatory propulsion. Fish Physiol. 2005, 23, 425–468. [Google Scholar]
- Lauder, G.V.; Madden, P.G. Fish locomotion: Kinematics and hydrodynamics of flexible foil-like fins. Exp. Fluids 2007, 43, 641–653. [Google Scholar] [CrossRef]
- Rosic, M.L.N.; Thornycroft, P.J.; Feilich, K.L.; Lucas, K.N.; Lauder, G.V. Performance variation due to stiffness in a tuna-inspired flexible foil model. Bioinspir. Biomimetics 2017, 12, 016011. [Google Scholar] [CrossRef]
- Bose, N.; Lien, J.; Ahia, J. Measurements of the bodies and flukes of several cetacean species. Proc. R. Soc. B Biol. Sci. 1990, 242, 163–173. [Google Scholar] [CrossRef]
- DeBlois, M.C.; Motani, R. Flipper bone distribution reveals flexible trailing edge in underwater flying marine tetrapods. J. Morphol. 2019, 280, 908–924. [Google Scholar] [CrossRef]
- Katz, J.; Weihs, D. Hydrodynamic propulsion by large amplitude oscillation of an airfoil with chordwise flexibility. J. Fluid Mech. 1978, 88, 485–497. [Google Scholar] [CrossRef]
- Moore, M.N.J. Analytical results on the role of flexibility in flapping propulsion. J. Fluid Mech. 2014, 757, 599–612. [Google Scholar] [CrossRef] [Green Version]
- Heathcote, S.; Gursul, I. Flexible Flapping Airfoil Propulsion at Low Reynolds Numbers. AIAA J. 2007, 45. [Google Scholar] [CrossRef]
- Dewey, P.A.; Boschitsch, B.M.; Moored, K.W.; Stone, H.A.; Smits, A.J. Scaling laws for the thrust production of flexible pitching panels. J. Fluid Mech. 2013, 732, 29. [Google Scholar] [CrossRef]
- Quinn, D.B.; Lauder, G.V.; Smits, A.J. Maximizing the efficiency of a flexible propulsor using experimental optimization. J. Fluid Mech. 2015, 767, 430–448. [Google Scholar] [CrossRef] [Green Version]
- Lucas, K.N.; Johnson, N.; Beaulieu, W.T.; Cathcart, E.; Tirrell, G.; Colin, S.P.; Gemmell, B.J.; Dabiri, J.O.; Costello, J.H. Bending rules for animal propulsion. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lucas, K.N.; Thornycroft, P.J.; Gemmell, B.J.; Colin, S.P.; Costello, J.H.; Lauder, G.V. Effects of non-uniform stiffness on the swimming performance of a passively-flexing, fish-like foil model. Bioinspir. Biomimetics 2015, 10, 056019. [Google Scholar] [CrossRef] [Green Version]
- Zeyghami, S.; Moored, K.W. Effect of Nonuniform Flexibility on Hydrodynamic Performance of Pitching Propulsors. J. Fluids Eng. 2019, 141, 4041976. [Google Scholar] [CrossRef] [Green Version]
- Han, T.; Kurt, M.; Mivehchi, A.; Moored, K.W. Tailoring the Bending Pattern of Non-Uniformly Flexible Pitching Propulsors Enhances Propulsive Efficiency. In APS Division of Fluid Dynamics Meeting Abstracts; P27-002; American Physical Society: Seattle, WA, USA, 2019. [Google Scholar]
- Boschitsch, B.M.; Dewey, P.A.; Smits, A.J. Propulsive performance of unsteady tandem hydrofoils in an in-line configuration. Phys. Fluids 2014, 26, 051901. [Google Scholar] [CrossRef]
- Kurt, M.; Moored, K.W. Flow interactions of two-and three-dimensional networked bio-inspired control elements in an in-line arrangement. Bioinspir. Biomimetics 2018, 13, 045002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gopalkrishnan, R.; Triantafyllou, M.; Triantafyllou, G.; Barrett, D. Active vorticity control in a shear flow using a flapping foil. J. Fluid Mech. 1994, 274, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Muscutt, L.; Weymouth, G.; Ganapathisubramani, B. Performance augmentation mechanism of in-line tandem flapping foils. J. Fluid Mech. 2017, 827, 484–505. [Google Scholar] [CrossRef] [Green Version]
- Kurt, M.; Eslam Panah, A.; Moored, K.W. Flow interactions between low aspect ratio hydrofoils in in-line and staggered arrangements. Biomimetics 2020, 5, 13. [Google Scholar] [CrossRef] [Green Version]
- Mignano, A.P.; Kadapa, S.; Tangorra, J.L.; Lauder, G.V. Passing the wake: Using multiple fins to shape forces for swimming. Biomimetics 2019, 4, 23. [Google Scholar] [CrossRef] [Green Version]
- Kurt, M.; Mivehchi, A.; Moored, K.W. Two-dimensionally stable self-organization arises in simple schooling swimmers through hydrodynamic interactions. arXiv 2021, arXiv:2102.03571. [Google Scholar]
- Tytell, E.D.; Lauder, G.V. The hydrodynamics of eel swimming: I. Wake structure. J. Exp. Biol. 2004, 207, 1825–1841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kinsey, T.; Dumas, G.; Lalande, G.; Ruel, J.; Méhut, A.; Viarouge, P.; Lemay, J.; Jean, Y. Prototype testing of a hydrokinetic turbine based on oscillating hydrofoils. Renew. Energy 2011, 36, 1710–1718. [Google Scholar] [CrossRef]
- Ribeiro, B.L.R.; Frank, S.L.; Franck, J.A. Vortex dynamics and Reynolds number effects of an oscillating hydrofoil in energy harvesting mode. J. Fluids Struct. 2020, 94, 102888. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, B.L.R.; Su, Y.; Guillaumin, Q.; Breuer, K.S.; Franck, J.A. Wake-foil Interactions and Energy Harvesting Efficiency in Tandem Oscillating Foils. arXiv 2021, arXiv:2103.05892. [Google Scholar]
- Verma, S.; Novati, G.; Koumoutsakos, P. Efficient collective swimming by harnessing vortices through deep reinforcement learning. Proc. Natl. Acad. Sci. USA 2018, 115, 5849–5854. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Nagy, M.; Graving, J.M.; Bak-Coleman, J.; Xie, G.; Couzin, I.D. Vortex phase matching as a strategy for schooling in robots and in fish. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Dewey, P.A.; Quinn, D.B.; Boschitsch, B.M.; Smits, A.J. Propulsive performance of unsteady tandem hydrofoils in a side-by-side configuration. Phys. Fluids 2014, 26, 041903. [Google Scholar] [CrossRef]
- David, M.J.; Govardhan, R.N.; Arakeri, J.H. Thrust generation from pitching foils with flexible trailing edge flaps. J. Fluid Mech. 2017, 828, 70–103. [Google Scholar] [CrossRef]
- MacKowski, A.W.; Williamson, C.H. Effect of pivot location and passive heave on propulsion from a pitching airfoil. Phys. Rev. Fluids 2017, 2. [Google Scholar] [CrossRef]
- Ayancik, F.; Zhong, Q.; Quinn, D.B.; Brandes, A.; Bart-Smith, H.; Moored, K.W. Scaling laws for the propulsive performance of three-dimensional pitching propulsors. J. Fluid Mech. 2019, 871, 1117–1138. [Google Scholar] [CrossRef] [Green Version]
- Triantafyllou, G.S.; Triantafyllou, M.; Grosenbaugh, M. Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 1993, 7, 205–224. [Google Scholar] [CrossRef]
- Buchholz, J.H.; Smits, A.J. The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 2008, 603, 331. [Google Scholar] [CrossRef] [Green Version]
- Floryan, D.; Van Buren, T.; Smits, A.J. Efficient cruising for swimming and flying animals is dictated by fluid drag. Proc. Natl. Acad. Sci. USA 2018, 115, 8116–8118. [Google Scholar] [CrossRef] [Green Version]
- Moored, K.W.; Quinn, D.B. Inviscid scaling laws of a self-propelled pitching airfoil. AIAA J. 2018, 57, 3686–3700. [Google Scholar] [CrossRef] [Green Version]
- King, J.T.; Green, M.A. Experimental study of the three-dimensional wakes produced by trapezoidal panels with varying trailing edge geometry and piching amplitude. In AIAA SciTech; American Institute of Aeronautics and Astronautics: San Diego, CA, USA, 2019. [Google Scholar]
- Bernitsas, M.; Ray, D.; Kinley, P. KT, KQ and Efficiency Curves for the Wageningen b-Series Propellers; Technical Report; University of Michigan: Ann Arbor, MI, USA, 1981. [Google Scholar]
- Ayancik, F.; Fish, F.E.; Moored, K.W. Three-dimensional scaling laws of cetacean propulsion characterize the hydrodynamic interplay of flukes’ shape and kinematics. J. R. Soc. Interface 2020, 17. [Google Scholar] [CrossRef] [Green Version]
- Ramananarivo, S.; Mitchel, T.; Ristroph, L. Improving the propulsion speed of a heaving wing through artificial evolution of shape. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475. [Google Scholar] [CrossRef] [Green Version]
- Van Buren, T.; Floryan, D.; Smits, A.J.; Han, P.; Bode-Oke, A.T.; Dong, H. Foil shapes for efficient fish-like propulsion. In AIAA SciTech; American Institute of Aeronautics and Astronautics: San Diego, CA, USA, 2019. [Google Scholar]
- Moore, M.N.J. Torsional spring is the optimal flexibility arrangement for thrust production of a flapping wing. Phys. Fluids 2015, 27, 091701. [Google Scholar] [CrossRef] [Green Version]
- Yeh, P.D.; Li, Y.; Alexeev, A. Efficient swimming using flexible fins with tapered thickness. Phys. Rev. Fluids 2017, 2, 1–9. [Google Scholar] [CrossRef]
- Floryan, D.; Rowley, C.W. Distributed flexibility in inertial swimmers. J. Fluid Mech. 2020, 888, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Tytell, E.D.; Standen, E.M.; Lauder, G.V. Escaping flatland: Three-dimensional kinematics and hydrodynamics of median fins in fishes. J. Exp. Biol. 2007, 211, 187–195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Wainwright, D.K.; Lindengren, R.E.; Lauder, G.V.; Dong, H. Tuna locomotion: A computational hydrodynamic analysis of finlet function. J. R. Soc. Interface 2020, 17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Licht, S.; Durham, N. Biomimetic robots for environmental monitoring in the surf zone and in very shallow water. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012. [Google Scholar]


| Case I | Case II | Case III | |
|---|---|---|---|
| 0.25–1.25 | 0.5 | 0.5 | |
| 0 | 0–0.4 | 0 | |
| 1 | 1 | 1–1.48 | |
| 0.25 | 0.25 | 0.25 | |
| f [Hz] | 1.3 | 1.3 | 1.3 |
| 0–2 with increments | |||
| U [m/s] | 0.094 | 0.094 | 0.094 |
| Performance Coefficients at Peak Efficiency | |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurt, M.; Mivehchi, A.; Moored, K. High-Efficiency Can Be Achieved for Non-Uniformly Flexible Pitching Hydrofoils via Tailored Collective Interactions. Fluids 2021, 6, 233. https://doi.org/10.3390/fluids6070233
Kurt M, Mivehchi A, Moored K. High-Efficiency Can Be Achieved for Non-Uniformly Flexible Pitching Hydrofoils via Tailored Collective Interactions. Fluids. 2021; 6(7):233. https://doi.org/10.3390/fluids6070233
Chicago/Turabian StyleKurt, Melike, Amin Mivehchi, and Keith Moored. 2021. "High-Efficiency Can Be Achieved for Non-Uniformly Flexible Pitching Hydrofoils via Tailored Collective Interactions" Fluids 6, no. 7: 233. https://doi.org/10.3390/fluids6070233
APA StyleKurt, M., Mivehchi, A., & Moored, K. (2021). High-Efficiency Can Be Achieved for Non-Uniformly Flexible Pitching Hydrofoils via Tailored Collective Interactions. Fluids, 6(7), 233. https://doi.org/10.3390/fluids6070233






