Abstract
We present a stabilized POD–Galerkin reduced order method (ROM) for a Leray model. For the implementation of the model, we combine a two-step algorithm called Evolve-Filter (EF) with a computationally efficient finite volume method. In both steps of the EF algorithm, velocity and pressure fields are approximated using different POD basis and coefficients. To achieve pressure stabilization, we consider and compare two strategies: the pressure Poisson equation and the supremizer enrichment of the velocity space. We show that the evolve and filtered velocity spaces have to be enriched with the supremizer solutions related to both evolve and filter pressure fields in order to obtain stable and accurate solutions with the supremizer enrichment method. We test our ROM approach on a 2D unsteady flow past a cylinder at Reynolds number . We find that both stabilization strategies produce comparable errors in the reconstruction of the lift and drag coefficients, with the pressure Poisson equation method being more computationally efficient.
1. Introduction
For about a couple of decades, reduced order models (ROMs) have emerged as an efficient tool for the approximation of problems governed by parametrized partial differential equations. This success is owed to the fact that ROMs can significantly reduce the computational cost required by classical full order models (FOMs), e.g., finite element method or finite volume method, when several solutions associated to different parameter values are needed. The basic ROM framework consists of two steps. During a first phase (called offline), a database of several solutions is collected by solving a FOM of choice for different parameter values. Then, during a second phase (called online), the database collected in the offline phase is used to compute the solution for newly specified values of the parameters in a short amount of time. For a comprehensive review on ROMs, we refer the reader to, e.g., [1,2,3,4,5,6,7,8].
The particular ROM we consider in this paper is based on a POD–Galerkin approach, which consists in extracting of the most energetic modes representing the system dynamics and projecting the governing equations onto the space spanned by these modes. For the specific application that we target, i.e., an incompressible fluid flow at moderately high Reynolds number, and it is well known that standard POD–Galerkin models lead to instabilities [9,10]. A successful way to cure these instabilities in advection dominated flows is to adopt subgrid-scale closure models. See, e.g., [11,12]. Thus, we choose to work with a large eddy simulation (LES) approach.
We focus on a variant of the so-called Leray model [13], where the small-scale effects are described by a set of equations to be added to the discrete Navier–Stokes equations. This extra problem acts as a differential low-pass filter [14]. For its actual implementation, we use the Evolve-Filter (EF) algorithm [15,16,17,18]. One of the novelties of our approach is that we use a finite volume (FV) method [19,20], while the vast majority of the works on Leray-type models use a finite element framework. Some of the reasons behind our interest in a FV approximation are the following: FV schemes are usually favored for practical, real-life applications; FV methods are considered robust, computationally efficient, and suitable when the conservation of the numerical flux is a crucial issue, as is the case in problems arising in fluid dynamics; nowadays many computational codes used in the industry, both commercial (e.g., CFX, FLUENT, STAR-CD) and open-source (e.g., OpenFOAM), are based on FV discretizations. Thus, with a FV approximation we hope to broaden the community of practitioners that use Leray-type models and ROMs. In the context of regularized ROMs, the Leray model and the EF algorithm have been thoroughly investigated. See, e.g., [21,22,23,24,25]. In all of these works, the filtering approach is only employed at reduced order level. In [26,27], for the first time the LES filtering is used also at the FOM level, i.e., to generate the snapshot data. Such an approach provides a ROM that is fully consistent with the FOM as the same mathematical framework is used during both the offline and online stages.
This paper could be seen as an extension of [26]. Therein, we used a pressure Poisson Equation (PPE) in the online stage [28,29,30] as a pressure stabilization technique. Here, we compare the PPE method with the supremizer enrichment of the velocity space [29,31,32,33], i.e., another technique that provides pressure stability. The main objective of this work is to test the accuracy and efficiency of these two methods within our LES filtering approach. We show that adapting the supremizer enrichment to the EF algorithm is not a trivial exercise. Indeed, the supremizer method becomes accurate only when the evolve and filtered velocity spaces are enriched by the supremizer solutions associated to both evolve and filter pressure fields. Since we are interested in the reconstruction of the pressure field at reduced order level, time is the only parameter we consider. We vary no physical and/or geometrical parameters. We test our framework on 2D flow past a cylinder with time-dependent Reynolds number [34,35].
2. The Full Order Model
In this section, we describe our Full Order Model (FOM). We consider a fixed domain with over a time interval of interest (, T) . The so-called Leray model couples the Navier–Stokes equations (NSE) with a differential filter as follows:
where is the fluid density, is the dynamic viscosity, is the fluid velocity, p is the fluid pressure, is the filtered velocity, and variable is a Lagrange multiplier to enforce the incompressibility constraint for . Parameter in Equation (3) can be interpreted as a filtering radius (that is, the radius of the neighborhood where the filter extracts information from the unresolved scales). In this paper, will be constant in space and time. More sophisticated choices are possible, but will not be considered here. Problem (1)–(4) is endowed with suitable boundary conditions
and the initial data in . Here, and . In addition, and are given. Note that we restrict our attention to homogeneous Neumann boundary conditions. Of course, the methodology we propose can be extended to non-homogeneous Neumann conditions, as well as other boundary conditions (e.g., Robin conditions) [36].
2.1. The Evolve-Filter Algorithm
First, we address the time discretization of model (1)–(4). Let , , with and , and let denote the approximation of a generic quantity y at the time .
With the aim of decoupling the Navier–Stokes system (1) and (2) from the filter system (3) and (4) at each time step, we adopt the Evolve-Filter (EF) algorithm [15,16,17]. This algorithm reads as follows: given and , at time :
- -
- Evolve: find intermediate velocity and pressure such thatwith boundary conditionsand initial condition in . In Equation (9), we set and . Moreover, we approximated the Eulerian time derivative with a Backward Differentiation Formula of order 2 (BDF2) [37].
- -
- Filter: find such thatwith boundary conditions
So, we accept and as the approximation of the fluid velocity and pressure at the time , respectively.
Remark 1.
Problem (13)-(14) can be seen as a generalized Stokes problem. In fact, by multiplying Equation (13) by and with a rearrangement of the terms we get:
where variable can be regarded as a filtered pressure. Problem (17), (14) can be seen as a time dependent Stokes problem with viscosity and the Eulerian time derivative approximated by the Backward Euler (or BDF1) scheme. Thus, problem (17) and (14) can be solved by adapting a standard linearized Navier–Stokes solver.
Remark 2.
It is known that the EF algorithm is over-diffusive, also when combined with a FV method. In [19], we showed that the Evolve-Filter-Relax algorithm [18] with nonlinear differential filters is a better choice, especially for realistic problems. Both the EF and the EFR algorithm require pressure stabilization. Thus, in this manuscript, we prefer to focus on the EF algorithm, which does not have the complication of non-linearity. For the application of our ROM approach with pressure stabilization to nonlinear LES filtering and associated assessment for 2D and 3D problems, the reader is referred to [27].
2.2. Space Discrete Problem by a Finite Volume Method
Concerning the space discretization, we use a FV method for both problem (9) and (10) and problem (17) and (14). We partition the computational domain into cells or control volumes , with , where is the total number of cells in the mesh. Let A be the surface vector of each face of the control volume (i.e., a vector that is perpendicular to the surface and has magnitude equal to the surface area), with .
In (18)–(20), and denote the average velocity and source term in control volume , respectively. Moreover, we denote with and the velocity and pressure associated to the centroid of face j normalized by the volume of .
In (21)–(23), we denoted with the average filtered velocity in control volume , while is the auxiliary pressure at the centroid of face j normalized by the volume of .
More details on the full discretization of both problems (18)–(20) and (21)–(23) are available in [19].
The EF algorithm has been implemented within the C++ finite volume library OpenFOAM® [38]. The linear system related to the problem (18) and (19) has been solved by using the PISO algorithm [39]. On the other hand, for problem (21) and (22) the SIMPLEC algorithm [40] (i.e., a slightly modified version of the SIMPLE algorithm [41]) has been chosen. We remark that both PISO and SIMPLEC are partitioned algorithms that perform a decoupling of the computation of the pressure from the computation of the velocity.
3. The Reduced Order Model
The Reduced Order Model (ROM) we propose draws inspiration from the framework introduced in [26]. In Section 3.1, we provide a description of the procedure used to build a POD–Galerkin ROM, whilst in Section 3.2, we propose two different strategies for pressure stabilization at reduced order level. Finally, Section 3.3 is focused on the method we apply to impose non-homogeneous Dirichlet boundary conditions (5) and (7) at the reduced order level. All the ROM computations are performed using ITHACA-FV [42], an in-house open source C++ library.
3.1. A POD–Galerkin Projection Method
We assume that the velocity fields and and pressure fields q and can be approximated by linear combinations of the dominant modes (basis functions) that are dependent on space variables only and multiplied by scalar coefficients that depend on the time:
In (24) and (25), denotes the cardinality of a reduced basis for the space field belongs to. Note that could be either a scalar or a vector field. Using (24) to approximate and in (9) and (10), we obtain
where and . Then, using (25) to approximate and in (17) and (14) we get:
The reader is referred, e.g., to [2,6,43,44,45,46,47,48] for an overview of several techniques proposed in the literature to generate the reduced basis spaces. Among these, we mention the Proper Orthogonal Decomposition (POD), the Proper Generalized Decomposition (PGD) and the Reduced Basis (RB) with a greedy sampling strategy. We opt for the method of snapshots. To this aim, we solve the FOM described in Section 2 for each time . The snapshots matrices are obtained from the full-order snapshots:
where the subscript h denotes a solution computed with the FOM and is the dimension of the space field in the FOM. Then, for each value of the dimension of the POD space one has to find the scalar coefficients and functions that minimize the error between the snapshots and their projection onto the POD basis. In the -norm, we have
Problem (31) is equivalent to the following eigenvalue problem:
where is the correlation matrix computed from the snapshot matrix , is the matrix of eigenvectors and is a diagonal matrix whose diagonal entries are the eigenvalues of [49]. Once problem (32) is solved, the basis functions are obtained as follows:
and the POD modes are:
where are chosen according to the eigenvalue decay. The reduced order model can be obtained through a Galerkin projection of the governing equations onto the POD spaces.
Let
where and are the basis functions in (24). At time , the reduced algebraic system for problem (26) and (27) is:
where vectors and contain the values of coefficients and in (24) at time . The term in (37) is related to the non-linear convective term:
where is a third-order tensor defined as follows
See [37,50] for more details.
In order to write the reduced algebraic system for problem (28) and (29), let
where and are the basis functions in (25). Such system at time is
where vectors and contain the values of coefficients and in (25) at time .
Finally, we obtain the initial conditions for the ROM algebraic system (37) and (38) by performing a Galerkin projection of the initial full order condition onto the POD basis spaces:
3.2. Pressure Fields Reconstruction and Pressure Stability
It is well known that the reduced problem (37)-(38) and (43)-(44) presents stability issues because the approximation spaces need to satisfy the inf-sup (Ladyzhenskaya-Brezzi-Babuska) condition [51,52]. In a standard finite element (FE) NSE framework, the inf-sup condition reads:
where is the FE space for the pressure approximation, is the FE space for the approximation of the velocity field, and is a constant that does not depend on the mesh size h. In order to obtain a stable and accurate reconstruction of the pressure field at the reduced level, different approaches have been proposed. One option is to use a global POD basis for both pressure and velocity field and same temporal coefficients [53,54]. Another option is represented by the supremizer enrichment method; see, e.g., [29,31,32,33]. Finally, one can take the divergence of the momentum equation to obtain a Poisson equation for the pressure that is projected onto a POD basis; see, e.g., [28,29]. This third method is called Poisson pressure Equation (PPE).
In this work, we test and compare the performances of two methods: the PPE method (already combined with the EF algorithm in [26]) and the supremizer enrichment method (not yet tested for the EF algorithm). As we will show, the extension of the supremizer enrichment method to the EF algorithm is not straightforward.
3.2.1. Pressure Poisson Equation Method
We take the divergence of Equation (9) and account for conditions (10) to obtain the Poisson pressure equation for the Evolve step:
So, at the Evolve step instead of solving (9) and (10), we solve the modified systems (9), (46) with boundary condition (11) and
where denotes the derivative with respect to outgoing normal n.
We proceed similarly for the Filter step. We take the divergence of Equation (17) and account for condition (14) to obtain the Poisson pressure equation:
The reader interested in enforcing non-homogeneous Neumann conditions for the pressure fields is referred to [55,56]. We remark that systems (9) and (10) and (17) and (14) are not equivalent to systems (9) and (46) and (17) and (48) for steady flows [55,56,57].
The residual associated with the non-linear term in Equation (51) is evaluated with the same strategy used for Equation (37). We have
where is a third-order tensor defined as follows
Using (25) to approximate in Equation (48), we get
3.2.2. Supremizer Enrichment Method
For a given pressure basis function, the supremizer is the solution that permits the realization of the inf-sup condition (45). One has to find the supremizer for each pressure basis function. Here, we use an approximated supremizer enrichment procedure: instead of pressure basis functions we use pressure snapshots. This procedure allows to drastically reduce the online computational cost. In fact, the supremizer basis functions do not depend on the particular pressure basis functions, but are computed directly from the pressure snapshots during the offline phase. The downside of this approximated procedure is that it is not possible to rigorously show that the inf-sup condition is satisfied. One only relies on heuristic criteria or checks during a post-processing stage.
For NSE, the supremizer relative to pressure snapshot is found by solving the following problem:
for . For more details, the reader is referred to [29,31,32,33]. For the EF algorithm, in addition to (59) and (60) one has to solve an analogous problem for each auxiliary pressure snapshot :
for . Once problems (59)–(62) are solved, two snapshots matrices of supremizer solutions are assembled:
A POD procedure is applied to the matrices above in order to obtain the supremizer POD basis functions:
where and conform to the notation introduced in Section 3.1. These velocity supremizer basis functions are added to the reduced velocity spaces, which become:
Let us call the supremizer enrichment method described above. In Section 4, we will show that does not lead to an accurate reconstruction of the pressure fields. To increase the accuracy, we add the supremizer solutions associated to both pressure fields to the evolve and filtered velocity spaces, i.e.:
We call the realization of the supremizer enrichment.
3.3. Implementation of Dirichlet Boundary Conditions: The Lifting Function Method
We apply the lifting function method to homogeneize the velocity fields snapshots, as well as to make them independent of the boundary conditions [29]. We notice that the lifting functions are problem-dependent, so they have to be divergence free in order to retain the divergence-free property of the basis functions and they have to satisfy the boundary conditions of the FOM.
The velocity snapshots are modified as follows:
where is the number of non-homogeneous Dirichlet boundary conditions, are the lifting functions, and and are suitable temporal coefficients. We apply the POD procedure described in Section 3.1 to the snapshots satisfying the homogeneous boundary conditions. Then, the boundary value is added back in this way:
4. Numerical Results
We consider 2D flow past a cylinder [34,35]. This well-known benchmark will allow us to assess the ability of the ROM approaches presented in Section 3 to reconstruct the time evolution of the velocity and pressure fields. We have thoroughly investigated the 2D flow past a cylinder with a finite volume FOM in [19] and with a ROM using a PPE approach in [26,27]. Here, we aim at comparing the supremizer enrichment method and the PPE method in terms of errors and speed-up.
We consider a 2.2 × 0.41 rectangular channel. Let the origin of the axes be at the bottom left corner of the channel. Inside the channel, there is a cylinder of radius 0.05 and center is located at (0.2, 0.2), The fluid filling the channel has density and viscosity . We enforce a no slip boundary condition on the upper and lower walls and on the cylinder. On the other hand at the inflow, we consider the following velocity profile:
and . Finally, at the outflow we enforce and . All the simulations run starting from the condition of fluid at rest. It should be noted that the Reynolds number is time dependent, with [34].
We use a hexaedral computational grid with and for a total of cells. The mesh quality is high: it is characterized by very low values of maximum non-orthogonality (36), average non-orthogonality (4), skewness (0.7), and maximum aspect ratio (2). Figure 1 shows a part of the mesh. We note that this mesh is the coarsest among all the meshes investigated in [19]. Therefore, it is the most challenging for our LES approach. We set , which allows us to obtain a maximum Courant–Friedrichs–Lewy number at the time when the velocity reaches its maximum value for both FOM and ROM simulations. Concerning the convective term, we adopt a second-order accurate Central Differencing scheme [58]. With this choice, we do not have to introduce artificial stabilization. So, the effect of the filter can be assessed.

Figure 1.
Part of the mesh under consideration.
We need to enforce a time-dependent non-uniform Dirichlet boundary condition at the inlet. For this purpose, we consider a divergence free function with the following non-uniform velocity distribution:
and uniform null values on the rest of the boundary.
We will compare our findings with those in [29]. The choice of Ref. [29] is due to the fact that therein the authors develop a NSE-ROM finite volume framework both with PPE and supremizer enrichment methods for the reconstruction of the pressure field.
We set and refer to [19] for details on this choice. The snapshots are collected every 0.1 (i.e., ) using an equispaced grid method in time. Therefore, the dimension of the correlation matrix in (32) is . For a convergence test as the number of snapshots increases, see [26]. Therein, we show that there is no substantial difference in the errors for the different sampling frequencies. Table 1 reports the first four cumulative eigenvalues for the velocity, pressure, and supremizer fields, based on (i.e., scaled with respect to the sum of) the first 15 most energetic POD modes. In order to retain 99.99% of the energy for the ROM, we need 2 modes for , 2 modes for q, 2 modes for , and 1 mode for . As for , we consider a number of supremizer modes greater than pressure modes as suggested in [29]: four modes for and three modes for . On the other hand, for we take into account an equal number of pressure and supremizer modes: two modes for and one mode for .

Table 1.
First four cumulative eigenvalues for the velocity, pressure and supremizer fields.
We calculate the relative error:
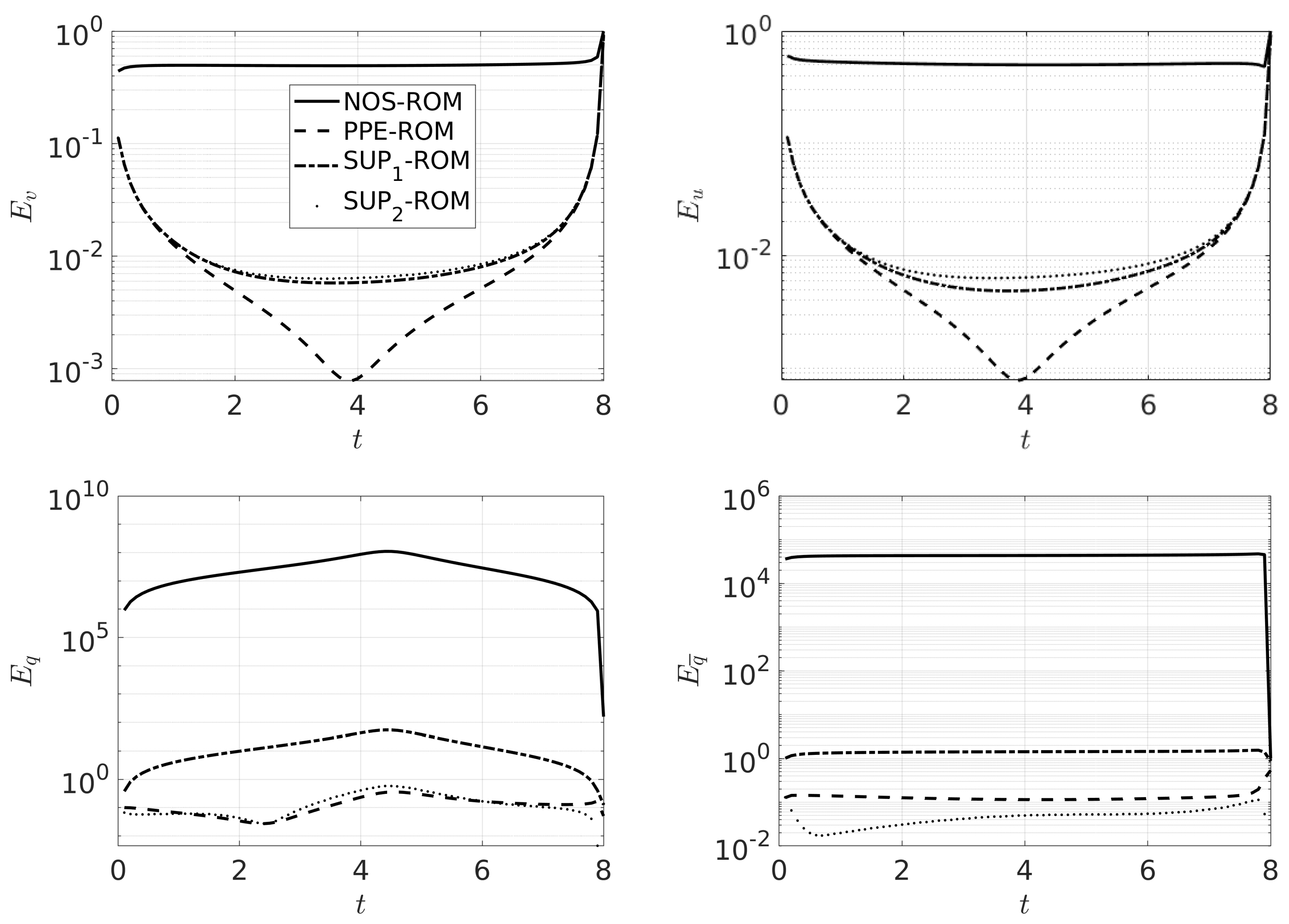
where and are the FOM approximation of a given field (i.e., , , or ) and the corresponding ROM approximation (i.e., , , or ), respectively. Figure 2 shows error (69) for the two velocity and pressure fields over time for the three different ROM techniques under investigation: PPE, and . We also present the errors related to the ROM computations with no stabilization technique, referred to as NOS. As one would expect, Figure 2 shows that the model with no stabilization is completely unreliable. From Figure 2, we see that the -ROM is a big improvement over NOS-ROM. However, while the errors for the velocity fields are acceptable, the pressure errors remain large and far above the values obtained with NSE in [29]. This shows that -ROM is not a reliable stabilization of the ROM for the EF algorithm. The -ROM produces much better results in terms of the pressure fields, with errors for the velocity fields that are comparable with those given by the -ROM. We speculate that the better performance of the model (which adds the supremizer solutions related to both pressure fields to the evolve and filtered velocity spaces) with respect to the model could be due to the strong coupling between the evolve velocity and the filter velocity ; however, the stability of the inf-sup ROM formulation for the EF algorithm needs to be investigate in more depth and will be the object of future work. Finally, from Figure 2, we observe that the PPE-ROM provides the lowest errors for the velocity fields, while the pressure errors are comparable (for q) or worse (for ) than the errors given by the -ROM. Our findings for the EF algorithm are in agreement with what observed in [29] for NSE. Indeed, therein it is shown that the PPE model produces better results for the velocity field, but worse results for the pressure field when compared to the supremizer enrichment model. For insights on the behavior of the errors at the first and last time steps of the simulation, we refer to [26].
Figure 2.
Time history of norm of the relative error for the velocity fields (top) and pressure fields (bottom) for NOS-ROM, PPE-ROM, -ROM, and -ROM. The legend in the top left panel is common to all the panels.
We report minimum, average, and maximum relative errors for PPE and in Table 2. The average errors for and q are comparable to the values obtained in [29].

Table 2.
Maximum, average, and minimum relative errors for the velocity and pressure fields for PPE-ROM and -ROM.
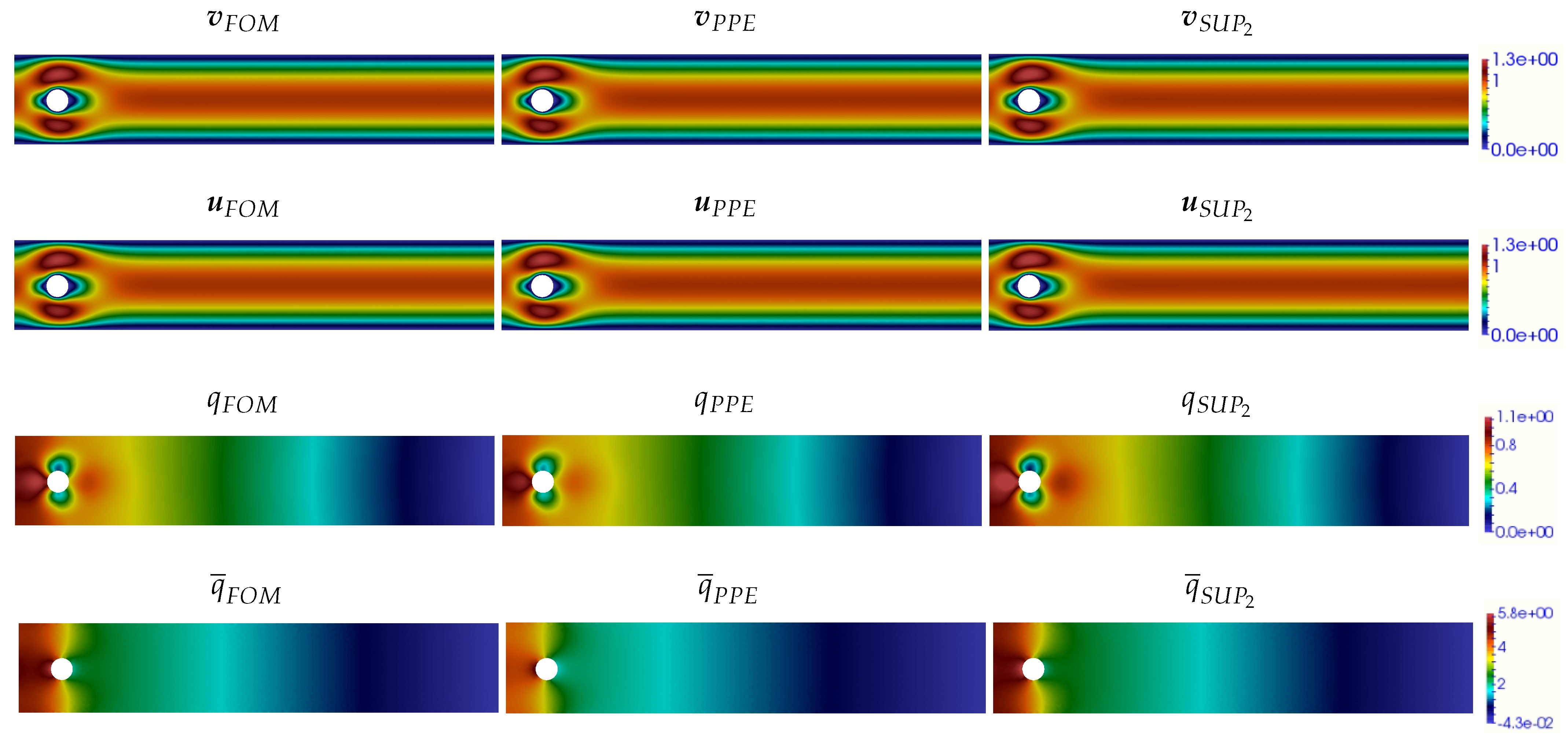
For a visual comparison, we report in Figure 3 velocity and pressure fields at computed by FOM, PPE-ROM, and -ROM. We observe that both PPE-ROM and -ROM can capture well the main flow features.
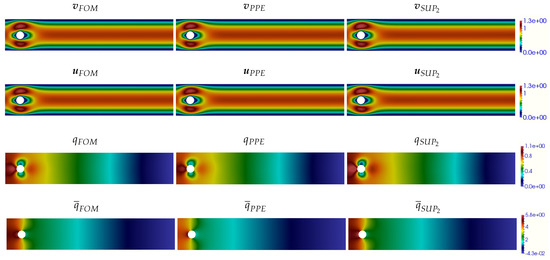
Figure 3.
Velocity fields (first row) and (second row) and pressure fields q (third row) and (fourth row) at time computed by FOM (left), PPE-ROM (center), and -ROM (right).
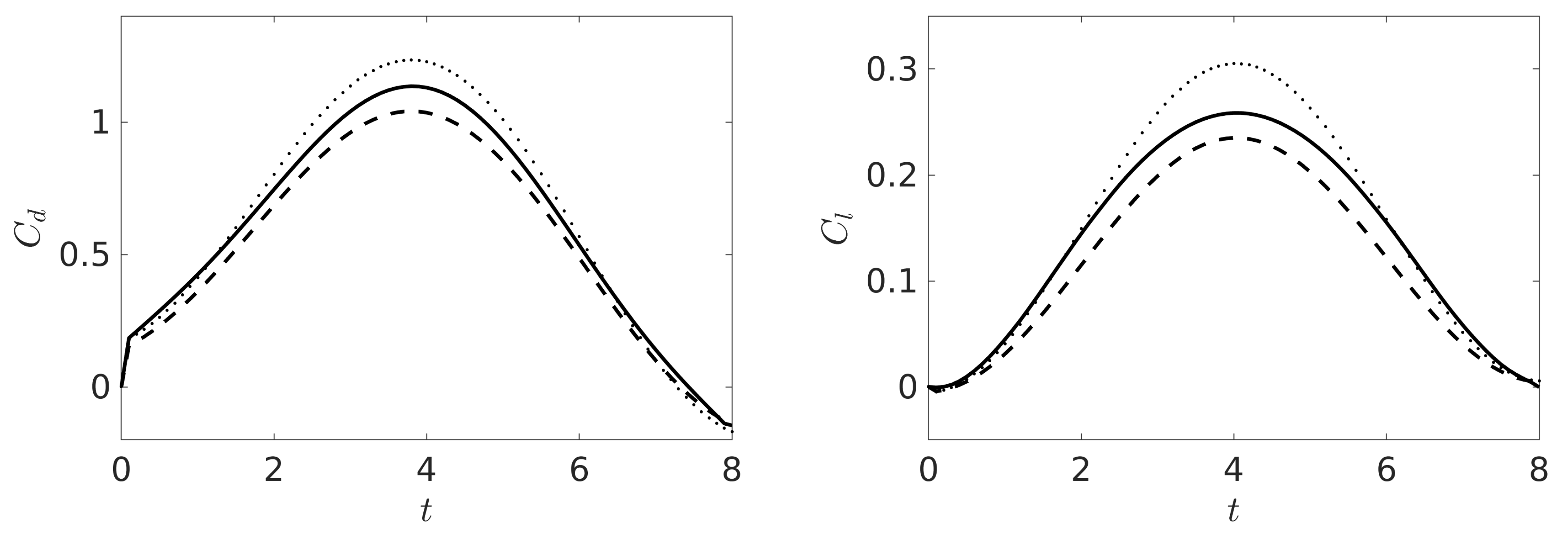
For a quantitative comparison of FOM, PPE-ROM, and -ROM, we consider the quantities of interest for this benchmark, i.e., the drag and lift coefficients [34,35]:
where is the maximum velocity at the inlet/outlet, is the cylinder diameter, S is the cylinder surface, and and are the tangential and normal unit vectors to the cylinder, respectively. See Figure 4 for the coefficients in (70) computed by the three approaches. We observe that the amplitude of both coefficients is slightly underestimated (resp., overestimated) by the PPE-ROM (resp., -ROM) over the entire time interval. The ROM reconstruction of the lift coefficient appears to be more critical, especially for the -ROM and around the center of the time interval. We note that, as expected [19], the over-diffusive nature of the EF algorithm (see Remark 2) used for both FOM and ROM smooths out the vortex shedding and completely dampens the related oscillations in the .
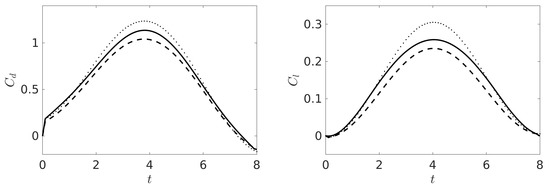
Figure 4.
Aerodynamic coefficients (left) and (right) computed by FOM (solid line), -ROM (dotted line), and PPE-ROM (dashed line).
For a further quantitative assessment of the reconstruction of the coefficients in (70), we computed the following errors
We notice that errors defined in (71) are different from the ones in [26], which are related to the maximum values only. Table 3 reports the errors (71) for PPE-ROM and -ROM. We see that the two ROM strategies provide comparable results: slightly lower than 9% relative error for the the drag coefficient and around 14% relative error for the lift coefficient.

Table 3.
Relative errors (71) for lift and drag coefficients for PPE-ROM and -ROM.
Finally, we provide some information on the computational cost. The total CPU time required by a FOM simulation is about 1900 s. The solution of the PPE-ROM algebraic systems (37), (51), (43) and (57) takes s (resulting in a speed-up of about 1180), while the solution of the -ROM systems (37), (38), (43) and (44) takes s (resulting in a speed-up of about 742). So, the -ROM is less efficient than the PPE-ROM. The additional cost of the -ROM comes from the supremizer modes, which increases the size of the reduced dynamical system. However, it is possible to assert that both ROMs allow to obtain a considerable speed-up.
5. Conclusions and Future Perspectives
We presented a POD–Galerkin based reduced order method for a Leray model implemented through the Evolve-Filter (EF) algorithm. Unlike the large majority of the works on Leray-type models, we choose a Finite Volume method for the space discretizaion because of its computational efficiency. The novelty of this work is the investigation and comparison of two techniques for the stabilization of the pressure fields: (i) Poisson Pressure equation, and (ii) supremizer enrichment. We showed that the standard supremizer enrichment, which works well for the Navier–Stokes equations with no filter, needs to be modified in order to obtain stable and accurate solutions with the EF algorithm. The modification consists in adding to the evolve and filter velocity spaces the supremizer solutions related to both evolve and filter pressure fields. We assessed our ROM through the classical 2D flow past a cylinder benchmark. We found that our ROM with both Poisson Pressure equation and modified supremizer enrichment captures the flow features with an accuracy comparable to ROMs applied to the Navier–Stokes equations with no filter [29]. Moreover, we quantified the relative error of the drag and lift coefficients computed by ROM and FOM and found that both stabilization approaches produce comparable errors. We have limited our assessment to a 2D problem, although obviously more interesting applications of LES arise in 3D. We have no reason to believe that the conclusions drawn here do apply to 3D problems. The reader interested in 3D applications of our ROM approach with the Poisson Pressure equation is referred to [26,27].
In the future, we would like to investigate in more depth the inf-sup stability of a ROM formulation with supremizer enrichment for the EF algorithm. In addition, we would like to extend to the EF algorithm other efficient stabilization techniques, such as the one proposed in [59].
Author Contributions
Conceptualization, M.G., A.Q. and G.R.; methodology, M.G. and A.Q.; software, M.G.; supervision, A.Q. and G.R.; writing—original draft preparation, M.G.; writing—review and editing, A.Q. and G.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Research Council Executive Agency by the Consolidator Grant project AROMA-CFD “Advanced Reduced Order Methods with Applications in Computational Fluid Dynamics”—GA 681447, H2020-ERC CoG 2015 AROMA-CFD, PI G. Rozza, and INdAM-GNCS 2019-2020 projects. This work was also partially supported by US National Science Foundation through grant DMS-1620384 and DMS-195353.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hesthaven, J.S.; Rozza, G.; Stamm, B. Certified Reduced Basis Methods for Parametrized Partial Differential Equations; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basis Methods for Partial Differential Equations; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Benner, P.; Ohlberger, M.; Patera, A.; Rozza, G.; Urban, K. Model Reduction of Parametrized Systems, 1st ed.; MS&A Series; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Benner, P.; Gugercin, S.; Willcox, K. A Survey of Projection-Based Model Reduction Methods for Parametric Dynamical Systems. SIAM Rev. 2015, 57, 483–531. [Google Scholar] [CrossRef]
- Bader, E.; Kärcher, M.; Grepl, M.A.; Veroy, K. Certified Reduced Basis Methods for Parametrized Distributed Elliptic Optimal Control Problems with Control Constraints. SIAM J. Sci. Comput. 2016, 38, A3921–A3946. [Google Scholar] [CrossRef]
- Benner, P.; Schilders, W.; Grivet-Talocia, S.; Quarteroni, A.; Rozza, G.; Silveira, L.M. Model Order Reduction; De Gruyter: Berlin, Germany; Boston, MA, USA, 2020. [Google Scholar]
- Longatte, E.; Erwan, L.; Pomarede, M.; Sigrist, J.F.; Hamdouni, A. Parametric study of flow-induced vibrations in cylinder arrays under single-phase fluid cross flows using POD-ROM. J. Fluids Struct. 2018, 78, 314–330. [Google Scholar] [CrossRef]
- Shinde, V.; Longatte, E.; Baj, F.; Hoarau, Y.; Braza, M. A Galerkin-free model reduction approach for the Navier–Stokes equations. J. Comput. Phys. 2018, 309, 148–163. [Google Scholar] [CrossRef]
- Carlberg, K.; Farhat, C.; Cortial, J.; Amsallem, D. The GNAT method for nonlinear model reduction: Effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 2013, 242, 623–647. [Google Scholar] [CrossRef]
- Moin, P.; Mahesh, K. Direct Numerical Simulation: A Tool in Turbulence Research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Wang, Z.; Akhtar, I.; Borggaard, J.; Iliescu, T. Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison. Comput. Methods Appl. Mech. Eng. 2012, 237–240, 10–26. [Google Scholar] [CrossRef]
- Aubry, N.; Holmes, P.; Lumley, J.L.; Stone, E. The dynamics of coherent structures in the wall region of a turbulent boundary layer. J. Fluid Mech. 1988, 192, 115–173. [Google Scholar] [CrossRef]
- Leray, J. Essai sur le mouvement d’un fluide visqueux emplissant l’espace. J. Mathématiques Pures Appliquées 1934, 63, 193–248. [Google Scholar]
- Bowers, A.; Rebholz, L. Numerical study of a regularization model for incompressible flow with deconvolution-based adaptive nonlinear filtering. Comput. Methods Appl. Mech. Eng. 2013, 258, 1–12. [Google Scholar] [CrossRef]
- Boyd, J.P. Two Comments on Filtering (Artificial Viscosity) for Chebyshev and Legendre Spectral and Spectral Element Methods: Preserving Boundary Conditions and Interpretation of the Filter as a Diffusion. J. Comput. Phys. 1998, 143, 283–288. [Google Scholar] [CrossRef]
- Fischer, P.; Mullen, J. Filter-based stabilization of spectral element methods. Comptes Rendus L’Academie Sci. Ser. I Math. 2001, 332, 265–270. [Google Scholar] [CrossRef]
- Dunca, A.; Epshteyn, Y. On the Stolz-Adams deconvolution model for the large-eddy simulation of turbulent flows. SIAM J. Math. Anal. 2005, 37, 1890–1902. [Google Scholar] [CrossRef]
- Layton, W.; Rebholz, L.; Trenchea, C. Modular Nonlinear Filter Stabilization of Methods for Higher Reynolds Numbers Flow. J. Math. Fluid Mech. 2012, 14, 325–354. [Google Scholar] [CrossRef]
- Girfoglio, M.; Quaini, A.; Rozza, G. A Finite Volume approximation of the Navier–Stokes equations with nonlinear filtering stabilization. Comput. Fluids 2019, 187, 27–45. [Google Scholar] [CrossRef]
- Girfoglio, M.; Quaini, A.; Rozza, G. Fluid–structure interaction simulations with a LES filtering approach in solids4Foam. Commun. Appl. Ind. Math. 2021. accepted. Available online: https://arxiv.org/abs/2102.08011 (accessed on 27 June 2021).
- Gunzburger, M.; Iliescu, T.; Schneier, M. A Leray regularized ensemble-proper orthogonal decomposition method for parameterized convection-dominated flows. IMA J. Numer. Anal. 2019, 40, 886–913. [Google Scholar] [CrossRef]
- Xie, X.; Wells, D.; Wang, Z.; Iliescu, T. Numerical analysis of the Leray reduced order model. J. Comput. Appl. Math. 2018, 328, 12–29. [Google Scholar] [CrossRef]
- Wells, D.; Wang, Z.; Xie, X.; Iliescu, T. An evolve-then-filter regularized reduced order model for convection-dominated flows. Int. J. Numer. Methods Fluids 2017, 84, 598–615. [Google Scholar] [CrossRef]
- Gunzburger, M.; Iliescu, T.; Mohebujjaman, M.; Schneier, M. An Evolve-Filter-Relax stabilized reduced order stochastic collocation method for the time-dependent Navier–Stokes equations. SIAM/ASA J. Uncertain. Quantif. 2019, 7, 1162–1184. [Google Scholar] [CrossRef]
- Xie, X.; Wells, D.; Wang, Z.; Iliescu, T. Approximate deconvolution reduced order modeling. Comput. Methods Appl. Mech. Eng. 2016, 313, 512–534. [Google Scholar] [CrossRef]
- Girfoglio, M.; Quaini, A.; Rozza, G. A POD-Galerkin reduced order model for a LES filtering approach. J. Comput. Phys. 2021, 436, 110260. [Google Scholar] [CrossRef]
- Girfoglio, M.; Quaini, A.; Rozza, G. A Hybrid Reduced Order Model for Nonlinear LES Filtering. Available online: https://arxiv.org/abs/2107.12933 (accessed on 27 June 2021).
- Akhtar, I.; Nayfeh, A.H.; Ribbens, C.J. On the stability and extension of reduced-order Galerkin models in incompressible flows. Theor. Comput. Fluid Dyn. 2009, 23, 213–237. [Google Scholar] [CrossRef]
- Stabile, G.; Rozza, G. Finite volume POD-Galerkin stabilised reduced order methods for the parametrised incompressible Navier–Stokes equations. Comput. Fluids 2018, 173, 273–284. [Google Scholar] [CrossRef]
- Isoz, M. POD-DEIM based model order reduction for speed-up of flow parametric studies. Ocean Eng. 2019, 186, 106083. [Google Scholar] [CrossRef]
- Rozza, G.; Veroy, K. On the stability of the reduced basis method for Stokes equations in parametrized domains. Comput. Methods Appl. Mech. Eng. 2007, 196, 1244–1260. [Google Scholar] [CrossRef]
- Ballarin, F.; Manzoni, A.; Quarteroni, A.; Rozza, G. Supremizer stabilization of POD-Galerkin approximation of parametrized steady incompressible Navier–Stokes equations. Int. J. Numer. Methods Eng. 2014, 102, 1136–1161. [Google Scholar] [CrossRef]
- Gerner, A.L.; Veroy, K. Certified Reduced Basis methods for parametrized saddle point problems. SIAM J. Sci. Comput. 2011, 34, A2812–A2836. [Google Scholar] [CrossRef]
- Turek, S.; Schäfer, M. Benchmark computations of laminar flow around cylinder. In Flow Simulation with High-Performance Computers II; Hirschel, E., Ed.; Vieweg: Braunschweig, Germany; Wiesbaden, Germany, 1996; Volume 52. [Google Scholar]
- John, V. Reference values for drag and lift of a two dimensional time-dependent flow around a cylinder. Int. J. Numer. Methods Fluids 2004, 44, 777–788. [Google Scholar] [CrossRef]
- Bertagna, L.; Quaini, A.; Veneziani, A. Deconvolution-based nonlinear filtering for incompressible flows at moderately large Reynolds numbers. Int. J. Numer. Methods Fluids 2016, 81, 463–488. [Google Scholar] [CrossRef]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Van Doormaal, J.P.; Raithby, G.D. Enhancements of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Stabile, G.; Rozza, G. ITHACA-FV—In Real Time Highly Advanced Computational Applications for Finite Volumes. Available online: https://mathlab.sissa.it/ithaca-fv (accessed on 30 January 2018).
- Rozza, G.; Huynh, D.B.P.; Patera, A.T. Reduced Basis approximation and a Posteriori error estimation for affinely parametrized elliptic coercive Partial Differential Equations. Arch. Comput. Methods Eng. 2008, 15, 229. [Google Scholar] [CrossRef]
- Chinesta, F.; Huerta, A.; Rozza, G.; Willcox, K. Model Order Reduction. In Encyclopedia of Computational Mechanics; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Kalashnikova, I.; Barone, M.F. On the stability and convergence of a Galerkin reduced order model (ROM) of compressible flow with solid wall and far-field boundary treatment. Int. J. Numer. Methods Eng. 2010, 83, 1345–1375. [Google Scholar] [CrossRef]
- Chinesta, F.; Ladeveze, P.; Cueto, E. A short review on Model Order Reduction based on Proper Generalized Decomposition. Arch. Comput. Methods Eng. 2011, 18, 395. [Google Scholar] [CrossRef]
- Dumon, A.; Allery, C.; Ammar, A. Proper General Decomposition (PGD) for the resolution of Navier–Stokes equations. J. Comput. Phys. 2011, 230, 1387–1407. [Google Scholar] [CrossRef][Green Version]
- Tsiolakis, V.; Giacomini, M.; Sevilla, R.; Othmer, C.; Huerta, A. Parametric Solutions of Turbulent Incompressible Flows in OpenFOAM via the Proper Generalised Decomposition. Available online: https://arxiv.org/abs/2006.07073 (accessed on 27 June 2021).
- Kunisch, K.; Volkwein, S. Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics. SIAM J. Numer. Anal. 2002, 40, 492–515. [Google Scholar] [CrossRef]
- Rozza, G. Reduced basis methods for Stokes equations in domains with non-affine parameter dependence. Comput. Vis. Sci. 2009, 12, 23–35. [Google Scholar] [CrossRef]
- Brezzi, F.; Bathe, K.J. A discourse on the stability conditions for mixed finite element formulations. Comput. Methods Appl. Mech. Eng. 1990, 82, 27–57. [Google Scholar] [CrossRef]
- Boffi, D.; Brezzi, F.; Fortin, M. Mixed Finite Element Methods and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bergmann, M.; Bruneau, C.H.; Iollo, A. Enablers for robust POD models. J. Comput. Phys. 2009, 228, 516–538. [Google Scholar] [CrossRef]
- Lorenzi, S.; Cammi, A.; Luzzi, L.; Rozza, G. POD-Galerkin method for finite volume approximation of Navier–Stokes and RANS equations. Comput. Methods Appl. Mech. Eng. 2016, 311, 151–179. [Google Scholar] [CrossRef]
- Orszag, S.A.; Israeli, M.; Deville, M. Boundary conditions for incompressible flows. J. Sci. Comput. 1986, 1, 75–111. [Google Scholar] [CrossRef]
- Johnston, H.; Liu, J.G. Accurate, stable and efficient Navier–Stokes solvers based on explicit treatment of the pressure term. J. Comput. Phys. 2004, 199, 221–259. [Google Scholar] [CrossRef]
- Li, L. A split-step finite-element method for incompressible Navier–Stokes equations with high-order accuracy up-to the boundary. J. Comput. Phys. 2020, 408, 213–237. [Google Scholar] [CrossRef]
- Lax, P.; Wendroff, B. System of conservation laws. Commun. Pure Appl. Math. 1960, 13, 217–237. [Google Scholar] [CrossRef]
- Stabile, G.; Zancanaro, M.; Rozza, G. Efficient Geometrical parametrization for finite-volume based reduced order methods. Int. J. Numer. Methods Eng. 2020, 121, 2655–2682. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).