Free Stream Behavior of Hydrogen Released from a Fluidic Oscillating Nozzle
Abstract
:1. Introduction
- After the startup of the system, a hydrodynamic instability in the interaction region causes the jet to attach to one of the walls W1 or W2 due to the Coanda effect.
- The jet is split into a main portion that exits the chamber through the outlet O and a smaller portion that loops back to the inlet.
- When reaching the inlet, this jet causes the main jet to detach from one wall and to fill the resulting recirculation bubble.
- The jet attaches to the opposite wall, and the cycle starts over.
2. Materials and Methods
2.1. Experimental Setup
2.2. Numerical Simulation
2.2.1. Governing Equations
2.2.2. Numerical Methodology
2.2.3. Computational Setup
3. Results
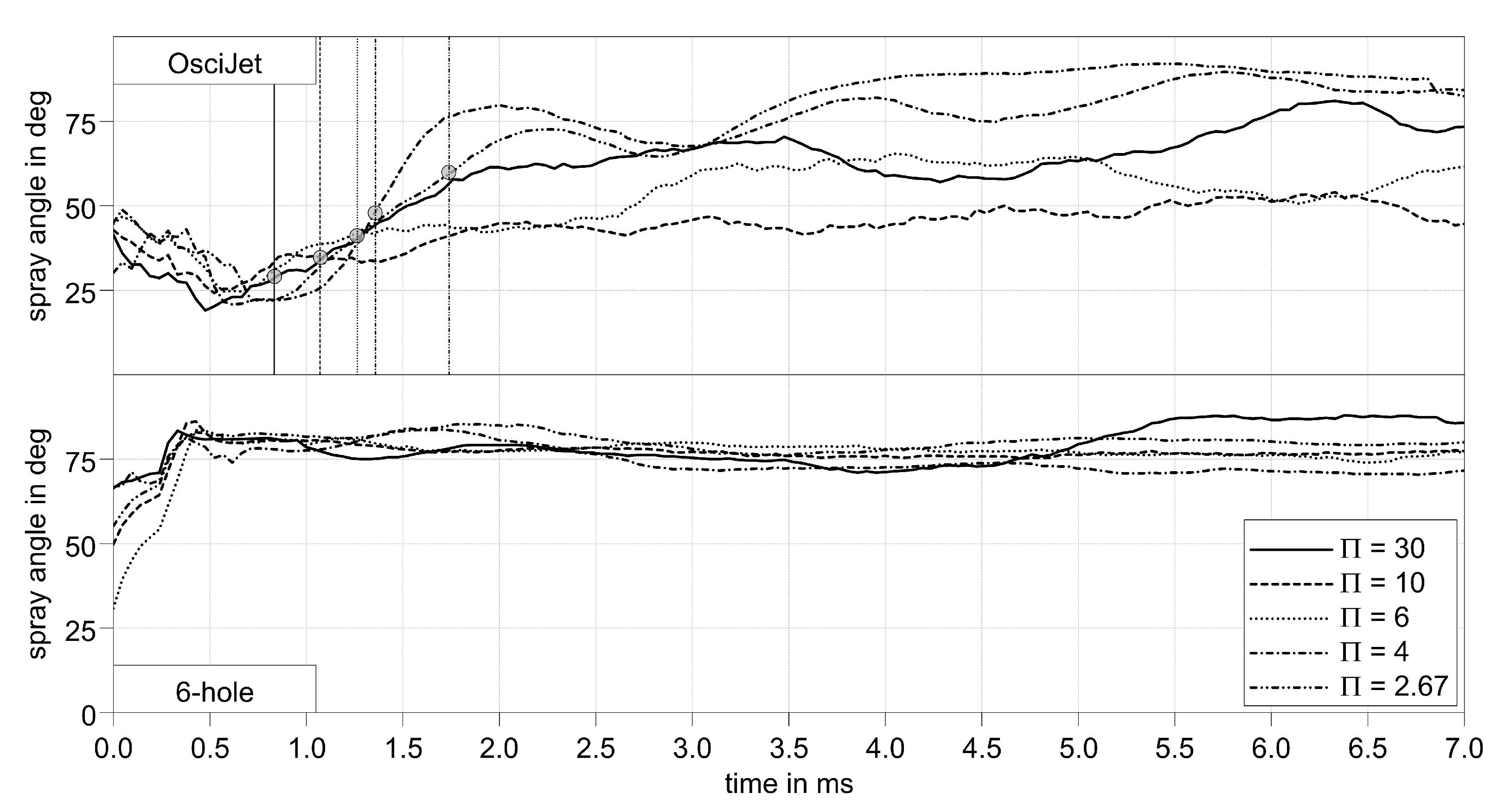
3.1. Experimental Results
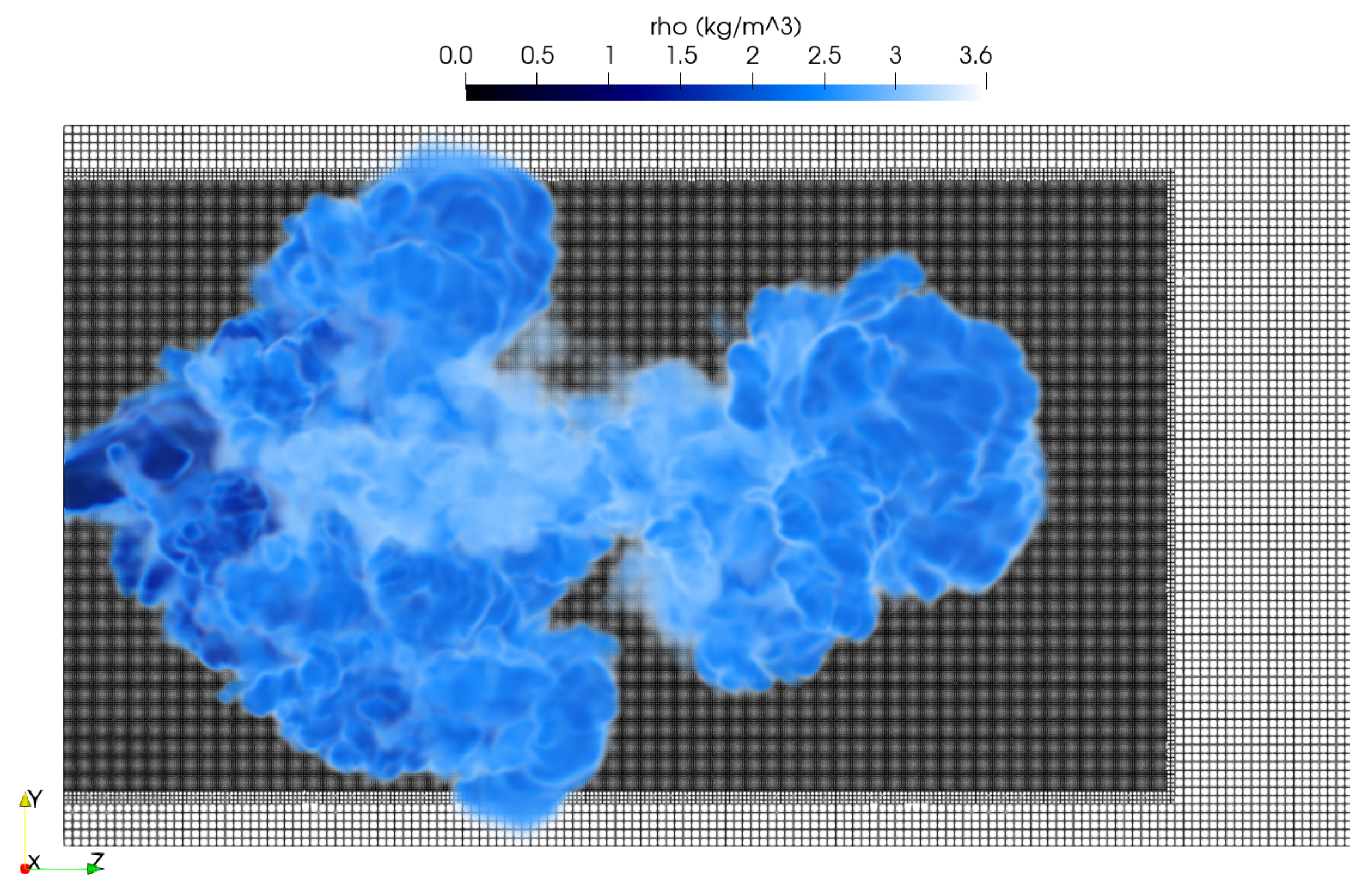
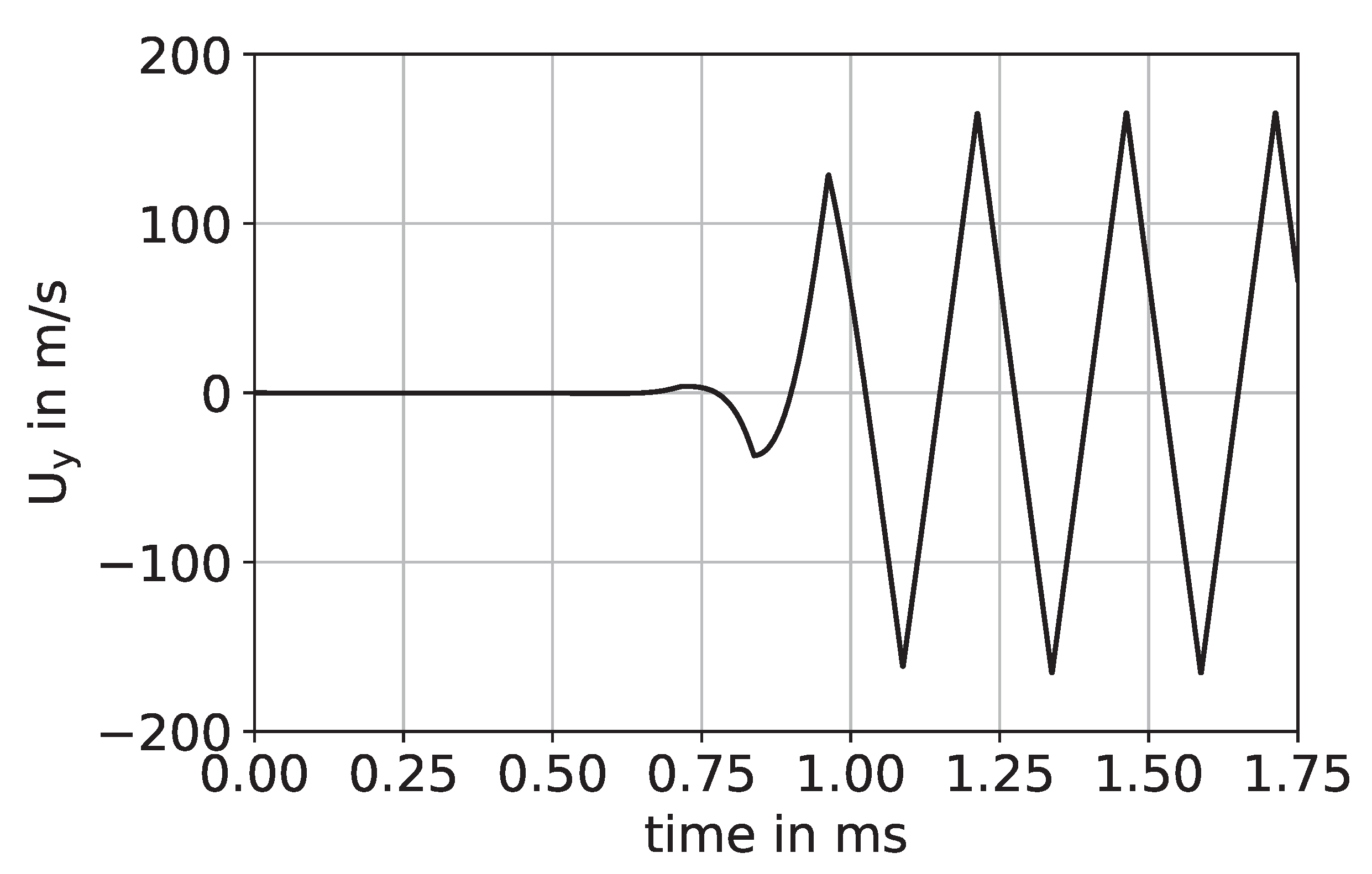
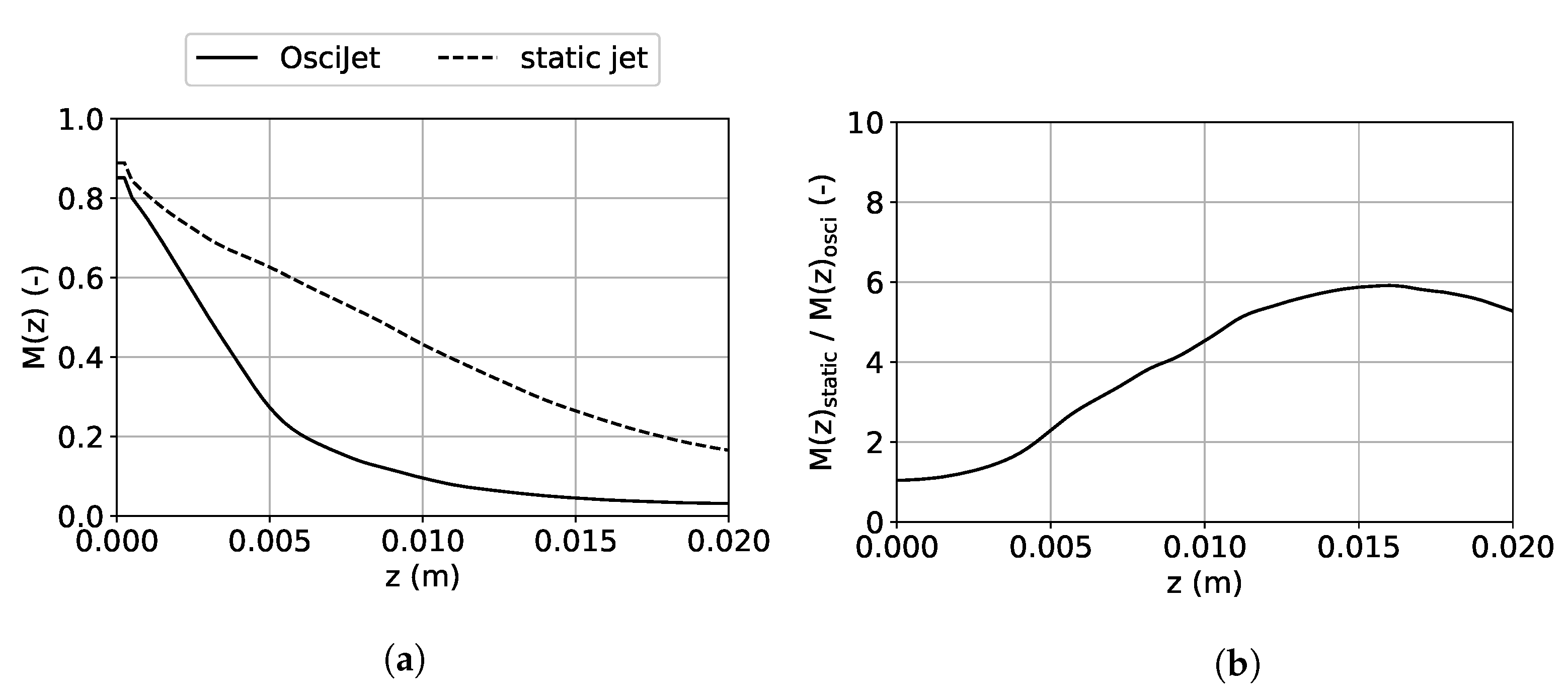
3.2. Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BDC | Bottom dead centre |
| CFD | Computational fluid dynamics |
| DI | Direct injection |
| ICE | Internal combustion engine |
| LED | Light emitting diode |
| LES | Large eddy simulation |
| SOI | Start of injection |
References
- EMCEL Welche Strafen folgen aus den CO2-Emissionsnormen für schwere Nutzfahrzeuge? Available online: https://emcel.com/de/co2-emissionsnormen-schwere-nutzfahrzeuge (accessed on 30 June 2021).
- The European Commission. Proposal for a Regulation of the European Parliament and of the Council Setting CO2 Emission Performance Standards for New Heavy-Duty Vehicles; The European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Munshi, S.; Garner, G.; Theissl, H.; Hofer, F.; Raser, B. Total Cost of Ownership (TCO) Analysis for HeavyDuty Hydrogen Fueled Powertrains; Technical Report. Westport Fuel Systems, AVL List GmbH, 2021. Available online: https://bit.ly/3dt5DDD (accessed on 30 June 2021).
- Koch, D.; Ebert, T.; Sousa, A. Transformation vom Diesel zum H2-Hoch-AGR-Magerkonzept. ATZheavy Duty 2020, 13, 32–41. [Google Scholar] [CrossRef]
- Lacarelle, A.; Paschereit, C.O. Increasing the passive scalar mixing quality of jets in crossflow with fluidics actuators. J. Eng. Gas Turbines Power 2012, 134, 021503. [Google Scholar] [CrossRef]
- Bobusch, B.C.; Berndt, P.; Paschereit, C.O.; Klein, R. Investigation of fluidic devices for mixing enhancement for the shockless explosion combustion process. In Active Flow and Combustion Control 2014; Springer: Berlin/Heidelberg, Germany, 2015; pp. 281–297. [Google Scholar]
- Spyropoulos, C.E. A sonic oscillator(Operational principles and characteristics of sonic oscillator- pneumatic clock pulse generator). In Proceedings of the Fluid Amplification Symposium, Washington, DC, USA, 26–28 May 1964; Volume 3, pp. 27–52. [Google Scholar]
- Warren, R.W. Fluid Oscillator. U.S. Patent US3016066A, 9 January 1962. [Google Scholar]
- Campagnuolo, C.J.; Lee, H.C. Review of Some Fluid Oscillators; Technical Report; Harry Diamond Labs: Adelphi, MD, USA, 1969. [Google Scholar]
- Weathers, T.M. NASA Contributions to Fluidic Systems. J. Spacecr. Rocket. 1973, 10, 417–418. [Google Scholar] [CrossRef]
- Stouffer, R.D. Fluidic Washer Systems for Vehicles. U.S. Patent US5749525A, 12 May 1998. [Google Scholar]
- Raghu, S. Fluidic oscillators for flow control. Exp. Fluids 2013, 54, 1455. [Google Scholar] [CrossRef]
- Woszidlo, R.; Wygnanski, I. Parameters governing separation control with sweeping jet actuators. In Proceedings of the 29th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 27–30 June 2011; p. 3172. [Google Scholar]
- Cerretelli, C.; Kirtley, K. Boundary layer separation control with fluidic oscillators. J. Turbomach. 2009, 131, 1–9. [Google Scholar] [CrossRef]
- Tesař, V. Microbubble generation by fluidics. Part I: Development of the oscillator. In Proceedings of the Colloquium Fluid Dynamics, Prague, Czech Republic, 24–26 October 2012. [Google Scholar]
- Gilmour, D.; Zimmerman, W. Microbubble intensification of bioprocessing. Adv. Microb. Physiol. 2020, 77, 1. [Google Scholar]
- Ćosić, B.; Waßmer, D.; Genin, F. Integration of Fluidic Nozzles in the New Low Emission Dual Fuel Combustion System for MGT Gas Turbines. Fluids 2021, 6, 129. [Google Scholar] [CrossRef]
- Gregory, J.; Tomac, M.N. A review of fluidic oscillator development and application for flow control. In Proceedings of the 43rd AIAA Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; p. 2474. [Google Scholar]
- Tesarř, V. Pressure-Driven Microfluidics. In Proceeding of the Engineering Mechanics, Svratka, Czech Republic, 12–15 May 2008. [Google Scholar]
- Tesarř, V. Taxonomic trees of fluidic oscillators. EPJ Web Conf. 2017, 143, 02128. [Google Scholar] [CrossRef] [Green Version]
- Foster, K.; Parker, G.A. Fluidics: Components and Circuits; John Wiley & Sons: Hoboken, NJ, USA, 1970. [Google Scholar]
- Bobusch, B.C. Fluidic Devices for Realizing the Shockless Explosion Combustion Process. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Willert, C.; Stasicki, B.; Klinner, J.; Moessner, S. Pulsed operation of high-power light emitting diodes for imaging flow velocimetry. Meas. Sci. Technol. 2010, 21, 075402. [Google Scholar] [CrossRef] [Green Version]
- Predelli, O.; Kracke, T.; Schmidt, W.; Meyerleitet, S. FI2RE. Mtz-Mot. Z. 2004, 65, 36–42. [Google Scholar] [CrossRef]
- Steuer, J.; Mladek, M.; Dengler, C.; Mayer, W.; Kracke, T.; Jakubek, P.; Brune, A.; Rick, R. Flexibles Motorsteuerungssystem für die Entwicklung innovativer Brennverfahren. ATZelektronik 2009, 4, 36–41. [Google Scholar] [CrossRef]
- Yoshizawa, A. Statistical theory for compressible turbulent shear flows, with the application to subgrid modeling. Phys. Fluids 1986, 29, 2152–2164. [Google Scholar] [CrossRef]
- Krüger, O.; Bobusch, B.C.; Woszidlo, R.; Paschereit, C.O. Numerical modeling and validation of the flow in a fluidic oscillator. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; p. 3087. [Google Scholar]
- Danckwerts, P. The definition and measurement of some characteristics of mixtures. Appl. Sci. Res. Sect. A 1952, 3, 279–296. [Google Scholar] [CrossRef]







| Pressure Boundary Condition | Mass Flow in g/s | Average Spray Velocity in m/s | ||||
|---|---|---|---|---|---|---|
| in bar | in bar | 6-hole | OsciJet | 6-hole | OsciJet | |
| 30 | 1 | 30.00 | 6.21 | 6.70 | 45.60 | 83.82 |
| 3 | 10.00 | 35.74 | 63.64 | |||
| 5 | 6.00 | 30.70 | 55.91 | |||
| 8 | 2 | 4.00 | 1.60 | 1.72 | 23.87 | 48.38 |
| 3 | 2.67 | 23.66 | 35.91 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fink, A.; Nett, O.; Schmidt, S.; Krüger, O.; Ebert, T.; Trottner, A.; Jander, B. Free Stream Behavior of Hydrogen Released from a Fluidic Oscillating Nozzle. Fluids 2021, 6, 245. https://doi.org/10.3390/fluids6070245
Fink A, Nett O, Schmidt S, Krüger O, Ebert T, Trottner A, Jander B. Free Stream Behavior of Hydrogen Released from a Fluidic Oscillating Nozzle. Fluids. 2021; 6(7):245. https://doi.org/10.3390/fluids6070245
Chicago/Turabian StyleFink, Anja, Oliver Nett, Simon Schmidt, Oliver Krüger, Thomas Ebert, Alexander Trottner, and Bojan Jander. 2021. "Free Stream Behavior of Hydrogen Released from a Fluidic Oscillating Nozzle" Fluids 6, no. 7: 245. https://doi.org/10.3390/fluids6070245
APA StyleFink, A., Nett, O., Schmidt, S., Krüger, O., Ebert, T., Trottner, A., & Jander, B. (2021). Free Stream Behavior of Hydrogen Released from a Fluidic Oscillating Nozzle. Fluids, 6(7), 245. https://doi.org/10.3390/fluids6070245






