1. Introduction
Open water flumes provide effective hands-on multidisciplinary learning tools for students matriculated in engineering programs, as well as in the physical education program [
1]. Senior students participating in the design and fabrication process of the flume obtained the opportunity to reinforce fundamental engineering concepts and to master valuable technical skills [
2,
3,
4]. The reported open flume was motivated by the need of a test chamber for an ongoing research on bladeless turbines, as well as the desire to have such device in the fluid mechanics laboratory. The current design was inspired by a small scale commercial water flow tank used in the investigation of vortex-induced autorotation and oscillation of straight cylinders [
5,
6], as well as the energy potential from such vibration modes of symmetric geometries [
7,
8]. Open channel tanks are paramount for various hydrodynamic research areas, such as designs of hydrokinetic energy harvesters, investigation of flow characteristics in the presence of obstacles, drag and lift of objects exposed to fluid flows, etc. The vortex-induced vibration (VIV) of objects exposed to flow has emerged as attractive potential sources of renewable energy. Additionally, the versatility of open channel flumes has allowed plethora of vibration modes to be experimented. Sun et al. used a 40 cm wide and long rectangular channel to convert vortex-induced vibration and galloping of blunt bodies into electricity via piezoelectric strips [
9]. In a small scale water tank, Cao et al. attempted to amplify the vibration amplitudes of piezoelectric strips by means of magnet fields [
10,
11]. Arionfard and Nishi utilized a small (30 cm × 1 m) water channel to investigate power harnessing potential of pivoted cylinder exposed to highly turbulent flow [
12]. The utilization of much larger size channels allows modeling of near-realistic flow and full-scale energy harvesters. Rostami and Fernandes studied the energy harvesting from the torsional galloping, fluttering, and autorotation modes of flat and S-shape plates using a 1.4 m, wide 22 m long water channel [
13,
14,
15,
16]. Furthermore, a 1 m wide water flume tank is used in the development of VIVACE (Vortex-Induced Vibration of Aquatic Clean Energy), which exploits the transverse-to-the-flow (lateral) oscillation mode of VIV at large range of Reynolds numbers using magnets attached to cylindrical bars as harvesters [
17,
18,
19]. An open channel with similar width but five times longer (about 42 m long) was recently used in the attempts to utilize the galloping modes of triangular cylindrical bars at much higher velocity [
20,
21]. Generally, interests in the designs of innovative hydrokinetic energy turbines have been well facilitated by open water flumes. The facility is adaptable for various types of turbines and its blades, as well as a range of measurement needs. Barber et al. studied the power and thrust improvement of axial turbines after the utilization of carefully designed adaptive pitch composite blades [
22]. A small commercial flow loop water tank was used in the investigation of wake behind the propellers of wind turbines [
23]. Open water flume experimentations of vertical axis hydrokinetic generators, such as Savonius and Darrieus turbines, have been intensified lately. These turbines are attractive renewable energy harvesters due to their simple designs, low-cost manufacturing, easy maintenance, and independence of flow direction. Talukdar et al. demonstrated that the performance of two-bladed semi-circular Savonius turbines is better than two-bladed elliptical and three-bladed semi-circular designs [
24]. On the other hand, Sarma et al. pointed out that the three-bladed Savonius model performs better in water than in air flow [
25]. It is interesting to note that placing an upstream obstacle can improve the performance of a modified two-bladed Savonius turbines [
26] and Darrieus turbines [
27]. Attempts to assemble and test the two turbines into one single hybrid unit have shown promising outcomes [
28,
29]. In the hydrology area, large size tanks facilitate investigations of particle sedimentation carried by water flow [
30], improvement of hyporheic zones due to riverbed restoration [
31], and effects of flood waves on river banks [
32] among many other studies. The open channel allows examination of flow qualities, such as head loss and turbulence, by placing out obstacles in its test section. Investigation of the head loss due to the presence of submerged baffle-posts [
33,
34] and examination of water turbulence due to rib roughness [
35] are examples of important studies to be carried out for better irrigation systems. Examinations on the interaction between vegetation and water flows shed light on the life quality of river. Here, the vegetation under investigation is carefully arranged along the base of the test chamber and its effects on water waves are studied using camera [
36]. Lastly, we would like to mention flume experimentations to test the drag and lift of 3D-printed models of swimmers [
1] that show the capability of water flume to accommodate large range of multidisciplinary applications. The transparent chamber of the flume certainly allows flow measurement by either direct observation [
33,
34] or flow visualization technology such as dye injection [
31], hydrogen bubble [
37], particle image velocimetry (PIV) [
23,
37,
38], planar laser-induced fluorescence (PLIF) [
39], stereoscopic digital particle image velocimetry (SDPIV) [
40], laser doppler velocimetry (LDV), and acoustic doppler velocimetry (ADV) [
30] methods. It is obvious that the versatility and easy-to-maintain characteristic of the open flume systems makes the device very attractive to be included in fluid mechanics and hydrology labs.
The presented work discusses the design and fabrication of a small size (15 cm wide and 75 cm long test chamber) open water flume with closed flow loop driven by a 3 hp centrifugal pump. The designs must consider limited funds, available space in the lab, and mobility requirement. The overall size of the system, the materials for the structural frame and the chambers, as well as the pump selection, can be determined by the flow requirement in the observation chamber and experiments that would be conducted. In this project, the maximum fund was set to be USD 10,000 and the overall size is governed by the size of the freight elevator in the school. The overall length of the system must be kept to about 2.5 m or shorter, so that it can fit in the school’s freight elevator. Reported in this paper are the pump selection process, structural analysis of the supporting frame, computational fluid dynamic analysis of the flume, manufacturing process, and conducted experimentations on the flow visualization using dye injection and investigation of drag forces on submerged objects. A brief discussion on the budget is presented before the paper is closed with a discussion and conclusion sections.
2. Basic Design and Pump Selection
This water flow tank is designed to provide straight uniform flow with an average speed of as much as 60 cm/s through its transparent observation chamber. The cross-sectional dimension of the observation chamber is planned to be at least 15 × 15 cm
2. The length of the observation chamber was designed to be 60 cm. This length is needed to provide enough observation room for vortex trail and wakes behind objects exposed to water flow. The final length of the test chamber is 75 cm. The selection of the maximum speed and chamber dimension was based on a commercial water flume used in experiments on vortex-induced oscillation of cylinders [
41]. An upstream manifold in a shape of converging chamber of about 44 cm is added to provide room for the water to reduce its turbulence and complex characteristics prior to enter the observation chamber. The height of the observation chamber was designed to be ~1.2 m, a little less than the average height of human eyes of ~1.4 m. The top side of the observation chamber is expected to be open to allow direct physical access to the flow and, more importantly, easy placement of objects exposed to the flow. Tight covering of the top side to achieve high speed of water flow is possible, but the pressure increase must carefully be calculated. The flow tank was designed to be mobile, so that it can be easily moved when needs arise. The overall length and width of the flow tank therefore is constrained to size of the school’s freight elevator of approximately 2.16 by 2.44 m
2. This size put limitation on the total length of the equipment to be about 2.5 m. The overall budget of this device is set to be less than USD 10,000, based on the maximum fund by the sponsor for this project: Vibration Institute. As the project is scheduled for a senior design project, the design and construction must be finished in two semesters.
The design process begins with a preliminary calculation for the pump specification, which would determine the pipe diameters, the dimension of supporting frames, and required power outlet. Detail calculation would require flowrates, height of the observation chamber, lengths, diameters, and materials of various pipes involved in the designs, as well as connections and pipe bends. In the absence of many of these parameters, the needed pump power can be calculated using the required flowrates and maximum elevation that needs to be overcome by the water. Other parameters need to be estimated.
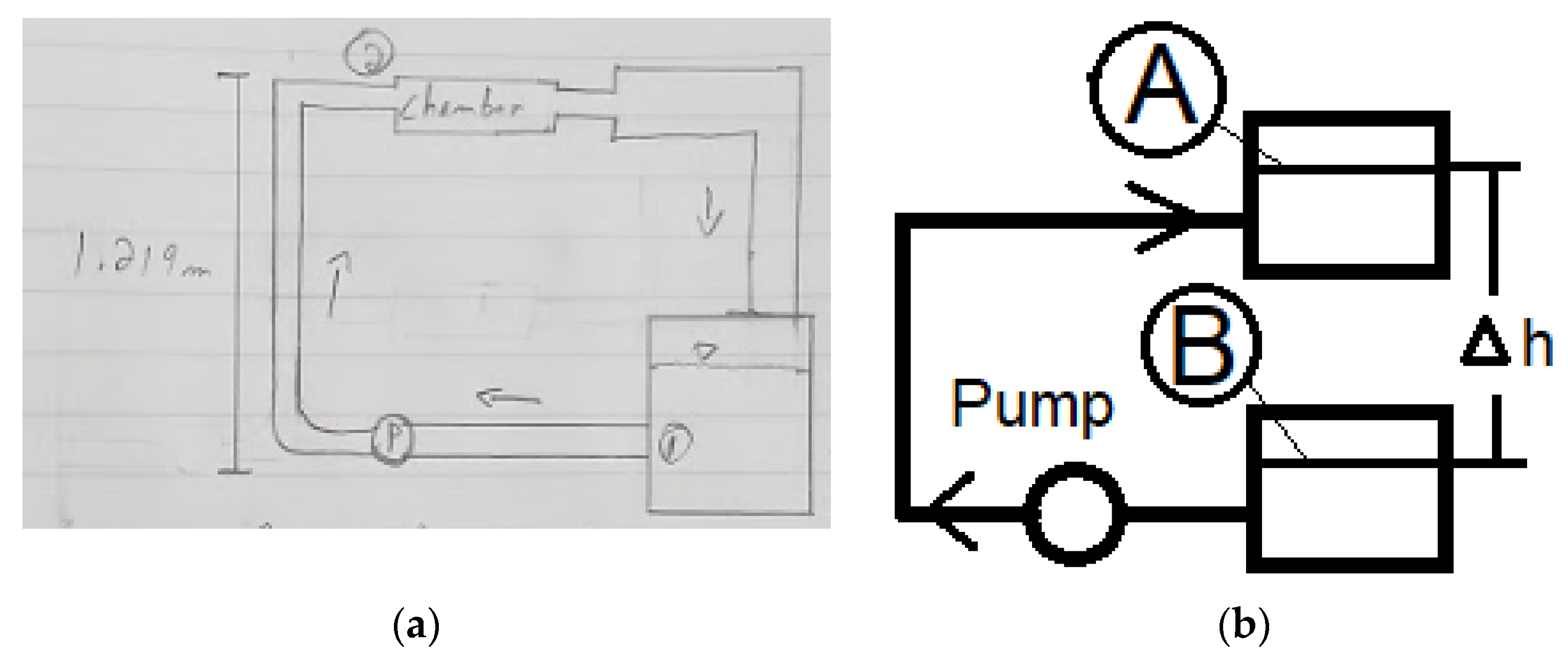
Figure 1 panel (a) shows an example of simple conceptual sketch of the water flow system drawn by students involved in this project. The flowrate can be determined from the demanded speed
of ~0.6 m/s and cross section area of the observation chamber of
, through the equation for flowrate
, or about 12,800 gph or 214 gpm.
Figure 1 panel (b) depicts a simple open flow diagram to represent the design of the water tank. The pump must overcome the height of the observation chamber and resistance by all pipes and chambers (major losses) and various connections (minor losses) along the loop. Note also that the effects of gravity on the returning channel from the observation chamber is not included in the calculation, as the power discount may not be significant. The flow diagram shown in
Figure 1 guides us in determining the Bernoulli equation to be used.
The total head
for the calculation of pump power can be obtained from the Bernoulli equation easily found in fluid mechanics text books [
42,
43];
The
represents the elevation difference between two end points in the flow diagram. In our case, we would take this as the largest height difference available in the water tank system, which is the height of the observation chamber. The second and third terms in the equation are known as the major and minor losses, losses that are caused by the wall friction along the pipes and channels in the system, and losses that are caused by any other obstacles in the system, respectively. For the major loss, the Darcy’s friction factor
is known to depend on the Reynolds numbers of the flow and roughness of the pipe. The
and
are length and diameter of pipe, respectively. In the third term, the constant
represents resistance factors for various obstacles along the loop, such as bends, junctions, entrances, etc. The Reynolds number is defined as
where
and
are the water density and absolute viscosity, respectively. In calculating the major and minor losses, the average speed
of the water should be taken at each section along the pipe where the loss is calculated, and the
represents hydraulic diameter of that particular section. As the detail geometry of the flume is not yet known, we assume the contribution of these losses to be simply double the elevation difference, hence the total head is
. It will be shown later that this estimation is larger than an alternative estimation based on possible major and minor losses in the flume. The required pump power can be calculated using [
42,
43]
In estimating the needed pump power, we took the density (
) and absolute viscosity (
) of water at atmospheric pressure and 20 °C to be 998 kg/m
3 and 0.001 Pa.s [
43,
44], respectively, while the gravitational constant
m/s
2. Not knowing the pump to be purchased yet, we estimated the pump efficiency
from commercial pump examples presented in textbooks [
43,
44]. Based on these examples, for the required flow rate of 214 gpm, the efficiency was found to be about
. Using these data, we can estimate the required pump power to be only
or about 1.06 hp. Note that the power calculation here is based on high flow rate but very low head loss, due to the very short pipe and minimal height involved in the current design. Consequently, such a pump, with such combination of low pump power and high flow rate, may not be available in the market. Here, students need to realize that the market availability of the pump puts a constraint in the design.
Alternatively, the major and minor losses could be estimated based on the possible materials and components to be used in the designs. This detail calculation process provides valuable realistic exercise for the students involved in this project.
Table 1 shows list of pipes and channels, as well as estimated major head losses. The mean velocity for each section is estimated from the flowrate of 0.0135 m
3/s based on the required flow speed of 60 cm/s. The major loss is defined as
and the friction factor for each section is determined from the Moody chart based on the associated Reynolds number and given roughness factors of the pipes [
42,
43,
44,
45]. Due to the short pipes involved in this design, this calculation renders net head much less than 1 m, well below the estimated head mentioned before. As expected, the required head is dominated by the height of the water column that must be overcome.
Similarly, the minor losses can be estimated by considering all possible pipe components that are to be included in the system and evaluate its contribution.
Table 2 shows the list of possible components to be installed in the system and its corresponding “
K” values obtained from a textbook [
42,
45]. The total
value is about 4, and this results in minor head loss of about 0.2 m, after assuming velocity of 1 m/s. Combined with the major head loss calculated above, the total would still be less significant compared to the head by elevation difference.
Three (3) pumps for minimum 190 gpm flow rate are selected from McMaster–Carr [
46]; (A) High-Efficiency Circulation Pumps for Water, Coolants, and Oil, (B) Harsh-Environment Self-Priming Circulation Pumps for Water and Coolants, and (C) High-Flow Inline Circulation Pumps for Water. Shown in
Table 3 are features of the three pumps considered for the system. The price range is approximately USD 1000 to 2000 (2018 price). The specification of these pumps shows that the flow rates and power requirement slightly above our design requirement and the prices are within the budget range.
In selecting the pump, students may be asked to setup a simple decision matrix. The matrix allows a group of students to quantify their opinions on factors that weigh the buying decision such as price, capacity, pump power, and type of fluids that can be handled by the pump. In using the matrix, each student in the design team gives score between 1 to 3 (as there are three pump candidates), indicating the level of preference, for each category. For example, a student who prefers to buy pump B as they think that the price is the most reasonable, not necessarily the cheapest, should score 3 for pump B under the category of “Price”. If the student considers that they prefer another pump for the power, then they can put a score of either 2 or 1 under the “Power” category for pump B. Students involved in the pump selection process collect their matrix, and the pump with highest total score should be selected.
Table 4 shows an example of such decision matrix performed by one student. This example shows that the student preferred to purchase pump B over the other two pumps.
The selected 3″-self-priming pump is manufactured by AMT, a Gorman–Rupp Company based in Mansfield, OH, USA [
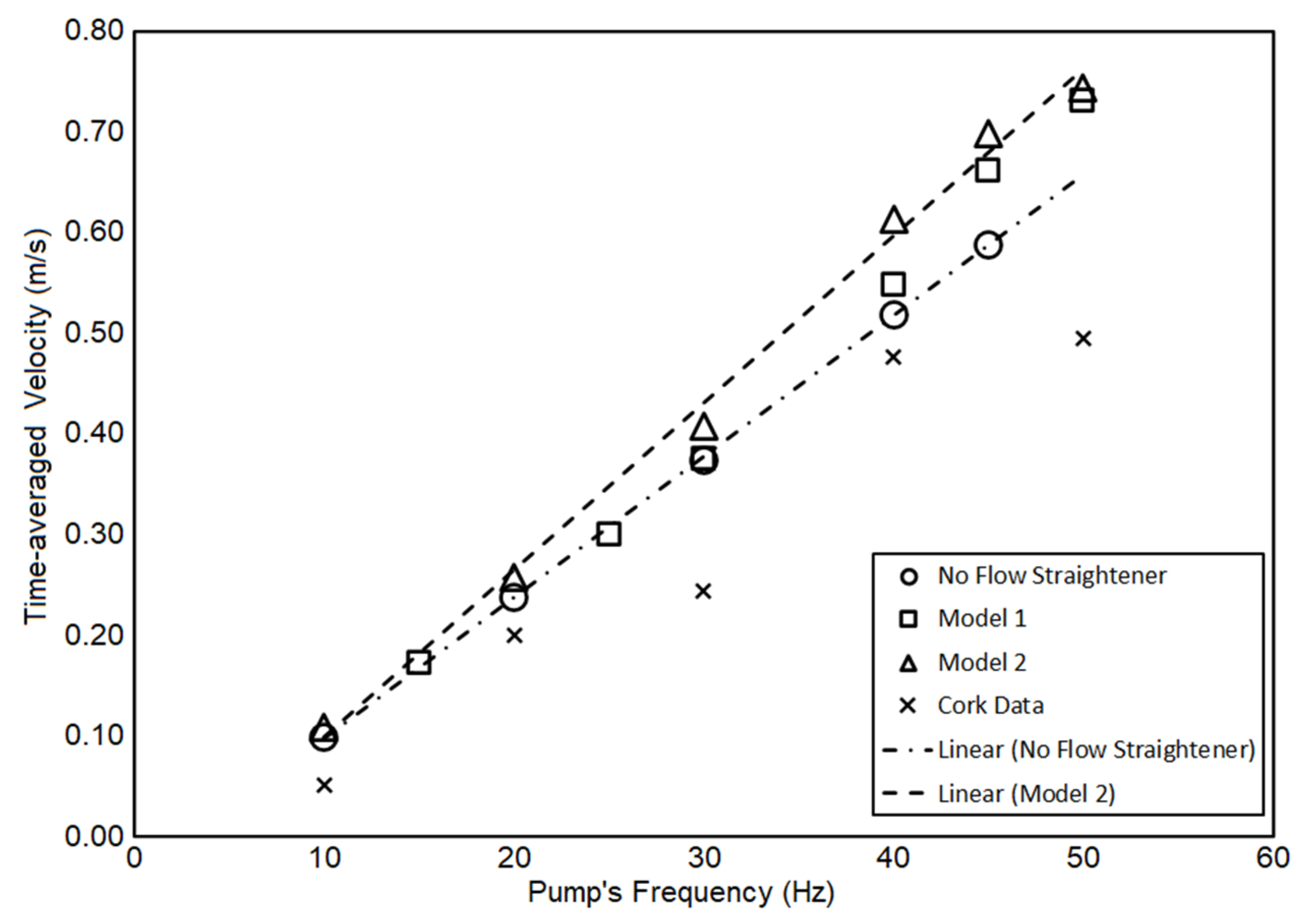
47]. This is a 3-phase pump that draws 10 Amps at 208–230 V. The stainless-steel impeller is encased in cast iron and capable of delivering 375 gpm maximum capacity of water at its 3450 rpm. The pump is selected due to its availability, capability in delivering 200 gpm, and affordability. Testing of the pump after the complete assembly indicates that the flow speed reaches 60 cm/s at the maximum 50 Hz input.
3. Static and Dynamic Analysis of Supporting Frame
Structural analysis is paramount to determine the integrity of the flow tank and its supporting frame.
Figure 2 panel (a) shows the final Computer Aided Design (CAD) drawing prepared by students and its major components. The final product of the water flow tank is shown on panel (b). The final total length of the water tank system is 2.51 m, which includes the 75 cm long observation chamber (1) and inlet manifold into the observation chamber (5) with enough entry length. In the discussion below, only the structural analysis of the supporting frame is presented.
The material chosen for the supporting frame is ASTM A513, which has a yield strength of 220.6 MPa (32,000 psi). Considering a safety factor of 1.3, the maximum yield strength for the system is
= 169.72 MPa (24,615 psi). The beam profile used is
cm
2 hollow square tubing with a thickness of 2.11 mm. The static analysis involves calculations of dead loads acting on the system, which includes the weight of the water and the tank.
Table 5 lists all possible static load items and its estimated amount. The list was prepared by students as part of the full static and dynamic structural analysis of the supporting frame. Several possible designs were analyzed and results from one design is presented here.
The maximum deflection of 0.0254 mm was discovered on one of the cross beams directly supporting the observation chamber. This value is considered very minimal, and it indicates that the selected channel is sufficiently strong. In this model, the frame is assumed to be supported by pins on its four bottom corners. Static loads, representing items listed in the
Table 5 are applied as point loads on several locations on top beams. The water weight is distributed throughout several points on the frame.
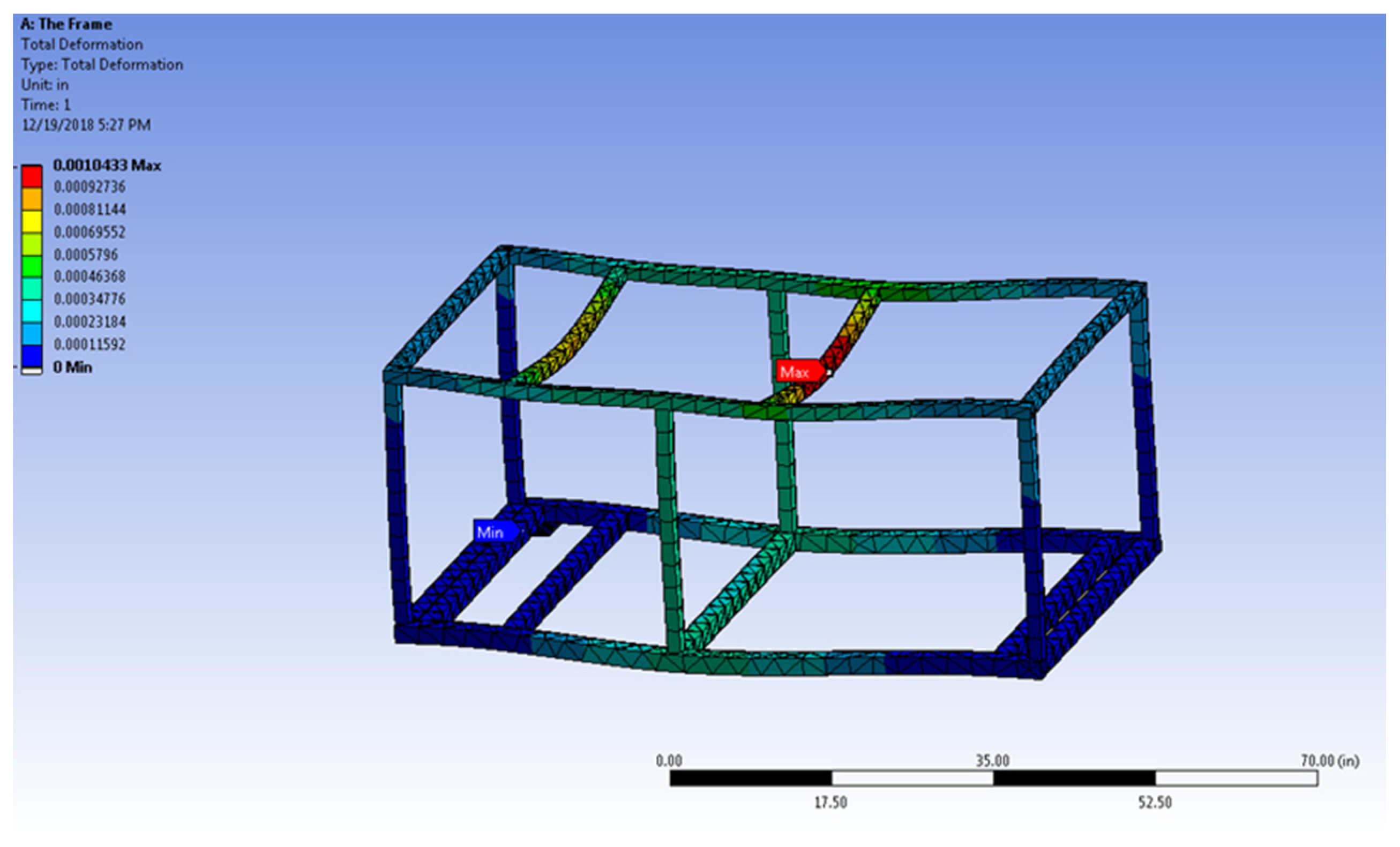
Figure 3 displays the deformation of the frame in the full 3D static analysis. As is expected, the bottom beams show minimum deformation due to the supports, while the top beams show large deformation due to the application of load.
Additionally, a dynamic modal analysis was performed using ANSYS (ANSYS Inc., Canonsburg, PA, USA) to check the mode shapes and natural frequencies of the supporting system. Outcomes from the modal analysis indicate possible resonance and amplification of deformation when the pump’s operating frequency is in the vicinity of the natural frequency of the support system. Due to the simple vibration load that is being considered, the modal analysis was set to find only the first six (6) natural frequencies. The resulting natural frequencies of the frame are presented in
Table 6. These natural frequencies were used in harmonic response analysis to determine the maximum deflection of the frame. The maximum deformation of 5.51 mm occurs for Mode 5 corresponding to the frequency of 73 Hz. Other frequencies result in maximum deformation of less than 2.54 mm. The first three (3) modes correspond to the operating frequencies of the pump of 0 to 60 Hz. Nevertheless, due to the rigidity of the structure, the amplification was found to be very minimal. The outcome suggests that the structure and material selection for this flow tank is sufficiently strong to sustain the vibration load by the pump. The study also shows that only the first 3 (or at most 4) modes need to be considered as the maximum operating frequency of the pump is only 60 Hz.
Table 6 shows the six (6) first natural frequencies of the supporting frame. The maximum deformation from the harmonic analysis, based on the given static load, is also shown in this table. A maximum deformation of 5.08 mm can potentially occur for Mode 5, corresponding to ~73 Hz. Other modes show maximum deformation of less than 2.54 mm.
The first, second, and third modes represent predominantly lateral deformation of the top beams due to the rigid support of the bottom beam. The lateral deformation can occur harmoniously between the parallel top beams (Modes 1 and 3), but it can also occur non-harmoniously as in Mode 2. Mode 3 shows lateral deformation in the long direction of the frame. While the dynamic analysis shows sufficient stiffness and unlikeliness for large amplification, rubber footings were placed underneath the pump’s platform to damp the vibration.
4. Computational Fluid Dynamics
Computational fluid dynamics (CFD) analysis suggests useful information for the design of various channels of the flume. Nevertheless, the CFD simulation and analysis provide hands-on exercise materials that allow students to better understand the dynamics of flow phenomena through visualization and parametric studies [
48]. Possible analysis to be performed ranges from two-dimensional to full three-dimensional study of either unsteady or steady water flow. Examples of topics to be studied include studying the flow characteristics in the observation chamber, pressure losses across the flume, undesired circulation zones, areas of turbulence, extreme stresses caused by fluid flow, etc. The computation domains of such studies can be either developed from scratch or imported from the structural mechanics CAD designs. In this section, results from a full 3D steady state analysis of water flows in a semi-loop model of the tank are briefly presented. The study is performed using the commercial package COMSOL Multiphysics 5.5 with CFD module (COMSOL Inc., Burlington, MA, USA). Most of the computations are performed using HP ProBook 640 G2 Notebook PC (Hewlett-Packard Company, Palo Alto, CA, USA). operated using 64-bit Windows 10 Enterprise version 1909 with a total capacity of ~465 GB. The computer has an installed RAM of 16 GB and is equipped with Intel
® Core™ i7-6600U CPU @ 2.60 GHz. One model is run using a desktop HP Compaq Elite 8300 CMT computer equipped with Intel
® Core TM i7-3770 CPU at 3.40 GHZ and 16.0 GB RAM.
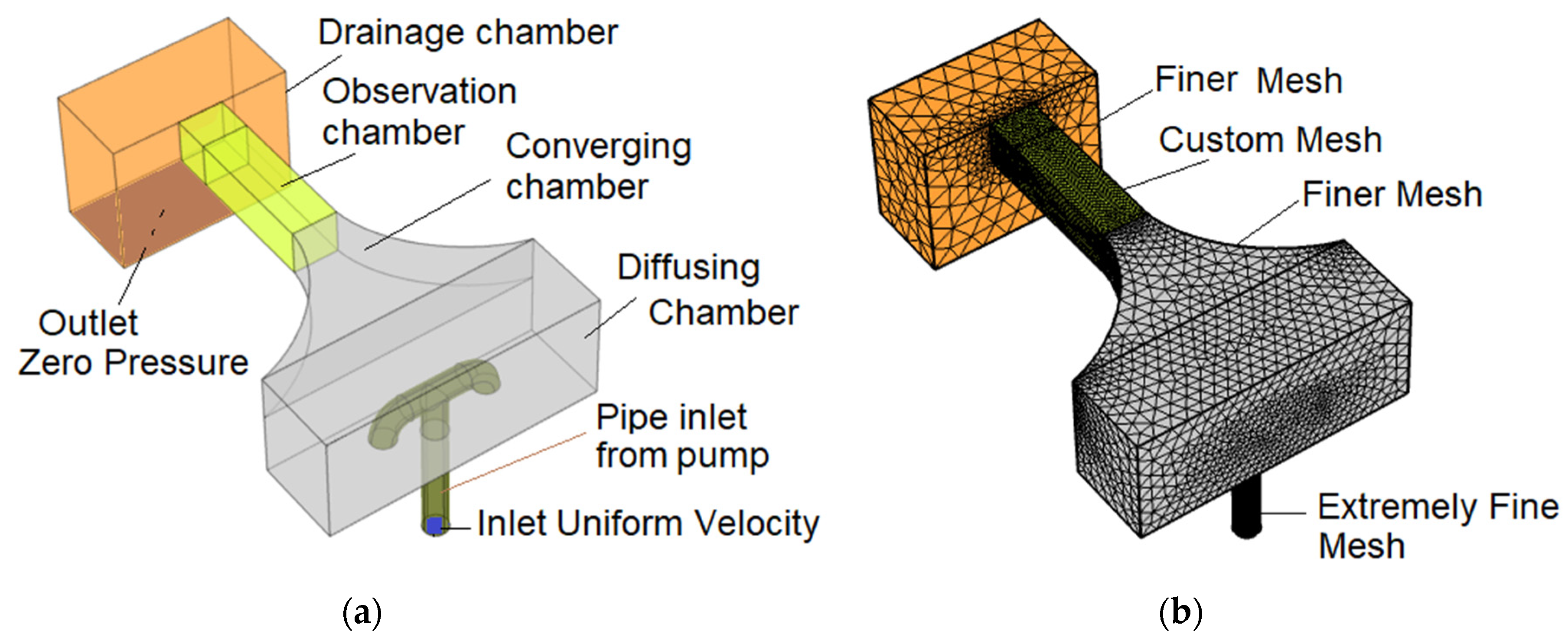
The computation domains can be differentiated into several parts, as shown in
Figure 4 panel (a). The pipe inlet domain represents the vertical cylindrical thick PVC pipe channel that delivers water from the pump’s exit into the main part of the water tank. This channel is 8 cm in internal diameter and the length is 40 cm. The pipe is extended into the diffusing chamber before it splits into two horizontal branches with the same internal diameter. The resulting T-pipe allows the water to be distributed in the diffusing chamber. The T-pipe also prevents the water to “shoot up” and put high pressure on the ceiling of the diffusing chamber. The next important domain is the converging chamber that functions to collect the water and channel it into the observation chamber. A flow straightener could be included in the converging section, however this part is not modeled due to its large amount of mesh. This simplification is justified by the computation results that indicate straight uniform flow in the observation chamber (Figure 6). The observation chamber is a 60 cm long prismatic pipe with a square cross section of 15 × 15 cm
2. At the end of the chamber, the water is collected in a rectangular drainage tank of
. The CFD model does not include a horizontal transparent plastic pipe that returns the water back from the drainage chamber into the centrifugal pump.
Several simplifications are implemented in the CFD model. For instance, the actual drainage chamber is converging downward, but in the model only the top 40 cm section is included. It is assumed that the inclusion of this part is sufficient to recreate necessary backflow effects that occur in the observation chamber. The converging chamber attached to the distal face of the observation chamber is made to be plain horizontal, parallel to the observation chamber. The actual configuration of this curved chamber includes a slight decline in the vertical direction into the entrance of the observation chamber. Lastly, in the CFD, the observation chamber is assumed to be a closed rectangular pipe. The actual observation chamber is open on its top side to allow direct access to the water.
The inlet boundary condition is located at the free end of the inlet pipe that represents the conduit between the centrifugal pump and water tank body. Not knowing the exact velocity profile produced by the centrifugal pump, a uniformly distributed velocity profile is assumed at the inlet. The exit boundary condition is located at the bottom of the drainage chamber and a zero-pressure outlet is assumed here. The actual pressure level required by the centrifugal pump to produce the flow can be obtained by adding known hydrostatic and dynamic pressures occurred at the exit level. The internal wall is assigned to the wall of the T-pipe domain, as this pipe is located inside the diffusion chamber. The physical T-pipe has a non-zero pipe thickness that has been ignored in this CFD modeling. This important feature certainly leads to a convenience and efficient mesh generation. The remaining walls are assumed to have zero velocity.
Figure 4 shows the complete model, domains, boundary conditions, and partial mesh generation that results in non-uniform mesh size throughout the domains.
CFD analysis requires a delicate balance between demands for accuracy of the outcomes versus the computational cost that are the direct results of both mesh generation and complexity of the selected flow model.
Table 7 lists CFD models studied in this work and their mesh generation scenarios. Models As and Bs are all meshed using “Global Mesh” method, where the same mesh size or scheme is applied uniformly on all domains of the model. However, models As are computed by means of “Laminar” flow model, while models Bs are executed using “Turbulent” flow model. The C, D, E, and F models are discretized using “Partial Refinement” method and are executed using “Turbulent” flow model. Effects of the two flow models will be explained later in this section. All models are computed using the HP ProBook laptop, except model D that is executed using the desktop computer. The Global Mesh method is straightforward, but for three-dimensional models this method may result in astronomical element numbers and computation time with possible less-than-sufficient accuracy at places of interest. In the current work, we later show that partial mesh refinement on places of interest should be practiced as a choice of practice in CFD modeling, particularly for three-dimensional modeling. In our work, the “Extremely Coarse” mesh option of COMSOL Multiphysics (COMSOL Inc., Burlington, MA, USA) for our model results in 21,011 elements. Increasing the accuracy by selecting the “Normal” mesh generation option multiplies the element number to 414,735 elements, almost 20 times more than “Extremely Coarse” option. However, the computational time needed to run the model using turbulence k-
scheme is multiplied from 6760 s to almost 286,538 s, 40 times longer. The partial refinement mesh generation, used for models C, D, E, and F, is performed by selecting domains or regions of interest (ROI) to be discretized finer than other domains. Here, the observation chamber, T-pipe, and inlet pipe are selected as the ROI so that the velocity profiles and other important aspects in the region can be studied more accurately. This method aims to reduce the amount of mesh and computational time, and to avoid unnecessary data collection in non-ROI parts such as the diffusing chamber, drainage chamber, and converging chamber. The Partial Refinement method certainly opens numerous possible mesh arrangements. To limit the study, we focus on mesh refinement of the ROI only. The refinement of the observation chamber sub domain will enhance accuracy of the velocity profiles in the region needed for possible two-dimensional modeling. On the other hand, the refinement of the inlet pipe and the T-pipe is expected to give accurate information on the amount of pump pressure needed in the design. These three domains will be refined using “Extremely Fine” mesh or customized mesh, while the remaining body will be meshed using either “Normal” of “Finer” scheme. For Model C, the ROI are meshed using “Extremely Fine”, while the remaining domains are meshed using “Normal”. For Models D and E, the mesh for the test chamber domain of Model C is further refined by reducing the “maximum element size” from 0.0318 to 0.015 m. Model D is the only model that is computed using the HP desktop computer. It should be noted that the “Normal” size used in the non-ROI domains of models C, D, and E employs “maximum element size” that is about triple than that of the “Normal” size used in Model B4 with global mesh method. Consequently, although the ROI domains of Models C, D, and E, are finely meshed, the total number of elements of these models are less than that of Model B4. The difference in the “maximum element size” is due to the different “Calibration” option offered by COMSOL (COMSOL Inc., Burlington, MA, USA). The mesh configuration for Model F is the finest among models with partial refinement mesh. Here, the mesh configuration of the ROI used in Model D is maintained, but the remaining domains are meshed using “Finer” mesh. This refinement results in 355,730 elements, and the computation time is 145,860 s, only half of the time needed by model B4.
Shown in
Figure 4 panel (b), results of Partial Refinement strategy where high mesh density (“Extremely fine mesh”) is applied on the observation chamber, pipe inlet, and T-junction domains. The remaining domains are discretized using “Finer” mesh. The minimum and maximum element sizes employed in the observation chamber are 5 mm and 15 mm, respectively. The application would result in at least 10 computation nodes across the 15 cm wide observation chamber, which should be enough for accuracy.
The volumetric flowrate () and mean velocity () in the observation chamber in the inlet pipe and observation chamber will be used to measure the accuracy of the solution. The volumetric flowrate across planes perpendicular to the long direction of the observation chamber must equal to that of the inlet. This flowrate can be obtained from the uniform inlet velocity provided at the pipe inlet; , where is the pipe diameter. The mean velocity in the observation chamber can be easily estimated using , where the cross-section area of the chamber is known as . As the outlet at the base of the drainage chamber is assumed to have a pressure drop, the flowrate at this location should also be verified.
Second only to the mesh generation, the selection of appropriate physical modeling of the fluid is the most crucial aspect of CFD modeling. The selection between Laminar and Turbulent models is often determined by Reynolds numbers involved in the problem. The laminar threshold for fully developed flow in long pipe with circular cross sections is typically around 2300, while for an open channel flow is 500. Students have to understand that the change from laminar to turbulent flow is a gradual transition, and therefore it is not practical to point out a single number to differentiate the two regimes. As pointed out by Lowe, the confusion over the critical Reynolds number is not new in the Fluid Mechanics community [
49]. Nevertheless, smaller Reynolds numbers should be treated as turbulent when the complex geometry of the domains include circulation zones that are best captured using turbulent models. In the current water tank design, the maximum expected mean velocity occurring in the 15 × 15 cm square observation chamber is 60 cm per second, which results in the Reynolds number of 90,000, which puts the model under turbulent category. A long list of turbulent models is available in COMSOL Multiphysics software (COMSOL Inc., Burlington, MA, USA). For this project, we selected the standard k-
model to serve our purpose. This suggested model is selected due to its popularity for industrial applications, easy convergence, and low memory requirement [
50]. Alternatively, the analysis on such water flume can be performed using k-
SST model [
51]. However, a comparison study performed on a water flume with 5 m wide and 17 m long test section suggest that the outcomes from the two different Turbulent models do not show significant differences [
52]. Heyrani et al. compare the performance of seven (7) turbulent models used in steady state modeling of a venturi flume. It was discovered that the k-
model performs slightly better than the k-
SST model [
53].
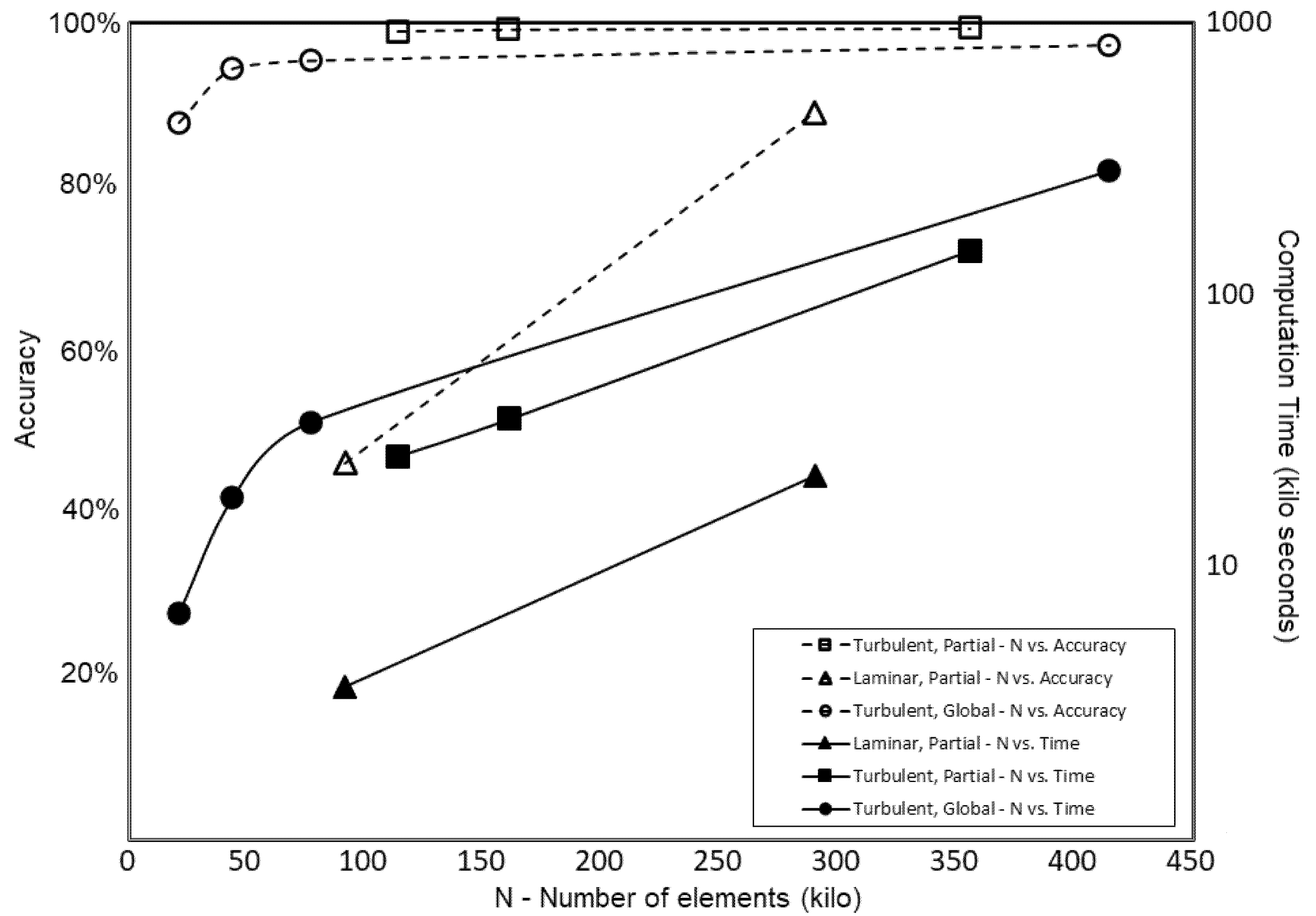
Figure 5 shows the accuracy and computation times that are plotted against the mesh number for different models. The graph shows that Turbulent model with Partial Refinement (rectangular markers) produces the best accuracy among the three models (Laminar model with Partial Refinement, Turbulent model with Global Mesh, and Turbulent model with Partial Refinement). Moreover, its computing time is less than the Turbulent model with Global Mesh (circular markers). The computing time of the Laminar model with Partial Refinement (triangular marker) is the lowest, but the accuracy is also very low. The laminar model should only be used to make sure that the CFD model can be properly executed. High accuracy can be easily achieved by the Turbulent model with Partial Refinement, even with a low amount of mesh.
Streamlines in the water tank when the mean inlet flow is 3 m/s are shown in
Figure 6. The streamlines are obtained using “standard point controlled” method and using “Number of Points” entry of 80 points. The streamlines on the left and right are obtained when the computation modules used are Laminar model and Turbulent k-
model, respectively. The streamlines from the Laminar model are parallel and straight in the observation chamber, but they are clearly absent from the circular flows in the drainage chamber, as well as in the diverging chambers that are demonstrated by the Turbulent model.
Observing the axial velocity profiles along the observation chamber, the Laminar model shows reasonable parabolic shapes (data are not shown here), however the amount of flow rate and mean velocity show deviation from the correct values. The profile of axial velocity along the observation chamber obtained from the Turbulent models are depicted in
Figure 7. Each velocity profile is obtained at the same horizontal mid-section of the observation chamber, but at different distances “Y” from the starting of the chamber (taken as the interface between the converging chamber and observation chamber). The development of the velocity profile can be observed in this figure as the profile changes into a more parabolic shape as the Y is increasing. The velocity profiles demonstrate the typical characteristic of turbulent profile consisting of a turbulent core in the middle and laminar sublayer near the wall [
45]. Note, however, that for the Model B4 (global mesh), the laminar sublayer is pronounced, while for Model F (partial refinement), it is very difficult to observe due to its small thickness. The accuracy of Model F in predicting the expected flowrate and mean velocity however is higher than that of Model B.
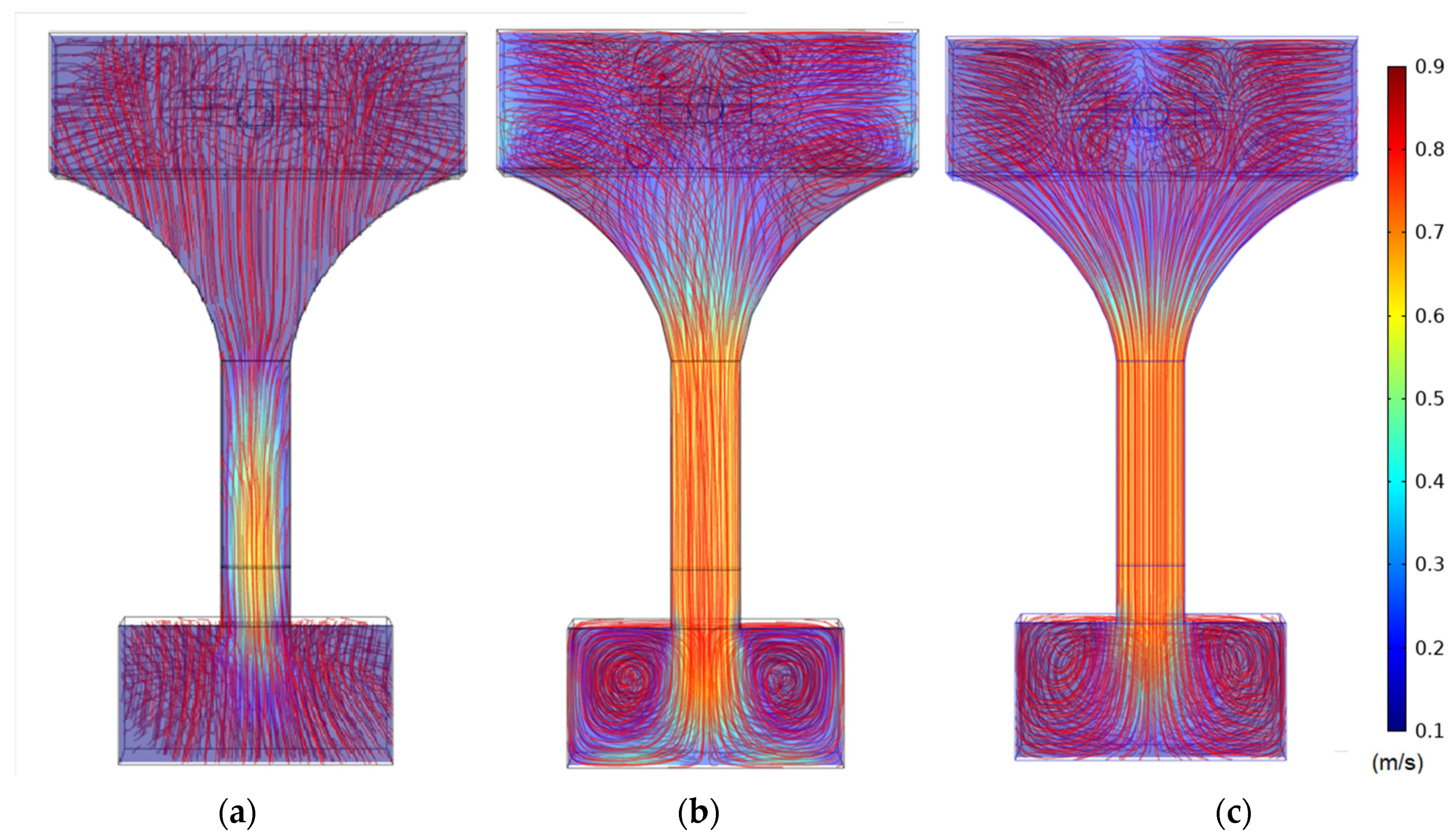
The velocity map and streamlines, viewed from the top of the flume, can be seen in
Figure 8. The flow direction goes from top to bottom (diffusing chamber to the drainage chamber). Panel (a) on the left shows the velocity map of laminar model, while panels (b) and (c) are from the turbulent model, but with different mesh schemes. All models present reasonable straight parallel streamlines in the observation chamber. The Laminar model shows gradual increase in speed as it enters the observation chamber, as can be observed from the changing color. On the contrary, the Turbulent models both show consistent average velocity along the observation chamber. The Laminar model fails to produce the twin circulation zones that occur in the drainage chamber. These circulation zones are physically observed during real experimentation. The two Turbulent models clearly show these circulation zones with slight difference. The circulation zones by the Model B4 (
Figure 8 panel (b)) are shown to be less chaotic than that of Model F (
Figure 8 panel (c)).
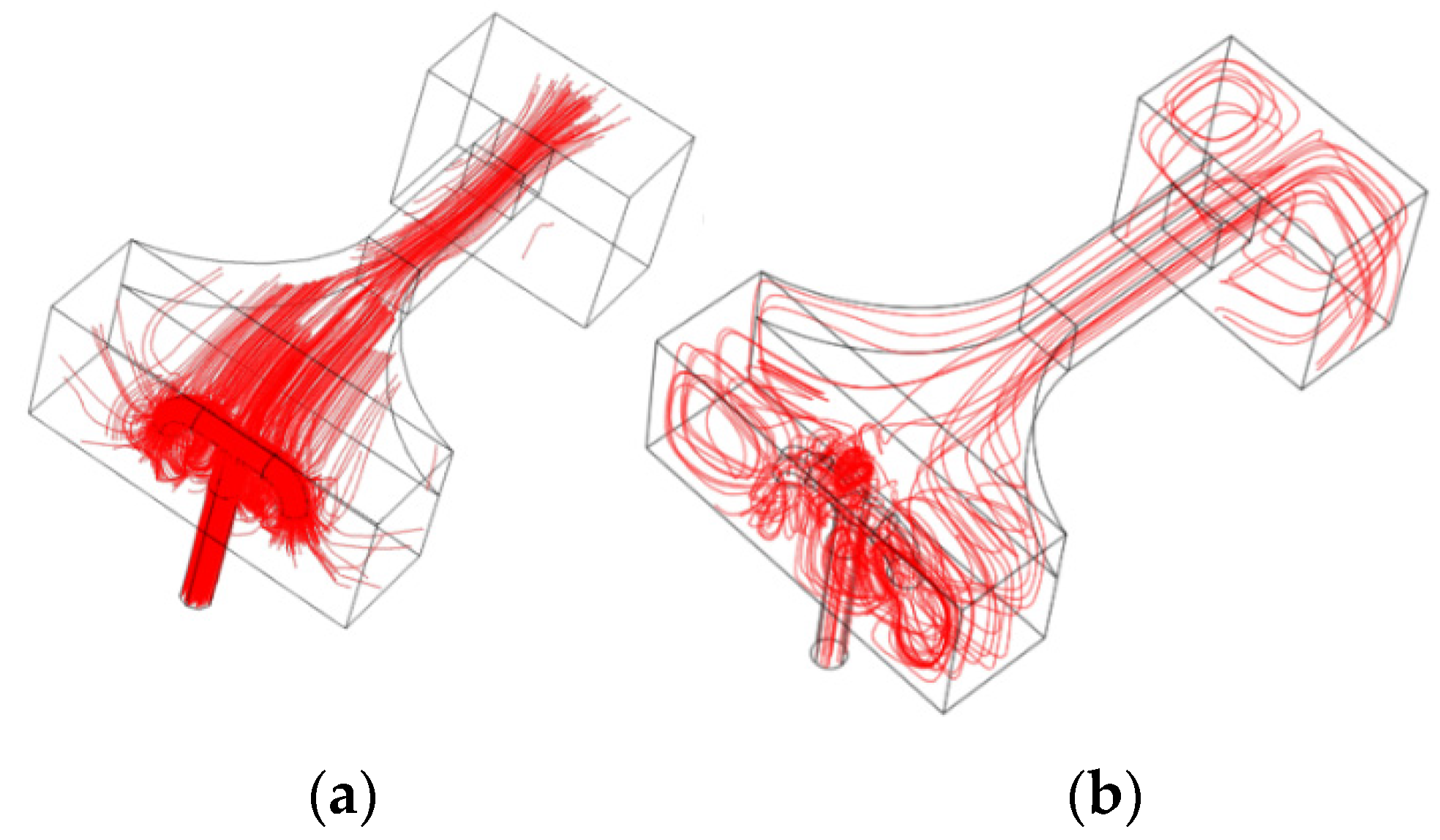
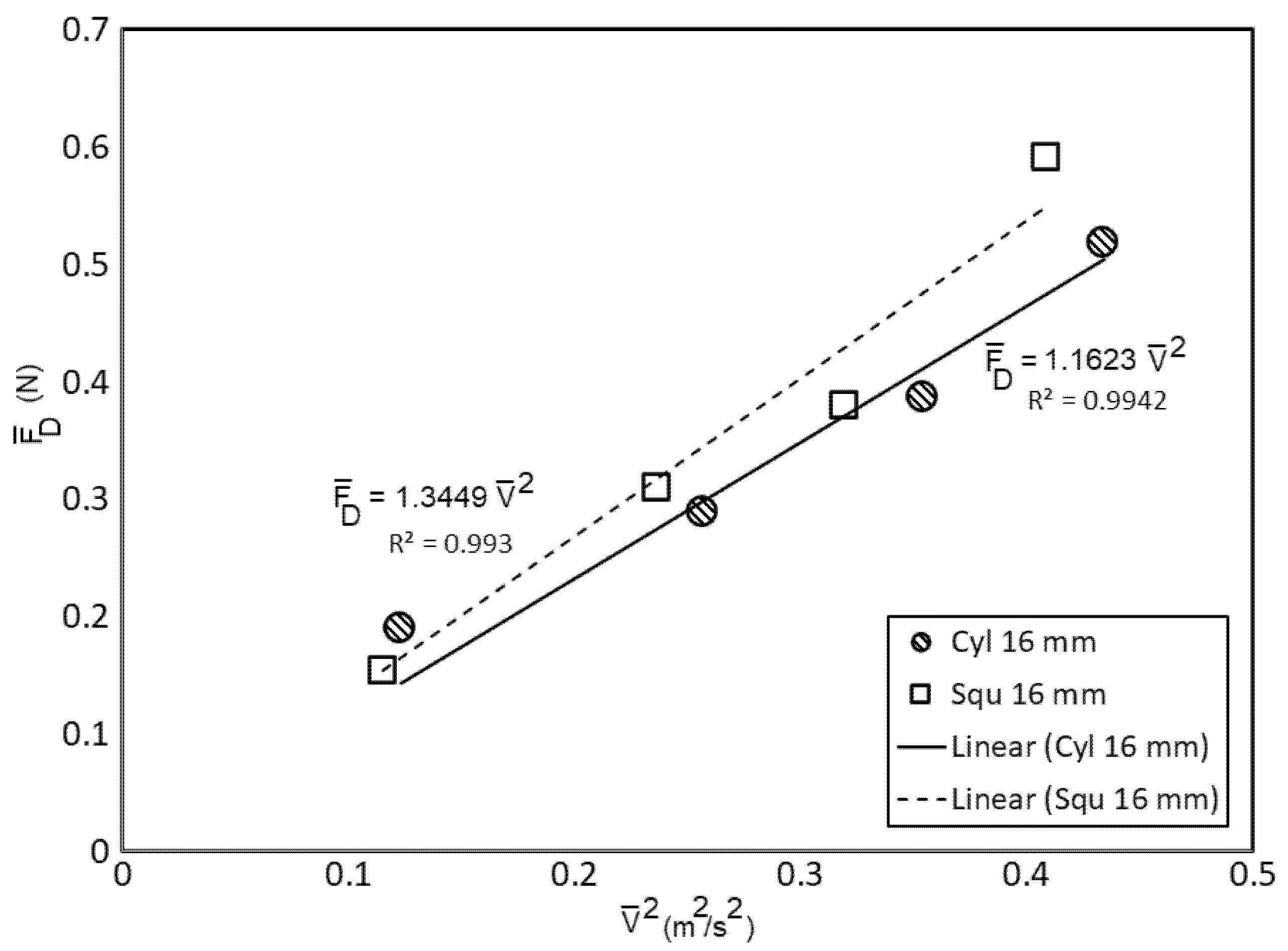
Vorticity is a local measure of the rotational motion of fluid particle relative to its own centroid, while the circulation can be considered as the measure of the rotational motion in global sense, relative to a distance reference point. After passing the observation chamber, water enters a short drainage chamber that is three times wider than the observation chamber but much deeper in the vertical sense. Here, due to the high speed in the observation chamber, the water shoots into the back wall of the chamber, but it also starts to fall due to the gravity. Hence, the stream splits into a pair of almost identical spiraling flows downward. Shown in
Figure 9 are streamlines projected on a two-dimensional plane cut across approximately the middle height of the drainage chamber. On each panel, the streamlines demonstrate a pair of spiraling circles running in opposite directions. Note that the flow is coming from the observation chamber located, according to these pictures, relatively above the rectangular areas shown in the panels. The color map describes local vorticity values, and the scales indicate that, on average, the two pairs have a similar amount but in opposite directions. In this figure, each panel represents a circulation zone in the chamber from the same Reynolds numbers, around 72 K (uniform inlet velocity of 3 m/s), but each is computed using different mesh density and element types used in the drainage chamber domain. On panel (a), the fluid model is laminar, and the elements used in the drainage chamber is tetrahedral. On panels (b), (c), and (d), the k-
Turbulent model is used, but the number of elements used (only in the drainage chamber) are 5498, 14,681, and 61,052, respectively. On panel (b), only tetrahedral elements are used, but various elements are used for results shown in panels (c) and (d). It can be seen that the utilization of various elements results in smooth vorticity map and streamlines that are less discrete. The symmetry of the circular flow is captured when the mesh density is very high but, generally, panel (c) shows that essential flow structure is sufficiently captured. The maximum and minimum values on the scales indicate the amount of vorticity details that can be captured by the respected mesh density. On panels (b), (c), and (d), while the maximum and minimum vorticity are different, the average values inside and around the cores of the circulation area is around 4 to 5. On panel (c) and (d), zones with large vorticity up to 20/s can be captured, but these areas are concentrated near the walls. As is expected, the large vorticity occurs near the walls where large shear strain is expected to occur. On panel (a), the Laminar model results in a pair of seemingly symmetric circulation zones. The zones, however, appear to be shifted to the side walls. Moreover, the vorticity map shows some level of local spins, but the distribution is different from that shown in other panels. The laminar model certainly has failed to produce the desired outcomes, despite of the high mesh density that has been employed.