Precise Method to Estimate the Herschel-Bulkley Parameters from Pipe Rheometer Measurements

Abstract

Accurate characterization of the rheological behavior of non-Newtonian fluids is critical in a wide range of industries as it governs process efficiency, safety, and end-product quality. When the rheological behavior of fluid may vary substantially over a relatively short period of time, it is desirable to measure its viscous properties on a more continuous basis than relying on spot measurements made with a viscometer on a few samples. An attractive solution for inline rheological measurements is to measure pressure gradients while circulating fluid at different bulk velocities in a circular pipe. Yet, extracting the rheological model parameters may be challenging as measurement uncertainty may influence the precision of the model fitting. In this paper, we present a method to calibrate the Herschel-Bulkley rheological model to a series of differential pressure measurements made at variable bulk velocities using a combination of physics-based equations and nonlinear optimization. Experimental validation of the method is conducted on non-Newtonian shear-thinning fluid based on aqueous solutions of polymers and the results are compared to those obtained with a scientific rheometer. It is found that using a physics-based method to estimate the parameters contributes to reducing prediction errors, especially at low flow rates. With the tested polymeric fluid, the proportion difference between the estimated Herschel-Bulkley parameters and those obtained using the scientific rheometer are −24% for the yield stress, 0.26% for the consistency index, and 0.30% for the flow behavior index. Finally, the computation requires limited resources, and the algorithm can be implemented on low-power devices such as an embedded single-board computer or a mobile device.

1. Introduction

Accurate characterization of non-Newtonian fluids is a critical issue in a wide range of domains from chemical to physical processing since it governs the process efficiency, safety, and end-product quality. Usually, the rheological properties are determined by sampling the fluid in the production system and measuring its characteristics with an off-line rheometer. However, the characterizations made off-line may be unsatisfactory when the viscous properties of the fluid change continuously. With non-Newtonian fluid, the in-line measurement of viscous properties is much more complicated than for Newtonian fluids where simple methods such as the tuning fork technique, for example, can be implemented even in very harsh conditions [1]. To meet the requirements of the industry for inline measurement of the viscous properties of non-Newtonian fluids, several methods have been developed. Most of them rely on the measurement of the fluid radial velocity profile losses along a known section of pipe. Different techniques were developed to estimate the velocity profile such as magnetic resonance imaging [2], laser velocimetry [3], ultrasound velocity profiling [4], and electrical resistance sensing [5]. Each technique comes with its own limitations due to the physical principles of the sensor, specific environmental constraints, cost, and/or safety. For instance, methods based on the measurement of the velocity profile are not adapted to investigate fluids that are opaque or which structure results in the diffraction of the probing signal that is sent by the radiating source, like for example with emulsions or fluids containing many solid particles.

An alternate approach to the one based on velocimetry consists of measuring the pressure gradient for various bulk fluid velocities while circulating the fluid in pipes [6]. This method has the advantage of working with fluids that are completely opaque to or that cause a high degree of diffraction of the radiations from possible illuminating sources. The inconvenience of the method is that measurements shall be made with multiple flow conditions in order to acquire enough information for calibrating a chosen rheological model. The choice of a rheological model depends on the type of fluid being measured. In turn, the minimum number of flow conditions is a function of the chosen rheological model. The simplest non-Newtonian rheological models have two parameters like the Bingham plastic or the power law models, while more realistic models have three parameters such as the Herschel-Bulkley [7], Robertson-Stiff [8], or Heinz-Casson models [9]. More complex models such as the ones from Carreaux [10] and Quemada [11] depend on four parameters.

The Herschel-Bulkley model is often used to describe the rheological behavior of non-Newtonian fluids, simply because it is a generalization of both the Bingham and power-law models. Therefore, we have chosen to use that model to describe the rheological behavior of the fluid being measured in the pipe rheometer. From differential pressure measurements, we derive a calculation method for the Hershel-Bulkley parameters using a combination of physics-based equations and non-linear optimization. The present method can accurately estimate the fluid rheologic characteristics based on pressure loss measurements and three hypotheses: the fluid rheological behavior can be approximated by the Herschel-Bulkley model, measurements are made in laminar flow conditions and slippage at the wall is negligible.

2. Herschel-Bulkley Flow in a Pipe

The Herschel-Bulkley (H-B) model, also referred to as the yield power law (YPL) model, is one of the many relations used to describe how certain viscous fluids behave; especially fluids that exhibit yield stress and for which the shear stress tends to behave like a power law at high shear rate.

The model relates the shear stress τ to the shear rate $\dot{\gamma }$ as follow [7]:

$$\tau ={\tau }_{\gamma }+K{\dot{\gamma }}^n,$$

(1)

where ${\tau }_{\gamma }$ is the yield stress, $K$ is the consistency index and $n$ is the flow behavior index. Note that the model reduces to the Bingham plastic rheological behavior when $n=1$, i.e., $\tau ={\tau }_{\gamma }+K\dot{\gamma }$ and the power law model when the yield stress is equal to zero, i.e., $\tau =K{\dot{\gamma }}^n$.

For parameter identification purposes, a linearized expression of Equation (1) is often used [12]:

$$\ln \left(\tau -{\tau }_{\gamma }\right)=\ln K+n\ln \dot{\gamma }.$$

(2)

2.1. Practical Estimation of the Herschel-Bulkley Parameters

The Herschel-Bulkley parameters for a particular fluid are usually found experimentally by measuring several pairs of data $\left(\tau , \dot{\gamma }\right)$ with a rheometer. Then, using an optimization method such as a direct search or a Newton-like method, the corresponding model is fitted, and its parameters are estimated. However, as shown by Kelessidis et al. [12], these methods often give a negative yield stress, ${\tau }_{\gamma }$, which is not physically meaningful. To overcome this challenge, different methods were developed which use the linearized model (Equation (2)) and require a prior estimation of ${\tau }_{\gamma }$. To fulfill this requirement, multiple approaches were tried: trial-and-error [13], graphical extrapolation of the rheogram [14], or golden section search [12], involving constrained optimization algorithms when needed. It is also possible to use machine learning algorithms, more specifically genetic algorithms, to directly determine the H-B parameters of a fluid, as shown in [15].

More recently, Mullineux showed in [14] that the resulting value of parameters $K$ and $\dot{\gamma }$ were very sensitive to the initial estimation of ${\tau }_{\gamma }$. The problem is that the estimation of ${\tau }_{\gamma }$ is heavily influenced by measurements at the lowest flow rates where uncertainty is the highest. Mullineux showed that for a fluid described by the following H-B parameters ${\tau }_{\gamma }=5 Pa$, $K=4 Pa.s^n$ and $n=0.35$, an error of 1 Pa on the estimation of ${\tau }_{\gamma }$ leads to an error of 12.5% on $K$ and 6% on $n$. Thus, he described a method to estimate the flow behavior index, n, independently from the determination of the two other parameters, therefore, allowing to estimate $K$ and ${\tau }_{\gamma }$ by simple linear regression. This method is especially interesting as it does not require extrapolation on uncertain data and returns the global optimum value for n.

When looking for the best H-B coefficients to model a fluid, an optimization step is usually required, and the method relies on the minimization of the least square error:

$$S={{\displaystyle \sum }}_{i=1}^m{\left[{\tau }_{\gamma }+K{\dot{\gamma }}_i^n-{\tau }_i\right]}^2,$$

(3)

where, $\left({\tau }_i; {\dot{\gamma }}_i\right)$ is one of the $m$ measured pairs of shear stress and shear rate. In [14], the author showed that in the case of Herschel-Bulkley fluids, minimizing S is equivalent to solving the following equation:

$$F\left(n\right)=\left|\begin{array}{ccc}m& \sum {\dot{\gamma }}_i{}^n& \sum {\dot{\gamma }}_i{}^n\ln {\dot{\gamma }}_i\\ \sum {\dot{\gamma }}_i{}^n& \sum {\dot{\gamma }}_i{}^{2n}& \sum {\dot{\gamma }}_i{}^n\ln {\dot{\gamma }}_i\\ \sum {\tau }_i& \sum {\dot{\gamma }}_i{}^n{\tau }_i& \sum {\dot{\gamma }}_i{}^n{\tau }_i\ln {\dot{\gamma }}_i\end{array}\right|=0.$$

(4)

It has been shown in [14] as well that $F\left(n\right)$ has only one root for $n\in \left]0;+\infty \right[$ which is the $n$ that minimizes the function described by Equation (3). $n$ is found using a simple root search method such as the bisection method, $K$ and ${\tau }_{\gamma }$ are then determined by performing a linear regression based on Equation (1) on the measured data. The advantage of this method is that it allows us to find the H-B parameters corresponding to the global minimum of $S$ at a very low computational cost.

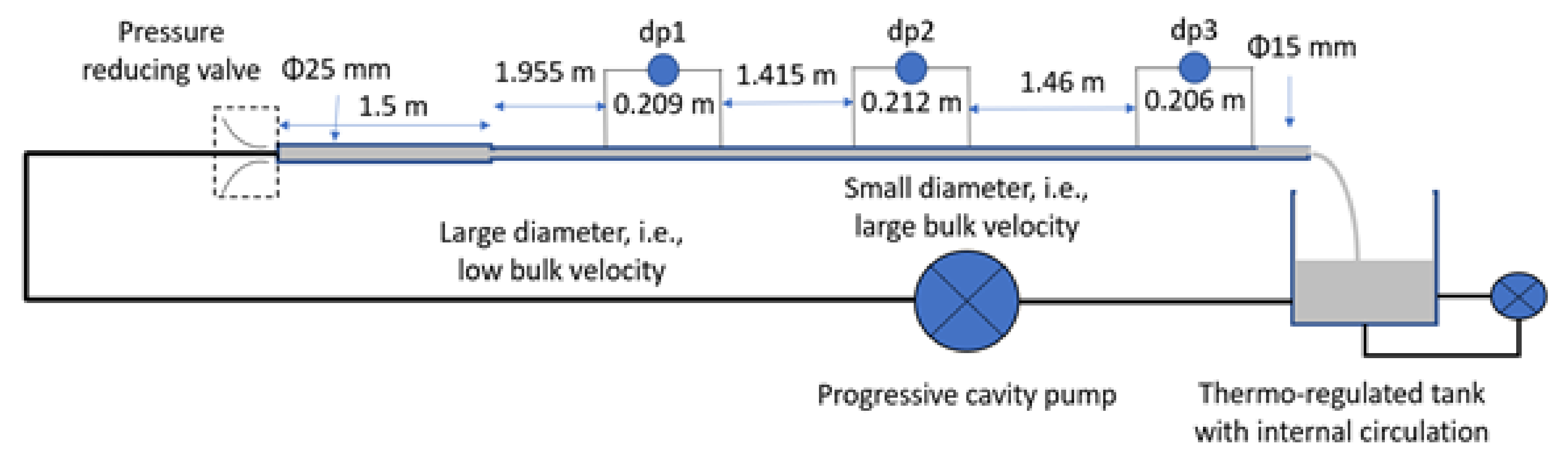
2.2. Laboratory Flow Loop

To test the described method of the present study, experiments have been conducted in a laboratory flow loop. A positive displacement pump circulates fluid stored in a thermo-regulated tank with internal circulation. First, the fluid flows into a pipe with an internal diameter of 25 mm and then into a glass tube with an internal diameter of 15.5 mm. Along the glass tube, there are three differential pressure sensors. The distances between the ports of the differential pressure sensors are 0.209 m, 0.212 m, and 0.206 m, from upstream to downstream, respectively. The first sensor is placed 1.955 m away from the change in diameter from 25 mm to 15.5 mm. The second sensor is positioned 1.415 m apart from the first one and the last sensor is separated from the previous by 1.46 m. A schematic representation can be found in figure 8 of [16], reproduced here as Figure 1. There is also a pressure-reducing valve placed 1.5 m upstream from the change in diameter. The purpose of this valve is to ensure that the fluid is fully sheared before it continues its journey inside the flow loop. In the case of non-thixotropic fluids, one sensor would have been enough, but since three series of measurements were available, we decided to use all of them to increase the amount of data.

All the experiments were conducted at an average controlled temperature of 27.9 °C. The temperature variations during the experiments have not exceeded ±0.6 °C. The first measurements have been made with an aqueous solution of Carbopol 980 having a density of 997 kg/m³ at 25 °C. This is a non-Newtonian fluid showing no signs of thixotropy and is well described by the Herschel-Bulkley model.

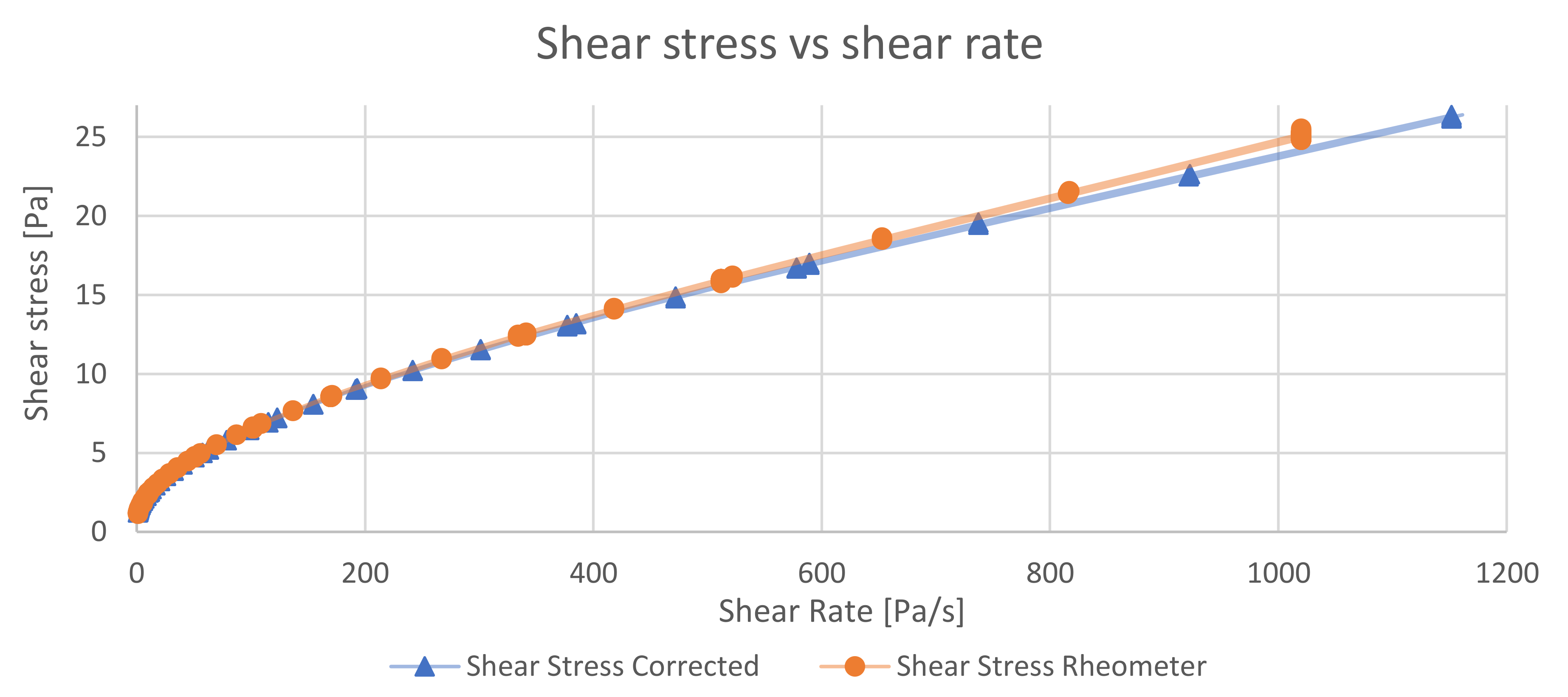
2.3. Rheometer and Data Correction

To confirm the results obtained with the pipe rheometer, a scientific rheometer was used (Physica MCR 301, manufactured by Anton Paar, headquarters: Graz, Austria). In a concentric rheometer configuration, the rotational speed is converted to a shear rate at the wall and the shear stress at the wall is deduced from the measured torque. However, the relationship between rotational speed and the shear rate at the wall is constant only for Newtonian fluids. For non-Newtonian fluids, the relationship is more complex and requires the utilization of all the measurements of shear rate and shear stresses in order to be estimated [17]. Similarly, the ratio of the torque to the shear stress is constant only for a Newtonian fluid. For non-Newtonian ones, corrections for end-effects shall be applied [18].

For this paper, we have applied a correction method based on Tikhonov regularization as described in [19]. Figure 2 shows the rheometer measurements and their corrected values for an aqueous solution of Carbopol 980 (Lubrizol, headquarters: Wickliffe, OH, USA).

After applying the correction on rheometer data and using the method from Mullineux for Herschel-Bulkley parameter identification, the following values for this fluid are found: $n_{Rheo}=0.6389, K_{Rheo}=0.2717 \mathrm{Pa}.{\mathrm{s}}^{\mathrm{n}}, {\tau }_{\gamma , rheo}=1.198 \mathrm{Pa}$.

3. Pipe Rheometer

The objective is to develop an algorithm able to estimate the H-B parameters of a fluid flowing in a pipe using only measurements of pressure loss along the pipe and the flow rate. Vajargah et al. [20,21] developed a similar method to estimate the rheology of drilling fluid during an oil well drilling operation, using only pressure loss measurements scattered along the drill string. In [21] they developed a pipe rheometer to measure the drilling mud characteristics on the rig surface. However, the authors used generic nonlinear optimization techniques to fit the rheological models. Other devices were developed for in-line fluid rheology measurements like a helicoidal pipe rheometer [22] to save space, or on-line dedicated sensors [23]. However, because of the high complexity brought by the geometry or the nature of the sensors, data was interpreted using a machine learning algorithm that needs to be trained and maintained thus raising the complexity of the apparatus and reducing reliability in an operational environment.

3.1. Background

Given the reasons evoked in Section 2.1, it is advisable to use Mullineux’s H-B parameters identification method instead of a regular nonlinear optimization technique. Thus, we need to calculate pairs of $\left(\tau , \dot{\gamma }\right)$ from our measured $\left(Q, \frac{dP}{dL}\right)$, where $Q$ is the volumetric flowrate and $\frac{dP}{dL}$ is the pressure gradient.

In laminar flow, the wall shear stress ${\tau }_w$ is directly proportional to the pressure gradient $\frac{dP}{dL}$:

$${\tau }_w=\frac{R}{2}\frac{dP}{dL},$$

(5)

where $R$ is the inner pipe radius.

To calculate the wall shear rate, we can use the Weissenberg-Rabinowitsch-Mooney (WRM) relation for a pipe developed in [24]. The WRM equation is mainly based on assumptions on the flow instead of the fluid and therefore can be applied to non-Newtonian fluids:

$${\dot{\gamma }}_w=\frac{3}{4}{\dot{\gamma }}_{N,w}+\frac{1}{4}{\dot{\gamma }}_{N,w}\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)},$$

(6)

with ${\dot{\gamma }}_{N,w}=\frac{4Q}{\pi R^3}$ being the wall shear rate in the case of a Newtonian fluid, and called apparent shear rate at the wall.

The main difficulty in calculating ${\dot{\gamma }}_w$ is that we need to estimate the quantity $\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)}$. Most of the time this quantity is evaluated by plotting $\ln \left({\dot{\gamma }}_{N,w}\right)$ as a function of $\ln \left({\tau }_w\right)$, applying a linear regression and using the slope as the derivative. However, this assumption is only true if ${\tau }_{\gamma }=0$ or in other words if we have a Power Law fluid. When a linear fit is not enough, it is generally advised to perform a polynomial fit [25]. However, in practice, a least-square polynomial fit tends to be inaccurate. Indeed, when collecting a lot of measurements, minor imprecisions of sensors or external perturbations produce a cloud of point which creates ambiguity when fitting a polynomial on the measurements. In addition, the polynomial fit is chosen for its ease of use and not because it corresponds to physical reality. In order to get a more accurate regression, we will derive a physics-based formula for $\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)}$:

First, let us express $\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)}$ as a function of the flow-rate Q:

$$\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)}=\frac{d\ln \left(\frac{4v}{R}\right)}{d\ln \left({\tau }_w\right)}=\frac{d\ln \left(\frac{4Q}{\pi R^3}\right)}{d\ln \left({\tau }_w\right)}=\frac{d\left(\ln \left(Q\right)+\ln \left(\frac{4}{\pi R^3}\right)\right)}{d\ln \left({\tau }_w\right)}=\frac{d\ln \left(Q\right)}{d\ln \left(\frac{R}{2}\frac{dP}{dL}\right)},$$

(7)

Using the equation developed by Kelessidis et al. in [12], we have:

$$Q=\frac{\pi n}{K^{1/n}}\frac{{\left({\tau }_w-{\tau }_{\gamma }\right)}^{1+\frac{1}{n}}}{{\left(\frac{{\tau }_w}{R}\right)}^3}\times \left[\frac{{\left({\tau }_w-{\tau }_{\gamma }\right)}^2}{1+3n}+\frac{2{\tau }_{\gamma }\left({\tau }_w-{\tau }_{\gamma }\right)}{1+2n}+\frac{{\tau }_{\gamma }{}^2}{1+n}\right]$$

(8)

Let´s express $\ln Q$ from Equation (8):

$$\begin{array}{cc}\ln Q=\ln \left(\frac{\pi n}{K^{1/n}}\right)\hfill & +\frac{n+1}{n}\ln \left({\tau }_w-{\tau }_{\gamma }\right)-3\ln \left({\tau }_w\right)+3\ln \left(R\right)\hfill \\ \hspace{1em}\hfill & +\ln \left[\left(1+n\right)\left(1+2n\right){\left({\tau }_w-{\tau }_{\gamma }\right)}^2+\left(1+n\right)\left(1+3n\right)2{\tau }_{\gamma }\left({\tau }_w-{\tau }_{\gamma }\right)+\left(1+2n\right)\left(1+3n\right){\tau }_{\gamma }{}^2\right]\hfill \\ \hspace{1em}\hfill & -\ln \left[\left(1+n\right)\left(1+2n\right)\left(1+3n\right)\right].\hfill \end{array}$$

(9)

By regrouping the constants, we obtain:

$$\ln Q=\frac{n+1}{n}\ln \left({\tau }_w-{\tau }_{\gamma }\right)-3\ln \left({\tau }_w\right)+\ln \left(C_2{\tau }_w{}^2+C_1{\tau }_w+C_0\right)+A,$$

(10)

with $A=\ln \left(\frac{\pi n}{K^{1/n}}\right)+3\ln \left(R\right)-\ln \left[\left(1+n\right)\left(1+2n\right)\left(1+3n\right)\right],$ $C_0=\left(6n-4n^2\right){\tau }_{\mathsf{\gamma }}{}^2$, $C_1=2n{\tau }_{\mathsf{\gamma }}\left(1+n\right)$ and $C_2=\left(1+n\right)\left(1+2n\right)$.

Let us now express $\ln Q$ as a function of $\ln \left({\tau }_w\right)$:

$$\ln Q\left[\ln \left({\tau }_w\right)\right]=\frac{n+1}{n}\ln \left(e^{\ln \left({\tau }_w\right)}-{\tau }_{\gamma }\right)-3\ln \left(e^{\ln \left({\tau }_w\right)}\right)+\ln \left(C_2{e}^{2\ln \left({\tau }_w\right)}+C_1{e}^{\ln \left({\tau }_w\right)}+C_0\right)+A,$$

(11)

Finally, we obtain:

$$\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)}=\frac{d\ln \left(Q\right)}{d\ln \left({\tau }_w\right)}=\frac{n+1}{n}\frac{{\tau }_w}{{\tau }_w-{\tau }_{\gamma }}-\frac{C_1{\tau }_w+2C_0}{C_2{\tau }_w^2+C_1{\tau }_w+C_0}-1.$$

(12)

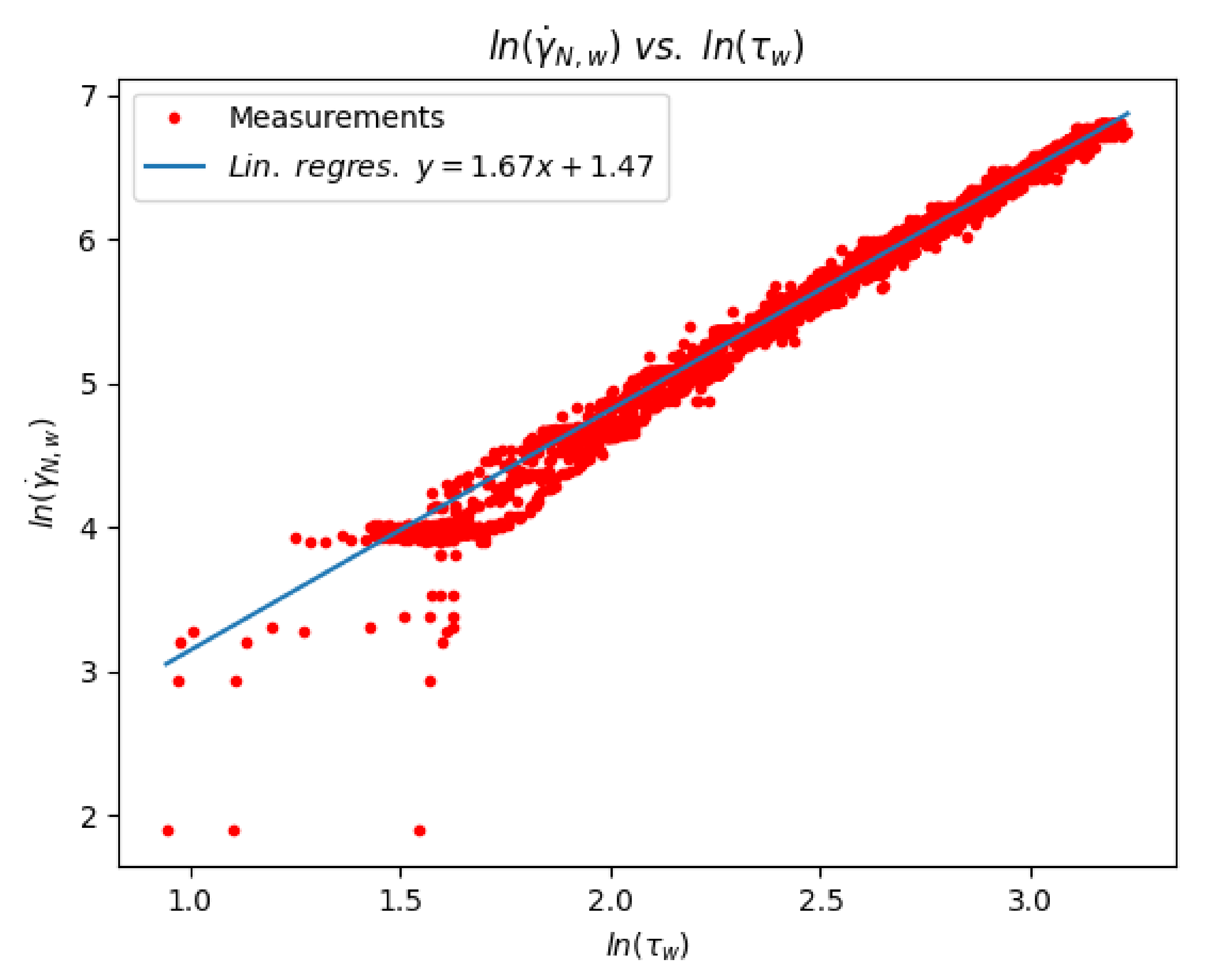
3.2. Experimental Determination of $\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)}$

As stated in Section 3.1, in order to compute accurately the derivative quantity (Equation (12)) it is better to avoid relying on curve fitting, however, a prior estimation of the H-B parameters is required in that case. The solution used here is to perform a nonlinear least square curve fitting with the Levenberg-Marquardt method [26] to fit Equation (8) on the measured pair data $\left(Q, \frac{dP}{dL}\right)$ and using Equation (5) to calculate ${\tau }_w$ from $\frac{dP}{dL}$. The Levenberg-Marquardt algorithm has been developed to solve non-linear least square curve fitting. It is a more robust method than more classical methods such as the Gauss-Newton and gradient descent algorithms, but the method can only find a local minimum and not necessarily the global one. Therefore it is an important point to choose values of the initial parameters that are close to the optimum. Consequently, it is very important to find a physically-based method to estimate those initial parameters.

An estimation of $n$ is obtained by calculating the limit of $\ln Q$ when ${\tau }_w$ goes toward infinity:

$$\underset{\ln {\tau }_w\to \infty }{\lim }\ln Q=\underset{{\tau }_w\to \infty }{\lim }\ln Q=\underset{{\tau }_w\to \infty }{\lim }\frac{1}{n}\ln {\tau }_w=+\infty .$$

(13)

The trend for ${\tau }_w\to \infty$ of $\ln Q$ is a line of slope equal to $\frac{1}{n}$ so we can do a linear regression on the last part of the curve ln(Q) as a function of ln(${\tau }_w)$, read the slope and use it to estimate $n$ (see Figure 3). This behavior is easily explained by the fact that Herschel-Bulkley fluids are power-law fluids with a yield stress, thus, when ${\tau }_w$ gets large, the influence of the yield stress disappears, and the behavior of the fluid can be described with a power law.

An initial estimation of the yield stress, ${\tau }_{\gamma }$, is obtained from the wall shear stress at a low flow rate. In Figure 4a, it is visible that there is a range of $\frac{dP}{dL}\in \left[0;1150\right] Pa.m^{-1}$ where either the fluid flows or it does not dependent on the measurements. This is due to the gelling property of the fluid: when left at rest, the fluid acts like an elastic solid. After a gelling period, there is a stress overshoot while increasing the shear strain. This behavior has been commonly observed on Carbopol fluids at different concentrations [27]. This stress overshoot depends on the chemical composition of the fluid but also the resting time. ${\tau }_{\gamma }$ is always smaller than the stress overshoot, therefore it is between the smallest value of the wall shear stress measured under viscous flow and the highest value corresponding to gel breaking. It is possible to obtain a rough estimation of ${\tau }_{\gamma }$ by taking a weighted average of the shear stress between the first flowing and the last non-flowing ${\tau }_w$ (shown in Figure 4b).

${\tau }_{\gamma }$ is estimated using a weighted average of the results shown in Figure 4b:

$${\tau }_{\gamma }=\frac{1}{m}{\displaystyle \sum }_{i=1}^m\mathbb{P}\left(Q>0|{\tau }_{w,i}-\frac{\epsilon }{2}\le {\tau }_w<{\tau }_{w,i}+\frac{\epsilon }{2}\right){\tau }_{w,i},$$

(14)

where m is the number of bins created for the histogram, $\epsilon$ is the shear stress span corresponding to a bin, and $i$ the index to run through the list of bins. The term $\mathbb{P}\left(Q>0|{\tau }_{w,i}-\frac{\epsilon }{2}\le {\tau }_w<{\tau }_{w,i}+\frac{\epsilon }{2}\right)$ is the probability that there was a fluid movement within the conditions defined by the current bin, in other words when the wall shear stress belongs to a given range of values. In addition, it is required to exclude data points whose wall shear stress is above the last non-flowing wall shear stress because it is known that the yield stress value is below the stress overshoot value. With the above-described method, we estimate an initial guess for the yield stress of ${\tau }_{\gamma }=1.19 \mathrm{Pa}$, which is an acceptable value when compared to the one obtained with the scientific rheometer measurements, i.e., ${\tau }_{\gamma , rheo}=1.20 \mathrm{Pa}$.

By rearranging Equation (8), we obtain an expression of the consistency index, $K$, that depends on $Q, \frac{dP}{dL}, n$ and ${\tau }_{\gamma }$:

$$K={\left[\frac{\pi n}{Q}\frac{{\left({\tau }_w-{\tau }_{\gamma }\right)}^{1+\frac{1}{n}}}{{\left(\frac{{\tau }_w}{R}\right)}^3}\times \left[\frac{{\left({\tau }_w-{\tau }_{\gamma }\right)}^2}{1+3n}+\frac{2{\tau }_{\gamma }\left({\tau }_w-{\tau }_{\gamma }\right)}{1+2n}+\frac{{\tau }_{\gamma }{}^2}{1+n}\right]\right]}^n,$$

(15)

The consistency index is then estimated by randomly sampling the measurements points in the set of pairs $\left(Q, \frac{dP}{dL}\right)$ and applying Equation (15) using the previously estimated values for n and ${\tau }_{\gamma }$ in order to determine $K$. The median value of all the calculations is taken in order to reduce the sensitivity of the estimation to outliers (see Figure 5).

The estimated Herschel-Bulkley parameters are now used as initial values for the Levenberg-Marquart optimization algorithm. The objective is to obtain an estimation for the Herschel-Bulkley parameters that are sufficiently precise to calculate $\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)}$ using Equation (12). The estimated parameters using the Levenberg-Marquart optimization are: ${\tau }_{\gamma , L-M}=1.03 Pa$, $K_{L-M}=0.256 Pa.s^n$, $n_{L-M}=0.649$.

Now, combining Equation (12) with the Weissenberg-Rabinowitsch-Mooney relation, i.e., Equation (6), it is possible to calculate the wall shear rate. Then by applying the calculated pairs $\left({\tau }_w, {\dot{\gamma }}_w \right)$, the method described by Mullineux, (see Section 2.3), the Herschel-Bulkley parameters are obtained based on the flow-loop measurements: ${\tau }_{\gamma , M}=0.909 Pa$, $K_M=0.272 Pa.s^n$, $n_M=0.641$. It is interesting to note that the consistency and flow behavior indices are closer to the ones obtained with the scientific rheometer measurements compared to those obtained with the Levenberg-Marquart optimization, $\frac{K_M-K_{Rheo}}{K_{Rheo}}\approx 0.26\%$, $\frac{K_{L-M}-K_{Rheo}}{K_{Rheo}}\approx -5.85\%$, $\frac{n_M-n_{Rheo}}{n_{Rheo}}\approx 0.30\%$, $\frac{n_{L-M}-n_{Rheo}}{n_{Rheo}}\approx 1.66\%$ while the new estimation of yield stress deviates more than the value obtained with the Levenberg-Marquart optimization, $\frac{{\tau }_{\gamma , M}-{\tau }_{\gamma , rheo}}{{\tau }_{\gamma , rheo}}\approx -24.12\%$,

$\frac{{\tau }_{\gamma , L-M}-{\tau }_{\gamma , rheo}}{{\tau }_{\gamma , rheo}}\approx -14.02\%$.

3.3. Results

Figure 6 presents the measured and calculated pressure losses as a function of the flow rate. The pressure losses curves obtained with the Levenberg-Marquart and Mullineux method are so close that they appear superimposed. Looking at the Herschel-Bulkley parameters produced by each method, only the yield stress varies with a substantial amount (approximatively −24% for the Mullineux method, and −12% for the Levenberg-Marquart optimization method, based on the pressure gradient measurements compared to the value obtained with the scientific rheometer). This result is to be expected, knowing that the measurements at low flow rate are scattered over a large range of pressure loss values. In addition, the low yield stress of this sample makes the determination of ${\tau }_{\gamma }$ even more sensitive to numerical and experimental noise. The resulting curves presented in Figure 6 are still in agreement with the measurements. One can notice that at a low flow rate the curves produced from the Levenberg-Marquart optimization and Mullineux methods are closer to the mean value of the measurements than the one obtained based on the Herschel-Bulkley parameters calibrated with the scientific rheometer measurements.

In Figure 7, the estimation made using Equation (12) shows a hyperbolic shape when the estimations made with a polynomial fit of the measured data show an almost flat curve. It is important to note that the hyperbolic shape is amplified with an increase of the yield stress ${\tau }_{\gamma }$ value of the fluid. Therefore it shows that it is not possible to estimate $\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)}$ using a polynomial fit of $\frac{\ln \left({\dot{\gamma }}_{N,w}\right)}{\ln \left({\tau }_w\right)}$ as it will result in errors while predicting the rheological behavior of the fluid at low shear stress (and therefore at low flow rate). 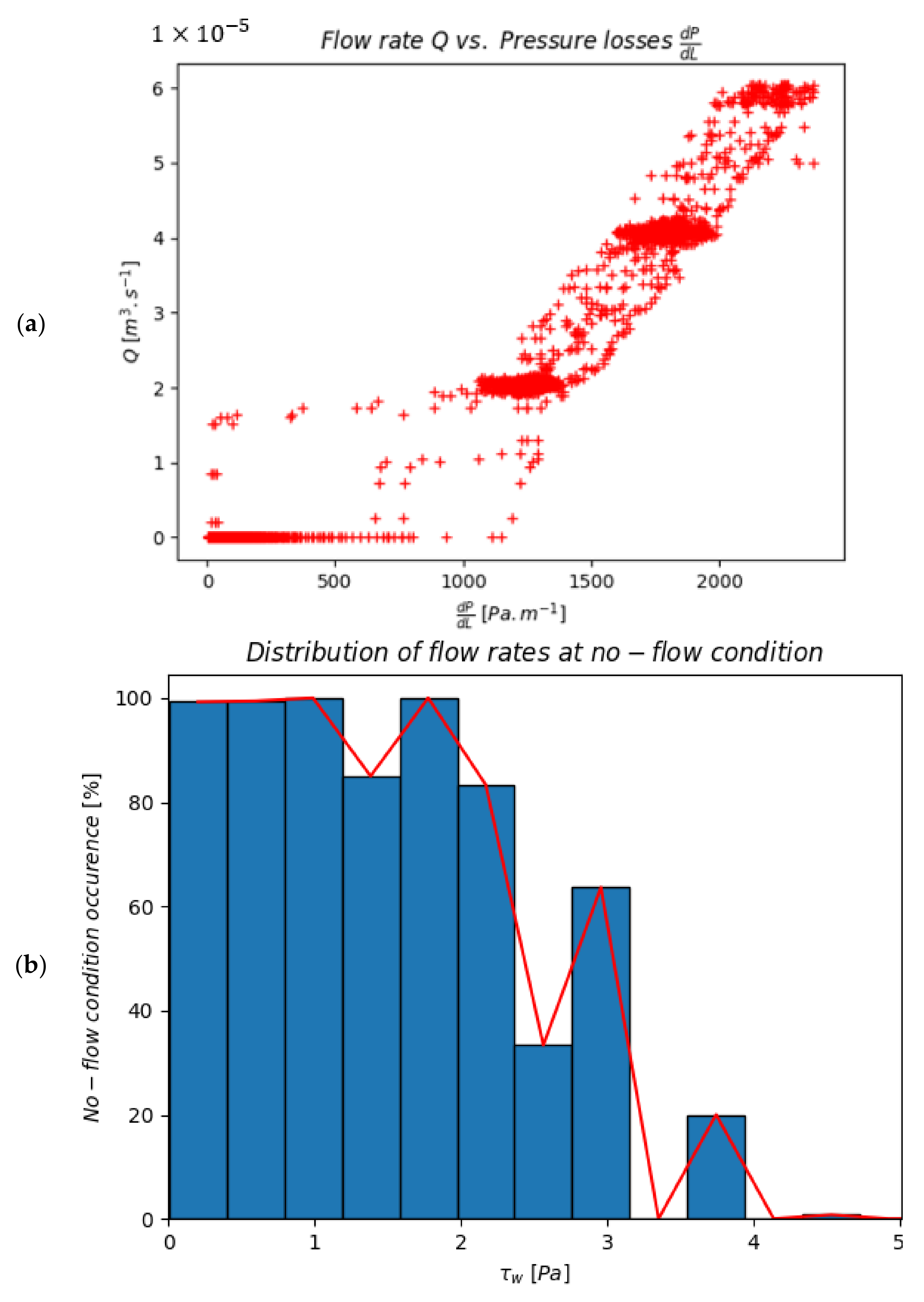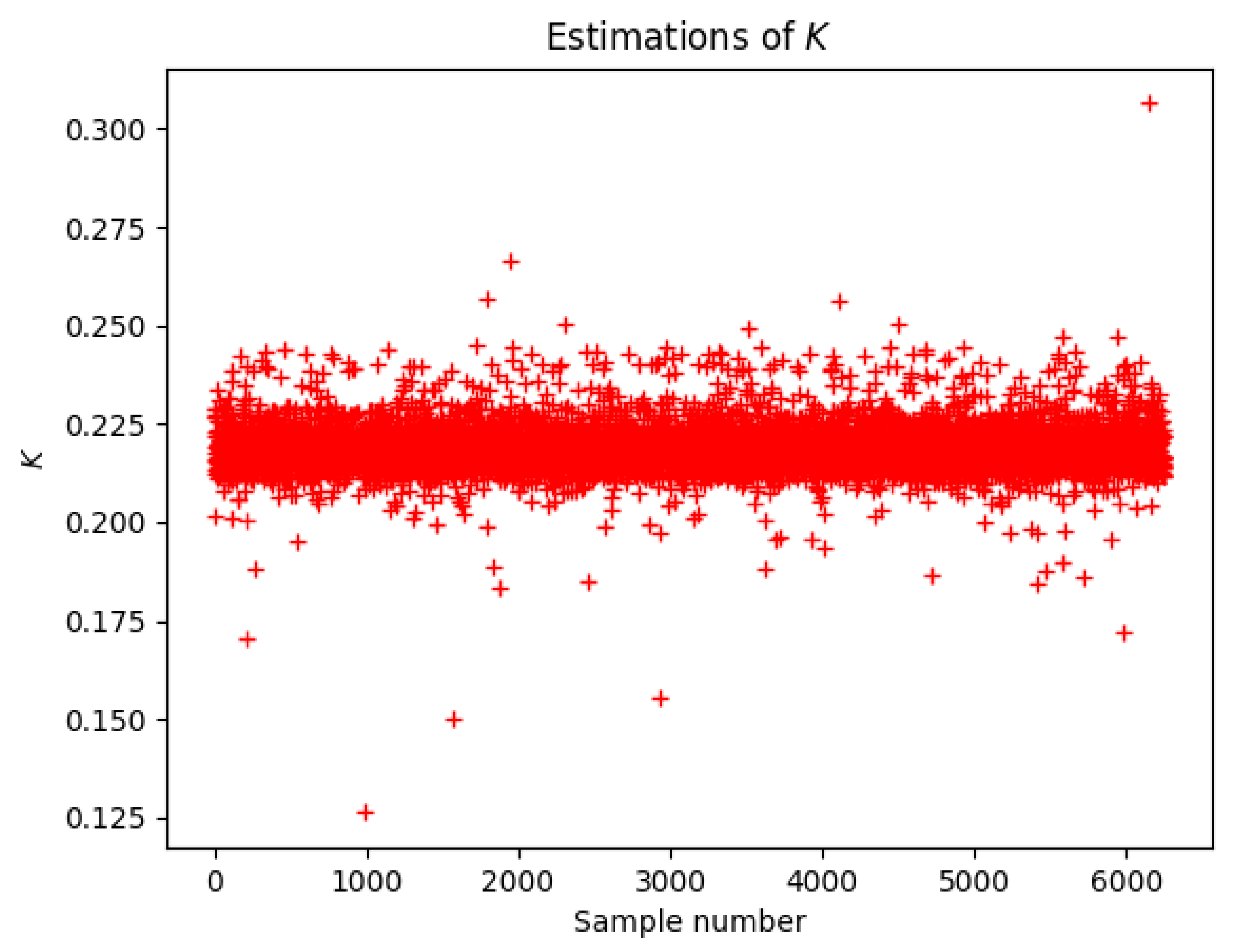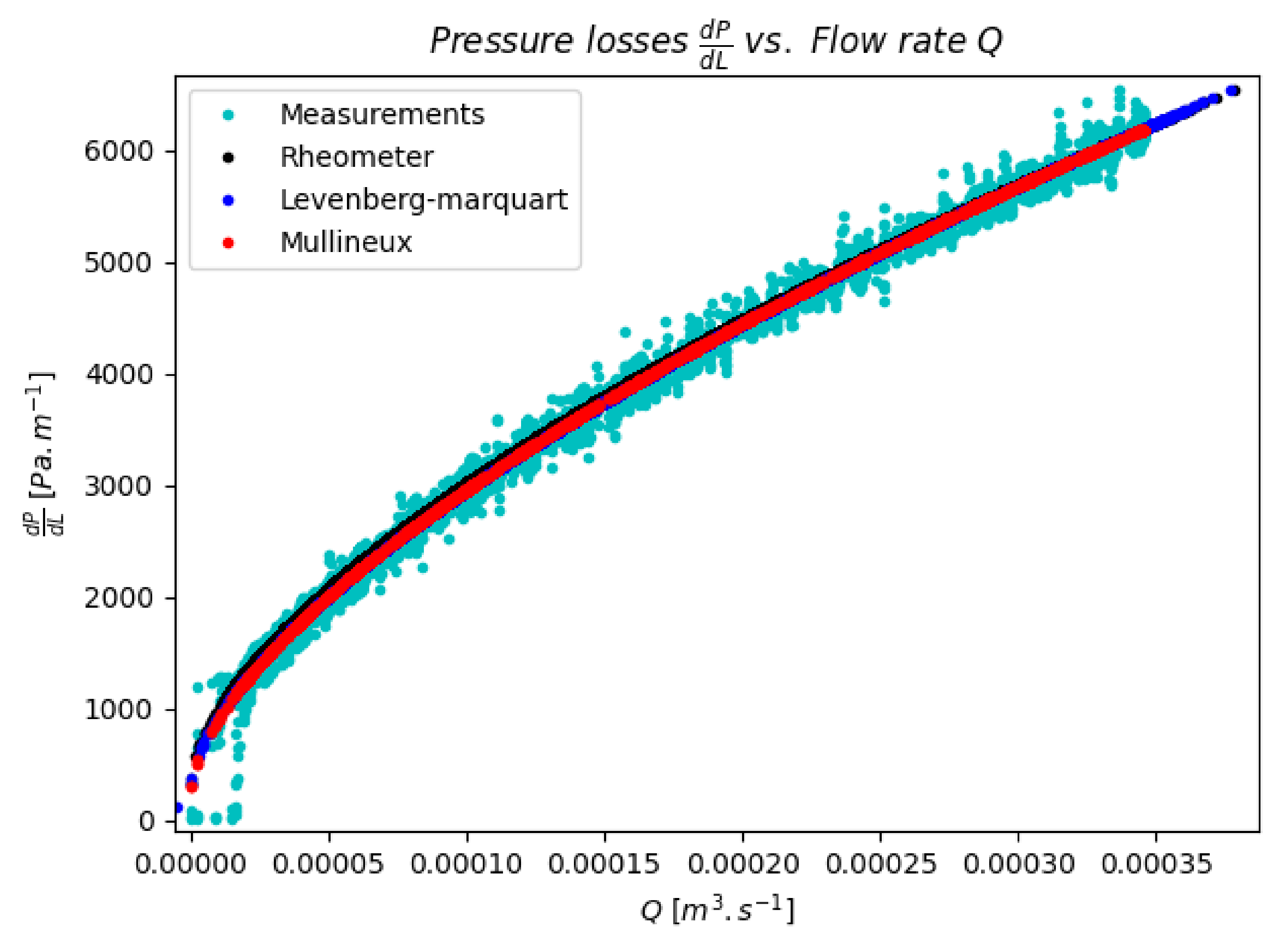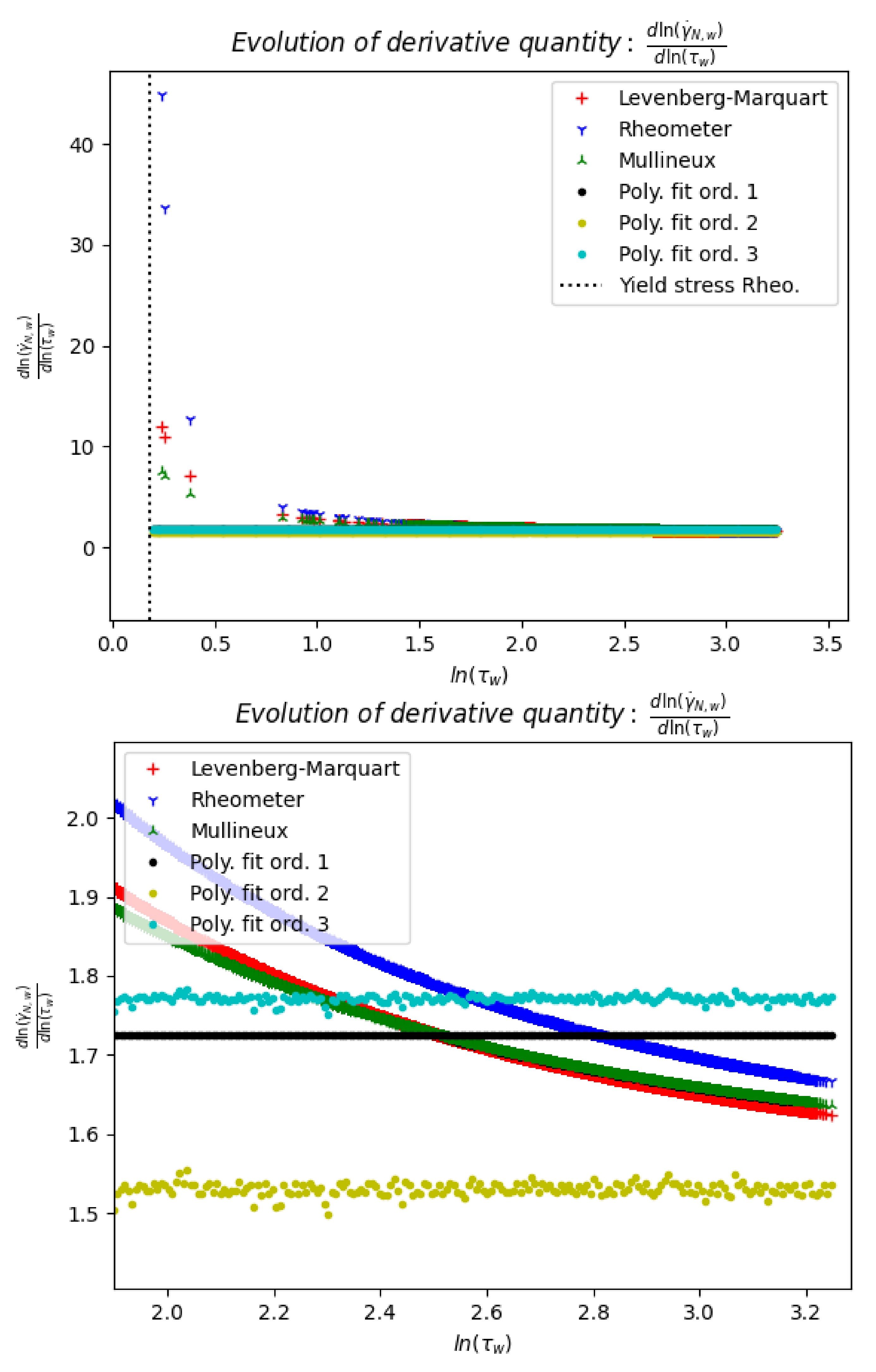Using a proper estimation of $\frac{d\ln \left({\dot{\gamma }}_{N,w}\right)}{d\ln \left({\tau }_w\right)}$ becomes more and more critical as the yield stress of the fluid increases.

4. Discussion

As shown in Figure 6, the parameters obtained with this algorithm are very close to those obtained with the scientific rheometer after correcting the measurements for non-Newtonian effects. However, it is important to mention that such results can only be obtained if the algorithm is applied on points that follow the Herschel-Bulkley behavior: it is required to remove outliers, remove measurements made at transitional and turbulent flow regimes and remove low flow rates data where gelling occurs. The method used here was to analyze the impact of the removal of data from the dataset. When removing the first extremum data, the value of the calculated parameters undergoes high amplitude variation, and the more outliers were removed, the more stable the parameters became. It was decided to cut the dataset where the variation of the dataset has the least influence on the result.

At the moment, the described algorithm is limited to circular pipes, but it can be adapted to other pipe geometry. Another interesting axis of research would be to extend this work to transitional and turbulent flow.

The calculations proposed in Section 3 do not require heavy computations and can be implemented on a single board computer (SBC) or a programmable logic controller (PLC). It is therefore possible to build an automatic non-Newtonian rheometer based on differential pressure measurements in a pipe that can provide continuous estimations of the Herschel-Bulkley parameters with an uncertainty that is of the same order of magnitude as those obtained with a Scientific rheometer.

5. Conclusions

It has been shown that:

• It is possible to estimate the Herschel-Bulkley rheological behavior parameters utilizing differential pressure measurements along a circular pipe made at different volumetric flow rates. The advantage of using pressure gradients to obtain information about the viscous properties of non-Newtonian fluid is that it does not put any specific requirements on the transparency of the fluid nor the possible negative side effects of diffractions when attempting to measure the fluid velocity field when the fluid contains large proportions of solid particles.
• The method described by Mullineux [14] to calibrate the Herschel-Bulkley parameters based on rheometer measurements, i.e., a series of pairs of shear rate and shear stress at the wall could also be transposed to the context of calibrating the parameters of Herschel-Bulkley fluid utilizing a series of pairs of volumetric flow rate and pressure gradients. The method has the advantage of being also precise at a low shear rate which is not the case of the method based on a logarithm development of the difference of the shear and yield stresses [12].
• The obtained precision of the calibrated parameters is of the same order of magnitude as the one obtained with a scientific rheometer.
• The calibration method based on the method from Mullineux is simple enough to be implemented on real-time computer systems such as single-board computers or programmable logic controllers, therefore allowing the possibility to devise real-time equipment that can measure continuously the rheological behavior of non-Newtonian fluids that follow the Herschel-Bulkley rheological behavior.

The possibility to measure continuously the rheological behavior of Herschel-Bulkley fluid in a setup where settling of particles is unlikely and which can be operated completely automatically and with a precision of the same order of magnitude as the one from a scientific rheometer, is important for industries that utilize non-Newtonian fluids with rheological characteristics that are likely to change with time.