1. Introduction
Magnetohydrodynamics (MHD) is the study of electrically conducting fluids moving through magnetic fields. A historical reference in the MHD field is the seminal paper by Hartman [
1], who followed the evidence from an electromagnetic pump (previously devised by himself) that led him to this novel field of investigation. The theory of MHD, as disclosed by Hartman [
1] and further enriched by Hartman and Lazarus [
2], consisted of the classic hydrodynamical equations combined with the general equations of electrodynamics. Later, Swedish physicist Hannes Alfvén received the Nobel Prize for officially initiating the field of MHD by introducing the full set of Navier–Stokes equations combined with the Maxwell’s equations [
3].
The attention in the present study is concentrated on low-Reynolds pulsatile flows, which come with interesting features. The theory predicts that high-frequency oscillatory channel flows acquire a boundary-layer character with peak velocity migrating closer to the wall with the increase of Womersley number [
4]. Early in the previous century, even before the theoretical foundation of oscillatory flows, Richardson and Tyler conducted experiments on alternating air flows observing the relocation of maximum velocity toward the boundary [
5]. Other experimental studies on oscillatory flows in pipes or other geometries cover a range of frequencies spanning (1) the quasi-steady, (2) intermediate, and (3) inertia-dominated regimes [
6,
7,
8]. The pulsatile flows are not only interesting from a scientific perspective but have a direct implication in modern telecommunication industry, which is in need of efficient liquid-cooling microchannels [
9]. While the standard Poiseuille flow is self-similar and bound to the Nusselt number, the low-Reynolds pulsatile flow presents with an enhanced thermal performance, which has been confirmed experimentally [
10]. An interesting possibility appears if an electrically conducting fluid is chosen as the medium, as an external magnetic field permits the adjustment of the flow profiles. Our knowledge though about MHD oscillatory flows derives mainly from analytical or numerical studies, which usually focalize on biological applications, while the experimental validation is still pending. An overview of bio-MHD theory and its applications in pulsatile biological flows (mainly blood) is available in the literature [
11].
A wide range of numerical methods have been employed for the solution of the full MHD problem [
12]. On the other hand, the search for analytic solutions is traditionally an important topic because analytic solutions represent the ground truth, thus enabling an accurate view of the underlying physics with minimum computational cost. Moreover, they are useful in the evaluation of numerical schemes and solvers. Analytic solutions can be hard to obtain, which is why they are scarce in the literature. In the field of oscillatory MHD flows, the analytic studies in the literature mainly refer to low-Reynolds flow regimes governed by Stokes equations. Ganesh et al. [
13] presented an analytical solution of oscillating MHD Stokes flow under an external transverse magnetic field considering porous plates with steady suction. Malathy et al. [
14] studied the pulsatile MHD flow in permeable beds by distinguishing the steady and oscillatory components of the solution. Kahshan et al. [
15] accounted for the slip boundary condition and seepage velocity through the walls to investigate steady-state MHD flow in permeable channels with application to hemodialyzers. The case of dusty fluid with an angular velocity was studied by Delhi Babu et al. [
16] to examine potential MHD effects considering periodic absorption through the walls.
The present study provides an analytic solution of velocity and pressure fields for the oscillatory MHD creeping flow considering periodic absorption both temporally and spatially, generalizing existing analytic solutions in the literature. The derivation is based on the mathematical approach also followed by Ganesh et al. [
13] and Haroon et al. [
17]. The analytic solution provided by the latter on steady (non-MHD) Stokes flow with periodic reabsorption proves to be a limit of the analytic solution introduced here. The flow behavior is visualized and analyzed under the effect of various parameters such as Womersley and Hartmann number, and the absorption coefficient.
3. Results and Discussion
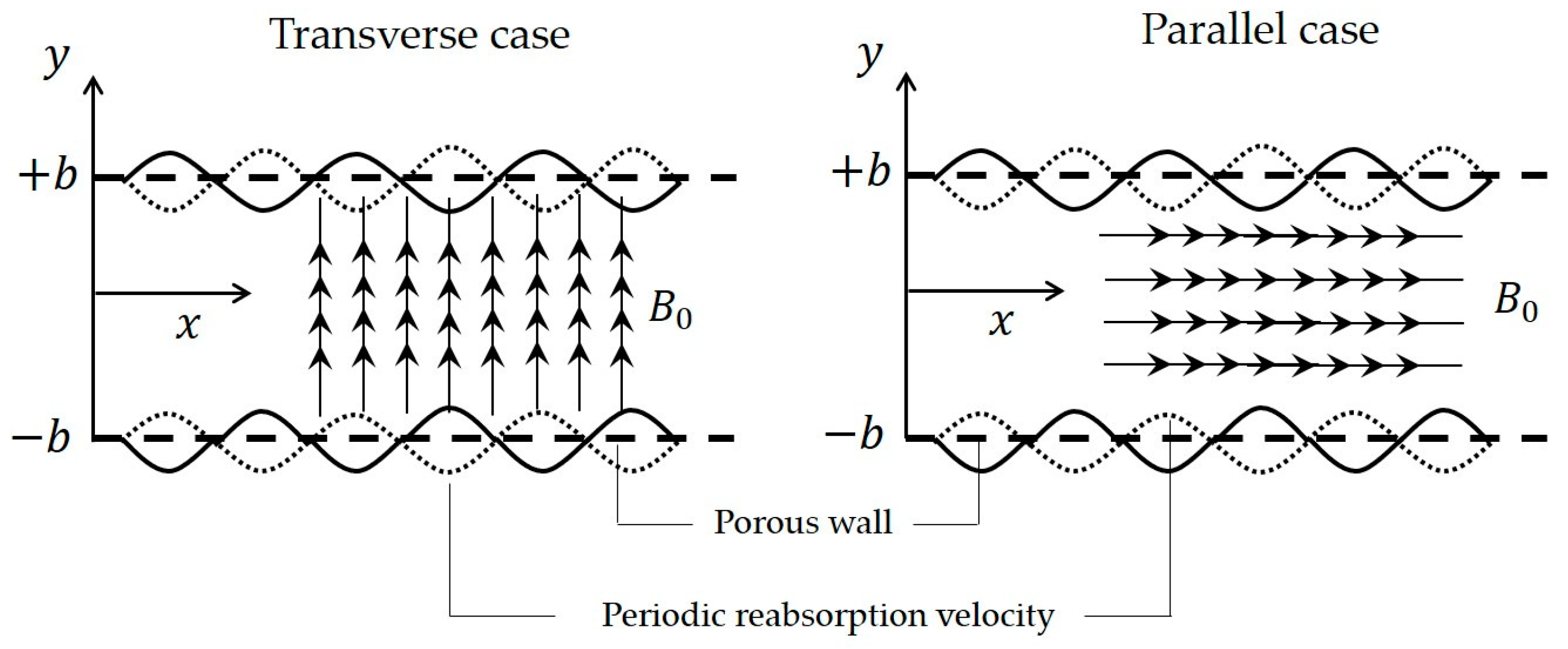
The flow conditions are studied under the effect of parameters: , , and . The absorption coefficient relates to the spatial reabsorption through the porous walls, Womersley number controls the pulsatile flow frequency, and the magnetic parameter M tunes the intensity of the magnetic field.
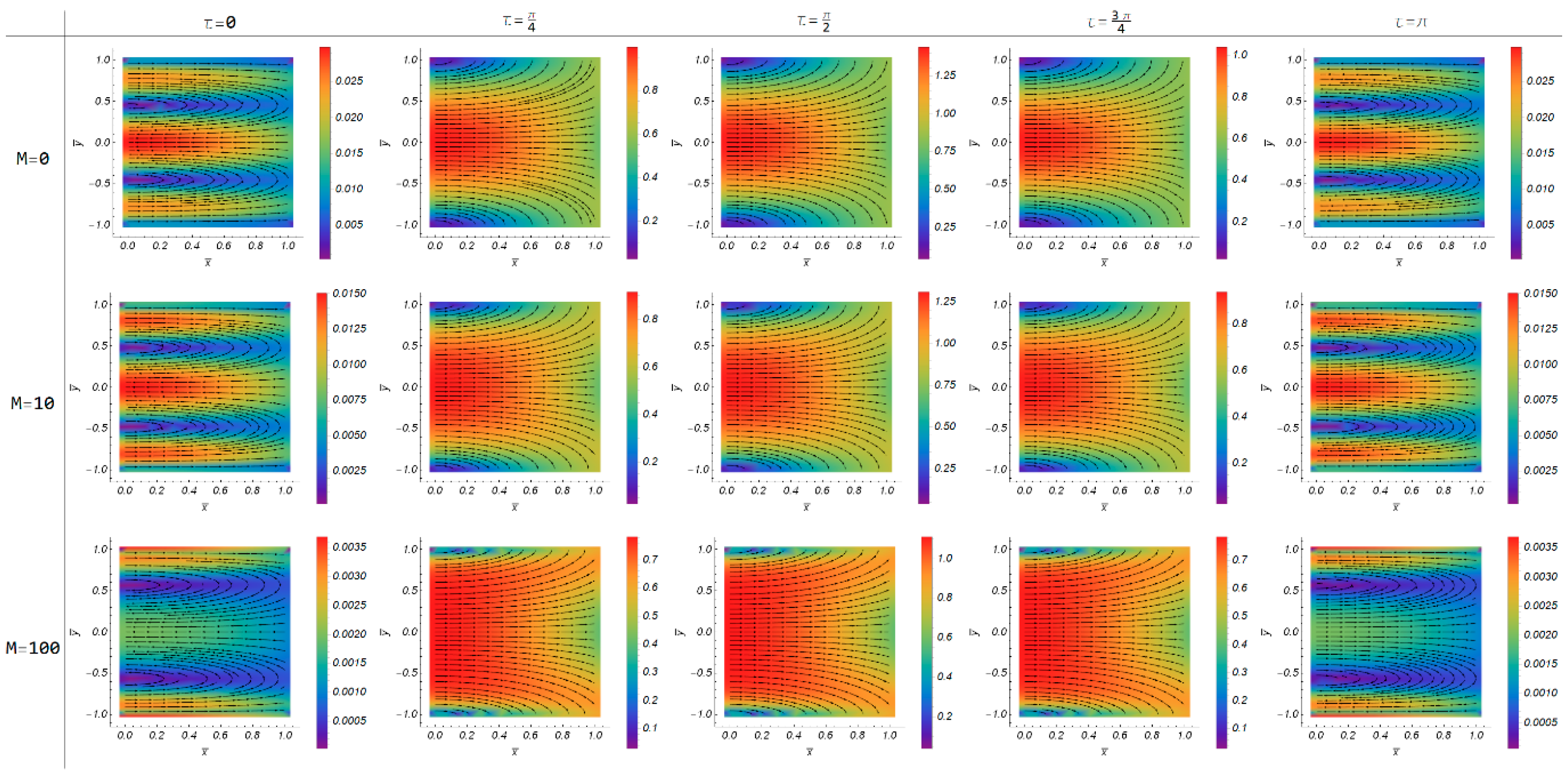
Figure 2 and
Figure 3 display the streamlines on top of velocity magnitude contours for the transverse and the parallel case, in the presence of a magnetic field with increasing intensity,
. The oscillatory flow is a result of the spatiotemporally periodic reabsorption and its interaction with the magnetic field. For the representation of the flow in
Figure 2 and
Figure 3, we used the imaginary part of the complex solution, Equations (2) and (3), as mandated by the boundary conditions in the real plane, Equation (4). In the transverse case (
Figure 2), the flow is decelerated with the increase of the magnetic field intensity. The deceleration is caused by the Lorentz Force, which removes momentum in the x-direction of the flow when the magnetic field acts normal to it. Conversely, when the magnetic field acts in parallel (
Figure 3), the maximum velocity of the fluid does not alter; rather, a restructuring of the flow is mostly observed, especially for
. In both cases, the central jet seems to be flattening, even splitting in multiple jets with the increase of magnetic field intensity. Last but not least, we note that the stability of the solution for different values of the parameters is not addressed in this study. However, we direct the interested reader to the studies by Von Kerczek et al. [
18] (on oscillating flow in a non-porous channel), and by Potter and Kutchey [
19] (on Hartmann–Poiseuille flow), which prove that flow stabilizes with the increase of Womersley or Hartmann numbers.
To get a deeper insight of the flow behavior, the amplitude
and phase angle
indexes are plotted for various combinations of the parameters in the following ranges:
, both for the transverse,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9, and the parallel case,
Figure 10,
Figure 11,
Figure 12,
Figure 13,
Figure 14 and
Figure 15. The indexes are calculated as follows: Starting from the solution of the
velocity component, as shown in Equation (22), we utilize the part of the expression that is a function of
and write it in the form of a typical complex number,
Substituting the complex number, Equation (40), back in the solution, Equation (22), the resulting expression is,
Utilizing the imaginary part of Equation (41),
is written in terms of
and
,
while the mean values of velocity amplitude and phase angle are given by
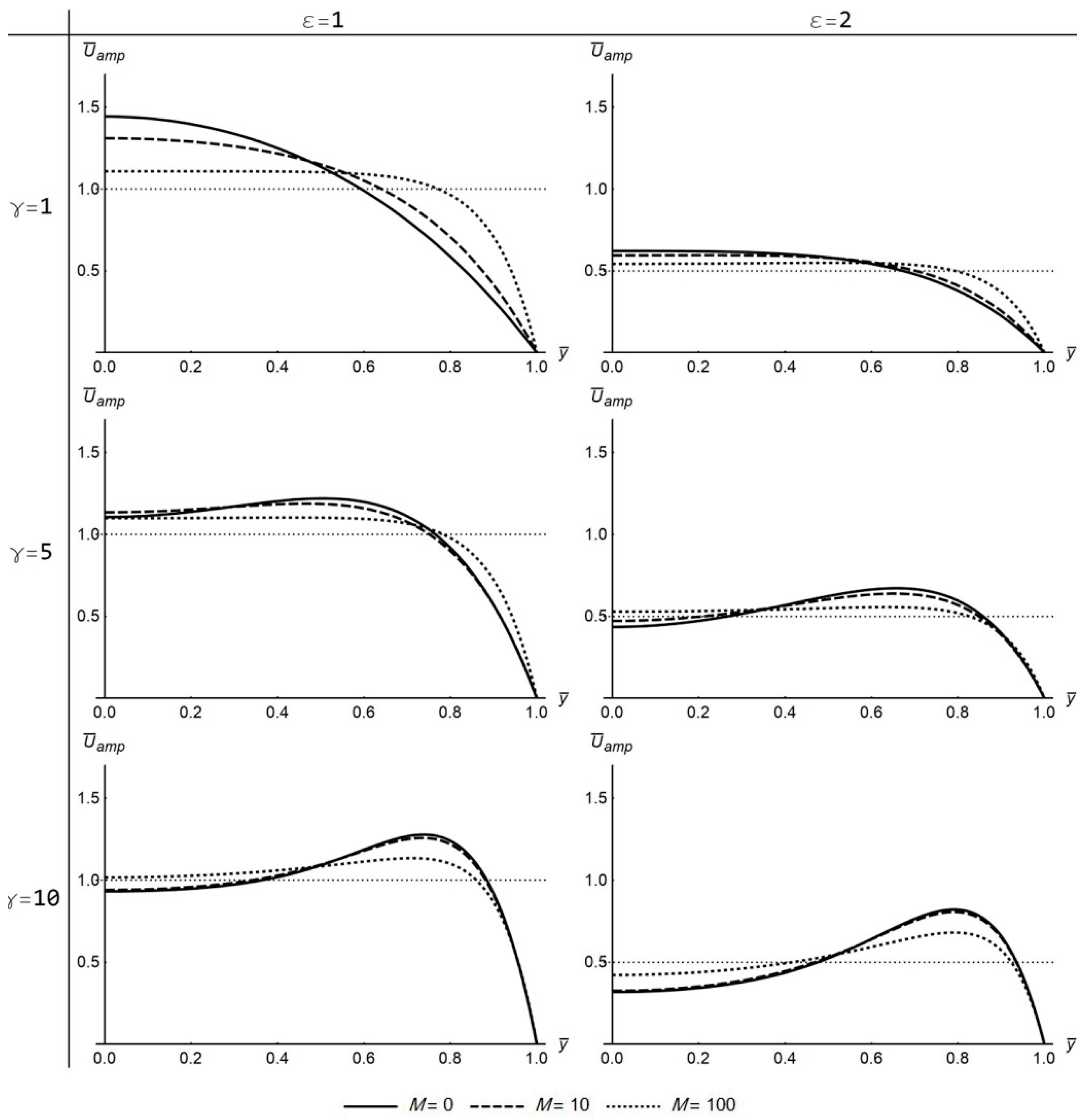
The next three paragraphs discuss the effect of the parameters ε and γ, without accounting for the magnetic field, thus considering
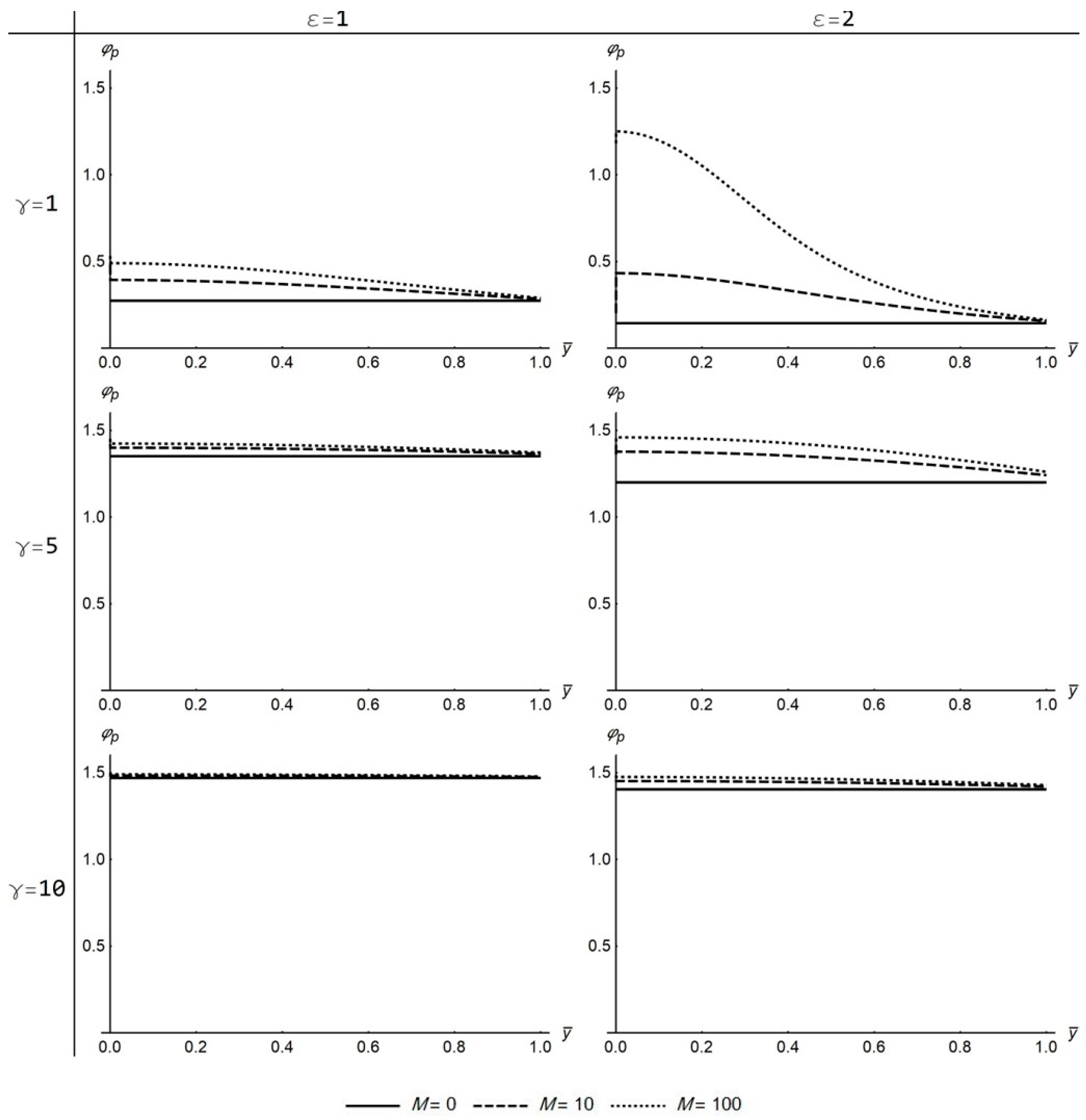
. For low values of Womersley number
, a quasi-steady
emerges with its maximum value converging to
, and the phase angle converging to
,
. The results are in agreement with the steady case without magnetic field published by Haroon et al. [
17]. For low values both of parameter
and ε, the maximum value converges to
(
). The amplitudes and phase angles of the
and
are derived in a similar way.
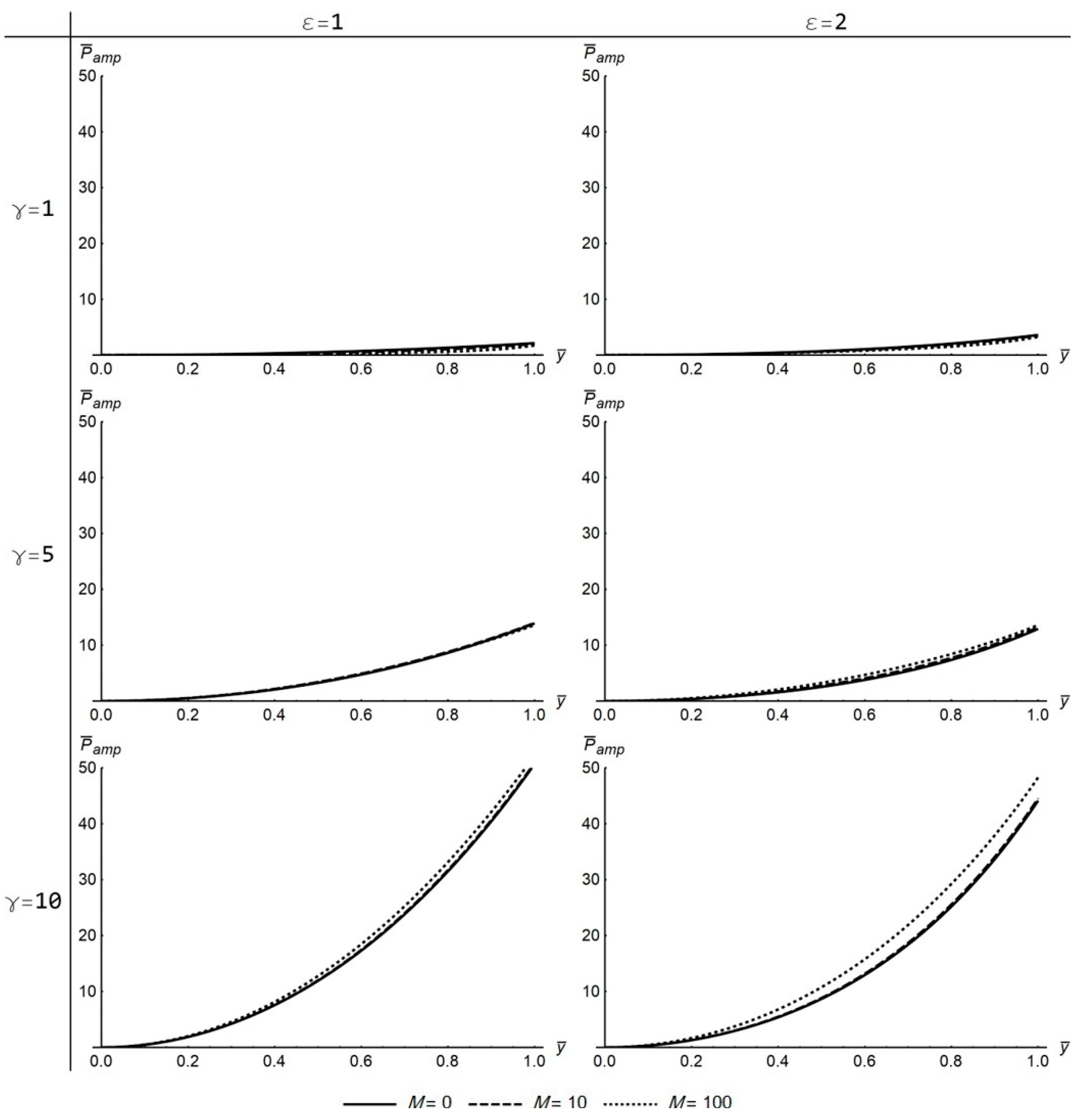
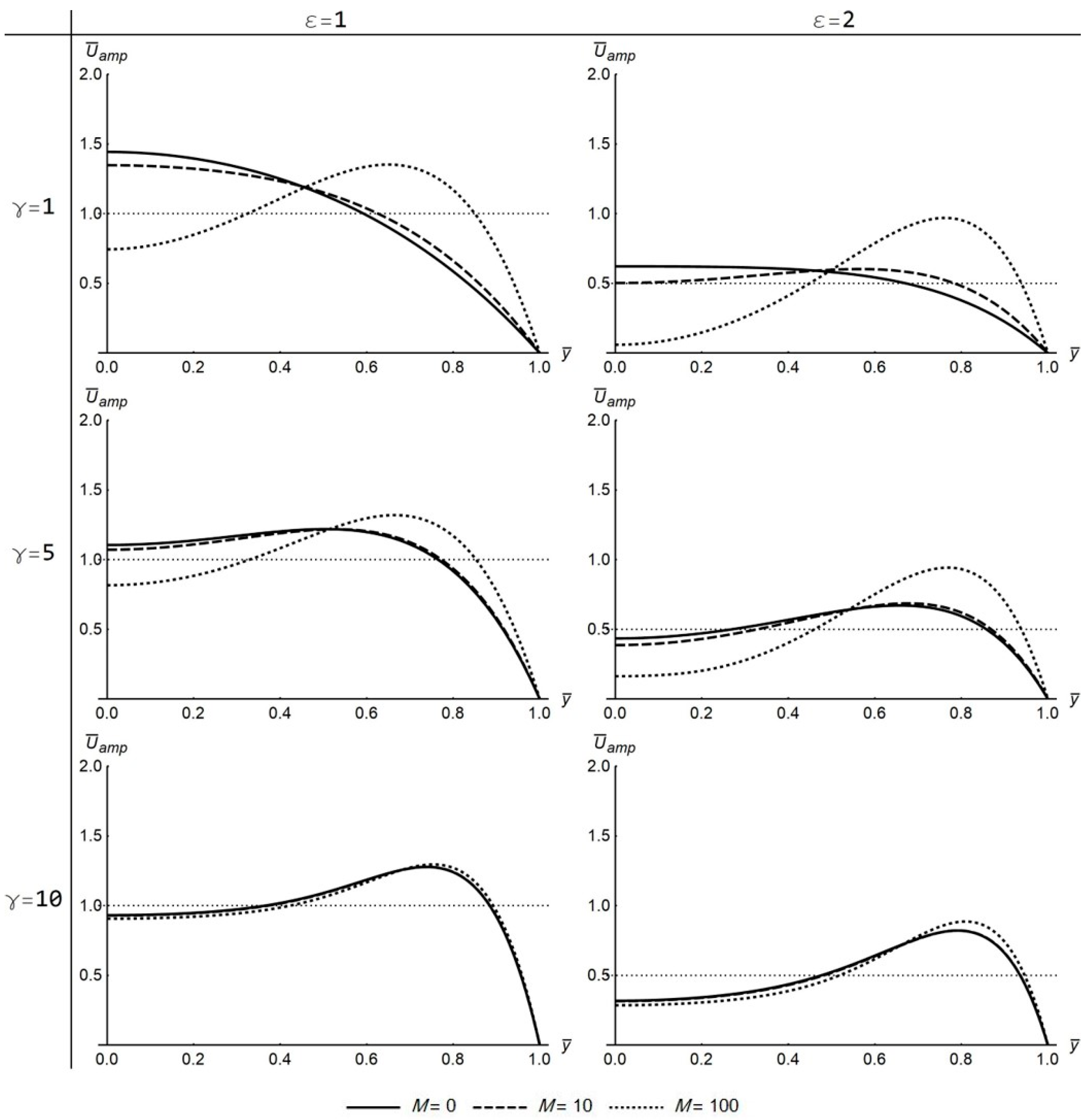
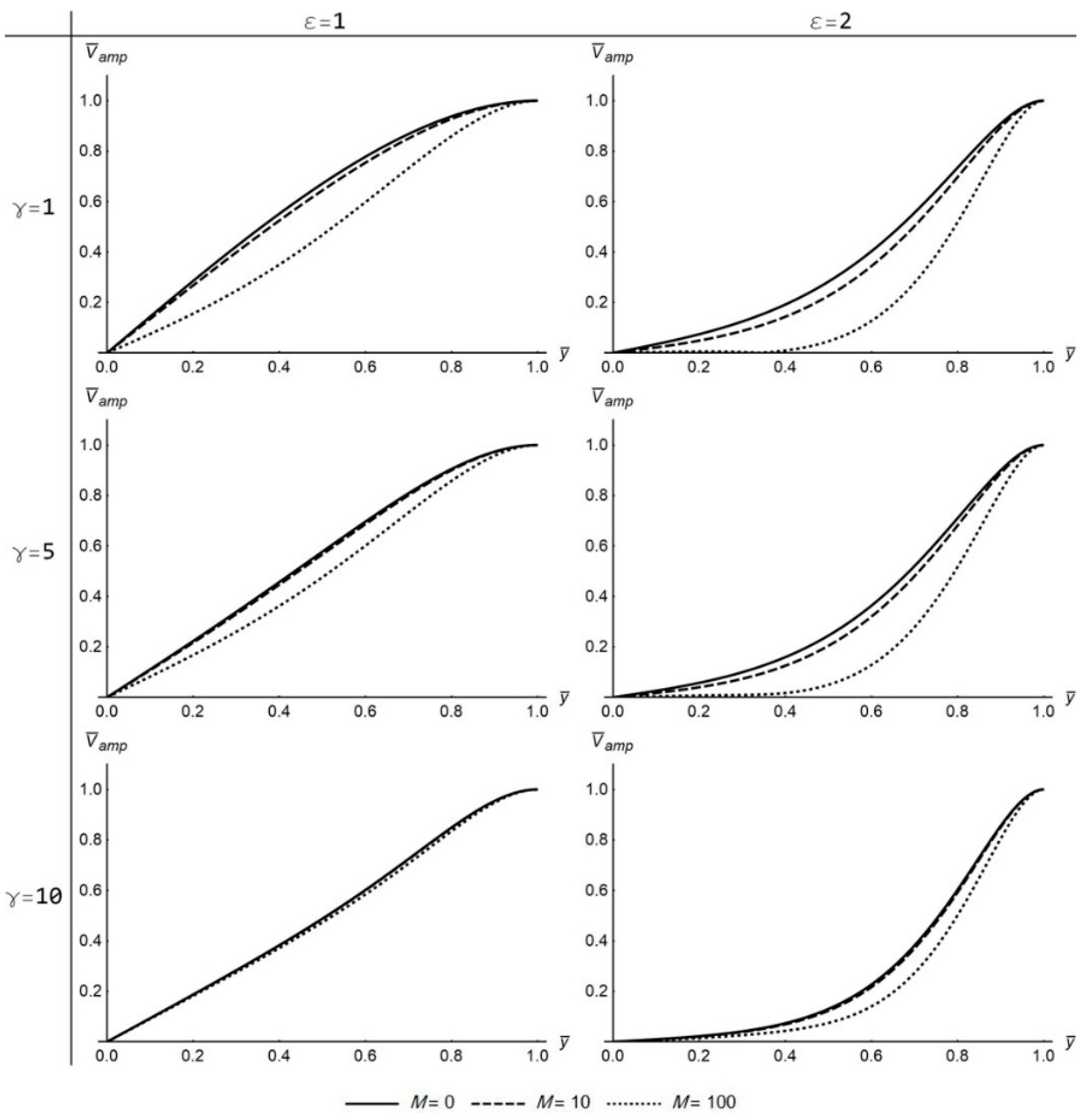
For high values of Womersley number (
),
is endowed by all the characteristics of oscillatory flow in a straight tube without porous walls [
20]. Specifically,
presents with a flattened inviscid-flow-like profile at the center of the channel converging to the value,
and to the value,
for
. The maximum
value is attained near the walls where a boundary layer forms, as presented by [
20], while
approaches the value
at the wall for
(
Figure 5 and
Figure 11).
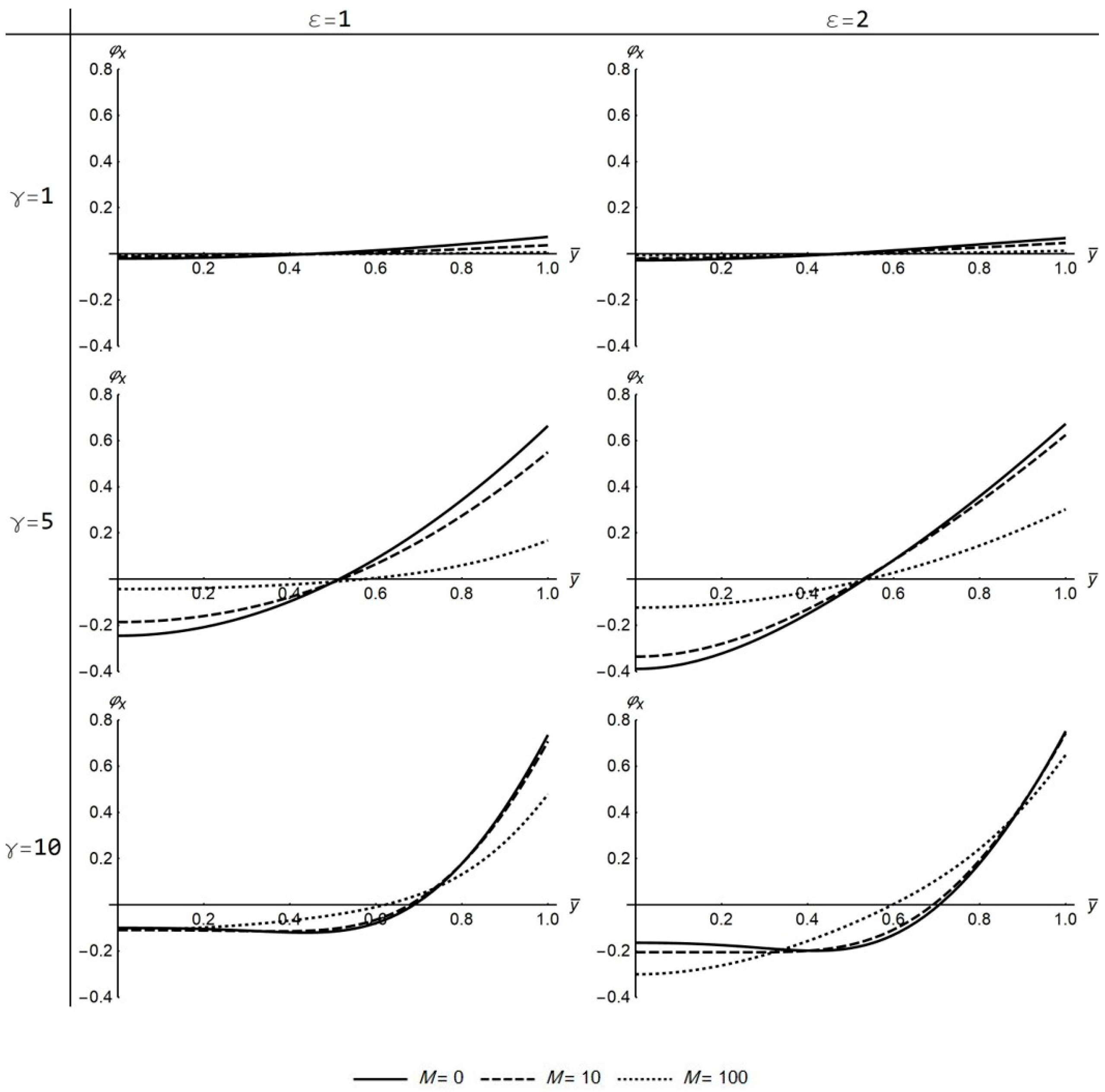
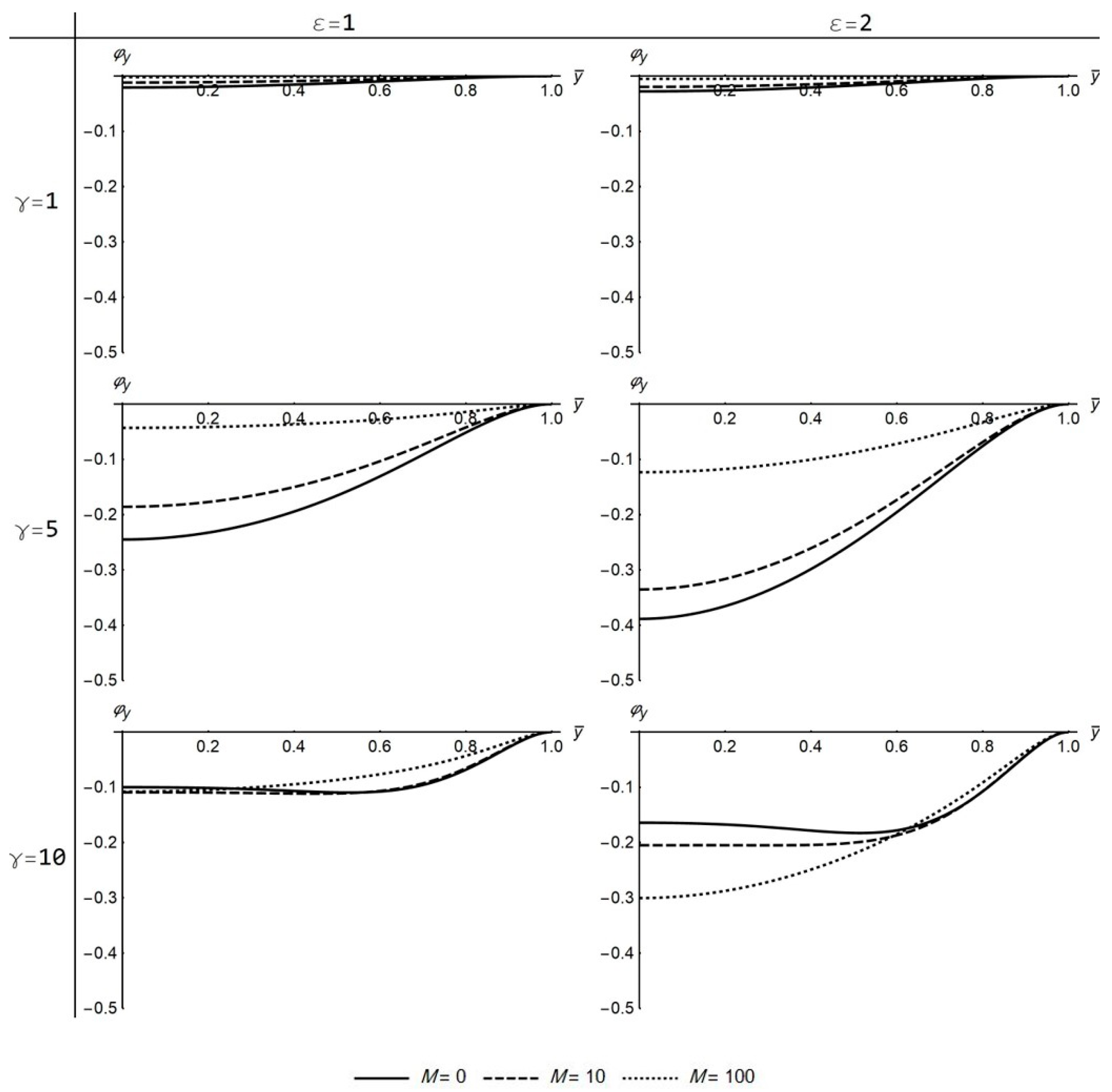
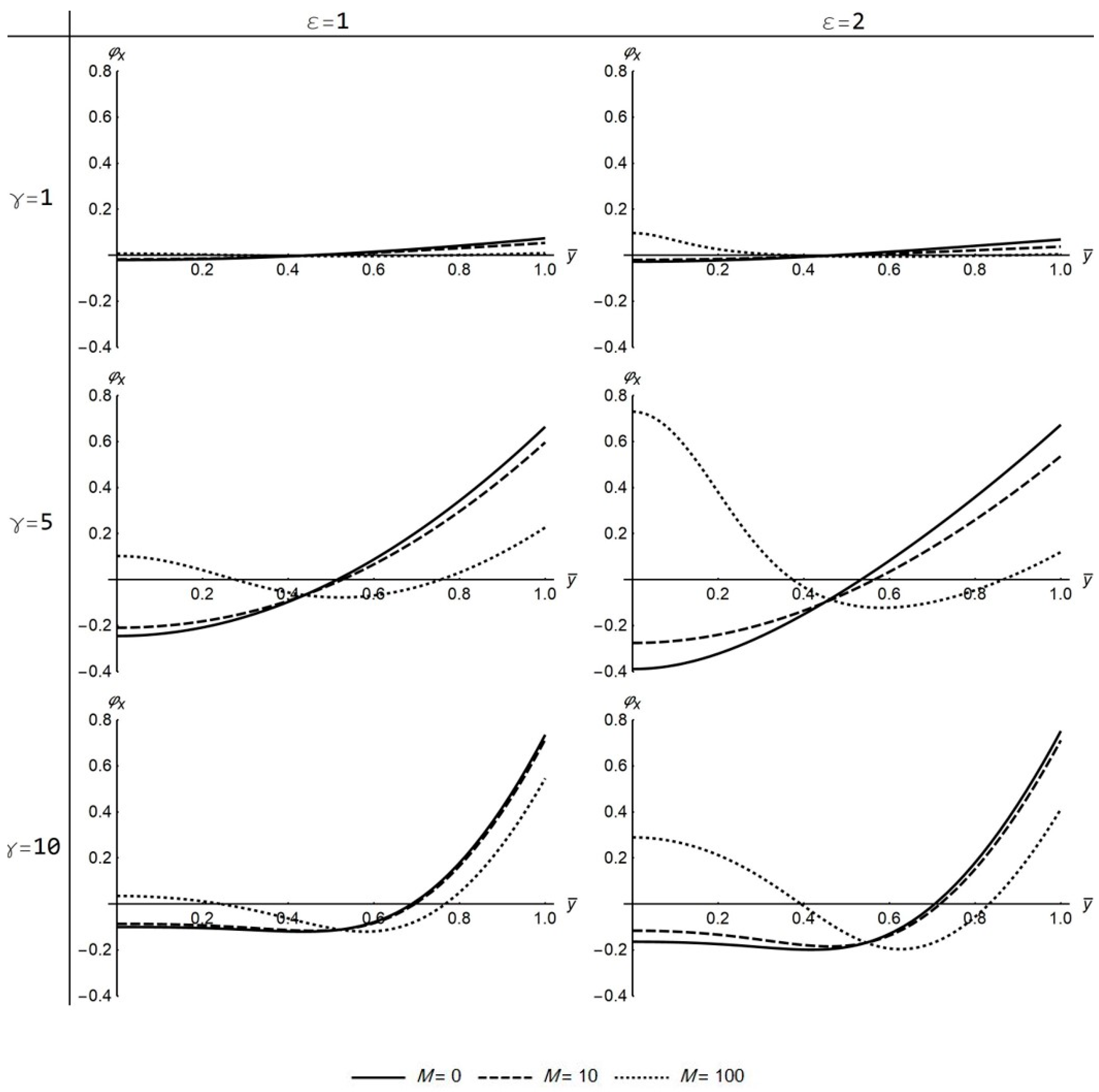
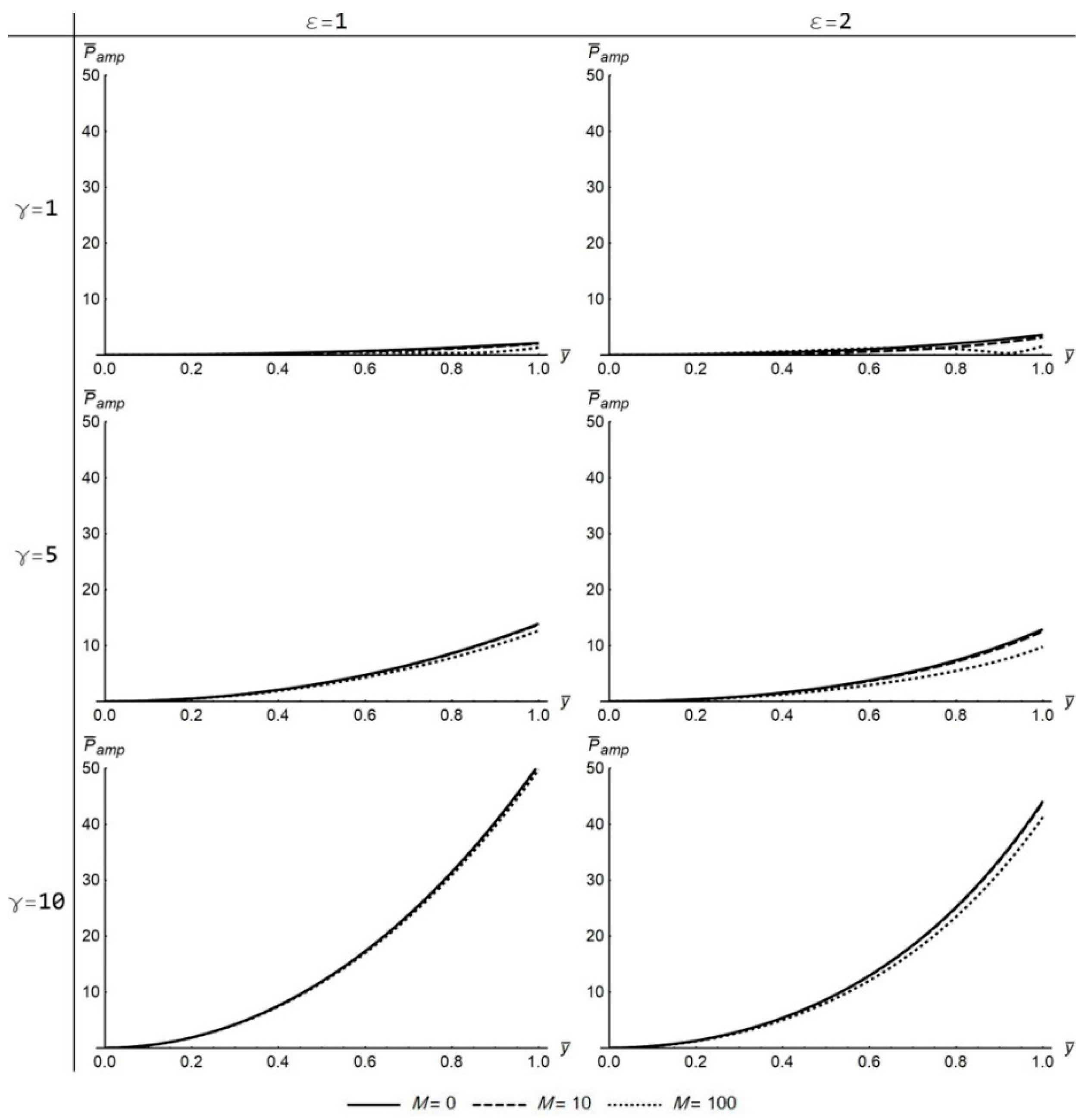
The
increases monotonically from the center toward the wall of the channel (
Figure 6 and
Figure 12), and the same applies to
(
Figure 8 and
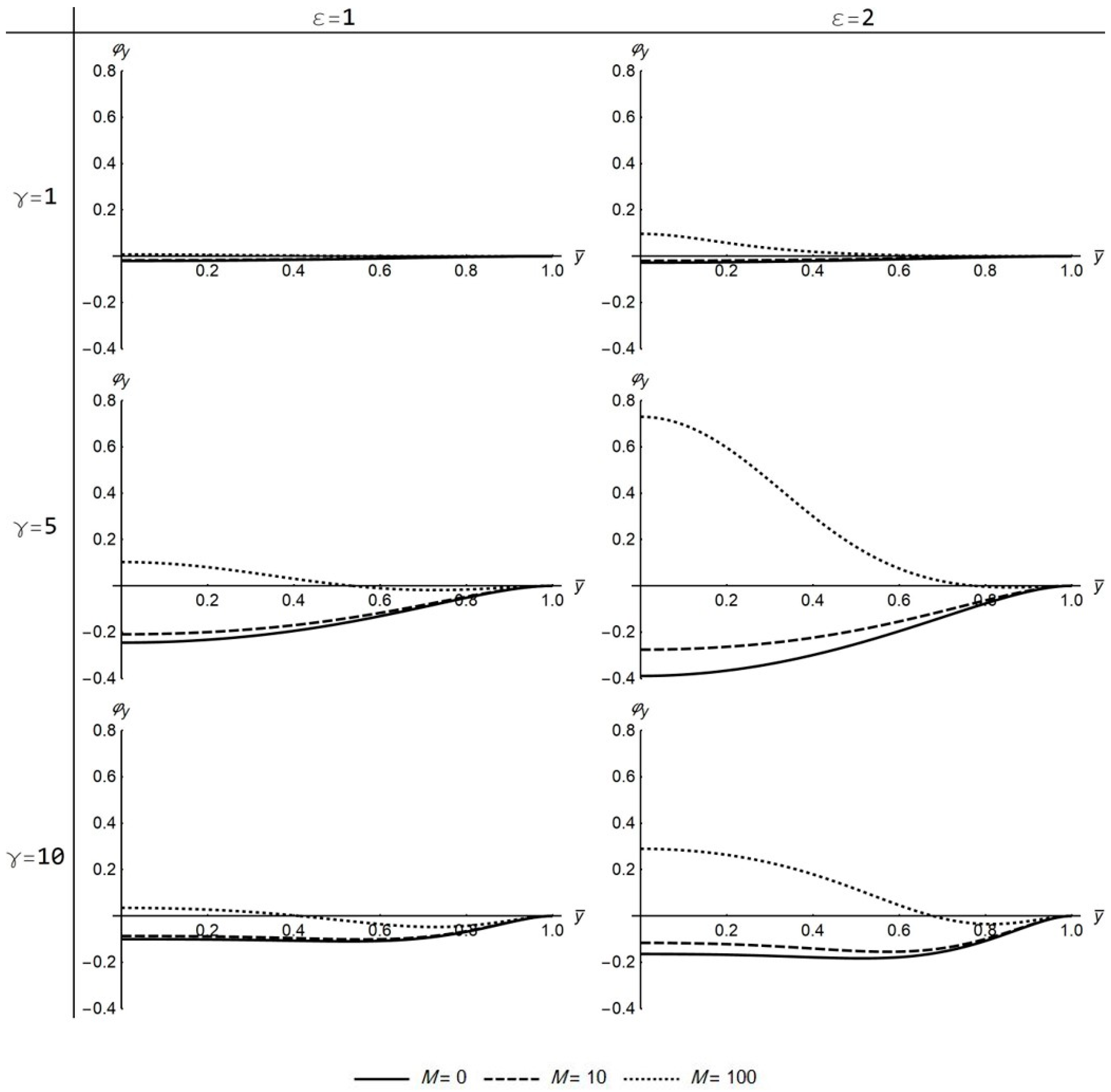
Figure 14). The
takes negative values both for low and high
γ values but increases as an absolute value with the increase of
ε (
Figure 7 and
Figure 13). The
increases with the increase of
γ (
Figure 8 and
Figure 14), while
is small for low
γ values. For high
γ values,
approaches the value
(
Figure 9 and
Figure 15).
The direction and magnitude of magnetic field has a traceable effect on the amplitude and the phase angle of the flow variables. Concerning the transverse case, the
profile is further flattening around the center of the channel with the increase of magnetic field intensity, irrespective of
ε and
γ (
Figure 4). However, near the wall, the intensification of magnetic field leads to an increase of
for low
γ values but to a slight decrease for high
γ values. On the other hand, for high
ε values, the spread between
profiles for increasing
M values is reduced, suggesting that the effect of the magnetic field is alleviated with the increase of absorption coefficient
ε. On the other hand, the
profiles do not alter drastically under the presence of stronger magnetic fields (
Figure 6). A noticeable difference between
and
profiles with increasing M values is that
slightly decreases for low
γ values but slightly increases for high
γ values.
The parallel magnetic field case distinguishes from the transverse at several points, but still some effects are shared between them. Here, the increase of magnetic field intensity reduces
near the center and reinforces it near the wall, which is noticeable especially for low
γ values (
Figure 10). For high
γ values, the magnetic field does not have a significant effect on
even at high intensity, which is a similarity between the parallel (
Figure 10) and the transverse case (
Figure 4). The biggest impact of the parallel magnetic field is concentrated on
that reduces with the increase of magnetic field intensity (
Figure 12). For high ε values, the decrease of
is even more striking when increasing the intensity of the magnetic field. In contrast to the transverse case, the
also reduces under stronger parallel magnetic fields, but the decrease is small, even at the highest magnetic intensity (
Figure 14). In general, the amplitude of the flow variables for high
γ values is not overly sensitive to the magnetic field, even at high intensities, independent of its direction. Seemingly, the high frequency oscillation neutralizes the effects of the magnetic field on the flow.