Consider the flow of an incompressible viscous liquid in a physical two-dimensional space over a flat bottom and with a free surface. We assume additionally that the fluid is homogeneous (i.e., density
is constant) and that the gravity acceleration
g is constant. For the sake of simplicity, in this study, we neglect all other forces (such as the Coriolis force and friction). Hence, we deal with pure viscous gravity waves. We introduce a Cartesian coordinate system
. The horizontal line
coincides with the still water level
, and the axis
points vertically upwards. The fluid layer is bounded below by the horizontal solid bottom
and above by the free surface
. The sketch of the fluid domain is shown in
Figure 1.
In order to make the equations dimensionless, we choose a characteristic horizontal length
ℓ (characteristic wavelength of the surface wave), vertical height of the free surface
A (departure from the mean position of the free boundary), and mean depth
d. All this enables us to define a characteristic velocity
. Then, one may define the dimensionless independent variables:
One could assume the fields to be small around the hydrostatic flow (which is lifted by the change in field from
to
p), so around
. However, such an assumption would be too particular for our nonlinearity assumption, which reads
. Since the linear case
must be satisfied also, we are justified in making this assumption. Then, we would be led to a linear system identical (up to changes of variables) to System (7) of [
5]. The study of this linear system is rather arduous and without interest to reproduce here. In the end, even though linearity is not the regime assumed here, it must be included in our study as a special case (if
). It suggests then to assume:
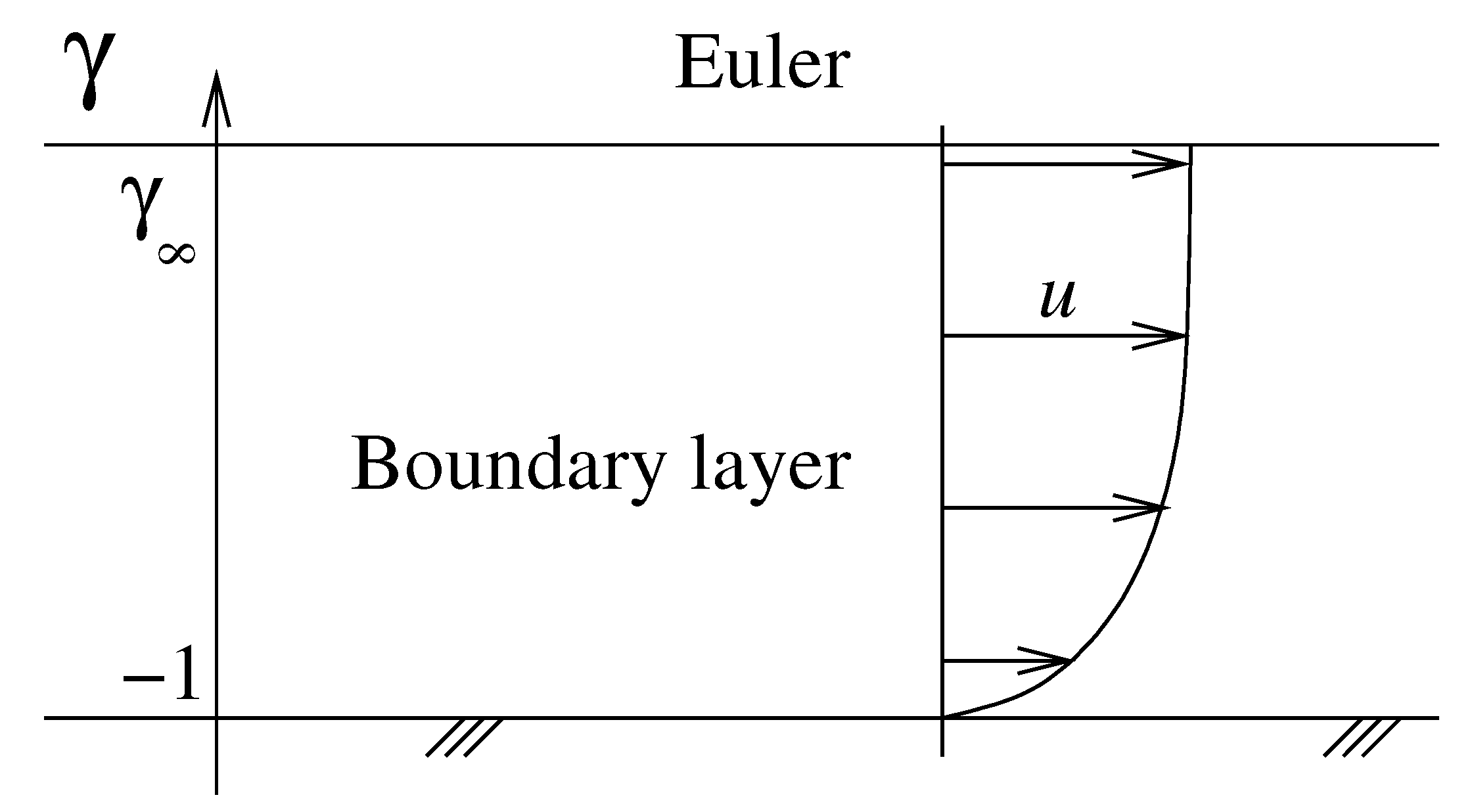
Below, we solve the problem in the bulk part where Euler’s equations are justified to apply (
Section 2.1) and, then, we try to solve the velocity in the boundary layer (
Section 2.2). In this last section, we are led to Prandtl’s equation that prohibits any further advance to the best of our knowledge. The sketch of the boundary layer fluid domain is depicted in
Figure 2.
2.1. Resolution in the Upper Part (Euler)
In the upper part,
and
are small. Therefore, one may drop the Laplacian and keep the following from (
1):
Here and below, for
or
v, we denote
. First, one may notice that the viscosity terms are no more present inside this part of the domain. It is argued in [
5] that one may (and even must) drop the fifth equation from this system due to the fact that the fluid is indeed no more viscous in this part of the domain.
It is classical to use (
4)
to get
where
is given by (
4)
. One may use this vertical velocity in (
4)
to compute
. Thanks to (
4)
, one has
Thus, we have both
v (thanks to (
5)) and
p (thanks to (
6)) and may rewrite (
4)
with the only fields
u and
:
To take off the dependence on
y of this equation, we integrate between the bottom of our upper part (
) and its upper free boundary (
). We define the following:
We also need a lemma that will enable us to commute the integration and the x differentiation under an assumption:
Lemma 1. Let F be a function defined in , such that, if then The proof is very simple and left to the interested reader. We apply it to (
7) because the
x differentiation of functions inside the square brackets commutes with our integral. Indeed, every function inside the brackets vanishes at
.
Thanks to Lemma 1, one may commute the
x differentiation of the square bracket in Equation (
7) with the integral since the terms in the square brackets vanish at
. An integration by parts of the integral
term, and the treatment of
leads to the following (below, we write
):
We need now the following (two-fold) assumption for
:
where
and
is already defined in (
8). Notice that the expansion of a function around its mean value
is not an assumption. A first way to see this assumption is that the discrepancy with the mean
is
and is small (
). Another way to formulate this assumption is to look at an expansion in
, in which one assumes that the zeroth-order term does not depend on
y and that the next order term is a zero-mean value. Therefore,
is perpendicular to
. Whatever the interpretation, the consequence of this assumption is that
(cross) terms in
vanish. This gives two different ways to see the real assumptions behind (
8) and (
11). Finally, this assumption is proven to be true in Lemma 11 (Equation (77)) of [
5] in the case of a Boussinesq flow (where
is small)
without the assumption of irrotationality in the Euler part of the flow. The horizontal velocity’s expansion is computed in the inviscid case:
Thus, the function is indeed the sum of its mean and an order 2 (in ) function of mean vanishing. We remind the reader that we still assume that we solve the Euler equations and not yet the Navier–Stokes ones in this part. Therefore, the assumption is coherent with the present derivation.
Upon this assumption, (
10) simplifies to
One must add (
4)
:
and look for an equation for
.
Remark 1. The attention may be drawn to the fact that, thanks to (11), where is given by (4). In the pure Euler case with no boundary layer (), since the flow does not cross the boundary. Therefore, we would not need to compute . We would have derived the classical SGN equation. We need to go further to obtain a closure of . 2.2. Resolution in the Boundary Layer
We write the system that applies in the layer, extracted from (
1):
This system may be rewritten with the change in variables justified in (
3)
, where
is positive and up to a large (but not too large)
. This change in variable is elicited by the
term. The change in variable to an order two in
raises this term to order zero. We also use the assumption (
2) on
such that
, where
R is a constant. We should have tilded the fields but would have dropped the tilde soon after. Therefore, we omit them. When precision is needed, we denote
as the horizontal velocity in the boundary layer. The system writes the following:
As is classical, we first compute
v (owing to (
16)
and (
16)
:
Then, we can compute the differentiated pressure from (
16)
that proves
. As a consequence,
where
is determined thanks to a matching condition at the bottom of the upper part (Euler part). From (
6) and owing to the already stated assumption (
11), the pressure in the boundary layer is as follows, up to
:
Then, one has the pressure in the boundary layer:
Last, we may gather
(from (
17)) and
(from (
19)) and rewrite (
16)
:
At this stage of the derivation, we recognize a Prandtl’s equation. It is then intuitive to assume the continuity relation on the horizontal velocity:
In the Boussinesq regime, the author of [
5] had a heat equation (instead of Prandtl’s equation) on
. It was solved with this (upper) boundary condition and the condition at
. Once the horizontal velocity (in the boundary) was determined, the author derived the vertical velocity. Then, the continuity condition on the vertical velocity gave the supplementary equation that closed the viscous Boussinesq system.
In our regime, we are led to a system (
13) and (
20) with boundary conditions depending on
. However, the nonlinearity is Prandtl-like and it still depends on
in a hopeless way because of the Prandtl term. Indeed, it is well-known that Prandtl’s equation still resists the best physicists and mathematicians. It was proven to be ill-posed in [
12] and partially well-posed later. At the current stage, we do not know how to derive a simpler model without unrealistic assumption. At this level, we could not see any more than the two following possible routes:
One may use the assumption, classical in the boundary layer community, that the profile is exponential of the type:
which vanishes at
(see (
16)
). Such a dependence on
x and
is assumed to be split, and this last assumption is very strong. Indeed, (
20) may then be rewritten:
This equation simplifies to the following:
Therefore, this first idea gets rid of the second-order derivative that came from the Laplacian. As a consequence, the viscosity is no longer taken into account and it is a deadlock. The error is to assume that the two dependences (
x and
) are not tied together. Therefore, we may not make such an assumption. The exact shape of the
dependence in the Boussinesq approximation is given in [
5] and recalled below.
One may assume the profile of the horizontal velocity in the boundary layer to be the one
proven in [
5] that is a convolution in time mixing
x and
:
where
R is a constant,
p is the dual variable of time
t through Laplace transform
, and
is its only root with a nonnegative real part of
p. However, the Boussinesq assumptions are incompatible with the ones we would do here and such a function would be untractable in Prandtl’s equation.
In the system (
13) and (
20), the
term must be found from the Euler part. Owing to Euler Equation (
4)
, one knows
(see (
14)). Finally, the system (in
) to which we are led is no better than
It still depends on
in addition to
and requires initial conditions in the whole boundary layer (for all
x and
). We expected a one-dimensional in space and one dimensional in time two-field (
and
) system as is classical for inviscid Boussinesq, viscous Boussinesq [
5], and inviscid Serre–Green–Naghdi [
9,
10,
13]. Therefore, we could not reach a reduced enough model.
The first equation of (
24) is not surprising. It contains
and a third-order space derivative of
as in the inviscid SGN system [
9,
10]. All the terms are the same as in the classical SGN system, apart from a coupling term depending on
.
is the upper boundary of the horizontal velocity in the boundary layer
which must satisfy a Prandtl equation. When one takes viscosity into account from the Boussinesq system, one obtains only two additional terms. One is a half derivative (in time), and the other depends on the initial conditions in the boundary layer. In the nonlinear case we are currently studying, we would have appreciated not having more complex terms. In (
24)
, the coupling is performed through
and the resolution of a Prandtl equation. Thus, we do need the initial condition in the boundary layer and the resolution of the Prandtl equation in that layer. This is not the goal of the reduced model.
As was said above, in the closest case (the linear viscid case), (
24)
is a parabolic heat-like equation on
. It may be solved explicitly, and it provides the
given in (
23) (see [
5]). This
enables us to compute the vertical velocity
thanks to (
17). Then, writing its matching condition at the frontier of the boundary layer with the vertical velocity computed in the Euler (inviscid) part provides a new condition. After some computations, this last condition writes
! Therefore, the nonlinear viscous case lags behind the linear viscous case and the derivation is currently blocked at the Prandtl’s step. Would it be possible to further simplify such a coupled Prandtl system similarly to the classical one? This is the main question left by the current study.