1. Introduction
Explaining the origin of planetary and stellar magnetic fields has been a scientific quest since Larmor [
1] hypothesized that magnetohydrodynamic (MHD) motions within the Sun, and by extension, the Earth, were responsible for the creation and maintenance of global magnetic fields. Numerical simulations of the geodynamo [
2,
3,
4] have established that MHD processes within the Earth are capable of creating magnetic fields similar to the actual geomagnetic field, including reversals of the dominant dipole component.
However successful these numerical simulations were in proving the MHD nature of the geodynamo, the fundamental origin of the dominant, quasi-steady geomagnetic dipole field still remained a mystery [
5]. In previous work, we showed that extending the statistical mechanics of ideal MHD turbulence opened the door to understanding the fundamental origin of the geodynamo [
6,
7] and then demonstrated that these ideal results appeared to apply to real (i.e., forced and dissipative) MHD turbulence [
8,
9]. In Reference [
9], we put forward the hypothesis that differences in the oblateness of the outer and inner boundaries of a spheroidal shell could cause dipole alignment. In the present work, we studied the analogue of this with a Fourier model by using stretching-shrinking factors
,
, and
(
is the smallest and
the largest of these factors). These factors change the relative lengths of the
x-,
y- and
z-directions in both
x-space and
k-space, as will be described in
Section 3.3.
We use a Fourier model as a surrogate for a spherical model because the statistical mechanics of ideal, rotating MHD turbulence are equivalent in the two cases [
7]. Both models are based on the MHD equations transformed from physical, or
x-space, to a dynamical system of interacting modes in
k-space. In either
x- or
k-space, there is no imposed magnetic field; only overall rotation is imposed. Here, the magnetic field is dynamically generated by MHD turbulence.
We find, in both Fourier and spherical cases, that the largest-scale (smallest wavenumber
k) magnetic field modes are very energetic and quasi-steady, i.e., random variables with large mean values subject to only very small fluctuations. The explanation of this is that there is a broken ergodicity: we expected all modes to be fluctuating zero-mean random variables and they mostly are—except for certain largest-scale modes, which will have a very large mean and comparatively very small fluctuations [
6]. (Not all of the smallest-
k modes need to have the same value—there is a dynamically broken symmetry.) The only requirement for this to occur is that the system have a non-zero magnetic helicity
. In the case of ideal rotating MHD turbulence,
is an integral invariant, along with the energy
E. In the forced, dissipative, quasi-equilibrium case, driven so that it has a large, relatively constant
, behavior is equivalent in that a largest-scale, quasi-steady ‘dipole’ component arises [
8,
9]. Although the Fourier and spherical models have equivalent ideal statistical mechanics and dynamical evolution in
k-space, they appear, of course, very different and are not comparable in
x-space, where the largest-scale mode in a periodic box has a sinusoidal shape, while in the spherical case it is a spherical harmonic dipole. (At times, we will refer to the largest-scale mode in the Fourier model as the ‘dipole’, although this is meant figuratively and not meant to imply that the
x-space structures are similar, only that the corresponding modes in
k-space are equivalent).
The smallest wavenumber
k magnetic field quasi-steady mode (or modes) may be thought of as a ‘mean field’, but it is not the mean field that is assumed to exist in ‘mean field electrodynamics’ (MFE) [
10]. The a priori MFE mean-field is introduced by altering the magnetic field evolution equation, thereby changing the fundamental nature of the MHD equations; the result is the MFE equations. Instead, basing our work on the MHD equations, we see that a quasi-steady, largest-scale component of the magnetic field emerges dynamically and has an explanation by a statistical mechanics with broken ergodicity and broken symmetry, as will be discussed at length in this paper. Thus, a ‘mean field’ emerges from MHD turbulence, per se, and there is no need to impose one a priori.
Let us add that the interesting question of geomagnetic reversals is not addressed here. This presumably depends on the equilibrium of an existing geomagnetic dipole orientation being destabilized by unseen processes in the Earth’s interior or by some natural bi-stability. Here, we are only concerned with a system that is in a state of equilibrium or quasi-equilibrium and important questions as to the cause of reversals are beyond the scope of this paper.
Our principal result is that without magnetic helicity there is no dipole field. Thus, if the Earth has a dipole field, we require that it have magnetic helicity. In fact, by measuring the strength of the Earth’s external dipole magnetic field and by mapping this mathematically onto the core-mantle boundary, we can estimate the value of the magnetic helicity in the core.
This principal result and all of the related results, we believe, further enhance the view that magnetic helicity and MHD turbulence play essential roles in understanding the fundamental cause of the geodynamo (and perhaps other astrophysical dynamos [
11,
12]). Next, we briefly review our numerical method, then summarize our new theoretical and computational results, followed by detailed explanations of how they were found.
2. Numerical Procedure
A Fourier spectral transform method [
13] on an
grid with
is used; the minimum wave number is
and the maximum wave number is
. Time-integration is performed with a third-order Adams Bashforth–Adams Moulton method [
14] with a time-step of
; initial magnetic and kinetic energy spectra are
, where
. Viscosity and magnetic diffusivity are set to zero so that the flow is ideal. (A grid size of
was used so that the ten runs of
Table 1 could be completed in a reasonable amount of time with the resources available, an 8-core Linux computer, each core running at
s
). The integral invariants of ideal MHD turbulence are the volume-averaged energy
E and magnetic helicity
, as well as the cross helicity
when there is no rotation. The ideal invariants changed less than 0.1% during the runs of
Table 1, while the kinetic helicity
, though it is an ideal invariant for hydrodynamic turbulence, fell to zero very quickly and had small fluctuations about that value. Further details concerning mathematical modeling and numerical procedure may be found in [
6,
8,
9].
3. Summary of Results
Here, we present a brief summary of the major results to be detailed later in this paper. In what follows, both a Fourier model (periodic box) [
9] and a spherical harmonic model (spherical shell) are employed, with the Fourier model serving numerically as a surrogate for the spherical harmonic model. While the periodic box is a 3-torus with no boundaries, the spherical shell model [
7] has homogeneous boundary conditions, i.e., the normal components of all fields are zero on the spherical surfaces bounding the internal, turbulent magnetofluid; these boundary conditions were introduced by [
15]. Here, these boundaries are not coincident with the Earth’s outer or inner core boundaries (whose precise topography is not well known, anyhow), but are set conceptually inside of them a short distance away at the top of each laminar boundary layer; at the core-mantle boundary (CMB), this laminar layer is estimated to be ∼160 m thick [
16] or about 0.07% of the thickness of the outer core. It is within this laminar boundary layer that the magnetic field gains a radial component, eventually becoming the external magnetic field. The external field is connected to the internal, turbulent magnetic field by assuming tangential continuity at the model’s upper boundary. This view of magnetic structure appears to be reflected in Figure 1 of Reference [
2]. The efficacy of this model is discussed in
Section 3.2, below.
Please note that what is meant by the ‘dipole part’ of a Fourier expansion is comprised of those coefficients that have the smallest wavenumbers. In addition, in regard to the magnetic field, the Fourier coefficients that have positive magnetic helicity are
and those with negative magnetic helicity are
; similarly, the Fourier coefficients that have positive kinetic helicity are
and those with negative kinetic helicity are
. The set of coefficients with the same wavevector
will be called a ‘Fourier mode’ and the mode
and the mode
are not independent because, for example,
; coefficients can have the same wavenumber
and there are no coefficients with
. The number of independent modes for
is
; in our simulations,
and
57,656. In what follows, for definiteness, we choose the global magnetic helicity
to be positive. The integral invariants of ideal MHD turbulence are, again, the energy
E and magnetic helicity
, as well as the cross helicity
when there is no rotation; these are all volume-averaged quantities as described in
Section 5, as are the magnetic energy
, kinetic energy
and related quantities.
3.1. Magnetic Dipole Energy and Magnetic Helicity
The energy in the dipole part of the magnetic field generated by MHD turbulence is equal to the absolute value of the magnetic helicity multiplied by the smallest wavenumber. This result was implicit in our previous formulations [
6,
7], but further analysis, discussed in more detail in
Section 9, reveals that
Here,
is the expectation value
of the dipole magnetic energy and the expectation value of the magnetic helicity is
, where
is a constant for ideal MHD turbulence; expectation values are defined in
Section 6. As discussed in
Section 4.2, the smallest possible wavenumber is
and is associated with the dipole, while the corresponding wavevector is
(in the symmetric case, there are three of them).
The result (
1) has been tested on ten new ideal MHD turbulence Fourier method simulations of
Table 1, as well as ten real (forced, dissipative) simulations, drawn from [
9] that are given in
Table 2. Let us denote the ratio of the right and left sides of (
1) as
. Averaging
R over the last 20% of each run gives a value
for each run, and then averaging the averages
gives us a mean
and standard deviation
for each of
Table 1 and
Table 2. Using the notation
, for the ten runs in
Table 1,
and for the ten runs in
Table 2,
. The significance of
Table 2 (real MHD turbulence) is that the values of
are commensurate with those found in
Table 1 (ideal MHD turbulence), i.e., real and ideal MHD turbulence behave similarly with regard to the theoretical prediction (
1).
The prediction (
1) can be visually verified, as seen in
Figure 1 and
Figure 2, where the lowest-wavenumber positive magnetic helicity coefficients
are normalized by
(since the expectation value of any coefficient’s energy is
or
, where
is the grid size) and by
in accordance with (
1); if all dipole coefficients had equal energies, their doubly normalized magnitudes would be
and if one of these coefficients had all the energy predicted by (
1), its magnitude would be unity. Thus, the theoretical prediction (
1) appears to be well confirmed through the Fourier method (periodic box) numerical simulations of both ideal and real MHD turbulence.
In addition to the energy
contained in the dipole modes of the magnetic field, given by (
1), the rest of the magnetic field has an energy
(‘
h’ stands for higher-wavenumber, non-dipole positive magnetic helicity components, as well as all negative magnetic helicity ones), while the velocity field has kinetic energy
; the total energy is
. In addition to (
1), we find
The essential result (
2), along with (
1), is discussed in
Section 9. Using (
1) and (
2), we clearly have
.
Next, we discuss the application of the principal result (
1) to the Earth’s outer core. We use the spherical shell model of [
7] and assume that ideal results are qualitatively applicable to the low-wavenumber (large length-scale) behavior of a real turbulent magnetofluid. This assumption was tested previously numerically on a Fourier model and seen to be a fairly good one at low wavenumber [
9]. Forced, dissipative MHD turbulence behaves very similarly to ideal MHD turbulence at the largest wavelengths and important measures of MHD turbulence are commensurate, as application of the ideal result (
1) to forced, dissipative numerical data shows us in
Table 2.
3.2. Knowledge of the Internal Toroidal Field
The Fourier model examines MHD turbulence in a periodic box, for which there is no ‘outside’ but only an ‘inside’. Thus, the results above are pertinent to the flow interior to the Earth’s fluid (outer) core. We have considered MHD turbulence in the outer core by developing a spherical shell model that uses spherical Bessel function-spherical harmonic expansions and have found that the statistical theory of ideal MHD turbulence developed for the Fourier model system also applies to this case [
7]. In this spherical shell model, there are poloidal
and toroidal
magnetic field coefficients, and it is the poloidal coefficients
that can be matched to the Gauss coefficients
and
at the outer boundary of the numerical model. The toroidal coefficients
are internal to the outer core and it had long been assumed that these were unknowable. However, consider the following results.
A turbulent magnetofluid in the rotating spherical shell model of [
7] has the ideal invariants energy
, where
, and magnetic helicity
. In that model, the magnetic energy
and helicity
are given by
The indices
l and
m are the degree and order of a spherical harmonic
, and
n denotes the
nth zero
of
at
, where
is a linear combination of spherical Bessel and Neumann functions. Please see [
7] for more details; in that paper, the smallest spherical shell dimensionless wavenumber for an Earth-like model is
(the next smallest wavenumber is
). The spherical shell version of (
1) is
The geomagnetic field is measured at the surface out to spherical harmonic degree
[
17], where about 93% of the magnetic energy at the Earth’s surface is in the dipole,
. However, at the CMB, only about 38% of its magnetic energy is locked up in the dipole
components; this percentage is probably high, as there is presumably more energy that is unaccounted for in the
components. The dipole’s Gauss coefficients
and
given by [
17] indicate that 97% of the dipole’s energy is held by
, so the dipole moment is closely aligned with the rotation axis.
Theoretically, we expect that the components
and
that have the smallest wave number
contribute most to
in (
4) [
7]. Truncating the summations (
3) and (
4) to the
and
terms and setting
, for
, we have
Therefore, if we know the major part of the poloidal dipole magnetic field, then we also know the major part of the toroidal dipole field:
Note that, if we had set , the result would be .
The important point here is that because we can relate the coefficients
to the Gauss coefficients
and
through the boundary conditions, we know both the poloidal coefficients
and, through (
7), the toroidal coefficients
in the outer core. Using the results in References [
7,
17], we find, with
,
Formulas in Reference [
7] tell us that the conversion factor is
for degree
, leading to an estimated mean value of the dipole magnetic field in the outer core of 3.02 mT, or 11.7 times that of average geomagnetic dipole field at the CMB, which is 0.259 mT, based on the 2015 International Geomagnetic Reference Field (IGRF) coefficients [
17]. Although the value of 3.02 mT comes from a model with homogeneous boundary conditions [
7], the model appears to have some robustness because 3.02 mT is compatible with the value of 2.5 mT estimated by [
18] as the mean strength of the total magnetic field in the Earth’s outer core. In addition, the IGRF data tells us that
J/m
and
J/m
.
In the case of the dipole,
, using
is appropriate because it is the minimum wavenumber
of the spherical shell model. However, for estimating higher multipole (
) field strengths, it is unclear which wavenumber
, or even how many, to use because the IGRF field components are indexed by degree
l and order
m, and, in the spherical shell model of [
7], there are many wavenumbers
associated with each spherical harmonic degree
l, but, at present, no obvious procedure for picking out which ones are important.
3.3. Differential Oblateness vs. Rotation in Dipole Alignment
In Reference [
9], we put forward the idea that a greater oblateness of the inner core boundary (ICB) with respect to the CMB in the
z-direction might influence dipole alignment. In the Fourier case, the analogy is that the periodic box would be stretched in the
z-direction compared to the
x- and
y-directions in
x-space; in
k-space, this would entail a shrinking in the
-direction compared to the
and
-directions (or some permutation of this). Thus,
,
, while
,
and
. A number of runs were performed, using various values of
,
and
, with
, as
Table 1 shows. In a numerical simulation with
, the effect of making one of the
smaller than the others is to give the positive magnetic helicity Fourier coefficient, say
with smallest wave number
, more energy than it would have if all the
; the reason for this is discussed in
Section 8.
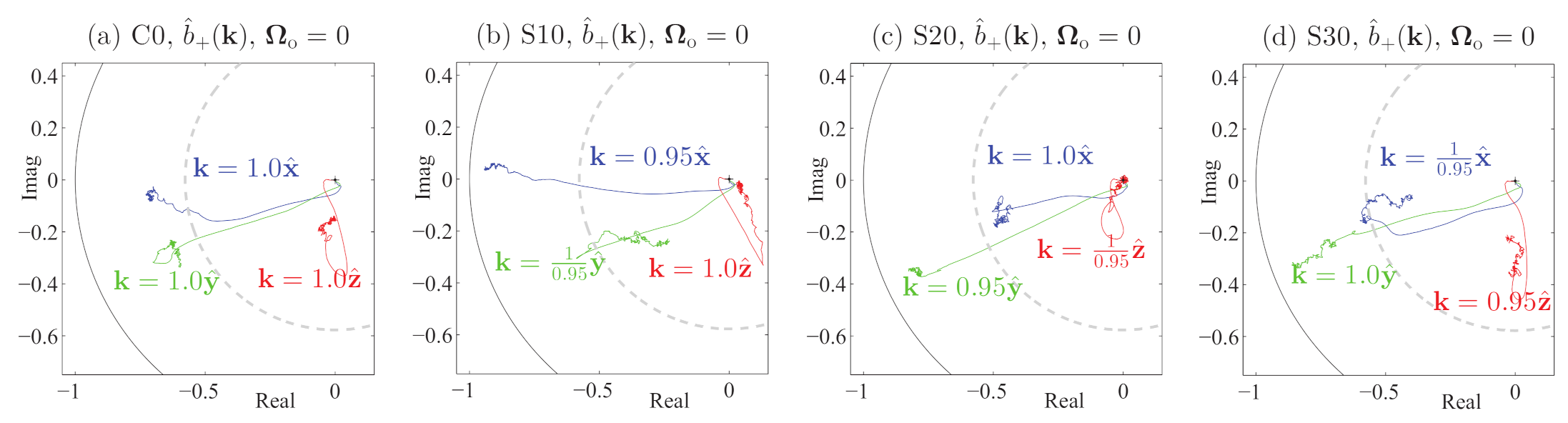
Let us again compare the evolution of the
,
, for the four runs C0, S10, S20, and S30 of
Table 1. This comparison is made using the trajectories shown in
Figure 1, where we plot the real vs. imaginary parts of the doubly normalized
. In
Figure 1, we see that, when the smallest wavevector is in the (b)
x-, (c)
y- or (d)
z-directions, it induces an increase in the magnitude of the corresponding
compared to (a), where all
. Although it was initially assumed that all coefficients would be zero-mean random variables [
19,
20], we clearly see ‘broken ergodicity,’ a concept defined by [
21]. Broken ergodicity in MHD turbulence was first noted by [
22]; in
Figure 1, the phenomenon of ‘broken symmetry’ [
23] also appears, in that nonlinear evolution can lead to a lack of equipartition even in the
run C0.
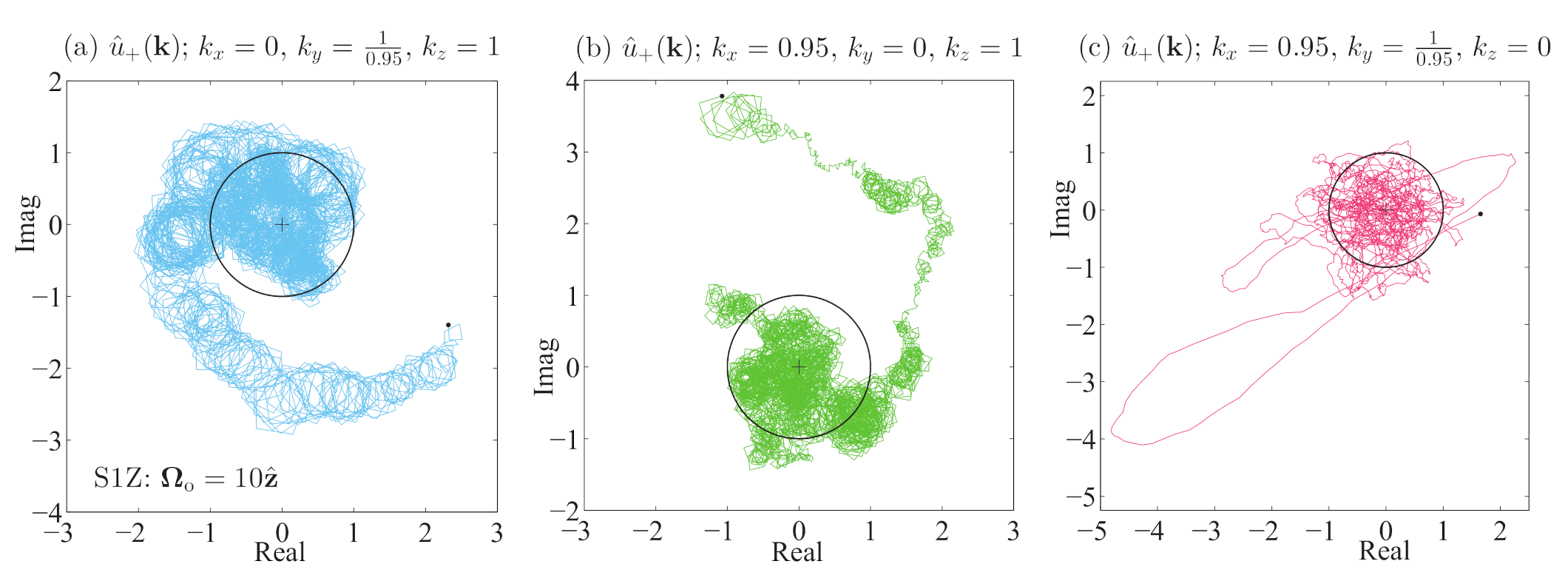
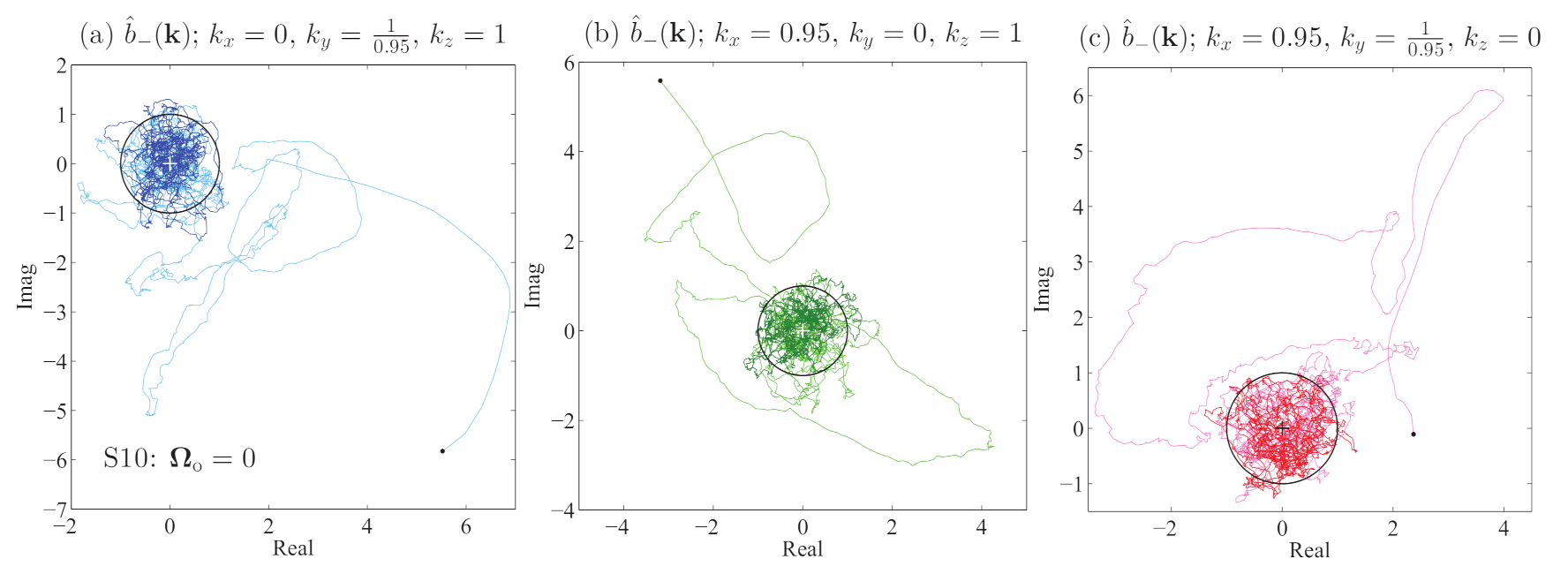
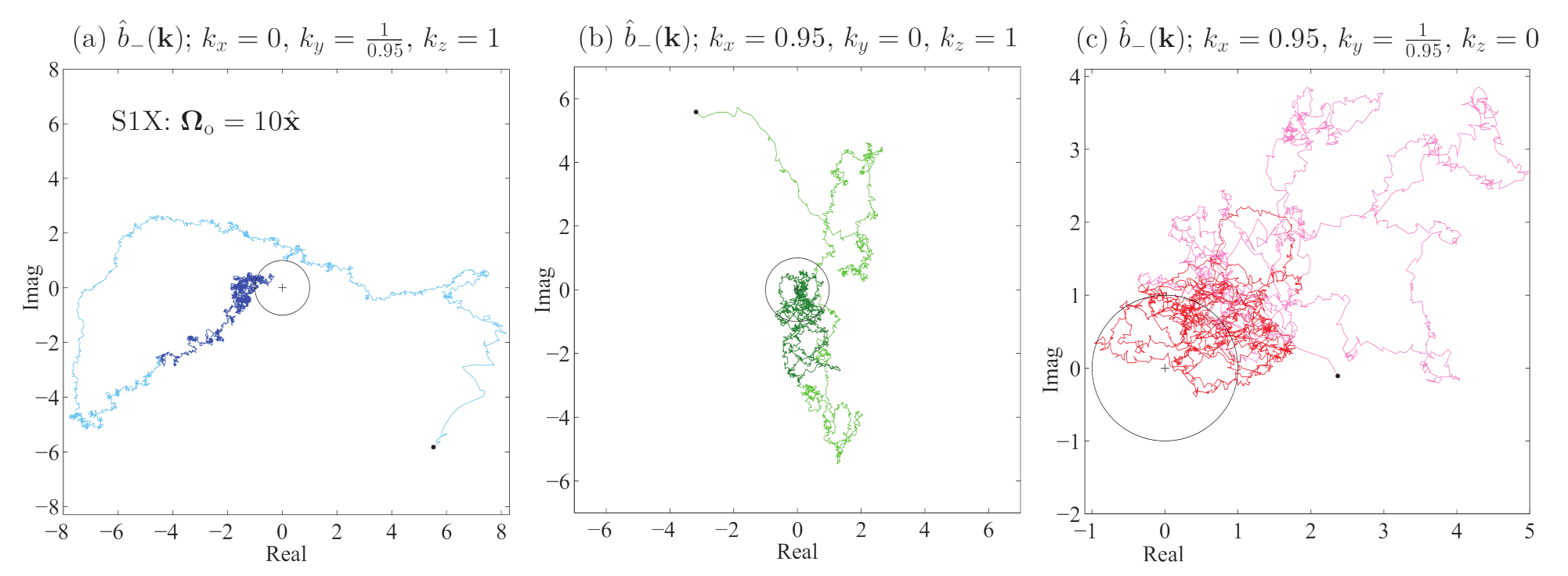
Next, consider
Figure 2 where (a) pertains to reference run S10 and
Figure 2b–d, which pertain to three runs whose parameters in
Table 1 are the same as run S10, except that they have an imposed rotation: in
Figure 2b, S1X has
, in (c), S1Y has
and in (d), S1Z has
.
Figure 2 shows that the effect of rotation overrides the effect of differential oblateness. The low-wavenumber, positive magnetic helicity coefficients
with
parallel to
develop much greater magnitude than those with
perpendicular to
. We discuss a possible reason for this in
Section 3.5 below.
3.4. Broken Ergodicity and Broken Symmetry
Figure 1 and
Figure 2 show that the dipole components
exhibit quasi-stationarity, i.e., coherent structure due to broken ergodicity and broken symmetry. We discuss these phenomena in greater detail in
Section 10. We believe we have a clearer understanding of their relationship and wish to summarize this here.
Assume
and define a vector
in a 3D complex space by
This has the dot product
. At least one of the components of
will have a large mean value of magnitude
that is much larger than the fluctuations it experiences, which are O
. The ‘dipole vector’
will thus evolve to become quasi-stationary and, while the
expectation value
is zero, the
time-average of
is almost constant and has a magnitude
greater than its standard deviation, as is seen in
Figure 1. This is the origin of broken ergodicity.
The phase space of independent Fourier components can also be subject to an arbitrary unitary transformation. While the choice of a particular set of initial conditions leads to a specific direction for the quasi-stationary vector , a unitary transformation can be made so as to point it in any direction we chose: The canonical ensemble represents all directions, which average to zero, but the dynamical system can only evolve so that points in one direction. This is the origin of broken symmetry.
Rotation, however, induces dipole alignment, though the reason why is not yet completely clear.
3.5. Rotation and Dipole Alignment
As mentioned above and shown in
Figure 1, differential oblateness can cause alignment, but, as shown in
Figure 2, rotation appears to be the absolute controlling factor. The rotation vector
enters explicitly into the basic equations only in the velocity Equation (
10) and not in the magnetic induction Equation (
11). However, it does enter into the magnetic induction equation implicitly through the electromotive field
because of the hydrodynamic inertial waves present in the velocity field
of a rotating system. While our discussion here will be brief, inertial waves, both Alfvén and hydrodynamic, are well known to be important in planetary cores, as discussed in detail by [
24] and [
25], respectively.
Here, we examine the inertial wave effects in the context of our Fourier model system. Since inertial waves may introduce a sinusoidal time variation into the electromotive field, the evolution of some of the Fourier magnetic dipole modes can be influenced: if
, then
and
are strongly affected, while
is not affected at all, to leading order in
. A qualitative appraisal is given more detail in
Section 11.
5. Global Quantities
There are various important global quantities that can be expressed as averages over either
x-space or, equivalently,
k-space. We define the volume average of a quantity
multiplied by a quantity
in a periodic box of side length
as
, where
Then, the volume-averaged energy
E, enstrophy
, mean-squared current
J, cross helicity
, magnetic helicity
and mean-squared vector potential
A (the last two defined in terms of the magnetic vector potential
, where
) are
Since all functions are periodic in
x-space, we can use Equations (
10) and (
11), along with integration by parts to derive the following relations [
33]:
When
and
, the quantities
E,
, and
are the traditional ideal invariants of MHD turbulence [
20,
34,
35]. If
, then (
38) indicates that
is no longer an ideal invariant. If an external mean magnetic field
was imposed, then
would also no longer be an ideal invariant [
33]; here, we will always have
. We note that ‘generalized helicities’
and
related to
and
can be defined [
36] and are ideal invariants even in the presence of nonzero
and
. However, we will only need to refer to
and
in this paper.
Although kinetic helicity
is not an ideal MHD invariant, it is an invariant of ideal fluid turbulence [
37]. Manipulating (
10), we find that, for a periodic box, we have
Note that and E are both conserved if and , i.e., in the case of ideal hydrodynamic turbulence.
Since
, then
. Using (
19), (
23) and (
25), we see that
Using this, energy
E, cross helicity
and magnetic helicity
are represented in
k-space by the quadratic sums:
In the ideal MHD case with either periodic or homogeneous b.c.s, E and are invariants, as is when , but other quantities, such as , , , and J, as well other functions of and , will generally be time-dependent, particularly in numerical simulations during the transition from initial conditions to an equilibrium state.
6. Statistical Mechanics
Here, we briefly discuss the statistical mechanics of ideal MHD turbulence. The Equations (
30) and (
31) form a finite dynamical system with a phase space defined by the independent real and imaginary components of
and
,
; we denote that these are coordinates in phase space and not dynamical variables by omitting
t from the arguments. If
and the number of independent
is
57,656, then the phase space has
461,248 dimensions. As pointed out by [
20], when
, the system has a Liouville theorem and whose phase space
represents a canonical ensemble where statistical properties depend on the constants of the motion. As just discussed, these constants, also known as ideal invariants, are the energy
E, the magnetic helicity
and, if
, the cross helicity
.
The statistical mechanics of ideal MHD turbulence are based on a probability density function of the form
Here,
E,
, and
are given by (
42), (
43) and (
44), respectively, and
Z is the partition function; in addition,
if
. [
20] initiated this approach and explicitly considered the dynamical system to be ergodic, an assumption that was unchallenged in the early work on ideal MHD turbulence [
19,
38]. It was finally challenged by [
22], when apparent non-ergodicity was first noticed and reported, and confirmed later [
39]. As already mentioned, this non-ergodicity is actually ‘broken ergodicity’ [
21]; again, a review of broken ergodicity for ideal MHD turbulence is given by [
6].
In the case of ideal MHD turbulence, expectation values of the various global quantities in (
35) and (
36), as well as any other phase functions, can be determined with respect to the probability density function (
45). Expectation values are integrations over the phase space
, i.e., for all possible values of the coordinates in
, which are the real and imaginary parts of
and
(again, the
t is omitted from the arguments because these are coordinates and not dynamical variables). Given a quantity
Q, the expectation value
is defined by
As an example, the velocity and magnetic field coefficients are expected to have zero mean values:
In the ideal case, the integral invariants
E,
, and possibly
, should have time-independent values
,
, and
that are equal to their expectation values:
In fact, we require that (
48) be true and use this to determine the ‘inverse temperatures’
,
and
in (
45). Whereas (
47) is an ‘ergodic hypothesis,’ (
48) is actually an a priori axiom on which the theory of ideal MHD turbulence is based, though justified by a posteriori numerical results. Ergodicity, or rather the lack of it, will be discussed in
Section 10.
7. Eigenvariables and Entropy
Placing the
k-space representation of
E,
and
, as given in (
42)–(
44), into the PDF (
45) gives an expression that contains modal 4×4 Hermitian covariance matrices in the argument of the exponential:
In
, the notation
means that only independent modes
are included, i.e., if
is included, then
is not. Here,
is the Hermitian adjoint (
means transpose) of the column vector
, where
The Hermitian (here, real, and symmetric) 4×4 covariance matrix
is
The circumflex indicates division by : , and .
Although the
in (
51) can also be expressed as 8 × 8 real symmetric matrices and the
as 8 × 1 real arrays [
19], finding eigenvalues and eigenvariables is facilitated by using the 4 × 4 matrices
and 4 × 1 complex arrays
, along with the properties of block matrices given by [
40].
The real, symmetric matrices
can be diagonalized (and more easily than the Hermitian matrices used previously [
6,
30,
41]) to yield the modal PDFs
The eigenvalues
are also written with a circumflex to indicate division by
, just as for
,
and
. Implicit in the form of
given above is the transformation
, where
SU(4) is a unitary transformation matrix (see below). Explicitly,
is
The energy expectation values for the complex eigenvariables
is
This energy contains equal contributions from the real and imaginary parts of . The exact forms of the and in terms of , and will be presented next.
7.1. Eigenvariables
The eigenvariables
in (
52) can be determined for ideal MHD turbulence through a modal unitary transformation [
6,
7,
30]. In the general case (nonrotating with zero mean magnetic field), the form of the transformation
is
Above,
with
for
; the functions
and
are, in terms of a third function
,
In terms of
, as defined above, the eigenvalues
(
) are
Although it appears that the eigenvalues given above are functions of the undetermined quantities
,
, and
, there is only one unknown to be determined:
. Theory [
6,
30] tells us that
Here,
and, again,
,
and
. Basic results of ideal MHD turbulence theory [
6] are that
and
; thus, in the expression for
, we have
. Noting that
and
are pseudoscalars, we see that
and
are also pseudoscalars and that
and
.
7.2. Entropy
We use (
52) to find the entropy functional
:
Above, the sum over
means, again, that only independent modes
are included (if
, then not
). The fact that there is only one unknown quantity
in (
62) means that the entropy functional of the system is a function of only one variable. As discussed by [
42], finding the (single) minimum of
gives us the value
that sets the values of
,
and
, as well as the system entropy
.
Both the non-rotating (
) and rotating cases (
), have
, and the first derivative of the entropy functional (
63) with respect to
is
Theory tells us that the denominators for the terms in
are positive and also that
. For the Fourier case we are discussing here,
, and for the spherical shell model of the outer core developed by [
7],
. We define a wavenumber
, so that
. For purposes of discussion, let us draw from examples found in [
9]: for run NM06,
,
and
, so that
, while, for run NM06c,
,
and
, so that
; either could be used as a representative value. (The difference between runs NM06 and NM06c is that the former had steady forcing and the latter had cyclic forcing).
The important point here is that dissipative, driven magnetofluids tend to have
. Defining
as the number of independent Fourier modes with smallest wavenumber
, the summation
can be broken up into the following:
Above, the first term on the right is negative, while all the rest are positive because
for
. (Even if
, so that there were a few more negative terms, the following development would still be valid.) In addition, all the terms in
are positive. In the limit that
,
Requiring is equivalent to requiring that ; from the relations given above, we see that a small number of negative terms (the “dipole” part, corresponding to the smallest wavenumber, ) must balance a very large number of positive terms. For a cubical periodic box (or a spherically symmetric shell), since the independent modes with are .
Putting the expressions in (
68) into
leads to
Defining the small quantity
, we get the cubic equation
We always have , but, in the non-rotating case (), we also have , so that (approximately) if ; or if .
However, the rotating case (
) case applies to essentially all planets (and stars) and, in this case, we have
. Setting
in (
70) leads, to first order in
,
This approximation is needed for theoretical development, but, when exactness is required, is determined by numerically finding the minimum of corresponding to and for a given run, as well as if .
From the expression (
71) for
, we can also determine the expectation value of the kinetic energy,
, as well as of the difference
:
We will now use these results, assuming , to show how the positive magnetic helicity eigenvariable has an energy expectation value of , while all of the other eigenvariables have expected energies . This will allow us to explain the large-scale coherent magnet structures (i.e., quasi-stationary dipole fields) that spontaneously arise within a turbulent magnetofluid such as is found in the Earth’s outer core.
8. Energy Expectation Values
In a rotating frame of reference, again,
so that
, for which
. Assuming
, so that
and thus
and
, (
55)–(
58) become:
Remember that the dynamical variables and carry negative and positive kinetic helicity, respectively, while and carry negative and positive magnetic helicity, respectively.
In the limit that
,
and the eigenvariables are as given in (
74), while the eigenvalues (
60)–(
61) become
In the rotating case,
and
are determined by putting
from (
71) into their respective expression as given in (
62) with
; the result is
Using these expressions, along with (
72), (
73) and (
75), gives us the unnormalized eigenvalues
, up to leading order:
The eigenvariables have real (
R) and imaginary (
I) parts, i.e.,
,
, each have the same eigenvalue
. The associated energies of the real (
R) and imaginary (
I) parts are
As defined in (
74), the index
refers to negative and
to positive kinetic helicity coefficients; similarly, the index
refers to negative and
to positive magnetic helicity coefficients. The relations (
77) and (
78) tell us that the expected energies with respect to helicity are
The sum of these over independent modes is plus a term of O(), as it should be. Again, for cubical periodic boxes or symmetrical spherical shells, , since all lowest-wavenumber modes are expected to have the same energy. However, for the non-rotating case, and, especially for the rotating case, there is always some dynamical symmetry breaking so that one of the lowest-wavenumber modes dominates dynamically, as will be discussed further shortly.
We have already seen how well the prediction (
84) works by considering
Figure 1 and
Figure 2, as well as
Table 1 and
Table 2, as discussed in
Section 3. To see the efficacy of (
81), consider
Figure 3, while, for (
82) and (
83), consider
Figure 4 and
Figure 5, respectively. Please note that
Figure 3c represents the general behavior originally expected of
all coefficients [
19,
20], i.e., that of a zero-mean random variable.
Figure 1 and
Figure 2 demonstrate that this expected ergodicity is clearly broken, while
Figure 3,
Figure 4 and
Figure 5 show that expected behavior may be slow in occurring.
10. Broken Ergodicity and Broken Symmetry
Here, we discuss the differences between the eigenvariables and all the other eigenvariables in regard to their dynamical behavior. It will be assumed that as differential oblateness is obviated by rotation and most planets and stars, do, in fact, rotate.
10.1. Broken Ergodicity
The expectation values (
81)–(
84) yield rms values
, so that
Again, from (
74),
and
. In (b), the expected magnitude is just the standard deviation because the associated mean of
may be taken as zero. In (a), however, the expected magnitude may represent the magnitude of the mean of
, rather than its standard deviation, for the following reasons.
Consider the modal dynamic Equations (
30) with
and (
31) with
. Furthermore, in (
30), because
, we have
and can then use (
85) to write
Using (
93a,b) as size estimates, we see that the rms values of the first two terms on the right are ∼
larger than the third term
, which is the same size as
in (
30).
In (
31),
can be written as
Again using (
93a,b), we also see that the rms value of the first term on the right is ∼
larger than the second term.
Using these estimates, estimate the rms sizes of the right sides of (
30) and (
31) as
From these and (
93), we get
What this implies dynamically is that, in equilibrium, the ‘dipole’ eigenvariables , which may be large, have, on average, fluctuations in magnitude comparable in size to the other , which are all very small. In particular, the fluctuations of these other are of the same size as their rms magnitudes and so they behave like zero-mean random variables, as expected. However, the rms values of one or more of the are so large compared to their fluctuations that they exhibit nonergodic behavior, i.e., they have relatively large mean values over very long times, i.e., the exhibit ‘broken ergodicity.’ This phenomenon will be made clearer in the next subsection, where we also discuss ‘broken symmetry.’
10.2. Broken Symmetry
We have seen that, dynamically, the magnitudes of a ‘dipole’ eigenvariable
, once large enough, can become effectively constant over a long time because its fluctuation in magnitude are very small. Often, one of the
, for
,
or
does not become as large as predicted by (
83). These predictions are just average values over the ensemble and to see what is really going on we must consider the sum of the expectation values (
86). As in
Section 10.1, we will use
so that
and
,
or
. What (
83) implies is that the six components of the three
define a six component vector in a 6D real space or a three component vector in a complex 3D space; for compactness, we define a vector
and dot product
in a 3D complex space:
The endpoint of
is a quasi-stationary point on the surface of the hypersphere of radius
in a 6D subspace of the
-D phase space
. The coordinates of the 6D space can undergo an arbitrary orthogonal rotation (or a unitary transformation in the complex 3D space) that puts the point of the vector on any desired point on the surface. Thus, although (
93a) predicts that all
will have the same magnitude, this does not take into account that a suitable orthogonal transformation of initial conditions in the whole phase space will lead to the evolution of
pointing in any direction its 6D space that we choose, at least for the non-rotating case.
The fact that
will exhibit broken ergodicity (i.e., it becomes quasi-stationary while undergoing only small fluctuations. However, initial conditions will also impose a particular direction on it, leading to a
broken symmetry amongst the
with regard to the expectation values (
83). The phenomenon of broken symmetry has been noted before [
23,
43], as we have also noted many times the appearance of broken ergodicity [
6,
22,
23,
39]. Here, we see how these aspects of MHD turbulence are connected.
In equilibrium, the magnitudes of the
, for
,
, and
are often not that different in the non-rotating ideal case but may vary appreciably, as
Figure 1a shows. However, when rotation is imposed in the ideal case, the eigenfunction
with
parallel to
has essentially all the dipole energy (regardless of the values of the
), as
Figure 2b–d demonstrate. In the real case of forced, dissipative MHD turbulence, this phenomenon is also usually observed numerically, although some forcing mechanism may disrupt this process, as seen in Figure 7 of Reference [
9].
However, alignment with the rotation axis seems fairly ubiquitous in numerical simulations, as well as in planets and stars. We will now discuss possible reasons for this ‘dipole alignment’.