Vibroconvective Patterns in a Layer under Translational Vibrations of Circular Polarization

Abstract

This article experimentally investigates thermal vibrational convection in horizontal layers, subject to circular translational oscillations in the horizontal plane. The definite direction of translational vibrations lacks investigation, and the case of a layer heated from above is considered. At large negative values of the gravitational Rayleigh number, the thermovibrational convection appears in a threshold manner with an increase in the vibration intensity. Our results show that in the case of strong gravitational stabilization, thermovibrational convection develops in the form of patterns with strong anisotropy of spatial periods in orthogonal directions. The vibroconvective patterns have the form of parallel rolls divided along their length into relatively short segments. The layer thickness determines the distance between the rolls, and the longitudinal wavelength, depends on the Rayleigh number. Convective cells are studied using the noninvasive thermohromic methodic. It is found that when using the tracers for flow visualization, the concentration and type of the visualizer particles have a serious impact on the shape of the observed vibroconvective structures. In particular, the presence of even a small number of tracers (used in the study of velocity fields by the PIV method) generates flows and intensifies the heat transfer below the threshold of thermovibrational convection excitation.

1. Introduction

The study of thermal vibrational convection (TVC) (Gershuni and Lyubimov [1]) is the object of high interest nowadays, in connection with its potential use in effectively controlling the convection and heat transfer in various technological devices, particularly at zero gravity (Gershuni and Zhukhovitskii [2], Mialdun et al. [3]). According to Gershuni and Lyubimov [1], TVC is the averaged convection, excited in a non-isothermal fluid by the oscillating force fields. This is done by the oscillating inertial forces arising in the non-inertial frame of reference associated with the cavity, as a result of the cavity vibrations. The non-isothermal liquid oscillations lead to the appearance of averaged mass forces as a result of nonlinear effects, which generates the averaged convective flows. The last has been well-studied, both theoretically and experimentally, in the case of linear translational vibrations of a cavity with a non-uniform in density (for example, non-isothermal or multi-component) liquid. Wide theoretical studies are carried out both in the limiting case of high vibration frequencies (using the equations of averaged convection) and in the region of arbitrary frequencies (Simonenko and Zen’kovskaja [4], Gershuni et al. [5], Smorodin et al. [6], Vorobev and Lyubimova [7], Lappa [8]], Crewdson and Lappa [9]). The thermal vibrational convection equations obtained by the averaging method in the approximation of high dimensionless frequencies $\omega \equiv \mathsf{\Omega }{h}^2/\nu \gg 1$ (Simonenko and Zen’kovskaja [4]) are often used. They correspond to the case when the characteristic size of the cavity $h$ is much greater than the thickness of the viscous boundary layers $\delta \equiv \sqrt{2\nu /\mathsf{\Omega }}$, and the oscillations of the fluid are inviscid. In this case, the thermovibrational mechanism is determined by the vibrational parameter $R_{\mathrm{v}}={\left(b\mathsf{\Omega }\beta \mathsf{\Theta }h\right)}^2/2\nu \chi$, where $b$ is the vibration amplitude, $\mathsf{\Omega }=2\pi f$—radian frequency of vibration, $\mathsf{\Theta }$—characteristic temperature difference, $\beta$, $\chi$ and $\nu$—coefficients of volumetric expansion, thermal conductivity, and kinematic viscosity of the fluid.

Linear translational vibrations, which have the preferred direction of oscillations, determines the shape of convective structures. For instance, in plane layers, the linear vibrations lead to two-dimensional convective structures, elongated in the general case across the vibration axis. Exceptions are the linear vibrations directed along the temperature gradient (Crewdson and Lappa [9]).

A more general case is the one, when the cavity performs translational oscillations of elliptical polarization, considered theoretically by Kozlov [10]. The case of circular translational vibrations, when the cavity moves along a circular path, is of special interest. This type of vibration has no preferred direction—it leads to a rotating inertial force field in a non-inertial reference frame associated with the cavity. A theoretical description of TVC (equations of thermal vibrational convection obtained by the averaging method in the high-frequency approximation) for this case, as well as the problem of vibroconvective stability of liquid in a horizontal layer with isothermal boundaries of different temperatures, are considered in Reference [10]. It is shown that in the horizontal layers, the vibrations of circular polarization in the horizontal plane act similarly to vibrations of linear polarization. The fundamental difference lies in the absence of a preferred direction. According to the results of the linear stability theory, at the threshold, the most dangerous disturbances are characterized only by the square of the wavenumber, while the shape of convective structures (two-dimensional rolls, hexagonal or rectangular convective cells) remains undefined. Determining the type of disturbances developing in the supercritical region requires a nonlinear analysis. In this regard, a theoretical study by Pesch et al. [11] is interesting, where thermal convection in a horizontal layer performing unidirectional and circular translational oscillations in its own plane is studied. The analysis is based on the Galerkin method, as well as on direct numerical simulations of the underlying Boussinesq equations, in contrast to Reference [10], where the equations of vibrational convection obtained by the averaging method in the high frequency approximation were used. The studies [11] were carried out in the region of moderate dimensionless frequencies and have demonstrated that in the case of circular shaking, the onset of convection corresponds to the transverse roll, like in the case of unidirectional vibrations, with the roll axis selected spontaneously.

Experimental study of thermovibrational convection in a horizontal layer performing circular translational oscillations is performed by Kozlov et al. in Reference [12]. Since the experiments were carried out in a gravity field, in addition to the vibrational mechanism, thermal convection was determined by the thermogravitational mechanism, which is characterized by the Rayleigh number $Ra=g\beta \mathsf{\Theta }{h}^3/\nu \chi$. To exclude the destabilizing effect of the gravitational convective mechanism, the case of a fluid stably stratified in the gravity field, when the layer is heated from above, is considered. The studies are carried out in the area of large negative values of the Rayleigh number, at $Ra\sim -{10}^5$. According to the experimental observations, the thermovibrational convection, in this case, develops in the form of two-dimensional rolls; the wavelength of convective structures is determined by the layer thickness. The visualization of convective structures was carried out with the help of calliroscope particles, which is a small amount were located at the lower (cold) boundary of the layer. The convection excitation threshold found experimentally is in good agreement with the results of the linear stability theory (Ivanova and Kozlov [13]). It is interesting, that the wavenumber of two-dimensional convective rolls, observed in the experiment, is significantly lower than one predicted by the linear theory for large negative values of the gravitational Rayleigh number; at the same time, it is in good agreement with the results of the theory in the absence of gravity. In accordance with (Ivanova and Kozlov [13]), an increase in the negative value of the Rayleigh number, along with an increase in the threshold value of the vibrational parameter $R_{\mathrm{v}}$, is accompanied by a sharp increase in the critical wavenumber.

Let us mention an interesting case of translational-rotational or pendulum vibrations of the cavity. Such combined vibrations result in an additional thermovibrational mechanism (Kozlov [14], Kozlov and Selin [15]) which is linear in density inhomogeneity, and thus, analogous to the Rayleigh mechanism of gravitational convection. It is important that in thin layers, due to the specific form of the isothermal component of the pulsation velocity, excited by the rotational component of vibrations, the combined translational-rotational vibrations result in the renormalization of the external static force field. One can see that the equations of thermal vibrational convection under pendulum vibrations in a complete nonlinear formulation have the same form as in the case of translational vibrations, both in the case of linear and circular ones, Kozlov [10]. The only difference is in the renormalization of the static force field. This allows to compensate the effect of gravity in ground-based experiments and to study thermovibrational convection in layers under conditions that simulate the microgravity. This was confirmed in an experimental study of thermovibrational convection in a layer oscillating as a plane pendulum (Ivanova and Kozlov [13]) and spherical pendulum (Kozlov and Selin [15]). By the way, the experiments have shown that the use of different types of visualizing particles has a significant effect on the structure of convective flows, up to the fact that convective cells appear to significantly lower the excitation threshold of thermovibrational convection. In the case of circular translational vibrations, the presence of even an insignificant number of particles of practically neutral buoyancy can change the heat transfer in the subthreshold region, without, however, affecting the excitation threshold of thermovibrational convection.

The aim of this work is the experimental study of the structure of vibroconvective flows in a horizontal layer heated from above and subjected to circularly polarized translational vibrations, as well as the study of the effect of different types of tracers on the structure of observed convective flows and convective heat transfer, in particular, below the excitation threshold of thermal vibrational convection. Along with the visualization of convective flows with the help of different types of tracers, the structure of vibroconvective cells was studied using a thermochromic film, which allows visualization of temperature fields in a liquid in the absence of tracers, that is, without disturbing the liquid.

2. Formulation and Methods

2.1. Problem Formulation

Convection in a horizontal plane layer with boundaries of different temperatures $T_1$ and $T_2$ is considered (Figure 1). The upper boundary temperature is higher than that of the lower one ($T_1>T_2$), so the gravity field plays a stabilizing role. The layer performs translational circular vibrations in the horizontal plane with an amplitude $b=4.4$ cm and frequency $\mathsf{\Omega }$, which varies in the interval $\mathsf{\Omega }=0-60$ s⁻¹. The oscillations are set using a mechanical vibrator, a description available in Kozlov et al. [12]. The radius vector $r$, drawn from the origin of a laboratory coordinate system $xyz$ to the origin of the moving system $x^{\prime }{y}^{\prime }{z}^{\prime }$ associated with the cavity, rotates with a frequency $\mathsf{\Omega }\equiv 2\pi f$ around the vertical axis z. Thus, the cavity performs translational displacement along the circle path (translational vibrations of circular polarization). At this, a spatially uniform inertial force field ${\mathsf{\Omega }}^{2}r$ rotates in the non-inertial frame of reference associated with the vibrating cavity. The direction of the inertial force field coincides with the vector $r$.

The layer used in the experiments (Figure 2) is formed by two parallel flat heat exchangers. The bottom heat exchanger is an aluminum plate 1, with channels through which the liquid of constant temperature is pumped. The heat exchanger is equipped with a heat flux sensor, which consists of a thin plate with low thermal conductivity 2 between the heat exchanger and top-mounted aluminum plate 3 with a thickness of 3 mm. The heat flux is measured according to the temperature drop $\Delta T$ at this thermal resistance. The thickness of the liquid layer in the experiments is $h=0.42$ cm or 0.32 cm, the lateral border diameter −13.8 cm. The upper heat exchanger 4 is transparent and serves to observe the convective structures in the layer. It is formed by two polished silicate glass plates 5 with a thickness of 4 mm, between which the fluid of a given temperature circulates. The temperature of the working surfaces of the liquid layer is measured by resistance thermometers with an accuracy 0.1 of °C. The temperature of the heat exchangers has constant values, due to the circulation of water at a given temperature coming from powerful jet thermostats. The working fluid is ethanol.

2.2. Experimental Technique and Procedure

In the course of the experiments, at given values of the temperature of the upper and lower heat exchangers, circular oscillations of a certain amplitude and frequency are reported to the cavity. The amplitude $b$ is measured accurately to the closest 0.1, mm using the marker at the cuvette. For this purpose, the moving cavity is photographed by high-resolution photo camera, and the radius of the marker trajectory is measured. The value of the amplitude is controlled in all the experiments. The radian frequency of vibration varies in the interval $\mathsf{\Omega }=0-60$ s⁻¹ and is kept constant at each step of the experiment with an accuracy of 0.1 s⁻¹.

At a monotonous stepwise increase of the vibration frequency (while controlling vibration amplitude), the temperature difference between the layer boundaries $\mathsf{\Theta }\equiv T_2-T_1$ and temperature drop $\Delta T$ at thermal resistance are measured. The measurements at each step are performed after the system reaches the stationary convection regime, which takes place five minutes after the vibration frequency change. The use of the transparent upper heat exchanger and the visualizing particles in the working fluid allows for the observation, and registration, of the convective patterns that form after the thermal convection excitation. A stroboscopic lamp, or a flash lamp, was used for the layer illumination.

To visualize the vibroconvective structures, along with traditional methods (using the traces—calliroscope or particles of Rezin-Amberlite), a thermochromic film was used in the experiments. This film is the microencapsulated liquid-crystal ink protected on both sides by a transparent polymer base. The ink changes its color when the temperature changes in a relatively narrow range, so the film can be used as a color temperature indicator. For the film used in the experiment, the activation range is from 30 °C to 35 °C. Outside this area, the film is black. At 30 °C, the film turns yellow-green and above 33 °C—blue and dark blue. The film with a thickness of 0.15 mm adheres to the lower boundary of the liquid layer over the heat flux sensor. To exclude the contact with the working fluid, the thermochromic film is additionally covered with a transparent film with a thickness equal to 0.10 mm. For the visualization of the vibroconvective patterns, the temperature at the cold lower boundary of the liquid layer is set slightly lower than 30 °C. In this case, under the conditions of convective equilibrium, the film at the surface has a uniform dark color. In the supercritical area, when the convective cells appear, the flows of the hot liquid descending from the upper boundary cause an increase in temperature near the surface of the lower layer boundary. As a result, the film changes its color in the areas of hot stream hitting. The experiments show that this technique resolves the convective cells even of a relatively small size. An important feature of the described technique is that it is not associated with the visualizing particles, which are added to the liquid and play the role of perturbations.

3. Results

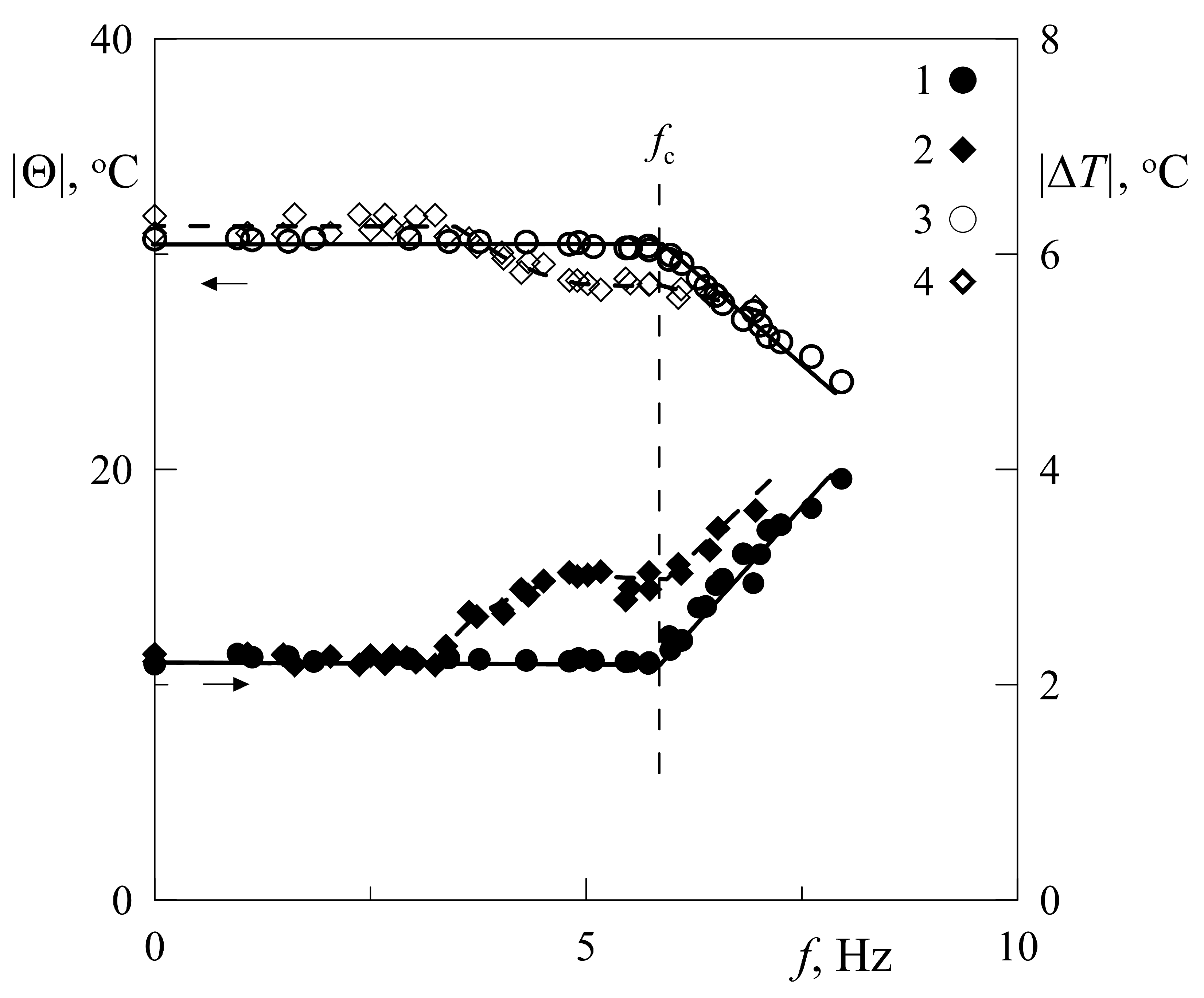
The liquid layer is heated from the top. At definite temperatures of heat exchangers and definite amplitude of vibrations, the frequency of vibrations is increased in a stepwise manner. In the absence of the visualizer in the range of low frequencies of vibrations, the temperature difference between the layer boundaries $\mathsf{\Theta }$ does not change with frequency; the liquid is in a quasi-equilibrium state (Figure 3, points 3). In this case, the heat flux, which is characterized by a temperature drop on $\Delta T$, remains unchanged (Figure 3, points 1). At reaching a certain critical frequency $f_c$ there is a threshold increase in heat flux through the layer $\Delta T$ (points 1), accompanied by a decrease in the temperature difference between the layer boundaries (points 3).

To visualize the vibroconvective flows, the calliroscope particles with the density slightly exceeding the density of the liquid were used, the characteristic particle size equals $40\pm 5$ μm. Experiments with and without particles added [12] showed that this visualizer does not affect the excitation threshold of vibrational convection, as well as the heat flux. Below the threshold of the thermovibrational convection excitation, at $f<f_c$, the particles were randomly distributed at the bottom of the cavity (Figure 4a). At the threshold, their redistribution in the form of periodically arranged rows is observed (Figure 4b). The photos of structures in Figure 4 are obtained in the conditions corresponding to the experiments presented in Figure 3 (points 1, 3). The photos show the top view of the working layer. At the top, a channel is visible through which the isothermal liquid is supplied to the central part of the upper transparent heat exchanger. In the top left part of fragment a, one can see the resistance thermometer sensor, which is a thin copper wire glued in the form of a snake to the inner boundary of the liquid layer. The sensor covers a relatively large area, which, unlike a point temperature sensor, makes it possible to measure the area-average boundary temperature even after developing cellular convection.

The results obtained in the experiments with the visualization by the Resin Amberlite particles (mass fraction less than 0.14%) with an average size $30\pm 10$ μm are shown by points 2, 4. At the vibration frequency $f<4$ Hz, the presence of the particles has practically no effect on the heat transfer. At the same time, already at these frequencies, the particles begin to gather in heaps located at a significant distance from each other (Figure 4c).

The presence of visualizer particles in the liquid leads to an increase in the heat flux through the layer, and as a result, the lowering of the temperature difference between the layer boundaries (Figure 3) in the frequency range ($f=4÷6$ Hz) up to the excitation threshold of thermovibrational convection in the absence of tracers. The particles of the visualizer form spatial periodic structures in the layer in the form of hills spaced at a considerable distance from each other (Figure 4c). With an increase in the intensity of vibrations, the distance between the hills decreases (Figure 4d). It can be assumed that, in this case, the intensification of heat transfer is caused by steady streaming flows [16], which are generated by hillocks as a result of fluid oscillations. In this case, the mounds themselves are formed by these averaged flows. This phenomenon, which was previously observed in Kozlov, Selin (Reference [15]), is of independent interest, but its description is beyond the scope of this work. It should be noted that a large number of studies have been devoted to the influence of vibrations on phase inclusions and their accumulation against the background of oscillations; a literature review can be found in Lappa (Reference [17]).

When the frequency exceeds the critical value ($f>f_c$), the structure of the hills and the distribution of the visualizer particles qualitative change. At $f=6.52$ Hz (Figure 4e), the visualizer particles form the elongated parallel rows similar to the case with the heavier particles of the calliroscope (Figure 4b). However, the structures formed by the lighter particles have a clearly visible periodic distribution of the particles along the rows length. It should be noted that in the supercritical area (at $f>f_c$), the change of $\Delta T$ and $\mathsf{\Theta }$, with the vibration frequency in the absence of tracers and in their presence are in qualitative agreement (Figure 3), which indicates the transition to the thermal vibrational convection mode.

The comparison of the fragments b and e in Figure 4 shows that in the supercritical area, the PIV particles visualize vibroconvective structures in the form of two-dimensional rolls, the distance between which is consistent with the results obtained using a calliroscope (Figure 4b). The question of the nature of the PIV particles accumulation into periodic heaps along the rows length remains open, if this distribution is associated with the interaction between the particles aggregations similar to ones observed in the subthreshold region (Figure 4d). The thermochromic visualization of the temperature distribution near the cold layer boundary answers this question. This technique excludes the presence of any particles that disturb the convective flows. Below the threshold of thermal vibrational convection excitation, at $f<6$ Hz in the considered case, the thermochromic film at the boundary of the layer has one color, which indicates the constancy of its temperature and the absence of convective structures. The photo of the film in the supercritical region (Figure 4f) demonstrates the presence of the spatial convective cells in the layer, and these cells are characterized by different spatial periods in perpendicular directions. The distance between the parallel rolls, which is characterized by the wavelength ${\lambda }_1$, corresponds to the thickness of the working layer, ${\lambda }_1~2h$. Such structures were previously observed in Reference [12]; it was shown that the distance between the parallel rolls is completely determined by the layer thickness. The visualization of convective flows with calliroscope in Reference [12] allowed an assumption about the two-dimensional form of the convective structures developing at the excitation threshold of the thermal vibrational convection. As one can see in Figure 4f, the convective cells are characterized not only by ${\lambda }_1$ but also by a spatial period ${\lambda }_2$. The reference directions of this spatial periods are perpendicular and the value of ${\lambda }_2$ is much less than that of ${\lambda }_1$.

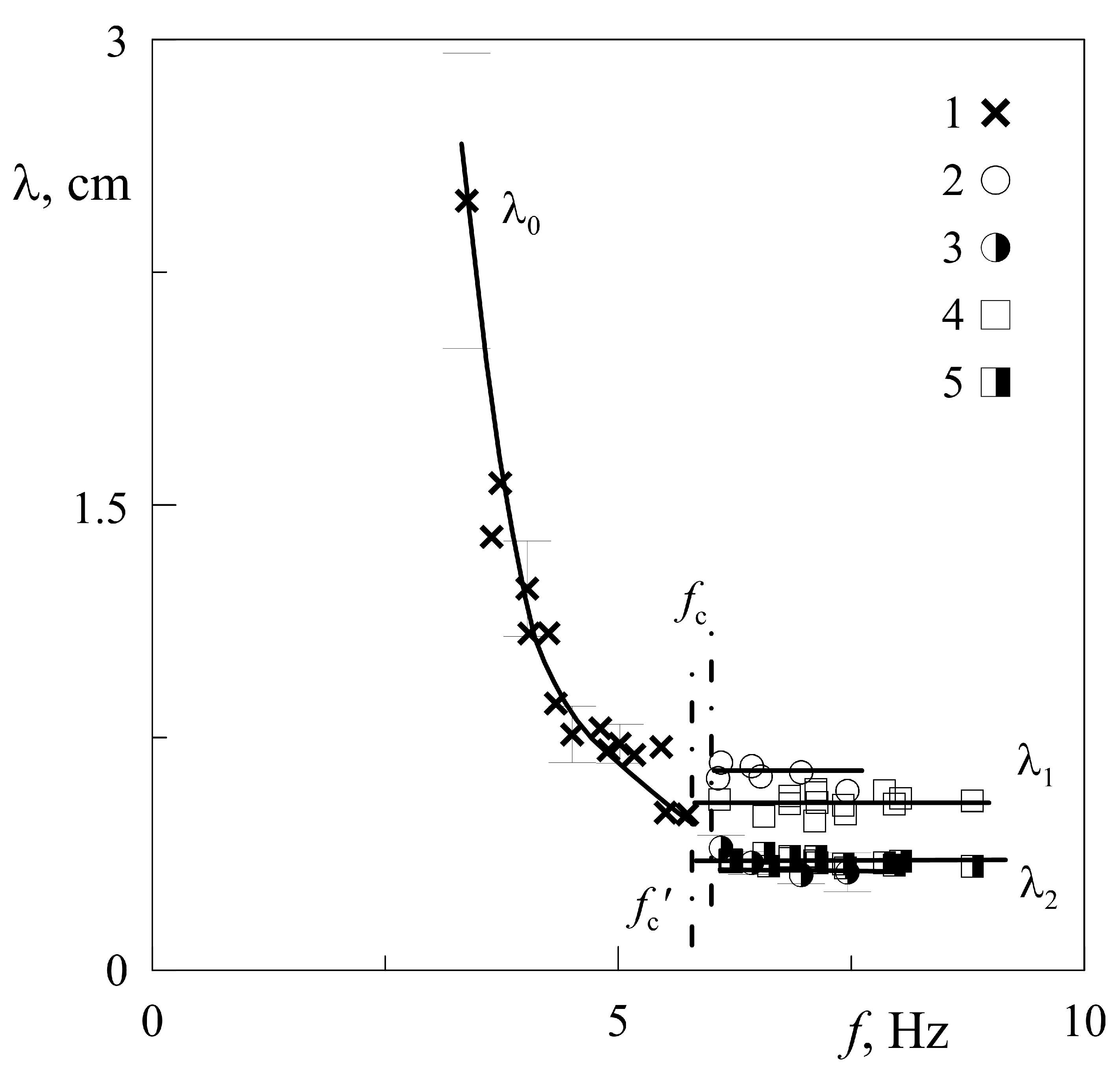
The characteristic linear dimensions of the structures (wavelength $\lambda$) depending on the vibration frequency are shown in Figure 5; the dashed lines $f_c$ indicates the threshold of convection excitation in layers $h=0.42$ cm. The visualizer is the Resin Amberlite particles, the layer is heated from above, $\mathsf{\Theta }=-30.7$. At a low frequency, the particles in the form of hillocks are distributed fairly uniformly in space, but without pronounced regularity. In Figure 5 points 1 correspond to the average distance between the hills tops. With increasing the vibration frequency, the average distance between the centers of adjacent hills ${\lambda }_0$ decreases. At frequency $f_c$ there is a redistribution of the particles and a qualitative change in the structures shape: The particles form the regular parallel rows. The average distance between the rows ${\lambda }_1$ is shown in Figure 5 by the points 2, and the average distance between the hills in a row ${\lambda }_2$ (at $f>f_c$)—by the points 3. The points 4 and 5 show the results of ${\lambda }_1$ and ${\lambda }_2$ measuring using the thermochromic technique of visualization of the convective flows in a layer $h=0.32$ cm ($f_c^{\prime }$—the threshold frequency). One can see, the thinner the layer, the shorter is the wavelength ${\lambda }_1$ (compare points 2 and 4).

It should be noted that under vibrations, the particles of the visualizer accumulate in the heaps relatively regularly located at the bottom of the cavity (Figure 4c,d) in the isothermal case too. The distance between the heaps is smaller than the non-isothermal case. With increasing the frequency, the distance between the heaps decreases monotonically. There is no redistribution of the particles at any frequency in an explored range; the distribution of the hillocks remains random, close to the hexagonal one.

In the experiments with using the calliroscope particles as a visualizer (concentration equals 0.02%) in the absence of heating, the regular patterns are not observed at any vibration parameters. The visualizer particles with relatively high density are randomly located at the bottom of the layer. Only when thermovibrational convection is excited, the visualizer distributes in the form of two-dimensional rows. This indicates that the presence of a small amount of the calliroscope particles in the liquid does not affect the excitation threshold of thermal vibrational convection. At the same time, the calliroscope particles do not visualize the flows with a relatively short wavelength.

4. Discussion

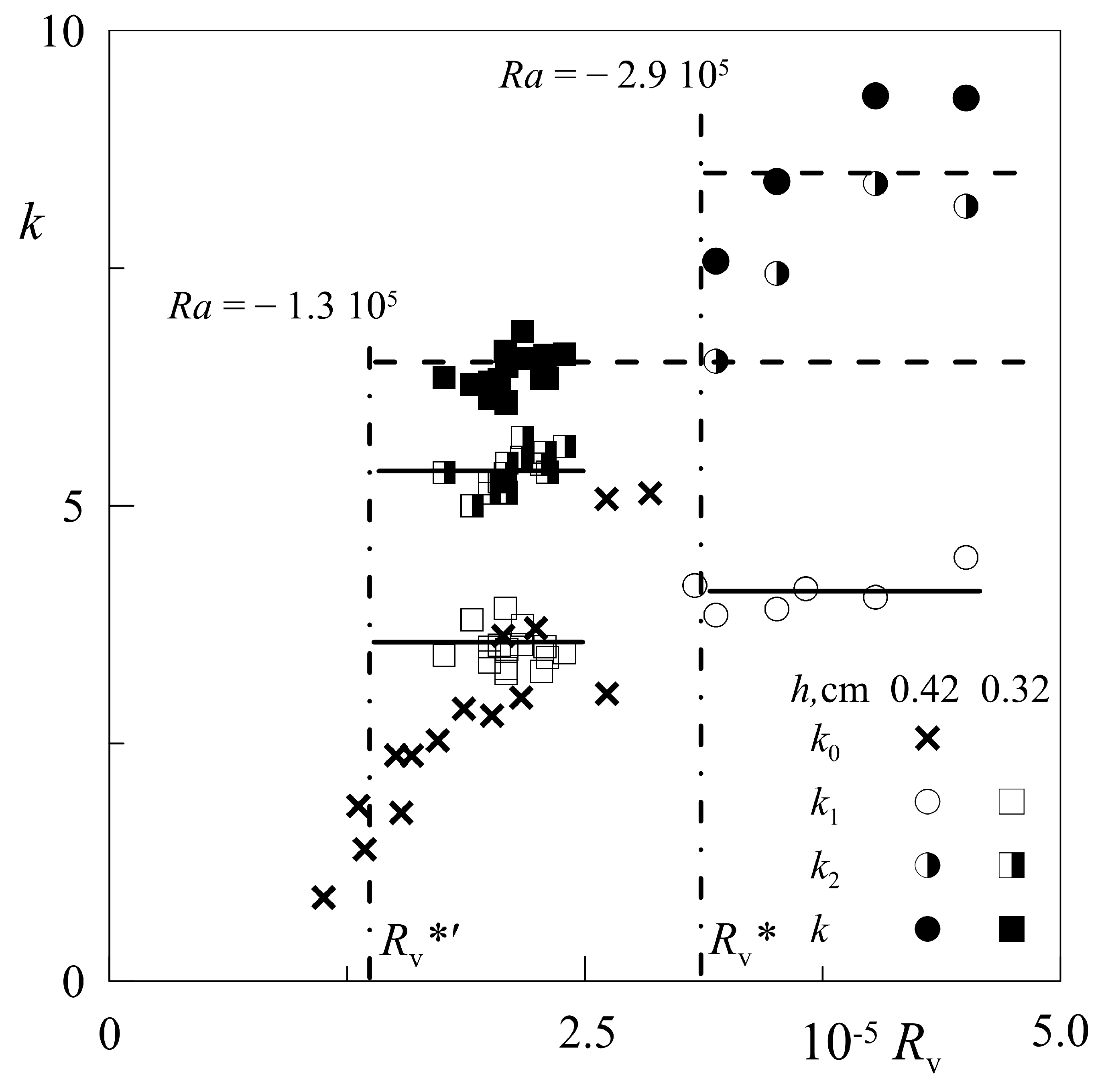
Figure 6 shows the dimensionless wavenumber $k$ of the spatial structures depending on the vibrational parameter $R_{\mathrm{v}}$. The experimental conditions and designations correspond to Figure 5. The wavenumber $k_0$ for the points corresponds to the case of spatial structures in the form of heaps located in an order similar to the hexagonal one (points 1 in Figure 5). To calculate the wavenumber, the equation for the hexagonal structures is used, $k_0={4\pi h/\sqrt{3}\lambda }_0$ [18].

To calculate the dimensionless wavenumber $k$ in the case of convective structures characterized by a periodic change in mutually perpendicular directions (points 2 and 3 in Figure 5), the term $k=\sqrt{k_1^2+k_2^2}$ is used. Here the wavenumber $k_1={2\pi h/\lambda }_1$ corresponds to the periodic distribution with a bigger wavelength (Figure 5, points 2 and 4), and $k_2=2\pi h/{\lambda }_2$ characterizes the distribution of the hills along each row.

It should be noted that the wavenumber $k_1$ in the supercritical region turns out to be constant and plactically the same in the layers of different thicknesses, $h=0.42$ and 0.32 cm (Figure 6, transparent circles and squares). Moreover, its value is close to the theoretical value $k=3.23$ [1] of the most dangerous disturbances in the problem of vibrational convection in plane layer in zero gravity. It is important to note that this wavenumber corresponds to the optimal size of two-dimensional convective rolls, consistent with the thickness of the liquid layer; the wavelength is close to twice the thickness of the layer. At the same time, the total wavenumber of the convective cells $k$ under the conditions of the performed experiment turns out to be much higher and is in good agreement with the theoretical value predicted by the linear theory of stability (shown by the dashed line). This is achieved due to the short-wave modulation of the structure of convective rolls along their length with the wavenumber $k_2=2\pi h/{\lambda }_2$. The results indicate that in the absence of a selected direction of translational vibrations (at the vibrations of circular polarization) under the conditions of a strong stabilizing effect of a static gravity field, the structure of vibroconvective cells is characterized by the strong inhomogeneity in perpendicular directions.

One can see that with increase of negative value of $Ra$ the threshold value of corresponding vibrational parameter $R_{\mathrm{v}}^{*}$ grows in good agreement with the theory [13]. At this, the critical value of total wavenumber $k$ also significantly grows; but the wavenumber $k_1$ practically does not change, it keeps the value, which corresponds to the vortexes occupying the whole layer thickness, and thus, providing the optimal heat transfer. The growth of $k$ with $\left|Ra\right|$, which also takes place in good agreement with the linear theory, happens due to rapid growth of $k_2$. Such a phenomenon is found for the first time and could be named “the beads instability”, it takes place at high negative Rayleigh numbers ($\left|Ra\right|>{10}^5$), due to strong interaction of two mechanisms, thermogravitational (playing the stabilizing role) and the destabilizing thermovibrational one. The dominant role of vibroconvective structures in the form of parallel rolls with a wavenumber $k_1~3$ discovered in the experiments is consistent with the results of theoretical analysis [11], where it was shown that in the case of circular shaking, when the system is isotropic in the time average sense, the onset of convection corresponds to the 2D system of rolls with the roll axis selected spontaneously, in the case of positive and negative values of $Ra$. Reference [11], however, corresponds to the smaller negative values of $\left|Ra\right|$ and moderate dimensionless frequencies ($\omega \sim 50$), while in the present study the dimensionless frequency of vibrations is an order higher ($\omega \sim 500$).

The experiments suggest that the increase of heat transfer in the subthreshold (in terms of vibrational thermal convection) area in the experiments with visualizer particles (PIV particles) located near the bottom of the cavity, is associated with the excitation of the averaged flows generated as a result of the system of heaps formation. As it has been mentioned, the appearance of the heaps is not of thermal origin. It should be noted that a similar phenomenon of the formation of a spatially ordered system of hills was observed on the surface of quartz sand in a cavity filled with liquid, performing high-frequency circular oscillations in the horizontal plane [19]. In that case, the emergence of a quasi-stationary “frozen” relief at the interface (liquefied granular medium and pure liquid), performing tangential circular oscillations, was associated with developing the Kelvin-Helmholtz instability. This fact was confirmed by comparison with a similar “frozen” relief at the boundary of liquids at circular vibrations of the cavity [20].

A similar distribution of the particles of the visualizer suspended near the bottom of the cavity was previously observed in a flat layer performing the oscillations of a spherical pendulum [15]. In this case, in agreement with the results of the present experiment, the wavenumber of structures increases with a dimensionless frequency and practically does not depend on the temperature conditions at the layer boundaries.

5. Conclusions

This article experimentally instigated the structure of the vibroconvective flows excited in the horizontal plane layer by the translational vibrations of circular polarization under conditions of high negative Rayleigh numbers. An important feature of the problem is the absence of a preferred direction of translational vibration. It was found that, in this case, the vibroconvective cells, developing in a threshold manner upon reaching the threshold value of the vibration parameter $R_{\mathrm{v}}$, are characterized by a strong heterogeneity of sizes in different directions. The wavenumbers, characterizing the spatial periods in perpendicular directions, differ several times; the convective structures have the form of a system of parallel rolls, with a regular change in their dimensions along the length. The transverse size of the rolls is consistent with the thickness of the liquid layer; at the same time, the total wavenumber of the vibroconvective cells is much higher and is consistent with the theoretical value predicted by the linear analysis of vibroconvective stability. Such a selection of the vibroconvective patterns (in the form of asymmetric cells) in the absence of a definite direction of vibrations is observed for the first time. It will be interesting to check if such an overcritical behavior (when the size of vibroconvective vortexes is near to the layer thickness) will remains at much higher negative values of $Ra$, when predicted by the linear theory wavenumber $k$ will be extremely high.

It was found that the presence of the relatively dense calliroscope particles in the liquid, which are located directly at the bottom of the layer, does not affect the excitation threshold of the thermal vibrational convection. At the same time, the particles of the visualizer close in density to the liquid, which are suspended near its boundary and under vibrations gather into the hillocks, cause the increase in heat transport in the subthreshold region (below the threshold of thermovibrational convection excitation). This is because the particles change the bottom surface profile, as a result of the redistribution, which leads to the steady flows and an increase in the heat transfer. With an increase in the dimensionless frequency, the wavenumber characterizing the spatial arrangement of the hills increases.