Experimental Study on Coherent Structures by Particles Suspended in Half-Zone Thermocapillary Liquid Bridges: Review
Abstract
1. Introduction
2. Materials and Methods
3. Thermocapillary-Driven Convection and Coherent Structures
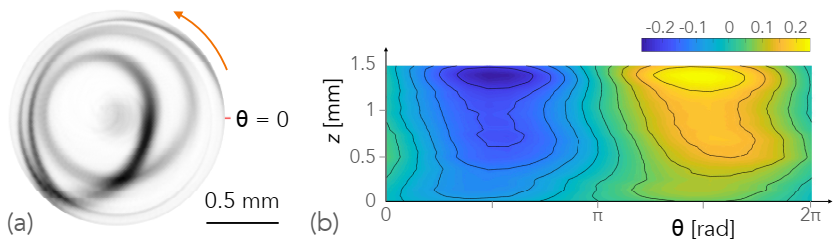
3.1. General View
3.2. Particle Path Lines to Form Coherent Structures
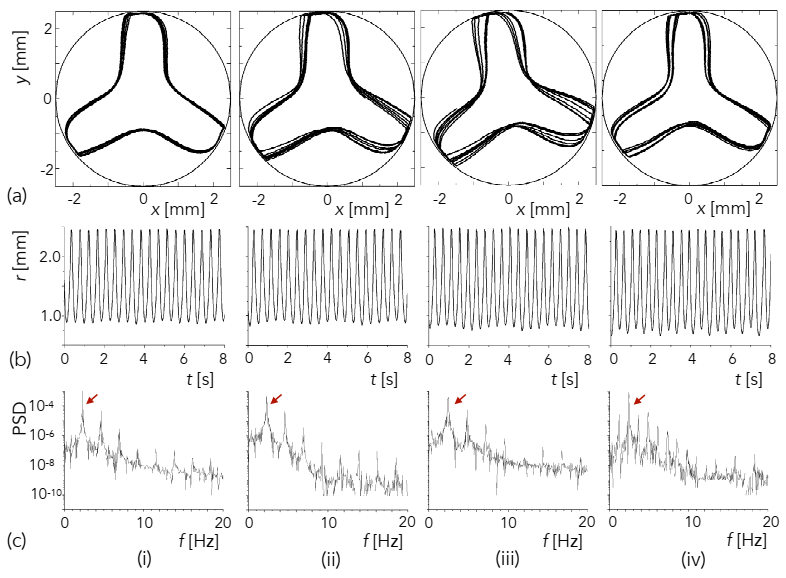
3.2.1. Path Lines
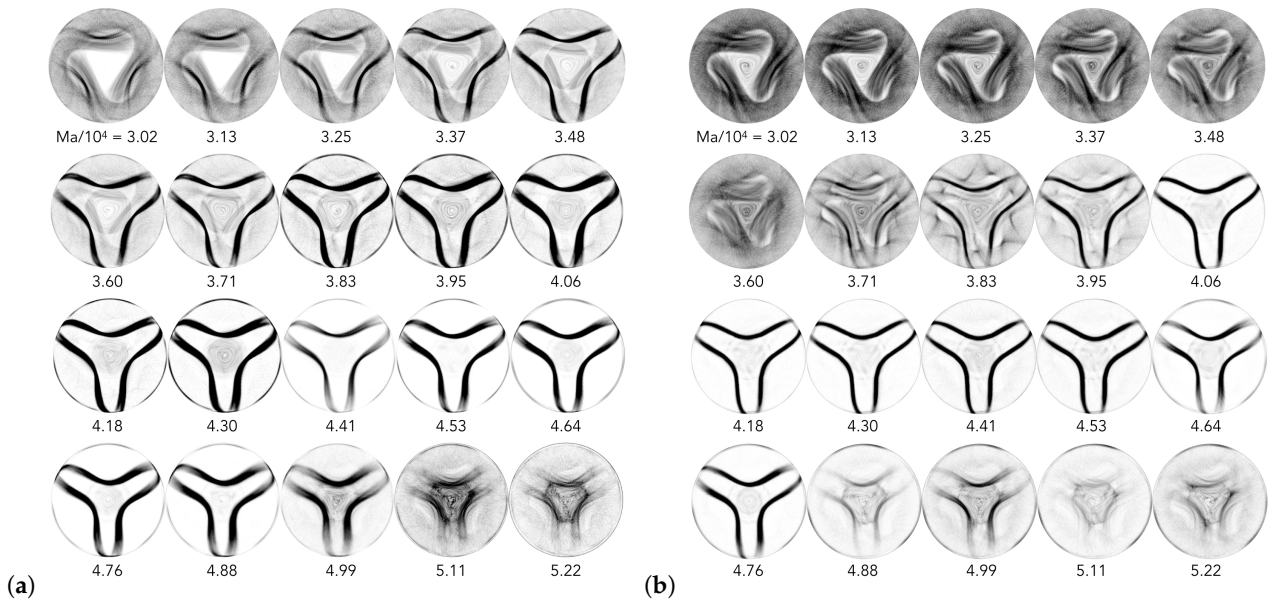
3.2.2. Pattern Map
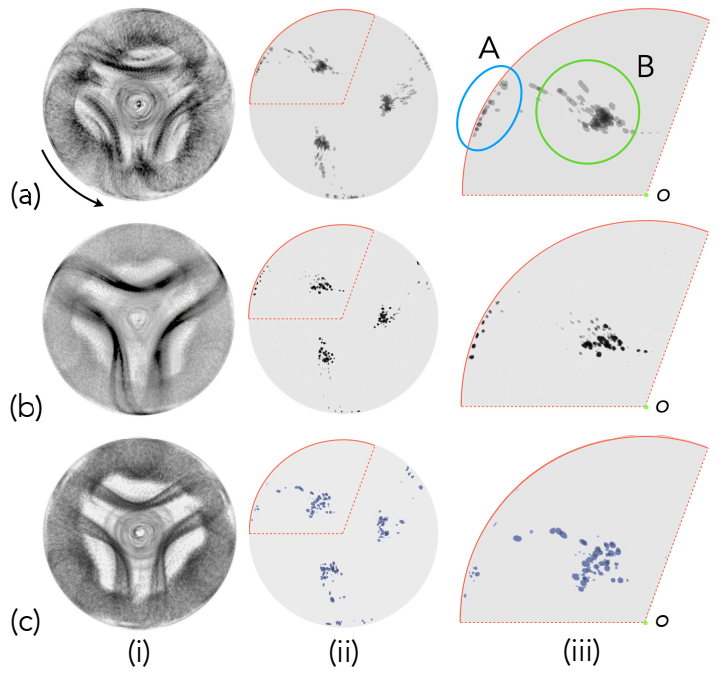
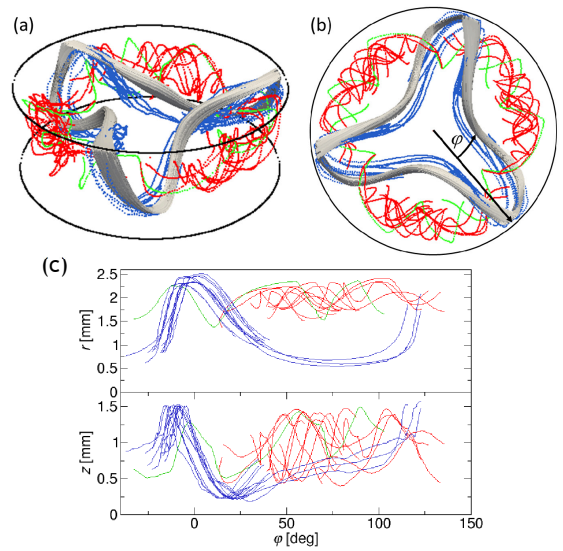
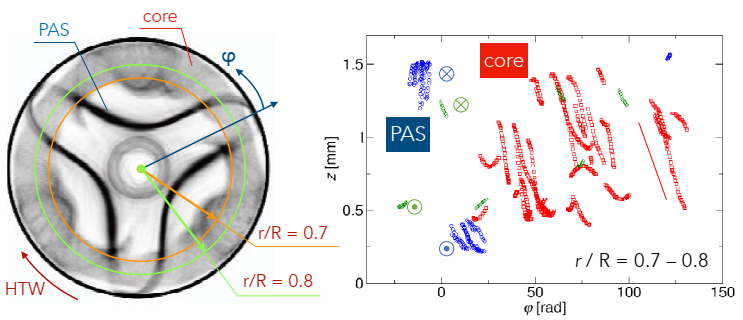
3.2.3. Particle Behaviours
3.2.4. On-Going Topics
4. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HTW | Hydrothermal wave |
| JEREMI | Japanese European Research Experiments on Marangoni Instability |
| PAS | Particle accumulation structure |
References and Notes
- Schwabe, D.; Hintz, P.; Frank, S. New features of thermocapillary convection in floating zones revealed by tracer particle accumulation structure (PAS). Microgravity Sci. Technol. 1996, 9, 163–168. [Google Scholar]
- Preisser, F.; Schwabe, D.; Scharmann, A. Steady and oscillatory thermocapillary convection in liquid columns with free cylindrical surface. J. Fluid Mech. 1983, 126, 545–567. [Google Scholar] [CrossRef]
- Wanschura, M.; Shevtsova, V.M.; Kuhlmann, H.C.; Rath, H.J. Convective instability mechanisms in thermocapillary liquid bridges. Phys. Fluids 1995, 7, 912–925. [Google Scholar] [CrossRef]
- Leypoldt, J.; Kuhlmann, H.C.; Rath, H.J. Three-dimensional numerical simulation of thermocapillary flows in cylindrical liquid bridges. J. Fluid Mech. 2000, 414, 285–314. [Google Scholar] [CrossRef]
- Ueno, I.; Tanaka, S.; Kawamura, H. Oscillatory and chaotic thermocapillary convection in a half-zone liquid bridge. Phys. Fluids 2003, 15, 408–416. [Google Scholar] [CrossRef]
- Xu, J.J.; Davis, S.H. Convective thermocapillary instabilities in liquid bridges. Phys. Fluids 1984, 27, 1102–1107. [Google Scholar] [CrossRef]
- Ogasawara, T.; Motegi, K.; Hori, T.; Ueno, I. Secondary instability induced by thermocapillary effect in half-zone liquid bridge of high Prandtl number fluid. Mech. Eng. Lett. 2019, 5, 1900014. [Google Scholar] [CrossRef]
- Tanaka, S.; Kawamura, H.; Ueno, I.; Schwabe, D. Flow structure and dynamic particle accumulation in thermocapillary convection in a liquid bridge. Phys. Fluids 2006, 18, 067103. [Google Scholar] [CrossRef]
- Schwabe, D.; Mizev, A.I.; Udhayasankar, M.; Tanaka, S. Formation of dynamic particle accumulation structures in oscillatory thermocapillary flow in liquid bridges. Phys. Fluids 2007, 19, 072102. [Google Scholar] [CrossRef]
- Yano, T.; Maruyama, K.; Matsunaga, T.; Nishino, K. Effect of ambient gas flow on the instability of Marangoni convection in liquid bridges of various volume ratios. Int. J. Heat Mass Transf. 2016, 99, 182–191. [Google Scholar] [CrossRef]
- Toyama, A.; Gotoda, M.; Kaneko, T.; Ueno, I. Existence conditions and formation process of second type of spiral loop particle accumulation structure (SL-2 PAS) in half-zone liquid bridge. Microgravity Sci. Technol. 2017, 29, 263–274. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Hori, T.; Ueno, I. Long-term behaviors of a single particle forming a coherent structure in thermocapillary-driven convection in half-zone liquid bridge of high Prandtl-number fluid. Int. J. Microgravity Sci. Appl. 2019, 36, 360203. [Google Scholar]
- Gotoda, M.; Toyama, A.; Ishimura, M.; Sano, T.; Suzuki, M.; Kaneko, T.; Ueno, I. Experimental study of coherent structures of finite-size particles in thermocapillary liquid bridges. Phys. Rev. Fluids 2019, 4, 094301. [Google Scholar] [CrossRef]
- Oba, T.; Toyama, A.; Hori, T.; Ueno, I. Experimental study on behaviors of low-Stokes number particles in weakly chaotic structures induced by thermocapillary effect within a closed system with a free surface. Phys. Rev. Fluids 2019, 4, 104002. [Google Scholar] [CrossRef]
- Takatsuka, M.; Tanaka, S.; Ueno, I.; Kawamura, H. Dynamic particle accumulation structure of Marangoni convection in liquid bridge—2. numerical simulation. In Proceedings of the Thermal Engineering Conference; Japan Society for Mechanical Engineers: Tokyo, Japan, 2002; pp. 307–308. [Google Scholar]
- Seki, T.; Tanaka, S.; Kawamura, H. Numerical simulation of particle accumulatoin structure in oscillatory thermocapillary convection of a liquid bridge. In Proceedings of the Thermal Engineering Conference; Japan Society for Mechanical Engineers: Tokyo, Japan, 2005; pp. 169–170. [Google Scholar]
- Hofmann, E.; Kuhlmann, H.C. Particle accumulation on periodic orbits by repeated free surface collisions. Phys. Fluids 2011, 23, 072106. [Google Scholar] [CrossRef]
- Melnikov, D.E.; Pushkin, D.O.; Shevtsova, V.M. Accumulation of particles in time-dependent thermocapillary flow in a liquid bridge: Modeling and experiments. Eur. Phys. J. Spec. Top. 2011, 192, 29–32. [Google Scholar] [CrossRef][Green Version]
- Lappa, M. Assessment of the role of axial vorticity in the formation of particle accumulation structures in supercritical Marangoni and hybrid thermocapillary-rotation-driven flows. Phys. Fluids 2013, 25, 012101. [Google Scholar] [CrossRef]
- Romanò, F.; Kuhlmann, H.C. Finite-size Lagrangian coherent structures in thermocapillary liquid bridges. Phys. Rev. Fluids 2018, 3, 094302. [Google Scholar] [CrossRef]
- Kawamura, H.; Nishino, K.; Matsumoto, S.; Ueno, I. Report on microgravity experiments of Marangoni convection aboard International Space Station. J. Heat Transf. 2012, 134, 031005. [Google Scholar] [CrossRef]
- Shevtsova, V.; Gaponenko, Y.; Kuhlmann, H.C.; Lappa, M.; Lukasser, M.; Matsumoto, S.; Mialdun, A.; Montanero, J.M.; Nishino, K.; Ueno, I. The JEREMI-project on thermocapillary convection in liquid bridges. Part B: Overview on impact of co-axial gas flow. Fluid Dyn. Mater. Process. 2014, 10, 197–240. [Google Scholar]
- Kuhlmann, H.C.; Lappa, M.; Melnikov, D.E.; Mukin, R.V.; Muldoon, F.H.; Pushkin, D.O.; Shevtsova, V.M.; Ueno, I. The JEREMI-Project on thermocapillary convection in liquid bridge. Part A: Particle Accumulation Structures. Fluid Dyn. Mater. Process. 2014, 10, 1–10. [Google Scholar]
- Chun, C.H.; Wuest, W. A micro-gravity simulation of the Marangoni convection. Acta Astronaut. 1978, 5, 681–686. [Google Scholar] [CrossRef]
- Lan, C.W.; Kim, Y.J.; Kou, S. A half-zone study of Marangoni convection in floating-zone crystal growth under microgravity. J. Cryst. Growth 1990, 104, 801–808. [Google Scholar] [CrossRef]
- Cao, Z.H.; Xie, J.C.; Tang, Z.M.; Hu, W.R. The influence of buoyancy on the onset of oscillatory convection in a half floating zone. Adv. Space Res. 1991, 11, 163–166. [Google Scholar] [CrossRef]
- Velten, R.; Schwabe, D.; Scharmann, A. The periodic instability of thermocapillary convection in cylindrical liquid bridges. Phys. Fluids A 1991, 3, 267–279. [Google Scholar] [CrossRef]
- Petrov, V.; Schatz, M.F.; Muehlner, K.A.; VanHook, S.J.; McCormick, W.D.; Swift, J.B.; Swinney, H.L. Nonlinear control of remote unstable states in a liquid bridge convection experiment. Phys. Rev. Lett. 1996, 77, 3779–3782. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Nishizawa, S.; Sakurai, M. Experimental results of oscillatory Marangoni convection in a liquid bridge under normal gravity. J. Jpn. Soc. Microgravity Appl. 1997, 14, 122–129. [Google Scholar]
- Hirata, A.; Sakurai, M.; Ohishi, N. Effect of gravity on Marangoni convection in a liquid bridge. J. Jpn. Soc. Microgravity Appl. 1997, 14, 130–136. [Google Scholar]
- Shevtsova, V.M.; Mojahed, M.; Legros, J.C. The loss of stability in ground based experiments in liquid bridges. Acta Astronaut. 1999, 44, 625–634. [Google Scholar] [CrossRef]
- Kamotani, Y.; Wang, L.; Hatta, S.; Wang, A.; Yoda, S. Free surface heat loss effect on oscillatory thermocapillary flow in liquid bridges of high Prandtl number fluids. Int. J. Heat Mass Transf. 2003, 46, 3211–3220. [Google Scholar] [CrossRef]
- Shiomi, J.; Kudo, M.; Ueno, I.; Kawamura, H.; Amberg, G. Feedback control of oscillatory thermocapillary convection in a half-zone liquid bridge. J. Fluid Mech. 2003, 496, 193–211. [Google Scholar] [CrossRef]
- Irikura, M.; Arakawa, Y.; Ueno, I.; Kawamura, H. Effect of ambient fluid flow upon onset of oscillatory thermocapillary convection in half-zone liquid bridge. Microgravity Sci. Technol. 2005, 16, 176–180. [Google Scholar] [CrossRef]
- Wang, A.; Kamotani, Y.; Yoda, S. Oscillatory thermocapillary flow in liquid bridges of high Prandtl number fluid with free surface heat gain. Int. J. Heat Mass Transf. 2007, 50, 4195–4205. [Google Scholar] [CrossRef]
- Tiwari, S.; Nishino, K. Effect of confined and heated ambient air on onset of instability in liquid bridges of high Pr fluids. Fluid Dyn. Mater. Process. (FDMP) 2010, 6, 109–136. [Google Scholar]
- Ueno, I.; Kawazoe, A.; Enomoto, H. Effect of ambient-gas forced flow on oscillatory thermocapillary convection of half-zone liquid bridge. Fluid Dyn. Mater. Process. (FDMP) 2010, 6, 99–108. [Google Scholar]
- Schwabe, D.; Mizev, A.I. Particles of different density in thermocapillary liquid bridges under the action of travelling and standing hydrothermal waves. Eur. Phys. J. Spec. Top. 2011, 192, 13–27. [Google Scholar] [CrossRef]
- Melnikov, D.E.; Pushkin, D.O.; Shevtsova, V.M. Synchronization of finite-size particles by a traveling wave in a cylindrical flow. Phys. Fluids 2013, 25, 092108. [Google Scholar] [CrossRef]
- Melnikov, D.E.; Watanabe, T.; Matsugase, T.; Ueno, I.; Shevtsova, V. Experimental study on formation of particle accumulation structures by a thermocapillary flow in a deformable liquid column. Microgravity Sci. Technol. 2014, 26, 365–374. [Google Scholar] [CrossRef]
- Gotoda, M.; Melnikov, D.E.; Ueno, I.; Shevtsova, V. Experimental study on dynamics of coherent structures formed by inertial solid particles in three-dimensional periodic flows. Chaos 2016, 26, 073106. [Google Scholar] [CrossRef]
- Yano, T.; Nishino, K.; Ueno, I.; Matsumoto, S.; Kamotani, Y. Sensitivity of hydrothermal wave instability of Marangoni convection to the interfacial heat transfer in long liquid bridges of high Prandtl number fluids. Phys. Fluids 2017, 29, 044105. [Google Scholar] [CrossRef]
- Yano, T.; Nishino, K.; Matsumoto, S.; Ueno, I.; Komiya, A.; Kamotani, Y.; Imaishi, N. Overview of “Dynamic Surf” project in Kibo—Dynamic behavior of large-scale thermocapillary liquid bridges in microgravity. Int. J. Microgravity Sci. Appl. 2018, 35, 350102. [Google Scholar]
- Yano, T.; Nishino, K.; Matsumoto, S.; Ueno, I.; Komiya, A.; Kamotani, Y.; Imaishi, N. Report on microgravity experiments of dynamic surface deformation effects on Marangoni instability in high-Prandtl-number liquid bridges. Microgravity Sci. Technol. 2018, 30, 599–610. [Google Scholar] [CrossRef]
- Yano, T.; Nishino, K.; Kawamura, H.; Ueno, I.; Matsumoto, S.; Ohnishi, M.; Sakurai, M. Space experiment on the instability of Marangoni convection in large liquid bridge—MEIS-4: Effect of Prandtl number. J. Phys. Conf. Ser. 2011, 327, 012029. [Google Scholar] [CrossRef]
- Yano, T.; Nishino, K.; Kawamura, H.; Ueno, I.; Matsumoto, S.; Ohnishi, M.; Sakurai, M. 3-D PTV measurement of Marangoni convection in liquid bridge in space experiment. Exp. Fluids 2012, 53, 9–20. [Google Scholar] [CrossRef]
- Sato, F.; Ueno, I.; Kawamura, H.; Nishino, K.; Matsumoto, S.; Ohnishi, M.; Sakurai, M. Hydrothermal wave instability in a high-aspect-ratio liquid bridge of Pr > 200 On-orbit experiments in the Japanese Experiment Module ’Kibo’ aboard the International Space Station. Microgravity Sci. Technol. 2013, 25, 43–58. [Google Scholar] [CrossRef]
- Yano, T.; Nishino, K.; Kawamura, H.; Ueno, I.; Matsumoto, S. Instability and associated roll structure of Marangoni convection in high Prandtl number liquid bridge with large aspect ratio. Phys. Fluids 2015, 27, 024108. [Google Scholar] [CrossRef]
- Nishino, K.; Yano, T.; Kawamura, H.; Matsumoto, S.; Ueno, I.; Ermakov, M.K. Instability of thermocapillary convection in long liquid bridges of high Prandtl number fluids in microgravity. J. Cryst. Growth 2015, 420, 57–63. [Google Scholar] [CrossRef]
- Matsugase, T.; Ueno, I.; Nishino, K.; Ohnishi, M.; Sakurai, M.; Matsumoto, S.; Kawamura, H. Transition to chaotic thermocapillary convection in a half zone liquid bridge. Int. J. Heat Mass Transf. 2015, 89, 903–912. [Google Scholar] [CrossRef]
- Pushkin, D.O.; Melnikov, D.E.; Shevtsova, V.M. Ordering of small particles in one-dimensional coherent structures by time-periodic flows. Phys. Rev. Lett. 2011, 106, 234501. [Google Scholar] [CrossRef] [PubMed]
- Kuhlmann, H.C.; Hofmann, E. The mechanics of particle accumulation structures in thermocapillary flows. Eur. Phys. J. Spec. Top. 2011, 192, 3–12. [Google Scholar] [CrossRef]
- Kuhlmann, H.C.; Muldoon, F.H. Particle-accumulation structures in periodic free-surface flows: Inertia versus surface collisions. Phys. Rev. E 2012, 85, 046310. [Google Scholar] [CrossRef] [PubMed]
- Kuhlmann, H.C.; Muldoon, F.H. On the different manifestations of particle accumulation structures (PAS) in thermocapillary flows. Eur. Phys. J. Spec. Top. 2013, 219, 59–69. [Google Scholar] [CrossRef]
- Mukin, R.V.; Kuhlmann, H.C. Topology of hydrothermal waves in liquid bridges and dissipative structures of transported particles. Phys. Rev. E 2013, 88, 053016. [Google Scholar] [CrossRef] [PubMed]
- Muldoon, F.H.; Kuhlmann, H.C. Origin of particle accumulation structures in liquid bridges: Particle-boundary-interactions versus inertia. Phys. Fluids 2016, 28, 073305. [Google Scholar] [CrossRef]
- Romanò, F.; Kuhlmann, H.C.; Ishimura, M.; Ueno, I. Limit cycles for the motion of finite-size particles in axisymmetric thermocapillary flows in liquid bridges. Phys. Fluids 2017, 29, 093303. [Google Scholar] [CrossRef]
- Muldoon, F.H.; Kuhlmann, H.C. Coherent particulate structures by boundary interaction of small particles in confined periodic flows. Phys. D Nonlinear Phenom. 2013, 253, 40–65. [Google Scholar] [CrossRef]
- Gotoda, M.; Sano, T.; Kaneko, T.; Ueno, I. Evaluation of existence region and formation time of particle accumulation structure (PAS) in half-zone liquid bridge. Eur. Phys. J. Spec. Top. 2015, 224, 299–307. [Google Scholar] [CrossRef]
- Abe, Y.; Ueno, I.; Kawamura, H. Dynamic particle accumulation structure due to thermocapillary effect in noncylindrical half-zone liquid bridge. Ann. N. Y. Acad. Sci. 2009, 1161, 240–245. [Google Scholar] [CrossRef] [PubMed]
- Kuhlmann, H.C.; Mukin, R.V.; Sano, T.; Ueno, I. Structure and dynamics of particle-accumulation in thermocapillary liquid bridges. Fluid Dyn. Res. 2014, 46, 041421. [Google Scholar] [CrossRef]
- Niigaki, Y.; Ueno, I. Formation of particle accumulation structure (PAS) in half-zone liquid bridge under an effect of thermo-fluid flow of ambient gas. Trans. JSASS (Japan Soc. Aeronaut. Space Sci. Aerosp. Technol.) 2012, 10, Ph33–Ph37. [Google Scholar] [CrossRef]
- Kang, Q.; Wu, D.; Duan, L.; Hu, L.; Wang, J.; Zhang, P.; Hu, W. The effects of geometry and heating rate on thermocapillary convection in the liquid bridge. J. Fluid Mech. 2019, 881, 951–982. [Google Scholar] [CrossRef]
- Kang, Q.; Wu, D.; Duan, L.; Zhang, J.; Zhou, B.; Wang, J.; Han, Z.; Hu, L.; Hu, W. Space experimental study on wave modes under instability of thermocapillary convection in liquid bridges on Tiangong-2. Phys. Fluids 2020, 32, 034107. [Google Scholar]
- Wang, J.; Wu, D.; Duan, L.; Kang, Q. Transition to chaos of buoyant-thermocapillary convection in large-scale liquid bridges. Microgravity Sci. Technol. 2020, 32, 217–227. [Google Scholar] [CrossRef]
- Nishimura, M.; Ueno, I.; Nishino, K.; Kawamura, H. 3D PTV measurement of oscillatory thermocapillary convection in half-zone liquid bridge. Exp. Fluids 2005, 38, 285–290. [Google Scholar] [CrossRef]
- Romanò, F.; Kuhlmann, H.C. Private communications.
- Yazawa, S.; Kawamura, H. Experiment of Marangoni convection in a liquid bridge with a low to medium aspect ratio. In Proceedings of the National Heat Transfer Symposium of Japan (in Japanese), Hokkaido, Japan, 26–28 May 2010; p. SP409. [Google Scholar]
- Sasaki, Y.; Tanaka, S.; Kawamura, H. Particle accumulation structure in thermocapillary convection of small liquid bridge. In Proceedings of the 6th Japan/China Workshop on Microgravity Sciences, Saga, Japan, 22–26 October 2005. [Google Scholar]
- Sakata, T.; Ueno, I. (The University of Tokyo, Tokyo, Japan). Private communications.
- Fujimoto, S.; Ogasawara, T.; Ota, A.; Motegi, K.; Ueno, I. Effect of heat loss on hydrothermal wave instability in half-zone liquid bridges of high Prandtl number fluid. Int. J. Microgravity Sci. Appl. 2019, 36, 360204. [Google Scholar]
- Capobianchi, P.; Lappa, M. On the influence of gravity on particle accumulation structures in high aspect-ratio liquid bridges. J. Fluid Mech. 2021, 908, A29. [Google Scholar] [CrossRef]
- Barmak, I.; Romanò, F.; Kuhlmann, H.C. Particle accumulation in high-Prandtl-number liquid bridges. Proc. Appl. Math. Mech. 2019, 19, e201900058. [Google Scholar] [CrossRef]
- Barmak, I.; Romanò, F.; Kannan, P.K.; Kuhlmann, H.C. Coherent particle structures in high-Prandtl-number liquid bridges. Microgravity Sci. Technol. 2021, 33, 19. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ueno, I. Experimental Study on Coherent Structures by Particles Suspended in Half-Zone Thermocapillary Liquid Bridges: Review. Fluids 2021, 6, 105. https://doi.org/10.3390/fluids6030105
Ueno I. Experimental Study on Coherent Structures by Particles Suspended in Half-Zone Thermocapillary Liquid Bridges: Review. Fluids. 2021; 6(3):105. https://doi.org/10.3390/fluids6030105
Chicago/Turabian StyleUeno, Ichiro. 2021. "Experimental Study on Coherent Structures by Particles Suspended in Half-Zone Thermocapillary Liquid Bridges: Review" Fluids 6, no. 3: 105. https://doi.org/10.3390/fluids6030105
APA StyleUeno, I. (2021). Experimental Study on Coherent Structures by Particles Suspended in Half-Zone Thermocapillary Liquid Bridges: Review. Fluids, 6(3), 105. https://doi.org/10.3390/fluids6030105





