Time-Periodic Cooling of Rayleigh–Bénard Convection
Abstract
1. Introduction
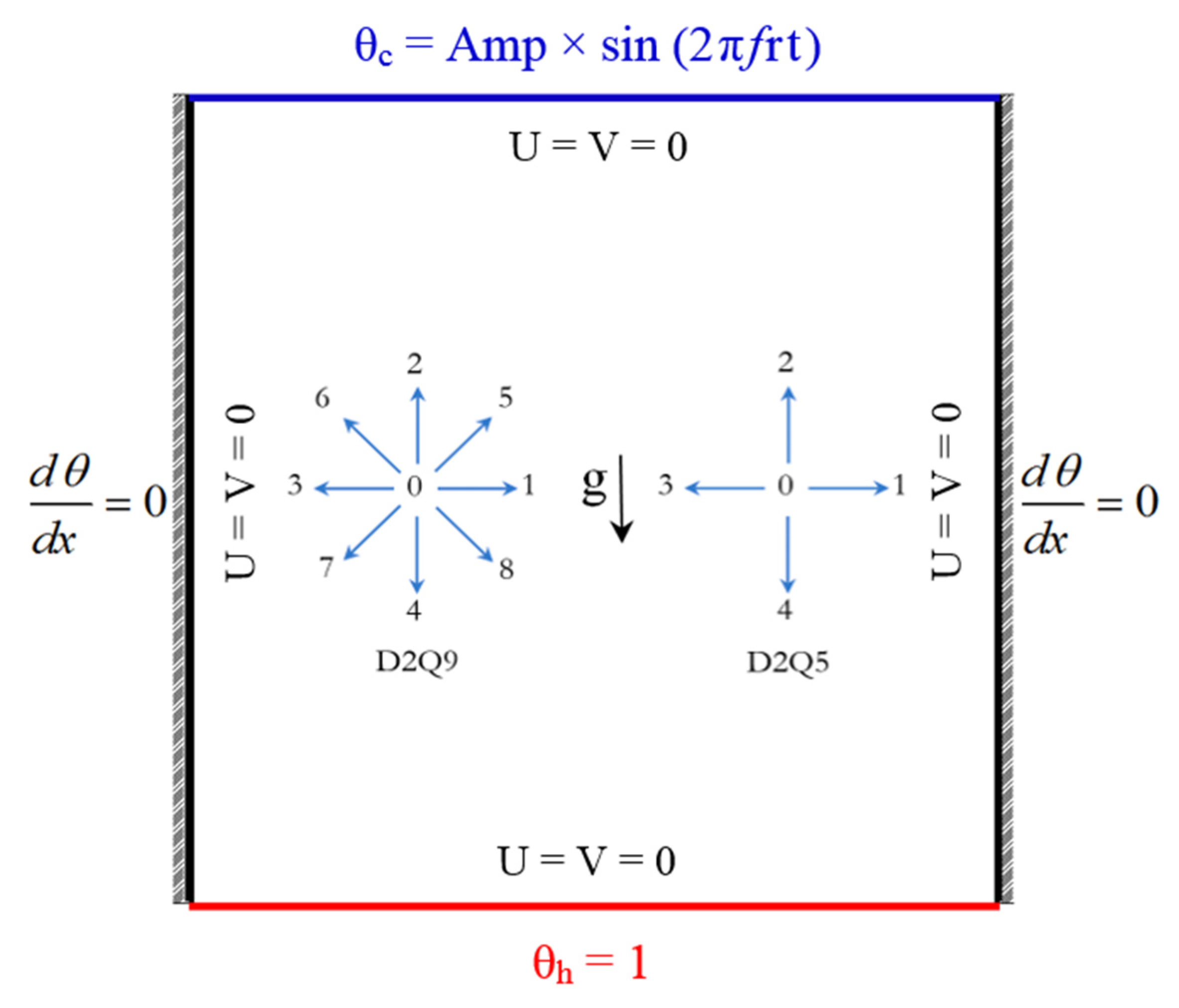
2. Mathematical Formulation
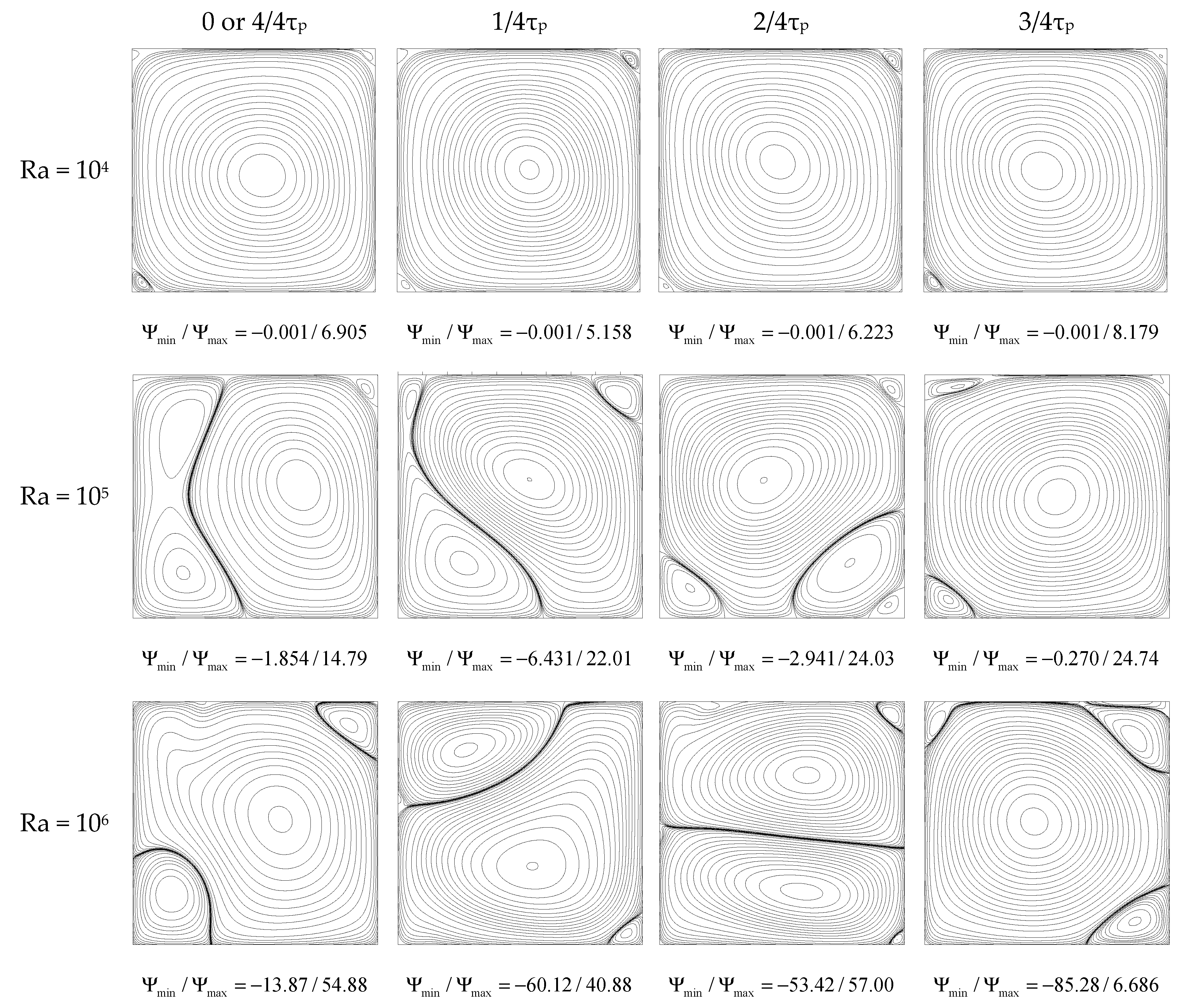
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| C | Lattice speed |
| cs | Sound speed (cs = 1/) |
| ci | Micro-discrete velocities |
| f | Frequence |
| f | Distribution function of momentum equation |
| feq | Distribution function for equilibrium momentum equations |
| G | Gravitational acceleration (m/s2) |
| Thermal distribution function | |
| H | Convective exchange coefficient |
| Correction term | |
| J | Components of momentum |
| L | Cavity length (m) |
| Moments | |
| Equilibrium moments | |
| M | Transformation matrix |
| N | Thermal transformation matrix |
| Nu | Average Nusselt number |
| Nux | Local Nusselt number |
| Pr | Prandtl number |
| rj | Position node |
| Ra | Rayleigh number |
| S | Matrix with Sj diagonal relaxation rates elements |
| t | Lattice time |
| tk | Time at a step k |
| T | Dimensional temperature |
| U | Dimensionless horizontal velocity component |
| V | Dimensionless vertical velocity component |
| x | Dimensional longitudinal coordinate |
| y | Dimensional vertical coordinate |
| X | Dimensionless longitudinal coordinate |
| Y | Dimensionless vertical coordinate |
| Subscript | |
| c | Cold |
| h | Hot |
| t | Time derivative |
| Greek symbols | |
| α | Thermal diffusivity coefficient (m2/s) |
| Coefficient of thermal expansion (K-1) | |
| The second order energy | |
| Dynamic viscosity (kg/m/s) | |
| Kinematic viscosity (m2/s) | |
| δt | Time step |
| Ψ | Dimensionless stream function |
| τ | Relaxation time |
| ρ | Density (Kg/m3) |
| θ | Dimensionless temperature |
| Diagonal relaxation matrix of | |
| Thermal source term vector | |
| Energy flux |
References
- Fiaschi, D.; Bandinelli, R.; Conti, S. A case study for energy issues of public buildings and utilities in a small municipality: Investigation of possible improvements and integration with renewables. Appl. Energy 2012, 97, 101–114. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Yang, L.; Yan, H.; Lam, J.C. Thermal comfort and building energy consumption implications—A review. Appl. Energy 2014, 115, 164–173. [Google Scholar] [CrossRef]
- Ameziani, D.; Bennacer, R.; Bouhadef, K.; Azzi, A. Effect of the days scrolling on the natural convection in an open ended storage silo. Int. J. Therm. Sci. 2009, 48, 2255–2263. [Google Scholar] [CrossRef]
- Himrane, N.; Ameziani, D.E.; Bouhadef, K.; Bennacer, R. Storage Silos Self Ventilation: Interlinked Heat and Mass Transfer Phenomenon. Numer. Heat Transf. Part A Appl. 2014, 66, 379–401. [Google Scholar] [CrossRef]
- Yang, R.; Wang, L. Multi-objective optimization for decision-making of energy and comfort management in building automation and control. Sustain. Cities Soc. 2012, 2, 1–7. [Google Scholar] [CrossRef]
- Enescu, D. A review of thermal comfort models and indicators for indoor environments. Renew. Sustain. Energy Rev. 2017, 79, 1353–1379. [Google Scholar] [CrossRef]
- Manz, H.; Schaelin, A.; Simmler, H. Airflow patterns and thermal behavior of mechanically ventilated glass double façades. Build. Environ. 2004, 39, 1023–1033. [Google Scholar] [CrossRef]
- Dimoudi, A.; Androutsopoulos, A.; Lykoudis, S. Experimental work on a linked, dynamic and ventilated, wall component. Energy Build. 2004, 36, 443–453. [Google Scholar] [CrossRef]
- De Dear, R.J.; Akimoto, T.; Arens, E.A.; Brager, G.; Candido, C.; Cheong, K.W.D.; Li, B.; Nishihara, N.; Sekhar, S.C.; Tanabe, S.; et al. Progress in thermal comfort research over the last twenty years. Indoor Air 2013, 23, 442–461. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Oxford University Press: London, UK, 1961. [Google Scholar]
- Drazin, P.; Reid, W.; Busse, F.H. Hydrodynamic Stability. J. Appl. Mech. 1982, 49, 467–468. [Google Scholar] [CrossRef]
- Ouertatani, N.; Cheikh, N.B.; Beya, B.B.; Lili, T. Numerical simulation of two-dimensional Rayleigh–Bénard convection in an enclosure. Comptes Rendus Mécanique 2008, 336, 464–470. [Google Scholar] [CrossRef]
- Turan, O.; Chakraborty, N.; Poole, R.J. Laminar Rayleigh-Bénard convection of yield stress fluids in a square enclosure. J. Non-Newtonian Fluid Mech. 2012, 171, 83–96. [Google Scholar] [CrossRef]
- Park, H. Rayleigh–Bénard convection of nanofluids based on the pseudo-single-phase continuum model. Int. J. Therm. Sci. 2015, 90, 267–278. [Google Scholar] [CrossRef]
- Aghighi, M.S.; Ammar, A.; Metivier, C.; Gharagozlu, M. Rayleigh-Bénard convection of Casson fluids. Int. J. Therm. Sci. 2018, 127, 79–90. [Google Scholar] [CrossRef]
- Kebiche, Z.; Castelain, C.; Burghelea, T. Experimental investigation of the Rayleigh–Bénard convection in a yield stress fluid. J. Non-Newton. Fluid Mech. 2014, 203, 9–23. [Google Scholar] [CrossRef]
- Chavanne, X.; Chilla, F.; Chabaud, B.; Castaing, B.; Hebral, B. Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 2001, 13, 1300–1320. [Google Scholar] [CrossRef]
- Chillà, F.; Schumacher, J. New perspectives in turbulent Rayleigh-Bénard convection. Eur. Phys. J. E 2012, 35, 58. [Google Scholar] [CrossRef]
- Zhu, X.; Mathai, V.; Stevens, R.J.A.M.; Verzicco, R.; Lohse, D. Transition to the Ultimate Regime in Two-Dimensional Rayleigh-Bénard Convection. Phys. Rev. Lett. 2018, 120, 144502. [Google Scholar] [CrossRef]
- Bhadauria, B.S. Time-periodic heating of Rayleigh–Benard convection in a vertical magnetic field. Phys. Scr. 2006, 73, 296–302. [Google Scholar] [CrossRef]
- Kaviany, M. Onset of Thermal Convection in a Fluid Layer Subjected to Transient Heating From Below. J. Heat Transf. 1984, 106, 817–823. [Google Scholar] [CrossRef]
- Kaviany, M.; Vogel, M. Effect of Solute Concentration Gradients on the Onset of Convection: Uniform and Nonuniform Initial Gradients. J. Heat Transf. 1986, 108, 776–782. [Google Scholar] [CrossRef]
- Lage, J. Convective currents induced by periodic time-dependent vertical density gradient. Int. J. Heat Fluid Flow 1994, 15, 233–240. [Google Scholar] [CrossRef]
- Aniss, S.; Souhar, M.; Belhaq, M. Asymptotic study of the convective parametric instability in Hele-Shaw cell. Phys. Fluids 2000, 12, 262–268. [Google Scholar] [CrossRef]
- Bhadauria, B.S.; Bhatia, P.K. Time-periodic Heating of Rayleigh-Benard Convection. Phys. Scr. 2002, 66, 59–65. [Google Scholar] [CrossRef]
- Umavathi, J.C. Rayleigh–Benard convection subject to time dependent wall temperature in a porous medium layer saturated by a nanofluid. Meccanica 2015, 50, 981–994. [Google Scholar] [CrossRef]
- Himrane, N.; Ameziani, D.E.; Nasseri, L. Study of thermal comfort: Numerical simulation in a closed cavity using the lattice Boltzmann method. SN Appl. Sci. 2020, 2, 1–7. [Google Scholar] [CrossRef]
- Abourida, B.; Hasnaoui, M.; Douamna, S. Transient Natural Convection in a Square Enclosure with Horizontal Walls Submitted to Periodic Temperatures. Numer. Heat Transf. Part A Appl. 1999, 36, 737–750. [Google Scholar] [CrossRef]
- Raji, A.; Hasnaoui, M.; Firdaouss, M.; Ouardi, C. Natural Convection Heat Transfer Enhancement in a Square Cavity Periodically Cooled from Above. Numer. Heat Transf. Part A Appl. 2013, 63, 511–533. [Google Scholar] [CrossRef]
- Eidel’Man, E.D. Excitation of an electric instability by heating. Physics-Uspekhi 1995, 38, 1231–1246. [Google Scholar] [CrossRef]
- Éidel’Man, E.D. Influence of the thickness of the liquid layer on the ratio of the dimensions of a convection cell. Tech. Phys. 1998, 43, 1275–1279. [Google Scholar] [CrossRef]
- Nevskii, S.; Sarychev, V.; Konovalov, S.; Granovskii, A.; Gromov, V. Formation Mechanism of Micro- and Nanocrystalline Surface Layers in Titanium and Aluminum Alloys in Electron Beam Irradiation. Metals 2020, 10, 1399. [Google Scholar] [CrossRef]
- Mohamad, A. Lattice Boltzmann Method; Springer: London, UK, 2011; Volume 70. [Google Scholar]
- Guo, Y.; Bennacer, R.; Shen, S.; Ameziani, D.; Bouzidi, M. Simulation of mixed convection in slender rectangular cavity with lattice Boltzmann method. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 130–148. [Google Scholar] [CrossRef]
- Khali, S.; Nebbali, R.; Ameziani, D.E.; Bouhadef, K. Numerical investigation of non-Newtonian fluids in annular ducts with finite aspect ratio using lattice Boltzmann method. Phys. Rev. E 2013, 87, 053002. [Google Scholar] [CrossRef] [PubMed]
- D’Humieres, D. Generalized Lattice-Boltzmann Equations. In Proceedings of the 18th International Symposium, Rarefied Gas Dynamics, Vancouver, BC, Canada, 26–30 July 1994; pp. 450–458. [Google Scholar]
- Lallemand, P.; Luo, L.-S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef]
- Wang, G.; Meng, X.; Zeng, M.; Ozoe, H.; Wang, Q.W. Natural Convection Heat Transfer of Copper–Water Nanofluid in a Square Cavity With Time-Periodic Boundary Temperature. Heat Transf. Eng. 2013, 35, 630–640. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Ghernaout, B.; Teggar, M.; Benchatti, A.; Benarab, F.-Z. Onset of Natural Convection and Transition Laminar-Oscillatory Convection Flow in Rayleigh-Bénard Configuration. Int. J. Heat Technol. 2016, 34, 151–157. [Google Scholar] [CrossRef]
- Kwak, H.S.; Hyun, J.M. Natural convection in an enclosure having a vertical sidewall with time-varying temperature. J. Fluid Mech. 1996, 329, 65–88. [Google Scholar] [CrossRef]
- Soong, C.; Tzeng, P.; Hsieh, C. Numerical study of bottom-wall temperature modulation effects on thermal instability and oscillatory cellular convection in a rectangular enclosure. Int. J. Heat Mass Transf. 2001, 44, 3855–3868. [Google Scholar] [CrossRef]
- Kazmierczak, M.; Chinoda, Z. Buoyancy-driven flow in an enclosure with time periodic boundary conditions. Int. J. Heat Mass Transf. 1992, 35, 1507–1518. [Google Scholar] [CrossRef]
- Wang, Q.-W.; Wang, G.; Zeng, M.; Ozoe, H. Upward Heat Flux through the Horizontal Fluid Layer of Water with Sinusoidal Wall Temperature at the Top or Bottom Boundary. Numer. Heat Transf. Part A Appl. 2007, 52, 817–829. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasseri, L.; Himrane, N.; Ameziani, D.E.; Bourada, A.; Bennacer, R. Time-Periodic Cooling of Rayleigh–Bénard Convection. Fluids 2021, 6, 87. https://doi.org/10.3390/fluids6020087
Nasseri L, Himrane N, Ameziani DE, Bourada A, Bennacer R. Time-Periodic Cooling of Rayleigh–Bénard Convection. Fluids. 2021; 6(2):87. https://doi.org/10.3390/fluids6020087
Chicago/Turabian StyleNasseri, Lyes, Nabil Himrane, Djamel Eddine Ameziani, Abderrahmane Bourada, and Rachid Bennacer. 2021. "Time-Periodic Cooling of Rayleigh–Bénard Convection" Fluids 6, no. 2: 87. https://doi.org/10.3390/fluids6020087
APA StyleNasseri, L., Himrane, N., Ameziani, D. E., Bourada, A., & Bennacer, R. (2021). Time-Periodic Cooling of Rayleigh–Bénard Convection. Fluids, 6(2), 87. https://doi.org/10.3390/fluids6020087







