1. Introduction
“Life is like a journey” as stated by an anonymous philosopher. But in the case of living beings like mammals, life literally begins with a journey. It begins with a long journey of hundreds of millions of sperms, passing through the reproductive tracks of the female trying to reach the oviducts, with an ultimate aim to unite with one of the eggs. However, only a few excellent travelers will reach the eggs indicating the complexity of the flow paths and the environments experienced by the sperms. This remarkable journey has attracted growing interest over the past several decades [
1,
2,
3,
4,
5,
6,
7], to understand the mechanisms used by the sperms to swim through different complex environments with the potential of using the findings to solve some of the significant problems faced nowadays like human infertility and to save some mammal species from extinction. Among the applications, solving human infertility can have a huge impact on the lives of many people. It is estimated that about 70 million couples around the world cannot conceive a child [
8] due to infertility and that that nearly
of men is affected by infertility [
9,
10]. The male infertility is due to several factors such as low sperm count, low sperm quality, low sperm motility etc. In addition, it is also observed that the average sperm density has been decreasing during the past several decades [
11]. Therefore it is desired to study the sperm swimming to achieve a better understanding of sperm motility.
There are different types of swimming organisms in nature ranging from large whales to micro-organisms like bacteria. Depending on their size and speed, these swimmers experience different types of flow regimes while swimming. For large creatures such a fishes, the inertial forces of the fluid are dominant while for micro organisms the viscous forces of the fluid plays a significant role. To correlate the inertial forces to the viscous forces of a fluid, an important non-dimensional parameter, Reynolds number (Re), is used and defined as,
where
is the kinematic viscosity of the fluid,
U is the reference speed, and
L is swimmer length. If numerical methods are used to study the fluid–structure interaction of swimmers, the swimming speed is usually unknown, and determined by the fluid–structure interaction solver. In this case, the traveling wave speed is usually used as the reference speed [
12], which defines a Reynolds number larger than the one defined by the forward swimming speed. Regarding sperm swimming, there are several factors that should be considered. In general, the sperm length is less than
µm, while the sperm speed is less than
µm/s [
13]. Such parameters define a Reynolds number of
indicating that the sperm should swim in a special way different from larger and faster swimmers [
3]. Considering the facts that the traveling wave speed is generally larger than the forward speed and that most body fluid is shear-thinning-like non-Newtonian fluid, the effective Reynolds number for sperm swimming could be of
. In addition, the motion of ambient fluids should be taken into account as well, which in general have much higher velocities compared to the sperm speed. Therefore we can conclude that the flow regimes involved in sperm swimming cover both Stokes and laminar flows, which have been respectively covered by Lauga [
14] and Childress [
15].
The dominantly used strategy for a sperm swimming through a fluid is to make traveling wave (from head to tail) motion [
7] and/or to improve its frequency so that
(where
is the ratio of lateral oscillating speed to the forward swimming speed) to break the time-reversal symmetry [
16]. This is different from the large animals which use both traveling and flapping motions [
12,
17,
18]. The traveling wave can be described by [
19,
20]
where
is the distance measured from the head of the sperm,
and
are respectively the prescribed displacement of the body in
y-and
z-directions,
is the amplitude,
c is the traveling wave phase speed, and
is the wave length. Three additional non-dimensional numbers are introduced, i.e., non-dimensional amplitude
, traveling-wave Reynolds number
and wave number
, where
is the maximum or average amplitude. In the cases where the motion is driven by a prescribed function [
21] or an internal moment, the traveling wave is used to describe the driving function or moment. If non-Newtonian fluid is considered, extra parameter(s) will be introduced [
22,
23], and the definition of Reynolds number should be modified. Without loss of generality, we take the power-law fluid as an example [
24] of which the dynamic viscosity is
where
is the power-law consistency index,
n is the power-law fluid behavior index, and
is the shear rate. It should be noted that the Einstein summation convention is applied in Equation (5). One additional parameter, i.e.,
n, is introduced. The power-law fluids of
,
and
are respectively the shear-thinning, shear-thickening and Newtonian fluids. The definition of Reynolds number is modified to [
18,
22,
25]
In addition to the flow regimes and sperm kinematics discussed above, the sperm material properties should be considered in the fluid–structure interaction simulations, e.g., bending rigidity, stretching rigidity, structure damping, and mass [
20,
21]. Therefore, many methods have been developed to address the fluid–structure interaction of sperm in order to study different aspects involved in this topic. In this paper, we present a review of the numerical methods used in this topic from an engineering perspective to understand the swimming mechanism of sperm. The earliest simplified theories used to evaluate the forces on the sperm are first introduced. Then the boundary-element method that solves Stokes flow is introduced. Finally, the Cartesian grid based methods are introduced.
The rest of this paper is organized as follows.
Section 2 summarizes several simplified theories. The boundary–element method for flagellar propulsion in Stokes flow is introduced in
Section 3.
Section 4 presents driving-configuration-function model based on immersed boundary method (IBM). An integrative model based on IBM is introduced in
Section 5. A Singular-Value Decomposition based on the Generalized Finite Difference method for the simulation of fluid–structure interaction problems in a viscous fluid is discussed in
Section 6.
Section 7 gives an IBM based on finite difference method.
Section 8 proposes an immersed boundary–lattice Boltzmann method based driving moment function. Final conclusions are given in
Section 9.
3. Boundary-Element Method for Flagellar Propulsion in Stokes Flow
The boundary-element method has been extensively used to study the fluid field and forces induced by flagellar motion in Stokes flow where the fluid inertia is ignorable (see Refs. [
19,
34,
35,
36,
37] for several examples). The fluid dynamics considered is described by
The sperm/flagellar motion including position and velocity can be either described [
19,
34,
35,
36] or obtained from fluid–structure interaction [
37]. For the prescribed motion, the position of the swimmer can be written as (see e.g., Ref. [
19])
where
Y and
Z are traveling wave functions. If fluid–structure interaction is considered, Montenegro-Johnson et al. [
37] employed the following equation to describe the sperm/flagellar dynamics
where
is the fluid viscous force,
E is the bending rigidity,
M is the internal moment, and
T is the tension. Compared to the model in
Section 8, this model does not consider structure damping. In addition, the internal driving moment appears as the form of
in
Section 8.
At the fluid–structure interface, the non-slip/non-penetration boundary condition applies, and can be described as
Note that these equations are applicable to the fluid motion around the micro-organism, where the Reynolds number based on the length of the organism and swimming velocity (including forward speed and lateral vibration speed whichever is larger) is extremely small. The flow solution of Equations (
23) and (
26) can be obtained by
where
is the Kronecker delta,
is a unit outward normal on the fluid–structure interface, and
is the traction field that can be obtained by taking
to a boundary point [
19].
The primary advantage of using boundary-element method here is that the dimension of the problem is reduced by one, and thus it reduces the number of algebraic equations and avoids mesh generation for two- and three-dimensional problems. Therefore, this method could save computational cost. However, this method ignores fluid inertia and nonlinearity, and thus the associated phenomena cannot be captured.
4. Driving-Configuration-Function Model Based on IBM
A model with both driving and configuration functions was developed by Fauci and McDonald [
21] to study the sperm motility. In this model, the immersed boundary method (IBM) [
38,
39,
40,
41] was developed to couple the sperm dynamics with the fluid dynamics. Based on this method, the surface force acting on the fluid by the sperm is spread onto the volumetric fluid grids by
where
is the Lagrangian force density on the fluid,
is the point on the sperm, and
is Dirac’s delta function. The Lagrangian force at a node
i on the sperm is calculated by
where
is the elastic energy of the sperm model.
consists of three parts: cell energy (or head energy) with a prescribed configuration function, flagellum energy with driving function, and joint energy that couples the flagellum to the cell body. Therefore,
where
,
and
are respectively cell energy, flagellum energy and joint energy.
If the cell is divided into
m points and the flagellum is divided into
points,
,
and
can be written as
where
and
are respectively the stretching and bending coefficients of the cell,
and
are respectively the stretching and bending coefficients of the flagellum,
is the constant used to force the flagellum orthogonal to the cell body at the point of attachment,
and
are respectively the prescribed configuration function and driving function, and
. In Equation (
35), periodic boundary should be applied, i.e.,
and
. In Equation (36), the moment free at both ends is applied in the bending energy calculation. The last point
of the flagellum is connected to the first point
on the cell body by the joint energy (see Equation (37)). The last term of Equation (37) is used to drive an orthogonal connection.
is used to maintain a prescribed shape. For example, a configuration of
prescribes an equilibrium configuration of the points along the cell body equally-spaced along a circle of radius
. Coefficients
and
determine how closely the equilibrium configuration is enforced.
is chosen so that a sine wave of amplitude is passed along the flagellum. Because the motion of flagellum includes both passive and active parts, it is hard to generate a specific amplitude profile. In general, , where is the wave length.
The non-slip/non-penetration boundary condition is achieved by using
The Navier-Stokes equations are solved by using the projection method of Chorin with periodic boundary conditions and the velocity field is solved by an implicit scheme. The implicit method is used for the calculation of Equation (
32). Such treatment could enhance the numerical stability. In practice, a few hundred to one thousand time steps per period of undulation should be used; the number of time steps per period of undulation should increase with the undulation amplitude as well.
The major advantage of this method is associated with the driving function used. is actually the prescribed motion in the body-fixed frame of reference, which interacts with the fluid forces. In addition, the fluid inertia and nonlinearity are considered. The internal driving mechanism is unclear in this method. In addition, the structure inertia is not considered.
5. An Integrative Model Based on IBM
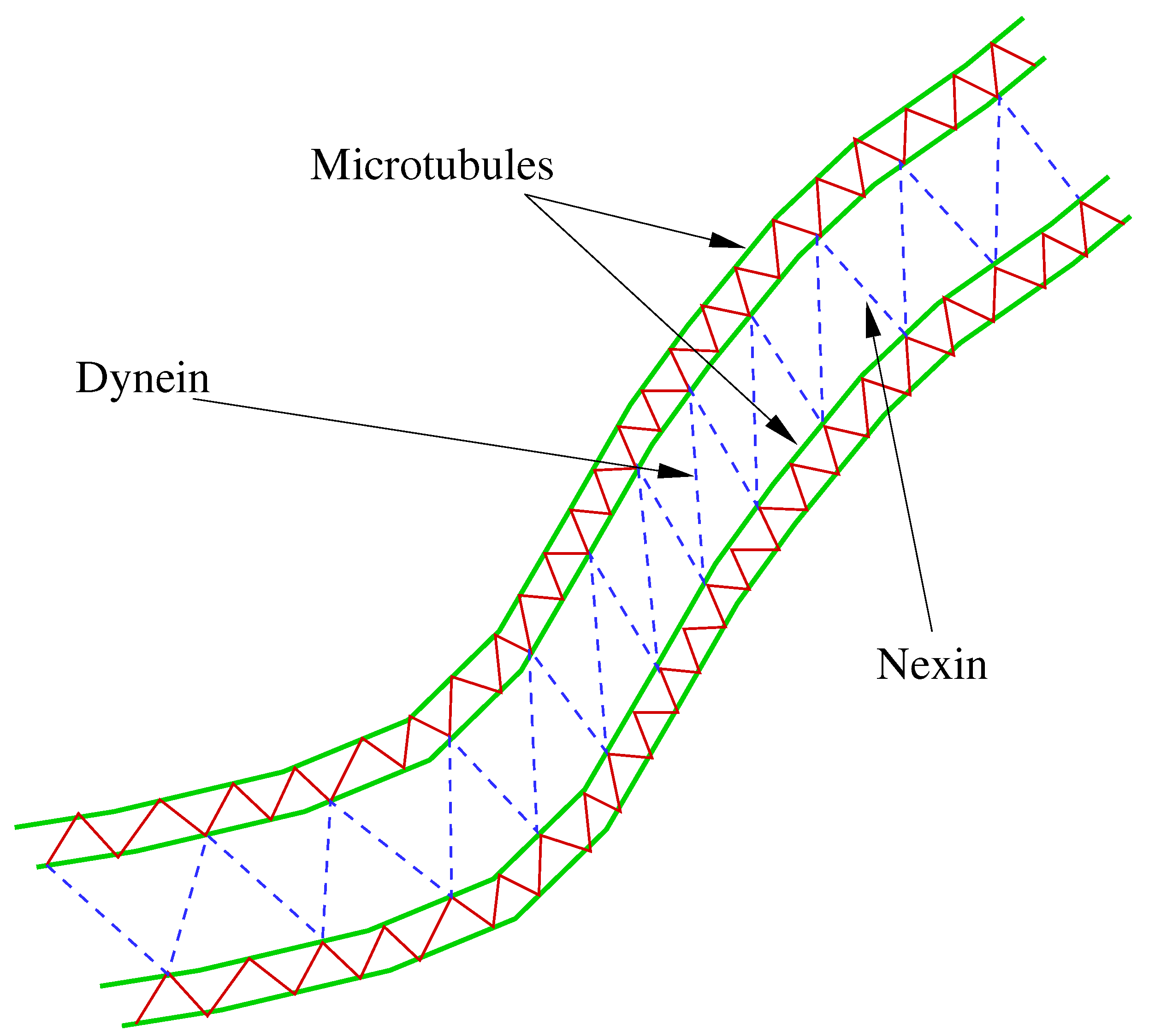
An integrative model based on IBM, which considers an axoneme consisting of two microtubules, was developed by Dillon et al. [
5,
42,
43,
44]. In this model, the microtubule is modeled as a pair of filaments with diagonal cross-links. The microtubules are linked by nexins and dyneins (dynamic diagonal elastic links) (see
Figure 1).
The immersed boundary method is employed to couple this cilia dynamics with the fluid dynamics. It spreads the surface force onto the volumetric fluid grids in the vicinity of the boundary and treats it as a body force through the following expression
where
is the Lagrangian force density on the fluid by the
k-th filament,
is the point on the
k-th filament, and
is Dirac’s delta function. The Lagrangian force can be written as
where
is the elastic force arising from the deformation of the microtubules (including contributions from the filaments and the cross links),
is the force caused by the elongation of nexin links,
is induced by the contraction of the dynein links,
is the tethering force to prevent movement of cell wall, and
is the tethering force to prevent movement of the axoneme base.
The microtubule forces at node
i of
k-th filament is denoted by
, and can be written as
where
denotes those points linked to node
i by filament segment and the cross-links,
is the stretching coefficient between nodes
i and
, and
is the rest length between nodes
i and
. The calculation of
is the same as Equation (
41).
,
and
at node
i, denoted by
, can be written as,
where
denotes those points linked to node
i, and
is the stretching coefficient between nodes
i and
.
Dillon et al. [
43] also introduced a simple curvature control algorithm to control the flagellar waveform. In this algorithm, individual dyneins are selected from LR (
left to right) or RL (
right to left) families at each time step according to the local curvature at the site of the dynein at a time
in the past. The choice of modes is determined by the sigh of the lagged local curvature. Initially the shape of the axoneme has a pair of bends, and the resulting bend propagation depends on this curvature control mechanism when the simulation begins. Details of this method can be found in Ref. [
43].
The advantage of this method is associated with the facts that it applied curvature control method to achieve swimming motion, and that it includes microtubule structure details, with the cost of algorithm complexity. This method does not consider structure inertia.
6. SVD-GFD Method on a Hybrid Meshfree-Cartesian Grid
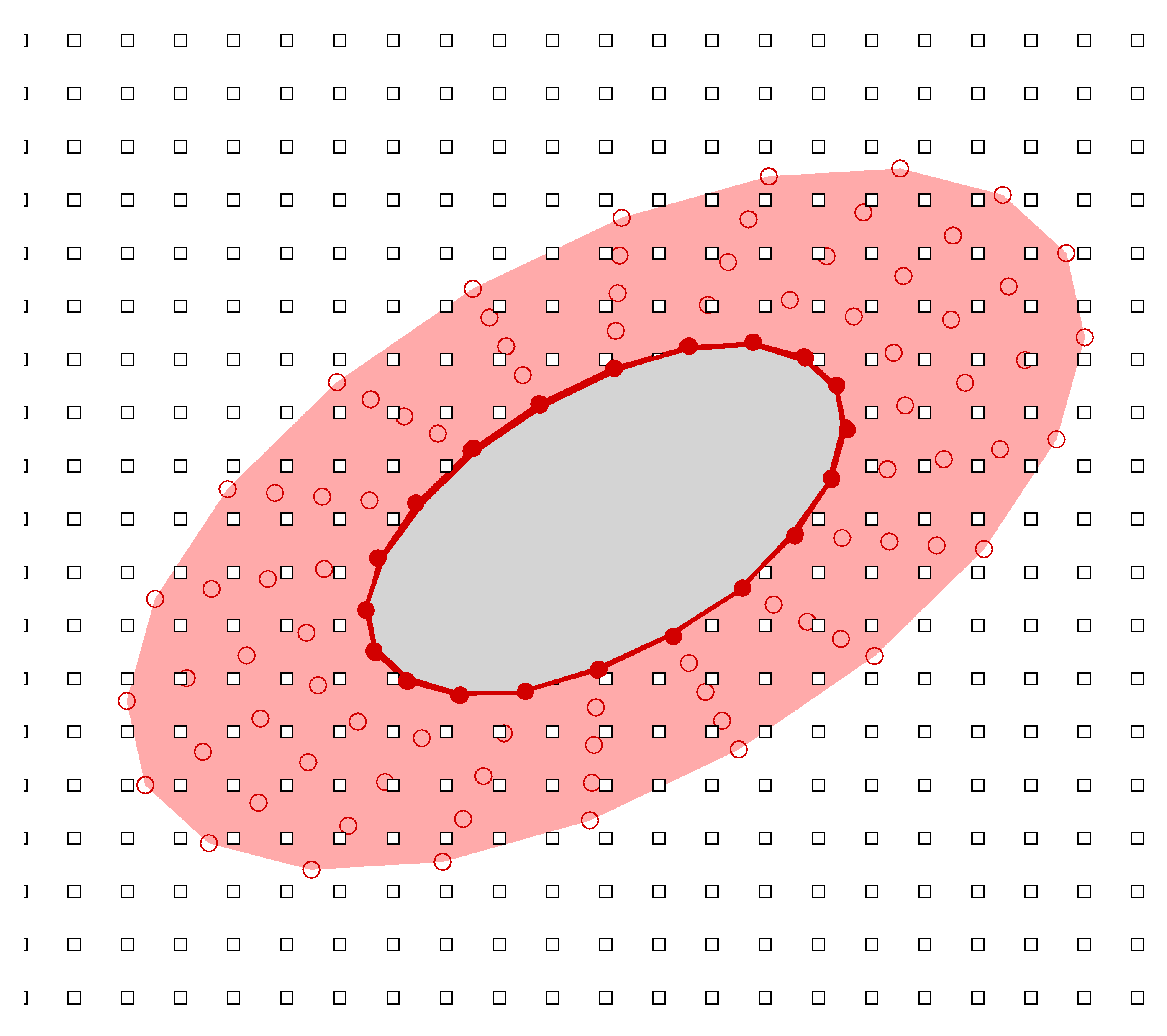
In Ref. [
45], Yeo et al. presented a Singular-Value Decomposition (SVD) based Generalized Finite Difference (GFD) method for the simulation of fluid–structure interaction problems in a viscous fluid. This method was originally developed for moderate and large Reynolds number swimming problems, e.g., fish swimming and manoeuvring. However, this method can be directly extended to sperm swimming. In this method, computation is carried out on a hybrid grid comprising meshfree nodes around the undulating swimming body which are convected in tandem with the changing shape and motion of the body and Cartesian nodes in the background (as shown in
Figure 2). Both types of grids employ the arbitrary Lagrangian–Eulerian (ALE) formulation of the incompressible Navier–Stokes equations to calculate the fluid dynamics
where
denotes the convection velocity of the computational grids. At the meshfree nodes and a small number of Cartesian nodes (which contain meshfree nodes in its
neighbourhood), derivative approximation is carried out by a GFD scheme that uses the SVD procedure for error minimization [
45]. The GFD method is based on the Taylor series approximation where the derivative components
of a function
at a given position
are related to its function values
at
n support nodes
by
In general,
support nodes are needed to approximate the second-order derivative components of
. The derivatives are obtained as the solution of the over-determined linear system (
44) by the method of SVD, which minimizes the
-norm (least square) of the residual error vector.
At other Cartesian nodes which do not contain meshfree nodes in its neighbourhood, traditional finite difference method is used.
Once the fluid dynamics is acquired, the forces on the swimming body can be obtained. Finally, the motion of the body is governed by (also see Ref. [
18])
where
m is the mass of the body,
is the moment of inertia about centroid (
) of the body,
is the orientation angle of the body center line,
is the linear velocity of the mass centroid,
is the angular velocity of the body,
represents an external force such as gravitational force,
is the fluid forces, and
is the fluid moment about centroid. In the body-frame, the body performs motion with prescribed kinematics to achieve cyclic swimming and turning manoeuvres. Similar swimmer dynamics model has been extensively used to study fish-like and sperm-like swimming (see for example Refs. [
12,
17,
20,
46]). Equations (
47)–(50) governing the centroidal translation and rotation of the swimming body are integrated by a Crank–Nicolson like implicit scheme.
We would like to highlight several major advantages of this method. It combines the advantages of mesh-free discretization for precise definition of bodies and good resolution of boundary regions with the efficiency of standard Cartesian finite difference scheme, so that the interpolation is kept at a very minimal level associated with fresh nodes creation. Furthermore, the density of mesh-free nodes around bodies may be freely varied to give necessary resolution within boundaries. Finally, both meshfree nodes and background Cartesian nodes can be convected if necessary. This will be particularly useful in problems where the swimming body travels over extended distances. Though this method considers structure inertia, it uses the prescribed kinematics, which is not affected by the fluid force, to achieve cyclic swimming and turning manoeuvres.
7. IBM Based on Finite Difference Method
IBM based on finite difference method was extended by Qin et al. [
20] to study a small swimmer (e.g., sperm) in a viscous fluid. This method consists of three parts: swimmer dynamics, fluid dynamics and fluid-structure interaction.
In this method, the swimmer dynamics is the same as that used in Refs. [
12,
17,
45], and is described by Equations (
47)–(50). Therefore, it will not be repeated here. In the fluid dynamics solver, the fractional step method was adopted to solve the Navier–Stokes Equation (
43) without mesh movement (i.e.,
). Fully implicit time advancement and the Crank–Nicolson scheme were respectively used for the discretization of the diffusion and convection terms on a staggered Cartesian grid. Decoupling of the velocity and pressure was achieved by using a variation of Chorin’s projection method (see Ref. [
47] for the details of this method).
The major difference of this method compared to Ref. [
45] is that the immersed boundary method is employed to handle the fluid–structure coupling, which spreads the surface force onto the volumetric fluid grids in the vicinity of the boundary and treats it as a body force through the following expression
where
is the mass ratio (with
being the structure linear density,
being fluid density and
L being the swimmer length), Re is the Reynolds number defined by
(this definition was also used in Ref. [
12]),
is the Lagrangian force density on the fluid by the swimmer body,
is Dirac’s delta function. In this work, the feedback forcing scheme [
48,
49,
50] is used to calculate the Lagrangian force density, i.e.,
where
and
are positive constants,
is the Lagrangian velocity obtained from both prescribed motion,
is the interpolated velocity from flow field according to
and
is the position integrated by using
,
In the implementation, Equation (
52) is not directly used. Instead, the equations below are used to calculate the Lagrangian force,
where the second term of the Lagrangian force is usually less than the first term unless the flagellum shape changes sharply with time or the body swims very fast. This fact is useful for choosing appropriate values of
and
. Details regarding values of
and
can be found in Ref. [
47].
Qin et al. [
20] applied this method to study a small swimmer (e.g., sperm) in a viscous fluid. They found that for a very small swimmer such as sperm swimming at very low Reynolds numbers, the traveling-wave beating propels the swimmer forward and the asymmetrical parabola beating changes the swimming direction. Similar observation was obtained by the method in
Section 8 which applies an internal driving moment to generate the beating motion of a sperm. Qin et al. also found that if the distance between the swimmer and a wall is less than the wavelength, the wall effect on the swimmer motion is strong, which is consistent with fish swimming as discussed in Ref. [
51]. Another interesting observation was that the swimmer approaches the wall due to the net torque generated by the non-uniform distribution of the pressure along the flagellum.
Compared to Ref. [
45], this method uses IBM, and thus it is more efficient regarding the boundary condition treatment. We also note that an explicit scheme was used in Ref. [
20] for equations governing the sperm dynamics, while a Crank–Nicolson like scheme was used in Ref. [
45]. Therefore, a much smaller
(e.g.,
) was used for both structure and fluid dynamics in Ref. [
20], while
was used in Ref. [
45]. Actually, at each fluid–structure interaction, the integration of structure dynamic equations can be further split into several substeps depending on the stiffness and/or mass ratio, as did in Refs. [
52,
53,
54]. Similar to the SVD-GFD method on a hybrid meshfree-Cartesian grid in
Section 6, this method uses the prescribed kinematics independent of hydrodynamics to achieve cyclic swimming and turning manoeuvres.
8. IB-LBM Based Driving Moment Method
Here we introduce an internal driving nonlinear model based on the immersed boundary–lattice Boltzmann method (IB-LBM) [
23,
55,
56,
57,
58,
59,
60,
61]. In this method, the sperm is simplified as a nonlinear beam. To drive the swimming motion, an internal moment is introduced into the beam equation [
59]. Therefore, the geometrically nonlinear motion for the sperm is described as
where
s is the arch length from the leading edge to the tail,
is the stretching stress,
is the stretching coefficient,
is the bending rigidity,
is the damping coefficient,
is the Lagrangian position vector of the sperm,
is the normal pointing to the left hand side when
s is increasing,
is the driving moment, and
is the fluid stress. Both head and tail are shear-free and subjected to driving moment, which can be described by
and
.
The incompressible viscous fluid dynamics is solved by using LBM [
62,
63] where the kinematics of the fluid is governed by the discrete LBE of a single relaxation time model [
55,
62,
63,
64,
65,
66]
where
is the distribution function for particles,
is the particle velocity,
is the position,
is the size of the time step,
is the equilibrium distribution function,
represents the nondimensional relaxation time, and
is the body force term. In the D2Q9 model, the nine possible particle velocities are given by
where
is the lattice spacing. In Equation (
58),
and
are acquired by [
64,
67]
where
are the weights given by
,
for
1 to 4 and
for
5 to 8,
is the velocity of the fluid,
is the sound speed, and
is the fluid body force. The relaxation time is related to the fluid kinematic viscosity by
Finally, the fluid density, velocity and pressure are computed by
The immersed boundary method is employed to handle the moving boundary, which spreads the surface force onto the volumetric fluid grids in the vicinity of the boundary and treats it as a body force through the following expression
where
is the Lagrangian force density on the fluid by the elastic boundary,
is Dirac’s delta function. The regularized body force is the same as
in Equation (60), and it enters the kinetic equation of the fluid, Equation (
58), through
. Since
is the reaction force of hydrodynamic force on the sperm,
, it can be written as
where
,
,
and
are respectively the viscous, stretching, bending, and internal driving forces.
The velocity of a point on the sperm is interpolated from the flow field, and the position of the sperm is updated explicitly by
where
is the velocity of the sperm.
The method ignores the internal structure details and the molecular motor mechanisms of the sperm. Instead, an internal driving moment is employed to drive the swimming motion. By designing a suitable driving moment, one is able to reproduce the traveling wave motion, turning maneuver, and other motions. Furthermore, the structure inertia can be incorporated by using the method in Ref. [
55]. In practice, the driven force is sometimes explicitly provided [
68,
69], i.e.,
where
is the force amplitude. The leading edge trajectory, and speeds in
x- and
y-directions presented in Ref. [
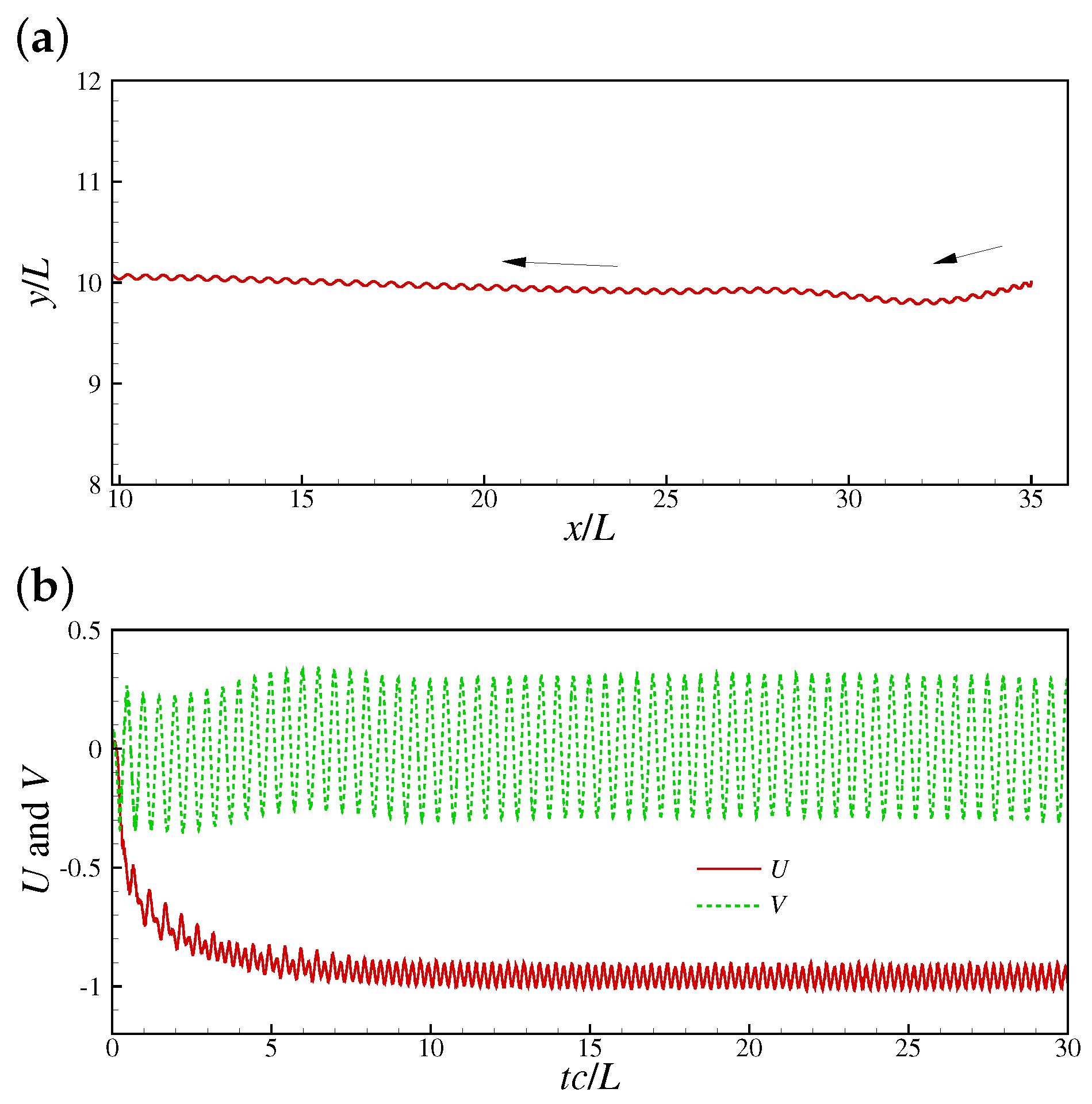
59] are shown in
Figure 3. The pressure distributions around a swimming sperm in 2D and 3D space by Liu et al. [
69] are shown in
Figure 4.
9. Conclusions
In this article, a number of previous efforts focusing on the theoretical and numerical methods for sperm swimming have been introduced from an engineering perspective. Specifically, the governing equations and parameters for sperm swimming in fluid are first presented and discussed. The simplified theoretical methods, including Taylor’s swimming sheet and cylinder, the resistive force theory and the slender body theory, are then introduced. Finally, numerical methods, including boundary-element method for flagellar propulsion in Stokes flow, driving-configuration-function model based on IBM, an integrative model based on IBM, SVD-GFD method on a hybrid meshfree-Cartesian grid, IBM based on finite difference method and IB-LBM based driving moment method, are provided. The methods include IBMs and non-IBMs. IBMs are normally based on the delta function which is a first-order approach in space. The major advantage of these methods is the simplicity in handling boundary conditions at the fluid-structure interacts. For the non-IBMs solving FSI systems, effort is required to handle the computational mesh, bringing benefit of higher accuracy in space.
Actually, among the hundreds of millions of sperm cells that begin the journey up the oviducts, only a few excellent travelers will ever reach their destination. They have to swim in the right direction over distances that are around 1000 times their own length. In addition, they are exposed to complex currents along the way. During their journey, the sperms might explore the hydrodynamic benefits from other sperms around them or the flexible walls so that they have better opportunities to reach the destination. There may be both collaboration and competition between sperms. Therefore, significant work needs to be done to gain better understanding of this complex process. There are several issues for further research in this area.
First, the control strategy of driving moment is an interesting topic considering the “fierce race” during the journey up the oviducts. The complex currents and the moving wall require excellent control strategy which has not been studied. The combination of numerical methods with artificial intelligence, which has been introduced in high-Reynolds-number swimmers [
70,
71], is an attractive strategy to achieve this. Second, the sperm-sperm and sperm-wall interactions are important during this journey. In previous numerical experiments, it was found that two tandem sperms enjoy benefits from the interaction in terms of acceleration and forward speed. However, instability occurs during the swimming, and thus it may need extra energy for the sperm to recover from instability. In addition, the interaction among large number of sperms and walls is not well understood. The challenges are the swimming stability, control and the response of the sperm to the complex environments which could be addressed by artificial intelligence. Third, chemotaxis is an important feature of sperms. It is the movement in response to a chemical stimulus from egg (and/or oviduct). Understanding of sperm chemotaxis is of importance to understand its swimming mechanism and driving moment control. Fourth, it is desired to study the non-Newtonian effects on the swimming performance of sperms considering most body fluids behave according to non-Newtonian rheologies which have strong effects on fluid–structure interaction at low Reynolds numbers. Fifth, the beating of the sperm tail is subjected to fluctuations in internal forces due to the noise in the activity of the motors, which could be modelled by Brownian motion [
72,
73] which should be considered in the numerical modelling. Finally, collaboration and competition between sperms [
73], and optimization, also need further study in the modelling.