Two-Phase Turbulence Statistics from High Fidelity Dispersed Droplet Flow Simulations in a Pressurized Water Reactor (PWR) Sub-Channel with Mixing Vanes
Abstract
1. Introduction
2. Numerical Setup
2.1. Governing Equations
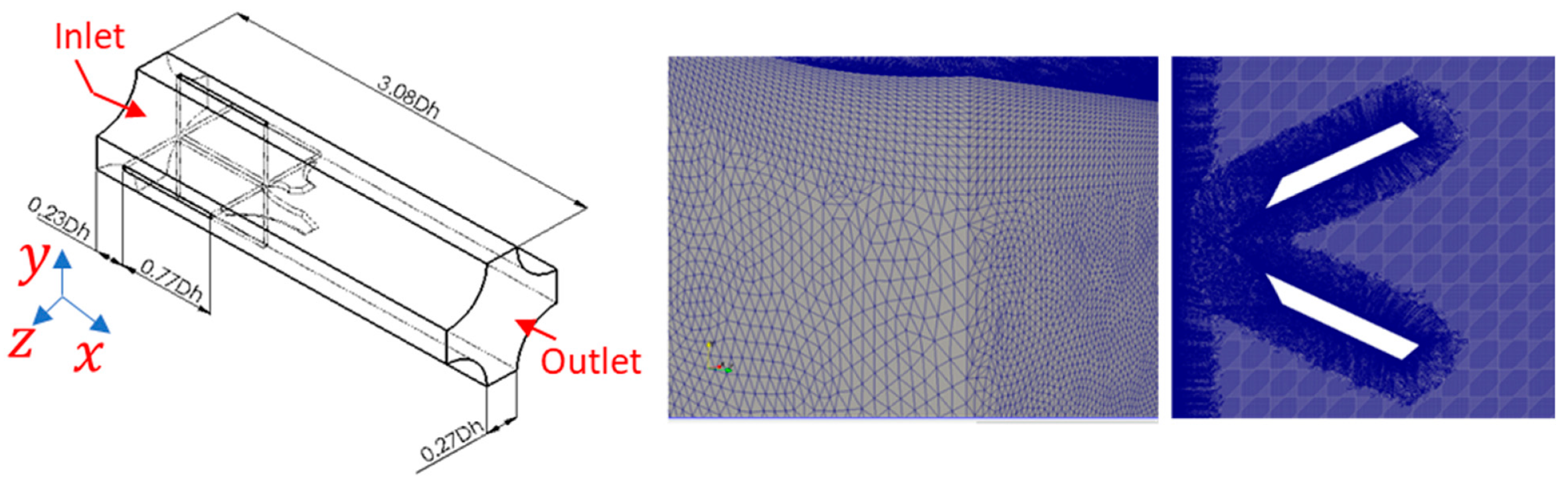
2.2. Geometry and Simulation Properties
3. Results and Discussion
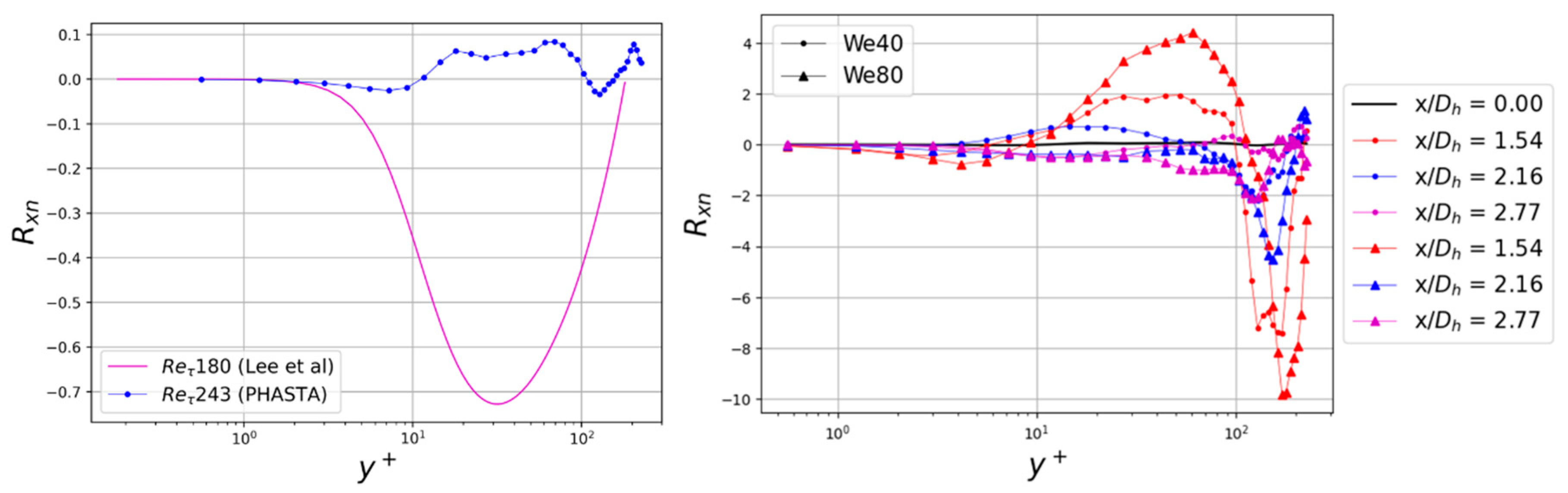
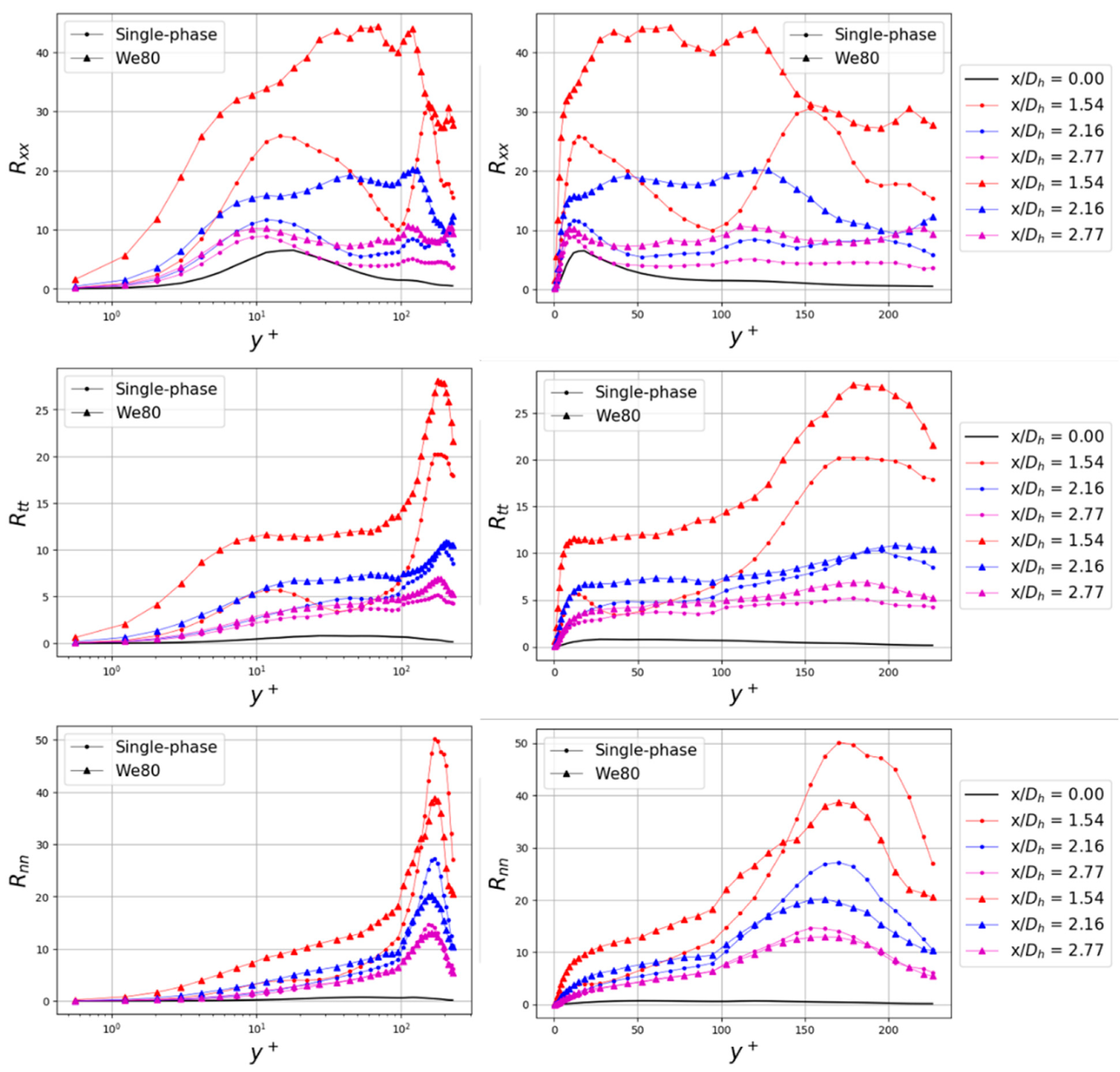
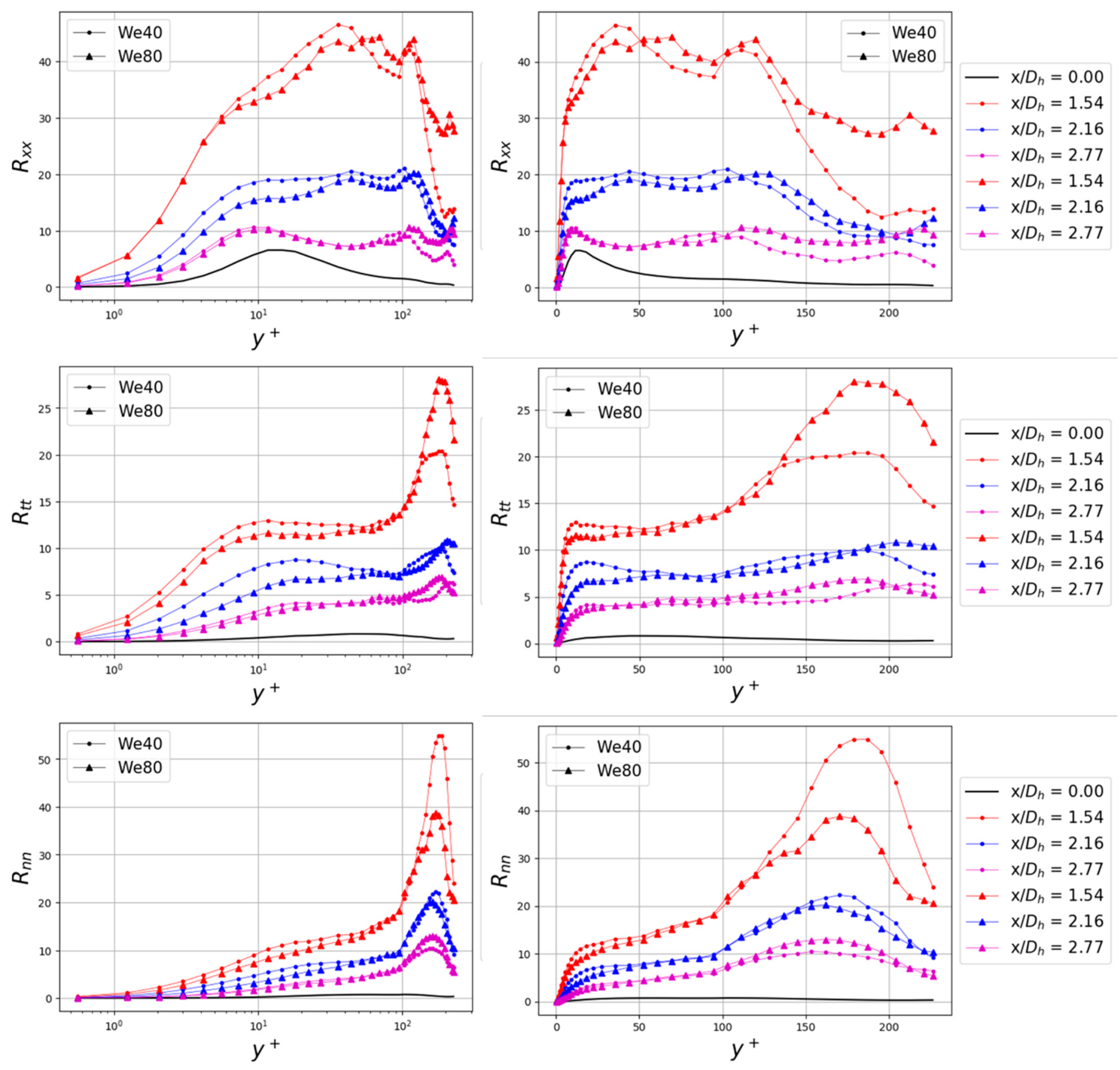
3.1. Turbulence Analysis
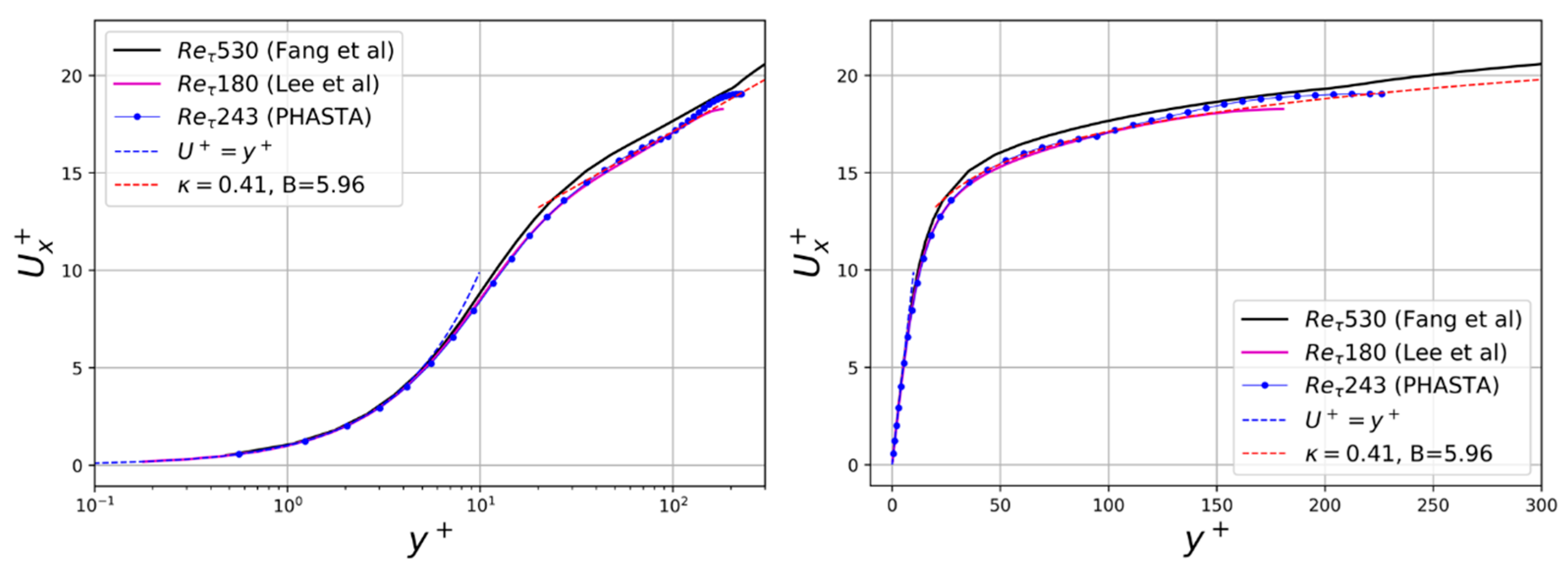
3.1.1. Verification of Inlet Turbulent Flow Features
3.1.2. Effect of Mixing Vanes and Droplets on Downstream Turbulence
3.1.3. Axial Evolution of Downstream Turbulence
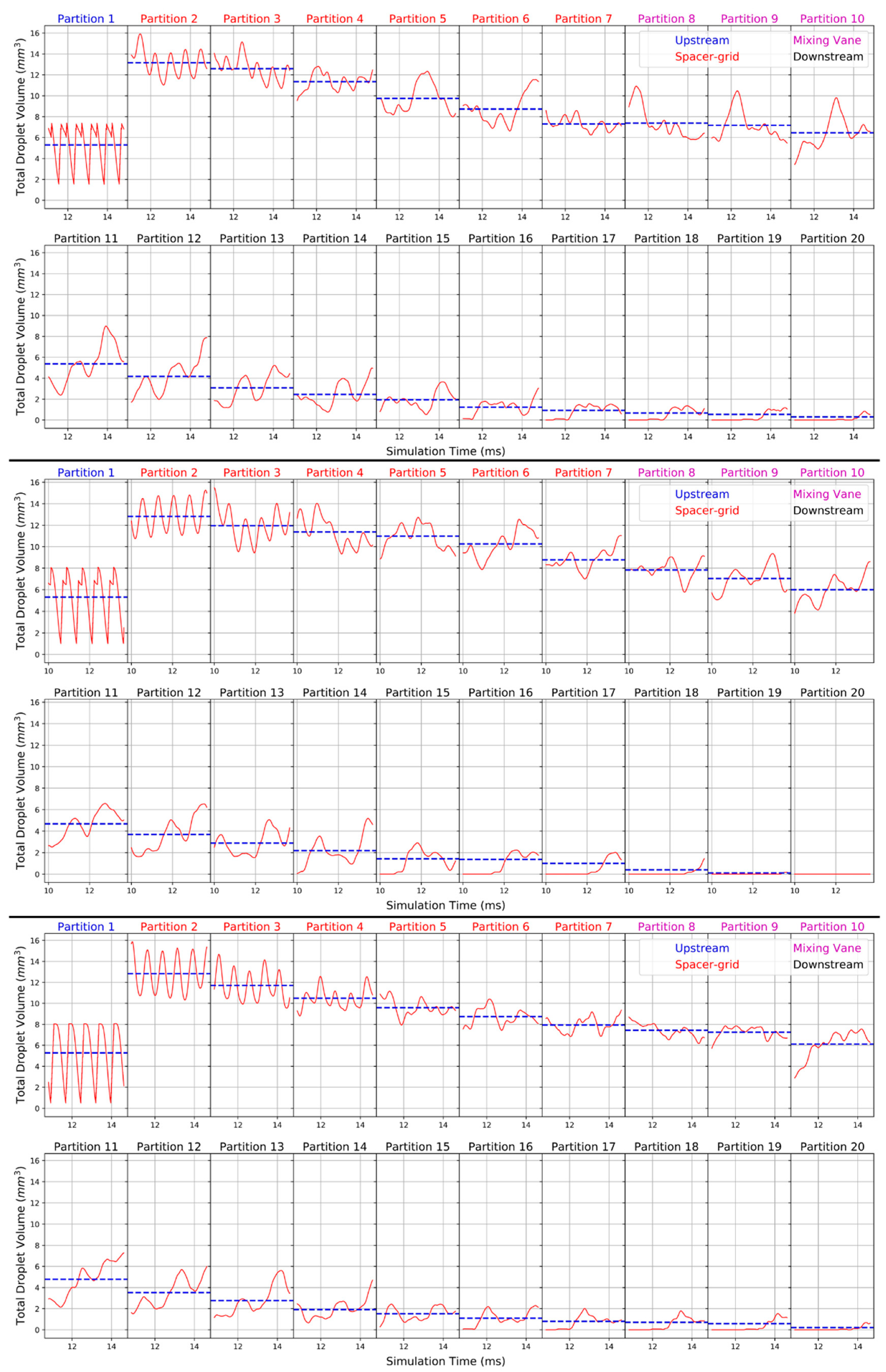
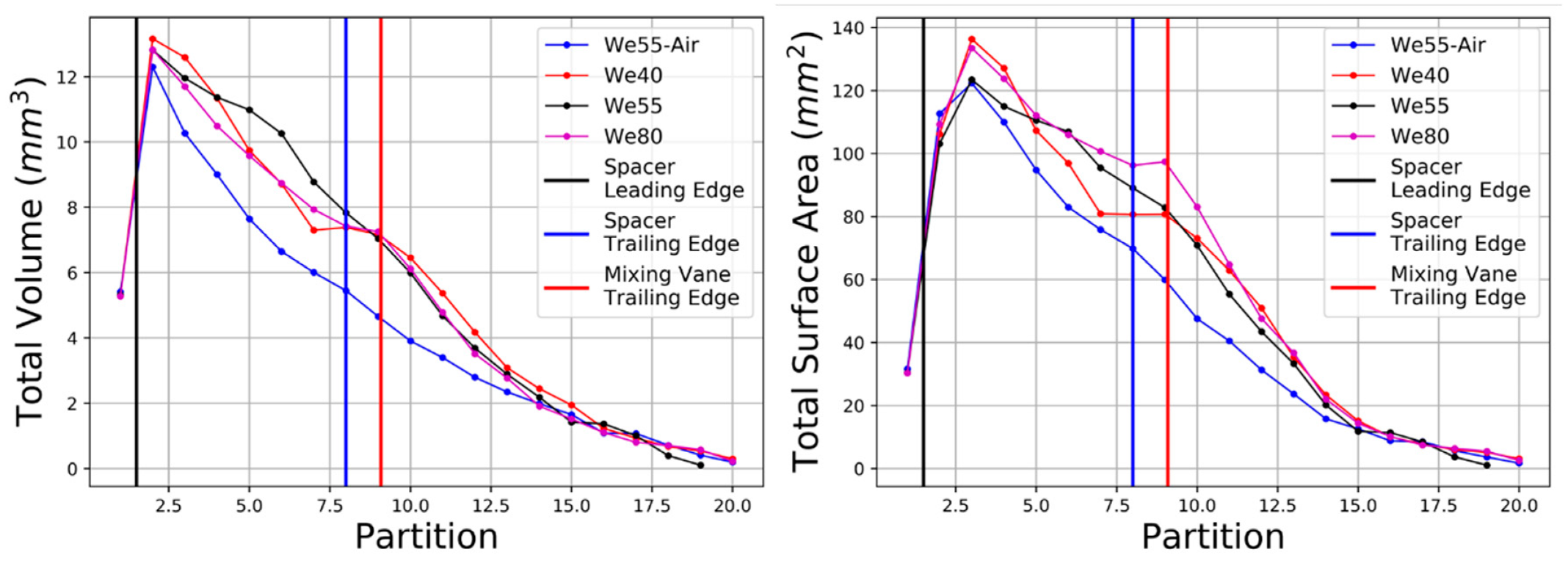
3.2. Axial Evolution of Droplet Sauter Mean Diameter
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Hochreiter, L.; Cheung, F.; Lin, T.; Baratta, A.; Frepoli, C. Dispersed Flow Heat Transfer under Reflood Conditions in a 49-Rod Bundle: Test Plan and Design—Results from Tasks 1–10; PSU ME/NE-NRC-04-98-041; Pennsylvania State University: State College, PA, USA, 2000. [Google Scholar]
- Meholic, M.J. The Development of a Non-Equilibrium Dispersed Flow Film Boiling Heat Transfer Modeling Package. Ph.D. Thesis, The Pennsylvania State University, The Graduate School, College of Engineering, State College, PA, USA, August 2011. [Google Scholar]
- Takenaka, N.; Akagawa, K.; Fujii, T.; Nishida, K. Experimental study on flow pattern and heat transfer of inverted annular flow. Nucl. Eng. Des. 1990, 120, 293–300. [Google Scholar] [CrossRef]
- Hammouda, N.; Groeneveld, D.; Cheng, S. An experimental study of subcooled film boiling of refrigerants in vertical up-flow. Int. J. Heat Mass Transf. 1996, 39, 3799–3812. [Google Scholar] [CrossRef]
- Andreani, M.T.; Yadigaroglu, G. Dispersed Flow Film Boiling; Thermal-Hydraulic Laboratory, Paul Scherrer Institute (PSI): Villigen, Switzerland, 1989. [Google Scholar]
- Yoder, G.L.; Rohsenow, W.M. Dispersed Flow Film Boiling; Heat Transfer Laboratory, Department of Mechanical Engineering, Massachusetts Institute of Technology: Cambridge, MA, USA, 1980. [Google Scholar]
- Lee, N. PWR FLECHT SEASET Unblocked Bundle, Forced and Gravity Reflood Task Data Evaluation and Analysis Report; No.10; The Commission: Brussels, Belgium, 1982. [Google Scholar]
- Bajorek, S.M.; Cheung, F.-B. Rod bundle heat transfer thermal-hydraulic program. Nucl. Technol. 2018, 205, 307–327. [Google Scholar] [CrossRef]
- Andreani, M.; Yadigaroglu, G. Difficulties in modeling dispersed-flow film boiling. Heat Mass Transf. 1992, 27, 37–49. [Google Scholar] [CrossRef]
- Hochreiter, L. Rod Bundle Heat Transfer Facility: Steady-State Steam Cooling Experiments; United States Nuclear Regulatory Commission, Office of Nuclear Regulatory: Washington, DC, USA, 2014. [Google Scholar]
- Riley, M.P. Spacer Grid Induced Heat Transfer Enhancement in a Rod Bundle under Reflood Conditions; Pennsylvania State University: State College, PA, USA, 2014. [Google Scholar]
- Miller, D.J.; Cheung, F.; Bajorek, S. Investigation of grid-enhanced two-phase convective heat transfer in the dispersed flow film boiling regime. Nucl. Eng. Des. 2013, 265, 35–44. [Google Scholar] [CrossRef]
- Riley, M.; Mohanta, L.; Cheung, F.; Bajorek, S.; Tien, K.; Hoxie, C. Experimental studies of spacer grid thermal hydraulics in the dispersed flow film boiling regime. Nucl. Technol. 2015, 190, 336–344. [Google Scholar] [CrossRef]
- Yao, S.C.; Hochreiter, L.E.; Leech, W.J. Heat-Transfer Augmentation in Rod Bundles Near Grid Spacers. J. Heat Transf. 1982, 104, 76–81. [Google Scholar] [CrossRef]
- Avramova, M. Development of an Innovative Spacer Grid Model Utilizing Computational Fluid Dynamics within a Sub-Channel Analysis Tool; Pennsylvania State University: State College, PA, USA, 2007. [Google Scholar]
- Hochreiter, L.; Cheung, F.; Lin, T.; Frepoli, C.; Sridharan, A.; Todd, D.; Rosal, E.R. Rod Bundle Heat Transfer Test Facility Test Plan and Design; NUREG CR-6975; US Nuclear Regulatory Commission: Washington, DC, USA, 2010. [Google Scholar]
- Cheung, F.; Bajorek, S. Dynamics of droplet breakup through a grid spacer in a rod bundle. Nucl. Eng. Des. 2011, 241, 236–244. [Google Scholar] [CrossRef]
- Wachters, L.; Smulders, L.; Vermeulen, J.; Kleiweg, H. The heat transfer from a hot wall to impinging mist droplets in the spheroidal state. Chem. Eng. Sci. 1966, 21, 1231–1238. [Google Scholar] [CrossRef]
- Senda, J. Experimental Studies on the Behavior of a Small Droplet Impinging upon a Hot Surface. In Proceedings of the ICLASS-82, Madison, WI, USA, 20–24 June 1982. [Google Scholar]
- Behzadi, A.; Issa, R.; Rusche, H. Modelling of dispersed bubble and droplet flow at high phase fractions. Chem. Eng. Sci. 2004, 59, 759–770. [Google Scholar] [CrossRef]
- Gosman, A.D.; Lekakou, C.; Politis, S.; Issa, R.I.; Looney, M.K. Multidimensional modeling of turbulent two-phase flows in stirred vessels. AIChE J. 1992, 38, 1946–1956. [Google Scholar] [CrossRef]
- Lance, M.; Bataille, J. Turbulence in the liquid phase of a uniform bubbly air–water flow. J. Fluid Mech. 1991, 222, 95. [Google Scholar] [CrossRef]
- Wang, S.K.; Lee, S.J.; Jones, O.C.; Lahey, R.T. 3-D turbulence structure and phase distribution measurements in bubbly two-phase flows. Int. J. Multiph. Flow 1987, 13, 327–343. [Google Scholar] [CrossRef]
- Lee, S.L.; Lahey, R.T.; Jones, O.C. The Prediction of Two-Phase Turbulence and Phase Distribution Phenomena Using a K-κ Model. Jpn. J. Multiph. Flow 1989, 3, 335–368. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College London, University of London, London, UK, 2002. [Google Scholar]
- Balachandar, S.; Eaton, J.K. Turbulent Dispersed Multiphase Flow. Annu. Rev. Fluid Mech. 2010, 42, 111–133. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E. CFD modeling of bubble-induced turbulence. Int. J. Multiph. Flow 2013, 55, 138–155. [Google Scholar] [CrossRef]
- Rasquin, M.; Smith, C.; Chitale, K.; Seol, E.S.; Matthews, B.A.; Martin, J.L.; Sahni, O.; Loy, R.M.; Shephard, M.S.; Jansen, K.E. Scalable Implicit Flow Solver for Realistic Wing Simulations with Flow Control. Comput. Sci. Eng. 2014, 16, 13–21. [Google Scholar] [CrossRef]
- Bolotnov, I.A. Phasta-NCSU Git Repository. Available online: https://github.com/PHASTA/phasta-ncsu (accessed on 1 December 2020).
- Nagrath, S.; Jansen, K.E.; Lahey, R.T. Computation of incompressible bubble dynamics with a stabilized finite element level set method. Comput. Methods Appl. Mech. Eng. 2005, 194, 4565–4587. [Google Scholar] [CrossRef]
- Fang, J.; Mishra, A.V.; Bolotnov, I.A. Interface Tracking Simulation of Two-phase Bubbly Flow in A PWR Subchannel. In Proceedings of the International Embedded Topical Meeting on Advances in Thermal Hydraulics—2014, American Nuclear Society 2014 Annual Meeting (ATH ‘14), Reno, NV, USA, 15–19 June 2014. [Google Scholar]
- Bolotnov, I.A.; Jansen, K.E.; Drew, D.A.; Oberai, A.A.; Lahey, R.T.; Podowski, M.Z. Detached direct numerical simulations of turbulent two-phase bubbly channel flow. Int. J. Multiph. Flow 2011, 37, 647–659. [Google Scholar] [CrossRef]
- Fang, J.; Cambareri, J.; Li, M.; Saini, N.; Bolotnov, I.A. Interface-Resolved Simulations of Reactor Flows. Nucl. Technol. 2020, 206, 133–149. [Google Scholar] [CrossRef]
- Zimmer, M.D.; Bolotnov, I.A. Slug-to-churn vertical two-phase flow regime transition study using an interface tracking approach. Int. J. Multiph. Flow 2019, 115, 196–206. [Google Scholar] [CrossRef]
- Saini, N.; Bolotnov, I.A. Interface capturing simulations of droplet interaction with spacer grids under DFFB condi-tions. Nucl. Eng. Des. 2020, 364, 110685. [Google Scholar] [CrossRef]
- Lu, J.; Biswas, S.; Tryggvason, G. A DNS study of laminar bubbly flows in a vertical channel. Int. J. Multiph. Flow 2006, 32, 643–660. [Google Scholar] [CrossRef]
- Santarelli, C.; Fröhlich, J. Direct Numerical Simulations of spherical bubbles in vertical turbulent channel flow. Influence of bubble size and bidispersity. Int. J. Multiph. Flow 2016, 81, 27–45. [Google Scholar] [CrossRef]
- Chang, C.-W.; Dinh, N. Classification of machine learning frameworks for data-driven thermal fluid models. Int. J. Therm. Sci. 2019, 135, 559–579. [Google Scholar] [CrossRef]
- Ma, T.; Santarelli, C.; Ziegenhein, T.; Lucas, D.; Fröhlich, J. Direct numerical simulation–based Reynolds-averaged closure for bubble-induced turbulence. Phys. Rev. Fluids 2017, 2, 034301. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Liu, Y.; Dinh, N.; Sato, Y.; Niceno, B. Data-driven modeling for boiling heat transfer: Using deep neural networks and high-fidelity simulation results. Appl. Therm. Eng. 2018, 144, 305–320. [Google Scholar] [CrossRef]
- Bao, H.; Feng, J.; Dinh, N.; Zhang, H. Computationally efficient CFD prediction of bubbly flow using physics-guided deep learning. Int. J. Multiph. Flow 2020, 131, 103378. [Google Scholar] [CrossRef]
- Saini, N. High-fidelity Interface Capturing Simulations of the Post-LOCA Dispersed Flow Film Boiling Regime in a Pres-Surized Water Reactor Sub-Channel. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2020. [Google Scholar]
- Whiting, C.H.; Jansen, K.E. A stabilized finite element method for the incompressible Navier-Stokes equations using a hierarchical basis. Int. J. Numer. Methods Fluids 2001, 35, 93–116. [Google Scholar] [CrossRef]
- Ibanez, D.A.; Seol, E.S.; Smith, C.W.; Shephard, M.S. PUMI: Parallel unstructured mesh infrastructure. ACM Trans. Math. Softw. (TOMS) 2016, 42, 17. [Google Scholar] [CrossRef]
- Sahni, O.; Carothers, C.D.; Shephard, M.S.; Jansen, K.E. Strong Scaling Analysis of a Parallel, Unstructured, Implicit Solver and the Influence of the Operating System Interference. Sci. Program. 2009, 17, 261–274. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Nagrath, S.; Jansen, K.E.; Lahey, R.T. Three Dimensional Simulation of Incompressible Two-Phase Flows Using a Stabilized Finite Element Method and a Level Set Approach; Preprint; Elsevier Science: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Fatemi, E.; Sussman, M. An efficient interface preserving Level-Set Re-distancing algorithm and its application to interfacial incompressible fluid flow. SIAM J. Sci. Statist. Comput. 1995, 158, 36. [Google Scholar]
- Chen, N.H. An Explicit Equation for Friction Factor in Pipe. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Lee, M.; Moser, R.D. Direct numerical simulation of turbulent channel flow up to Re_tau 5200″. J. Fluid Mech. 2015, 774, 395–415. [Google Scholar] [CrossRef]
- Thomas, A.M.; Fang, J.; Bolotnov, I.A. Estimation of shear-induced lift force in laminar and turbulent flows. In Proceedings of the International Topical Meeting on Advances in Thermal Hydraulics—2014 (ATH ′14), Reno, NV, USA, 15–19 June 2014. [Google Scholar]
- Busco, G.; Merzari, E.; Hassan, Y.A. Invariant analysis of the Reynolds stress tensor for a nuclear fuel assembly with spacer grid and split type vanes. Int. J. Heat Fluid Flow 2019, 77, 144–156. [Google Scholar] [CrossRef]
- Wierzba, A. Deformation and breakup of liquid drops in a gas stream at nearly critical Weber numbers. Exp. Fluids 1990, 9, 59–64. [Google Scholar] [CrossRef]
- Jin, Y.; Miller, D.J.; Qiao, S.; Rau, A.; Kim, S.; Cheung, F.-B.; Bajorek, S.M.; Tien, K.; Hoxie, C.L. Uncertainty analysis on droplet size measurement in dispersed flow film boiling regime during reflood using image processing technique. Nucl. Eng. Des. 2018, 326, 202–219. [Google Scholar] [CrossRef]
- Papka, M.; Coghlan, S.; Isaacs, E.; Peters, M.; Messina, P. Mira: Argonne’s 10-Petaflops Supercomputer; Argonne National Laboratory (ANL): Argonne, IL, USA, 2013. [Google Scholar]
- Gottfried, B.; Lee, C.; Bell, K. The leidenfrost phenomenon: Film boiling of liquid droplets on a flat plate. Int. J. Heat Mass Transf. 1966, 9, 1167–1188. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Fang, J.; Rasquin, M.; Bolotnov, I.A. Interface tracking simulations of bubbly flows in PWR relevant geometries. Nucl. Eng. Des. 2017, 312, 205–213. [Google Scholar] [CrossRef]
- Nagib, H.M.; Chauhan, K.A. Variations of von Kármán coefficient in canonical flows. Phys. Fluids 2008, 20, 101518. [Google Scholar] [CrossRef]
- Avramova, M.N.; Salko, R.K. CTF Theory Manual; Technical Report for the Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2016. [Google Scholar] [CrossRef]













| Properties | Single Phase | We55-Air (Saini et al. [35]) | Properties @ 30 Psi, Steam Superheat 100 K | ||
|---|---|---|---|---|---|
| We40 | We55 | We80 | |||
| Density ratio () | 1000 | 1029.59 | |||
| Viscosity ratio () | 48 | 13.49 | |||
| Bulk Reynolds number, | 11,822 | ||||
| Friction Reynolds number, | 242.539 | ||||
| Mean inlet gas velocity, | 7.0 | ||||
| Collision Weber number, (Equation (14)) | - | 55 | 40 | 55 | 80 |
| Aerodynamic Weber number, (Equation (17)) | - | 0.319 | 0.253 | 0.348 | 0.507 |
| Injected absolute droplet velocity, | 2.05 | 1.97 | |||
| Injected droplet diameter, | - | 1.0 | |||
| Injected droplet Reynolds number, | 643.71 | 654.67 | |||
| Surface tension coefficient, | - | 0.091 | 0.118 | 0.086 | 0.059 |
| Gravity, | −9.81 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saini, N.; Bolotnov, I.A. Two-Phase Turbulence Statistics from High Fidelity Dispersed Droplet Flow Simulations in a Pressurized Water Reactor (PWR) Sub-Channel with Mixing Vanes. Fluids 2021, 6, 72. https://doi.org/10.3390/fluids6020072
Saini N, Bolotnov IA. Two-Phase Turbulence Statistics from High Fidelity Dispersed Droplet Flow Simulations in a Pressurized Water Reactor (PWR) Sub-Channel with Mixing Vanes. Fluids. 2021; 6(2):72. https://doi.org/10.3390/fluids6020072
Chicago/Turabian StyleSaini, Nadish, and Igor A. Bolotnov. 2021. "Two-Phase Turbulence Statistics from High Fidelity Dispersed Droplet Flow Simulations in a Pressurized Water Reactor (PWR) Sub-Channel with Mixing Vanes" Fluids 6, no. 2: 72. https://doi.org/10.3390/fluids6020072
APA StyleSaini, N., & Bolotnov, I. A. (2021). Two-Phase Turbulence Statistics from High Fidelity Dispersed Droplet Flow Simulations in a Pressurized Water Reactor (PWR) Sub-Channel with Mixing Vanes. Fluids, 6(2), 72. https://doi.org/10.3390/fluids6020072






