Next Article in Journal
Filaments, Fronts and Eddies in the Cabo Frio Coastal Upwelling System, Brazil
Next Article in Special Issue
Numerical Modeling of Sperm Swimming
Previous Article in Journal
Numerical Prediction of Turbulent Spray Flame Characteristics Using the Filtered Eulerian Stochastic Field Approach Coupled to Tabulated Chemistry
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Fluids
Volume 6
Issue 2
10.3390/fluids6020053
fluids-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

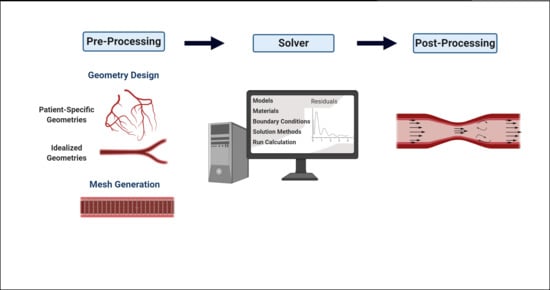
Blood Flow Modeling in Coronary Arteries: A Review

by
Violeta Carvalho
1,
Diana Pinho
1,2,3,4,†,
Rui A. Lima
1,2,*,
José Carlos Teixeira
1 and
Senhorinha Teixeira
5
1
MEtRICs Research Center, Mechanical Engineering Department, University of Minho, Campus de Azurém, 4800-058 Guimarães, Portugal
2
CEFT, Faculdade de Engenharia da Universidade do Porto (FEUP), R. Dr. Roberto Frias, 4200-465 Porto, Portugal
3
Research Centre in Digitalization and Intelligent Robotics (CeDRI), Instituto Politécnico de Bragança, Campus de Santa Apolónia, 5300-253 Bragança, Portugal
4
Center for MicroElectromechanical Systems (CMEMS-UMinho), University of Minho, Campus de Azurém, 4800-058 Guimarães, Portugal
5
ALGORITMI Centre (CAlg), University of Minho, 4800-058 Guimarães, Portugal
*
Author to whom correspondence should be addressed.
†
Current Affiliation: INL—International Iberian Nanotechnology Laboratory, Av. Mestre José Veiga, 4715-330 Braga, Portugal
Fluids 2021, 6(2), 53; https://doi.org/10.3390/fluids6020053
Submission received: 29 November 2020 / Revised: 10 January 2021 / Accepted: 20 January 2021 / Published: 23 January 2021
(This article belongs to the Special Issue Computational Biofluid Mechanics)
Browse Figures
Versions Notes

Abstract

:
Atherosclerosis is one of the main causes of cardiovascular events, namely, myocardium infarction and cerebral stroke, responsible for a great number of deaths every year worldwide. This pathology is caused by the progressive accumulation of low-density lipoproteins, cholesterol, and other substances on the arterial wall, narrowing its lumen. To date, many hemodynamic studies have been conducted experimentally and/or numerically; however, this disease is not yet fully understood. For this reason, the research of this pathology is still ongoing, mainly, resorting to computational methods. These have been increasingly used in biomedical research of atherosclerosis because of their high-performance hardware and software. Taking into account the attempts that have been made in computational techniques to simulate realistic conditions of blood flow in both diseased and healthy arteries, the present review aims to give an overview of the most recent numerical studies focused on coronary arteries, by addressing the blood viscosity models, and applied physiological flow conditions. In general, regardless of the boundary conditions, numerical studies have been contributed to a better understanding of the development of this disease, its diagnosis, and its treatment.

Graphical Abstract

1. Introduction

Cardiovascular diseases are responsible for a critical number of deaths every year worldwide, accounting for nearly 31% of all deaths, most of which are associated with atherosclerosis, a disease that causes unusual hemodynamic conditions in arteries [1,2,3]. Briefly, atherosclerosis is a silent, multifactorial, and complex disease initiated when lipids and immune cells are accumulated in the arterial wall, resulting in the formation of a plaque [4,5]. This has been correlated to local biological, biomechanical, and systemic factors [6,7,8]. Among these factors, local hemodynamics has been indicated as the major cause [9,10,11]. In particular, wall shear stress (WSS) is a well-known predictor of coronary atherosclerosis progression. While regions of low wall shear stress have been commonly recognized as prone to plaque development, high values of WSS are related to plaque destabilization [12,13,14,15,16]. Moreover, a recent study has also proved that patients with COVID-19 are at high risk for thrombotic arterial and venous occlusions. Considering the mortality rate caused by this virus itself until today and its relation with atherosclerosis development, this becomes an even more complex situation [17].
Although the presence of this pathology has quite serious damage regardless of the arteries affected, the situation is aggravated when this pathology develops in coronary arteries. When those are affected, the agglomeration of fatty materials creates an occlusion, which restricts the blood flow to the heart muscle leading to a decreased supply of blood, oxygen, and other vital nutrients fundamental for the proper functioning of this organ. Eventually, the reduced blood flow may cause chest pain or a heart attack if there is a complete blockage of the artery [18,19]. A common approach used to treat this pathology is balloon angioplasty and placement of an intracoronary stent. This allows restoring the blood flow keeping the artery open, nevertheless, the risk of restenosis is still present [20,21].
Considering the global impact of this disease, it is of utmost importance to obtain deeper knowledge about the blood flow hemodynamics. For this reason, extensive research has been done in this area, by applying either experimental and/or numerical methods. Although numerous experimental hemodynamic studies are found in the literature, by applying either in vitro [22,23,24,25,26,27,28], in vivo [29,30,31,32,33], or ex vivo [34,35,36] approaches, there are some drawbacks associated as reported elsewhere [19,37,38,39,40,41]. For this reason, lately, computational approaches have been the preferred method of several researchers [42,43,44,45,46]. These have become a valuable tool for evaluating and predicting the disease formation, and also for testing the performance of new devices for its treatment. By having the capability of constructing more realistic virtual models, getting fast and accurate results, and thoroughly testing different physiological conditions, some limitations of hemodynamic experimental techniques used can be overcome by the computational models [45,47,48,49,50,51]. However, this does not mean that those models can completely replace experimental tests since it is still quite challenging to perform realistic blood flow modeling [52].
Due to several advantages of using numerical simulations, computational atherosclerosis studies have gained popularity in recent years [53]. In general, to perform numerical simulations three main steps have to be accomplished, the pre-processing, the solver, and the post-processing. Firstly, it is necessary to define the geometry of the problem, followed by the mesh generation. Secondly, the fluid properties of blood, the flow physics model, and the boundary conditions are defined in order to solve the mathematical model. Finally, after the problem being solved, the results are analyzed. These steps are drafted as follows in Figure 1.
Over the years, researchers have modeled blood flow within arteries by using different geometries, diverging in two directions, using either stenotic geometries with idealized shapes (e.g., half-sphere [54], ellipsoid [55], gaussian equation [56], cosine function [57], among others proposed by the authors themselves [58,59]) or realistic coronary artery models extracted from patient’s medical data [60,61,62,63,64,65].
After defining the geometry, the blood properties have to be set to solve the problem accurately. Blood is a complex mixture of cells, proteins, lipoproteins, and ions which are transports nutrients and wastes. Due to the presence of red blood cells, the viscosity of blood is increased and affects the behavior of the fluid. Moreover, although considering the blood as a Newtonian fluid is generally accepted as a good approximation for large vessels, in the microcirculatory system, and also in the presence of stenosis, the assumption is not true. At these locations, the non-Newtonian behavior is more evident due to the ability of red blood cells to form aggregates, termed rouleaux, at low shear rates. Moreover, other aspects that should be taken into account are the cyclic nature of the heart pump, which creates pulsatile conditions, and also the elastic behavior observed in the arteries’ wall [66,67,68].
Although the aforementioned characteristics of blood, namely, the vessel wall elasticity, non-Newtonian viscosity, and particles in the fluid, and body forces are physiologically relevant, the analysis of blood flow can be greatly simplified by neglecting some of the properties [68]. For this reason, in the literature, there is a vast diversity of articles that apply different boundary conditions to simulate blood flow, and attention must be taken since the performance of CFD models is directly dependent on the blood rheology, physiological flow conditions, mechanical properties of blood vessels, among other mechanical and biological factors set to solve the problem. In this regard, in the present paper, a review of the geometries, boundary conditions, and flow properties proposed by several authors for coronary models is provided by discussing and presenting the current knowledge on the advantages and also the drawbacks of blood viscosity models and physiological flow conditions available.

2. Blood Flow Studies in Coronary Arteries

Despite the progress done in experimental studies and blood flow measurement techniques, there are still some challenges associated with them [19]. For instance, in vitro WSS measurements are extremely difficult to perform and the velocity measurements have high associated errors. These, combined with other complications of directly measuring quantities of interest, have motivated the use of computer simulations to predict them in silico [69].
The earliest numerical detailed studies solving the flow problem in constricted tubes were conducted by Lee and Fung (1970) [70]. After that, other studies in this field conducted by Caro et al., (1971) [71], Glagov et al., (1989) [72], and Ku et al., (1985) [73] are important references in this area and should be highlighted. Ever since, CFD approaches have been progressively adopted by most researchers as the preferred technique for numerical modeling of hemodynamics. Owing to the continued growth of computational power, these have become an increasingly reliable tool for measuring biomechanical factors vital for clinical decision-making and surgical planning. However, the proper selection of the flow boundary conditions has to be done, otherwise, the findings can be considered uncertain, weak, and unrealistic [74]. In this regard, the different geometries, boundary conditions, and flow characteristics applied by some researchers in the last ten years are summarized in Table 1.
From the above-mentioned investigations, it can be seen that, regardless of the type of geometry, the majority of authors consider that the blood is a non-Newtonian fluid, usually approximated by the Carreau model, with a laminar behavior. Regarding the boundary conditions, in most cases, the wall is considered rigid, and at the inlet, a pulsatile velocity is applied. At the outlet, the condition set mainly depends on the study, but either the default conditions are maintained, or pressures are applied, time-dependent or constant values.

2.1. Geometrical Parameters and Stenosis Severity

Before studying directly stenotic coronary arteries, some authors have dedicated their time to study the effect of geometrical parameters, such as the branch curvatures, tortuosities, and the angulations of the arteries, and relating them to the development of atherosclerosis, by resorting to idealized geometries, or the combination of patient-specific models with idealized ones [6,87,89]. In general, regardless of the type of geometry, it has been shown that there is a direct correlation between wide angulation in the coronary artery branches and hemodynamic changes, such as disturbed flow and low WSS, possibly inducing the development of atherosclerosis [87,89]. Although consistent observations between idealized and patient-specific models have been demonstrated by Chaichana et al., (2011) [89], the same is not true when talking about the arteries’ curvature and tortuosity, since small variations can lead to different hemodynamic simulated results [6]. It was shown that the specific curvature of each branch of the coronary bifurcation affects the hemodynamics of the remaining three branches, which can cause an increase in atherosusceptibility [6]. In view of this, it can be verified that the selection of the geometrical parameters of the artery model plays an important role and can lead to different hemodynamic results.
Nevertheless, when the aim is to investigate the effect of stenosis severity, the results presented in the literature have shown to be in good agreement independently of the model used, idealized, or patient-specific. Generally, an increase in the velocity and WSS at the stenosis throat is observed. This increased WSS can disturb the plaque formed and lead to plaque rupture, and consequently to heart failure. Besides the WSS, other shear stress indices have been studied such as the time average wall shear stress (TAWSS), and the oscillatory stress index (OSI). While the TAWSS has the same trend as WSS, the OSI distribution has a maximum value in the region downstream of the stenosis. Moreover, in this location, the prevalence of recirculation zones is also verified [60,64,75,86,90,91]. Both high OSI, low WSS, and disturbed flows in the post stenotic section are important factors that can promote the formation of atherosclerotic plaques [59,68,92].
A different way to study the effect of stenosis in blood flow hemodynamics was addressed by Doutel et al., (2018) [93]. They developed a methodology to create three-dimensional irregular stenosis with different degrees of occlusion in artery models for both numerical and in vitro hemodynamic studies. This methodology is quite interesting since it allows the creation of realistic stenosis in a fast way for hemodynamic studies. Furthermore, the authors proved that the irregular shape of the stenosis and their specific morphology affects the flow field, creating diverse values of WSS for each case.

2.2. Newtonian and Non-Newtonian Assumptions

Besides the effect of stenosis, several studies have emphasized the importance of considering the non-Newtonian behavior of blood and selecting the proper model to better represent the in vivo conditions [56,94]. An interesting study was undertaken by Razavi et al. (2011) [56], in which six non-Newtonian models and a Newtonian model were compared. The data obtained showed that the power-law model produces higher deviations in comparison with other models, overstating the non-Newtonian behavior, regarding the velocity and WSS values. On the other hand, the generalized power-law and modified-Casson models are more similar to the Newtonian state, though, they underestimate the non-Newtonian behavior. In contrast to the previous models, the Carreau and Carreau–Yasuda models represented moderate IG values (cut-off value above which flow can be assumed as non-Newtonian), demonstrating to be the suitable models to mimic the blood behavior. Other authors have also compared Newtonian and non-Newtonian models. Chaichana et al., (2012) [60] compared the effect of the non-Newtonian power-law generalized model with a Newtonian fluid; however, similar results were obtained for both cases, in terms of velocity fields and WSS measurements. On the other hand, Gaudio et al. (2018) [91] compared the Newtonian and non-Newtonian Carreau–Yasuda model. Their results showed that the velocity for the Carreau–Yasuda model is slightly lower when compared to the Newtonian model, but the non-Newtonian effects are most important in shear stress indices distributions. Carvalho et al., (2020) [78] have similar results; however, they used the Carreau non-Newtonian model. Another interesting study was performed by Pinto et al., (2020) [95]. They investigated several viscoelastic models, namely the Generalized Oldroyd-B (GOB) model, the Multi-mode Giesekus and Simplified Phan-Thien/Tanner (sPTT) models in order to conclude which model is the most accurate to simulate the blood flow, and compared those with the Carreau model and also with a Newtonian model. The authors verified that the non-linear viscoelastic multi-mode models (Giesekus and sPTT) cause an overall reduction of the velocity in regions of higher velocity gradients. In general, the researchers concluded that the sPTT model should be the preferred option since the Giesekus model introduces the second normal stress difference, which so far has not been reported for blood.

2.3. Turbulence Modeling and Wall Assumptions

Although various investigations consider the blood flow as laminar, due to the pulsatile nature of blood flow through arteries, and the presence of stenosis, the transition from laminar to turbulent flow condition can occur. For this reason, some authors have explored some turbulent models in computational simulations [42,59,64,77,78,86,96]. By observing Table 1 it can be seen that the majority uses or the standard k-ω or the k-ω SST turbulent model. The main difference between these two models is that the SST model accounts for the laminar to turbulent transition, and it seems to be the most suitable for blood flow studies [64,97]. However, in a study conducted by Straatman et al. (2016) [97], both models were compared with experimental data, and the k-ω SST turbulent model provided the best overall results.
Furthermore, hemodynamic studies mainly assume the wall to be rigid, however, over the years, fluid-structure interaction (FSI) has received increasing interest due to its ability to simultaneously model blood flow and arterial wall deformations [79,81,98,99,100,101]. Among the several investigations that have emerged in this area, one of the most cited works in the literature was performed by Torii et al. (2009) [99], wherein the effects of compliance in WSS calculations were studied. Although more recent studies have been conducted to evaluate if there are significant differences between flexible and rigid walls, the main results are in good agreement. It is stated that there are negligible differences in TAWSS and OSI values, although, in the distal region of the artery, differences in instantaneous WSS profiles and velocity measurements were perceptible [57,99]. Regardless of the interesting results obtained in the literature, since arteries have a high degree of stiffness, in most cases, the effects of elasticity are very small, and thus, an assumption of rigid tube flow is reasonable [68].

3. Conclusions and Future Perspectives

Due to the great progress that has been made recently in the development of CFD methods, these have become extremely fundamental for hemodynamic studies, allowing researchers to obtain a better understanding of atherosclerosis in a rapid and accurate fashion. However, there are still unsolved challenges that have to be addressed in future hemodynamic studies. In the present review, the application of computational simulations by using different physiological conditions of blood flow, several rheological models, and boundary conditions, were discussed.
Although huge advancements have been made in imaging techniques to obtain patient-specific images, this step is time-consuming, and it is still a challenging task for all researchers. For this reason, nowadays, idealized models continue to be widely used by researchers, since these allow to obtain important and relevant results, without requiring much computational time and without the need to collect the medical images, which is highly time-consuming. In this regard, a promising study was proposed by Doutel et al., (2018) [93] wherein artificial, but realistic stenosis can be generated.
It was also noted that, although the modelling of blood as a Newtonian fluid is a good approximation for large vessels with high shear rates, the assumption of non-Newtonian behavior of blood flow has been increasingly used in the presence of stenosis. From the overall studies, the most used models are the Carreau and the Carreau-Yasuda, and these have also been indicated as the most appropriate to simulate the blood rheology by Razavi et al., (2011) [56]. Nevertheless, currently, one cannot say which is the right model, because there is not yet enough evidence in the literature to prove which model fully expresses the complex nature of blood rheology and its dependence on many biological factors [50]. Accordingly, it is of great importance to obtain proper models for CFD analysis that take into account the non-Newtonian behavior of blood. For this purpose, more experimental studies are needed. Regarding the boundary conditions, few studies have evaluated the impact of using different inlet and outlet boundary conditions [74,102], and therefore, it would be interesting, in future studies, to investigate what are the profiles more adequate to study the blood flow behavior in coronary arteries.
Despite the great efforts that have been made so far, the blood has been mainly modeled as a single-phase fluid. However, blood is a mixture of plasma, red blood cells, white blood cells, and platelets. Therefore, the consideration of multiphase models is of great importance when modeling atherosclerotic lesions. Although some studies have already applied these models [42,83,103,104,105], the research is still in the beginning. Moreover, it should be also noted that the use of these models is a promising option for studying nanoparticle-mediated targeted drug delivery treatment of atherosclerosis. In this context, a promising study was conducted by Zhang et al., (2020) [83]. The authors used an Eulerian-Lagrangian approach coupled with FSI to investigate the impact of plaque morphology on magnetic nanoparticles targeting under the action of an external field.
Due to the continuous improvements acquired in computational methods, in the following years more amazing and complex hemodynamic studies will be performed. The work of Zhao et al. (2019) [82] should be highlighted since their numerical approach has a great potential to achieve more realistic simulations. They have simulated 4D hemodynamic profiles of time-resolved blood flow. The results proved that these simulations can provide extensive information about blood flow, both qualitatively and quantitatively that may be advantageous for future investigations of clinical diagnosis and treatment of atherosclerosis.
To conclude, although computational methods have been extensively used for atherosclerosis investigations in recent years, they are expected to become more popular and more effective to simulate the blood flow in the cardiovascular system, and consequently, they will promote medical innovation at an affordable cost. However, to this end, active collaborations between engineers and medical staff are needed to assure the successful application of this technique in atherosclerosis treatment.

Author Contributions

Conceptualization, V.C. and S.T.; Writing-Original Draft Preparation, V.C.; Writing—Review and Editing, V.C., D.P., R.A.L., J.C.T. and S.T.; Supervision, R.A.L. and S.T.; Funding Acquisition, J.C.T., R.A.L. and S.T. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported through the R&D Units Project Scope: UIDB/00319/2020, UIDB/04077/2020, NORTE-01-0145-FEDER-030171, and NORTE-01-0145-FEDER-029394, funded by COMPETE2020, NORTE 2020, PORTUGAL 2020, and FEDER.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. World Health Organization (WHO). Cardiovasc. Dis. Fact Sheet No.317, 2017. Available online: https://www.who.int/nmh/publications/fact_sheet_cardiovascular_en.pdf (accessed on 20 January 2021).
  2. Haverich, A.; Boyle, E.C. Atherosclerosis Pathogenesis and Microvascular Dysfunction, 1st ed.; Springer: New York, NY, USA, 2019; ISBN 9783030202446. [Google Scholar]
  3. Libby, P.; Buring, J.E.; Badimon, L.; Hansson, G.K.; Deanfield, J.; Bittencourt, M.S.; Tokgözoğlu, L.; Lewis, E.F. Atherosclerosis. Nat. Rev. Dis. Prim. 2019, 5, 1–18. [Google Scholar] [CrossRef] [PubMed]
  4. Badimon, L.; Vilahur, G. Thrombosis formation on atherosclerotic lesions and plaque rupture. J. Intern. Med. 2014, 276, 618–632. [Google Scholar] [CrossRef] [PubMed]
  5. Lusis, A.J. Atherosclerosis. Nature 2000, 407, 233–241. [Google Scholar] [CrossRef] [PubMed]
  6. Kashyap, V.; Arora, B.B.; Bhattacharjee, S. A computational study of branch-wise curvature in idealized coronary artery bifurcations. Appl. Eng. Sci. 2020, 4, 100027. [Google Scholar] [CrossRef]
  7. Sun, Y.; Guan, X. Autophagy: A new target for the treatment of atherosclerosis. Front. Lab. Med. 2018, 2, 68–71. [Google Scholar] [CrossRef]
  8. Carpenter, H.J.; Gholipour, A.; Ghayesh, M.H.; Zander, A.C.; Psaltis, P.J. A review on the biomechanics of coronary arteries. Int. J. Eng. Sci. 2020, 147, 103201. [Google Scholar] [CrossRef]
  9. Lopes, D.; Puga, H.; Teixeira, J.; Lima, R. Blood flow simulations in patient-specific geometries of the carotid artery: A systematic review. J. Biomech. 2020, 111, 110019. [Google Scholar] [CrossRef]
  10. Zaromytidou, M.; Siasos, G.; Coskun, A.U.; Lucier, M.; Antoniadis, A.P.; Papafaklis, M.I.; Koskinas, K.C.; Andreou, I.; Feldman, C.L.; Stone, P.H. Intravascular hemodynamics and coronary artery disease: New insights and clinical implications. Hell. J. Cardiol. 2016, 57, 389–400. [Google Scholar] [CrossRef]
  11. Doutel, E.; Carneiro, J.; Campos, J.B.L.M.; Miranda, J.M. Experimental and numerical methodology to analyze flows in a coronary bifurcation. Eur. J. Mech. B Fluids 2018, 67, 341–356. [Google Scholar] [CrossRef]
  12. Nisco, G.D.; Hoogendoorn, A.; Chiastra, C.; Gallo, D.; Kok, A.M.; Morbiducci, U.; Wentzel, J.J. The impact of helical flow on coronary atherosclerotic plaque development. Atherosclerosis 2020, 1–8. [Google Scholar] [CrossRef]
  13. Samady, H.; Eshtehardi, P.; McDaniel, M.C.; Suo, J.; Dhawan, S.S.; Maynard, C.; Timmins, L.H.; Quyyumi, A.A.; Giddens, D.P. Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease. Circulation 2011, 124, 779–788. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Han, D.; Starikov, A.; Hartaigh, B.; Gransar, H.; Kolli, K.K.; Lee, J.H.; Rizvi, A.; Baskaran, L.; Schulman-Marcus, J.; Lin, F.Y.; et al. Relationship between endothelial wall shear stress and high-risk atherosclerotic plaque characteristics for identification of coronary lesions that cause ischemia: A direct comparison with fractional flow reserve. J. Am. Heart Assoc. 2016, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
  15. Siasos, G.; Sara, J.D.; Zaromytidou, M.; Park, K.H.; Coskun, A.U.; Lerman, L.O.; Oikonomou, E.; Maynard, C.C.; Fotiadis, D.; Stefanou, K.; et al. Local Low Shear Stress and Endothelial Dysfunction in Patients With Nonobstructive Coronary Atherosclerosis. J. Am. Coll. Cardiol. 2018, 71, 2092–2102. [Google Scholar] [CrossRef] [PubMed]
  16. Soulis, J.V.; Fytanidis, D.K.; Seralidou, K.V.; Giannoglou, G.D. Wall shear stress oscillation and its gradient in the normal left coronary artery tree bifurcations. Hippokratia 2014, 18, 12–16. [Google Scholar] [PubMed]
  17. Zuo, Y.; Estes, S.K.; Ali, R.A.; Gandhi, A.A.; Yalavarthi, S.; Shi, H.; Sule, G.; Gockman, K.; Madison, J.A.; Zuo, M.; et al. Prothrombotic autoantibodies in serum from patients hospitalized with COVID-19. Sci. Transl. Med. 2020, 3876, 1–17. [Google Scholar] [CrossRef]
  18. Pandey, R.; Kumar, M.; Majdoubi, J.; Rahimi-Gorji, M.; Srivastav, V.K. A review study on blood in human coronary artery: Numerical approach. Comput. Methods Program. Biomed. 2020, 187, 105243. [Google Scholar] [CrossRef]
  19. Carvalho, V.; Maia, I.; Souza, A.; Ribeiro, J.; Costa, P.; Puga, H.; Teixeira, S.F.C.F.; Lima, R.A. In vitro stenotic arteries to perform blood analogues flow visualizations and measurements: A Review. Open Biomed. Eng. J. 2020, 14, 87–102. [Google Scholar] [CrossRef]
  20. LaDisa, J.F.; Olson, L.E.; Douglas, H.A.; Warltier, D.C.; Kersten, J.R.; Pagel, P.S. Alterations in regional vascular geometry produced by theoretical stent implantation influence distributions of wall shear stress: Analysis of a curved coronary artery using 3D computational fluid dynamics modeling. Biomed. Eng. Online 2006, 5, 1–11. [Google Scholar] [CrossRef] [Green Version]
  21. Griggs, R.; Wing, E.F.G. Cecil Essentials of Medicine, 9th ed.; Elsevier: New York, NY, USA, 2016; ISBN 9781437718997. [Google Scholar]
  22. Kabinejadian, F.; Ghista, D.N.; Su, B.; Kaabi Nezhadian, M.; Chua, L.P.; Yeo, J.H.; Leo, H.L. In vitro measurements of velocity and wall shear stress in a novel sequential anastomotic graft design model under pulsatile flow conditions. Med. Eng. Phys. 2014, 36, 1233–1245. [Google Scholar] [CrossRef]
  23. Hewlin, R.L.; Kizito, J.P. Development of an Experimental and Digital Cardiovascular Arterial Model for Transient Hemodynamic and Postural Change Studies: “A Preliminary Framework Analysis”. Cardiovasc. Eng. Technol. 2018, 9. [Google Scholar] [CrossRef]
  24. Park, S.M.; Min, Y.U.; Kang, M.J.; Kim, K.C.; Ji, H.S. In vitro hemodynamic study on the stenotic right coronary artery using experimental and numerical analysis. J. Mech. Med. Biol. 2010, 10, 695–712. [Google Scholar] [CrossRef]
  25. Souza, A.; Souza, M.S.; Pinho, D.; Agujetas, R.; Ferrera, C.; Lima, R.; Puga, H.; Ribeiro, J. 3D Manufacturing of Intracranial aneurysm biomodels for flow visualizations: A low-cost fabrication process. Mech. Res. Commun. 2020, 107, 103535. [Google Scholar] [CrossRef]
  26. Bento, D.; Lopes, S.; Maia, I.; Lima, R.; Miranda, J.M. Bubbles moving in blood flow in a microchannel network: The effect on the local hematocrit. Micromachines 2020, 11, 344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  27. Pinho, D.; Carvalho, V.; Gonçalves, I.M.; Teixeira, S.; Lima, R. Visualization and measurements of blood cells flowing in microfluidic systems and blood rheology: A personalized medicine perspective. J. Pers. Med. 2020, 10, 249. [Google Scholar] [CrossRef] [PubMed]
  28. Carvalho, V.; Sousa, P.; Pinto, V.; Ribeiro, R.; Costa, P.; Teixeira, S.F.C.F.; Lima, R.A. Hemodynamic studies in coronary artery models manufactured by 3D printing. In Proceedings of the International Conference Innovation in Engineering, Guimarães, Portugal, 28–30 June 2021. accepted. [Google Scholar]
  29. Stepniak, K.; Ursani, A.; Paul, N.; Naguib, H. Development of a phantom network for optimization of coronary artery disease imaging using computed tomography. Biomed. Phys. Eng. Express 2019, 5, 45019. [Google Scholar] [CrossRef]
  30. Sjostrand, S.; Widerstrom, A.; Ahlgren, A.R.; Cinthio, M. Design and fabrication of a conceptual arterial ultrasound phantom capable of exhibiting longitudinal wall movement. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 11–18. [Google Scholar] [CrossRef]
  31. Papathanasopoulou, P.; Zhao, S.; Köhler, U.; Robertson, M.B.; Long, Q.; Hoskins, P.; Xu, X.Y.; Marshall, I. MRI measurement of time-resolved wall shear stress vectors in a carotid bifurcation model, and comparison with CFD predictions. J. Magn. Reson. Imaging 2003, 17, 153–162. [Google Scholar] [CrossRef]
  32. Chayer, B.; Hoven, M.; Cardinal, M.-H.; Hongliang, L.; Lopata, R.; Cloutier, G. Atherosclerotic carotid bifurcation phantoms with stenotic soft inclusion for ultrasound flow and vessel wall elastography imaging. Phys. Med. Biol. 2019, 64, 95025. [Google Scholar] [CrossRef]
  33. Goudot, G.; Poree, J.; Pedreira, O.; Khider, L.; Julia, P.; Alsac, J.; Laborie, E.; Mirault, T.; Tanter, M.; Messas, E.; et al. Wall Shear Stress Measurement by Ultrafast Vector Flow Imaging for Atherosclerotic Carotid Stenosis. Eur. Heart J. 2019, 40. [Google Scholar] [CrossRef]
  34. Karimi, A.; Navidbakhsh, M.; Shojaei, A.; Faghihi, S. Measurement of the uniaxial mechanical properties of healthy and atherosclerotic human coronary arteries. Mater. Sci. Eng. C 2013, 33, 2550–2554. [Google Scholar] [CrossRef]
  35. Karimi, A.; Navidbakhsh, M.; Shojaei, A.; Hassani, K.; Faghihi, S. Study of plaque vulnerability in coronary artery using Mooney-Rivlin model: A combination of finite element and experimental method. Biomed. Eng. Appl. Basis Commun. 2014, 26, 1–7. [Google Scholar] [CrossRef]
  36. Santamore, W.; Walinsky, P.; Bove, A.; Cox, R.; Carey, R.A.; Spann, J.F. The effects of vasoconstriction on experimental coronary artery stenosis. Am. Heart J. 1980, 100, 852–858. [Google Scholar] [CrossRef]
  37. Friedman, M.H.; Giddens, D.P. Blood flow in major blood vessels—Modeling and experiments. Ann. Biomed. Eng. 2005, 33, 1710–1713. [Google Scholar] [CrossRef] [PubMed]
  38. Rezvan, A.; Ni, C.W.; Alberts-Grill, N.; Jo, H. Animal, in vitro, and ex vivo models of flow-dependent atherosclerosis: Role of oxidative stress. Antioxid. Redox Signal. 2011, 15, 1433–1448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  39. Yazdi, S.G.; Geoghegan, P.H.; Docherty, P.D.; Jermy, M.; Khanafer, A. A Review of Arterial Phantom Fabrication Methods for Flow Measurement Using PIV Techniques. Ann. Biomed. Eng. 2018, 46, 1697–1721. [Google Scholar] [CrossRef]
  40. Fröhlich, E.; Salar-behzadi, S. Toxicological Assessment of Inhaled Nanoparticles: Role of in Vivo, ex Vivo, in Vitro, and in Silico Studies. Int. J. Mol. Sci. 2014, 15, 4795–4822. [Google Scholar] [CrossRef]
  41. Rodrigues, R.; Sousa, P.; Gaspar, J.; Bañobre-López, M.; Lima, R.; Minas, G. Organ-on-a-chip: A Preclinical Microfluidic Platform for the Progress of Nanomedicine. Small 2020, 1–19. [Google Scholar] [CrossRef]
  42. Carvalho, V.; Rodrigues, N.; Ribeiro, R.; Costa, P.; Teixeira, J.C.F.; Lima, R.; Teixeira, S.F.C.F. Hemodynamic study in 3D printed stenotic coronary artery models: Experimental validation and transient simulation. Comput. Methods Biomech. Biomed. Eng. 2020, 1–14. [Google Scholar] [CrossRef]
  43. Pandey, R.; Kumar, M.; Srivastav, V.K. Numerical computation of blood hemodynamic through constricted human left coronary artery: Pulsatile simulations. Comput. Methods Program. Biomed. 2020, 197, 105661. [Google Scholar] [CrossRef]
  44. Lopes, D.; Puga, H.; Teixeira, J.C.; Teixeira, S.F. Influence of arterial mechanical properties on carotid blood flow: Comparison of CFD and FSI studies. Int. J. Mech. Sci. 2019, 160, 209–218. [Google Scholar] [CrossRef]
  45. Elhanafy, A.; Elsaid, A.; Guaily, A. Numerical investigation of hematocrit variation effect on blood flow in an arterial segment with variable stenosis degree. J. Mol. Liq. 2020, 313, 113550. [Google Scholar] [CrossRef]
  46. Carvalho, V.; Carneiro, F.; Ferreira, A.C.; Gama, V.; Teixeira, J.C.F.; Teixeira, S.F.C.F. Numerical study of the unsteady flow in simplified and realistic iliac bifurcation models. Comput. Methods Biomech. Biomed. Engin. 2021. under review. [Google Scholar]
  47. Carvalho, V.; Rodrigues, N.; Ribeiro, R.; Costa, P.F.; Lima, R.A.; Teixeira, S.F.C.F. 3D Printed Biomodels for Flow Visualization in Stenotic Vessels: An Experimental and Numerical Study. Micromachines 2020, 11, 549. [Google Scholar] [CrossRef]
  48. Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2007; ISBN 9780131274983. [Google Scholar]
  49. Hoving, A.M.; de Vries, E.E.; Mikhal, J.; de Borst, G.J.; Slump, C.H. A Systematic Review for the Design of In Vitro Flow Studies of the Carotid Artery Bifurcation. Cardiovasc. Eng. Technol. 2019, 11, 111–127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  50. Yilmaz, F.; Gundogdu, M.Y. A critical review on blood flow in large arteries; relevance to blood rheology, viscosity models, and physiologic conditions. Korea Aust. Rheol. J. 2008, 20, 197–211. [Google Scholar]
  51. Lee, J.; Smith, N.P. The multi-scale modelling of coronary blood flow. Ann. Biomed. Eng. 2012, 40, 2399–2413. [Google Scholar] [CrossRef] [Green Version]
  52. Lieber, B.B.; Siebes, M.; Yamaguchi, T. Correlation of hemodynamic events with clinical and pathological observations. Ann. Biomed. Eng. 2005, 33, 1695–1703. [Google Scholar] [CrossRef]
  53. Zhang, J.-M.; Zhong, L.; Su, B.; Wan, M.; ShyaYap, J.; Tham, J.P.L.; Poh Chua, L.; Ghista, D.N.; San Tan, R. Perspective on CFD studies of coronary artery disease lesions and hemodynamics: A review Jun-Mei. Int. J. Numer. Method. Biomed. Eng. 2014, 30, 659–680. [Google Scholar] [CrossRef]
  54. Sriyab, S. Mathematical Analysis of Non-Newtonian Blood Flow in Stenosis Narrow Arteries. Comput. Math. Methods Med. 2014, 2014, 479152. [Google Scholar] [CrossRef]
  55. Chen, C.X.; Ding, Y.; Gear, J.A. Numerical simulation of atherosclerotic plaque growth using two-way fluid-structural interaction. ANZIAM J. 2012, 53, 277. [Google Scholar] [CrossRef]
  56. Razavi, A.; Shirani, E.; Sadeghi, M.R. Numerical simulation of blood pulsatile flow in a stenosed carotid artery using different rheological models. J. Biomech. 2011, 44, 2021–2030. [Google Scholar] [CrossRef] [PubMed]
  57. Mulani, S.S.; Jagad, P.I. Analysis of the Effects of Plaque Deposits on the Blood Flow through Human Artery. Int. Eng. Res. J. 2015, 41, 2319–3182. [Google Scholar]
  58. Wu, J.; Liu, G.; Huang, W.; Ghista, D.N.; Wong, K.K.L. Transient blood flow in elastic coronary arteries with varying degrees of stenosis and dilatations: CFD modelling and parametric study. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1835–1845. [Google Scholar] [CrossRef]
  59. Carvalho, V.; Rodrigues, N.; Lima, R.A.; Teixeira, S.F.C.F. Modeling blood pulsatile turbulent flow in stenotic coronary arteries. Int. J. Biol. Biomed. Eng. 2020, 14, 1998–4510. [Google Scholar] [CrossRef]
  60. Chaichana, T.; Sun, Z.; Jewkes, J. Computational Fluid Dynamics Analysis of the Effect of Plaques in the Left Coronary Artery. Comput. Math. Methods Med. 2012, 2012, 504367. [Google Scholar] [CrossRef]
  61. Shanmugavelayudam, S.K.; Rubenstein, D.A.; Yin, W. Effect of geometrical assumptions on numerical modeling of coronary blood flow under normal and disease conditions. J. Biomech. Eng. 2010, 132, 1–8. [Google Scholar] [CrossRef]
  62. Chaichana, T.; Sun, Z.; Jewkes, J. Hemodynamic impacts of various types of stenosis inthe left coronary artery bifurcation: A patient-specific analysis. Phys. Med. 2013, 29, 447–452. [Google Scholar] [CrossRef] [Green Version]
  63. Dabagh, M.; Takabe, W.; Jalali, P.; White, S.; Jo, H. Hemodynamic features in stenosed coronary arteries: CFD analysis based on histological images. J. Appl. Math. 2013, 2013, 11. [Google Scholar] [CrossRef] [Green Version]
  64. Kamangar, S.; Salman Ahmed, N.J.; Badruddin, I.A.; Al-Rawahi, N.; Husain, A.; Govindaraju, K.; Yunus Khan, T.M. Effect of stenosis on hemodynamics in left coronary artery based on patient-specific CT scan. Biomed. Mater. Eng. 2019, 30, 463–473. [Google Scholar] [CrossRef]
  65. Kim, H.J.; Vignon-Clementel, I.E.; Coogan, J.S.; Figueroa, C.A.; Jansen, K.E.; Taylor, C.A. Patient-specific modeling of blood flow and pressure in human coronary arteries. Ann. Biomed. Eng. 2010, 38, 3195–3209. [Google Scholar] [CrossRef]
  66. Rubenstein, D.A.; Yin, W.; Frame, M. Biofluid Mechanics, 2nd ed.; Elsevier: New York, NY, USA, 2015; ISBN 9780128009444. [Google Scholar]
  67. Formaggia, L.; Perktold, K.; Quarteroni, A. Cardiovascular Mathematics- Modeling and Simulation of the Circulatory System, 1st ed.; Springer: New York, NY, USA, 2009; Volume 53, ISBN 9788578110796. [Google Scholar]
  68. Ku, D. Blood flow in arteries. Annu. Rev. Fluid Mech. 1997, 29, 399–434. [Google Scholar] [CrossRef]
  69. Kissas, G.; Yang, Y.; Hwuang, E.; Witschey, W.R.; Detre, J.A.; Perdikaris, P. Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2020, 358, 112623. [Google Scholar] [CrossRef]
  70. Lee, J.; Fung, Y. Flow in Locally Constricted Tubes at Low Reynolds Numbers. J. Appl. Mech. 1970, 37, 9–16. [Google Scholar] [CrossRef]
  71. Caro, C.G.; Fitz-Gerald, J.M.; Schroter, R.C. Atheroma and arterial wall shear. Observation, correlation and proposal of a shear dependent mass transfer mechanism for atherogenesis. Proc. R. Soc. London Ser. B Biol. Sci. 1971, 177, 109–159. [Google Scholar] [CrossRef]
  72. Glagov, S.; Zarins, C.K.; Giddens, D.P.; Ku, D.N. Mechanical Factors in the Pathogenesis, Localization and Evolution of Atherosclerotic Plaques. In Diseases of the Arterial Wall; Springer: Berlin/Heidelberg, Germany, 1989; pp. 217–239. [Google Scholar] [CrossRef]
  73. Ku, D.N.; Giddens, D.P.; Zarins, C.K.; Glagov, S. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low and oscillating shear stress. Arterioscler. Thromb. Vasc. Biol. 1985, 5, 293–302. [Google Scholar] [CrossRef] [Green Version]
  74. Lodi Rizzini, M.; Gallo, D.; De Nisco, G.; D’Ascenzo, F.; Chiastra, C.; Bocchino, P.P.; Piroli, F.; De Ferrari, G.M.; Morbiducci, U. Does the inflow velocity profile influence physiologically relevant flow patterns in computational hemodynamic models of left anterior descending coronary artery? Med. Eng. Phys. 2020, 82, 58–69. [Google Scholar] [CrossRef]
  75. Biglarian, M.; Larimi, M.M.; Afrouzi, H.H.; Moshfegh, A.; Toghraie, D.; Javadzadegan, A.; Rostami, S.; Momeni, M.; Hassanzadeh, H.; Moshfegh, A.; et al. Computational investigation of stenosis in curvature of coronary artery within both dynamic and static models. Comput. Methods Program. Biomed. 2020, 185, 105170. [Google Scholar] [CrossRef]
  76. Kenjereš, S.; van der Krieke, J.P.; Li, C. Endothelium resolving simulations of wall shear-stress dependent mass transfer of LDL in diseased coronary arteries. Comput. Biol. Med. 2019, 114. [Google Scholar] [CrossRef]
  77. Kabir, M.A.; Alam, M.F.; Uddin, M.A. A numerical study on the effects of reynolds number on blood flow with spiral velocity through regular arterial stenosis. Chiang Mai J. Sci. 2018, 45, 2515–2527. [Google Scholar]
  78. Carvalho, V.; Rodrigues, N.; Lima, R.A.; Teixeira, S. Numerical simulation of blood pulsatile flow in stenotic coronary arteries: The effect of turbulence modeling and non-Newtonian assumptions. In Proceedings of the International Conference on Applied Mathematics & Computer Science, Athens, Greece, 2–4 June 2020. [Google Scholar]
  79. Jahromi, R.; Pakravan, H.A.; Saidi, M.S.; Firoozabadi, B. Primary stenosis progression versus secondary stenosis formation in the left coronary bifurcation: A mechanical point of view. Biocybern. Biomed. Eng. 2019, 39, 188–198. [Google Scholar] [CrossRef]
  80. Liu, B.; Zheng, J.; Bach, R.; Tang, D. Influence of model boundary conditions on blood flow patterns in a patient specific stenotic right coronary artery. Biomed. Eng. Online 2015, 14, S6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  81. Siogkas, P.K.; Papafaklis, M.I.; Sakellarios, A.I.; Stefanou, K.A.; Bourantas, C.V.; Athanasiou, L.S.; Exarchos, T.P.; Naka, K.K.; Michalis, L.K.; Parodi, O.; et al. Patient-specific simulation of coronary artery pressure measurements: An in vivo three-dimensional validation study in humans. Biomed Res. Int. 2014, 2015, 628416. [Google Scholar] [CrossRef] [Green Version]
  82. Zhao, Y.; Ping, J.; Yu, X.; Wu, R.; Sun, C.; Zhang, M. Fractional flow reserve-based 4D hemodynamic simulation of time-resolved blood flow in left anterior descending coronary artery. Clin. Biomech. 2019, 70, 164–169. [Google Scholar] [CrossRef] [PubMed]
  83. Zhang, X.; Luo, M.; Wang, E.; Zheng, L.; Shu, C. Numerical simulation of magnetic nano drug targeting to atherosclerosis: Effect of plaque morphology (stenosis degree and shoulder length). Comput. Methods Program. Biomed. 2020, 195, 105556. [Google Scholar] [CrossRef] [PubMed]
  84. Lo, E.W.C.; Menezes, L.J.; Torii, R. Impact of inflow boundary conditions on the calculation of CT-based FFR. Fluids 2019, 4, 60. [Google Scholar] [CrossRef] [Green Version]
  85. Doutel, E.; Viriato, N.; Carneiro, J.; Campos, J.B.L.M.; Miranda, J.M. Geometrical effects in the hemodynamics of stenotic and non-stenotic left coronary arteries—Numerical and in vitro approaches. Int. J. Numer. Method. Biomed. Eng. 2019, 35, 1–18. [Google Scholar] [CrossRef]
  86. Mahalingam, A.; Gawandalkar, U.U.; Kini, G.; Buradi, A.; Araki, T.; Ikeda, N.; Nicolaides, A.; Laird, J.R.; Saba, L.; Suri, J.S. Numerical analysis of the effect of turbulence transition on the hemodynamic parameters in human coronary arteries. Cardiovasc. Diagn. Ther. 2016, 6, 208–220. [Google Scholar] [CrossRef] [Green Version]
  87. Rabbi, M.F.; Laboni, F.S.; Arafat, M.T. Computational analysis of the coronary artery hemodynamics with different anatomical variations. Inform. Med. Unlocked 2020, 19, 100314. [Google Scholar] [CrossRef]
  88. Malota, Z.; Glowacki, J.; Sadowski, W.; Kostur, M. Numerical analysis of the impact of flow rate, heart rate, vessel geometry, and degree of stenosis on coronary hemodynamic indices. BMC Cardiovasc. Disord. 2018, 18, 1–16. [Google Scholar] [CrossRef]
  89. Chaichana, T.; Sun, Z.; Jewkes, J. Computation of hemodynamics in the left coronary artery with variable angulations. J. Biomech. 2011, 44, 1869–1878. [Google Scholar] [CrossRef] [Green Version]
  90. Zhang, J.M.; Zhong, L.; Luo, T.; Huo, Y.; Tan, S.Y.; Wong, A.S.L.; Su, B.; Wan, M.; Zhao, X.; Kassab, G.S.; et al. Numerical simulation and clinical implications of stenosis in coronary blood flow. BioMed Res. Int. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
  91. Gaudio, L.T.; Caruso, M.V.; De Rosa, S.; Indolfi, C.; Fragomeni, G. Different Blood Flow Models in Coronary Artery Diseases: Effects on hemodynamic parameters. In Proceedings of the Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Honolulu, HI, USA, 18–21 July 2018; Volume 2018, pp. 3185–3188.
  92. Berger, S.A.; Jou, L. Flows in Stenotic Vessels. Annu. Rev. Fluid Mech. 2000, 32, 347–382. [Google Scholar] [CrossRef]
  93. Doutel, E.; Carneiro, J.; Campos, J.B.L.M.; Miranda, J.M. Artificial stenoses for computational hemodynamics. Appl. Math. Model. 2018, 59, 427–440. [Google Scholar] [CrossRef]
  94. Johnston, B.M.; Johnston, P.R.; Corney, S.; Kilpatrick, D. Non-Newtonian blood flow in human right coronary arteries: Steady state simulations. J. Biomech. 2004, 37, 709–720. [Google Scholar] [CrossRef] [Green Version]
  95. Pinto, S.I.S.; Romano, E.; António, C.C.; Sousa, L.C.; Castro, C.F. The impact of non-linear viscoelastic property of blood in right coronary arteries hemodynamics—A numerical implementation. Int. J. Non Linear Mech. 2020, 123, 103477. [Google Scholar] [CrossRef]
  96. Moreno, C.; Bhaganagar, K. Modeling of stenotic coronary artery and implications of plaque morphology on blood flow. Model. Simul. Eng. 2013, 2013, 1–14. [Google Scholar] [CrossRef] [Green Version]
  97. Straatman, A.G.; Ryval, J. Two-equation Turbulence Modeling of Pulsatile Flow in a Stenosed Tube. J. Biomech. Eng. 2016, 126, 625–635. [Google Scholar] [CrossRef]
  98. Ahmadi, M.; Ansari, R. Computational simulation of an artery narrowed by plaque using 3D FSI method: Influence of the plaque angle, non-Newtonian properties of the blood flow and the hyperelastic artery models. Biomed. Phys. Eng. Express 2019, 5, 45037. [Google Scholar] [CrossRef]
  99. Torii, R.; Wood, N.G.; Hadjiloizou, N.; Dowsey, A.W.; Andrew, R.; Hughes, A.D.; Justin, D.; Francis, D.; Mayet, J.; Yang, G.; et al. Fluid–structure interaction analysis of a patient-specific right coronary artery with physiological velocity and pressure waveforms. Commun. Numer. Methods Eng. 2009, 25, 565–580. [Google Scholar] [CrossRef]
  100. Kallekar, L.; Viswanath, C.; Anand, M. Effect of wall flexibility on the deformation during flow in a stenosed coronary artery. Fluids 2017, 2, 16. [Google Scholar] [CrossRef] [Green Version]
  101. Karimi, A.; Navidbakhsh, M.; Razaghi, R.; Haghpanahi, M. A computational fluid-structure interaction model for plaque vulnerability assessment in atherosclerotic human coronary arteries. J. Appl. Phys. 2014, 115. [Google Scholar] [CrossRef]
  102. Van der Giessen, A.G.; Groen, H.C.; Doriot, P.A.; de Feyter, P.J.; van der Steen, A.F.W.; van de Vosse, F.N.; Wentzel, J.J.; Gijsen, F.J.H. The influence of boundary conditions on wall shear stress distribution in patients specific coronary trees. J. Biomech. 2011, 44, 1089–1095. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  103. Wu, W.T.; Li, Y.; Aubry, N.; Massoudi, M.; Antaki, J.F. Numerical simulation of red blood cell-induced platelet transport in saccular aneurysms. Appl. Sci. 2017, 7, 484. [Google Scholar] [CrossRef]
  104. Buradi, A.; Mahalingam, A. Numerical Simulation of Pulsatile Blood Flow in an Idealized Curved Section of a Human Coronary. Int. J. Mech. Prod. Eng. 2016, 2016, 15–19. [Google Scholar]
  105. Buradi, A.; Morab, S.; Mahalingam, A. Effect of stenosis severity on shear-induced diffusion of red blood cells in coronary arteries. J. Mech. Med. Biol. 2019, 19, 1950034. [Google Scholar] [CrossRef]
Fluids 06 00053 g001 550
Figure 1. Main steps performed in numerical simulations.
Figure 1. Main steps performed in numerical simulations.
Fluids 06 00053 g001
Table
Table 1. Numerical studies of hemodynamics and the respective assumptions for numerical simulations.
Table 1. Numerical studies of hemodynamics and the respective assumptions for numerical simulations.
GeometrySchematic RepresentationModeling ApproachesFluidBoundary ConditionsAuthors
WallInletOutlet
Idealized 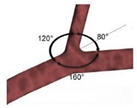Fluids 06 00053 i001LaminarNon-Newtonian (Carreau-Yasuda)RigidTime-dependent velocity profileZero gauge pressureKashyap et al., (2020) [6]
Idealized 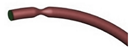Fluids 06 00053 i002LaminarNewtonianRigidTime-dependent mass flow profileZero surface tensionBiglarian et al., (2019) [75]
Idealized Fluids 06 00053 i003LaminarNon-Newtonian (Cross model)Rigid and FlexibleConstant inlet velocityConstant pressure outlet (10 kPa)Mulani et al., (2015) [57]
Idealized Fluids 06 00053 i004LaminarNewtonianRigid and FlexibleTime-dependent flowrate profileTime-dependent pressure profileWu et al., (2015) [58]
Idealized Fluids 06 00053 i005LaminarNewtonianRigidConstant inlet velocity (fully developed parabolic profile)Constant pressure outlet (13 kPa)Kenjereš et al., (2019) [76]
Idealized Fluids 06 00053 i006LaminarNewtonianRigidConstant inlet velocityZero gauge pressure Carvalho et al., (2020) [47]
Idealized Fluids 06 00053 i007k-ω turbulent modelNon-Newtonian (Carreau model)RigidSpiral boundary conditionwith a parabolic velocity profileZero gauge pressureKabir et al., (2018) [77]
Idealized Fluids 06 00053 i008k-ω turbulent model (SST)Non-Newtonian (Carreau model)RigidTime-dependent velocity profileZero gauge pressureCarvalho et al., (2020) [42]
Idealized Fluids 06 00053 i009k-ω turbulent model (SST)Non-Newtonian (Carreau model)Rigid Time-dependent velocity profileZero gauge pressure Carvalho et al., (2020) [59,78]
Idealized Fluids 06 00053 i010N.A1NewtonianFlexibleTime-dependent velocity profileTime-dependent pressure profileJahromi et al., (2019) [79]
Idealized Fluids 06 00053 i011LaminarNewtonianRigidTime-dependent velocity profileFlow partition implied in Murray’s lawDoutel et al., (2018) [11]
Patient-specific 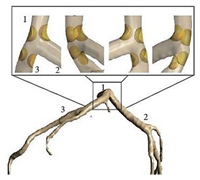Fluids 06 00053 i012LaminarNon-Newtonian (Generalized power-law model) and NewtonianRigid Time-dependent flow rate profileTime-dependent pressure profileChaichana et al., (2012) [60]
Patient-specific Fluids 06 00053 i013LaminarNon-Newtonian (Carreau model)Rigid Time-dependent velocity profileTime-dependent pressure profileLiu et al., (2015) [80]
Patient-specific Fluids 06 00053 i014LaminarNewtonianRigid and Flexible Time-dependent pressure profileParabolic velocity profileSiogkas et al., (2014) [81]
Patient-specific 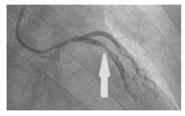Fluids 06 00053 i015N.ANewtonianRigid Time-dependent pressure profileConstant pressure outlet (9.85 kPa) Zhao et al., (2019) [82]
Patient-specific Fluids 06 00053 i016LaminarNon-Newtonian (Carreau model) Rigid Time-dependent velocity profileFlow partition implied in Murray’s lawPandey et al., (2020) [43]
Patient-specific Fluids 06 00053 i017LaminarNon-Newtonian (Carreau model)Rigid Various time-dependent velocity profilesFlow partition implied in Murray’s lawRizzini et al., (2020) [74]
Patient-specific 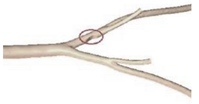Fluids 06 00053 i018N.ANon-Newtonian (Power-law model)Rigid Time-dependent velocity profilePressure outlet (N.A)Zhang et al., (2020) [83]
Patient-specific Fluids 06 00053 i019k-ω turbulent model (SST)Non-Newtonian (Bird-Carreau model)Rigid Time-dependent velocity profileConstant pressure outlet (10 kPa) Kamangar et al., (2019) [64]
Patient-specific Fluids 06 00053 i020LaminarNewtonianRigidTime-dependent flow rate profileTwo-Element Windkessel ModelLo et al., (2019) [84]
Patient-specific and Idealized 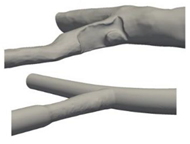Fluids 06 00053 i021LaminarNewtonian and Non-Newtonian (Carreau model)Rigid Constant inlet velocity and Time-dependent velocity profileN.ADoutel et al., (2019) [85]
Patient-specific and Idealized Fluids 06 00053 i022k-ω turbulent model (SST)Non-Newtonian (Carreau model)Rigid Time-dependent velocity profileOutflow conditionMahalingam et al., (2016) [86]
Patient-specific and Idealized 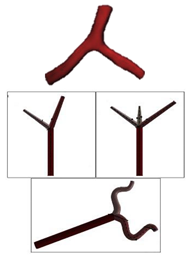Fluids 06 00053 i023N.ANon-Newtonian (Carreau model) Rigid Time-dependent velocity profileConstant pressure outlet (10 kPa) Rabbi et al., (2020) [87]
Patient-specific and Idealized 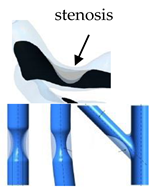Fluids 06 00053 i024LaminarNewtonianRigidConstant inlet mass flow and Time-dependent flow rateZero gauge pressureMalota et al., (2018) [88]
N.A—Not available. All images were adapted from [6,11,42,43,47,57,58,59,60,64,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88].
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Carvalho, V.; Pinho, D.; Lima, R.A.; Teixeira, J.C.; Teixeira, S. Blood Flow Modeling in Coronary Arteries: A Review. Fluids 2021, 6, 53. https://doi.org/10.3390/fluids6020053

AMA Style

Carvalho V, Pinho D, Lima RA, Teixeira JC, Teixeira S. Blood Flow Modeling in Coronary Arteries: A Review. Fluids. 2021; 6(2):53. https://doi.org/10.3390/fluids6020053

Chicago/Turabian Style

Carvalho, Violeta, Diana Pinho, Rui A. Lima, José Carlos Teixeira, and Senhorinha Teixeira. 2021. "Blood Flow Modeling in Coronary Arteries: A Review" Fluids 6, no. 2: 53. https://doi.org/10.3390/fluids6020053

APA Style

Carvalho, V., Pinho, D., Lima, R. A., Teixeira, J. C., & Teixeira, S. (2021). Blood Flow Modeling in Coronary Arteries: A Review. Fluids, 6(2), 53. https://doi.org/10.3390/fluids6020053

Article Metrics

Back to TopTop