Mechanical Forces Impacting Cleavage of Von Willebrand Factor in Laminar and Turbulent Blood Flow
Abstract
1. Introduction
2. Method
3. Laminar Flow
4. Turbulent Flow
5. Result and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Savage, B.; Saldívar, E.; Ruggeri, Z.M. Initiation of Platelet Adhesion by Arrest onto Fibrinogen or Translocation on von Willebrand Factor. Cell 1996, 84, 289–297. [Google Scholar] [CrossRef]
- Sadler, J.E. New Concepts in von Willebrand Disease. Annu. Rev. Med. 2005, 56, 173–191. [Google Scholar] [CrossRef]
- Savage, B.; Almus-Jacobs, F.; Ruggeri, Z.M. Specific Synergy of Multiple Substrate–Receptor Interactions in Platelet Thrombus Formation under Flow. Cell 1998, 94, 657–666. [Google Scholar] [CrossRef]
- Stockschlaeder, M.; Schneppenheim, R.; Budde, U. Update on von Willebrand Factor Multimers: Focus on High-Molecular-Weight Multimers and Their Role in Hemostasis. Blood Coagul. Fibrinolysis 2014, 25, 206–216. [Google Scholar] [CrossRef] [PubMed]
- Bharati, K.P.; Prashanth, U.R. Von Willebrand Disease: An Overview. Indian J. Pharm. Sci. 2011, 73, 7–16. [Google Scholar] [CrossRef] [PubMed]
- Sadler, J.E. Biochemistry and Genetics of von Willebrand Factor. Ann. Rev. Biochem 1998, 67, 395–424. [Google Scholar] [CrossRef] [PubMed]
- Springer, T.A. Von Willebrand Factor, Jedi Knight of the Bloodstream. Blood J. Am. Soc. Hematol. 2014, 124, 1412–1425. [Google Scholar] [CrossRef]
- Zheng, X.L. ADAMTS13 and von Willebrand Factor in Thrombotic Thrombocytopenic Purpura. Annu. Rev. Med. 2015, 66, 211–225. [Google Scholar] [CrossRef]
- Geisen, U.; Brehm, K.; Trummer, G.; Berchtold-Herz, M.; Heilmann, C.; Beyersdorf, F.; Schelling, J.; Schlagenhauf, A.; Zieger, B. Platelet Secretion Defects and Acquired von Willebrand Syndrome in Patients with Ventricular Assist Devices. J. Am. Heart Assoc. 2018, 7, e006519. [Google Scholar] [CrossRef]
- Vincentelli, A.; Susen, S.; Le Tourneau, T.; Six, I.; Fabre, O.; Juthier, F.; Bauters, A.; Decoene, C.; Goudemand, J.; Prat, A. Acquired von Willebrand Syndrome in Aortic Stenosis. N. Engl. J. Med. 2003, 349, 343–349. [Google Scholar] [CrossRef]
- Schneider, S.W.; Nuschele, S.; Wixforth, A.; Gorzelanny, C.; Alexander-Katz, A.; Netz, R.R.; Schneider, M.F. Shear-Induced Unfolding Triggers Adhesion of von Willebrand Factor Fibers. Proc. Natl. Acad. Sci. USA 2007, 104, 7899–7903. [Google Scholar] [CrossRef] [PubMed]
- Sing, C.E.; Alexander-Katz, A. Elongational Flow Induces the Unfolding of von Willebrand Factor at Physiological Flow Rates. Biophys. J. 2010, 98, L35–L37. [Google Scholar] [CrossRef] [PubMed]
- Doyle, P.S.; Shaqfeh, E.S. Dynamic Simulation of Freely-Draining, Flexible Bead-Rod Chains: Start-up of Extensional and Shear Flow. J. Non-Newton. Fluid Mech. 1998, 76, 43–78. [Google Scholar] [CrossRef]
- Alexander-Katz, A.; Netz, R.R. Dynamics and Instabilities of Collapsed Polymers in Shear Flow. Macromolecules 2008, 41, 3363–3374. [Google Scholar] [CrossRef]
- Sunthar, P.; Nguyen, D.A.; Dubbelboer, R.; Prakash, J.R.; Sridhar, T. Measurement and Prediction of the Elongational Stress Growth in a Dilute Solution of DNA Molecules. Macromolecules 2005, 38, 10200–10209. [Google Scholar] [CrossRef]
- Neelov, I.M.; Adolf, D.B.; Lyulin, A.V.; Davies, G.R. Brownian Dynamics Simulation of Linear Polymers under Elongational Flow: Bead–Rod Model with Hydrodynamic Interactions. J. Chem. Phys. 2002, 117, 4030–4041. [Google Scholar] [CrossRef]
- Venkataramani, V.; Sureshkumar, R.; Khomami, B. Coarse-Grained Modeling of Macromolecular Solutions Using a Configuration-Based Approach. J. Rheol. 2008, 52, 1143–1177. [Google Scholar] [CrossRef]
- Harrison, G.M.; Remmelgas, J.; Leal, L.G. The Dynamics of Ultradilute Polymer Solutions in Transient Flow: Comparison of Dumbbell-Based Theory and Experiment. J. Rheol. 1998, 42, 1039–1058. [Google Scholar] [CrossRef]
- Alexander-Katz, A.; Schneider, M.F.; Schneider, S.W.; Wixforth, A.; Netz, R.R. Shear-Flow-Induced Unfolding of Polymeric Globules. Phys. Rev. Lett. 2006, 97, 138101. [Google Scholar] [CrossRef]
- Bortot, M.; Ashworth, K.; Sharifi, A.; Walker, F.; Crawford, N.C.; Neeves, K.B.; Bark, D., Jr.; Di Paola, J. Turbulent Flow Promotes Cleavage of VWF (von Willebrand Factor) by ADAMTS13 (a Disintegrin and Metalloproteinase with a Thrombospondin Type-1 Motif, Member 13). Arterioscler. Thromb. Vasc. Biol. 2019, 39, 1831–1842. [Google Scholar] [CrossRef]
- Bortot, M.; Sharifi, A.; Ashworth, K.; Walker, F.; Cox, A.; Ruegg, K.; Clendenen, N.; Neeves, K.B.; Bark, D.; Di Paola, J. Pathologic Shear and Elongation Rates Do Not Cause Cleavage of Von Willebrand Factor by ADAMTS13 in a Purified System. Cell. Mol. Bioeng. 2020, 13, 379–390. [Google Scholar] [CrossRef] [PubMed]
- McNaught, A.D.; Wilkinson, A. Compendium of Chemical Terminology; Blackwell Science Oxford: Oxford, UK, 1997; Volume 1669. [Google Scholar]
- Koltzenburg, S.; Maskos, M.; Nuyken, O. Polymere: Synthese, Eigenschaften Und Anwendungen; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Frenkel, J. Orientation and Rupture of Linear Macromolecules in Dilute Solutions under the Influence of Viscous Flow. Acta Phys. URSS 1944, 19, 51–76. [Google Scholar]
- Vanapalli, S.A.; Ceccio, S.L.; Solomon, M.J. Universal Scaling for Polymer Chain Scission in Turbulence. Proc. Natl. Acad. Sci. USA 2006, 103, 16660–16665. [Google Scholar] [CrossRef]
- Horn, A.F.; Merrill, E.W. Midpoint Scission of Macromolecules in Dilute Solution in Turbulent Flow. Nature 1984, 312, 140–141. [Google Scholar] [CrossRef]
- Keller, A.; Odell, J.A. The Extensibility of Macromolecules in Solution; A New Focus for Macromolecular Science. Colloid Polym. Sci. 1985, 263, 181–201. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Kausch, H.-H. Chain Scission in Transient Extensional Flow Kinetics and Molecular Weight Dependence. J. Non-Newton. Fluid Mech. 1988, 30, 125–140. [Google Scholar] [CrossRef]
- Universal Scaling for Polymer Chain Scission in Turbulence, PNAS. Available online: https://www.pnas.org/content/103/45/16660.short (accessed on 23 November 2020).
- Perkins, T.T.; Smith, D.E.; Chu, S. Single Polymer Dynamics in an Elongational Flow. Science 1997, 276, 2016–2021. [Google Scholar] [CrossRef] [PubMed]
- Drag Reduction Fundamentals—Virk—1975—AIChE Journal. Wiley Online Library. Available online: https://aiche.onlinelibrary.wiley.com/doi/abs/10.1002/aic.690210402?casa_token=URnE3nKXNBkAAAAA:eSiXageo-olThvJFFEA_cy_Jr-nJKekdnKjiS6SXX7suJtIQSOXv-fT-oQllup_O2WTbgwLrI5AdMcY (accessed on 23 November 2020).
- Gold, P.I.; Amar, P.K.; Swaidan, B.E. Friction Reduction Degradation in Dilute Poly(Ethylene Oxide) Solutions. J. Appl. Polym. Sci. 1973, 17, 333–350. [Google Scholar] [CrossRef]
- Hershey, H.C.; Zakin, J.L. A Molecular Approach to Predicting the Onset of Drag Reduction in the Turbulent Flow of Dilute Polymer Solutions. Chem. Eng. Sci. 1967, 22, 1847–1857. [Google Scholar] [CrossRef]
- Virk, P.S.; Merrill, E.W. The Onset of Dilute Polymer Solution Phenomena. In Viscous Drag Reduction; Wells, C.S., Ed.; Springer: Boston, MA, USA, 1969; pp. 107–130. [Google Scholar]
- Odell, J.A.; Keller, A. Flow-Induced Chain Fracture of Isolated Linear Macromolecules in Solution. J. Polym. Sci. Part B Polym. Phys. 1986, 24, 1889–1916. [Google Scholar] [CrossRef]
- Steppich, D.M.; Angerer, J.I.; Sritharan, K.; Schneider, S.W.; Thalhammer, S.; Wixforth, A.; Alexander-Katz, A.; Schneider, M.F. Relaxation of Ultralarge VWF Bundles in a Microfluidic–AFM Hybrid Reactor. Biochem. Biophys. Res. Commun. 2008, 369, 507–512. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Jiang, Y.; Yang, D.; Scheiflinger, F.; Wong, W.P.; Springer, T.A. Flow-Induced Elongation of von Willebrand Factor Precedes Tension-Dependent Activation. Nat. Commun. 2017, 8, 324. [Google Scholar] [CrossRef] [PubMed]
- Fowler, W.E.; Fretto, L.J.; Hamilton, K.K.; Erickson, H.P.; McKee, P.A. Substructure of Human von Willebrand Factor. J. Clin. Investig. 1985, 76, 1491–1500. [Google Scholar] [CrossRef] [PubMed]
- Singh, I.; Shankaran, H.; Beauharnois, M.E.; Xiao, Z.; Alexandridis, P.; Neelamegham, S. Solution Structure of Human von Willebrand Factor Studied Using Small Angle Neutron Scattering. J. Biol. Chem. 2006, 281, 38266–38275. [Google Scholar] [CrossRef] [PubMed]
- Slayter, H.; Loscalzo, J.; Bockenstedt, P.; Handin, R.I. Native Conformation of Human von Willebrand Protein. Analysis by Electron Microscopy and Quasi-Elastic Light Scattering. J. Biol. Chem. 1985, 260, 8559–8563. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows. Meas. Sci. Technol. 2001, 12, 2020. [Google Scholar] [CrossRef]
- Lippok, S.; Radtke, M.; Obser, T.; Kleemeier, L.; Schneppenheim, R.; Budde, U.; Netz, R.R.; Rädler, J.O. Shear-Induced Unfolding and Enzymatic Cleavage of Full-Length VWF Multimers. Biophys. J. 2016, 110, 545–554. [Google Scholar] [CrossRef]
- Jhun, C.-S.; Reibson, J.D.; Cysyk, J.P. Effective Ventricular Unloading by Left Ventricular Assist Device Varies with Stage of Heart Failure: Cardiac Simulator Study. Asaio J. 2011, 57, 407–413. [Google Scholar] [CrossRef]
- Morabito, M.; Dong, C.; Wei, W.; Cheng, X.; Zhang, X.F.; Oztekin, A.; Webb, E. Internal Tensile Force and A2 Domain Unfolding of von Willebrand Factor Multimers in Shear Flow. Biophys. J. 2018, 115, 1860–1871. [Google Scholar] [CrossRef]
- Wu, T.; Lin, J.; Cruz, M.A.; Dong, J.; Zhu, C. Force-Induced Cleavage of Single VWFA1A2A3 Tridomains by ADAMTS-13. Blood 2010, 115, 370–378. [Google Scholar] [CrossRef]
- Ying, J.; Ling, Y.; Westfield, L.A.; Sadler, J.E.; Shao, J.-Y. Unfolding the A2 Domain of Von Willebrand Factor with the Optical Trap. Biophys. J. 2010, 98, 1685–1693. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Halvorsen, K.; Zhang, C.-Z.; Wong, W.P.; Springer, T.A. Mechanoenzymatic Cleavage of the Ultralarge Vascular Protein von Willebrand Factor. Science 2009, 324, 1330–1334. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lin, J.; Sulchek, T.; Cruz, M.A.; Wu, J.; Dong, J.; Zhu, C. Domain-Specific Mechanical Modulation of VWF–ADAMTS13 Interaction. MBoC 2019, 30, 1920–1929. [Google Scholar] [CrossRef] [PubMed]
- Morshed, K.N.; Bark, D., Jr.; Forleo, M.; Dasi, L.P. Theory to Predict Shear Stress on Cells in Turbulent Blood Flow. PLoS ONE 2014, 9, e105357. [Google Scholar] [CrossRef]
- Schroeder, C.M. Single Polymer Dynamics for Molecular Rheology. J. Rheol. 2018, 62, 371–403. [Google Scholar] [CrossRef]

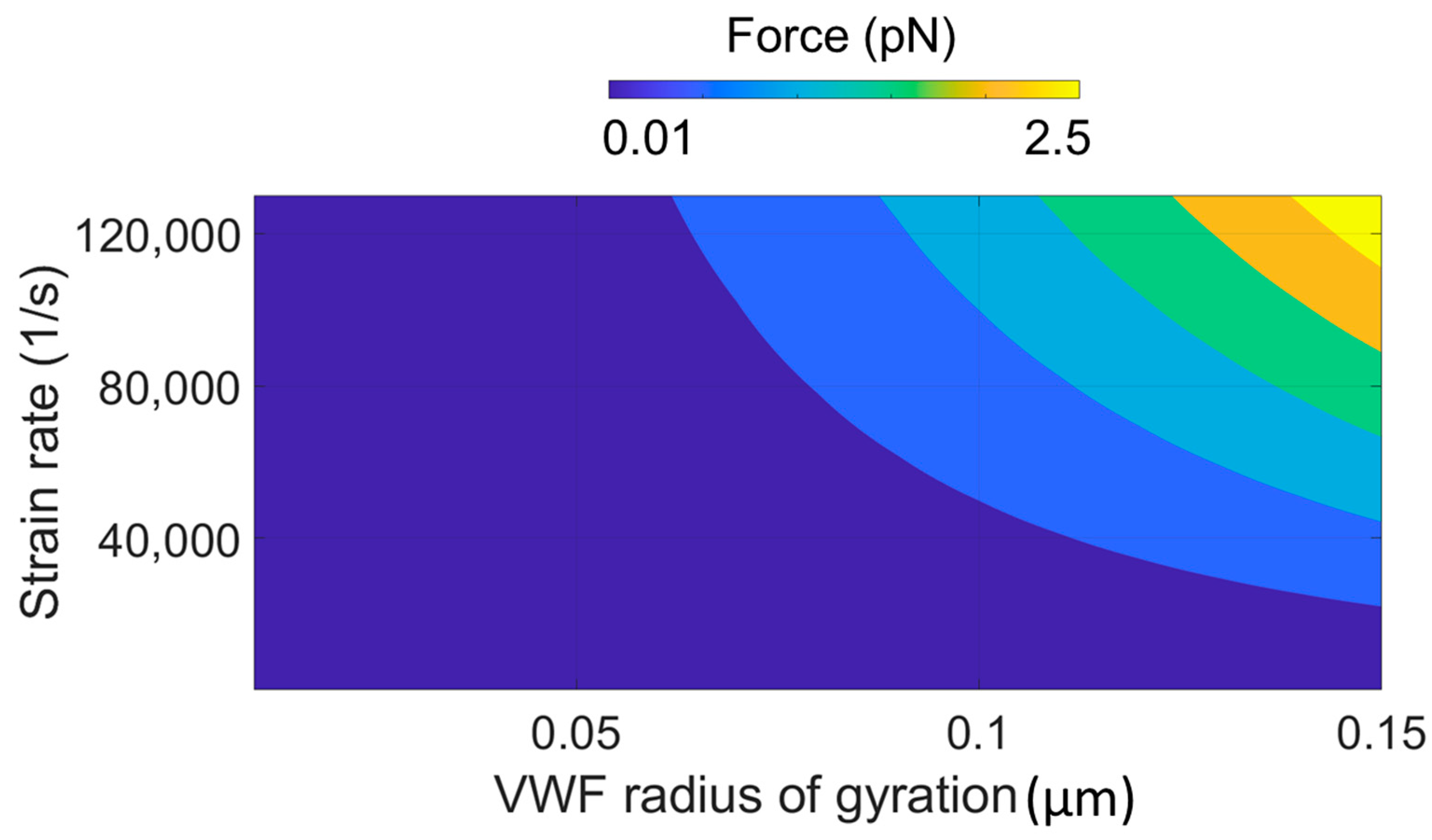
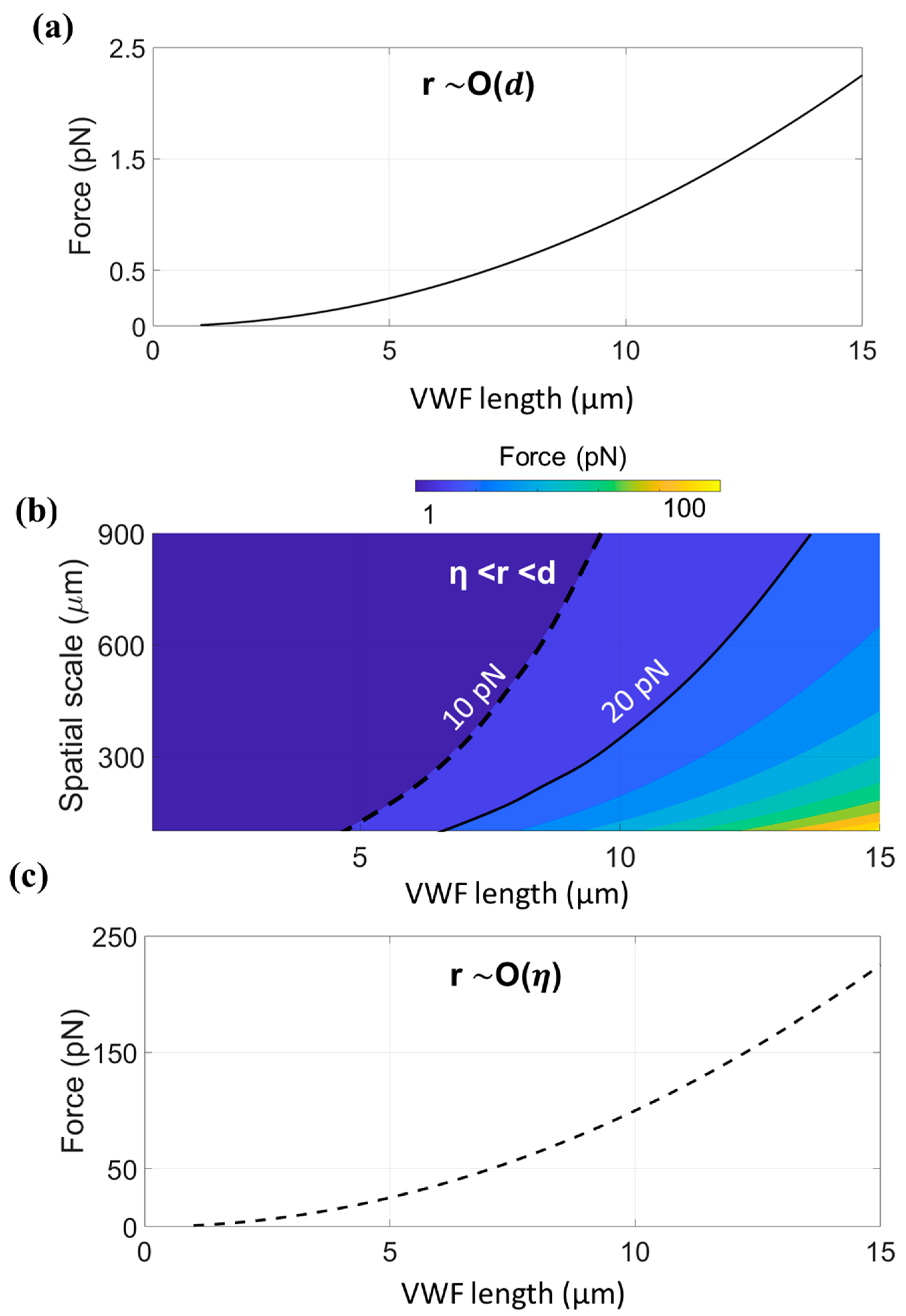
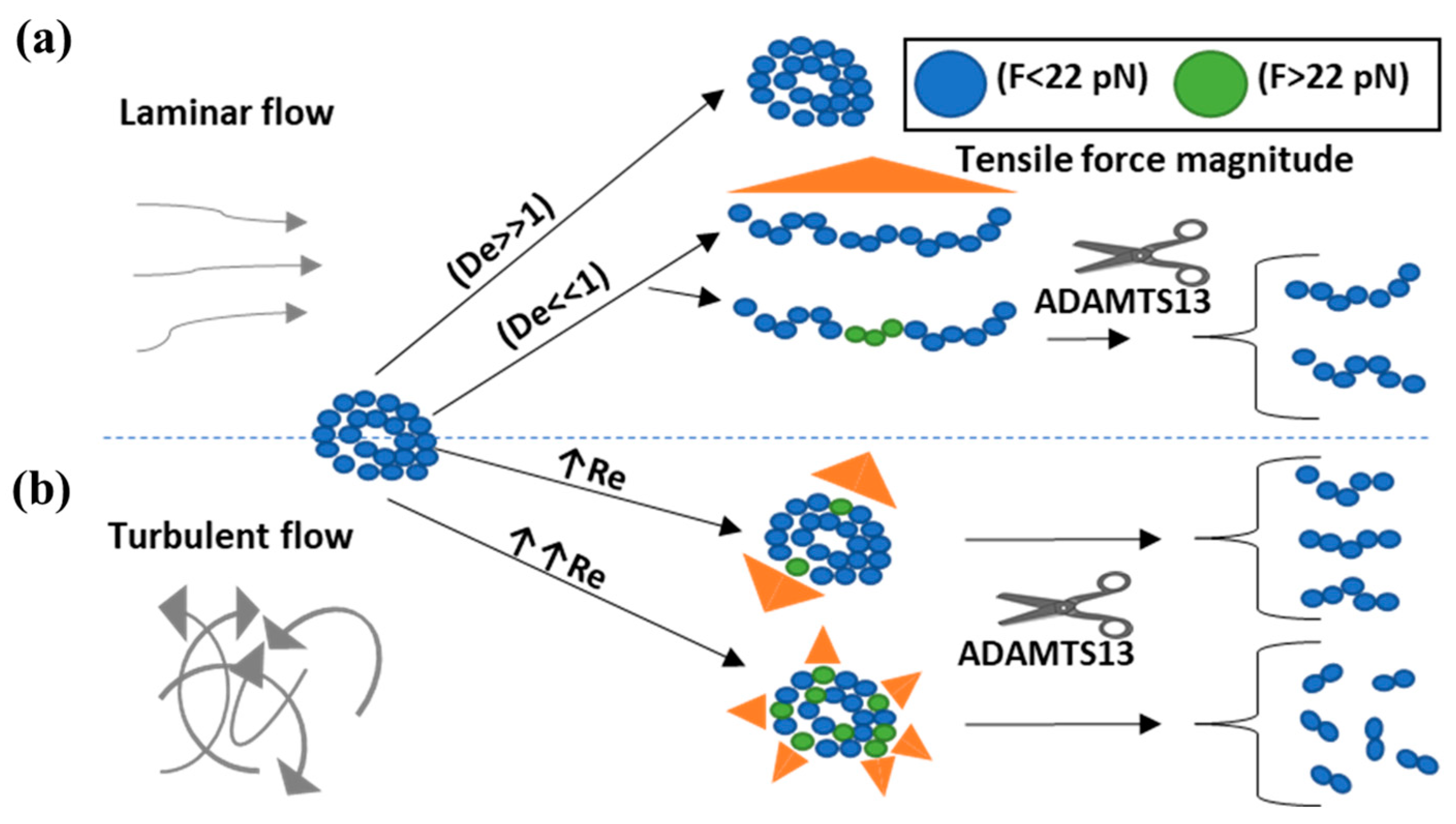
| Case | Flow Regime | Extended | Unfolded | Cleaved | Ref. | |||
|---|---|---|---|---|---|---|---|---|
| 1 | Laminar | 200–3000 | N/A | 0.2–0.5 | NM | NM | No | [20,21] |
| 2 | Laminar | 4000–5000 | N/A | NM | Yes | Yes | No | [42] |
| 3 | Laminar | 10,000 | N/A | 1200–8400 | NM | NM | Yes | [42] |
| 4 | Laminar | 5000–10,000 | N/A | 0.1–0.3 | Yes | Yes | NM | [11] |
| 5 | Laminar | 200–130,000 | N/A | 0.001–0.1 | NM | NM | No | [21] |
| 6 | Turbulent | 2000–6000 | 10–40 | 0.0002–0.001 | NM | NM | Yes | [20] |
| 7 | Turbulent | 5000–10,000 | 20–35 | 0.0001–0.001 | NM | NM | Yes | [21] |
| 8 | Turbulent | 300,000 | NM | 10 | NM | NM | Yes | [43] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharifi, A.; Bark, D. Mechanical Forces Impacting Cleavage of Von Willebrand Factor in Laminar and Turbulent Blood Flow. Fluids 2021, 6, 67. https://doi.org/10.3390/fluids6020067
Sharifi A, Bark D. Mechanical Forces Impacting Cleavage of Von Willebrand Factor in Laminar and Turbulent Blood Flow. Fluids. 2021; 6(2):67. https://doi.org/10.3390/fluids6020067
Chicago/Turabian StyleSharifi, Alireza, and David Bark. 2021. "Mechanical Forces Impacting Cleavage of Von Willebrand Factor in Laminar and Turbulent Blood Flow" Fluids 6, no. 2: 67. https://doi.org/10.3390/fluids6020067
APA StyleSharifi, A., & Bark, D. (2021). Mechanical Forces Impacting Cleavage of Von Willebrand Factor in Laminar and Turbulent Blood Flow. Fluids, 6(2), 67. https://doi.org/10.3390/fluids6020067






