A Review of Vortex Methods and Their Applications: From Creation to Recent Advances
Abstract
1. Introduction
2. Vortex Methods for Inviscid Incompressible Flows
2.1. General Description and Formulation
2.2. Convergence Issues
3. Viscous Vortex Methods
3.1. The Viscous Splitting and Random Walk Method
- (1)
- advection:
- (2)
- diffusion:where in the first step, the particles locations () are updated using the local flow velocity obtained with the Biot-Savart law and in the second one the vorticity () is modified at these new positions by the diffusion. The convergence of the viscous splitting method was proved by Beale and Majda in 1981 [39].
Random Walk Method (RW)
3.2. Deterministic Viscous Vortex Schemes
3.2.1. Particle Strength Exchange Method (PSE)
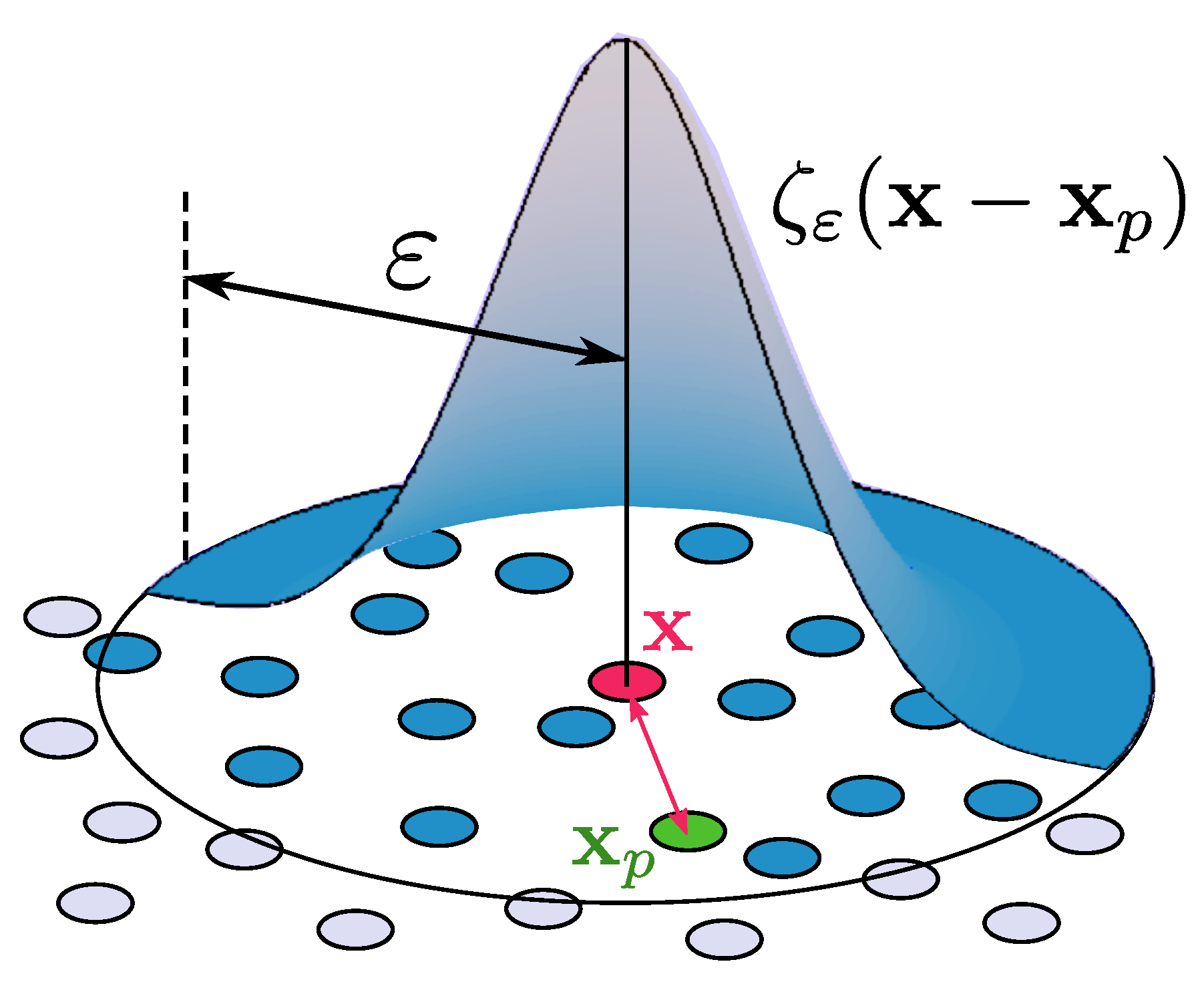
- Approximate the diffusion operator by an integral operator:where is a mollified diffusion kernel of order r, satisfying precise moment properties [22].
- The particle approximation of the diffusion equation can be obtained from the numerical integration of (35). The resulting vortex scheme is given by:where the particles trajectories are computed from (27) (based on Biot-Savart law), and satisfies the following ODEs:where the right hand side is obtained from (35) through a discretization of the integral operator taking the particle positions as quadrature points.
3.2.2. Core-Spreading Method (CSM)
3.2.3. Diffusion Velocity Method (DVM)
4. Spatial Adaptation and Hybrid Vortex Methods
4.1. The Meshless Rezoning Methods
4.2. The Remeshing Methods
4.2.1. Remeshing Kernels
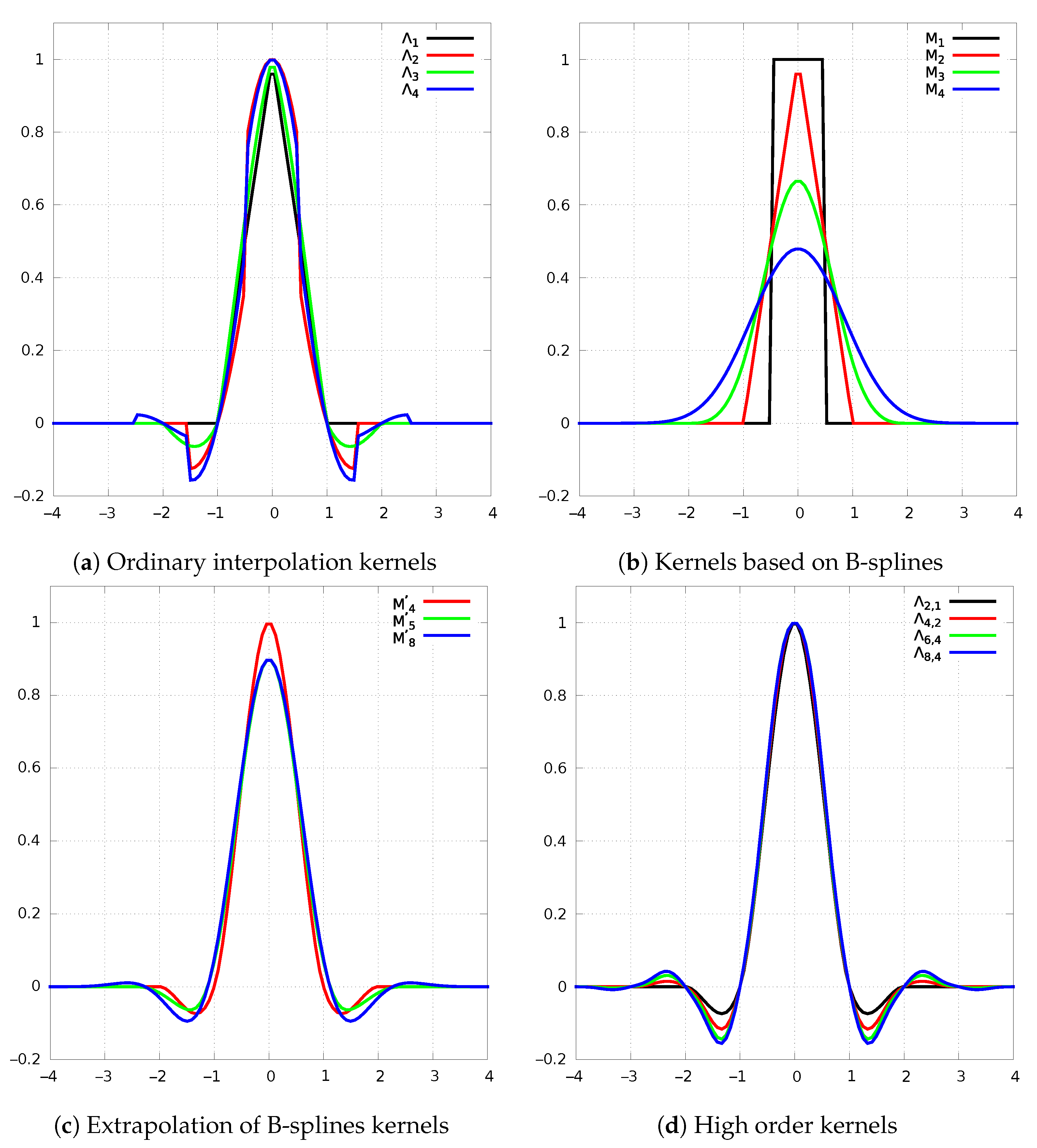
The Ordinary Interpolation Kernels
The B-Splines-Based Kernels
Extrapolation of B-Splines-Based Kernels
High Order Kernels
- P1: W has support in ,
- P2: W is even and piecewise polynomial of degree M in intervals of the form ,
- P3: W is of class ,
- P5: W satisfies the interpolation property (55).
4.2.2. The Directional Splitting
- advection + remeshing in the X-direction on
- advection + remeshing in the Y-direction on
- advection + remeshing in the X-direction on
4.3. Hybrid Vortex Methods
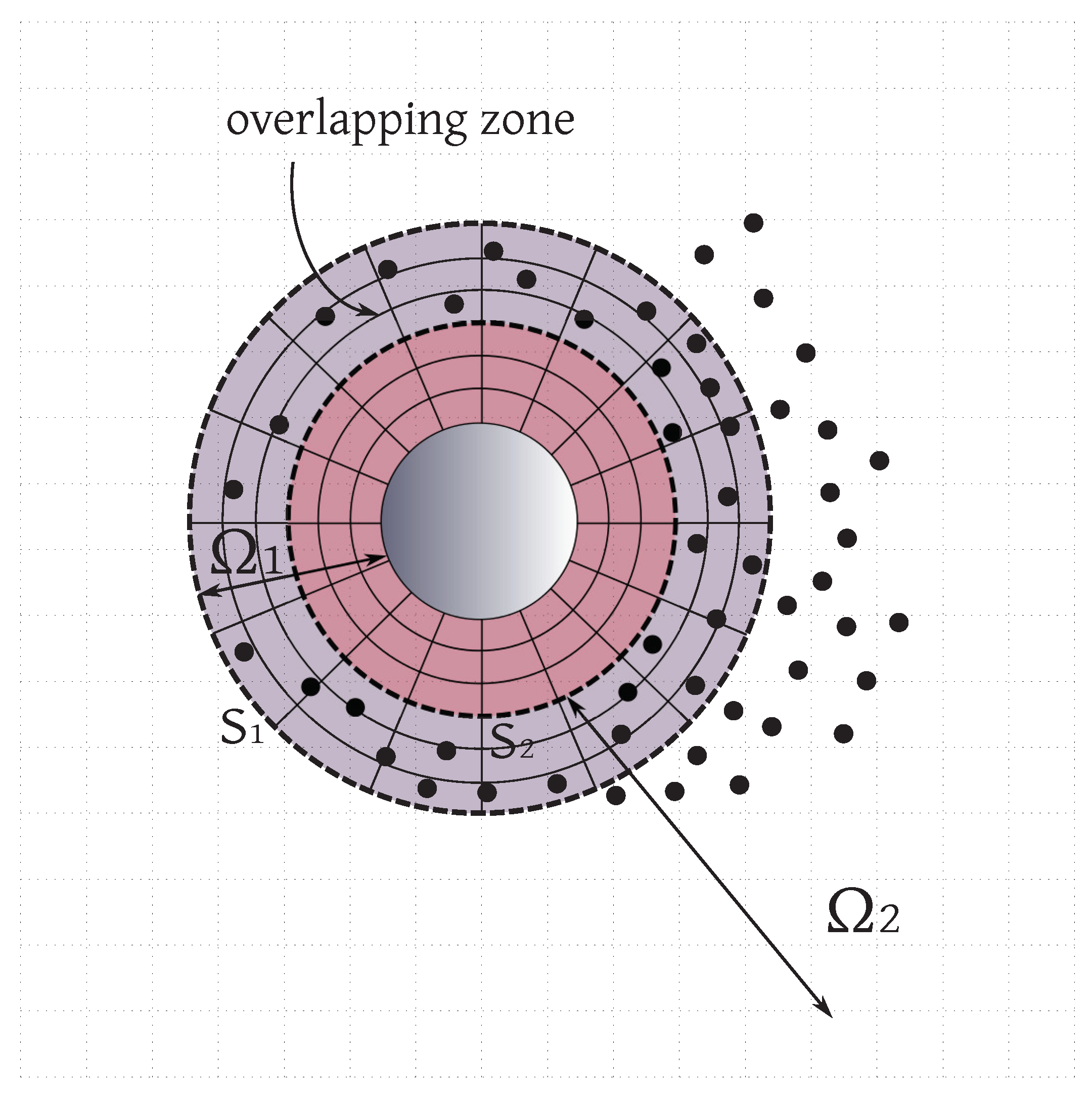
4.3.1. The Eulerian-Lagrangian Domain Decomposition Method
4.3.2. From Vortex-In-Cell (VIC) to Semi-Lagrangian Vortex Methods
- Poisson equation:
- (a)
- Assign particle vorticity values to the grid using a P2M formula.
- (b)
- Compute the velocity field solving the following equation on the grid:
- Advection:
- (a)
- Interpolate the velocity field on the particles using a M2P formula.
- (b)
- Perform a Lagrangian advection of the particles and get their new positions and vorticity:
- (c)
- Assign vorticity values and element volumes to the grid using a P2M formula.
- Stretching (in three-dimensions only):
- (a)
- Solve the stretching equation on the grid by differentiation of the velocity field:Note: One can also write the stretching equation in its conservative form, namely
- Diffusion:
- (a)
- Solve the diffusion equation on the grid and get the final grid values for the vorticity field:
- (b)
- Interpolate the particle values from the grid using a M2P formula.
- Possibility to use Fast Poisson solvers for the velocity computation instead of direct summations using the Biot-Savart integral,
- Easy treatment of the viscous effects using finite-differences schemes on the grid (or finite-volumes schemes, spectral schemes) for the resolution of the diffusion equation,
- Easiness of implementation compared to domain decomposition methods,
- Basis for mixing VM with other methods, easy model coupling,
- Prevalence of the less restrictive Lagrangian CFL condition (Equation (25)) for the whole stability,
- Satisfaction of the particle overlapping condition all along the simulation through remeshing procedures, whose computational cost may be greatly decreased by the use of directional splitting schemes (see Section 4.2.2),
- Limitation of the diffusive effects in the advection step thanks to the Lagrangian framework (provided the use of regular and high order remeshing kernels like or more generally ).
5. Treatment of the Boundary Conditions
5.1. Boundary Treatment Based on Viscous Splitting and Vorticity Creation
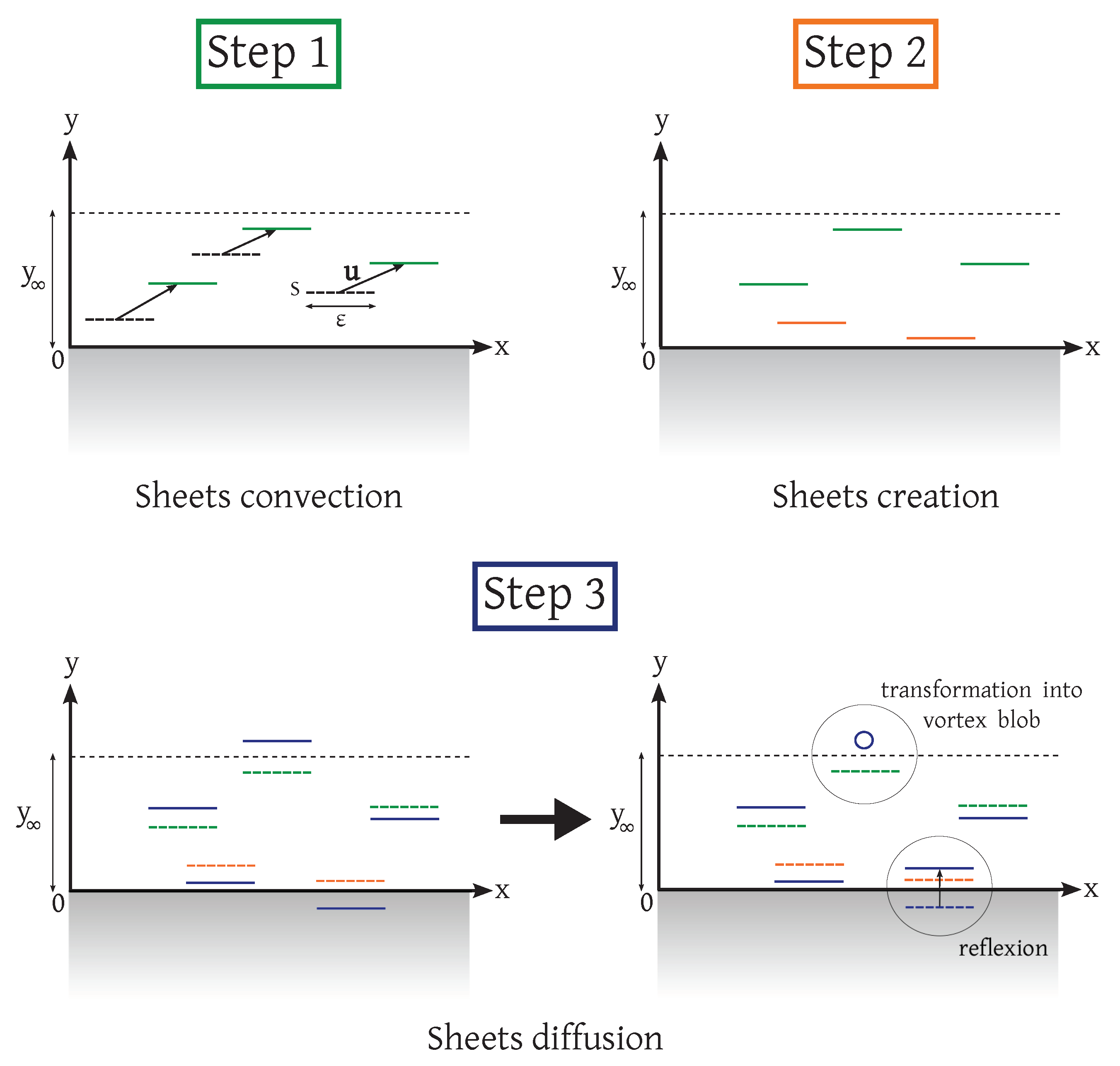
- Computation of u on the wall () and creation of new sheets at the boundary with strengths in order to impose the no-slip boundary condition (these strength values directly come from the integration of Equation (65)). As explained by Chorin in [106], the velocity field is here extended across the wall by the anti-symmetry . As a consequence and a vortex sheet is generated at .
- Diffusion of the vortex sheets in the y direction using a Random Walk approach (see Section 3.1). If a sheet arises in the far-field region (), it is transformed into a vortex blob. If a sheet crosses the boundary, moving into the body, it is reflected on the other side.
5.2. Boundary Treatment Based on Vorticity Flux Conditions
5.2.1. The Continuous Problem
5.2.2. The Integral Formulation
- The diffusion is solved in the domain with a PSE scheme for instance (the diffusion scheme needs to be based on a change of vorticity strength),
- The PSE scheme in complemented by distributing this vorticity flux onto the existing vortex blobs so that vorticity enters the domain.
5.2.3. Improvements of Vorticity Flux Boundary Conditions
5.3. Boundary Treatment Based on Immersed Boundary Methods
5.3.1. The Brinkman Vortex Penalization Method
5.3.2. The Immersed Interface Vortex Method
6. Algorithmic Issues
6.1. Fast Vortex Methods
6.2. Performance-Computing Improvements Using GPUs
6.3. Adapted Grids, Multiresolution Aspects and LES Models
6.3.1. Adaptive Mesh Refinement (AMR)
6.3.2. Subgrid Scale Vortex Methods
7. Applications and Issues
7.1. Hydrodynamics
7.2. Aerodynamics
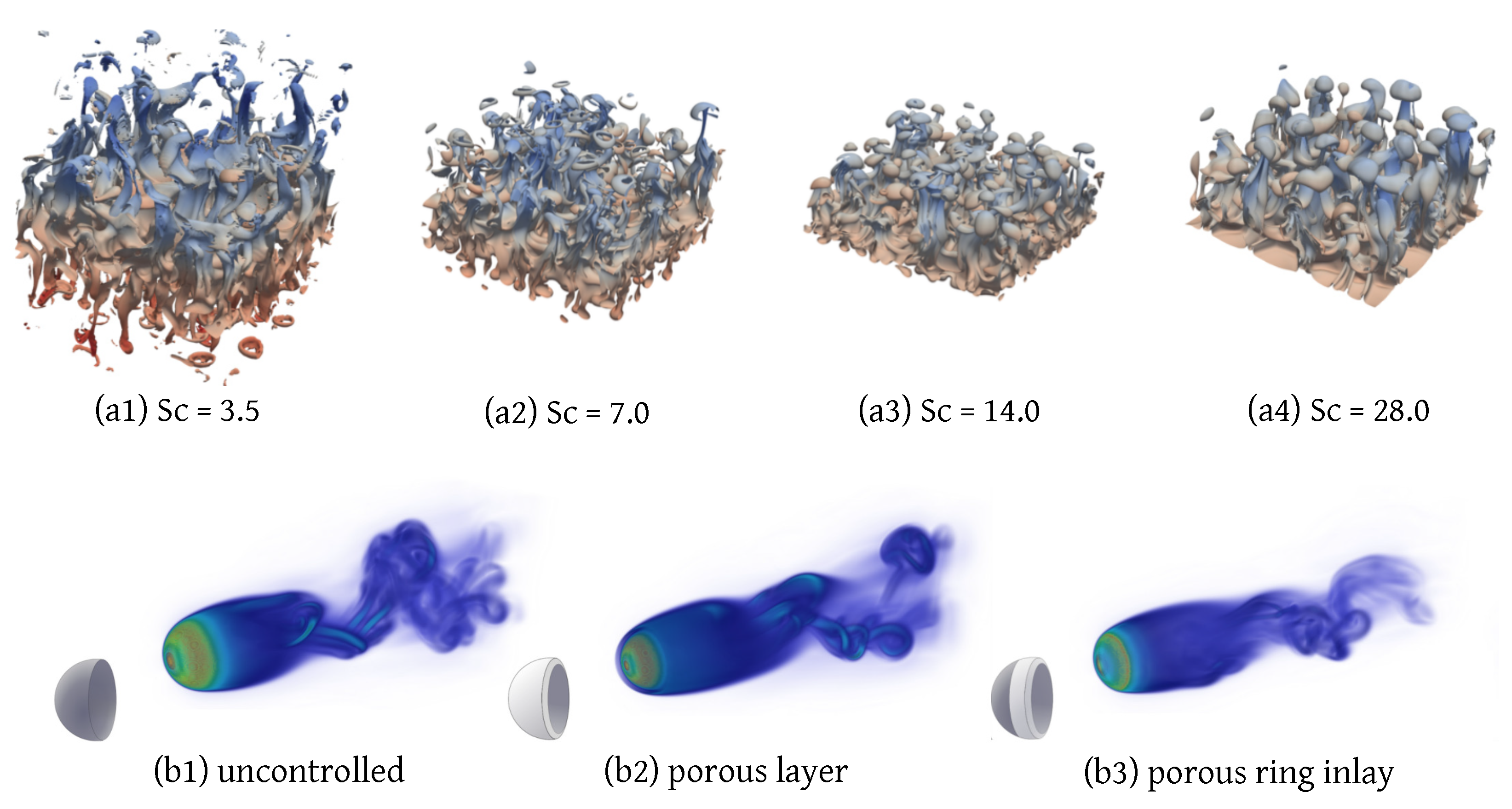
7.3. Scalars Transport
7.4. Porous Flows
| Application | Flow Regime | Governing Equations | Numerical Method | Particle Remeshing | Poisson Solver | Boundary Treatment | Grid Type | Simulation | Processor Type | |
|---|---|---|---|---|---|---|---|---|---|---|
| [9] | Swimming of articulated bodies | , | Navier-Stokes equations | VPM with multi-body solver | Tensorial scheme | FFT solver | Brinkman penalization | Cartesian uniform | 2-D DNS | CPU |
| [7,86] | Optimization of fish schooling | Navier-Stokes equations | VPM with CMA-ES algorithm | Tensorial scheme | FFT solver | Brinkman penalization | Cartesian uniform | 3-D DNS | CPU | |
| [152] | Reinforcement learning for swimmers | Navier-Stokes equations | VPM with RL algorithm | Tensorial scheme | FMM solver | Brinkman penalization | Wavelets-based AMR | 2-D DNS | CPU | |
| [14] | Dynamics of aircraft wings wake | Navier-Stokes equations | VPM based on SGS model | Tensorial scheme | FMM solver | - | Cartesian uniform | 3-D LES | CPU | |
| [12] | Dynamics of rotorcraft wakes | Navier-Stokes equations | VPM based on SGS and ILL model | Tensorial scheme | FFT solver | ILL method | Cartesian uniform | 3-D LES | CPU | |
| [13] | Dynamics of rotorcraft and aircraft wakes | , | Navier-Stokes equations | Hybrid method based on SGS model | - | FMM-GPU solver | BEM method | Body-fitted grid (near-body) | 3-D LES | CPU-GPU |
| [153] | Passive scalar turbulent transport | Navier-Stokes equations | Semi Lagrangian VM | Directional scheme | FFT solver | - | Cartesian uniform | 3-D DNS | CPU-GPU | |
| [141] | Sediment flow | , 7, 14, 28 | Navier-Stokes equations | Semi Lagrangian VM | Directional scheme | FFT solver | - | Cartesian uniform | 3-D DNS | CPU-GPU |
| [20,155] | Flow control using porous media | , | Navier-Stokes equations | Semi Lagrangian VM | Directional scheme | FFT solver | Brinkman penalization | Cartesian uniform | 3-D DNS | CPU |
| [156] | Rock dissolution at pore-scale | Dissolution regime () | Darcy Brinkman-Stokes equations | Semi Lagrangian method (for reaction equations) | Directional and schemes | FFT solver | penalization | Cartesian uniform | 3-D DNS | CPU-GPU |
8. Conclusions and Perspectives
8.1. Conclusions
8.2. Future Research Perspectives
- Turbulent and high Reynolds number flow simulations. The recent researches highlight the road map for this target with two possibilities. The first option consists in proposing modern turbulence models for the velocity-vorticity filtered Navier-Stokes equations (i.e., LES-like approaches), based for example on those already developed by Mansfield et al. [148] on one side or Cocle et al. [151] on the other side. The second view, that takes its idea from the inherent nature of vortex methods, is the multi-resolution approach (based on the pioneer works of Cottet and Wray [147,157]) which consists in using two different levels of resolution for vorticity (fine level) and the velocity (coarse level). This multi-resolution would have a deep interest in problems where important Schmidt numbers are involved like in heat transfer (e.g., thermal conduction and convection [158]), passive-scalar transport [153] or sedimentation flows [141].
- Fluid Structure Interactions (FSI). The handling of no-slip boundary conditions has long been one of the main difficulties of vortex methods. The implementation of the Brinkman penalization method has significantly improved this drawback in the context of Vortex-Particle-Mesh methods. However, this approach is limited because of its low order and accuracy. The very recent introduction of immersed interface method (IIM) [131,132] and immersed lifting line approach (ILL) [12,99] introduced a real improvement and allows us to start a real progress in the challenging field of FSI.
- Environmental and industrial particular flows. Vortex methods belong to the family of particle methods with direct treatment of particles. Therefore, their application to problems like sediment transport [141,159] or internal multi-phase flows in industry with particle mixing, dispersion, deposition, and particle-wall collision [160], seems natural and deserves a special place in the future perspectives.
- Multi-phase flows. Besides the industrial fluid/particles two-phase flows evoked above, vortex methods also have a role to play in the handling of multi-phase flows in general, with for instance the development of models able to capture interfaces between two phases and to handle surface tension, variable fluid properties and high mass density-ratio flows. To the authors knowledge, only few works based on vortex methods have been dedicated to this topic [161].
- Finally, future vortex computations need to be continually strengthened with novel high performance computing parallelism techniques (hybrid multi-CPU/multi-GPU) and powerful algorithms (like the very recent 2D-3D Poisson solver released in 2021 by Caprace et al. [162]) in order to achieve more complex flow approximations.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | Computational fluids dynamics |
| ODE | Ordinary differential equation |
| VM | Vortex methods |
| SPH | Smooth particle hydrodynamics |
| CFL | Courant-Friedricks-Levy |
| LCFL | Lagrangian Courant-Friedricks-Levy |
| RW | Random walk |
| PSE | Particle strength exchange |
| CSM | Core spreading method |
| DVM | Diffusion velocity method |
| CCF | Convolution of cut-off function |
| VRM | Vortex redistribution method |
| RBF | Radial basis functions |
| RPD | Regular point distributions |
| DVH | Diffused vortex hydrodynamics |
| VPM | Vortex-particle-mesh |
| VIC | Vortex-in-cell |
| P2M | Particle to Mesh |
| M2P | Mesh to Particle |
| FMM | Fast multiple method |
| DNS | Direct numerical simulation |
| LES | Large eddy simulation |
| BEM | Boundary elements method |
| IBM | Immersed boundary method |
| FFT | Fast Fourier Transform |
| GPU | Graphics processing unit |
| CPU | Central processing unit |
| AMR | Adaptive mesh refinement |
| FWT | Fast wavelet transform |
| LTS | Local time stepping |
| SGS | Sub-grid scale |
| SFS | Sub-filter scale |
| CMA-ES | Covariance Matrix Adaptation - Evolutionary Strategy |
| RL | Reinforcement learning |
| ILL | Immersed lifting line |
| HPC | High performance computing |
| FSI | Fluid structure interaction |
Nomenclature
| t | time |
| x, y | spacial locations |
| Q | solution vector in given continuous system |
| F | source term in given continuous system |
| Ω | computational domain |
| u | velocity field |
| δ | Dirac distribution |
| p | particle |
| volume of particle p (denoted in 2D) | |
| location of particle p | |
| denomination of the smoothing radial symmetric function in Lagrangian methods | |
| ε | radius of the smoothing radial symmetric function |
| Γ | circulation |
| × | cross product |
| ω | vorticity field (denoted ω in 2D) |
| initial vorticity field (denoted in 2D) | |
| quantity approximation | |
| far-field velocity | |
| local circulation around (denoted in 2D) | |
| ⋆ | convolution product |
| G | Green’s function |
| K | |
| ζ | smooth cutoff function |
| smoothing radial symmetric function in Vortex blobs methods (based on ζ and on blob radius ε) | |
| quantity evaluated on mollified blob particles | |
| h | particle spacing or grid spacing |
| time step | |
| ν | fluid viscosity |
| Reynolds number. Also , , and for based on length, chord, diameter and width respectively | |
| mollified diffusion kernel of given order, used in PSE schemes | |
| diffusion velocity | |
| ⊗ | tensor product |
| viscous vorticity | |
| W | interpolation/remeshing kernel |
| S | support of kernel W |
| half of grid points constituting the support of kernel W () | |
| ordinary interpolation/remeshing kernel of maximum order p | |
| B-splines interpolation/remeshing kernel of maximum order p | |
| Monaghan interpolation/remeshing kernel | |
| interpolation/remeshing kernel of regularity r and maximum order p | |
| basis functions in interpolation/remeshing process | |
| velocity of the solid immersed body | |
| any location on the solid surface | |
| wall normal vorticity flux | |
| surface of the solid body | |
| vortex sheet element at the surface | |
| strength of vortex sheet element | |
| H | Heavyside function |
| s | tangent vector to the surface |
| surface curvature at point s | |
| basis vectors in cylindrical coordinate system | |
| χ | characteristic function of the solid body |
| λ | non-dimensionalized Brinkman penalization factor |
| threshold for refinement and compression, respectively, in wavelet-based AMR method | |
| spatial filter of size Δ in LES | |
| τ | subgrid scale stress tensor in LES |
| eddy viscosity in Smagorinsky model | |
| C | coefficient in Smagorinsky model |
| rate-of-strain tensor in Smagorinsky model | |
| low-pass filtered quantities in LES model | |
| subgrid scale vorticity stress in LES | |
| subfilter scale torque in LES | |
| Schmidt number | |
| κ | diffusivity of the advected scalar in transport problems. |
References
- Gingold, R.; Monaghan, J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monaghan, J. Why particle methods work. SIAM J. Sci. Stat. Comput. 1982, 3, 422–433. [Google Scholar] [CrossRef]
- Monaghan, J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Shadloo, M.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Lind, S.; Rogers, B.; Stansby, P. Review of smoothed particle hydrodynamics: Towards converged Lagrangian flow modelling. Proc. R. Soc. A 2020, 476, 20190801. [Google Scholar] [CrossRef]
- Gazzola, M.; Chatelain, P.; van Rees, W.M.; Koumoutsakos, P. Simulations of single and multiple swimmers with non-divergence free deforming geometries. J. Comput. Phys. 2011, 230, 7093–7114. [Google Scholar] [CrossRef]
- van Rees, W.; Gazzola, M.; Koumoutsakos, P. Optimal shapes for anguilliform swimmers at intermediate Reynolds numbers. J. Fluid Mech. 2013, 722. [Google Scholar] [CrossRef]
- Gazzola, M.; Hejazialhosseini, B.; Koumoutsakos, P. Reinforcement Learning and Wavelet Adapted Vortex Methods for Simulations of Self-propelled Swimmers. SIAM J. Sci. Comput. 2014, 36, B622–B639. [Google Scholar] [CrossRef]
- Bernier, C.; Gazzola, M.; Ronsse, R.; Chatelain, P. Simulations of propelling and energy harvesting articulated bodies via vortex particle-mesh methods. J. Comput. Phys. 2019, 392, 34–55. [Google Scholar] [CrossRef]
- Gazzola, M.; Mimeau, C.; Tchieu, A.; Koumoutsakos, P. Flow mediated interactions between two cylinders at finite Re numbers. Phys. Fluids 2012, 24, 043103. [Google Scholar] [CrossRef]
- Parthasarathy, T.; Chan, F.; Gazzola, M. Streaming-enhanced flow-mediated transport. J. Fluid Mech. 2019, 878, 647–662. [Google Scholar] [CrossRef]
- Caprace, D.G.; Chatelain, P.; Winckelmans, G. Wakes of rotorcraft in advancing flight: A large-eddy simulation study. Phys. Fluids 2020, 32, 087107. [Google Scholar] [CrossRef]
- Stock, M.; Gharakhani, A.; Stone, C. Modeling rotor wakes with a hybrid OVERFLOW-vortex method on a GPU cluster. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010; p. 4553. [Google Scholar]
- Cocle, R.; Winckelmans, G.; Daeninck, G. Combining the Vortex-In-Cell and parallel Fast Multipole methods for efficient domain decomposition simulations. J. Comput. Phys. 2008, 227, 9091–9120. [Google Scholar] [CrossRef]
- Chatelain, P.; Duponcheel, M.; Caprace, D.G.; Marichal, Y.; Winckelmans, G. Vortex particle-mesh simulations of vertical axis wind turbine flows: From the airfoil performance to the very far wake. Wind Energy Sci. 2017, 2, 317–328. [Google Scholar] [CrossRef]
- Balty, P.; Caprace, D.G.; Waucquez, J.; Coquelet, M.; Chatelain, P. Multiphysics simulations of the dynamic and wakes of a floating Vertical Axis Wind Turbine. J. Phys. Conf. Ser. 2020, 1618, 062053. [Google Scholar] [CrossRef]
- Huberson, S.; Rivoalen, E.; Voutsinas, S. Vortex particle methods in aeroacoustic calculations. J. Comput. Phys. 2008, 227, 9216–9240. [Google Scholar] [CrossRef]
- Samarbakhsh, S.; Kornev, N. Simulation of a free circular jet using the vortex particle intensified LES (VπLES). Int J. Heat Fluid Flow 2019, 80, 108489. [Google Scholar] [CrossRef]
- Poncet, P.; Hildebrand, R.; Cottet, G.H.; Koumoutsakos, P. Spatially distributed control for optimal drag reduction of the flow past a circular cylinder. J. Fluid Mech. 2008, 599, 111–120. [Google Scholar] [CrossRef]
- Mimeau, C.; Mortazavi, I.; Cottet, G.H. Passive control of the flow around a hemisphere using porous media. Eur. J. Mech. B Fluids 2017, 65, 213–226. [Google Scholar] [CrossRef]
- Gustafason, K.; Sethian, J. (Eds.) Vortex Methods and Vortex Motion; SIAM: Philadelphia, PA, USA, 1991. [Google Scholar]
- Cottet, G.H.; Koumoutsakos, P. Vortex Methods—Theory and Practice; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Yokota, R.; Obi, S. Vortex Methods for the Simulation of Turbulent Flows: Review. J. Fluid Sci. Technol. 2011, 6, 14–29. [Google Scholar] [CrossRef][Green Version]
- Mimeau, C. Conception and Implementation of a Hybrid Vortex Penalization Method for sOlid-Fluid-Porous Media: Application to the Passive Control of Incompressible Flows. Ph.D. Thesis, Université de Grenoble, Grenoble, France, 2015. [Google Scholar]
- Prager, W. Die Druckverteilung an Korpern in ebener Potentialstromung. Phys. Z. 1928, 29, 865–869. [Google Scholar]
- Rosenhead, L. The Formation of vortices from a surface of discontinuity. Proc. R. Soc. Lond. Ser. A 1931, 134, 170–192. [Google Scholar]
- Chorin, A.J.; Bernard, P.S. Discretization of a Vortex Sheet, with an Example of Roll-Up. J. Comput. Phys. 1973, 13, 423–429. [Google Scholar] [CrossRef]
- Anderson, C.; Greengard, C. On vortex methods. SIAM J. Numer. Anal. 1985, 22, 413–440. [Google Scholar] [CrossRef]
- Cottet, G.H. A new approach for the analysis of Vortex Methods in two and three dimensions. Annales de l’I. H. P. Analyse non Linéaire 1988, 5, 227–285. [Google Scholar] [CrossRef][Green Version]
- Leonard, A. Numerical simulation of interacting vortex filaments. In Proceedings of the IV International Conference on Numerical Methods of Fluid Dynamics, Boulder, CO, USA, 24–28 June 1974; Springer: New York, NY, USA, 1975. [Google Scholar]
- Leonard, A. Vortex methods for flow simulation. J. Comput. Phys. 1980, 37, 289–335. [Google Scholar] [CrossRef]
- Leonard, A. Computing three-dimensional incompressible flows with vortex elements. Ann. Rev. Fluid Mech. 1985, 17, 523–559. [Google Scholar] [CrossRef]
- Angelidis, A.; Neyret, F. Simulation of smoke based on vortex filament primitives. In Proceedings of the ACM-SIGGRAPH/EG Symposium on Computer Animation (SCA), Los Angeles, CA, USA, 29–31 July 2005. [Google Scholar]
- Hald, O. Convergence of vortex methods II. SIAM J. Numer. Anal 1979, 16, 726–755. [Google Scholar] [CrossRef]
- Beale, J.; Majda, A. Vortex methods II: High order accuracy in 2 and 3 dimensions. Math. Comput. 1982, 32, 29–52. [Google Scholar]
- Knio, O.; Ghoniem, A.F. Numerical study of a three-dimensional vortex method. J. Comput. Phys. 1990, 86, 75–106. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical study of slighly viscous flow. J. Fluid Mech. 1973, 57, 785–796. [Google Scholar] [CrossRef]
- Prandtl, W. Uber Flussigkeitbewegung bei sehr kleiner Reibung. In Proceedings of the Fourth Mathematics Congress, Heidelberg, Germany, 8–13 August 1904; pp. 484–491. [Google Scholar]
- Beale, J.T.; Majda, A. Rates of convergence for viscous splitting of the Navier-Stokes equations. Math. Comput. 1981, 37, 243–259. [Google Scholar] [CrossRef]
- Marchioro, C.; Pulvirenti, M. Hydrodynamics in two dimensions and vortex theory. Commun. Math. Phys. 1982, 84, 483–503. [Google Scholar] [CrossRef]
- Goodman, J. Convergence of the random vortex method. Commun. Pure Appl. Math. 1987, 40, 189–220. [Google Scholar] [CrossRef]
- Long, D.G. Convergence of the random vortex method in two dimensions. J. Am. Math. Soc. 1988, 1, 779–804. [Google Scholar] [CrossRef]
- Chorin, A.J. Computational Fluid Mechanics; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- van Dommelen, L.L. Computation of unsteady separation using Lagrangian procedures. In Proceedings of the IUTAM Symposium on Boundary Layer Separation, London, UK, 26–28 August 1986; pp. 73–87. [Google Scholar]
- Smith, P.; Stansby, P. An efficient surface algorithm for random-particle simulation of vorticity and heat transport. J. Comput. Phys. 1989, 81, 349–371. [Google Scholar] [CrossRef]
- Slaouti, A.; Stansby, P. Flow around two circular cylinders by the random-vortex method. J. Fluids Struct. 1992, 6, 641–670. [Google Scholar] [CrossRef]
- Wang, S.C. Control of Dynamic Stall. Ph.D. Thesis, FAMU-FSU, College of Engineering, Tallahassee, FL, USA, 1995. [Google Scholar]
- Lewis, R.I. Vortex Element Methods for Fluid Dynamic Analysis of Engineering Systems; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Milinazzo, F.; Saffman, P.G. The calculation of large Reynolds number two-dimensional flow using discrete vortices with random walk. J. Comput. Phys. 1977, 23, 380–392. [Google Scholar] [CrossRef]
- Gharakhani, A.; Ghoniem, A. Three-Dimensional Vortex Simulation of Time Dependent Incompressible Internal Viscous Flows. J. Comput. Phys. 1997, 134, 75–95. [Google Scholar] [CrossRef]
- Degond, P.; Mas-Gallic, S. The weighted particle method for convection-diffusion equations. Math. Comput. 1989, 53, 485–526. [Google Scholar]
- Cottet, G.H.; Mas-Gallic, S. Une méthode de décomposition pour une équation de type convection-diffusion combinant résolution explicite et méthode particulaire. C. R. Acad. Sci. Paris 1983, 297, 133–136. [Google Scholar]
- Cottet, G.H.; Mas-Gallic, S. A particle method to solve the Navier-Stokes system. Numer. Math. 1990, 57, 1–23. [Google Scholar] [CrossRef]
- Koumoutsakos, P.; Leonard, A. High-resolution simulations of the flow around an impulsively started cylinder using vortex methods. J. Fluid Mech. 1995, 296, 1–38. [Google Scholar] [CrossRef]
- Ploumhans, P.; Winckelmans, G.S.; Salmon, J.K.; Leonard, A.; Warren, M.S. Vortex Methods for Direct Numerical Simulation of Three-Dimensional Bluff Body Flows: Applications to the Sphere at Re=300, 500 and 1000. J. Comput. Phys. 2002, 178, 427–463. [Google Scholar] [CrossRef]
- Yokota, R.; Sheel, T.; Obi, S. Calculation of isotropic turbulence using a pure Lagrangian vortex method. J. Comput. Phys. 2007, 226, 1589–1606. [Google Scholar] [CrossRef][Green Version]
- Kuwahara, K.; Takami, H. Numerical studies of two-dimensional vortex motion by a system of point vortices. J. Phys. Soc. Jpn. 1973, 34, 247–253. [Google Scholar] [CrossRef]
- Greengard, C. The core spreading vortex method approximates the wrong equation. J. Comput. Phys. 1985, 61, 345–348. [Google Scholar] [CrossRef]
- Rossi, L.F. Resurrecting core spreading vortex methods: A new scheme that is both deterministic and convergent. SIAM J. Sci. Stat. Comput. 1996, 17, 370–397. [Google Scholar] [CrossRef]
- Barba, L.; Leonard, A.; Allen, C. Advances in viscous vortex methods—Meshless spatial adaption based on radial basis function interpolation. Int. J. Numer. Methods Fluids 2005, 47, 387–421. [Google Scholar] [CrossRef]
- Fronteau, J.; Combis, P. A lie admissible method of integration of Folkler-Plank equations with non linear coefficients (exact and numerical solutions). Hadronic J. 1984, 7, 911–930. [Google Scholar]
- Ogami, Y.; Akamatsu, T. Viscous flow simulation using the discrete vortex model—The diffusion velocity model. Comput. Fluids 1991, 19, 433–441. [Google Scholar] [CrossRef]
- Beaudoin, A.; Huberson, S.; Rivoalen, E. Simulation of anisotropic diffusion by means of a diffusion velocity method. J. Comput. Phys. 2003, 186, 122–135. [Google Scholar] [CrossRef]
- Clarke, N.; Tutty, O. Construction and validation of a discrete vortex method for the two-dimensional incompressible Navier-Stokes equations. Comput. Fluids 1994, 23, 751–783. [Google Scholar] [CrossRef]
- Lucchesi, M.; Allouch, S.; Le Maitre, O.; Mustapha, K.; Knio, O. Particle simulation of space–fractional diffusion equations. Comput. Part. Mech. 2020, 7, 491–507. [Google Scholar] [CrossRef]
- Rivoalen, E.; Huberson, S.; Hauville, F. Simulation numérique des équations de Navier-Stokes 3D par une méthode particulaire. C. R. Acad. Sci. Ser. IIB Mech. Phys. Chem. Astron. 1997, 324, 543–549. [Google Scholar] [CrossRef]
- Fishelov, D. A new vortex scheme for viscous flows. J. Comput. Phys. 1990, 86, 211–224. [Google Scholar] [CrossRef][Green Version]
- Shankar, S.; van Dommelen, L. A new diffusion procedure for vortex methods. J. Comput. Phys. 1996, 127, 88–109. [Google Scholar] [CrossRef]
- Barba, L. Vortex Method for Computing High-Reynolds Number Flows: Increased Accuracy with a Fully Mesh-Less Formulation. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2004. [Google Scholar]
- Rossinelli, D.; Koumoutsakos, P. Vortex methods for incompressible flow simulations on the GPU. Vis. Comput. 2008, 24, 699–708. [Google Scholar] [CrossRef]
- Henshaw, W.; Kreiss, H.O.; Reyna, L. On the smallest scale for the compressible Navier-Stokes equations. Theor. Comput. Fluid Dyn. 1989, 1, 65–95. [Google Scholar]
- Krasny, R. A study of singularity formation in a vortex sheet by the point vortex approximation. J. Fluid Mech. 1986, 167, 65–93. [Google Scholar] [CrossRef]
- Beale, J.T. On the accuracy of vortex methods at large times. In Computational Fluid Dynamics and Reacting Gas Flows; Engquist, B., Majda, A., Luskin, M., Eds.; Springer: New York, NY, USA, 1988; pp. 19–32. [Google Scholar]
- Choquin, J.P.; Lucquin-Desreux, B. Accuracy of a deterministic particle method for the Navier-Stokes equations. Int. J. Numer. Fluids 1988, 8, 1439–1458. [Google Scholar] [CrossRef]
- Russo, G.; Strain, J. Fast triangulated vortex methods for the 2D Euler equations. J. Comput. Phys. 1994, 111, 291–323. [Google Scholar] [CrossRef]
- Strain, J. Fast adaptive 2D vortex methods. J. Comput. Phys. 1997, 132, 108–122. [Google Scholar] [CrossRef]
- Schrader, B.; Sbalzarini, I.; Redoux, S. Discretization correction of general integral PSE operators for particle methods. J. Comput. Phys. 2010, 229, 4159–4182. [Google Scholar] [CrossRef]
- Eldredge, J.; Colonius, T.; Leonard, A. A general deterministic treatment of derivatives in particle methods. J. Comput. Phys. 2002, 180, 686–709. [Google Scholar] [CrossRef]
- Rossi, E.; Colagrossi, A.; Bouscasse, B.; Graziani, G. The Diffused Vortex Hydrodynamics Method. Commun. Comput. Phys. 2015, 18, 351–379. [Google Scholar] [CrossRef]
- Huberson, S.; Jollès, A. Correction de l’erreur de projection dans les méthodes particules/maillage. La Recherche Aérospatiale 1990, 4, 1–6. [Google Scholar]
- Cottet, G.H.; Magni, A. TVD remeshing schemes for particle methods. C. R. Acad. Sci. Paris 2009, 347, 1367–1372. [Google Scholar] [CrossRef]
- Magni, A.; Cottet, G.H. Accurate, non-oscillatory remeshing schemes for particle methods. J. Comput. Phys. 2012, 231, 152–172. [Google Scholar] [CrossRef]
- Schoenberg, I.J. Contributions to the problem of approximation of equidistant data by analytic functions. Q. Appl. Math. 1946, 4, 112–141. [Google Scholar] [CrossRef]
- Magni, A. Méthodes Particulaires Avec Remaillage: Analyse Numérique, Nouveaux Schémas Et Applications Pour La Simulation D’équations De Transport. Ph.D. Thesis, Université de Grenoble, Grenoble, France, 2011. [Google Scholar]
- Monaghan, J. Extrapolating B-splines for interpolation. J. Comput. Phys. 1985, 60, 253–262. [Google Scholar] [CrossRef]
- Gazzola, M.; van Rees, W.M.; Koumoutsakos, P. C-start: Optimal start of larval fish. J. Fluid Mech. 2012, 698, 5–18. [Google Scholar] [CrossRef]
- Bergdorf, M.; Koumoutsakos, P. A Lagrangian particle-wavelet method. SIAM Multiscale Model. Simul. 2006, 5, 980–995. [Google Scholar] [CrossRef]
- Cottet, G.H.; Etancelin, J.M.; Perignon, F.; Picard, C. High order Semi-Lagrangian particles for transport equations: Numerical analysis and implementation issues. ESAIM Math. Model. Numer. Anal. 2014, 48, 1029–1060. [Google Scholar] [CrossRef]
- Cottet, G.H. Particle-grid domain decomposition methods for the Navier-Stokes equations in exterior domains. Lect. Appl. Math. Ser. Am. Math. Soc. N. Y. 1991, 28, 100–118. [Google Scholar]
- Cottet, G.H.; Koumoutsakos, P.; Ould-Salihi, M. Vortex Methods with Spatially Varying Cores. J. Comput. Phys. 2000, 162, 164–185. [Google Scholar] [CrossRef][Green Version]
- Huberson, S.; Voutsinas, S. Particles and grid. Comput. Fluids 2002, 31, 607–625. [Google Scholar] [CrossRef]
- Guermond, J.L.; Huberson, S.; Shen, W.Z. Simulation of 2D external viscous flows by means of a domain decomposition method. J. Comput. Phys. 1993, 108, 343–352. [Google Scholar] [CrossRef]
- Christiansen, J. Numerical solution of hydrodynamics by the method of point vortices. J. Comput. Phys. 1973, 13, 363–379. [Google Scholar] [CrossRef]
- Mortazavi, I.; Giovannini, A. The simulation of vortex dynamics downstream of a plate separator using a vortex-finite element method. Int. J. Fluid Dyn. 2001, 5, 31–48. [Google Scholar]
- Ould-Salihi, M.; Cottet, G.H.; El Hamraoui, M. Blending finite-difference and vortex methods for incompressible flow computations. SIAM J. Sci. Comp. 2000, 22, 1655–1674. [Google Scholar] [CrossRef]
- Gallizio, F. Analytical and Numerical Vortex Methods to Model Separated Flows. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2009. [Google Scholar]
- van Rees, W.M.; Leonard, A.; Pullin, D.; Koumoutsakos, P. A comparison of vortex and pseudo-spectral methods for the simulation of periodic vortical flows at high Reynolds numbers. J. Comput. Phys. 2011, 230, 2794–2805. [Google Scholar] [CrossRef]
- Mimeau, C.; Gallizio, F.; Cottet, G.H.; Mortazavi, I. Vortex penalization method for bluff body flows. Int. J. Numer. Meth. Fluids 2015, 79, 55–83. [Google Scholar] [CrossRef]
- Caprace, D.G.; Winckelmans, G.; Chatelain, P. An immersed lifting and dragging line model for the Vortex Particle-Mesh method. Theor. Comput. Fluid Dyn. 2020, 34, 21–48. [Google Scholar] [CrossRef]
- Mimeau, C.; Cottet, G.H.; Mortazavi, I. Direct numerical simulations of three-dimensional flows past obstacles with a vortex penalization method. Comput. Fluids 2016, 136, 331–347. [Google Scholar] [CrossRef]
- Morgenthal, G.; Walther, J.H. An immersed interface method for the Vortex-In-Cell algorithm. Comput. Struct. 2007, 85, 712–726. [Google Scholar] [CrossRef]
- Kudela, H.; Kozlowski, T. Vortex-in-cell method for exterior problems. J. Theor. Appl. Mech. 2009, 47, 779–796. [Google Scholar]
- Cottet, G.H.; Poncet, P. Simulation and control of three-dimensional wakes. Comput. Fluids 2004, 33, 697–713. [Google Scholar] [CrossRef]
- Creusé, E.; Giovannini, A.; Mortazavi, I. Vortex simulation of active control strategies for transitional backward-facing step flows. Comput. Fluids 2009, 38, 1348–1360. [Google Scholar] [CrossRef]
- Kornev, N. Hybrid method based on embedded coupled simulation of vortex particles in grid based solution. Comput. Part. Mech. 2018, 5, 269–283. [Google Scholar] [CrossRef]
- Chorin, A.J. Vortex sheet approximation of boundary layers. J. Comput. Phys. 1978, 27, 428–442. [Google Scholar] [CrossRef]
- Smith, P.; Stansby, P. Impulsively started flow around a circular cylinder by the vortex method. J. Fluid Mech. 1988, 194, 45–77. [Google Scholar] [CrossRef]
- Sethian, J.A.; Ghoniem, A.F. Validation Study of Vortex Methods. J. Comput. Phys. 1988, 74, 283–317. [Google Scholar] [CrossRef][Green Version]
- Cheer, A.J. Numerical study of incompressible slightly viscous flow past blunt bodies and airfoils. SIAM J. Sci. Stat. Comput. 1983, 4, 685–705. [Google Scholar] [CrossRef]
- Mortazavi, I.; Micheau, P.; Giovannini, A. Numerical convergence of vortex method for a high Reynolds number 2D bluff-body flow. C. R. Mec. 2002, 330, 409–416. [Google Scholar] [CrossRef]
- Chorin, A.J. Vortex models and boundary layer instability. SIAM J. Sci. Stat. Comput. 1980, 1, 1–21. [Google Scholar] [CrossRef]
- Fishelov, D. Vortex Methods for Slightly Viscous Three Dimensional Flow. SIAM J. Sci. Stat. Comput. 1990, 3, 399–424. [Google Scholar] [CrossRef]
- Gharakhani, A.; Ghoniem, A. Simulation of the piston driven flow inside a cylinder with an eccentric port. J. Fluids Eng. 1998, 120, 319–326. [Google Scholar] [CrossRef]
- Anderson, C.; Reider, M. Investigation of the use of Prandtl/Navier-Stokes Equation Procedures for Two-Dimensional Incompressible Flows. Phys. Fluids 1994, 6, 2380–2389. [Google Scholar] [CrossRef]
- Walther, J.H.; Larsen, A. Two dimensional discrete vortex method for application to bluff body aerodynamics. J. Wind Eng. Ind. Aerodyn. 1997, 67–68, 183–193. [Google Scholar]
- Cottet, G.H. A vorticity creation algorithm for the Navier-Stokes equations in arbitrary domain. In Navier-Stokes Equations and Related Non-Linear Problems; Sequeira, A., Ed.; Plenum Press Publishers: New York, NY, USA, 1994. [Google Scholar]
- Koumoutsakos, P.; Leonard, A.; Pépin, F. Boundary conditions for viscous vortex methods. J. Comput. Phys. 1994, 113, 52–61. [Google Scholar] [CrossRef]
- Casciola, C.M.; Piva, R.; Bassanini, P. Vorticity generation on a flat surface in 3D flows. J. Comput. Phys. 1996, 129, 345–356. [Google Scholar] [CrossRef]
- Poncet, P. Méthodes Particulaires Pour la Simulation des Sillages Tridimensionnels. Ph.D. Thesis, Université Joseph Fourier–Grenoble I, Grenoble, France, 2001. [Google Scholar]
- Cottet, G.H.; Poncet, P. Advances in direct numerical simulation of 3D wall-bounded flows by Vortex-In-Cell methods. J. Comput. Phys. 2003, 193, 136–158. [Google Scholar] [CrossRef]
- Cooper, C.; Barba, L. Panel-free boundary conditions for viscous vortex methods. In Proceedings of the AIAA Computational Fluid Dynamics Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar]
- Ploumhans, P.; Winckelmans, G.S. Vortex methods for high-resolution simulations of viscous flow past bluff bodies of general geometry. J. Comput. Phys. 2000, 165, 354–406. [Google Scholar] [CrossRef]
- Poncet, P. Analysis of an immersed boundary method for three-dimensional flows in vorticity formulation. J. Comput. Phys. 2009, 228, 7268–7288. [Google Scholar] [CrossRef]
- Caltagirone, J.P. Sur l’intéraction fluide-milieu poreux: Application au calcul des efforts exercés sur un obstacle par un fluide visqueux. C. R. Acad. Sci. Paris 1994, 318, 571–577. [Google Scholar]
- Angot, P.; Bruneau, C.H.; Fabrie, P. A penalization method to take into account obstacles in incompressible viscous flows. Numer. Math. 1999, 81, 497–520. [Google Scholar] [CrossRef]
- Kevlahan, N.; Ghidaglia, J.M. Computation of turbulent flow past an array of cylinders using a spectral method with Brinkman penalization. Eur. J. Mech. 2001, 20, 333–350. [Google Scholar] [CrossRef]
- Morency, F.; Beaugendre, H.; Gallizio, F. Aerodynamic force evaluation for ice shedding phenomenon using vortex in cell scheme, penalisation and level set approaches. Int. J. Comput. Fluid Dyn. 2012, 26, 435–450. [Google Scholar] [CrossRef]
- Coquerelle, M.; Cottet, G.H. A vortex level-set method for the two-way coupling of an incompressible fluid with colliding rigid bodies. J. Comput. Phys. 2008, 227, 9121–9137. [Google Scholar] [CrossRef]
- Hejlesen, M.; Koumoutsakos, P.; Leonard, A.; Walther, J. Iterative Brinkman penalization for remeshed vortex methods. J. Comput. Phys. 2015, 280, 547–562. [Google Scholar] [CrossRef]
- Gillis, T.; Winckelmans, G.; Chatelain, P. An efficient iterative penalization method using recycled Krylov subspaces and its application to impulsively started flows. J. Comput. Phys. 2017, 347, 490–505. [Google Scholar] [CrossRef]
- Marichal, Y.; Chatelain, P.; Winckelmans, G. Immersed interface interpolation schemes for particle–mesh methods. J. Comput. Phys. 2016, 326, 947–972. [Google Scholar] [CrossRef]
- Gillis, T.; Winckelmans, G.; Chatelain, P. A 2D immersed interface Vortex Particle-Mesh method. J. Comput. Phys. 2019, 394, 700–718. [Google Scholar] [CrossRef]
- LeVeque, R.J.; Li, Z. The immersed interface method for elliptic equations with discontinuous coefficients and singular sources. SIAM J. Numer. Anal. 1994, 31, 1019–1044. [Google Scholar] [CrossRef]
- Rossinelli, D.; Hejazialhosseini, B.; van Rees, W.M.; Gazzola, M.; Bergdorf, M.; Koumoutsakos, P. MRAG-I2D: Multi-resolution adapted grids for remeshed vortex methods on multicore architectures. J. Comput. Phys. 2015, 288, 1–18. [Google Scholar] [CrossRef]
- Greengard, L.; Rokhlin, V. A fast algorithm for particle simulations. J. Comput. Phys. 1987, 73, 325–348. [Google Scholar] [CrossRef]
- Marzouk, Y.M.; Ghoniem, A.F. K-means clustering for optimal partitioning and dynamic load balancing of parallel hierarchical N-body simulations. J. Comput. Phys. 2005, 207, 493–528. [Google Scholar] [CrossRef]
- Yokota, R.; Narumi, T.; Sakamaki, R.; Kameoka, S.; Obi, S.; Yasuoka, K. Fast multipole methods on a cluster of GPUs for the meshless simulation of turbulence. Comput. Phys. Commun. 2009, 180, 2066–2078. [Google Scholar] [CrossRef]
- Giannopoulou, O.; Colagrossi, A.; Di Mascio, A.; Mascia, C. Chorin’s approaches revisited: Vortex Particle Method vs. Finite Volume Method. Eng. Anal. Bound. Elem. 2019, 106, 371–388. [Google Scholar] [CrossRef]
- Hu, Q.; Gumerov, N.; Yokota, R.; Barba, L.A.; Duraiswami, R. Scalable fast multipole methods for vortex element methods. In Proceedings of the 2012 SC Companion: High Performance Computing, Networking Storage and Analysis, Salt Lake City, UT, USA, 10–16 November 2012; pp. 1408–1409. [Google Scholar]
- Rossinelli, D.; Bergdorf, M.; Cottet, G.H.; Koumoutsakos, P. GPU accelerated simulations of bluff body flows using vortex particle methods. J. Comput. Phys. 2010, 229, 3316–3333. [Google Scholar] [CrossRef]
- Keck, J.B. Numerical Modelling and High Performance Computing for Sediment Flows. Ph.D. Thesis, Université Grenoble Alpes, Grenoble, France, 2019. [Google Scholar]
- Yokota, R.; Barba, L.A.; Narumi, T.; Yasuoka, K. Petascale turbulence simulation using a highly parallel fast multipole method on GPUs. Comput. Phys. Commun. 2013, 184, 445–455. [Google Scholar] [CrossRef]
- Bergdorf, M.; Cottet, G.H.; Koumoutsakos, P. Multilevel adaptive particle methods for convection-diffusion equations. Multiscale Model. Sim. 2005, 4, 328–357. [Google Scholar] [CrossRef]
- Rasmussen, J.T.; Cottet, G.H.; Walther, J.H. A multiresolution remeshed Vortex-In-Cell algorithm using patches. J. Comput. Phys. 2011, 230, 6742–6755. [Google Scholar] [CrossRef]
- El Ossmani, M.; Poncet, P. Efficiency of Multiscale Hybrid Grid-Particle Vortex Methods. Multiscale Model. Simul. 2010, 8, 1671–1690. [Google Scholar] [CrossRef]
- Sagaut, P.; Deck, S.; Terracol, M. Multiscale and Multiresolution Approaches in Turbulence. LES, DES and Hybrid RANS/LES Methods: Applications and Guidelines; Imperial College Press: London, UK, 2013. [Google Scholar]
- Cottet, G.H. Artificial Viscosity Models for Vortex and Particle Methods. J. Comput. Phys. 1996, 127, 199–208. [Google Scholar] [CrossRef]
- Mansfield, J.; Knio, O.; Meneveau, C. A Dynamic LES Scheme for the Vorticity Transport Equation: Formulation and a Priori Tests. J. Comput. Phys. 1998, 145, 693–730. [Google Scholar] [CrossRef]
- Mansfield, J.; Knio, O.; Meneveau, C. Dynamic LES of Colliding Vortex Rings Using a 3D Vortex Method. J. Comput. Phys. 1999, 152, 305–745. [Google Scholar] [CrossRef]
- Pinon, G.; Bratec, H.; Huberson, S.; Pignot, G.; Rivoalen, E. Vortex method for simulation of a 3D round jet in a cross-stream. J. Turbul. 2005, 6, N18. [Google Scholar] [CrossRef]
- Cocle, R.; Dufresne, L.; Winckelmans, G. Investigation of multiscale subgrid scale models for LES of instabilities and turbulence in wake vortex systems. In Complex Effects in Large Eddy Simulations, Lecture Notes in Computational Science and Engineering (LNCSE); Springer: Berlin/Heidelberg, Germany, 2007; Volume 56. [Google Scholar]
- Novati, G.; Verma, S.; Alexeev, D.; Rossinelli, D.; van Rees, W.; Koumoutsakos, P. Synchronisation through learning for two self-propelled swimmers. Bioinspir. Biomim. 2017, 12, 036001. [Google Scholar] [CrossRef]
- Etancelin, J.M.; Cottet, G.H.; Pérignon, F.; Picard, C. Multi-CPU and multi-GPU hybrid computations of multi-scale scalar transport. In Proceedings of the 26th International Conference on Parallel Computational Fluid Dynamics, Trondheim, Norway, 20–22 May 2014; pp. 83–84. [Google Scholar]
- Etancelin, J.M. Couplage de Modèles, Algorithmes Multi-échelles et Calcul Hybride. Ph.D. Thesis, Université de Grenoble, Grenoble, France, 2014. [Google Scholar]
- Mimeau, C.; Mortazavi, I.; Cottet, G.H. Passive Flow Control Around a Semi-Circular Cylinder Using Porous Coatings. Int. J. Flow Control 2014, 6, 43–60. [Google Scholar]
- Etancelin, J.M.; Moonen, P.; Poncet, P. Improvement of remeshed Lagrangian methods for the simulation of dissolution processes at pore-scale. Adv. Water Resour. 2020, 146, 103780. [Google Scholar] [CrossRef]
- Cottet, G.H.; Wray, A. Anisotropic grid-based formulas for subgrid-scale models. In Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 1997. [Google Scholar]
- Ostilla-Monico, R.; Yang, Y.; van der Poel, E.; Lohse, D.; Verzicco, R. A multiple-resolution strategy for Direct Numerical Simulation of scalar turbulence. J. Comput. Phys. 2015, 301, 308–321. [Google Scholar] [CrossRef]
- Keck, J.B.; Cottet, G.H.; Meiburg, E.; Mortazavi, I.; Picard, C. Double-diffusive sedimentation at high Schmidt numbers: Semi-Lagrangian simulations. Phys. Rev. Fluids 2021. to appear. [Google Scholar]
- Iso, Y.; Kamemoto, K. A Grid-Free Lagrangian Approach of Vortex Method and Particle Trajectory Tracking Method Applied to Internal Fluid-Solid Two-Phase Flows. J. Fluids Eng. 2008, 130, 011401. [Google Scholar] [CrossRef]
- Lorieul, G. Development and Validation of a 2D Vortex-Particle-Mesh Method for Incompressible Multi-Phase Flows. Ph.D. Thesis, Université Catholique de Louvain, Ottignies-Louvain-la-Neuve, Belgium, 2018. [Google Scholar]
- Caprace, D.G.; Gillis, T.; Chatelain, P. FLUPS—A Fourier-based Library of Unbounded Poisson Solvers. SIAM J. Sci. Comput. 2021, 43, C31–C60. [Google Scholar] [CrossRef]





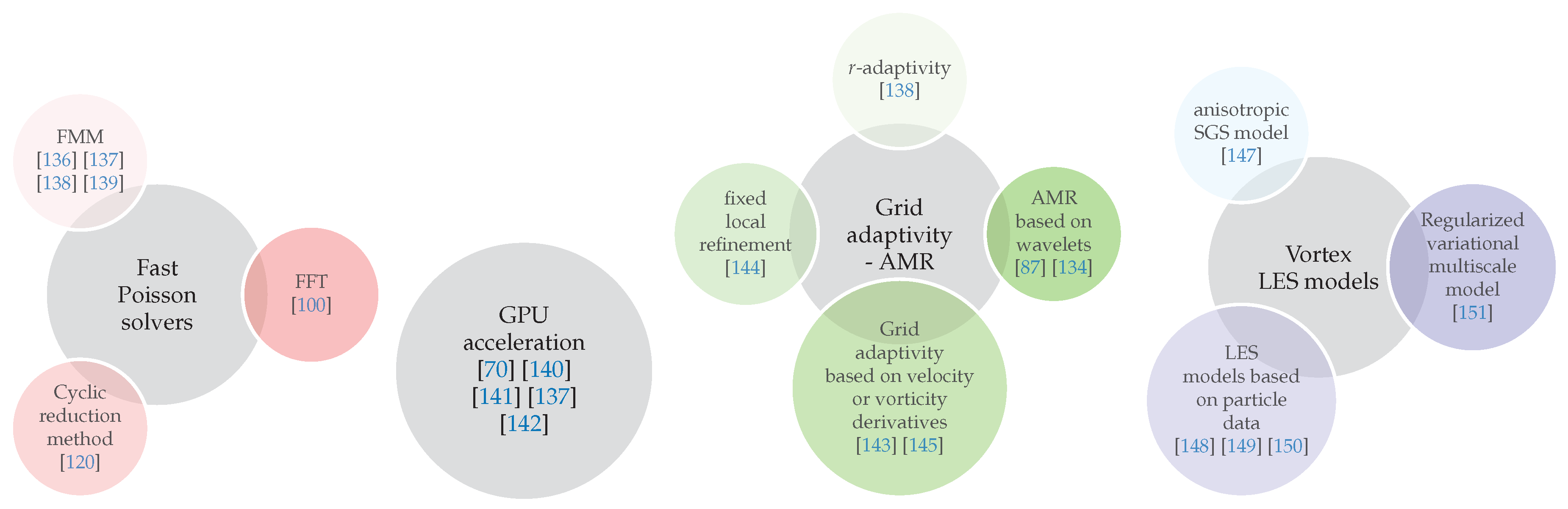
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mimeau, C.; Mortazavi, I. A Review of Vortex Methods and Their Applications: From Creation to Recent Advances. Fluids 2021, 6, 68. https://doi.org/10.3390/fluids6020068
Mimeau C, Mortazavi I. A Review of Vortex Methods and Their Applications: From Creation to Recent Advances. Fluids. 2021; 6(2):68. https://doi.org/10.3390/fluids6020068
Chicago/Turabian StyleMimeau, Chloé, and Iraj Mortazavi. 2021. "A Review of Vortex Methods and Their Applications: From Creation to Recent Advances" Fluids 6, no. 2: 68. https://doi.org/10.3390/fluids6020068
APA StyleMimeau, C., & Mortazavi, I. (2021). A Review of Vortex Methods and Their Applications: From Creation to Recent Advances. Fluids, 6(2), 68. https://doi.org/10.3390/fluids6020068






