Numerical Flow Characterization around a Type 209 Submarine Using OpenFOAM †
Abstract
1. Introduction
2. Numerical Method
2.1. DARPA SUBOFF and Type 209/1300 Submarine Geometry
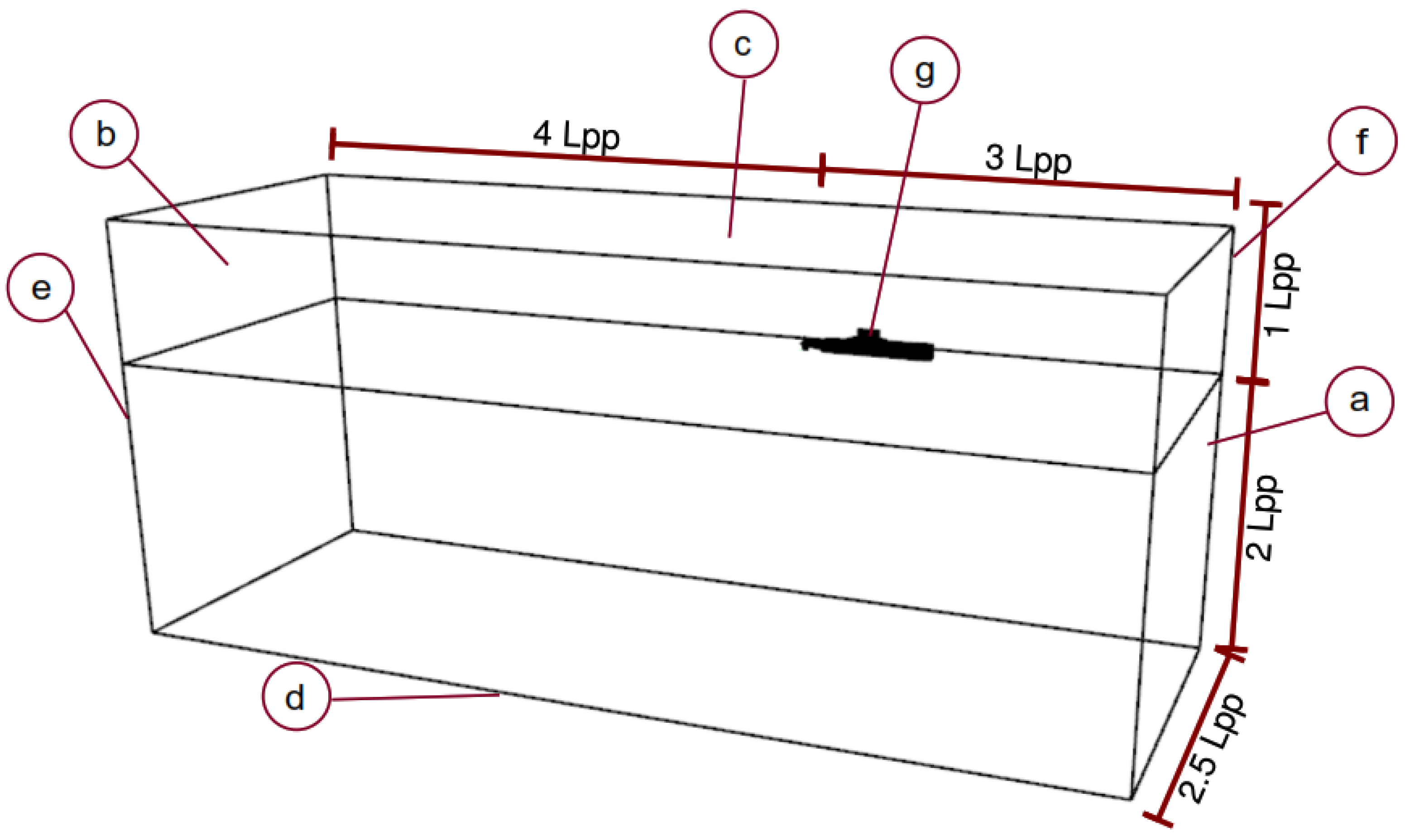
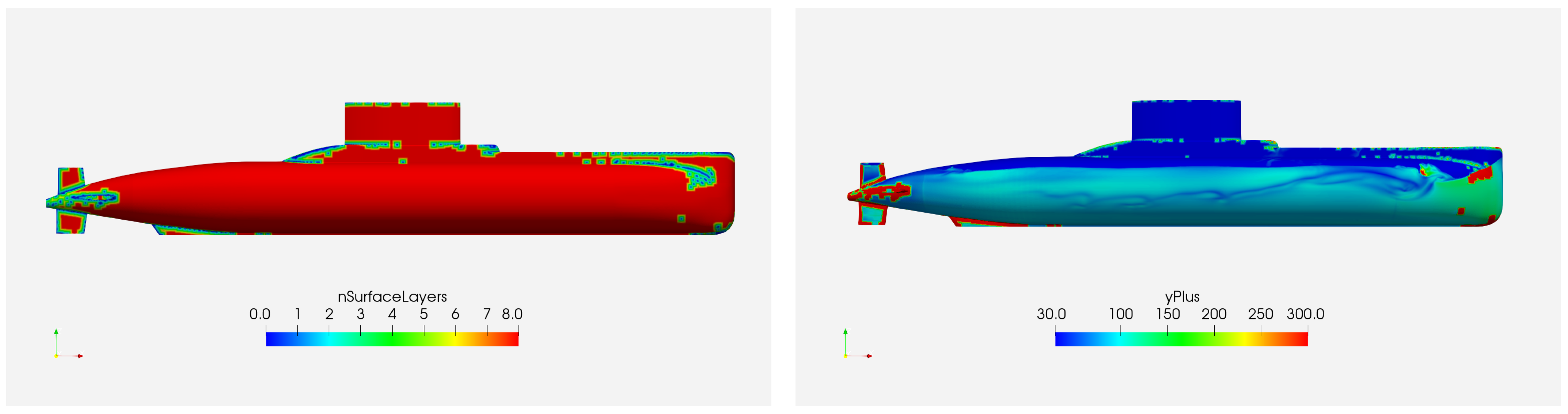
2.2. Simulation Setup for Submarines
2.3. Test Matrix
3. Results
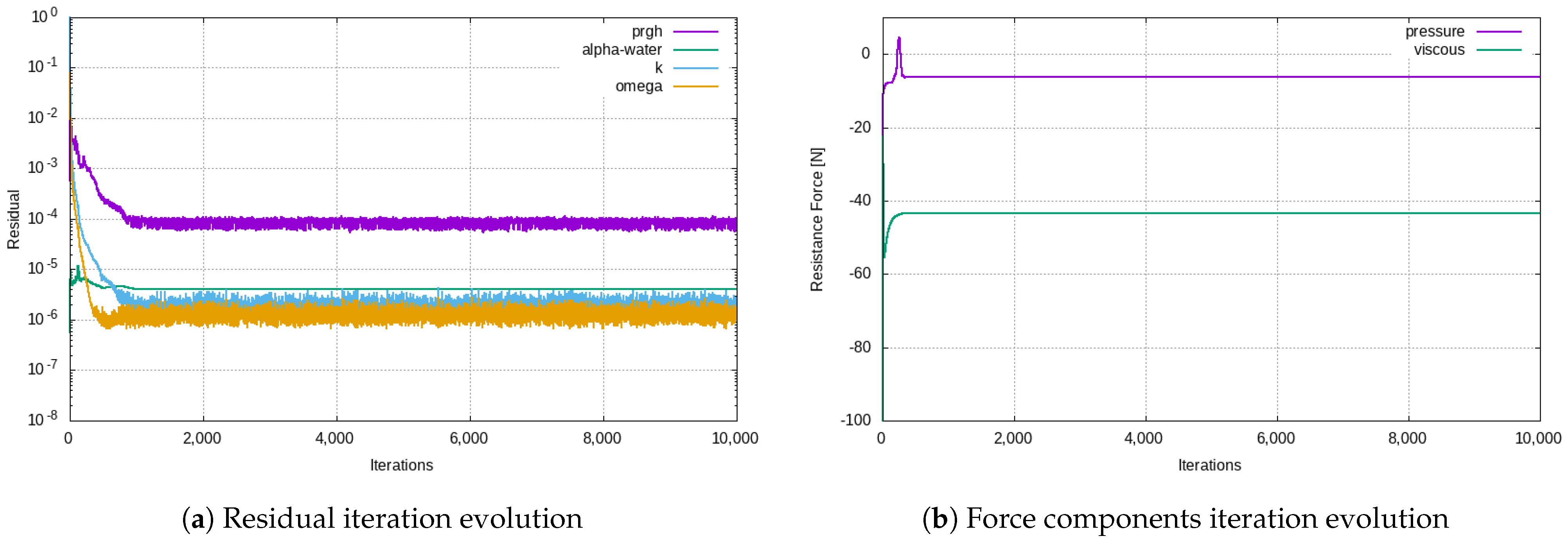
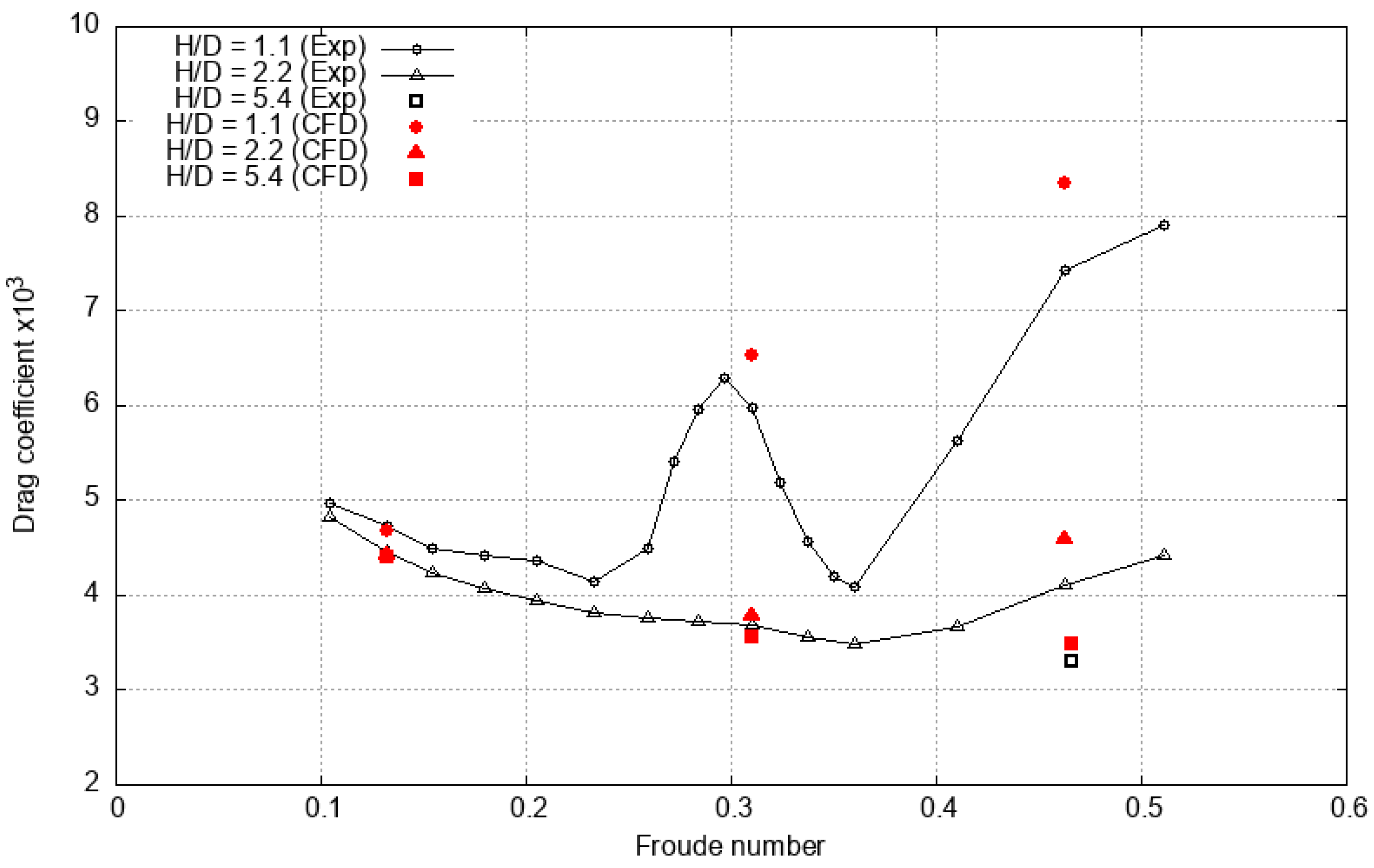
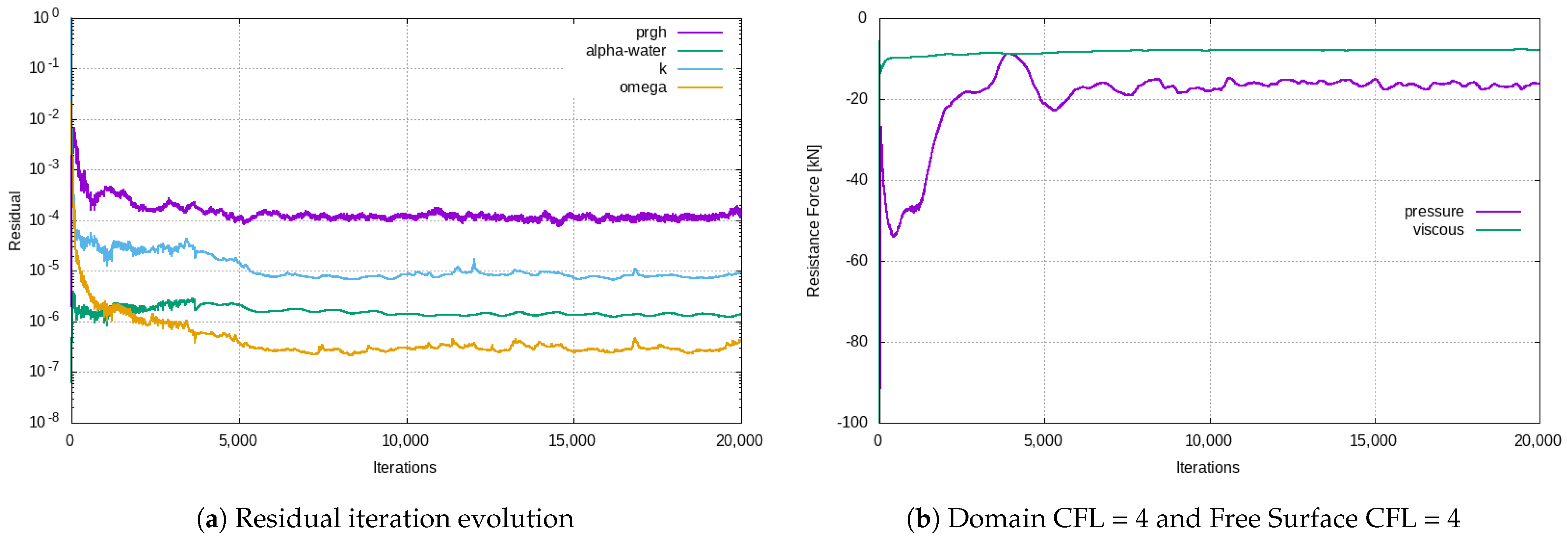
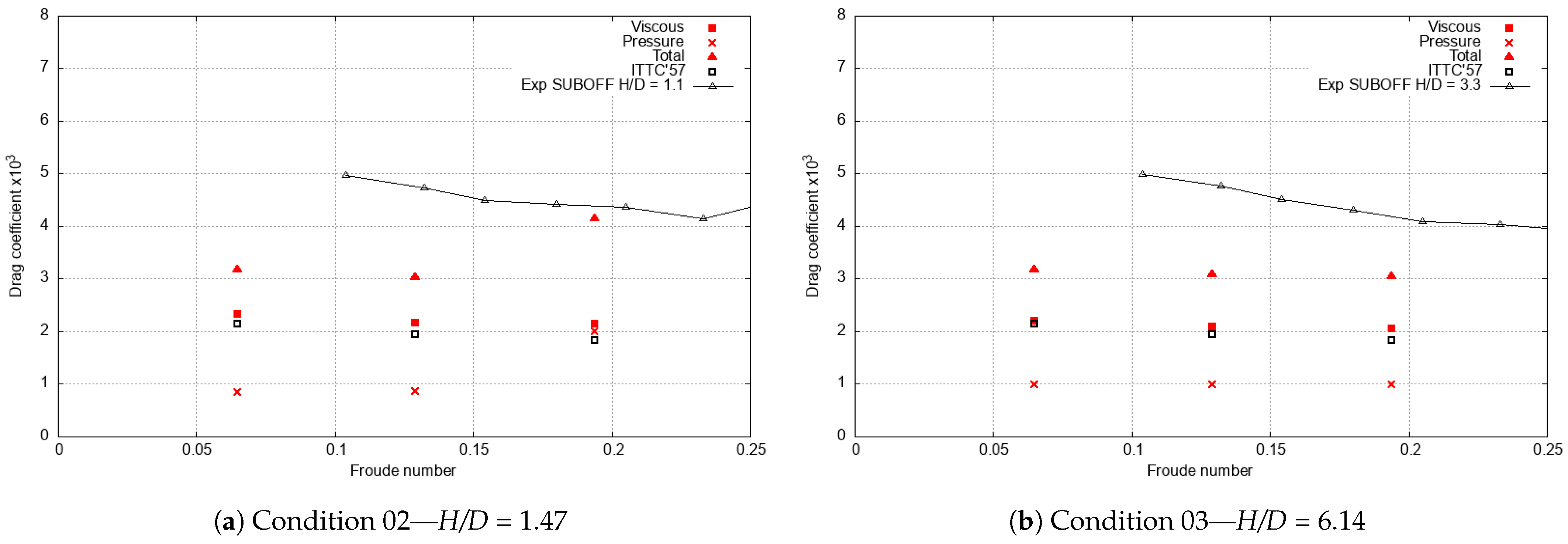
3.1. Verification and Validation
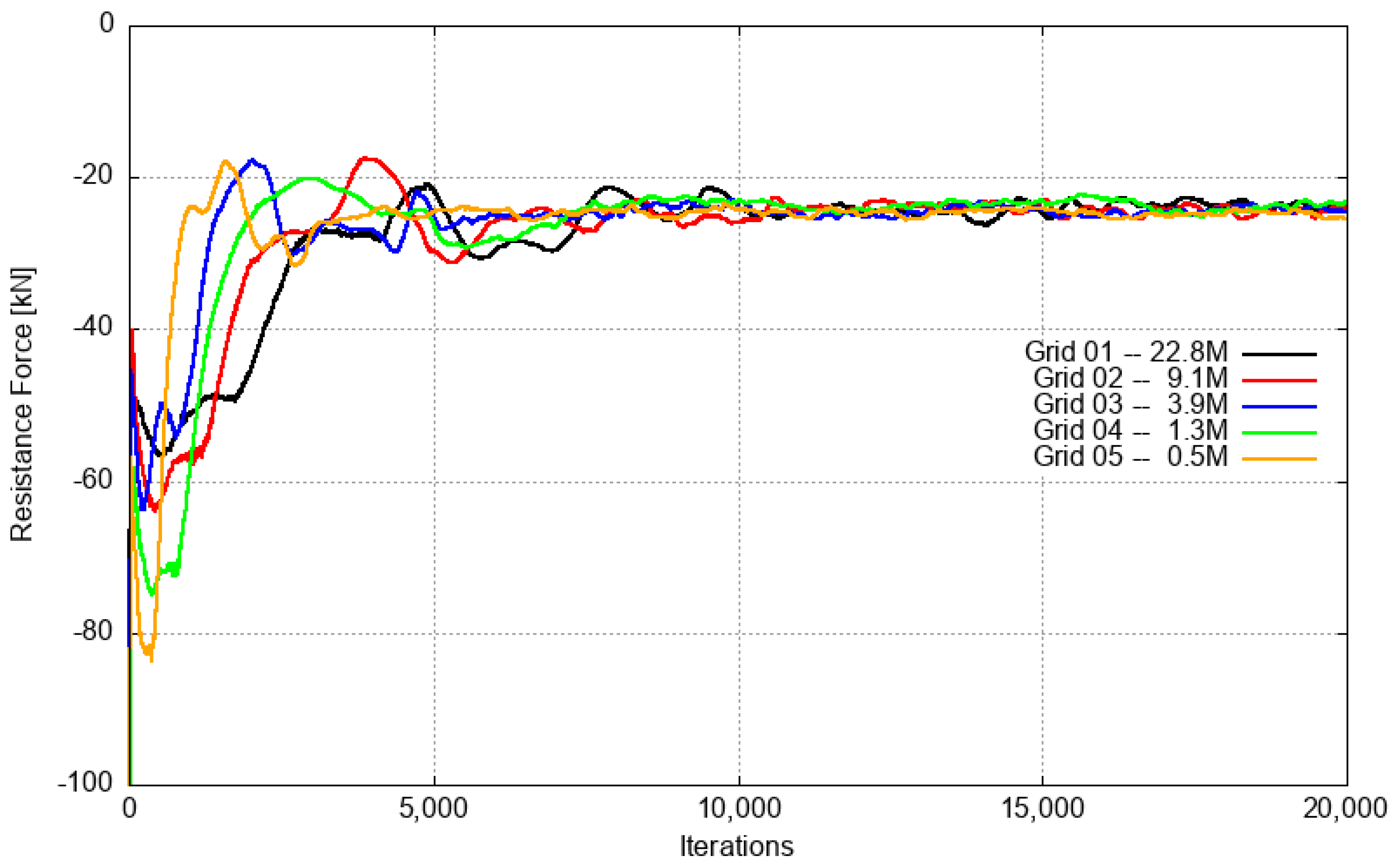
3.2. Grid Convergence for Type 209 at Full-Scale
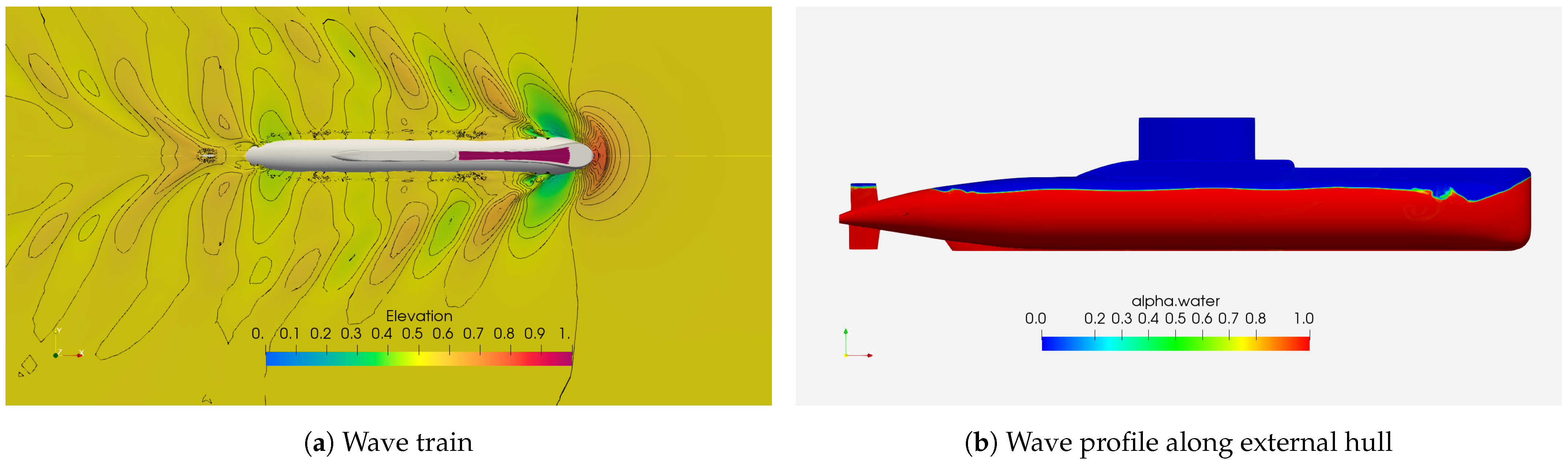
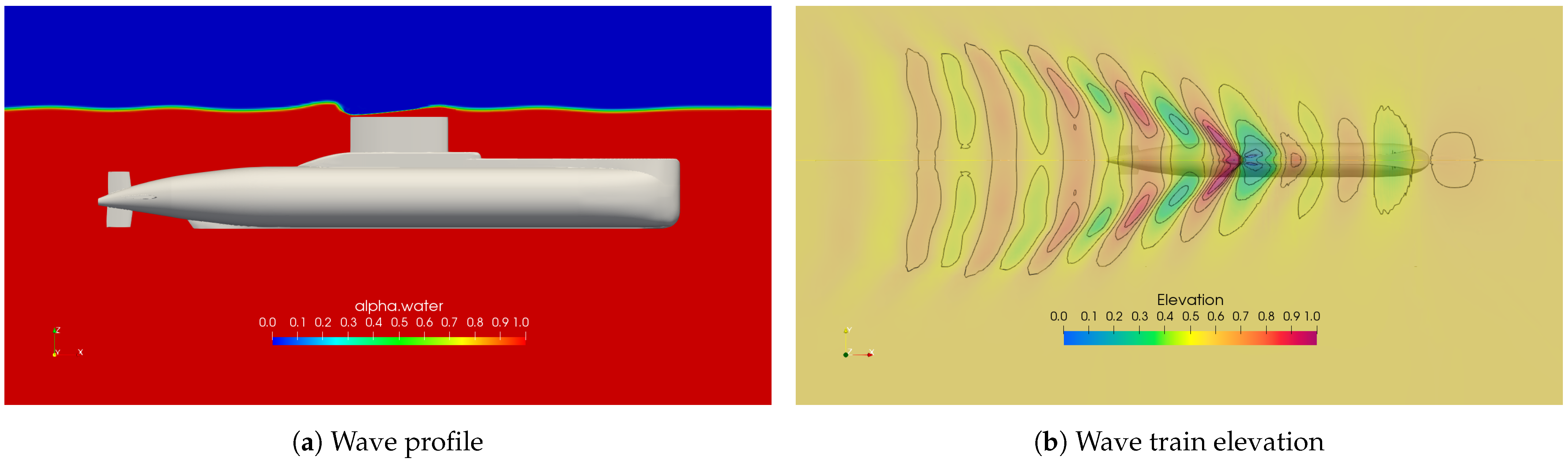
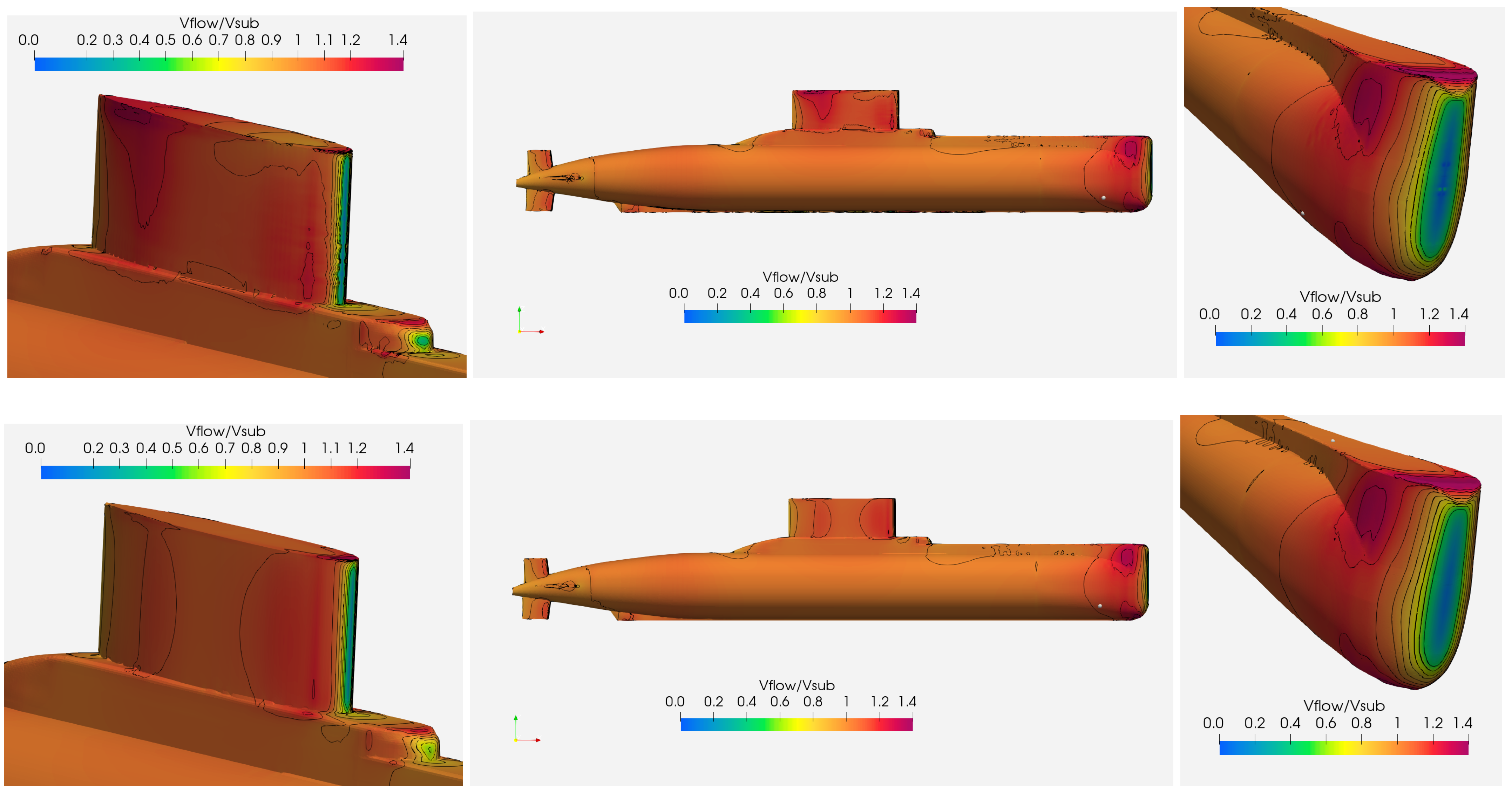
3.3. Flow Characterization at Condition 01: Surface Depth—H/D = 0.33
3.4. Free-Surface Depth Influence on Flow Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AUV | Autonomous Underwater Vehicle |
| CFD | Computational Fluid Dynamics |
| CSSRC | China Ship Scientific Research Centre |
| DARPA | Defense Advanced Research Projects Agency |
| DDES | Delayed Detached Eddy Simulation |
| DES | Detached eddy simulation |
| HDW | Howaldtswerke-Deutsche Werft |
| IHSSS | Iranian Hydrodynamic Series of Submarines |
| ITTC | International Towing Tank Conference |
| MRF | Moving Reference Frame |
| RANSE | Reynolds-averaged Navier–Stokes equations |
| VOF | Volume of Fluid |
References
- ITTC. Uncertainty Analysis in CFD Verification and Validation Methodology and Procedures. In ITTC—Recommended Procedures and Guidelines; 28th ITTC Executive Committee: Wuxi, China, 2017; Chapter 7.5-03-01-01. [Google Scholar]
- Stern, F.; Wilson, R.; Shao, J. Quantitative V&V of CFD simulations and certification of CFD codes. Int. J. Numer. Meth. Fluids 2006, 50, 1335–1355. [Google Scholar] [CrossRef]
- Liu, H.L.; Huang, T.T. Summary of DARPA SUBOFF Experimental Program Data; Technical Report CRDKNSWC/HD-1298-11; Naval Surface Warfare Center, Carderock Division (NSWCCD): West Bethesda, MD, USA, 1998. [Google Scholar]
- Huang, T.T.; Liu, H.L.; Groves, N.C. Experiments of the DARPA SUBOFF Program; Technical Report DTRC/SHD-1298-02; Davidson Taylor Research Center: Bethesda, MD, USA, 1989. [Google Scholar]
- Gross, A.; Kremheller, A.; Fasel, H. Simulation of Flow over SUBOFF Bare Hull Model. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2011. [Google Scholar] [CrossRef]
- Lungu, A. DES-based computation of the flow around the DARPA suboff. IOP Conf. Ser. Mater. Sci. Eng. 2019, 591, 12053. [Google Scholar] [CrossRef]
- Vasileva, A.; Kyulevcheliev, S. Numerical Investigation of the Free Surface Effects on underwater vehicle resistance. In Proceedings of the Fourteenth International Conference on Marine Sciences and Technologies, Varna, Bulgaria, 10–12 October 2018; Black Sea: Varna, Bulgaria, 2018; pp. 100–104. [Google Scholar]
- Gourlay, T.; Dawson, E. A Havelock source panel method for Near-surface Submarines. J. Mar. Sci. Appl. 2015, 14, 215–224. [Google Scholar] [CrossRef]
- Di Felice, F.; Felli, M.; Liefvendahl, M.; Svennberg, U. Numerical and experimental analysis of the wake behavior of a generic submarine propeller. In Proceedings of the First Internationnal Symposium on Marine Propulsors, Trondheim, Norway, 22–24 June 2009; p. 7. [Google Scholar]
- Takahashi, K. Numerical Simulations of Comprehensive Hydrodynamics Performance of DARPA SUBOFF Submarine. Master’s Thesis, Florida Institute of Technology, Melbourne, FL, USA, 2019. [Google Scholar]
- Liefvendahl, M.; Troëng, C. Computation of Cycle-to-Cycle Variation in Blade Load for a Submarine Propeller, using LES. In Proceedings of the Second International Symposium on Marine Propulsors, Hamburg, Germany, 15–17 June 2011; p. 7. [Google Scholar]
- Chase, N. Simulations of the DARPA Suboff Submarine Including Self-Propulsion with the E1619 Propeller. Master’s Thesis, University of Iowa, Iowa City, IA, USA, 2012. [Google Scholar] [CrossRef]
- Dogrul, A.; Sezen, S.; Delen, C.; Bal, S. Self-propulsion simulation of DARPA suboff. In Proceedings of the 17th International Congress of the International Maritime Association of the Mediterranean (IMAM 2017), Lisbon, Portugal, 9–11 October 2017; Maritime Transportation and Harvesting of Sea Resources, Tecnico Lisboa: Lisbon, Portugal, 2017; Volume 1, pp. 503–511. [Google Scholar]
- Delen, C.; Sezen, S.; Bal, S. Computational Investigation of Self Propulsion Performance of Darpa Suboff Vehicle. Tamap J. Eng. 2017, 2017, 4. [Google Scholar]
- Moonesun, M.; Javadi, M.; Charmdooz, P.; Mikhailovich, K. Evaluation of submarine model test in towing tank and comparison with CFD and experimental formulas for fully submerged resistance. Indian J. Mar. Sci. 2013, 42, 1049–1056. [Google Scholar]
- Sezen, S.; Dogrul, A.; Delen, C.; Bal, S. Investigation of self-propulsion of DARPA Suboff by RANS method. Ocean. Eng. 2018, 150, 258–271. [Google Scholar] [CrossRef]
- Duman, S.; Bal, S. Propeller effects on maneuvering of a submerged body. In Proceedings of the 3rd International Meeting—Progress in Propeller Cavitation and its Consequences: Experimental and Computational Methods for Predictions, Istanbul, Turkey, 15–16 November 2018. [Google Scholar]
- Chase, N.; Thad, M.; Carrica, P.M. Overset simulation of a submarine and propeller in towed, self-propelled and maneuvering conditions. Int. Shipbuild. Prog. 2013, 60, 171–205. [Google Scholar] [CrossRef]
- Chase, N.; Carrica, P.M. Submarine propeller computations and application to self-propulsion of DARPA Suboff. Ocean Eng. 2013, 60, 68–80. [Google Scholar] [CrossRef]
- Nematollahi, A.; Dadvand, A.; Dawoodian, M. An axisymmetric underwater vehicle-free surface interaction: A numerical study. Ocean Eng. 2015, 96, 205–214. [Google Scholar] [CrossRef]
- Moonesun, M.; Mikhailovich, Y. Minimum immersion depth for eliminating free surface effect on submerged submarine resistance. Turk. J. Eng. Sci. Technol. 2015, 1, 36–46. [Google Scholar]
- Moonesun, M.; Ghasemzadeh, F.; Korneliuk, O.; Korol, Y.; Valeri, N.; Yastreba, A.; Ursalov, A. Effective depth of regular wave on submerged submarine. Indian J. Geomar. Sci. 2019, 48, 1476–1484. [Google Scholar] [CrossRef]
- Moonesun, M.; Mahdian, A.; Korneliuk, O.; Korol, Y.; Bandarinko, A.; Valeri, N. Evaluation of submarine motions under irregular ocean waves by panel method. Indian J. Geomar. Sci. 2019, 48, 1485–1495. [Google Scholar]
- Zhang, N.; Zhang, S.L. Numerical simulation of hull/propeller interaction of submarine in submergence and near surface conditions. J. Hydrodyn. 2014, 26, 50–56. [Google Scholar] [CrossRef]
- Vali, A.; Saranjam, B.; Kamali, R. Experimental and numerical study of a submarine and propeller behaviors in submergence and surface conditions. J. Appl. Fluid Mech. 2018, 11, 1297–1308. [Google Scholar] [CrossRef]
- Carrica, P.M.; Kim, Y.; Martin, J.E. Near-surface self propulsion of a generic submarine in calm water and waves. Ocean Eng. 2019, 183, 87–105. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Zhang, T.; Pang, Y.; Chen, Q. Numerical simulation study on the effects of course keeping on the roll stability of submarine emergency rising. Appl. Sci. 2019, 9, 3285. [Google Scholar] [CrossRef]
- Moonesun, M.; Mikhailovich, K.Y.; Tahvildarzade, D.; Javadi, M. Practical scaling method for underwater hydrodynamic model test of submarine. J. Korean Soc. Mar. Eng. 2014, 38, 1217–1224. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yoon, H.K.; Park, Y.; Park, C. Estimation of Hydrodynamic Derivatives of Full-Scale Submarine using RANS Solver. J. Ocean. Eng. Technol. 2018, 32, 386–392. [Google Scholar] [CrossRef]
- The OpenFOAM Foundation. OpenFOAM v7 User Guide; The OpenFOAM Foundation: London, UK, 2019; p. 237. [Google Scholar]
- Groves, N.C.; Huang, T.T.; Chang, M.S. Geometric Characteristics of DARPA SUBOFF Models (DTRC MODEL Nos. 5470 and 5471); Technical Report DTRC/SHD-1298-01; David Taylor Research Center: Bethesda, MD, USA, 1989.
- Liu, Z.H.; Xiong, Y.; Wang, Z.Z.; Wang, S.; Tu, C.X. Numerical simulation and experimental study of the new method of horseshoe vortex control. J. Hydrodyn. 2010, 22, 572–581. [Google Scholar] [CrossRef]
- Jasak, H.; Vukčević, V.; Gatin, I.; Lalović, I. CFD validation and grid sensitivity studies of full scale ship self propulsion. Int. J. Nav. Archit. Ocean. Eng. 2019, 11, 33–43. [Google Scholar] [CrossRef]
- ITTC. Practical Guidelines for Ship CFD Applications. In ITTC—Recommended Procedures and Guidelines; 26th ITTC Executive Committee: Rio de Janeiro, Brazil, 2011; Chapter 7.5-03-02-03. [Google Scholar]
- Neulist, D. Experimental Investigation into the Hydrodynamic Characteristics of a Submarine Operating Near the Free Surface; Technical Report; Australian Maritime College: Launceston, Australia, 2011. [Google Scholar]
- Islam, H.; Guedes Soares, C. Uncertainty analysis in ship resistance prediction using OpenFOAM. Ocean Eng. 2019, 191, 1–16. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 0780011–0780014. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Dubief, Y.; Delcayre, F. On coherent-vortex identification in turbulence. J. Turbul. 2000, 1, 37–41. [Google Scholar] [CrossRef]


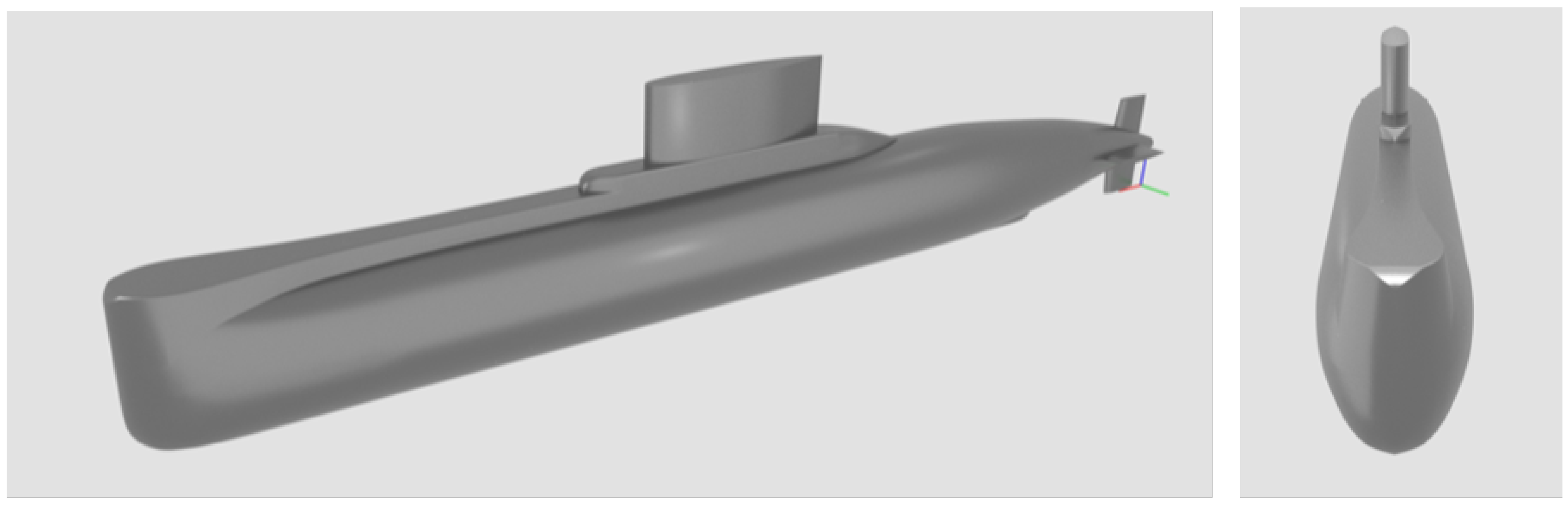



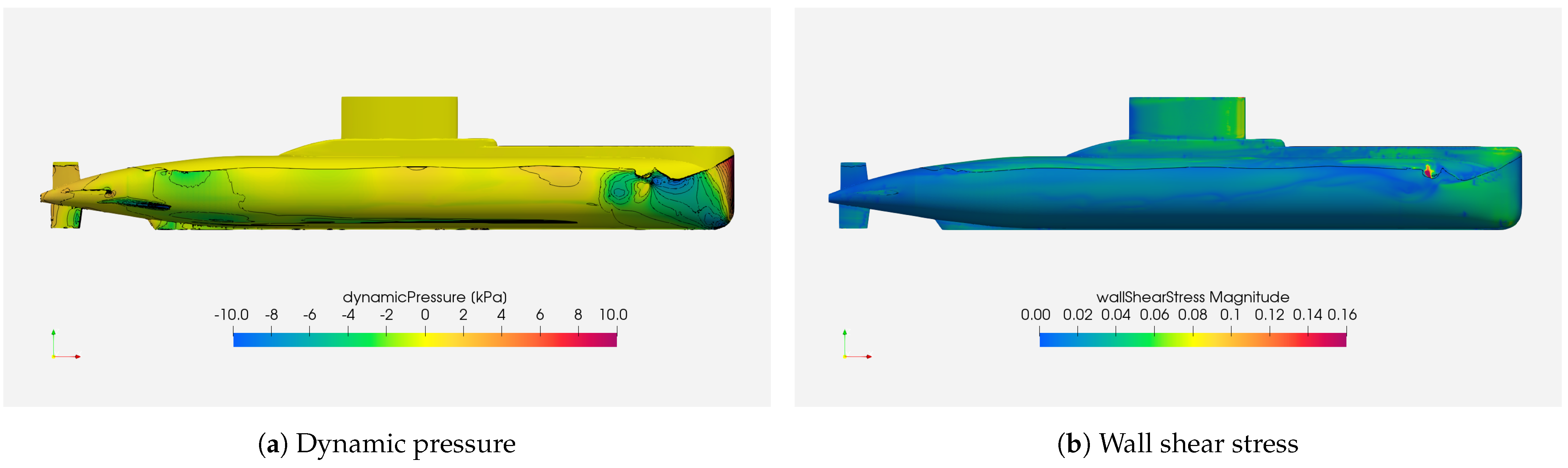

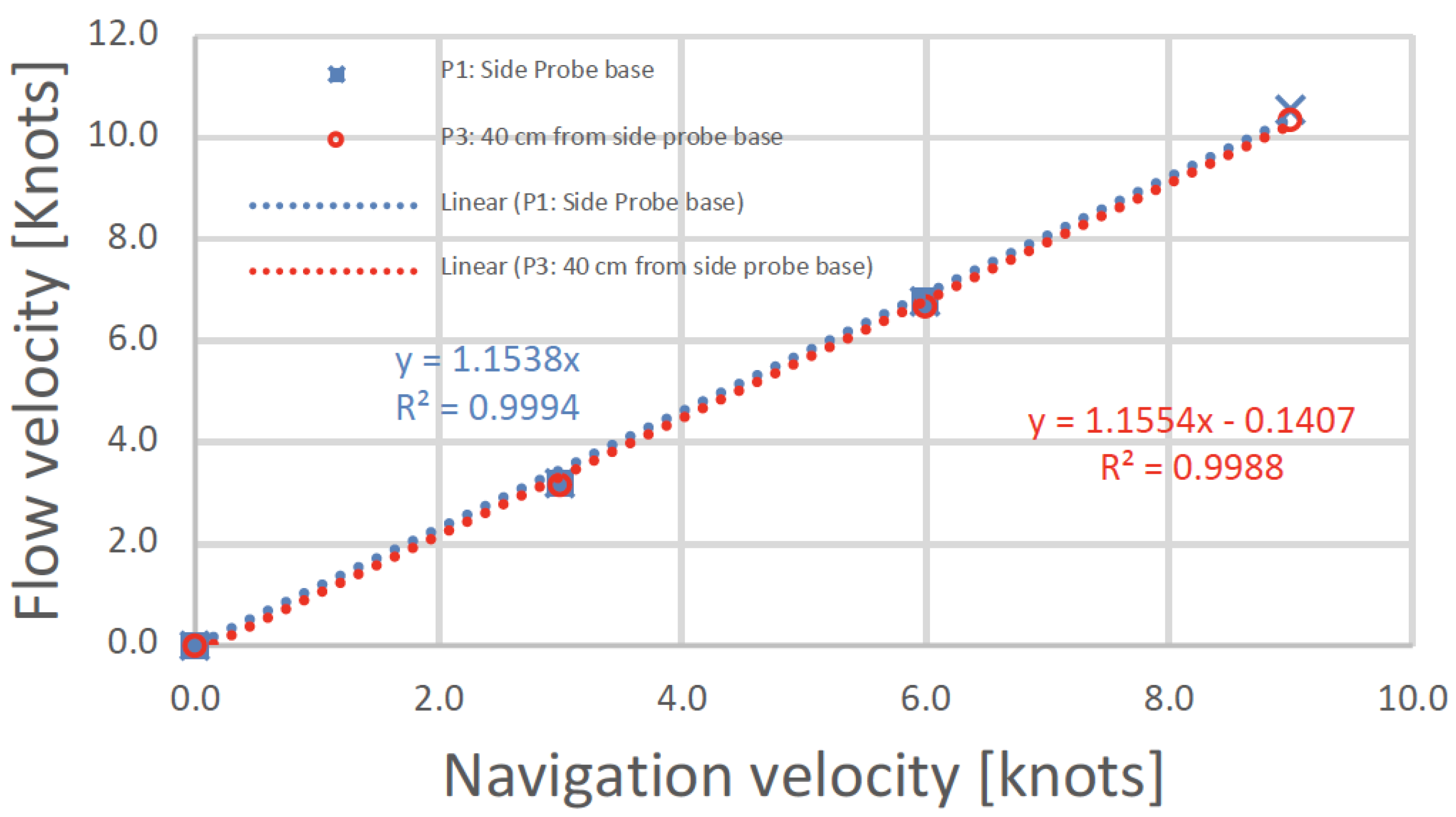
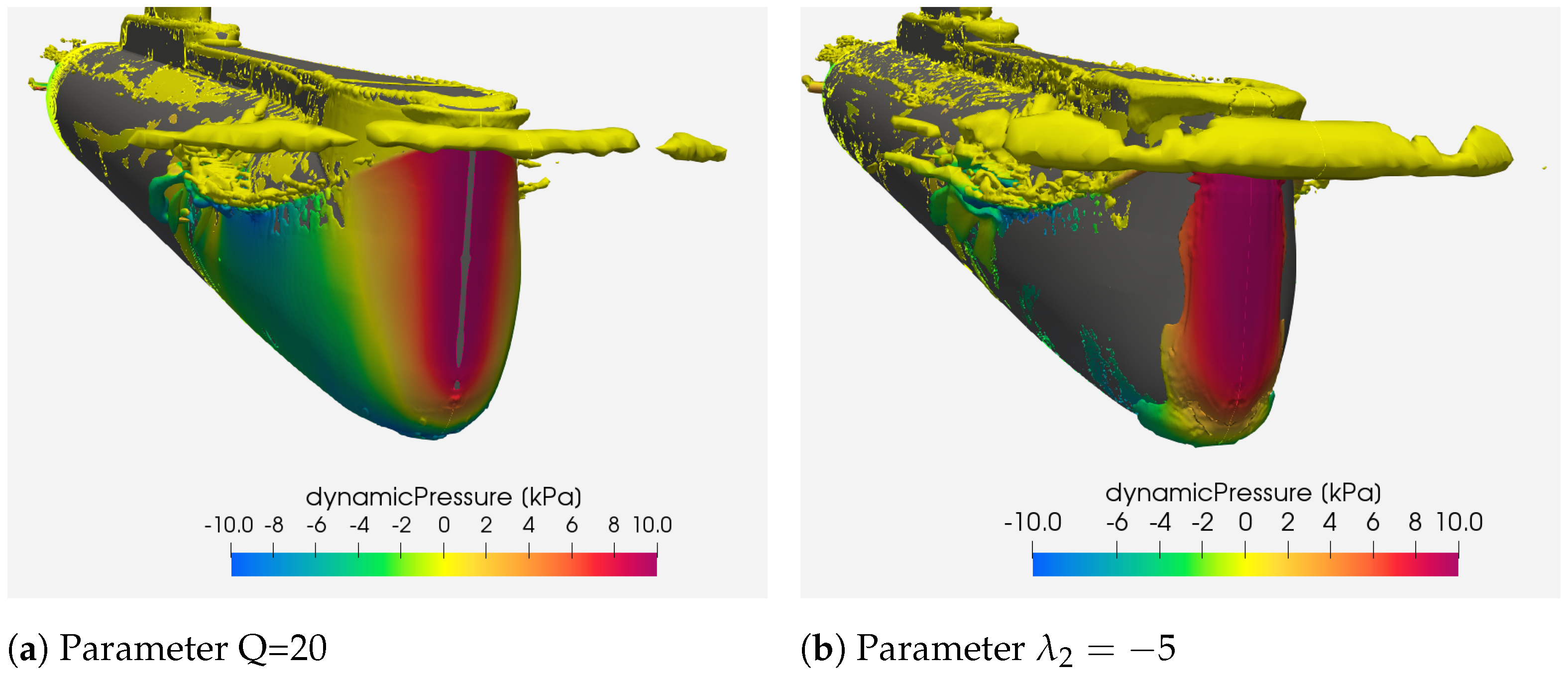
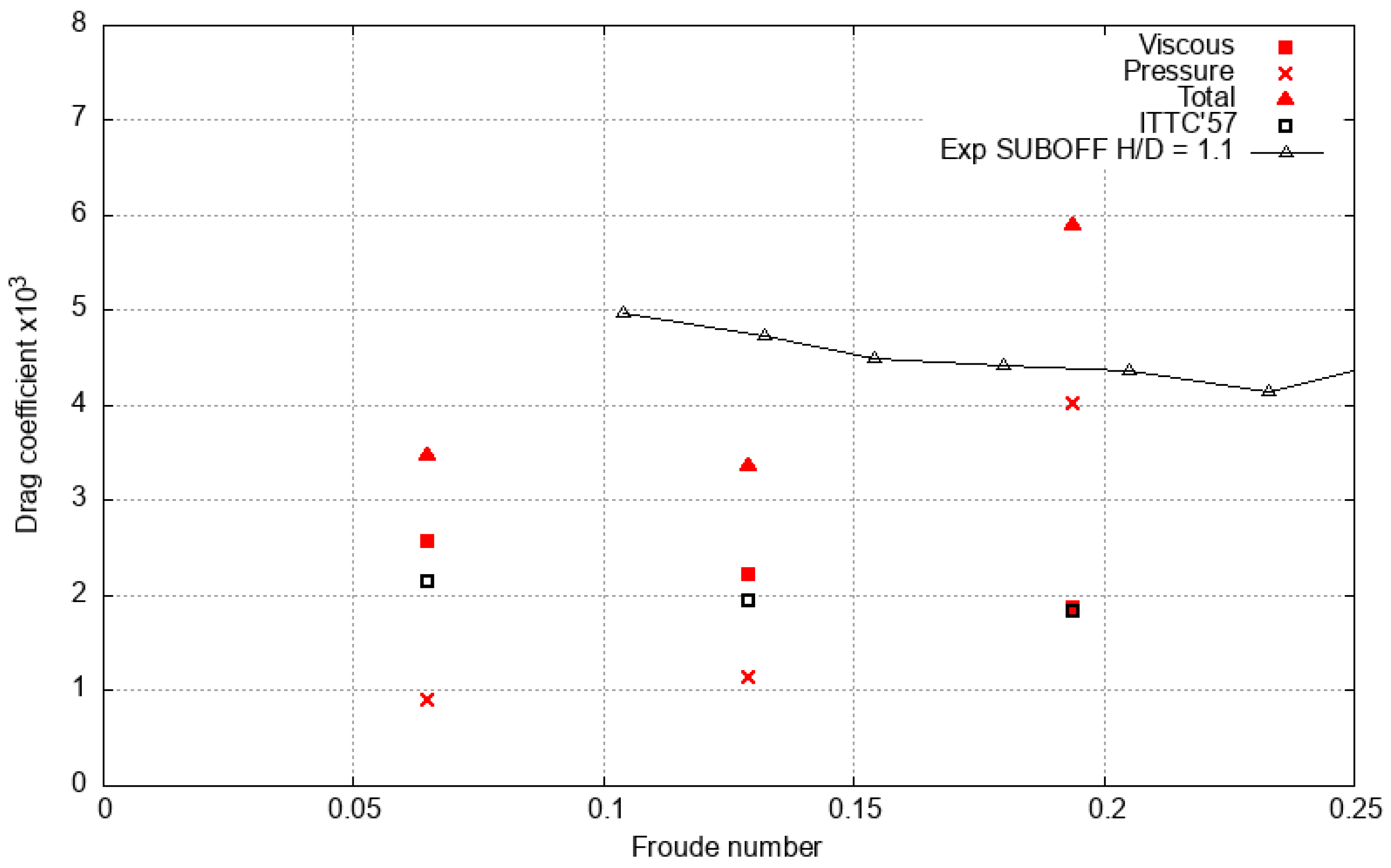

| Parameter | Symbol | SUB-OFF Model Scale | SUB-OFF Equivalent Prototype Scale | Type 209/1300 |
|---|---|---|---|---|
| Length between perpendiculars [m] | L | 4.356 | 58.167 | 58.167 |
| Length-Diameter ratio | 8.575 | 8.575 | 9.950 | |
| Draft-Diameter ratio | 0.863 | 0.863 | 0.863 | |
| Length percentage of fore body | 0.233 | 0.233 | 0.189 | |
| Length percentage of parallel middle body | 0.512 | 0.512 | 0.496 | |
| Length percentage of aft body | 0.255 | 0.255 | 0.314 | |
| Relative sail location | 0.21 | 0.21 | 0.40 | |
| Wetted area of hull at surface [m2] | 4.760 | 848.759 | 775.220 | |
| Wetted area of hull + sail [m2] | 6.160 | 1098.394 | 1182.420 | |
| Wetted surface area of sail [m2] | 0.184 | 32.855 | 83.258 | |
| Displacement at surface condition [tons] | 0.650 | 1547.675 | 1309.950 | |
| Displacement submerged hull + sail [tons] | 0.703 | 1674.560 | 1578.00 |
| Control Point | X (m) | Y (m) | Z (m) |
|---|---|---|---|
| P1 | 53.82 | −2.34 | 1.34 |
| P2 | 50.64 | −0.53 | 7.02 |
| P3 | 53.82 | −2.68 | 1.14 |
| P4 | 50.64 | −0.53 | 7.41 |
| Label | Name | U | |
|---|---|---|---|
| a | Inlet | fixedValue | fixedFluxPressure |
| b | Side | symmetryPlane | symmetryPlane |
| c | Atmosphere | pressureInletOutletVelocity | totalPressure |
| d | bottom | fixedValue | fixedFluxPressure |
| e | outlet | outletPhaseMeanVelocity | zeroGradient |
| f | midPlane | symmetryPlane | symmetryPlane |
| g | hull | movingWallVelocity | fixedFluxPressure |
| # | Grid Type | DARPA SUBOFF | Type 209/1300 |
|---|---|---|---|
| 1 | Finer | 11,986,756 | 22,832,329 |
| 2 | Fine | 4,500,437 | 9,145,512 |
| 3 | Medium | 1,576,885 | 3,892,550 |
| 4 | Coarse | 600,071 | 1,348,794 |
| 5 | Coarser | 215,582 | 514,008 |
| H/D | Fr | Source | |
|---|---|---|---|
| 0.132 | 4.730 | ||
| 1.1 | 0.310 | 5.980 | Neulist [35] |
| 0.463 | 7.440 | ||
| 0.132 | 4.460 | ||
| 2.2 | 0.310 | 3.690 | Neulist [35] |
| 0.463 | 4.110 | ||
| 5.4 | 0.466 | 3.310 | Liu and Huang [3] |
| Simulation | Navigation Condition | Velocity [Knots] | Coarse Grid | Intermediate Grid | Fine Grid |
|---|---|---|---|---|---|
| 1–3 | 9.0 | X | X | X | |
| 4 | C1: Surface depth | 6.0 | X | ||
| 5 | 3.0 | X | |||
| 6 | 9.0 | X | |||
| 7–9 | C2: Periscope depth | 6.0 | X | X | X |
| 10 | 3.0 | X | |||
| 11 | 9.0 | X | |||
| 12–14 | C3: Deep-water | 6.0 | X | X | X |
| 15 | 3.0 | X |
| Grid Density | Number of Cells | Pressure | Viscous | Total | % SD | Exp Value | % Error | Avg. |
|---|---|---|---|---|---|---|---|---|
| Coarser | 215,582 | 30.840 | 82.840 | 113.685 | 0.004 | 20.6% | 103.24 | |
| Coarse | 600,071 | 21.643 | 86.270 | 107.913 | 0.009 | 14.4% | 58.29 | |
| Medium | 1,576,885 | 17.631 | 86.271 | 103.902 | 0.798 | 94.29 | 10.2% | 43.39 |
| Fine | 4,500,437 | 12.508 | 86.954 | 99.461 | 0.002 | 5.5% | 23.06 | |
| Finer | 11,986,756 | 10.884 | 87.813 | 98.696 | 0.097 | 4.7% | 16.48 |
| Grid | Coarser—G5 | Coarse—G4 | Medium—G3 | Fine—G2 | Fine—G1 | Richardson Extrapolation | Exp Value—S |
|---|---|---|---|---|---|---|---|
| 3.985 | 3.783 | 3.642 | 3.486 | 3.460 | 3.433 | 3.305 | |
| 5.1% | 3.7% | 4.3% | 0.8% | ||||
| 0.202 | 0.141 | 0.156 | 0.027 |
| Analysis Set | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1–3 | 0.172 | 0.2% | 4.98 | 4.842 | 1.4% | 0.8% | 0.6% | 3.433 |
| 2–4 | 1.107 | |||||||
| 3–5 | 0.695 | 14.3% | 0.90 | 0.433 | 8.9% | 4.0% | 2.7% | 3.501 |
| Grid Density | Number of Cells | Pressure (N) | Viscous (N) | Total (N) | SD (N) |
|---|---|---|---|---|---|
| Coarser | 524,008 | 17,560.51 | 7390.06 | 24,950.57 | 446.85 |
| Coarse | 1,348,794 | 15,602.31 | 7927.64 | 23,529.95 | 336.51 |
| Medium | 3,892,550 | 16,467.29 | 7807.49 | 24,274.78 | 292.47 |
| Fine | 9,145,512 | 16,640.02 | 7768.89 | 24,408.91 | 450.07 |
| Finer | 22,832,329 | 15,709.69 | 8113.64 | 23,823.22 | 459.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paredes, R.J.; Quintuña, M.T.; Arias-Hidalgo, M.; Datla, R. Numerical Flow Characterization around a Type 209 Submarine Using OpenFOAM. Fluids 2021, 6, 66. https://doi.org/10.3390/fluids6020066
Paredes RJ, Quintuña MT, Arias-Hidalgo M, Datla R. Numerical Flow Characterization around a Type 209 Submarine Using OpenFOAM. Fluids. 2021; 6(2):66. https://doi.org/10.3390/fluids6020066
Chicago/Turabian StyleParedes, Ruben J., Maria T. Quintuña, Mijail Arias-Hidalgo, and Raju Datla. 2021. "Numerical Flow Characterization around a Type 209 Submarine Using OpenFOAM" Fluids 6, no. 2: 66. https://doi.org/10.3390/fluids6020066
APA StyleParedes, R. J., Quintuña, M. T., Arias-Hidalgo, M., & Datla, R. (2021). Numerical Flow Characterization around a Type 209 Submarine Using OpenFOAM. Fluids, 6(2), 66. https://doi.org/10.3390/fluids6020066







