Influence of Particle Mass Fraction over the Turbulent Behaviour of an Incompressible Particle-Laden Flow

Abstract

The presence of spherical solid particles immersed in an incompressible turbulent flow was numerically investigated from the perspective of the particle mass fraction (PMF or ${\varphi }_m$), a measure of the particle-to-fluid mass ratio. Although a number of different changes have been reported to be obtained by the presence of solid particles in incompressible turbulent flows, the present study reports the findings of varying ${\varphi }_m$ in the the turbulent behaviour of the flow, including aspects such as: turbulent statistics, skin-friction coefficient, and the general dynamics of a particle-laden flow. For this purpose, a particle-laden turbulent channel flow transporting solid particles at three different friction Reynolds numbers, namely $R{e}_{\tau }=180$, 365, and 950, with a fixed particle volume fraction of ${\varphi }_v={10}^{-3}$, was employed as conceptual flow model and simulated using large eddy simulations. The value adopted for ${\varphi }_v$ allowed the use of a two-way coupling approach between the particles and the flow or carrier phase. Three different values of ${\varphi }_m$ were explored in this work ${\varphi }_m\approx 1,2.96$, and $12.4$. Assessment of the effect of ${\varphi }_m$ was performed by examining changes of mean velocity profiles, velocity fluctuation profiles, and a number of other relevant turbulence statistics. Our results show that attenuation of turbulence activity of the carrier phase is attained, and that such attenuation increases with ${\varphi }_m$ at fixed Reynolds numbers and ${\varphi }_v$. For the smallest Reynolds number case considered, flows carrying particles with higher ${\varphi }_m$ exhibited lower energy requirements to sustain constant fluid mass flow rate conditions. By examining the flow velocity field, as well as instantaneous velocity components contours, it is shown that the attenuation acts even on the largest scales of the flow dynamics, and not only at the smaller levels. These findings reinforce the concept of a selective stabilising effect induced by the solid particles, particularly enhanced by high values of ${\varphi }_m$, which could eventually be exploited for improvement of energetic efficiency of piping or equivalent particles transport systems.

1. Introduction

Designing reliable and efficient fluid transport systems requires thoughtful consideration of energy requirements and power availability to move a fluid under given conditions of mass flow rate, pressure gradient, and friction losses. This argument is even more stringent when the system must transport multiphase flow, for instance solid particles suspended in a fluid stream. In practice, the energy requirements to overcome head losses must be properly supplied by pumping devices, i.e., pumps or compressors. These devices, in conjunction with the piping transport system, should be designed to meet the specific fluid transport requirements, but should also aim to have an efficient energy consumption or performance. As a matter of fact, one of the key parameters used in the design and analysis of piping systems for fluid transport is typically the friction or head loss. Therefore, it is up to the designer to consider producing and ensuring operating conditions such that the energy requirements or energy losses can be reduced as much as possible. Accordingly, it has become common to constantly pursue strategies aiming to improve the efficiency of fluid transport systems. To achieve this goal, a wide range of flow control techniques have been proposed and implemented in recent years as presented in Gad-el Hak [1], García-Mayoral and Jiménez [2], and Quadrio [3]. Some strategies have been focused on modifying the geometry of the walls bounding the flow, for instance through the prescription of the so-called riblets (see García-Mayoral and Jiménez [2]). Such elements generate a modification of the boundary layer behavior, usually by delaying its detachment location, which in turn generates lower shear stresses in the wall, decreasing the skin friction drag consequently. This flow control technique was studied experimentally by Choi [4] and numerically in Choi et al. [5]. Now considered as one of the seminal works performed in the field of passive flow control, Choi et al. [5] used direct numerical simulations to study in depth the mechanisms of drag reduction in turbulent flows induced by riblet-mounted surfaces, already observed and reported in the experiments of Choi [4]. In Choi et al. [5] mean-velocity profile shifting is observed to be directly related to drag modulation in the log-law region, although main differences were found only in the region bounded by the inner portion of the turbulent boundary layer. By examining turbulence statistics, they proposed a drag reduction mechanism induced by the presence of riblets in which the small scale spacings between riblets were able to reduce viscous drag by restricting dynamical interaction between streamwise vortices and high-speed fluid streaks induced by the vortices. Some other strategies have been focused on directly altering the turbulent boundary layer, therefore changing the flow dynamics in the near-wall region. One of these techniques which was recently proposed and widely studied is the imposition of controlled oscillatory motions to the bounding wall of a flow, as discussed by Quadrio et al. [6], Quadrio [3], Duque-Daza et al. [7], and Ricco and Hicks [8]. This flow control technique has shown to induce drag reduction in turbulent flows as a consequence of a modulation of the turbulent activity in the near-wall region of the associated bounding layer.

An alternative flow control technique which seems to also produce an important level of drag reduction, particularly in turbulent incompressible flows, is the injection of additives to be transported in the form of suspended particles in the flow, as discussed in Lumley [9], Ptasinski et al. [10], and Gyr and Bewersdorff [11]. In this regard, Ptasinski et al. [10] reported a substantial reduction of drag when small flexible polymers were injected in a turbulent channel flow at a friction Reynolds number of $R{e}_{\tau }=180$. These findings have been corroborated, to some extent, by other studies such as Dubief et al. [12] and Gillissen et al. [13]. Moreover, the ability exhibited by suspended additives injected in turbulent flows to reduce the skin-friction drag has motivated other researchers to explore the possibility of modulating the turbulent dynamics precisely through the injection of solid spherical particles, as presented and discussed by Zhao et al. [14].

However, the effects of the addition of particles on turbulent flow dynamics are complex and not fully known because the amount of involved parameters such as particle diameter, particle Stokes number, volume fraction and mass loading. In the specific case of channel flow, in some regimes, particles promote drag reduction and in others drag enhancement, with a complicated interplay between fluid turbulence attenuation or augmentation and the contribution of particle stresses to overall drag (Costa et al. [15]). In the literature there is a large set of works focused on particle laden turbulent channel flows in general. Some noteworthy efforts are the works on particle dispersion models by Taniere and Arcen [16] and Zhao et al. [17]. The studies on particle transport properties as presented by Sommerfeld and Lain [18], Laín and Sommerfeld [19], and a discussion of the relevant elementary processes driving the interaction between fluid and solid particles in confined environments, are found in Sommerfeld and Lain [20], as are the works on turbulence modulation due solely to the presence of particles as discussed in Gualtieri et al. [21] and Kuerten et al. [22], and the development of models for flows laden with particles of finite size by Kidanemariam et al. [23]. In Zhao et al. [14], the authors report turbulent skin-drag reduction for a fluid travelling through a smooth channel when particles with a particle response time of ${\tau }_p^{+}=30$ were injected. Likewise, Rossetti and Pfeffer [24] reported experimental evidence of drag reductions in both vertical and horizontal channel flows with diluted glass particles in a range of Reynolds numbers ($Re$) from $10.000$ to $25.000$. Li et al. [25] and Yamamoto et al. [26] carried out large eddy simulations (LES) and direct numerical simulations (DNS) of turbulent particle laden flows for vertical channels with gravity included, in order to compare their results with those previously obtained by Kulick et al. [27]. In both studies, it was found that the presence of particles with mass loading of 1 and $0.4$ generated an increase of the mean flow velocity in the main direction. Yamamoto et al. [26] argued that this change in the velocity flow was a direct effect of the presence of gravity in the main direction of the flow. This argument was later questioned by Zhao et al. [14] who, as already mentioned, obtained drag reduction in a similar case using DNS simulations without considering gravitational effects. Analysis of the physics underlying the turbulence modulation by the particle phenomenon has also been explored in Zhao et al. [28] and Lee and Lee [29]. The effect of the particle volume fraction and particle response time on the particle–turbulence interactions was studied and discussed by Zhao et al. [28], who proposed that the modulation could be explained in terms of mechanical energy exchange between the two phases. Lee and Lee [29], employing DNS to explore the effect of the particle volume fraction ${\varphi }_v$, whilst keeping the particle mass fraction ${\varphi }_m$ fixed, determined that turbulence in the near-wall region was affected by the particles in different ways depending on the Stokes number.

Among the recent previous works dealing with turbulence attenuation and particle drag modification, the following studies deserve attention.

Vreman [30] performed two-way coupled DNS simulations of point particles in a downward pipe flow, considering the action of the gravity as well as inter-particle collisions. As the objective was to compare the results with experimental data, there is no attempt to compare the cases with and without gravity. Fluid turbulence attenuation due to the presence of particles is discussed for a wide range of mass loading ratios, concluding that there are at least two mechanisms involved: the classical one, due to the dissipation added by the particles, and a second one present in inhomogeneous flows due to the slip velocity between particles and fluid close to the wall, collisions and consequent influence on fluid variables. Moreover, budgets of Reynolds stresses for both phases are discussed, showing that the particle-fluid interaction in the turbulent kinetic energy equation, for intermediate and large mass fractions, is no longer dissipative but productive. For low mass loadings, particles tend to accumulate in the wall vicinity but for a higher solid loading the particle concentration profile becomes uniform or even shows accumulation in the center of the pipe.

Capecelatro et al. [31] deal with vertical channel flow (R_eτ = 300) laden with point particles. Gravity is included in the simulations, the forces acting on the particles include, besides drag, the fluid pressure and stresses forces but no lift forces. Inter-particle collisions are described by means of a modified soft-sphere approach. The two-way simulations were addressed to study the particles effect on fluid turbulence analyzing the transition between dilute to dense flow regimes. From the obtained results two-phase energy balances are carried out to identify the transition between the mean shear production of turbulent kinetic energy and the so-called “drag production” occurring at high mass loadings. According to the mass loading, three regimes of fluid turbulence generation mechanisms can be distinguished: the classical means shear mechanism is the main one for low mass fractions (lower than 1); for intermediate loadings (up to around 10), a moderate coupling between the phases relaminarizes the flow; finally, for high mass fractions (larger than 10), the work performed by the mean interphase slip velocities is mainly responsible for the fluid kinetic energy generation. These authors remark that fluid flow relaminarization does not imply drag reduction, but better a transition from drag production at the channel walls to the particle surfaces.

Battista et al. [32] carried out DNS simulations of the flow laden with point particles in a pipe flow without considering gravity. Two-way coupling effects are incorporated by means of the so-called Exact Regularized Point Particle (ERPP) method which was extended to deal with the interphase momentum coupling between both phases close to the wall. In this study, nor inter-particle collisions or lift forces are included. The authors study the influence of particle Stokes number, particle to fluid density ratio and mass loading on the two-way coupling effects for a fixed friction Reynolds number of 180. As a result, they found that, in all the simulated cases, either particles do not alter or increase the drag regarding the uncoupled configuration. This fact is attributed to the extra stress produced by the particles that increases the momentum flux towards the wall eventually augmenting the viscous stresses and the drag.

Wang et al. [33] compare the results of two point-particle DNS simulations, performed with independent codes, with the experimental results of Fong et al. [34] in the configuration of vertical channel flow. The authors claimed that the study was one of the first “to perform one-to-one comparisons of particle-laden flow statistics between numerical models and experiments”. In fact, one of the employed codes was that of Capecelatro et al. [31] while the other was based on Richter and Sullivan [35]; inter-particle collisions were taken into account in both codes but neither of them included lift forces in the particle equation of motion. Computations are performed for two values of particle volume fraction within the very dilute to dilute regimes, where two-way coupling starts to be relevant. For the low volume loading, both codes agreed fairly well with the experiments in all available variables, with the exception that the numerical codes predict near the wall more particles than the experiments; this fact is attributed to the lack of an explicit lift force acting on the particles. For the higher mass loading, experiments suggested a strong turbulence modification which was not observed in the computations. Owing to the uncertainties associated with experimental measurements and the limitations of point particle DNS, the authors conclude that a one-to-one comparison between simulations and experiments is still a challenge and that further research is needed to develop reliable predictive models for turbulent flows laden with particles.

Zhou et al. [36] analyze the effect of mass loading on turbulence modulation in channel flows also employing a two-way coupling approach as in the present work. Computations were performed using direct numerical simulations for turbulent channel flows at $R{e}_{\tau }=180$, with the particle mass loading ranging from 0 to 0.96, but keeping a fixed Stokes number $St=30$. They report an attenuation of the velocity fluctuations in the spanwise and wall-normal directions. Their results also show an attenuation of the Reynolds shear stress with mass loading. They found that the near-wall vortices became weaker and the spacing between streaks became wider as the ${\varphi }_m$ increased. They argue that this effect seems to produce a damping effect on the fluctuations of the streamwise velocity. They analyzed the TKE and the Reynolds stresses budget and found that all the budget terms of the transport equations were also attenuated by the particles.

Costa et al. [15,37] made a step forward carrying out particle resolved simulations, using the Immersed Boundary Method (IBM), of channel flow including inter-particle interactions. In these computations, two-way coupling effects are naturally included as the motion of particles is driven by the forces and torques exchanged with the fluid. As a result of such simulations, the role of the shear lift force and inter-particle collisions on particle dynamics and interaction with the fluid is highlighted. In particular, the lift force (Saffman mechanism) is responsible for the resuspension of particles close to the wall causing a reduction of the particle residence time in the low speed streaks; as a result, also the particle slip velocity near the wall is increased, which in turn generates hot spots of high shear stress favoring drag increase. Moreover, in Costa et al. [15], two regimes of turbulence modulation are pointed out: for low mass fractions turbulence variables are hardly modified and the increase of particle concentration near the wall produces an augmentation of overall drag; for higher mass loadings, interphase coupling becomes complex and particles affect turbulent dynamics along the complete flow, attenuating fluid Reynolds Stress but enhancing particle velocity correlations which eventually lead to a moderate increase of the total drag. However, these authors point out that the increasing drag trend could be reverted at even higher mass loadings.

Given the progress observed in recent years in terms of the characterization of turbulent flows laden with particles, and due to the relative reduced level of information regarding drag reduction caused by spherical solid particles, it seems relevant to investigate the relation among particles properties and the possible levels of turbulent skin-drag reduction to be achieved. Therefore, the work discussed in the present paper focuses on the characterization of the effect of the particles mass fraction, herein denoted as PMF or ${\varphi }_m$, over the turbulent behavior of the carrier phase as well as the possibility to achieve turbulent skin-friction drag reduction for incompressible turbulent channel flows laden with spherical solid particles at low Reynolds numbers, similarly to the studies of Zhao et al. [28], Lee and Lee [29], and Zhao et al. [14]. However, in the present study, particular emphasis was placed on values of particle mass fraction presumed to produce observable drag reductions on the carrier phase. To accomplish this goal, large eddy simulations for a turbulent particle laden channel flow with friction Reynolds numbers of 180, 365 and 950 were performed. According to the best of our knowledge, LES simulations have not been extensively used to study turbulent skin-friction drag reduction as a consequence of the presence of spherical solid particles on the flow. From this perspective our goal is twofold: first, to contribute to the understanding of “turbulent flow modulation by injection of spherical particles” by numerically studying the effect of varying the particle mass fraction (${\varphi }_m$), whilst maintaining the particle volume fraction (${\varphi }_v$) constant; second, to explore and discuss the use of LES approach for simulating and exploring the physics of turbulent particle-laden flows.

This paper is organized as follows: initially, in Section 2, we present the main features of the mathematical and computational models used for both the continuous and the discrete phases. In the third section (Section 3), we discuss details of the set of numerical tests used for the validation process, as well as some considerations about the SGS modelling effect. 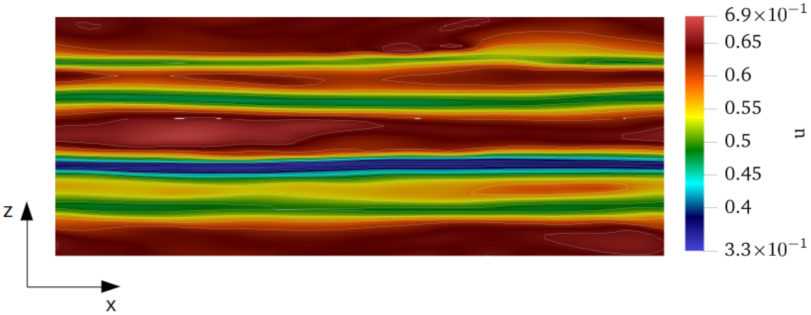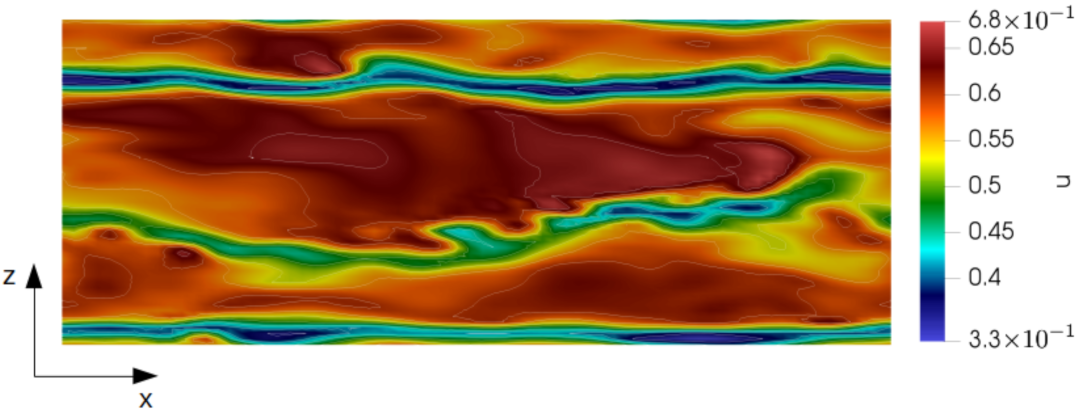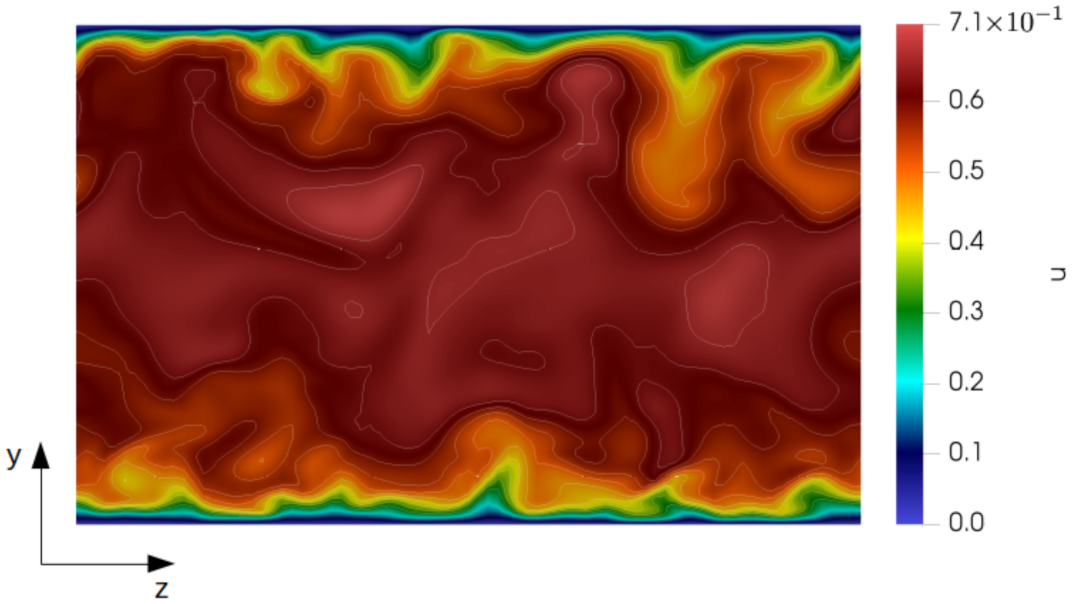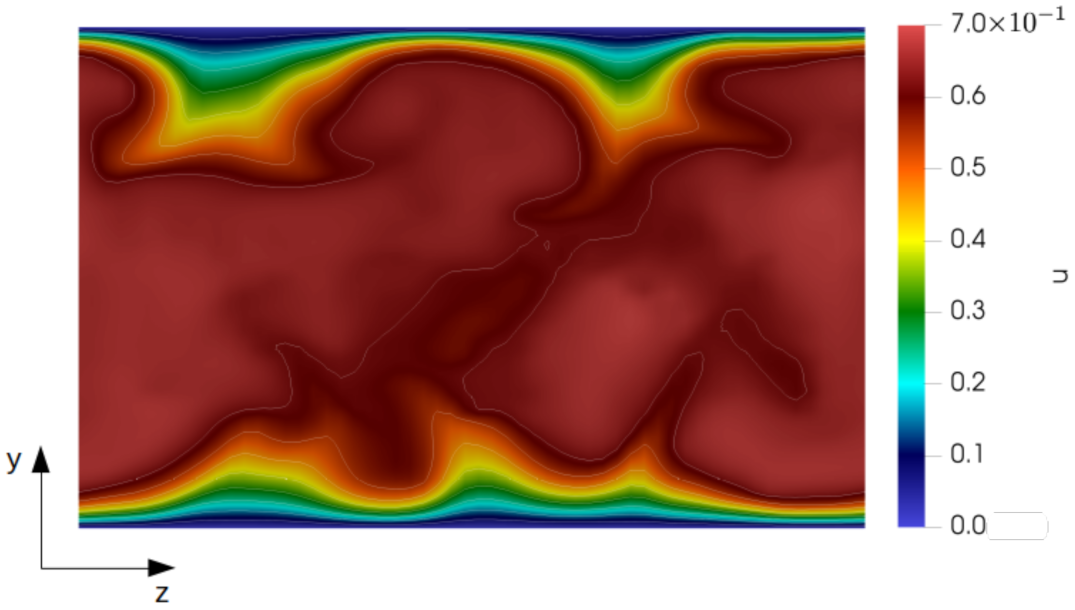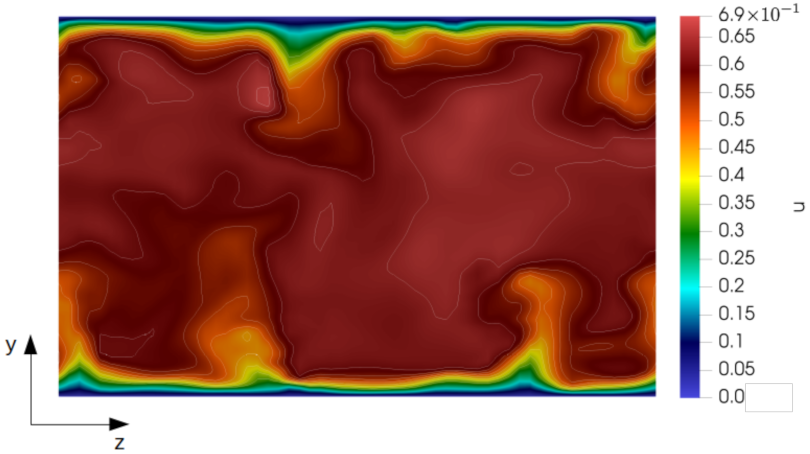The results of the numerical experiments are presented and discussed in the Section 4, where the effect of the PMF (${\varphi }_m$) on the turbulent mean velocity profile is discussed in the first section (Section 4.1), the findings on modulation of the velocity fluctuations are detailed and discussed in the second part of such section (Section 4.2), and in the third part (Section 4.3) we present our observations about the effect of the particle mass fraction on the general turbulence dynamics from a visual perspective by examining some instantaneous velocity contours. A short discussion on the changes in skin-friction drag and the relation between the skin-friction coefficient and an explicit momentum source is presented in Section 4.4. We conclude our article by drawing a set of conclusions based on the evidence discussed throughout the paper.

2. Modelling Methodology

The mathematical model adopted in the present work is based on an Eulerian–Lagrangian approach. We solve the fluid continuity and momentum equations on an Eulerian grid. The particle’s motion is governed by Newton’s law thus following a conventional Lagrangian approach. The fluid is herein named the carrier phase, whereas the particles are named the disperse phase. The computational model is based on a point-particle approximation for modelling the effects of the disperse phase. Modelling of the turbulent dynamics of the flow was performed by using a LES approach. The computational implementation was based on the set of C++ libraries of OpenFOAM (OF), an open source CFD toolbox that allows customization and implementation of in-house coding within its programming base.

2.1. Carrier Phase

A plane channel was adopted as main flow configuration, with no-slip walls as top and bottom boundaries, and periodic boundary conditions in the streamwise and spanwise directions. In this case, the carrier phase of the particle-laden flow was simulated using a turbulent LES incompressible solver on an Eulerian grid. The sub-grid scale dynamics was modelled by using the Coherent Structures Sub-Grid-Scale (SGS) model proposed by Kobayashi [38] and validated in Ramirez-Pastran and Duque-Daza [39]. In order to maintain constant fluid mass flow rate conditions in the streamwise direction, a dynamically computed momentum source was prescribed as a volumetric momentum source. This extra streamwise momentum term, herein named $\Phi$, was included in the LES-filtered Navier–Stokes Equations (Equation (2)). This momentum source term is usually interpreted either as an explicit pressure gradient or as a volumetric force acting over the entire carrier phase. In the present work $\Phi$ was also employed as an alternative mechanism to gauge the modification of the flow viscous resistance introduced by the particles.

The relatively high particle volumetric fraction employed in this work demanded the use of a two way coupling approach to capture the interaction between the discrete and carrier phases. The two-way coupling was implemented by introducing an additional momentum source term, independent from $\Phi$, and labelled as $S{U}^p$ (see Equation (2)), and which represents the momentum exchanged between the particles and the flow. This $S{U}^p$ term can be computed from the force on each individual particle following the action-reaction principle of Newton’s 3rd law, as discussed by Balachandar and Eaton [40], Zhao and Andersson [41]. Further discussion and additional details on the two-way coupling approach used in this work are presented in next section (see Section 2.2). It follows that the mathematical model for the carrier phase can be established as,

$$\frac{\partial \overline{u_i}}{\partial x_i}=0$$

(1)

$$\frac{\partial \overline{u_i}}{\partial t}+\frac{\partial \overline{u_i}\overline{u_j}}{\partial x_j}=\nu \frac{{\partial }^2\overline{u_i}}{\partial x_j^2}-\frac{\partial {\tau }_{ij}^R}{\partial x_j}+{\Phi }_i+S{U}_i^p$$

(2)

where $\overline{u}$ represents the LES filtered velocity field, and ${\tau }_{ij}^R$ is the residual stress tensor (see Sagaut [42]), also commonly called the sub-grid stress tensor. Note that in this paper the following convention was adopted: $u_1=u$, $u_2=vs.$ and $u_3=w$, representing streamwise, wall-normal, and spanwise velocity components. Furthermore, uppercase letters denote filtered variables, lowercase letters stand for instantaneous values and the prime symbol (${}^{\prime }$) is used to indicate fluctuating components of a given variable. According to LES methodology, a part of the velocity field is resolved explicitly and the other is modelled. To define the threshold that separates the spatial scales of the velocity field that must be resolved explicitly and those that must be modelled, it is necessary to use a spatial filter. This filter can be prescribed explicitly by the use of some mathematical expressions, or implicitly by using a characteristic length ($\Delta$) as a spatial filter. The scales that are to be modelled are also called sub grid scales. For the LES filtering, a characteristic length equivalent to $\Delta ={\left({\Delta }_x{\Delta }_y{\Delta }_z\right)}^{1/3}$, with ${\Delta }_i$ being the $i-th$ direction grid size, was employed as spatial filter. Furthermore, in LES modelling a residual stress tensor appears as part of the LES-filtering process and is defined as,

$${\tau }_{ij}^R=\overline{u_i{u}_j}-\left(\overline{u_i}\right)\left(\overline{u_j}\right)$$

(3)

which, expressed in spherical and deviatoric components, can also be written as,

$${\tau }_{ij}^R={\tau }_{ij}^r+\frac{2}{3}{k}_R{\delta }_{ij}$$

(4)

where ($k_R$) is the residual turbulent kinetic energy, representing the spherical part and defined as,

$$k_R=\frac{1}{2}{\tau }_{ii}^R$$

(5)

The spherical part of the residual stress tensor in LES, as discussed by Lar Kermani et al. [43], includes just a negligible portion of the turbulent kinetic energy, and hence the spherical part of it can be safely ignored. The remaining deviatoric part of the residual stress tensor, in the present study, was modelled with the “Q”-Coherent-Structures model, or simply the CS model, proposed by Kobayashi [38]. Although the Coherent Structures SGS (CS) model is conceptually based on the original Smagorinsky model (see Smagorinsky [44]), this CS model exhibits essentially the same performance as the dynamic Smagorinsky model for (non-) rotating homogeneous turbulences and turbulent channel flows (Kobayashi [38]). The CS model avoids the relatively high dissipative features of the original Smagorinsky model and performs well in a range of different applications as presented by Liu and Lai [45] and Okaze et al. [46]. The reliability of the CS-SGS model and its suitability for engineering applications can be appreciated in a few important features: it does not need to average or clip the model parameter; it does not need to use an explicit wall-damping function; finally, it does not require adjustment of the fixed-parameter. Liu and Lai [45] made two-point space–time correlation and Fourier spectrum analysis of large-eddy simulations of a compressible parallel jet flow at Reynolds number 2000 and Mach number 0.9 using different SGS models, including the CS proposed by Kobayashi [38], and found its performance and predictive capabilities comparable to direct numerical simulation (DNS) results of the same study case.

Numerically, the CS model is based on the original technique proposed by Smagorinsky [44], although in the model proposed by Kobayashi [38] the so-called Smagorinsky coefficient “C” is calculated from the second invariant (Q) of the velocity gradient tensor. Smagorinsky [44], originally proposed to express the deviatoric part of the residual stress tensor as

$${\tau }_{ij}^r=-2C{\Delta }^2\left|\overline{S_{ij}}\right|\overline{S_{ij}}$$

(6)

where “C” is the so-called Smagorinsky coefficient, “$\Delta$” is the spatial filter and “$\overline{S_{ij}}$” is the filtered strain tensor. In the Q-coherent structures model, however, the coefficient “C” is defined as,

$$C=\frac{1}{22}{\left|F_{CS}\right|}^{3/2}{F}_{\Omega }$$

(7)

where $F_{CS}=Q/E$ represents a coherent-structures function, $E=1/2\left(\overline{{\Omega }_{ij}}\overline{{\Omega }_{ij}}+\overline{S_{ij}}\overline{S_{ij}}\right)$ the filtered shear magnitude, and $F_{\Omega }=1-F_{CS}$ is a decay energy suppression function. The second invariant of the velocity gradient tensor (Q) was defined by Hunt et al. [47] as,

$$Q=\frac{1}{2}\left(\overline{{\Omega }_{ij}}\overline{{\Omega }_{ij}}-\overline{S_{ij}}\overline{S_{ij}}\right)$$

(8)

with ${\Omega }_{ij}$ representing the vorticity tensor. In Kobayashi’s model it is only necessary to calculate vorticity values to solve explicitly the velocity flow fields involved in the filtered N-S equations, which usually translates into a low computational cost and a relatively higher efficiency, at least in comparison with the dynamic model proposed by Germano [48]. Additionally, the coherent structure model is numerically stable, even without the use of an averaging process (see Kobayashi [38]).

2.2. Discrete Phase

The discrete phase was simulated using a Lagrangian approach and, as mentioned previously, a point-particle approximation was adopted as particles idealisation. In the point-particle approach it is assumed that each particle behaves physically like a moving source point, as explained and discussed by Marchioli [49], Kuerten [50], Balachandar [51]. As part of this approximation, all the simulations were prescribed so that the particle size used for each simulation was always smaller than the resolved fluid length scale, though always keeping a fixed particle volume fraction. Two values of particle volume fraction (${\varphi }_v$ or PFV) were prescribed in this work: ${\varphi }_v=2.7\times {10}^{-5}$ was used in the validation tests; and ${\varphi }_v=1.1\times {10}^{-3}$ was set for the main set of simulations. According to Elghobashi [52], for this range of ${\varphi }_v$ values, it is adequate to consider a two-way coupling between the phases if the normalised particle relaxation time is low (${\tau }_p/{\tau }_{\kappa }<{10}^2$, approximately, with ${\tau }_{\kappa }$ representing the Kolmogorov time). The particles motion was computed using the standard momentum conservation equations for solid particles, so the velocity and position of each $i-th$ particle are computed by solving Equations (9) and (10), as follows,

$$\frac{\mathrm{d}{\mathbf{x}}_i^p}{\mathrm{d}t}={\mathbf{u}}_i^p$$

(9)

$${\mathbf{m}}_p\frac{\mathrm{d}{\mathbf{u}}_i^p}{\mathrm{d}t}={\mathbf{F}}_i^p$$

(10)

where ${\mathbf{x}}^p$ is the particle’s position, ${\mathbf{m}}_p$ is the mass of the particle, ${\mathbf{u}}^p$ is the particle’s velocity, and ${\mathbf{F}}_i^p$ represents the total force being exerted over the $i-$th particle.

When LES is used for modelling turbulence of particle-laden flows, as it is the case of this work, it is necessary to assess if the SGS velocities might influence the particle dynamics, the turbulent behaviour of the carrier phase, or both (Kuerten et al. [22]). The characteristics of the particles and flow conditions adopted in the present work allowed us to neglect the effect of the SGS scales over the particle dynamics, hence precluding the need for any modelling of the SGS velocities effect (additional details in Section 3).

The dynamic model adopted in this paper for estimating the forces acting over each particle ($F_i^P$) follows the model proposed by Maxey and Riley [53] and discussed by Zhao and Andersson [41], where the the motion of the particles is governed by different individual forces, including: Stokes drag force, Saffman lift force, Magnus lift force, buoyancy force, added mass force, pressure gradient force, and Basset history force. In any case, due to the characteristics considered in this work for particles as well as for the flow, it was not necessary to take into account all these forces. For instance, as ${\rho }_p>>{\rho }_f$ then forces such as added mass, Basset history force and buoyancy, were deemed as negligible, and therefore safe to be disregarded, as discussed by Alletto and Breuer [54]. The walls were assumed to be completely smooth, so no wall-induced rotation motion was considered into the dynamics of the particles, which also allowed for the Magnus lift force to be ignored. In order to make the solution of the coupled turbulent flow-particles system more readily attainable, the Saffman lift force was also neglected, as proposed by Zhao et al. [14]. The collision effects between particles were not taken into account due to the low particle volumetric fraction (PVF). Furthermore, particle-wall collisions were set as completely elastic. Accordingly, the only force acting over the particles that was taken into account in this work was the drag force. This force can be mathematically modelled as follows (see Laín and Sommerfeld [55]),

$${\mathbf{F}}_D={\displaystyle \frac{3}{4}}{\displaystyle \frac{{\rho }_f}{{\rho }_p}}{m}_p\frac{C_D}{d_p}({\mathbf{u}}^f-{\mathbf{u}}^p)|{\mathbf{u}}^f-{\mathbf{u}}^p|$$

(11)

with ${\mathbf{u}}^f$ being the fluid velocity at particle position. In the previous expression, the drag coefficient is estimated by,

$$C_d=\left\{\begin{array}{cc}\frac{24}{R{e}_p}\left(1+0.15R{e}_p^{0.687}\right)& R{e}_p\le 1000\\ 0.44& R{e}_p>1000\end{array}\right.$$

(12)

with $R{e}_p=\frac{{\rho }_f{d}_p|{\mathbf{u}}^f-{\mathbf{u}}^p|}{{\mu }_f}$.

In accordance with the models just outlined, the term ${\mathbf{F}}_i^p$ used to compute the particles motion was obtained from Equation (11). In the point-particle approach used in this work it is possible to have several particles in a given discrete volume $\Delta$. Therefore, the feedback force from n particles within the given volume $\Delta$ adds up to

$$S{U}_i^p=-{\displaystyle \frac{1}{\Delta }}\sum _{i=1}^n{\mathbf{F}}_i^p$$

(13)

This $S{U}^p$ term representing the force per unit volume was then included in the momentum Equation (Equation (2)) to account for the effect of the solid particles on the fluid motion. This is known as the point-force approximation to two-way coupling (Balachandar and Eaton [40], Zhao and Andersson [41]) Therefore, and given the considerations regarding the particles and flow features in the present work, ${\mathbf{F}}_D$ was deemed to be the only significant interaction between particles and fluid to be included in $S{U}^p$. This force was computed for each particle within the computational domain, and the particle trajectories estimated using Equations (9) and (10). In any case, once values of ${\mathbf{F}}_D$ were obtained for each solid particle (per-particle property), the term $S{U}^p$ (a per-cell property) was calculated in every computational cell as a particle-average using only the particles contained in that specific cell, which provided a closure between particles and flow interaction.

2.3. Complementary Details of the Computational Model

Assessment of the effect of the particle mass fraction—PMF (${\varphi }_m$) was performend through numerical experiments on a benchmark turbulent channel geometry: a plane channel of height $2h$, with smooth non-slip walls as top and bottom boundaries, and periodic boundary conditions in the streamwise and spanwise directions, as presented in Figure 1. In this figure, the x, y, and z coordinates identify the streamwise, wall-normal, and spanwise directions, respectively.

The computational model was solved using the set of C++ libraries and solvers of OpenFOAM which allow to obtain numerical solution of systems of partial differential equations through spatial discretization based on the finite volume method (FVM). OpenFOAM (OF) has become one important tool for CFD researchers and practitioners alike, and its use is becoming more widespread in the numerical modelling community (see Ramirez-Pastran and Duque-Daza [39], Weller et al. [56], Hrvoje et al. [57], Jasak [58], Chen et al. [59], Iturrioz et al. [60]). Particularly, in line with the scope of this work, an incompressible turbulent flow solver has been selected to simulate the evolution and dynamics of the carrier phase presented in Equations (1) and (2) (see Ramirez-Pastran and Duque-Daza [39]). This selection was based on the fact that the OF libraries also provide numerical tools for modelling the solid particles in particle-laden incompressible flows, with minimum modifications. Time integration of the evolution of the transport phase was performed using a blended backward Crank–Nicholson scheme. The coupling between velocity and pressure for the carrier phase was achieved by using a coupling between the PISO algorithm with intermediate SIMPLE relaxation iterations, denominated PIMPLE method within OF framework, and which has been validated and explained in detail in Robertson et al. [61].

The other additional term $\Phi$ in the momentum Equation (Equation (2)) was employed to enforce a constant fluid mass flow rate in the periodic channel. As it is well known, the fluid mass flow rate in such flow configuration depends directly on the bulk velocity, so the $\Phi$-term served as a mechanism to gauge the amount of additional energy necessary to keep the bulk velocity constant, and at a given mass flow rate. Accordingly, changes on the value of this control source term $\Phi$ were deemed to be required for compensating viscous dissipation and particles inertia. In other words, $\Phi$ was employed as a sort of indirect measure of the friction losses present in the flow, as well as of the global effect of the presence of the particles.

The present work was focused on a gravity-free particles-laden flow setup, as appreciated from the mathematical model, and which could eventually be identified as a vertical channel flow. However, gravity in vertical channels laden with particles has a non-trivial effect and its inclusion has consequences. For instance, depending on the inertia of the particles and their level of interaction with the flow, it is both possible to find accumulation of particles either closer to the walls or to the center of the channel, among other effects. As mentioned previously, some works have considered gravity and assessed its effects on particles-laden vertical channels (see Li et al. [25], Yamamoto et al. [26], Vreman [30], Capecelatro et al. [31]). Nevertheless, the reasoning for neglecting gravity in our work was twofold. First, we wanted to avoid a possible gravity’s masking effect on the interaction between particles and fluid for the set of parameters selected. Second, by ignoring the gravity, we were able to use the data from both bounding walls of the channel (see Figure 1) to assess the changes and impact on the turbulent flow, and therefore to obtain sooner in the simulations the required ensemble averages of the turbulence modulation estimators, which in turn reduced the computational effort, usually a critical factor of turbulent flow simulations in industry related applications. Equally, neglecting gravity is an approach that has been successfully employed by other authors that following a similar strategy have either simplified the mathematical model or been able to clearly identify other effects that might be hindered by the inclusion of a gravitational force. Battista et al. [32] carried out DNS simulations of the flow laden with point particles in a pipe flow without considering gravity, and still were able to study the influence of particle Stokes number, particle to fluid density ratio and mass loading on the two-way coupling effects for a fixed friction Reynolds number of 180.

3. Validation of Computational Model

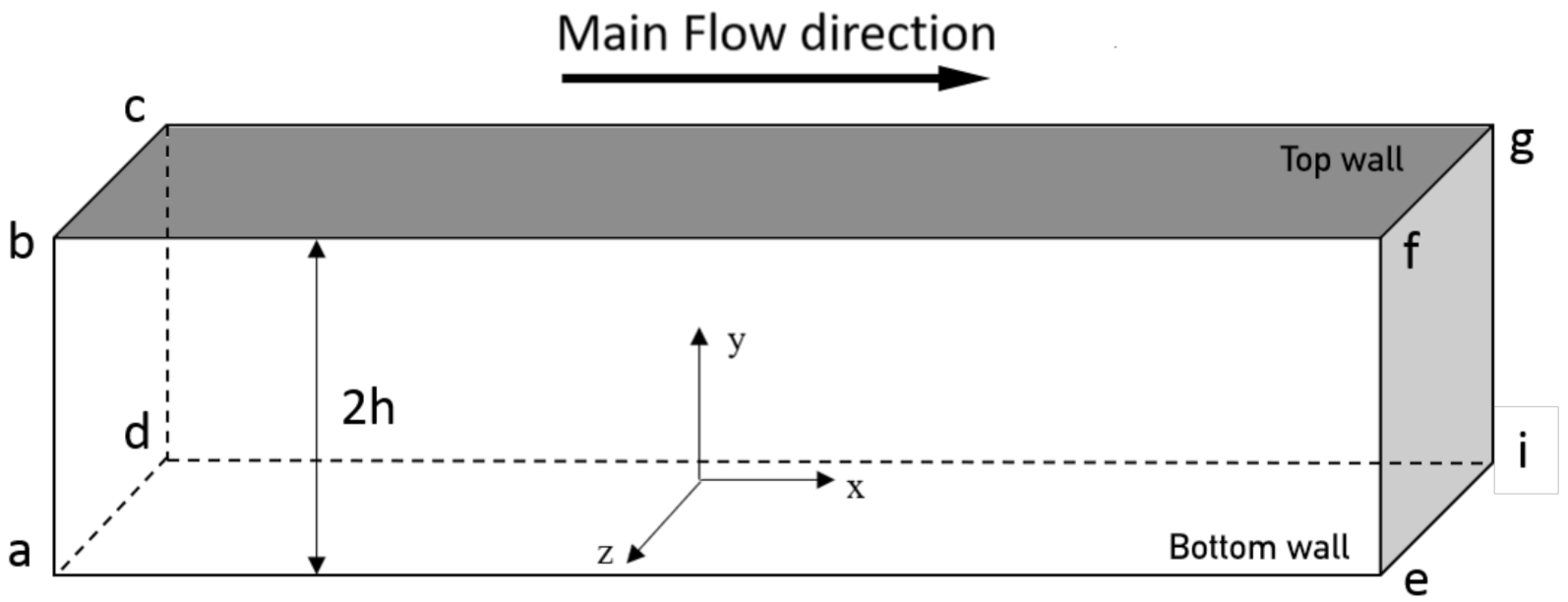
The computational methodology was validated using two different configurations of particle-laden flows. The main goal of these tests was to assess the consistency of the integrated computational model (fluid-particles). Results of these validation tests were compared against data published by Dritselis and Vlachos [62] and Dritselis and Vlachos [63]. The dimensions of the computational domain used in the validation process matched up those employed by Dritselis and Vlachos [63], i.e., $2\pi h\times 2h\times \pi h$, in $x,y,$ and z, respectively, with h defining the half-height of the channel, as shown in Figure 1. The flow characteristics and main features of the particles for the validation tests were prescribed as defined in Dritselis and Vlachos [62], namely a nominal average friction velocity $u_{\tau }$ = 0.18 m/s, Reynolds number of 5600 based on constant bulk velocity, particle volume fraction ${\varphi }_v=2.7\times {10}^{-5}$, and particle mass fraction ${\varphi }_m\approx 0.2$, corresponding to a particle to fluid density ratio of $S=7333$. In

Table 1. Particle diameter and relaxation time used in validation tests. $PL-1$ and $PL-2$ are case designations.

Case	${\mathit{Re}}_{\mathit{\tau }}$	${\mathit{d}}_{\mathit{p}}$ ($\mathsf{\mu }$m)	${\mathit{d}}_{\mathit{p}}^{+}$	${\mathit{\tau }}_{\mathit{p}}^{+}$
PL-1	180	21	0.248	25
PL-2	180	58	0.7	200

, the values of particle diameter are presented (in $\mathsf{\mu }$m, and in wall units “+”), and the relaxation time (also in wall-units) for the two validation cases considered in this work, which have been labelled as PL-1 and PL-2. The computational mesh used for both tests consisted of $100\times 200\times 80$ cells in x, y and z directions, respectively. Dimensionless wall-units were computed using the equivalent particle-free case friction velocity $u_{\tau }$, and the kinematic viscosity $\nu$ as normalisation factors, for instance: ${\tau }_p^{+}=\left({\tau }_p{u}_{\tau }^2\right)/\nu$ and $d_p^{+}=\left(d_p{u}_{\tau }\right)/\nu$. It is important to highlight that the non-dimensionalization in wall-units used in this work follows the wall-scaling proposed in Dritselis and Vlachos [62]. Other works, like Capecelatro et al. [31], employ slightly different definitions for the Stokes numbers based on friction velocity, so some care must be taken comparison are to be drawn between different results. As a simple example, a factor equals to $R{e}_{\tau }$ must be applied to the definition of the Stokes number based on friction velocity as defined in Capecelatro et al. [31] to obtain the equivalent non-dimensional Stokes number used throughout this paper.

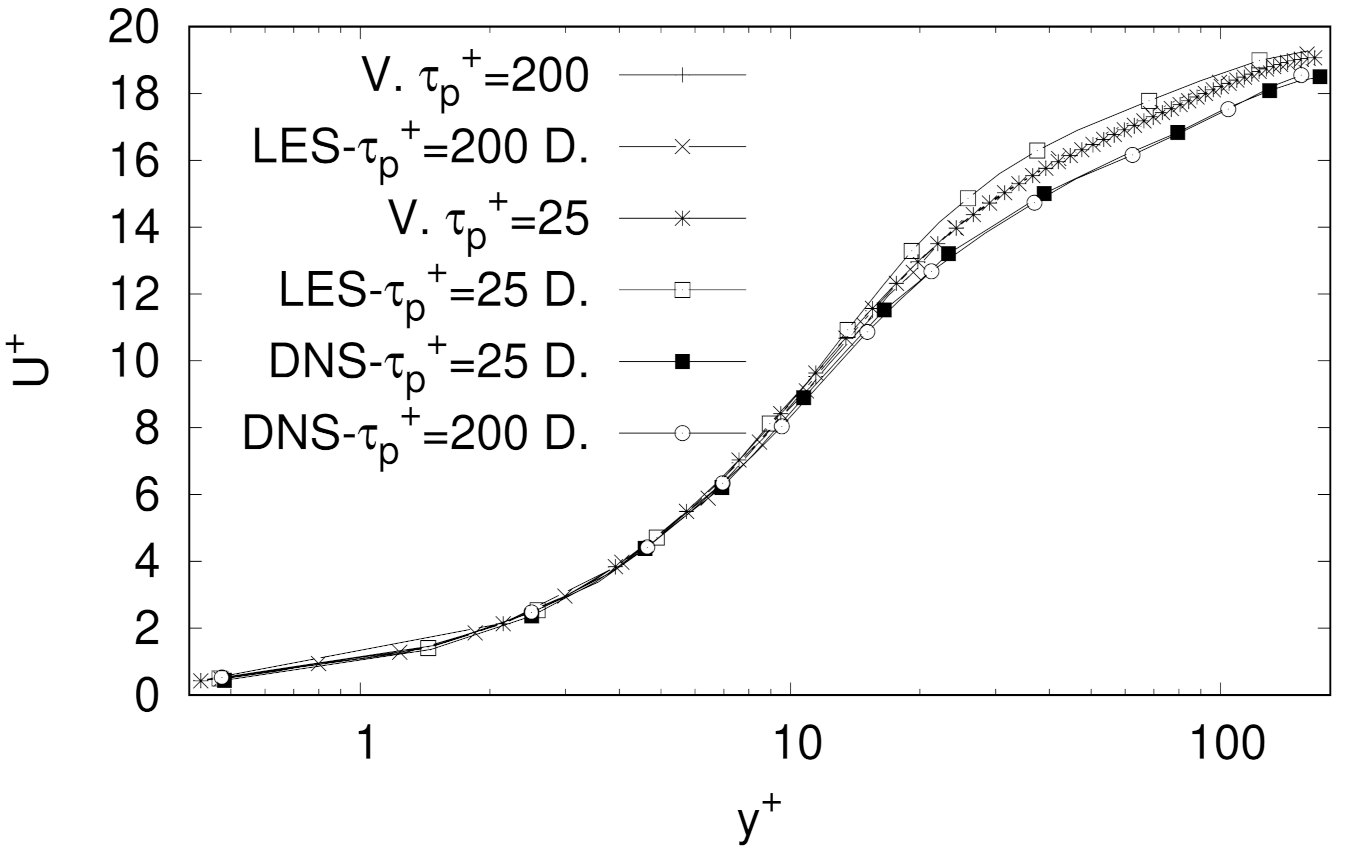
Results of our validation tests are presented in Figure 2 together with the LES and DNS results presented by Dritselis and Vlachos [63] and Dritselis and Vlachos [62], respectively. The following nomenclature has been used in this figure: $V.{\tau }_p^{+}=200$: Validation case with ${\tau }_p^{+}=200$; $V.{\tau }_p^{+}=25$: Validation case with ${\tau }_p^{+}=25$; $LES-{\tau }_p^{+}=200D$: LES results from Dritselis and Vlachos [63] for ${\tau }_p^{+}=200$; $LES-{\tau }_p^{+}=25D$: Dritselis and Vlachos [63] for ${\tau }_p^{+}=25$; $DNS-{\tau }_p^{+}=200D$: DNS results from Dritselis and Vlachos [62] for ${\tau }_p^{+}=200$; $DNS-{\tau }_p^{+}=25D$: DNS results from Dritselis and Vlachos [62] for ${\tau }_p^{+}=25$.

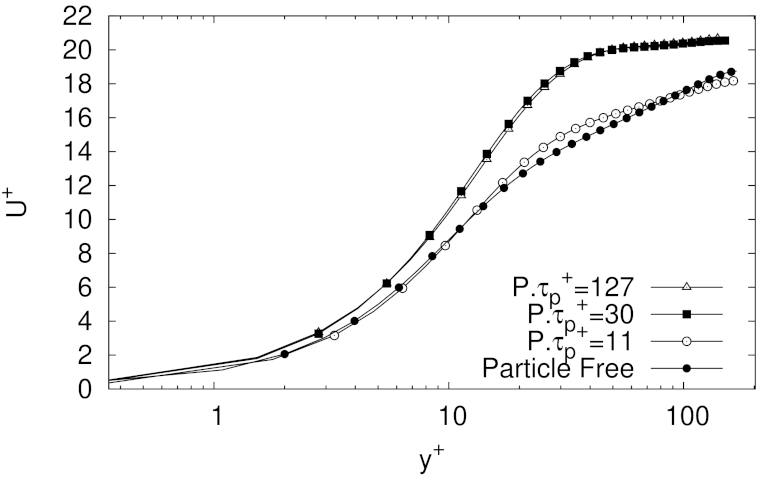
By examining the mean velocity profiles, shown in Figure 2, it seems clear that our computational model is completely able of capturing first order moment statistics. In general, it is clear that some of the important features of the mean velocity profiles, as computed by DNS, have been captured in both tests. For instance, the largest error on the mean velocity profile brought about by our model was around 2.7% for the flow laden with particles of ${\tau }_p^{+}=200$ (PL-2 case) which, as it can be seen in Figure 2, is the case with the largest deviation from the DNS results, specially in the log-law region. In any case, we do not claim our model features DNS-like resolution in the sub-viscous layer, rather than our model capabilities perform well within the range of accuracy expected for LES simulations.

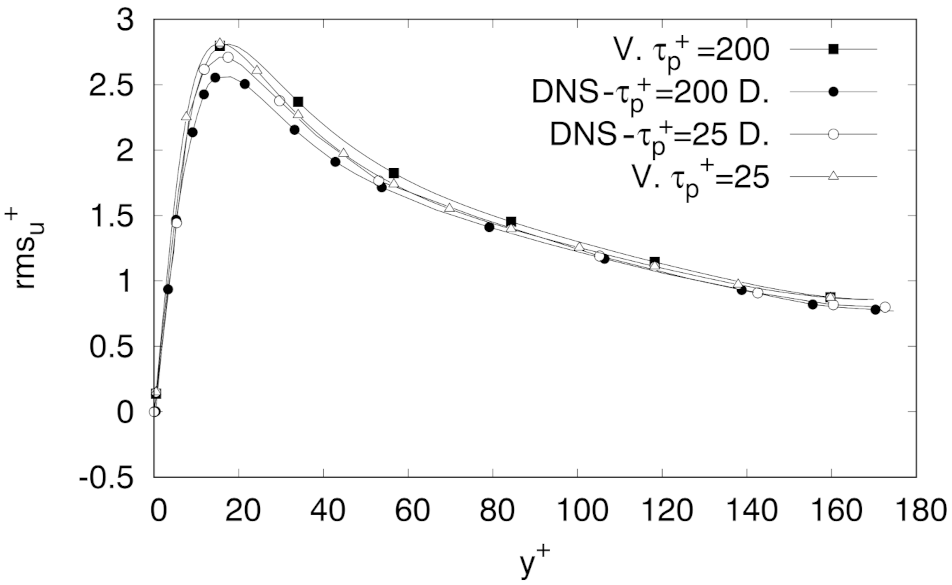
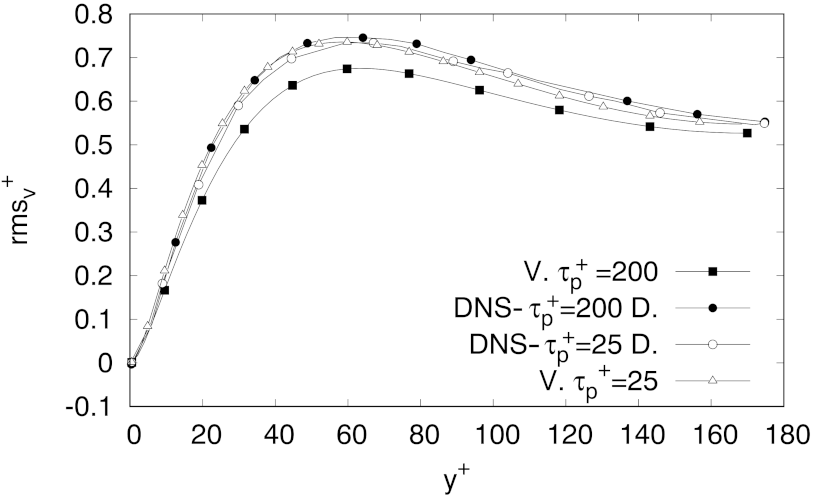
Equally, as it can be appreciated from the results presented in Figure 3, Figure 4 and Figure 5, it seems apparent that our model was also able to adequately predict profiles of velocity fluctuations in the streamwise, wall-normal, and spanwise directions. The results presented in these figures include the LES experiments by Dritselis and Vlachos [63], DNS experiments performed by Dritselis and Vlachos [62], and the results obtained with our model. The nomenclature in these figures is the same as in Figure 2.

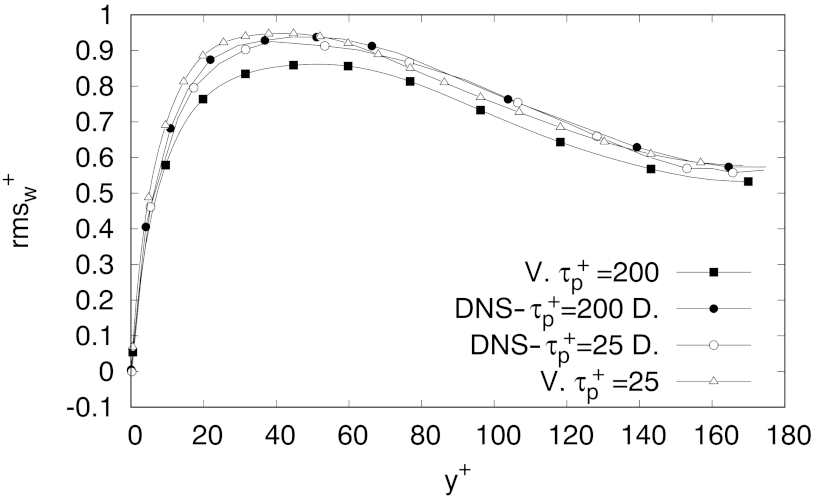
Values of the spanwise fluctuations (Figure 5) were within a margin of about 12 % of error, whereas profiles of the velocity fluctuations in the other directions were captured within even smaller margins of error. As the goal of this work is to critically asses the effect of ${\varphi }_m$, special attention was paid to three quality estimators in the velocity fluctuation profiles:

• The “wall-normal position” of the peak in wall-units (position P);
• The maximum peak value, regardless of its position (amplitude A);
• The velocity fluctuation value predicted by our model at the location of the maximum peak in DNS profiles, (DNS peak amplitude $DN{S}_P^A$)

A relative error was computed for every estimator using the DNS results reported by Dritselis and Vlachos [62], and the error computed for each of these three criteria (estimators) is presented as percentage in

Table 2. Relative error of prediction of peak values and positions of $rm{s}_u^{+}$ (in percentage). Nomenclature: P, Position; A, Amplitude; $DN{S}_P^A$, DNS Peak Amplitude.

	P	A	${\mathit{DNS}}_{\mathit{P}}^{\mathit{A}}$
${\tau }_p^{+}=200$	5	8.63	8.33
${\tau }_p^{+}=25$	0	3.11	3.11

,

Table 3. Relative error of prediction of peak values and positions of $rm{s}_v^{+}$ (in percentage). Nomenclature: P, Position; A, Amplitude; $DN{S}_P^A$, DNS Peak Amplitude.

	P	A	${\mathit{DNS}}_{\mathit{P}}^{\mathit{A}}$
${\tau }_p^{+}=200$	11.88	7.76	8.59
${\tau }_p^{+}=25$	8.63	0.28	0

and

Table 4. Relative error of prediction of peak values and positions of $rm{s}_w^{+}$ (in percentage). Nomenclature: P, Position; A, Amplitude; $DN{S}_P^A$, DNS Peak Amplitude.

	P	A	${\mathit{DNS}}_{\mathit{P}}^{\mathit{A}}$
${\tau }_p^{+}=200$	0	7.69	7.69
${\tau }_p^{+}=25$	0	2.51	2.51

, for $rm{s}_u^{+}$, $rm{s}_v^{+}$, and $rm{s}_w^{+}$, respectively. As observed in those tables, the estimator with the highest level of error was the position P, in the case for ${\tau }_p^{+}=200$, for the wall-normal velocity fluctuation profile ($v_{\mathrm{rms}}^{\prime }$). The next largest error was found in the value of $DN{S}_P^A$ for the same case. Nevertheless, in both cases, the error was below 12%, and some estimators even presented a null error, estimated within the margin of precision of the data acquired from DNS plots and DNS available data (see Table 2, Table 3 and Table 4).

Accordingly with the results presented, it seems clear that the adopted computational model and methodology were reasonably accurate and reliable. The low level of errors in the predictions of amplitudes and positioning of the peaks in the velocity fluctuations profiles, as well as the similarity of the mean velocity profiles to those reported by DNS results, and the arguably low level of error in the those profiles, allowed us to conclude that the model was able to reproduce reliably the first and second order moments of the statistics of turbulent particle-laden channel flow at the low Reynolds numbers explored, and the target of the present work.

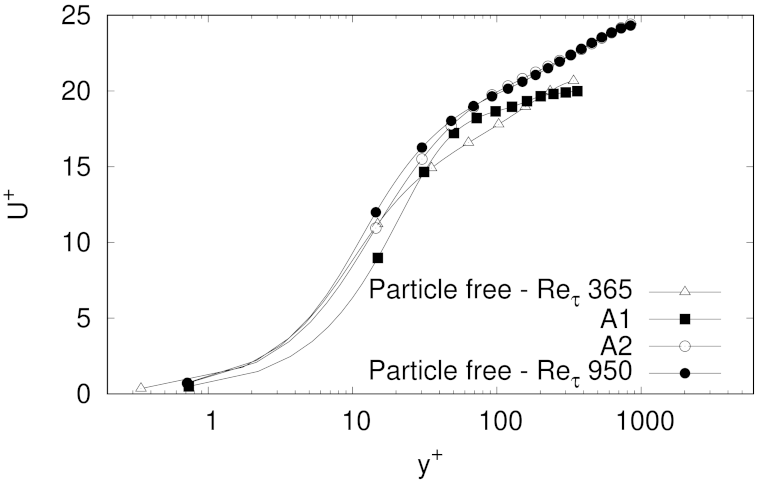
The turbulence modulation in the carrier phase induced by the presence of solid particles, and more concretely the influence of the particle mass fraction (${\varphi }_m$) was explored from two perspectives: (i) particle-laden flows were simulated at a fixed friction Reynolds number of $R{e}_{\tau }=180$ but with three different mass fraction values; (ii) the flow response to a fixed value of ${\varphi }_m$ was explored in flows with higher nominal friction Reynolds numbers of $R{e}_{\tau }=365$ and $R{e}_{\tau }=950$. The computational domain employed for these numerical experiments was a box with dimensions $8h\times 2h\times \pi h$, in the x, y, and z directions, and all simulations were performed considering particles with diameter of $d_p=264$ $\mathsf{\mu }$m, and same volume fraction of ${\varphi }_v\approx 0.0011$.

Different values of Particle Mass Fraction ${\varphi }_m$ ($S={\rho }_p/{\rho }_f$) were set by varying particle’s densities, somehow emulating the use of different materials, and prescribed as equivalent to: (i) gum, ${\varphi }_m=1.0$ ($S=950$), (ii) aluminium, ${\varphi }_m=2.96$ ($S=2700$); and (iii) lead, ${\varphi }_m=12.4$ (S = 11,350). For simplicity, these cases have been herein labelled simply as low (LMF), medium (MMF) and high (HMF) particles mass fraction cases (see

Table 5. Particles characteristics used in the production simulations for the High (HMF), Medium (MMF), and Low (LMF) particles mass fraction.

Case	${\mathit{Re}}_{\mathit{\tau }}$	${\mathit{d}}_{\mathit{p}}$ ($\mathsf{\mu }$m)	${\mathit{d}}_{\mathit{p}}^{+}$	${\mathit{\tau }}_{\mathit{p}}^{+}$	S
LMF	180	264	0.462	11	950
MMF	180	264	0.462	30	2700
HMF	180	264	0.462	127	11,350

). In all the numerical experiments of the present work a reference fluid density of ${\rho }_f=1000$ kg m${}^{-3}$ was adopted, and assumed to be equivalent to cold water. For the experiments at higher friction Reynolds numbers ($R{e}_{\tau }=365$ and 950), the volume fraction was also set as ${\varphi }_v\approx 0.0011$, although a single mass fraction was employed, and equivalent to the MMF case defined in the experiments at $R{e}_{\tau }=180$, i.e., ${\varphi }_m=2.96$, or equivalently $S=2700$. These simulations have been labelled simply as higher-$R{e}_{\tau }$ simulations in some of the following sections of this paper, and identified as cases A1 and A2. A summary of these two sets of simulations is presented in Table 5 and

Table 6. Particles characteristics of the higher-$R{e}_{\tau }$ simulations.

Case	${\mathit{Re}}_{\mathit{\tau }}$	${\mathit{d}}_{\mathit{p}}$ ($\mathsf{\mu }$m)	${\mathit{d}}_{\mathit{p}}^{+}$	${\mathit{\tau }}_{\mathit{p}}^{+}$
A1 (MMF)	365	264	0.96	139
A2 (MMF)	950	264	2.53	863

, with values given in wall-units for the particles characteristics. Experiments at higher friction Reynolds numbers are summarized in Table 6.

Details of the size and refinement of the computational meshes employed in these tests are presented in

Table 7. Mesh size, in terms of number of cells, used in the numerical simulations.

Case	${\mathit{N}}_{\mathit{x}}$	${\mathit{N}}_{\mathit{y}}$	${\mathit{N}}_{\mathit{z}}$
$R{e}_{\tau }=180$ (${\tau }_p^{+}=11$, 30, 127)	80	200	80
$R{e}_{\tau }=365$ (${\tau }_p^{+}=139$ (A1))	100	260	60
$R{e}_{\tau }=950$ (${\tau }_p^{+}=863$ (A2))	110	320	80

and

Table 8. Grid resolution/refinement employed for the numerical simulations (normalised in inner wall units).

Case	$\Delta {\mathit{y}}_{\mathit{min}}^{+}$	$\Delta {\mathit{y}}_{\mathit{max}}^{+}$
$R{e}_{\tau }=180$ (${\tau }_p^{+}=11$, 30, 127)	0.46	4.64
$R{e}_{\tau }=365$ (${\tau }_p^{+}=139$ (A1))	0.68	3.4
$R{e}_{\tau }=950$ (${\tau }_p^{+}=863$ (A2))	1.43	15.11

, in terms of number of cells in streamwise ($N_x$), wall-normal ($N_y$), and spanwise ($N_z$) directions, and of the wall-normal resolution at the wall ($\Delta y_{min}^{+}$) and at centre of the channel ($\Delta y_{max}^{+}$). The grid resolution adopted for each numerical experiment was defined through grid independence tests. As it can be seen in Table 7 and Table 8, although final mesh resolution adopted for the higher Reynolds numbers cases was not as good as that employed for the simulations at $R{e}_{\tau }=180$, it was fine enough to provide results within less than 8% of error margin when compared against the DNS mean velocity profile obtained by Lee and Moser [64].

As mentioned previously, the spatial filter $\Delta ={\left({\Delta }_x{\Delta }_y{\Delta }_z\right)}^{1/3}$ was adopted as the smallest resolved scale of the flow. Solid particles were then treated as material points (i.e., point particle approach) with a much smaller size than $\Delta$, as recommended by Marchioli [49] and Kuerten [50]. This approach, labelled by other authors as point-force models (Dritselis and Vlachos [62]), is accurate as long as the particle diameter is smaller than the Kolmogorov length scale and the grid spacing, which makes the point-particle LES methodology very attractive for exploring flows from moderate to high Reynolds number conditions (Balachandar [51]). In the present work we aimed to comply with such constrain by ensuring that the particle diameter was consistently smaller than the minimum spatial filter used in every simulation. Comparison between values of minimum ${\Delta }^{+}$, particle response time ${\tau }_p^{+}$ (indicating particle size), particle diameter, as well as the corresponding value of particle mass fraction for each ${\tau }_p^{+}$ are presented in

Table 9. Comparison between minimum ${\Delta }^{+}$, ${\tau }_p^{+}$, ${\varphi }_m$, and $d_p^{+}$ for each simulation.

Case	${\mathit{Re}}_{\mathit{\tau }}$	${\mathit{d}}_{\mathit{p}}^{+}$	${\mathbf{\Delta }}_{min}^{+}$	${\mathit{\tau }}_{\mathit{p}}^{+}$ ($\mathit{St}$)	${\mathit{\varphi }}_{\mathit{m}}$	S
PL-1 (Validation)	180	0.248	4.119	25	0.2	7333
PL-2 (Validation)	180	0.700	4.119	200	0.2	7333
LMF	180	0.462	3.761	11	1	950
MMF	180	0.462	3.761	30	2.96	2700
HMF	180	0.462	3.761	127	12.4	11,350
A1 (higher-$R{e}_{\tau }$)	365	0.960	7.215	139	2.96	2700
A2 (higher-$R{e}_{\tau }$)	950	2.530	15.84	863	2.96	2700

. For convenience, the values used in the validation tests presented in the previous section are also included in this table, where the Stokes number $St$ is indicated also as ${\tau }_p^{+}$.

In all the simulations of the present work a standard workflow methodology was adopted: (i) First, benchmark particle-free cases were solved and then evolved until reaching a statistically steady state; (ii) next, particles were injected throughout the entire computational domain in random positions; (iii) then once the particle distribution and the velocity profiles had reached a statistical steady state, the process of obtaining turbulent statistics was restarted; (iv) finally, turbulent statistics were computed for at least 120 additional characteristic times ($t_c=L_x/U_b$).

SGS Modelling Effect on the Particles Dynamics

As the flow dynamics related to the SGS length and time scales are modelled, rather than simulated, there are a number of discussions highlighting the importance of considering the influence of such a SGS modelling over the velocity field seen by the particles. Initially, Yeh and Lei [65] were the first to investigate particle dispersion behavior in turbulent flows using LES. However, they assumed a negligible effect of the SGS models on the particle dynamics and hence did not use any SGS additional model to predict the behavior of the particles. This assumption was also followed in other studies as in Dritselis and Vlachos [63], Mallouppas and van Wachem [66], and Marchioli et al. [67]. Other authors have expressed that the influence of the SGS can not be neglected unless the fraction of energy removed from the fluid velocity field is small. Marchioli [49] stresses that it is necessary to consider the influence of SGS fluid velocities to provide reliable estimations of the particle kinetic properties. Other phenomena, like preferential particle concentration, has recently also been considered as sensitive to the inclusion of the SGS effects on the particle dynamics (see Kuerten [50], and Minier [68]).

Note that it is important to consider that in LES simulations using two-way (and four-way) coupling, a careful balance between mesh resolution and the use of SGS model must be observed to prevent too large erroneous predictions of the interphase drag force due to the presence of the particles. As shown by Ireland and Desjardins [69], numerical errors in the drag force are tied to inaccuracies in the numerical implementation of the drag model for systems with two-way coupling. Many conventional implementations employ the undisturbed fluid velocity in the drag models, but the issue lies in that this variable is not resolved but rather modelled based on the disturbed fluid velocity. In fact, it is arguably inappropriate to use any SGS correction when the filter size, usually the mesh size as in the present work, is larger than the particle diameter. In these cases, a counterintuitive behavior is observed where drag predictions tend to become less accurate as the grid resolution improves—an interesting effect observed and discussed in Ireland and Desjardins [69], Gualtieri et al. [70], Moore et al. [71], Horwitz and Mani [72].

Nevertheless, some of these studies established that when the particle response time is large compared to the typical time scales of the turbulent flow and to the smallest time scale resolved in the LES, the SGS of the fluid velocity field does not play a significant role on the particle motion (Kuerten [50]), therefore precluding the need of a SGS model for the particle equation. Marchioli [49] expressed that in LES particle-laden simulations based on two-way coupling, the level of influence of the SGS can be estimated with the sub-grid Stokes number:

$$S{t}_{SGS}={(l^{*}/\Delta )}^{2/3}$$

(14)

where $l^{*}$ is approximately ${\left({\tau }_p^3ϵ\right)}^{1/2}$ with ${\tau }_p$ representing the particle response time and $ϵ$ the turbulence dissipation rate. In Equation (14), $l^{*}$ is an estimation of the size of the eddies for which the particle-fluid relative velocity is maximum. Marchioli [49] established two critical limits: (i) if $S{t}_{SGS}\ll 1$, the particles are extremely sensitive to subgrid turbulence fluctuations and a SGS model is required; (ii) if $S{t}_{SGS}\gg 1$, the particles become SGS-inertial respect to the SGS eddies and hence no SGS modelling is required.

Accordingly, in order to evaluate the necessity for SGS modelling for the particles motion in this work, values of $S{t}_{SGS}$ estimated for each simulation are presented in

Table 10. Values of $S{t}_{SGS}$ for each simulation. S and ${\tau }_p$ values included for comparison.

Case	${\mathit{Re}}_{\mathit{\tau }}$	S	${\mathit{\tau }}_{\mathit{p}}$ (s)	${\mathit{St}}_{\mathit{SGS}}$
LMF	180	950	0.18	0.54
MMF	180	2700	0.49	1.54
HMF	180	11,350	2.07	6.49
A1	365	2700	0.52	4.25
A2	950	2700	0.48	16.12

. It can be seen that, except for the case at $R{e}_{\tau }=180$ and $S=950$, all computed values of $S{t}_{SGS}$ are larger than unity. For this reason, in the present work, no SGS modelling was used for the particles motion. However, it is clear that the results of particles motion for the case with $S{t}_{SGS}<1$ must be taken with some care.

4. Results and Discussion

In order to assess the possible turbulence modulation effects of ${\varphi }_m$ on the carrier phase, the results of the numerical experiments have been grouped in terms of effects on the mean velocity profiles, on the velocity fluctuations profiles, and identification of flow pattern modulation using instantaneous velocity components contours. Where they are considered appropriate, profiles are presented in wall units using the friction velocity $u_{\tau }$ and the kinematic viscosity $\nu$ as normalisation factors, as indicated previously. A brief discussion is also presented on the apparent correlation between the trends exhibited by the momentum source term $\Phi$ introduced in the momentum equations and the skin friction drag.

4.1. Effect of ${\varphi }_m$ on Mean Velocity Profiles

In Figure 6, the mean velocity profiles attained at $R{e}_{\tau }=180$ for the three different PMF values ${\varphi }_m=1,2.96,12.4$, corresponding to the LMF, MMF, and HMF cases, respectively, are compared with the turbulent mean velocity profile for the particles-free (PF) case. In line with results from other works, the PMF has been indicated in the plots using the corresponding particle response time in wall-units, also indicated previously in Table 9. The first observation is that the more dramatic impact is produced by particles with MMF and HMF, whereas particles with LMF did not produce a significant change in the profile. The difference between the mean velocity profiles for both cases is more pronounced in regions between the buffer layer and the channel centre. It is clear that in the cases where particles with medium (MMF) and high (HMF) mass fractions were loaded in the flow, i.e., cases with ${\tau }_p^{+}=30$ (${\varphi }_m=2.96$) and ${\tau }_p^{+}=127$ (${\varphi }_m=12.4$), the mean velocity profile exhibited a log-law region with a higher slope and an apparent early onset of the outer layer. Both profiles present the standard “plateau” characteristic of the outer layer, but with the defect region starting from $y^{+}=50$. This suggests that the velocity attained the value of the mean outer velocity at an earlier position in the wall-normal direction. This can be effectively described as a reduction of the boundary layer thickness. This apparent homogenisation of the velocity profile towards the centre of the channel was accompanied by a reduction of the friction velocity estimated at the wall. For the MMF and HMF cases, the measured friction velocity was $u_{\tau }=0.03$ m/s, whereas for the LMF and particle-free cases it was $u_{\tau }=0.035$ m/s. The reduction on the friction velocity seems to be also reflected on the shift of the non-dimensional mean velocity profile to higher values, compared to the PF case. For the MMF and HMF cases, the friction velocity of the carrier phase was reduced in 14% in comparison to the particles-free case. Note that for the LMF case, there was not evident effect of the solid particles on the mean velocity profile of the carrier phase. It seems then that the particle mass fraction ${\varphi }_m$ has a strong influence on the turbulent behaviour of the carrier phase. This argument, in our case, is by default extended to the particle response time ${\tau }_p^{+}$ as the experiments were performed at constant ${\varphi }_v$ and with particles with same diameter $d_p^{+}$. In contrast, it is observed that particles of low ${\varphi }_m$ do not generate significant changes on the mean turbulent velocity profile of the carrier phase.

The mean velocity profiles obtained in the experiments at higher higher-$R{e}_{\tau }$ are presented in Figure 7. It is clear that, for the particle-free cases, the mean velocity profiles closely follow the widely accepted shape of a sub-viscous region right next to the wall, followed by a buffer layer, and a region dominated by the log-law behavior, as discussed by Marusic et al. [73]. In any case, the results illustrate that the modification of the mean velocity profile followed a similar trend to that induced by the particles at $R{e}_{\tau }=180$ with medium and high ${\varphi }_m$, but only in the case at $R{e}_{\tau }=365$. In the other case, for the flow at $R{e}_{\tau }=950$, although there was some attenuation in the wake region of the mean velocity profile, the overall effect was almost imperceptible. Note that although not completely explicit from the plots, the gradients measured in the near-wall region were both smaller than those measured in their particle-free (PF) counterpart. This can also be deduced by comparing the friction velocities which for the flow at $R{e}_{\tau }=365$ (A1 case) was $u_{\tau }=0.073$, while in the flow at $R{e}_{\tau }=950$ (A2 case) was $u_{\tau }=0.188$. This clearly indicates that there seems to be a lower skin friction drag and in consequence lower losses by viscous friction. This is corroborated by just visual inspection when the instantaneous velocity field is extracted from the data, as presented later in this work. It seems clear that in fact the particle mass fraction ${\varphi }_m$, and therefore the particle response time ${\tau }_p^{+}$ play an important role on altering the mean velocity profiles in turbulent flow. In any case, there seems to be a threshold limit value below which such an effect ceases to be really significant. Furthermore, once a ${\varphi }_m$ value is selected, the effect is also attenuated at higher Reynolds numbers. In our case, the ${\varphi }_m$ value that produced higher attenuation of the boundary layer for $R{e}_{\tau }=180$ and $R{e}_{\tau }=365$, was unable to produce any significant effect on the flow at $R{e}_{\tau }=950$.

Such fact can be understood as follows. According to Marchioli [74], particles tend to accumulate into low speed streaks depending on its Stokes number, $St$, defined as the quotient between the particle response time and the viscous time scale ${\tau }_{\nu }=\nu /\left(u_{\tau }^2\right)$, i.e., ${\tau }_p^{+}$. It is found in Marchioli et al. [75] in one-way coupling DNS simulations that such segregation is maximum for particles with $St\approx 25$, which is a close value of the MMF (around 30). It is known, that in two-way coupling simulations, particles accumulated in the low speed streaks interrupt the autonomous turbulence generation mechanism, affecting very much all the carrier flow variables.

On the other hand, as $R{e}_{\tau }$ increases, the viscous scales progressively decrease so the same particles immersed in higher $R{e}_{\tau }$ flows, possess larger and larger Stokes numbers. As $St$ increases particle motion tends to be ballistic being not much influenced by the carrier phase fluctuating dynamics (and vice versa) and, consequently in absence of gravity, the particles tend to be more homogeneously distributed through all the channel, weakening the two-way coupling effects. As a result, particles with large $St$ numbers (for a fixed mass loading as in the present case) disrupt less the carrier flow that particles with lower $St$ numbers between 20 and 120 as it happens for flows at $R{e}_{\tau }=180$ and 365. In fact, the velocity profiles for $R{e}_{\tau }=180$ in MMF ($St=30$) and HMF ($St=127$) are pretty much similar, although there are differences for the fluctuating velocities. As it is seen, from Table 9, the $St$ for the HMF and A1 is very similar, so a comparable effect on fluid velocities could be expected at least from a qualitative point of view. This can be recognised in the comparison of the fluctuating velocity components where the relation between the clean flow variables and the two-way coupling profiles is similar in the HMF and A1 cases.

4.2. Effect on Velocity Fluctuation Profiles

Another important effect of loading the turbulent flow with particles is to produce a dramatic modification of the fluctuations of the velocity components, when compared against the particle free flow. Clearly this should also be reflected in the turbulent intensity of the carrier phase. Profiles in the wall-normal direction of the root-mean squared (rms) fluctuations of the streamwise, wall-normal and spanwise components are presented, in wall-units (${}^{+}$), in the plots in Figure 8, Figure 9 and Figure 10. The profile associated with the rms of the Reynolds shear stress is shown in Figure 11. Initially, a comparison of the MMF and LMF cases against the particle free case shows that in the main flow direction the fluctuation levels increase in regions around the buffer layer, but decrease in the central zone of the channel for the MMF case and keep above the PF profile for the LMF experiment. On the other hand, it can be seen that HMF particles strongly attenuate the velocity fluctuations intensity of the carrier phase in streamwise direction. Such attenuation, in contrast to the observed in the cases with MMF and LMF particles, generates a reduction of the peak value in the $rm{s}_u^{+}$ profile, which is even lower than the peak value observed for the same profile in the particles free case (see Figure 8). Another feature that can be observed in wall-normal Figure 8 is that the peak value for the HMF case is nearer to the wall in comparison to the same profile for the particles free case. The latter is presumably a consequence of a redistribution of the moment exchange caused by a redistribution of the particles in near-wall regions, and the effect seems to be related to the momentum exchange exerted between solid particles and the carrier phase.

It is observed that in wall-normal and spanwise directions, a reduction of the velocity fluctuations was attained for all cases. Nevertheless, the major reduction is presented for the HMF case. Such reduction of the velocity fluctuations seems to be related with a presumable relaminarization process of the carrier phase flow as a consequence of the presence of the solid particles. This particular observation seems to be ratified by examining the instantaneous velocity contours that will be discussed in Section 4.3.

According to the results above presented and to the main goal of this paper, it looks important to remember to the reader that the turbulent modulation generated by solid particles over the carrier phase has been somehow characterised also by other authors. For example, Gore and Crowe [76] proposed a critical value for the particle diameter from which turbulence modulation occurs. This critical value has been also corroborated by other experimental and numerical studies such as Eaton [77]. In this paper, the solid particles with the highest mass fraction are those which cause the highest level of turbulence attenuation, which agree with the observations of Wu et al. [78], as well as the statements of Balachandar and Eaton [40].

When observing the components of velocity fluctuations in the wall-normal and spanwise directions, it is clear a drastic reduction of the fluctuations in the near wall region as well as in the central portion of the channel. Such observations coincide with the results reported by Kulick et al. [27], Dritselis and Vlachos [79], Dritselis and Vlachos [62], Zhao et al. [28] and Li et al. [80]. According to the behaviour of the velocity fluctuations presented in Figure 8, Figure 9 and Figure 10, it is clear that the greater turbulent intensity exchange between the flow and particles is presented in the wall-normal and spanwise directions. This behaviour in the turbulent dynamics of the flow seems to be directly linked with a higher resistance of particles to be moved in directions different to the streamwise direction, most likely due to particle inertia, specially considering the Stokes numbers explored. This response, it seems, has to be compensated with the momentum contributed by the carrier phase from such directions and therefore an increase in the fluid fluctuating velocity anisotropy is attained.

The changes on the velocity anisotropy mentioned above can be also evidenced in Figure 11 where the profile of the cross component $u^{{}^{\prime }}{v}^{{}^{\prime }}$ of the Reynolds stress tensor is presented. It is evident that the solid particles attenuate the momentum exchange between the streamwise and the Figure flow directions due to turbulent effects. One extremely interesting observation is that for the HMF case (${\tau }_p^{+}=127$) the Reynolds shear stress is practically zero which indicates that this mechanism of turbulence production has been essentially nullified.

As evidenced in Figure 12, Figure 13, Figure 14 and Figure 15 an attenuating effect of the turbulence over the carrier phase was also obtained for both A1 and A2 cases as a consequence of the presence of solid particles, consistent with previous results. However, in these cases, the highest levels of attenuation in the velocity fluctuations are attained for the case $A1$. Moreover, it seems that the highest reduction of the velocity fluctuation intensities are presented in spanwise and wall-normal direction, respectively. Hence, the lower percentage of reduction observed in streamwise direction is presumably a consequence of a redistribution of the direction where momentum exchange is done on the carrier phase as consequence of solid particles. The solid particles tends to attenuate the velocity fluctuations intensities in all directions, although part of the attenuated energy in spanwise and wall-normal directions seems to be redistributed to the streamwise direction by the particles presence.

4.3. Instantaneous Velocity Contours

A complementary approach employed in this work to evaluate the effects of the solid particles was through the examination of instantaneous fluid velocity contours of the streamwise component, extracted at given reference planes. From the previous results it is clear that the particles produce noticeable effects in the near-wall region as well as in the outer region of the boundary layer. The impact of the presence of particles can be then visually appreciated by simple comparison against the particle-free case, shown in Figure 16. To examine the effect in the near wall region, velocity contours were produced at an $xz-$plane located at $y^{+}=35$, and are presented in Figure 17, Figure 18 and Figure 19. The cases presented, without exception, show that the main result of injecting particles was to produce an arguably more organised sequence of low- and high-speed streamwise streaks, in some cases describing almost a straight line without significant mixing between streaks. The effect is more noticeable as the PMF is higher as appreciated in the graphs. For instance, in the LMF-case, the streaks are still not completely straight, although clearly more aligned than in the particle-free case, and exhibiting a streamwise length close to $90\%$ of the channel length in the $x-$direction. On the other hand, the HMF case presents low-speed streaks that are essentially straight, fully aligned with the direction of the flow, and covering the complete extension of the channel in the $x-$direction. This behaviour is similar to that observed in studies where drag reduction in channel flows was obtained due to the presence of polymers and solid particles (Zhao et al. [14], White and Mungal [81]). It is important to mention that the level of the apparent alignment effect observed in the carrier phase for the HMF and MMF cases was not the result of a change in the effective viscosity of the transport phase, as the values of turbulent viscosity ${\mu }_T$ obtained in this study (but not shown in this paper) were much lower than the prescribed kinematic viscosity value of the carrier phase. The effect on the outer region of the boundary layer (central region of the channel) can be appreciated observing the instantaneous velocity profiles of the streamwise velocity component in $yz-$planes, such as those presented in Figure 20, Figure 21 and Figure 22. From the velocity contours presented, as in the $xz-$planes, there is an apparent reduction on turbulent activity in general, compared to the particle-free case (Figure 20), with a clear increase of the spanwise separation between streaks, and a clear homogenization of the flow in the central region of the channel.

4.4. Analysis of the Effect of Particle Mass Fraction on Momentum Balance and Skin-Friction Coefficient

Analysis of the global effect of the particle mass fraction ${\varphi }_m$ over the dynamics of the flow is usually presented in terms of pressure losses or pressure gradient variations. However, as our computational model was prescribed as periodic in the streamwise direction, it precluded an analysis of pressure gradients. In order to produce a constant mass flow rate, the simulations were performed with the prescription of a momentum source term $\Phi$ acting on the main flow direction, and varied dynamically to ensure the target bulk velocity, as discussed earlier. Therefore, instead of focusing on pressure losses directly, we examine the amount of additional momentum required to sustain a target flow, and the attained friction coefficient for the LMF, MMF, and HMF cases. By examining $\Phi$ and comparing its trend with the skin-friction coefficient $C_f$ for each case, it was possible to confirm that the mass fraction effectively creates a global effect of reducing skin-friction drag. The values of $\Phi$ and $C_f$ attained for the particles free case, as well as for the three main target cases LMF (${\tau }_p^{+}=11$), MMF (${\tau }_p^{+}=30$), HMF (${\tau }_p^{+}=127$) are presented in

Table 11. Skin-friction coefficient $C_f$ and momentum source term $\Phi$ values for the LMF, MMF, and HMF cases. $\Phi$ values are time averages.

Case	${\mathit{C}}_{\mathit{f}}$	$\mathbf{\Phi }$
PF	0.0082	0.01281
LMF	0.0078	0.01237
MMF	0.0057	0.0098
HMF	0.0051	0.0075

. Clearly, there is a reduction of the required extra momentum term, which reflects also the beneficial effect of injecting particles, specially in terms of energy requirements for a given flow rate. This reduction of momentum source is clearly also supported by a decrease of the skin-friction coefficient. It is arguably obvious that alterations of the source term are brought about by skin-friction drag reduction in the carrier phase, although there is not a linear relation between these two quantities, as the reported values suggest. The decrease of skin-friction drag clearly induces a decrease of the energy losses by drag in the walls, which seems to be then also captured by the lower extra input requirements to sustain any given flow rate. When comparing the values of the term $\Phi$ for the particles free case against the particle laden cases (see Table 11), it is clear that in the LMF case, there is not a significant change. In contrast, for the MMF and HMF cases, the drag attenuation effect was more pronounced, as it can be appreciated from Table 11. Moreover, although not presented in the table, we observed that the values of $\Phi$ in the higher-$R{e}_{\tau }$ cases were approximately 37% and 59% lower for $R{e}_{\tau }=$365 and $R{e}_{\tau }=$950, respectively. It is important to highlight that the reductions observed for the source term $\Phi$ are not linearly proportional to those observed in $C_f$, and a convenient conversion between $\Phi$ and skin-friction drag must still be produced for a wider range of $R{e}_{\tau }$ and PMF values.

5. Conclusions

In this paper, the results of numerical tests designed to assess the ability of spherical solid particles to modify or attenuate turbulence intensity, and therefore to generate potential turbulent skin-friction drag reduction on the carrier phase, have been presented. The numerical experiments were based on LES simulations of a turbulent incompressible particle-laden channel flow using two-way coupling approach. The numerical experiments were carried for three mass loading values ${\varphi }_m=1,2.96,12.4$ for channel flow at $R{e}_{\tau }=180$ with a fixed particle volume fraction of ${\varphi }_v=1\times {10}^{-3}$. As the density of the particles was adjusted to prescribe the particle mass fractions, three different Stokes numbers were used for the experiments at $R{e}_{\tau }=180$, i.e., ${\tau }_p^{+}=11$ (${\varphi }_m=1$), ${\tau }_p^{+}=30$ (${\varphi }_m=2.96$), and ${\tau }_p^{+}=127$ (${\varphi }_m=12.4$). In this manner, our experiments and results can be interpreted as the analysis of the combined effects of particle mass fraction and Stokes number. Experiments at two higher $R{e}_{\tau }$ were performed for a fixed ${\varphi }_m=2.96$, at $R{e}_{\tau }=365$ corresponding to a ${\tau }_p^{+}=139$, and at $R{e}_{\tau }=950$ corresponding to a ${\tau }_p^{+}=863$.

One of the main conclusions is that at higher values of the particle mass fraction, the amount of turbulent skin-friction drag reduction obtained in the carrier phase was also larger. This conclusion, however, bears only for experiments at a fixed Reynolds number. Results for flows with high and medium particle mass fractions showed some levels of flow relaminarization, and therefore also a clear measurable level of turbulent skin-friction drag reduction. This relaminarization effect has also been reported by Capecelatro et al. [31] and identified as the main characteristic of one of three regimes in a transition mechanism of the turbulence-generation dynamics in a particle-laden flow with mass loading in the range $2\le {\varphi }_m\le 4$.

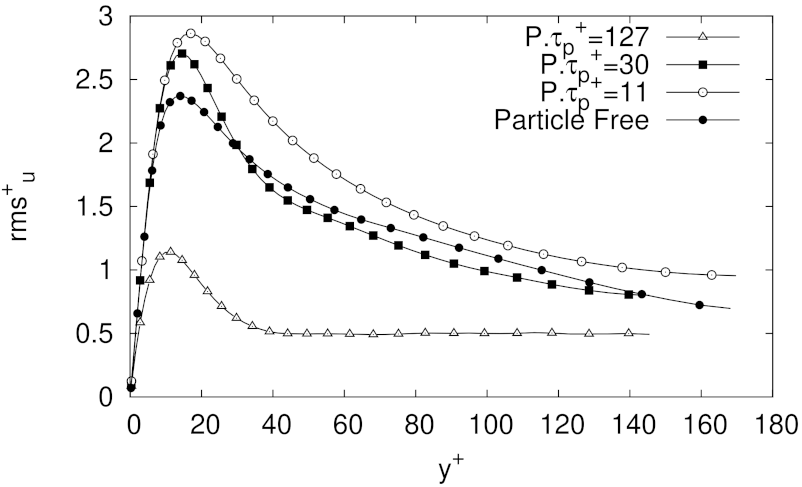
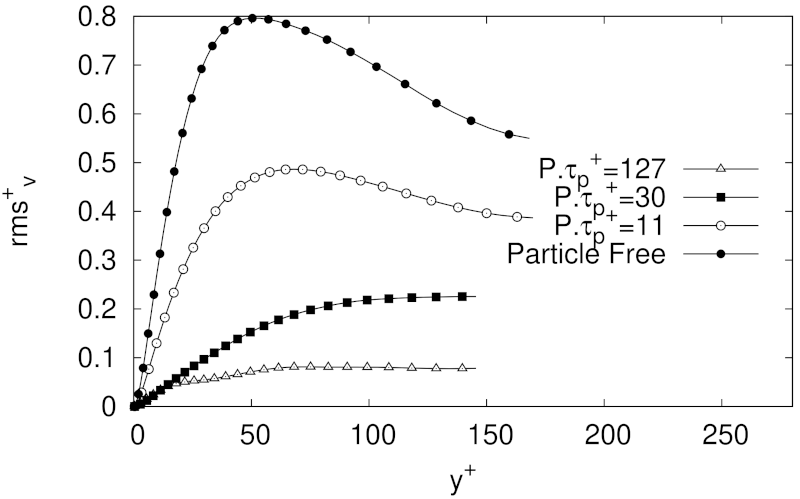
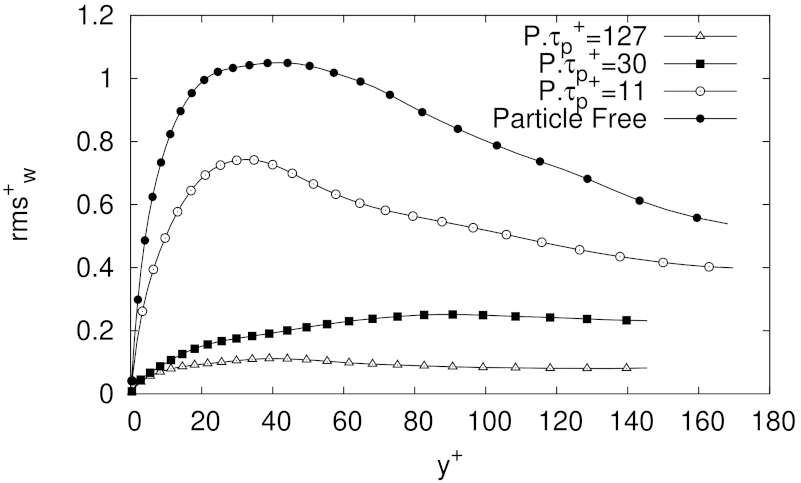
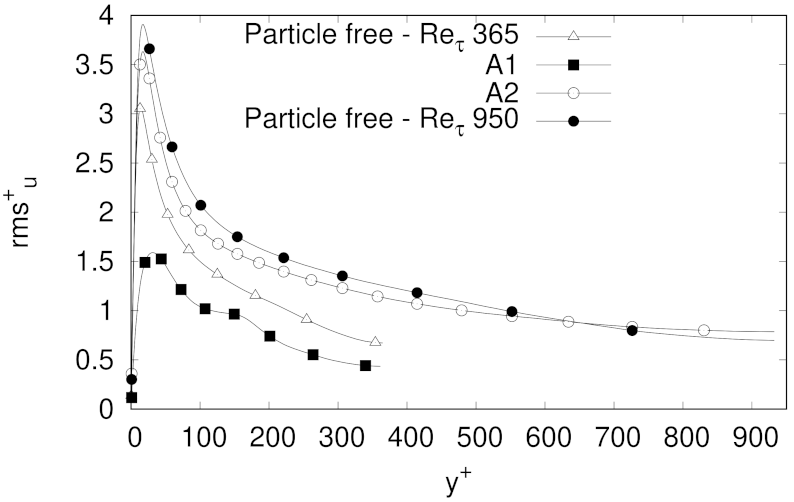
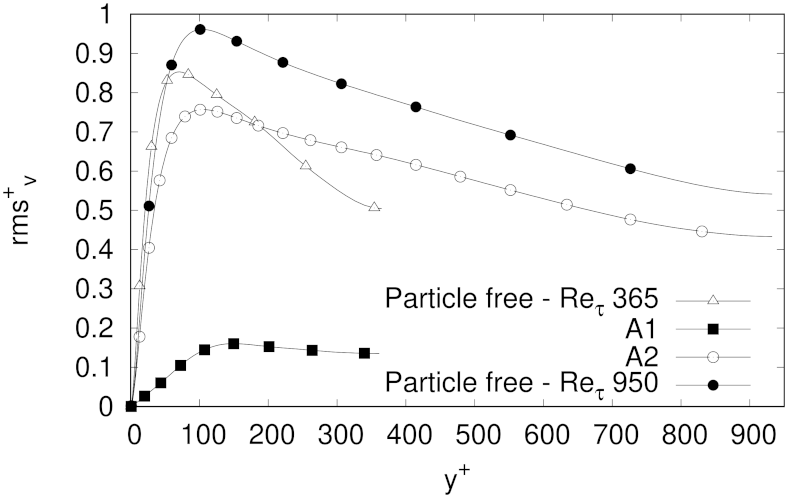
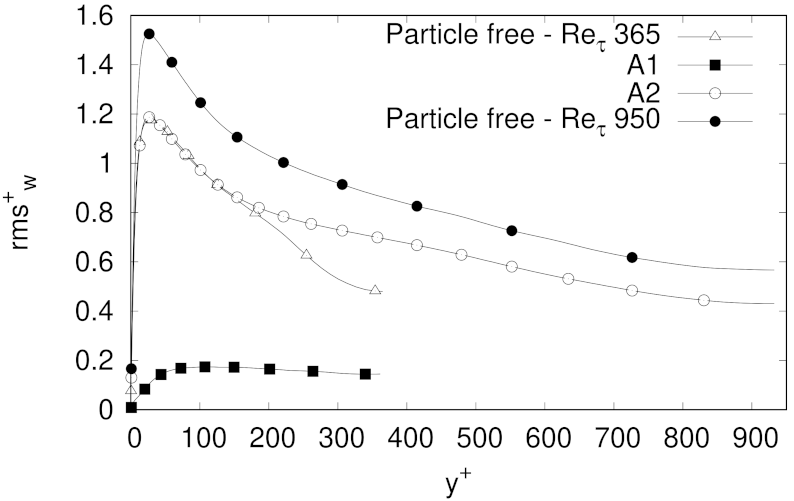
The effect of spherical solid particles with same levels of mass fraction as in the MMF case was assessed for three different friction Reynolds numbers, i.e., 180, 365, 950. In comparison to the particles free case, the velocity fluctuations profiles in wall-normal and spanwise directions of the explored cases showed a clear reduction in intensity, but keeping in general the profiles shape. The attenuation of the velocity fluctuations was more evident with higher values of mass fraction, although at higher Reynolds numbers the reduction in turbulence intensities was not as dramatic as for the cases at $R{e}_{\tau }=180$. In any case, the experiments clearly showed some level of flow homogenization, which increases with PMF at low friction Reynolds numbers.

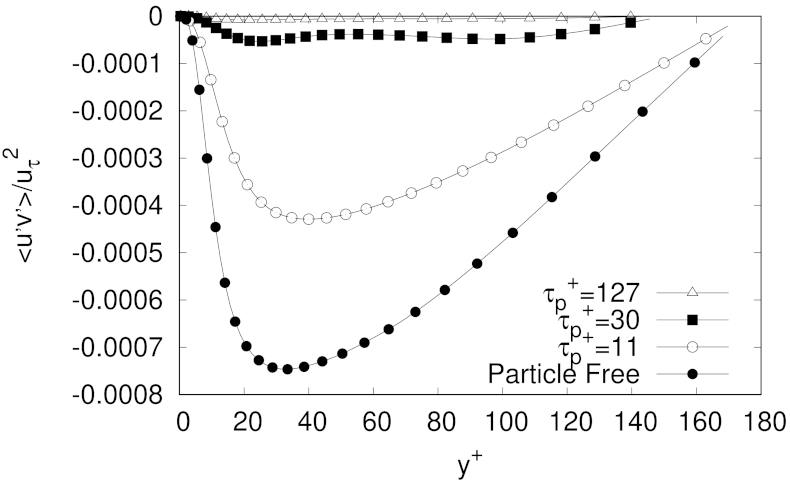
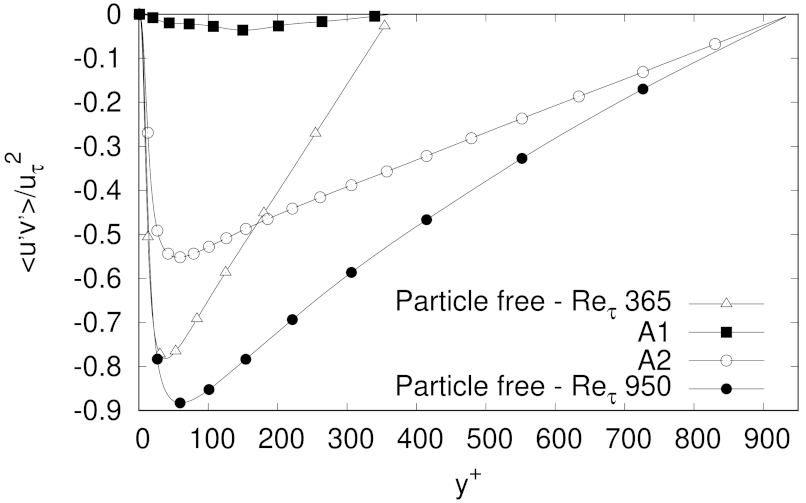
The lowest percentage of turbulent skin-drag reduction was observed for the lowest Reynolds number at the lowest particle mass fraction explored, i.e., our LMF case with ${\tau }_p^{+}=11$. As turbulent skin-friction drag reduction was observed on the carrier phase for almost all cases analysed in this paper, it was not surprising to observe for such cases an enhancement of the turbulence anisotropy, as well as a reduction of the intensity of the Reynolds stresses components, and of $C_f$ and $\Phi$. In fact, the results indicating turbulence activity reduction for the LMF, MMF and HMF cases, reinforce a picture where the turbulence intensities attenuation is related to the particle inertia, given that as $St$ (or equivalently ${\tau }_p^{+}$) increases, particles are more inertial, interact less with the fluid and they do not need to be so strongly accelerated by the fluid, so the pressure gradient needed to keep the fluid mass flow decreases (particles with larger inertia are more efficient in damping turbulence, at least when they are accumulated in the low speed streaks. For very large inertia particles tend to be more uniformly distributed along the channel).

One important conclusion to be drawn is that, contrary to some common belief, drag reduction can be achieved without a complete relaminarization of the flow. For instance, as shown by the results presented in this work, it was possible to attain reduction in the additional $\Phi$ term, as well as a reduction of the skin-friction coefficient, and therefore of the head loss, without a complete reduction of the turbulence intensity. In fact, for some of the cases where a great reduction of turbulent skin-drag was observed, changes of turbulent fluctuations were different in each direction. Strong turbulent streamwise velocity fluctuations were still obtained for cases with strong drag reduction. These results are in line with similar findings reported by the DNS study of Zhou et al. [36] where an increase of streamwise velocity fluctuations was accompanied by a decrease of the spanwise and wall-normal fluctuations, together with some levels of reduced skin friction drag. in fact, our numerical experiments show that the LES numerical model employed in the present work was able to produce results in line with those reported by DNS experiments, corroborating some of the findings presented in Capecelatro et al. [31] and also the general trends reported by Zhou et al. [36], at least for mean velocity profiles and first order moment statistics, i.e., velocity fluctuations.

Finally, when analyzing the behavior of both, mean velocity and the velocity fluctuation profiles, the turbulence modulation generated by the solid particles over the carrier phase compared to the free particles case becomes evident. Even when a reduction of the friction velocity was observed for the HMF and MMF cases, such reduction does not represent a change of the fluid mass flow rate. Therefore, according to the results obtained, it is presumed that one of the main impacts of this type of solid particles is to generate an increase of the laminar to turbulent transition Reynolds number for this kind of flows. Furthermore, according to the aforementioned results and with the data shown in Table 11, it is possible to recognize that the LMF particles do not cause enough turbulence attenuation on the carrier phase to generate a significant relaminarization of the flow and therefore a subsequent decrease in the term $\Phi$. On the other hand, the use of HMF particles generates the highest levels of turbulence attenuation and the highest relaminarization effect of the carrier phase, which is also evidenced in the largest reduction of the $\Phi$ term obtained in the present simulations.

As a future work, it would be important and interesting to perform an analysis of the effect of the ${\varphi }_m$ with a model including the wall roughness model of Sommerfeld [82], to assess the impact of a more realistic wall bounding condition. Equally, it would be extremely relevant to validate the effect of considering non-ideal inelastic collisions between particles, and therefore of their potential as mechanism to modulate turbulent flows.

Additionally, it is important to note that the main outcome observed in our numerical experiments was mostly related to turbulence attenuation. Clearly it is possible to attain turbulence generation/production, which has been reported in numerical and experimental works. For instance, in Gai et al. [83] increase of turbulence intensity was reported to be linked to different mass loading conditions, and depending on the characteristics of the particles, such as mass density, volume fraction, mean diameter, or carrier phase flow properties. However, there was no observable turbulence generation for most of the set of parameters employed in the present work. Similar findings have been reported by Zhou et al. [36] who performed numerical experiments using DNS and two-way coupling for different particle mass loadings, in a similar fashion to our work but at a fixed Stokes number. They reported that all the TKE and the Reynolds stresses budget terms of the transport equations were attenuated by the particles, as well as the spanwise and wall-normal velocity fluctuations, although they also report that streamwise velocity fluctuations increased in comparison with the non-laden case. It seems that obtention of almost exclusively turbulence attenuation in our set of numerical experiments was mainly a consequence of the range of values selected and employed for the numerical experiments. It seems clear that more numerical experiments are required to explore a wider range of friction Reynolds numbers $R{e}_{\tau }$, Stokes numbers ${\tau }_p^{+}$, and mass fraction loadings (PMF ${\varphi }_m$ values) to further explore the potential effective ranges inducing turbulence modulation.