Semi-Implicit Finite Volume Procedure for Compositional Subsurface Flow Simulation in Highly Anisotropic Porous Media
Abstract
:1. Introduction
2. Mathematical Model
2.1. Transport Models
2.2. Compositional System of Equations
2.3. Compatibility Equations
2.3.1. Thermodynamic Equilibrium
2.3.2. Capillary Pressure
2.3.3. Volume Constraint
2.4. Second-Order Anisotropic Elliptic Operator
3. Numerical Model
3.1. Time Discretization and Mesh Definition
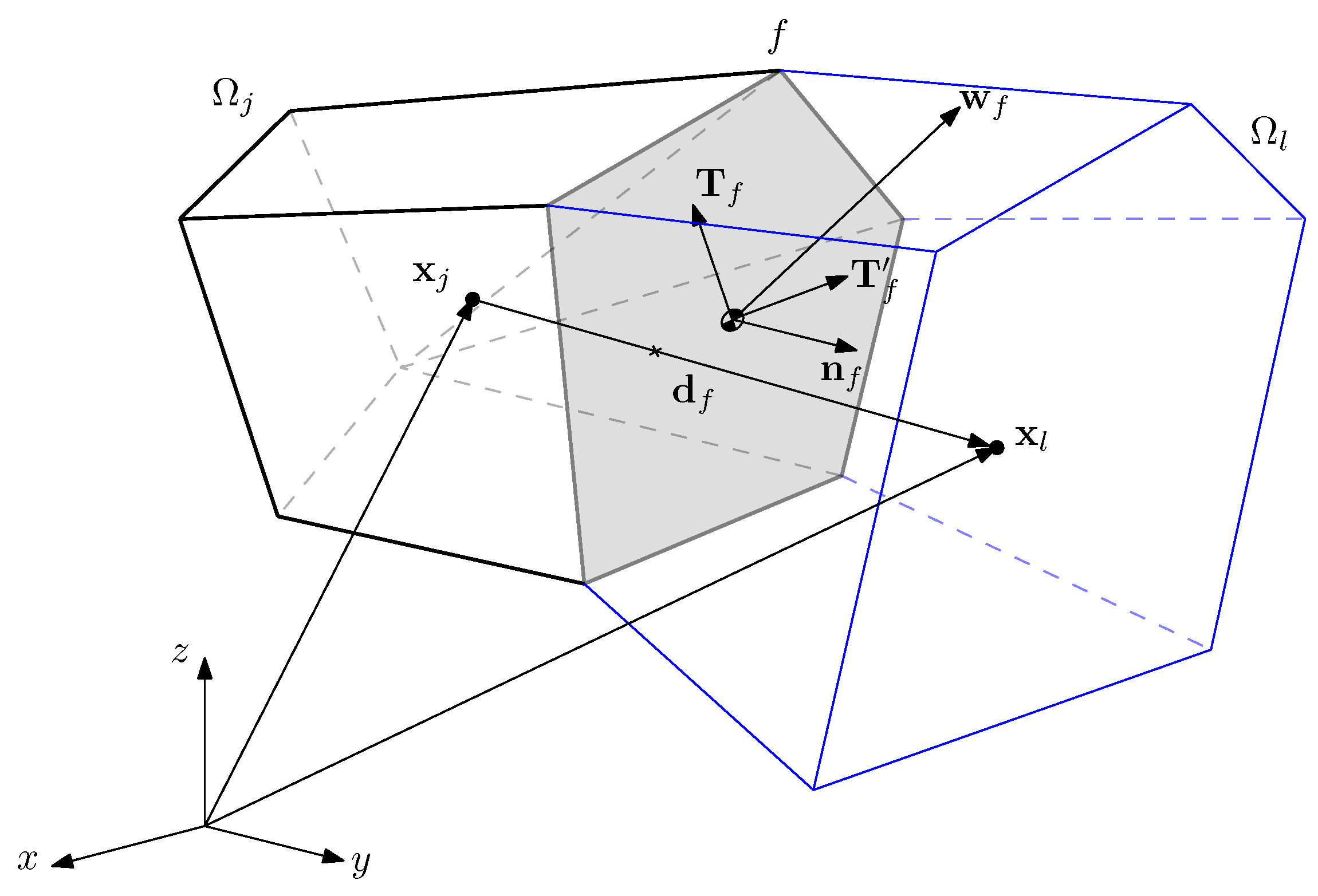
3.2. Finite Volume Integral Formulation
Accumulation Term
3.3. Advective Term
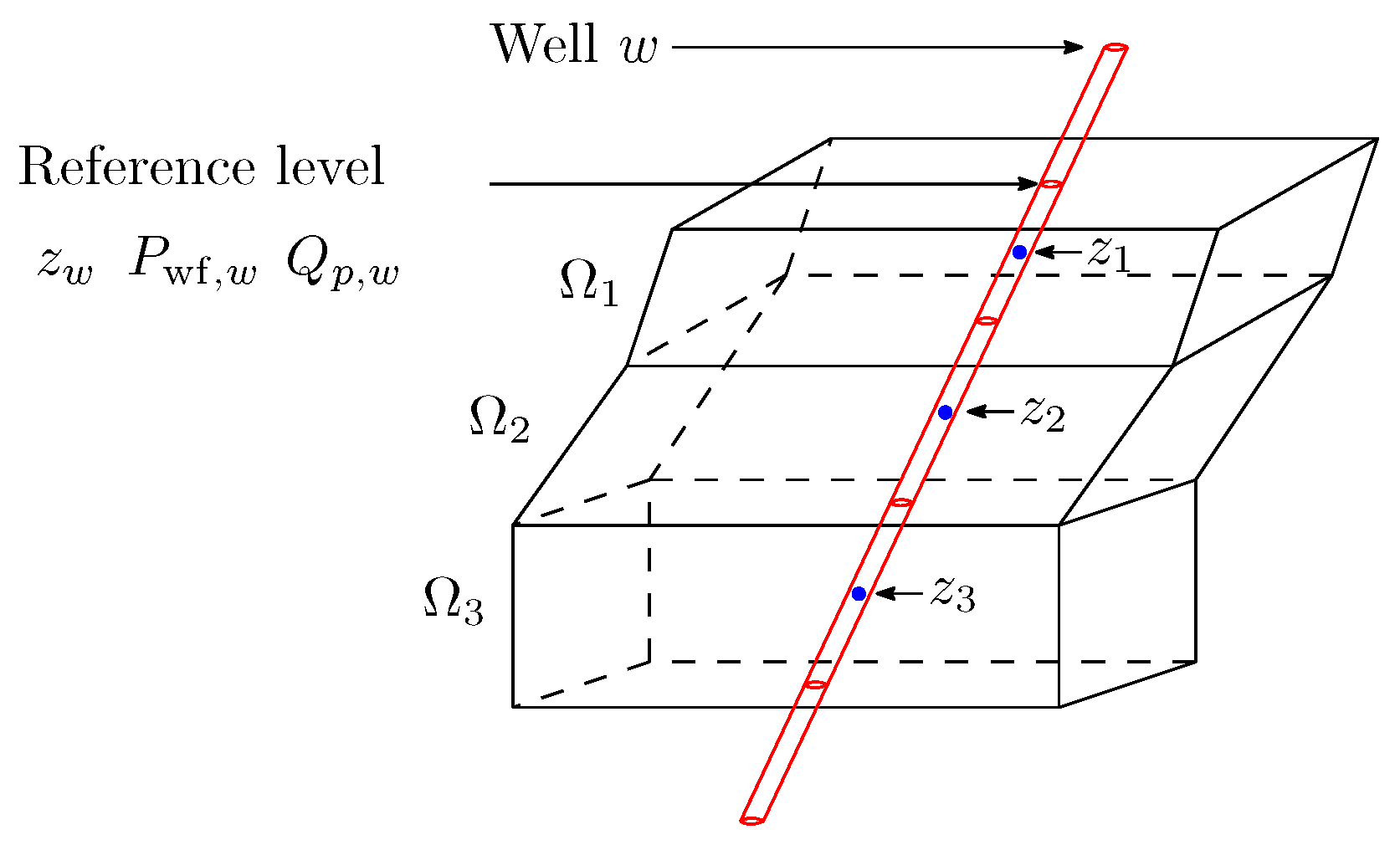
3.4. Source/Sink Term
Time Integration
4. Weighted Least Squares
4.1. General Formulation
WLS Solution
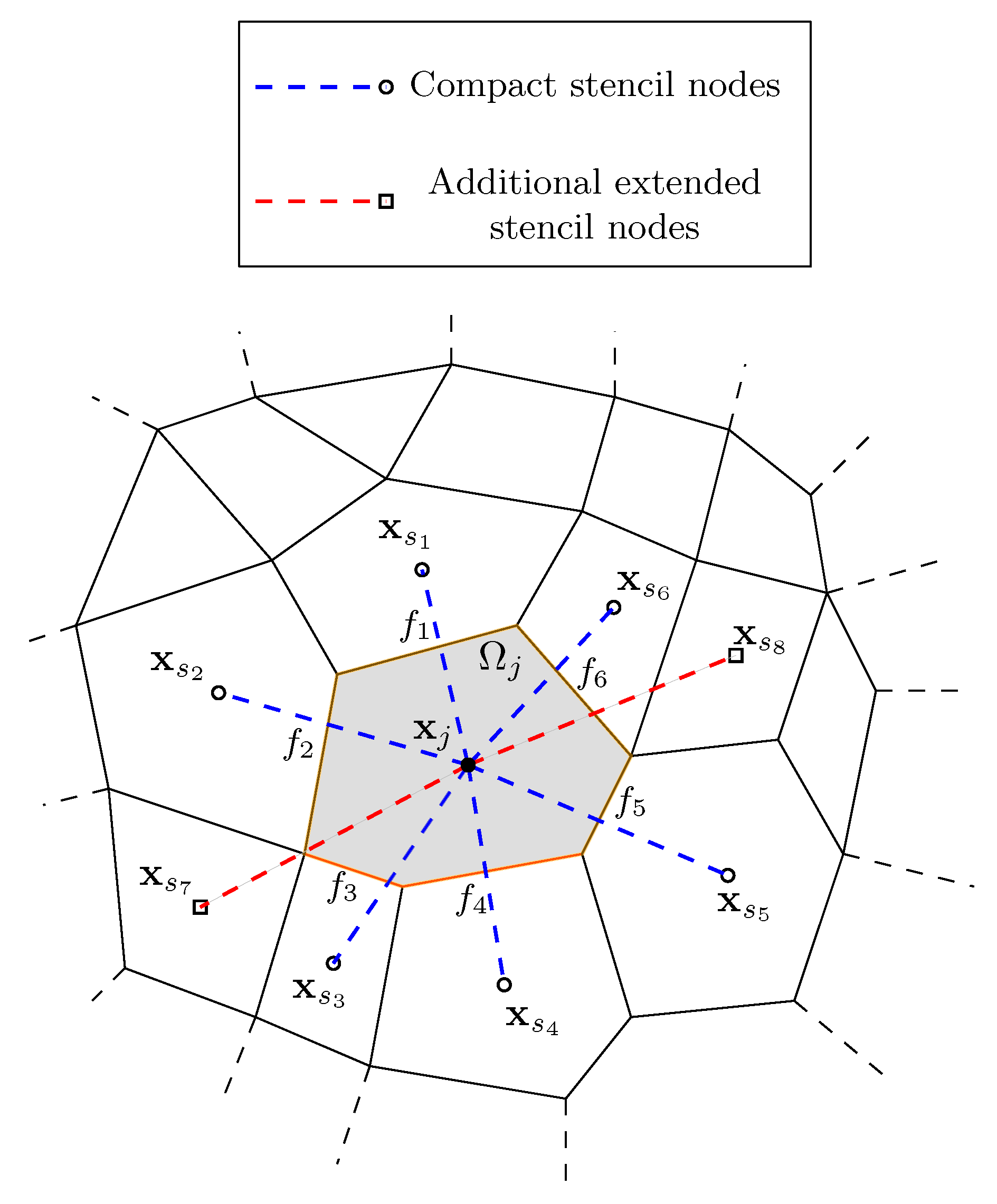
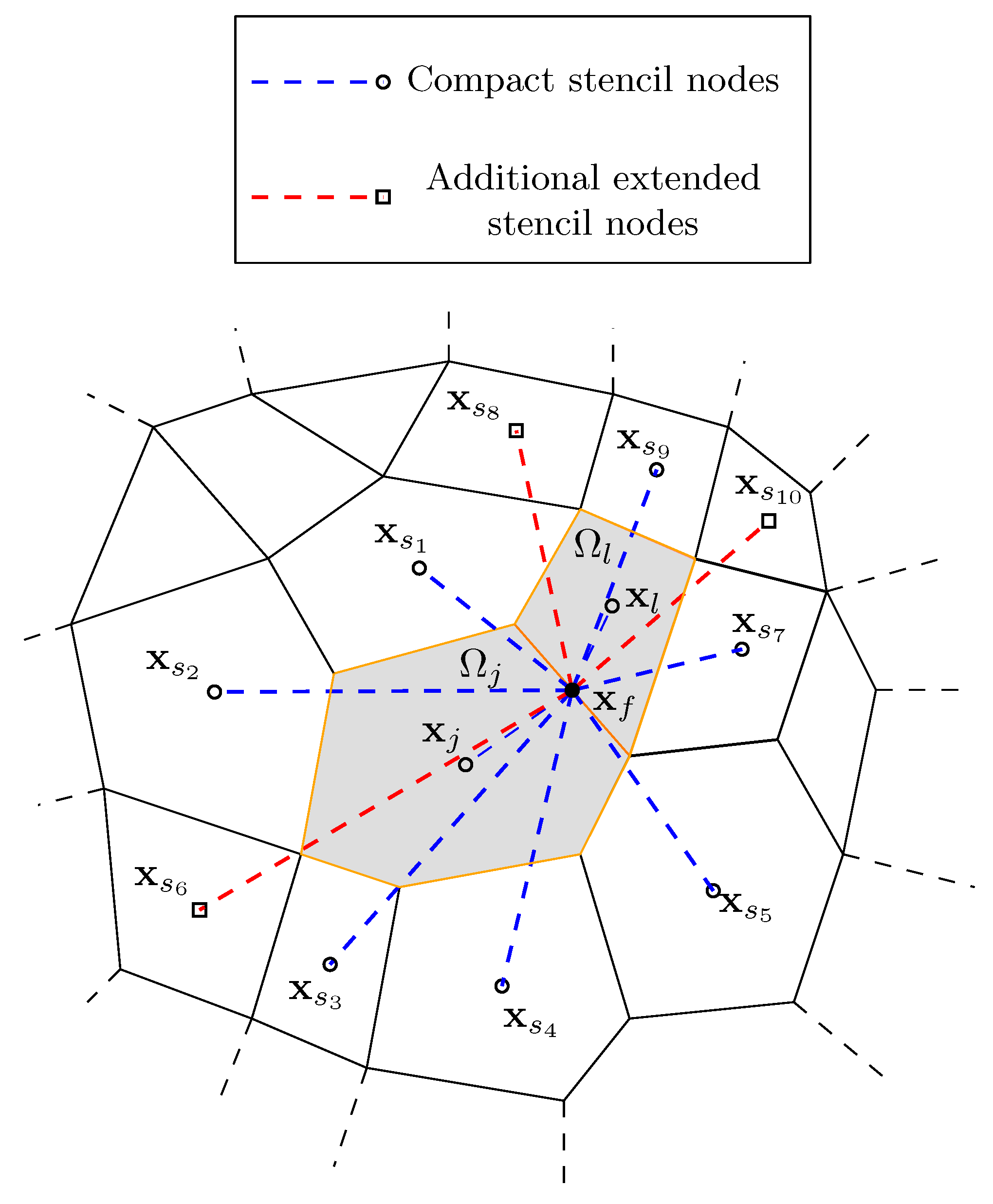
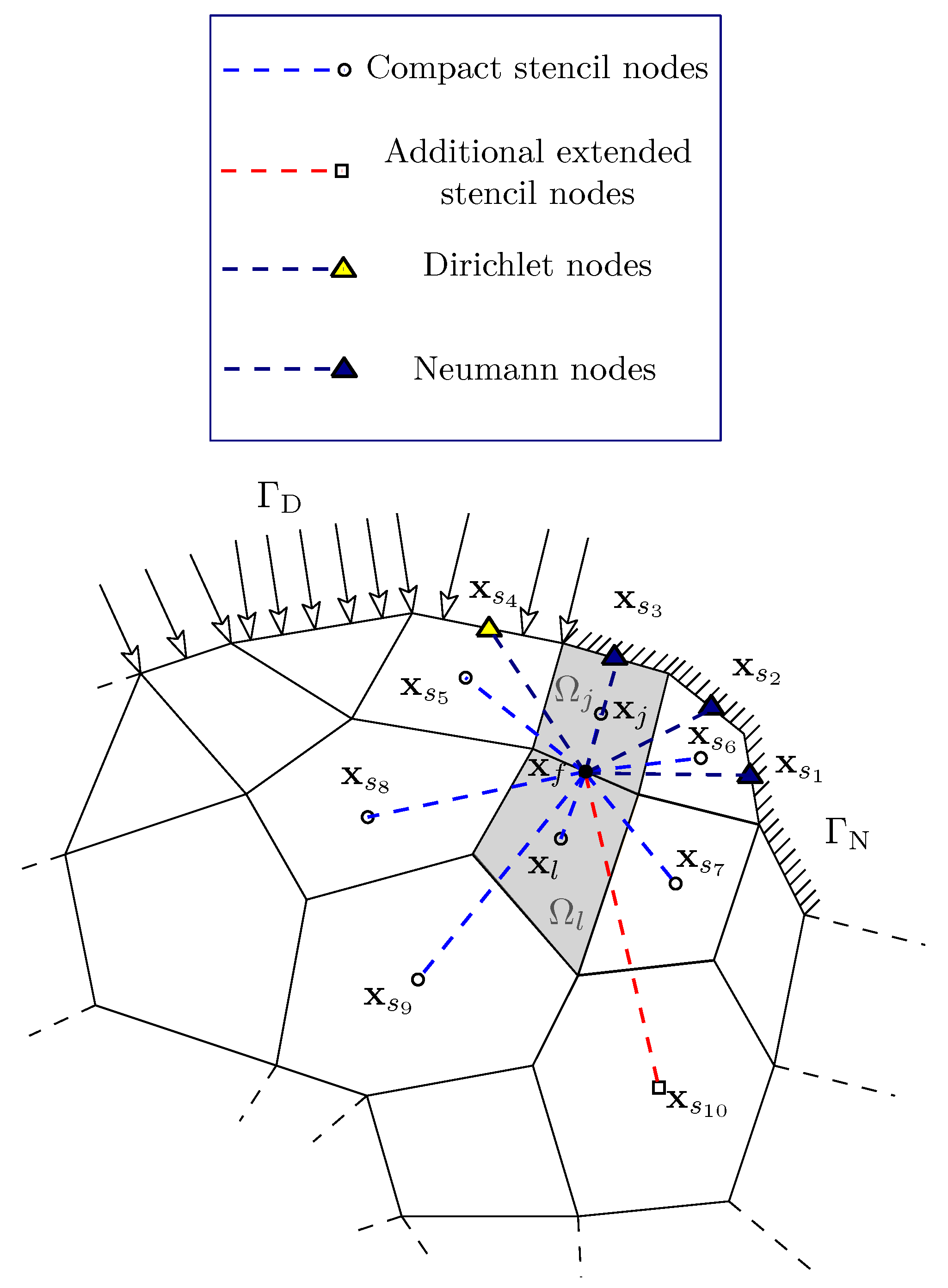
4.2. Stencil Definition
4.2.1. Cell Stencils
4.2.2. Face Stencils
4.2.3. Stencils at Boundaries
4.3. Gradient Reconstruction
4.4. Hessian Reconstruction
5. Semi-Implicit Implementation
| Algorithm 1 Semi-Implicit approach Pseudocode |
 |
6. Numerical Experiments and Discussion
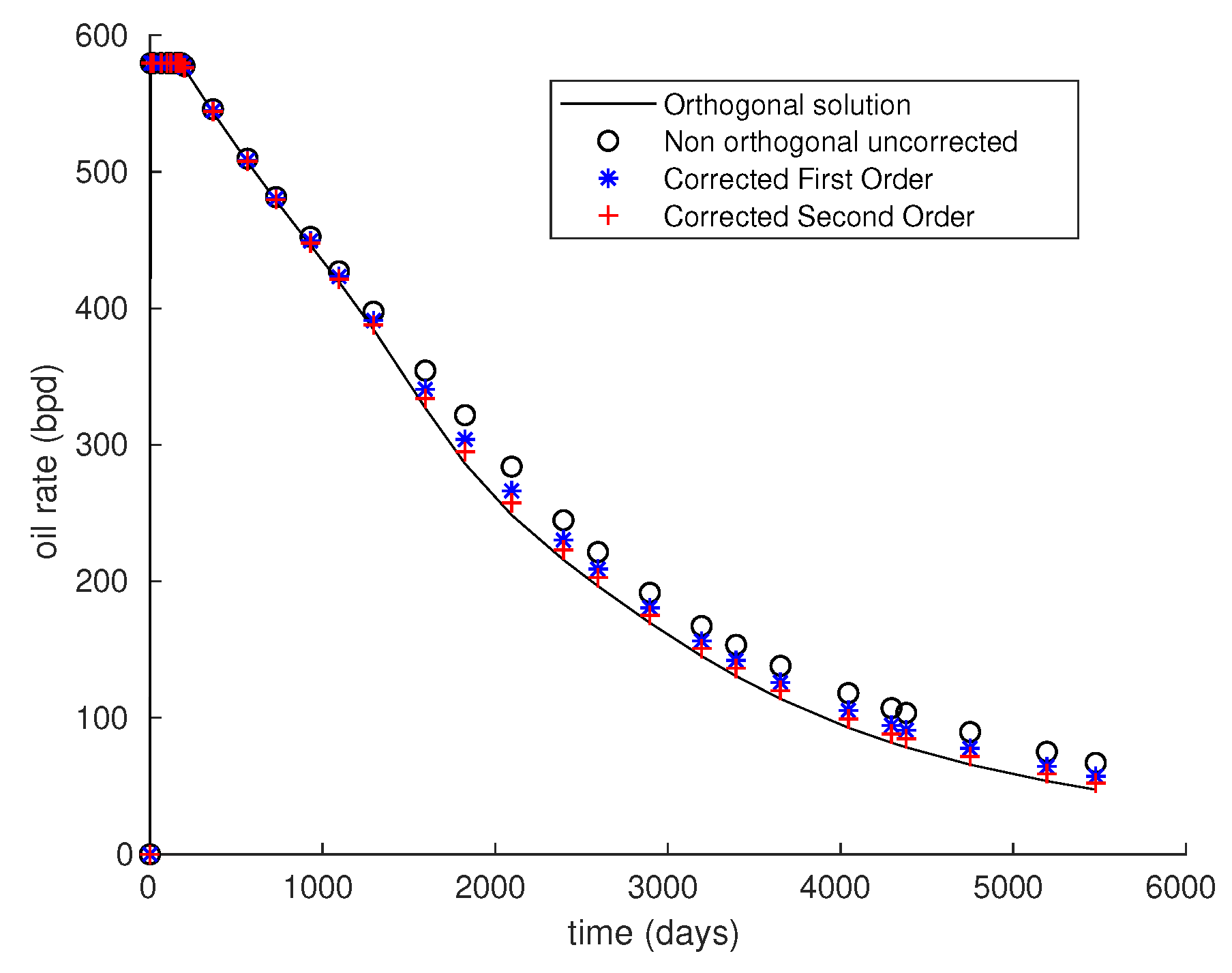
6.1. SPE Comparative Solution Project 3
Convergence Analysis
6.2. SPE Comparative Solution Project 2
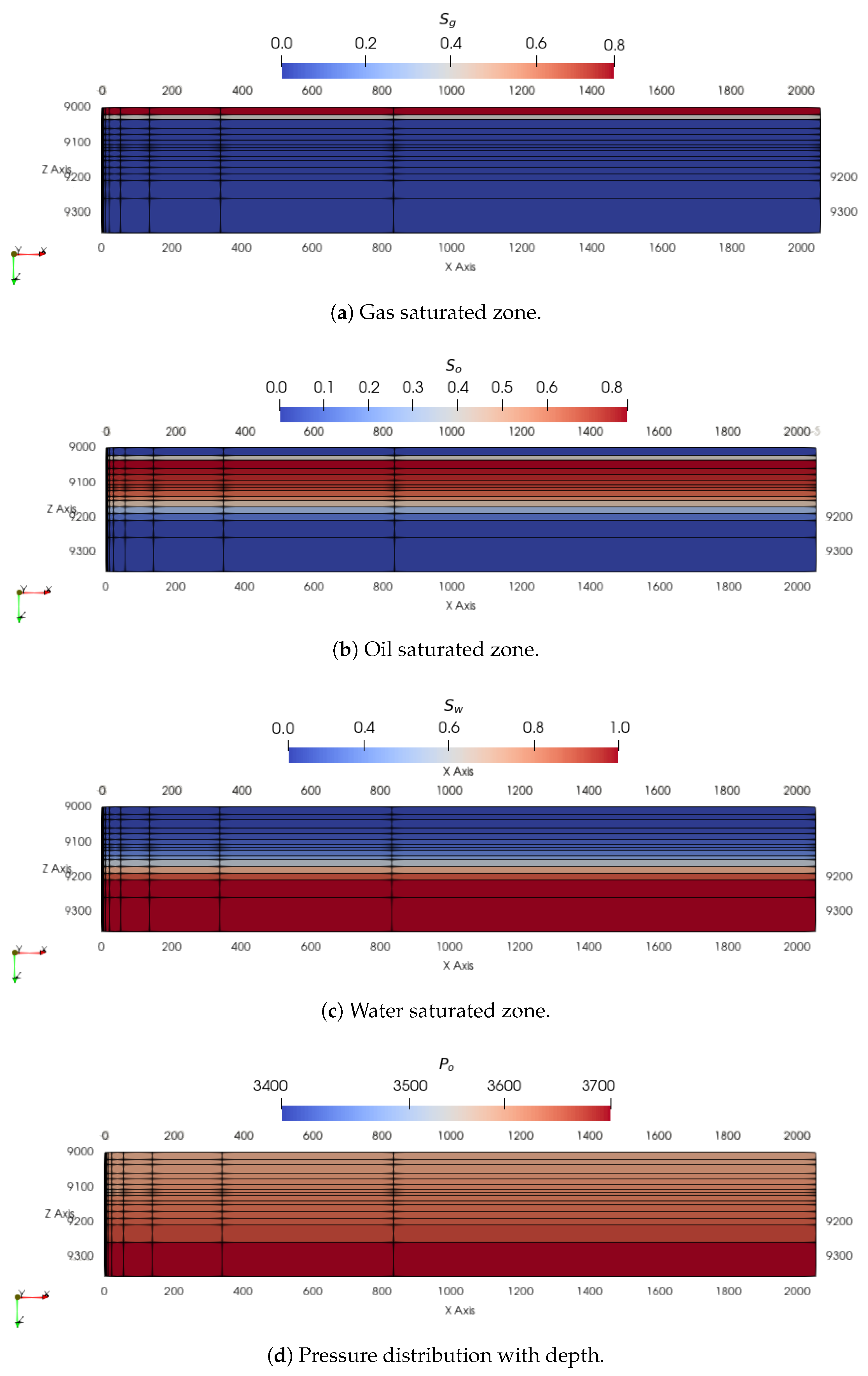
6.3. Colombian Volatile Oil Field Case
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Delshad, M.; Pope, G.; Sepehrnoori, K. A compositional simulator for modeling surfactant enhanced aquifer remediation, 1 formulation. J. Contam. Hydrol. 1996, 23, 303–327. [Google Scholar] [CrossRef]
- Neuman, S.P. Saturated-unsaturated seepage by finite elements. J. Hydraul. Div. 1973, 99, 2233–2250. [Google Scholar] [CrossRef]
- Cheah, E.P.; Reible, D.D.; Valsaraj, K.T.; Constant, W.; Walsh, B.W.; Thibodeaux, L.J. Simulation of soil washing with surfactants. J. Hazard. Mater. 1998, 59, 107–122. [Google Scholar] [CrossRef]
- Corapcioglu, M.Y.; Baehr, A.L. A compositional multiphase model for groundwater contamination by petroleum products: 1. Theoretical considerations. Water Resour. Res. 1987, 23, 191–200. [Google Scholar] [CrossRef]
- Singh, A.; Delfs, J.O.; Böttcher, N.; Taron, J.; Wang, W.; Görke, U.J.; Kolditz, O. A Benchmark Study on Non-isothermal Compositional Fluid Flow. Energy Procedia 2013, 37, 3901–3910. [Google Scholar] [CrossRef] [Green Version]
- Correia, N.; Robitaille, F.; Long, A.; Rudd, C.; Šimáček, P.; Advani, S. Analysis of the vacuum infusion moulding process: I. Analytical formulation. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1645–1656. [Google Scholar] [CrossRef]
- Michaud, V.; Mortensen, A. Infiltration processing of fibre reinforced composites: Governing phenomena. Compos. Part A Appl. Sci. Manuf. 2001, 32, 981–996. [Google Scholar] [CrossRef]
- Valencia, J.D.; Ocampo, A.; Mejía, J.M. Development and Validation of a New Model for In Situ Foam Generation Using Foamer Droplets Injection. Transp. Porous Media 2018, 131, 251–268. [Google Scholar] [CrossRef]
- Solano, H.; Valencia, J.; Mejía, J.; Ocampo, A. A Modeling Study for Foam Generation for EOR Applications in Naturally Fractured Reservoirs Using Disperse Surfactant in the Gas Stream. In Proceedings of the IOR 2019—20th European Symposium on Improved Oil Recovery, Pau, France, 8–11 April 2019. [Google Scholar]
- Pope, G.A.; Nelson, R.C. A chemical flooding compositional simulator. Soc. Pet. Eng. J. 1978, 18, 339–354. [Google Scholar] [CrossRef]
- Mohammadi, H.; Delshad, M.; Pope, G.A. Mechanistic modeling of alkaline/surfactant/polymer floods. SPE Reserv. Eval. Eng. 2009, 12, 518–527. [Google Scholar] [CrossRef]
- Bueno, N.; Mejía, J.M. Heavy oil in-situ upgrading evaluation by a laboratory-calibrated EoS-based reservoir simulator. J. Pet. Sci. Eng. 2020, 196, 107455. [Google Scholar] [CrossRef]
- Qin, X.; Wang, P.; Sepehrnoori, K.; Pope, G.A. Modeling asphaltene precipitation in reservoir simulation. Ind. Eng. Chem. Res. 2000, 39, 2644–2654. [Google Scholar] [CrossRef]
- Fazelipour, W.; Pope, G.A.; Sepehrnoori, K. Development of a fully implicit, parallel, EOS compositional simulator to model asphaltene precipitation in petroleum reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- Darabi, H. Development of a Non-Isothermal Compositional Reservoir Simulator to Model Asphaltene Precipitation, Flocculation, and Deposition and Remediation. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2014. [Google Scholar]
- Darabi, H.; Sepehrnoori, K. Modeling and Simulation of Near-Wellbore Asphaltene Remediation Using Asphaltene Dispersants. In Proceedings of the SPE Reservoir Simulation Symposium, Society of Petroleum Engineersr, Houston, TX, USA, 21–23 February 2015. [Google Scholar]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. In Solution of Equation in Rn (Part 3), Techniques of Scientific Computing (Part 3), Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 2000; Volume 7, pp. 713–1018. [Google Scholar] [CrossRef] [Green Version]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Kocberber, S. An automatic, unstructured control volume generation system for geologically complex reservoirs. In Proceedings of the SPE Reservoir Simulation Symposium. Society of Petroleum Engineers, Dallas, TX, USA, 8–11 June 1997. [Google Scholar]
- Ponting, D.K. Corner point geometry in reservoir simulation. In Proceedings of the ECMOR I-1st European Conference on the Mathematics of Oil Recovery, Cambridge, UK, 14–16 July 1989. [Google Scholar]
- Ding, Y.; Lemonnier, P. Use of corner point geometry in reservoir simulation. In Proceedings of the International Meeting on Petroleum Engineering. Society of Petroleum Engineers, Beijing, China, 14–17 November 1995. [Google Scholar]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002; Volume 31. [Google Scholar]
- Lie, K.A.; Krogstad, S.; Ligaarden, I.S.; Natvig, J.R.; Nilsen, H.M.; Skaflestad, B. Open-source MATLAB implementation of consistent discretisations on complex grids. Comput. Geosci. 2012, 16, 297–322. [Google Scholar] [CrossRef] [Green Version]
- Georgoulis, E.H.; Hall, E.; Houston, P. Discontinuous Galerkin Methods on hp-Anisotropic Meshes I: A Priori Error Analysis. 2006. Available online: https://www.researchgate.net/publication/28692961_Discontinuous_Galerkin_Methods_on_hp-Anisotropic_Meshes_I_A_Priori_Error_Analysis (accessed on 13 September 2021).
- Formaggia, L.; Perotto, S. Anisotropic error estimates for elliptic problems. Numer. Math. 2003, 94, 67–92. [Google Scholar] [CrossRef]
- Arbogast, T.; Wheeler, M.; Yotov, I. Mixed Finite Elements for Elliptic Problems with Tensor Coefficients as Cell-Centered Finite Differences. SIAM J. Numer. Anal. 1997, 34, 828–852. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.; Jones, J.; McCormick, S.; Russell, T. Control-volume mixed finite element methods. Comput. Geosci. 1997, 1, 289–315. [Google Scholar] [CrossRef]
- Faille, I. A control volume method to solve an elliptic equation on a two-dimensional irregular mesh. Comput. Methods Appl. Mech. Eng. 1992, 100, 275–290. [Google Scholar] [CrossRef]
- Pasdunkorale, A.J.; Turner, I.W. A second order finite volume technique for simulating transport in anisotropic media. Int. J. Numer. Methods Heat Fluid Flow 2003, 13, 31–56. [Google Scholar] [CrossRef] [Green Version]
- Jayantha, A.; Turner, P.I.W. A comparison of gradient approximations for use in finite-volume computational models for two-dimensional diffusion equations. Numer. Heat Transf. Part B Fundam. 2001, 40, 367–390. [Google Scholar] [CrossRef] [Green Version]
- Loudyi, D.; Falconer, R.; Lin, B. Mathematical development and verification of a non-orthogonal finite volume model for groundwater flow applications. Adv. Water Resour. 2007, 30, 29–42. [Google Scholar] [CrossRef]
- Klausen, R.A.; Russell, T.F. Relationships among some locally conservative discretization methods which handle discontinuous coefficients. Comput. Geosci. 2004, 8, 341–377. [Google Scholar] [CrossRef]
- Pettersen, Ø. Basics of reservoir simulation with the ECLIPSE reservoir simulator. In Lecture Notes; University of Bergen: Bergen, Norway, 2006; p. 114. [Google Scholar]
- C.M.G. GEM CMG User Guide; Computer Modelling Group Ltd.: Calgary, AB, Canada, 2019. [Google Scholar]
- C.M.G. Advanced Process and Thermal Reservoir Simulator CMG STARS; Computer Modelling Group Ltd.: Calgary, AB, Canada, 2009. [Google Scholar]
- Zyvoloski, G.A.; Robinson, B.A.; Dash, Z.V.; Trease, L.L. User’s Manual for the FEHM Application-A Finite-Element Heat-and Mass-Transfer Code. 1997. Available online: https://www.osti.gov/biblio/14902-user-manual-fehm-application-finite-element-heat-mass-transfer-code (accessed on 13 September 2021).
- Kolditz, O.; Bauer, S.; Bilke, L.; Böttcher, N.; Delfs, J.O.; Fischer, T.; Görke, U.J.; Kalbacher, T.; Kosakowski, G.; McDermott, C.I.; et al. OpenGeoSys: An open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 2012, 67, 589–599. [Google Scholar] [CrossRef]
- Giammarco, P.D.; Todini, E.; Lamberti, P. A conservative finite elements approach to overland flow: The control volume finite element formulation. J. Hydrol. 1996, 175, 267–291. [Google Scholar] [CrossRef]
- Cao, H. Development of Techniques for General Purpose Simulators. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Jiang, Y. Techniques for Modeling Complex Reservoirs and Advanced Wells. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2008. [Google Scholar]
- Wheeler, J. Integrated Parallel and Accurate Reservoir Simulator User’s Manual; Center for Subsurface Modeling, The University of Texas at Austin: Austin, TX, USA, 2007. [Google Scholar]
- Flemisch, B.; Darcis, M.; Erbertseder, K.; Faigle, B.; Lauser, A.; Mosthaf, K.; Müthing, S.; Nuske, P.; Tatomir, A.; Wolff, M.; et al. DuMux: DUNE for multi-phase, component, scale, physics, … flow and transport in porous media. Adv. Water Resour. 2011, 34, 1102–1112, New Computational Methods and Software Tools. [Google Scholar] [CrossRef]
- Bastian, P.; Blatt, M.; Dedner, A.; Engwer, C.; Klöfkorn, R.; Ohlberger, M.; Sander, O. A generic grid interface for parallel and adaptive scientific computing. Part I: Abstract framework. Computing 2008, 82, 103–119. [Google Scholar] [CrossRef]
- Bastian, P.; Blatt, M.; Dedner, A.; Engwer, C.; Klöfkorn, R.; Kornhuber, R.; Ohlberger, M.; Sander, O. A generic grid interface for parallel and adaptive scientific computing. Part II: Implementation and tests in DUNE. Computing 2008, 82, 121–138. [Google Scholar] [CrossRef]
- Baxendale, D.; Skaflestad, B.; Rasmussen, A.; Hove, J.; Rustad, A.B.; Lauser, A.; Skille, T.; Bao, K.; Sandve, T.H.; Blatt, M.; et al. OPEN POROUS MEDIA: Flow Documentation Manual; Equinox International Petroleum Consultants Pte. Ltd.: Tokyo, Japan, 2019. [Google Scholar]
- Lie, K.A. An Introduction to Reservoir Simulation Using MATLAB/GNU Octave: User Guide for the MATLAB Reservoir Simulation Toolbox (MRST); Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef] [Green Version]
- Krogstad, S.; Lie, K.A.; Møyner, O.; Nilsen, H.M.; Raynaud, X.; Skaflestad, B. MRST-AD—An open-source framework for rapid prototyping and evaluation of reservoir simulation problems. In Proceedings of the SPE Reservoir Simulation Symposium. Society of Petroleum Engineers, Houston, TX, USA, 23–25 February 2015. [Google Scholar]
- Juretić, F.; Gosman, A.D. Error Analysis of the Finite-Volume Method with Respect to Mesh Type. Numer. Heat Transf. Part B Fundam. 2010, 57, 414–439. [Google Scholar] [CrossRef]
- Au, A.D.; Behie, G.; Rubin, B.; Vinsome, P. Techniques for fully implicit reservoir simulation. In Proceedings of the SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers, San Antonio, TX, USA, 8–11 October 1980. [Google Scholar]
- Ascher, U.M.; Ruuth, S.J.; Wetton, B.T. Implicit-explicit methods for time-dependent partial differential equations. SIAM J. Numer. Anal. 1995, 32, 797–823. [Google Scholar] [CrossRef]
- Rodrigues, S.B. Improving the IMEX method with a residual balanced decomposition. arXiv 2017, arXiv:1705.04870. [Google Scholar]
- Di Castro, A. Elliptic Problems for Some Anisotropic Operators. Ph.D. Thesis, University of Rome “Sapienza”, Rome, Italy, 2009. [Google Scholar]
- Mihăilescu, M.; Pucci, P.; Rădulescu, V. Eigenvalue problems for anisotropic quasilinear elliptic equations with variable exponent. J. Math. Anal. Appl. 2008, 340, 687–698. [Google Scholar] [CrossRef] [Green Version]
- Civan, F. Porous Media Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3. [Google Scholar]
- Gaikwad, S.; Malashetty, M.; Prasad, K.R. An analytical study of linear and nonlinear double diffusive convection in a fluid saturated anisotropic porous layer with Soret effect. Appl. Math. Model. 2009, 33, 3617–3635. [Google Scholar] [CrossRef]
- Valdes-Parada, F.; Porter, M.; Wood, B. Bacterial Chemotaxis in Porous Media: Theory Derivation and Comparison with Experiments. In Proceedings of the AIP Conference Proceedings, Novosibirsk, Russia, 3–7 December 2010; pp. 131–138. [Google Scholar] [CrossRef]
- Valdés-Parada, F.J.; Porter, M.L.; Narayanaswamy, K.; Ford, R.M.; Wood, B.D. Upscaling microbial chemotaxis in porous media. Adv. Water Resour. 2009, 32, 1413–1428. [Google Scholar] [CrossRef]
- Ford, R.M.; Harvey, R.W. Role of chemotaxis in the transport of bacteria through saturated porous media. Adv. Water Resour. 2007, 30, 1608–1617. [Google Scholar] [CrossRef]
- Concha, F.; Barrientos, A. Mecánica racional moderna. In Vol. II Termodinámica del Medio Continuo, Serie en Mecánica Racional Moderna; Departamento de Ingeniería Metalúrgica, Universidad de Concepción: Concepción, Chile, 1993. [Google Scholar]
- Johnston, K.A.; Satyro, M.A.; Taylor, S.D.; Yarranton, H.W. Can a Cubic Equation of State Model Bitumen–Solvent Phase Behavior? Energy Fuels 2017, 31, 7967–7981. [Google Scholar] [CrossRef]
- Danesh, A. PVT and Phase Behaviour of Petroleum Reservoir Fluids; Developments in Petroleum Science 47; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Peng, D.Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Wang, Y. Implementation of a Two Pseudo-Component Approach for Variable Bubble Point Problems in GPRS. Master’s Thesis, Stanford University, Stanford, CA, USA, 2007. [Google Scholar]
- Abou-Kassem, J.H.; Islam, M.R.; Farouq-Ali, S. Petroleum Reservoir Simulations; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Aziz, K.; Settari, A. Petroleum Reservoir Simulation; Applied Science Publ. Ltd.: London, UK, 1979. [Google Scholar]
- Bear, J. Modeling Phenomena of Flow and Transport in Porous Media; Springer: Berlin/Heidelberg, Germany, 2018; Volume 31. [Google Scholar]
- Ivanenko, S.A. Selected Chapters on Grid Generation and Applications; Dorodnicyn Computing Centre of the Russ: Moscow, Russia, 2004. [Google Scholar]
- Berti, G. Generic Software Components for Scientific Computing. Ph.D. Thesis, Faculty of Mathematics, and Natural Science, Computer Science, BTU Cottbus, Cottbus, Germany, 2000. [Google Scholar]
- Elmahi, I.; Benkhaldoun, F.; Vilsmeier, R.; Gloth, O.; Patschull, A.; Hänel, D. Finite volume simulation of a droplet flame ignition on unstructured meshes. J. Comput. Appl. Math. 1999, 103, 187–205. [Google Scholar] [CrossRef]
- Islam, M.R.; Hossain, M.E.; Mousavizadegan, S.H.; Mustafiz, S.; Abou-Kassem, J.H. Advanced Petroleum Reservoir Simulation: Towards Developing Reservoir Emulators; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Terekhov, K.M.; Mallison, B.T.; Tchelepi, H.A. Cell-centered nonlinear finite-volume methods for the heterogeneous anisotropic diffusion problem. J. Comput. Phys. 2017, 330, 245–267. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of well-block pressures in numerical reservoir simulation (includes associated paper 6988). Soc. Pet. Eng. J. 1978, 18, 183–194. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of well-block pressures in numerical reservoir simulation with nonsquare grid blocks and anisotropic permeability. Soc. Pet. Eng. J. 1983, 23, 531–543. [Google Scholar] [CrossRef]
- Civan, F. Reservoir Formation Damage; Gulf Professional Publishing: Houston, TX, USA, 2015. [Google Scholar]
- Dragomir, S.; Fedotov, I. Approximating the Stieltjes integral via a weighted trapezoidal rule with applications. Math. Comput. Model. 2013, 57, 602–611. [Google Scholar] [CrossRef]
- Bjorck, A. Numerical Methods for Least Squares Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Siam: San francisco, CA, USA, 1995; Volume 15. [Google Scholar]
- Jayantha, P.A.; Turner, I.W. On the use of surface interpolation techniques in generalised finite volume strategies for simulating transport in highly anisotropic porous media. J. Comput. Appl. Math. 2003, 152, 199–216. [Google Scholar] [CrossRef] [Green Version]
- Trefethen, L.N.; Bau, D., III. Numerical Linear Algebra; Siam: San francisco, CA, USA, 1997; Volume 50. [Google Scholar]
- Sozer, E.; Brehm, C.; Kiris, C.C. Gradient calculation methods on arbitrary polyhedral unstructured meshes for cell-centered cfd solvers. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; Volume 1317. [Google Scholar]
- Ewing, R.; Lin, T.; Falk, R. Inverse and Ill-Posed problems in reservoir simulation. In Inverse and Ill-Posed Problems; Engl, H.W., Groetsch, C., Eds.; Academic Press: Cambridge, MA, USA, 1987; pp. 483–497. [Google Scholar] [CrossRef]
- Jasak, A.D.G.H. Residual error estimate for the finite-volume method. Numer. Heat Transf. Part B Fundam. 2001, 39, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. 1996. Available online: https://foam-extend.fsb.hr/wp-content/uploads/2016/12/Jasak_PhD_1996.pdf (accessed on 13 September 2021).
- Juretic, F. Error Analysis in Finite Volume CFD. Ph.D. Thesis, Imperial College London (University of London), London, UK, 2005. [Google Scholar]
- Moraes, A.; Lage, P.; Cunha, G.; da Silva, L.F.L.R. Analysis of the non-orthogonality correction of finite volume discretization on unstructured meshes. In Proceedings of the 22nd International Congress of Mechanical Engineering, Ribeirão Preto, Brazil, 3–7 November 2013; pp. 3519–3530. [Google Scholar]
- Kenyon, D.E.; Co, M.O.; Behie, O.A.; Systems, D.R. Third SPE Comparative Solution Project: Gas Cycling of Retrograde Condensate Reservoirs. J. Pet. Technol. 1987, 39, 981–997. [Google Scholar] [CrossRef]
- Weinstein, H.; Chappelear, J.; Nolen, J. Second comparative solution project: A three-phase coning study. J. Pet. Technol. 1986, 38, 345–353. [Google Scholar] [CrossRef]
- Wolfsteiner, C.; Durlofsky, L.J.; Aziz, K. Calculation of well index for nonconventional wells on arbitrary grids. Comput. Geosci. 2003, 7, 61–82. [Google Scholar] [CrossRef]
- Kramarenko, V.; Nikitin, K.; Vassilevski, Y. A finite volume scheme with improved well modeling in subsurface flow simulation. Comput. Geosci. 2017, 21, 1023–1033. [Google Scholar] [CrossRef]



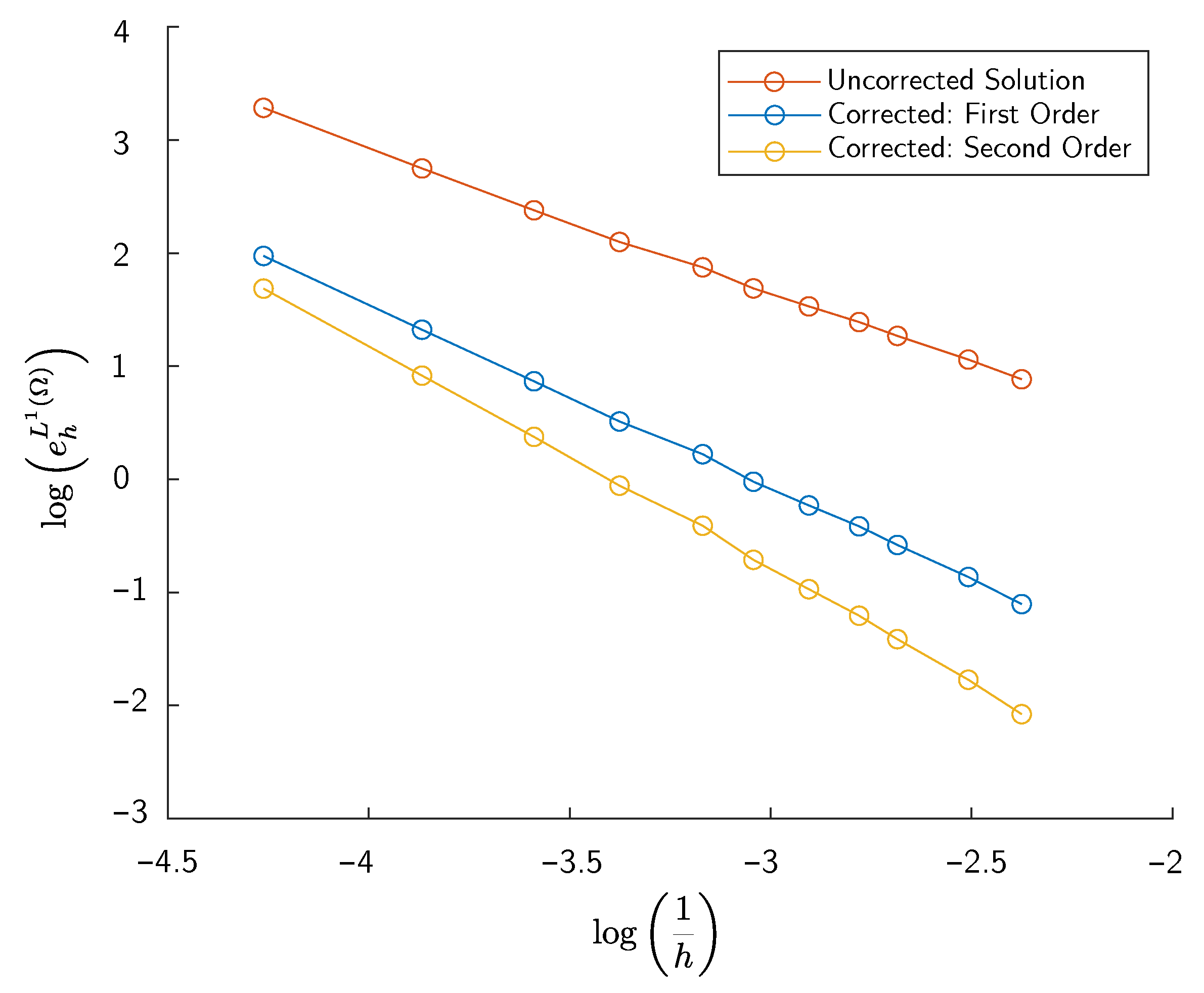
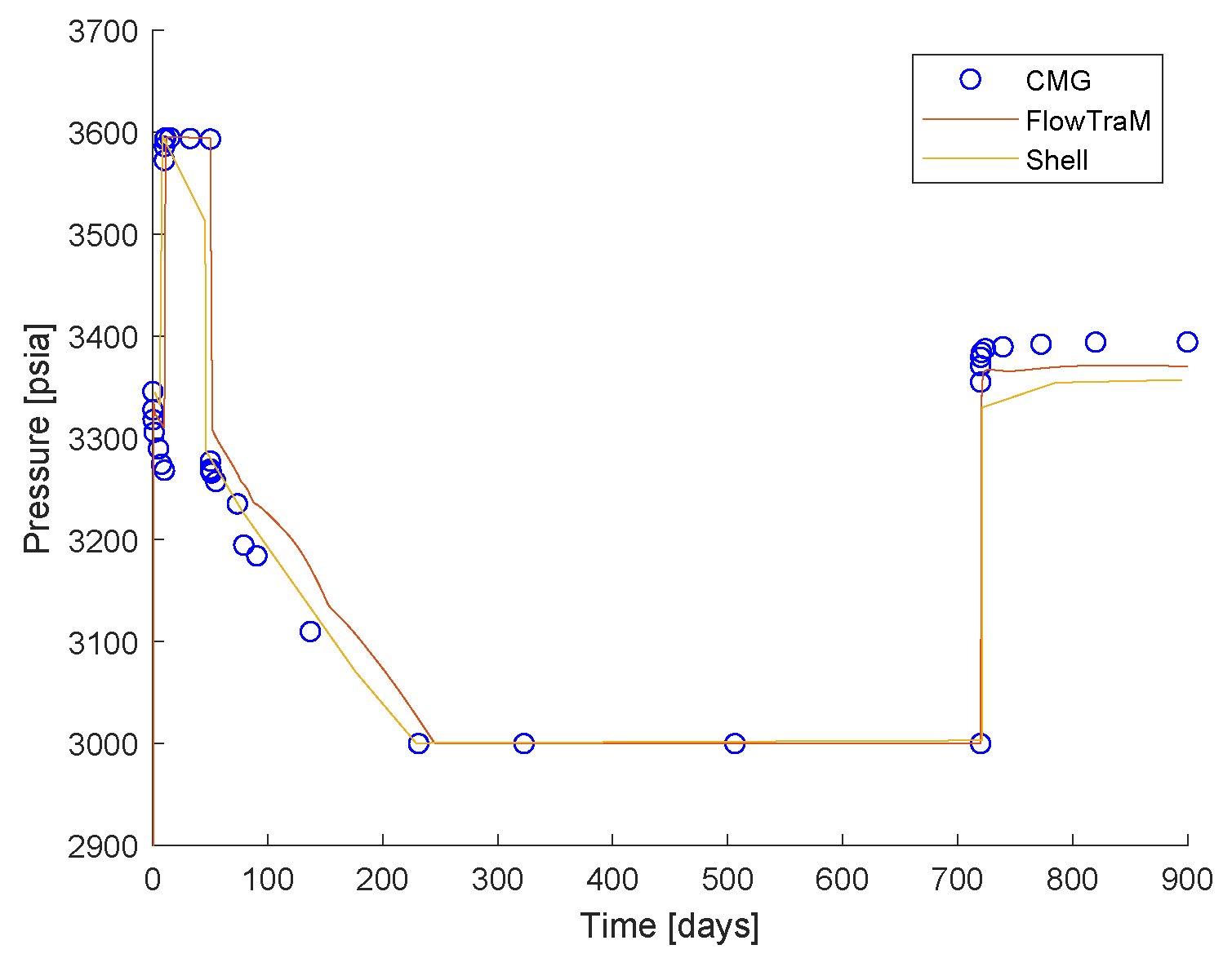
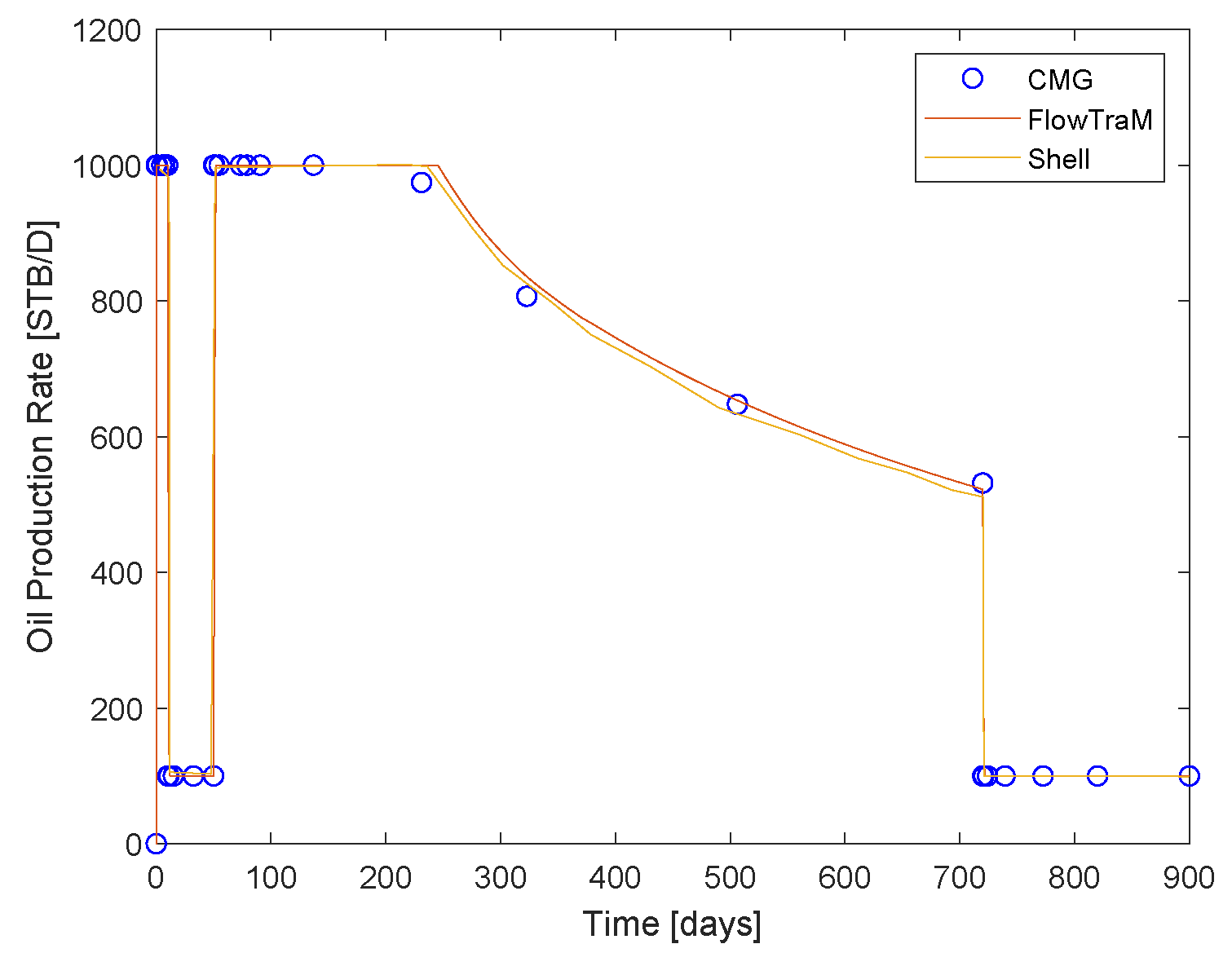
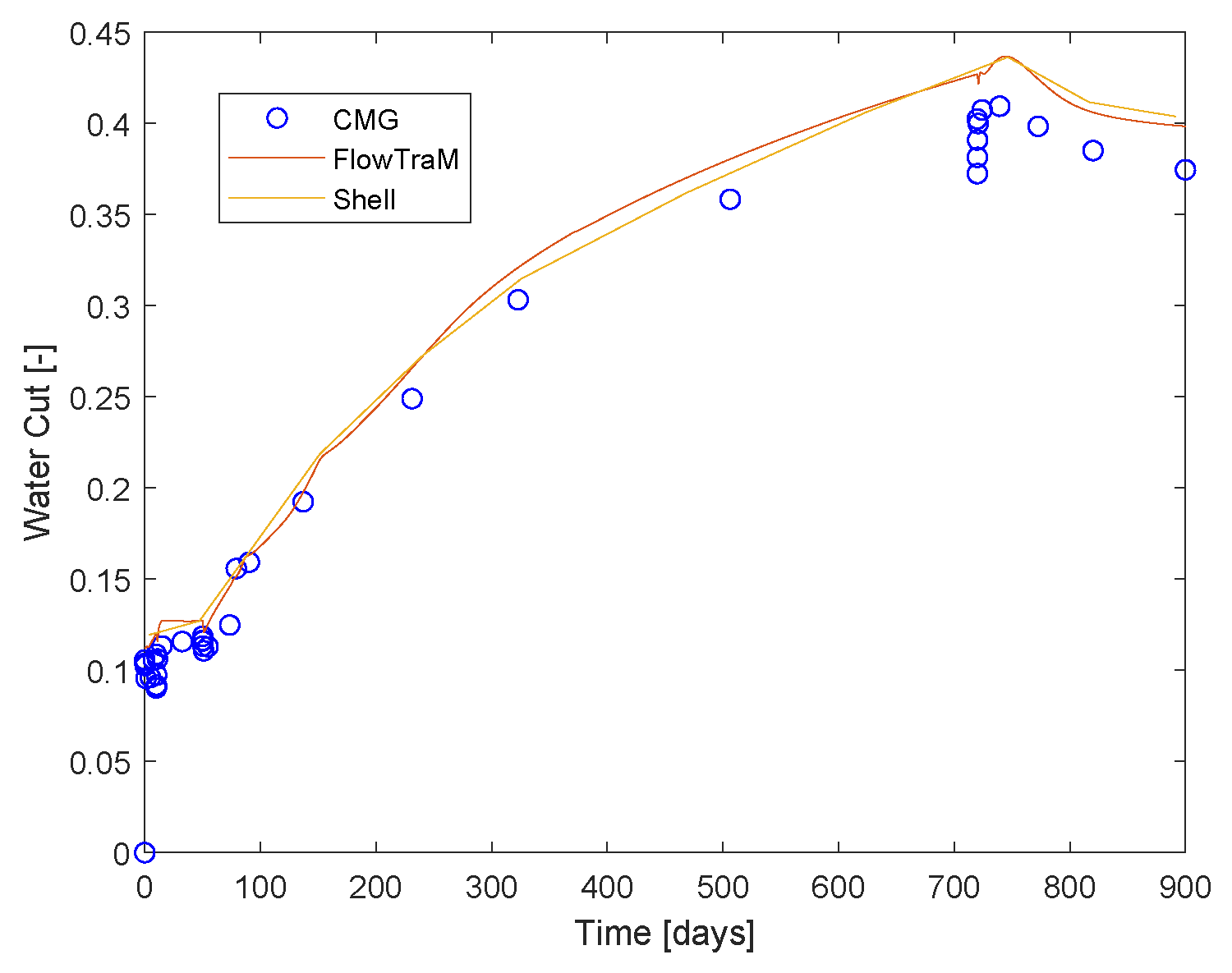
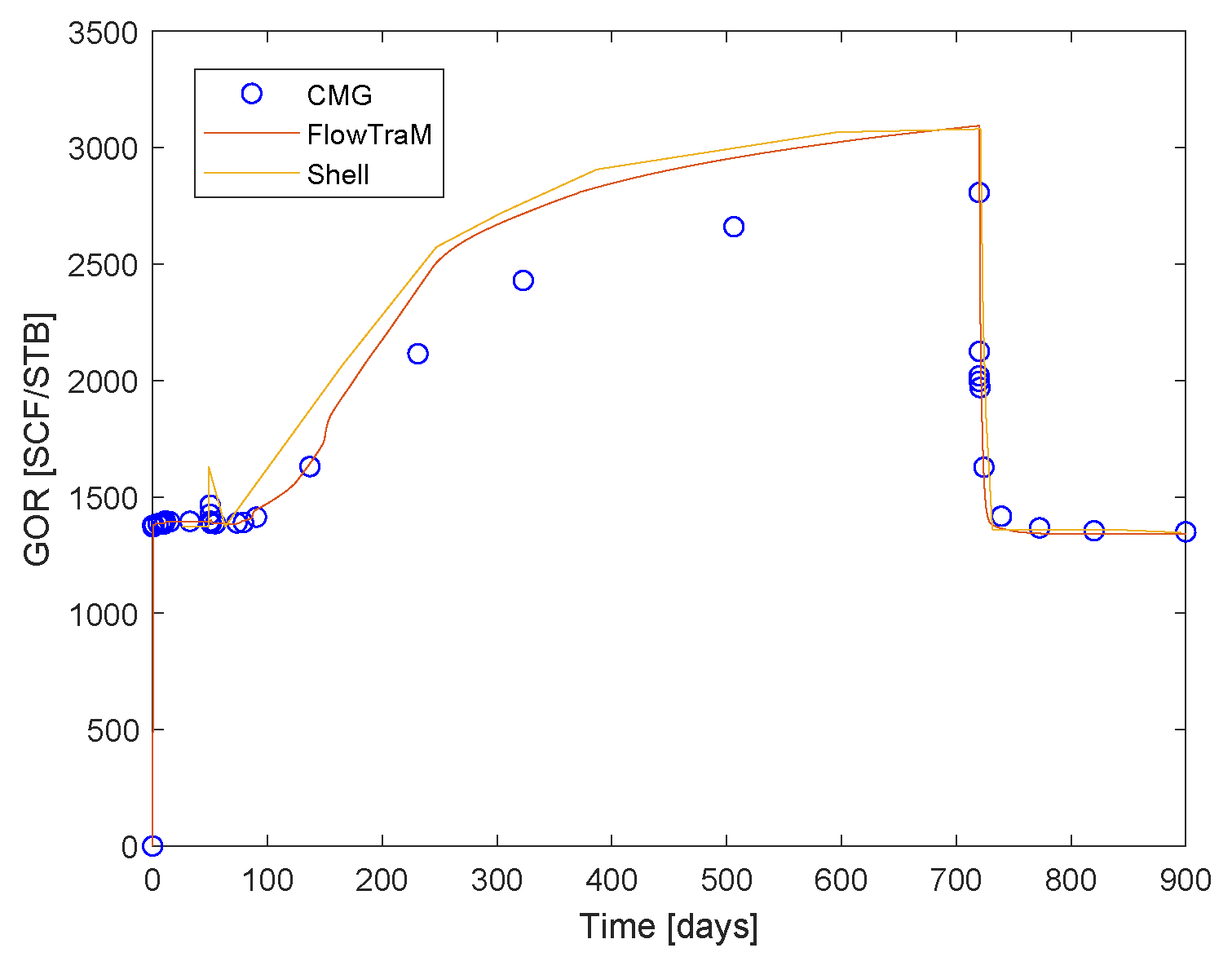
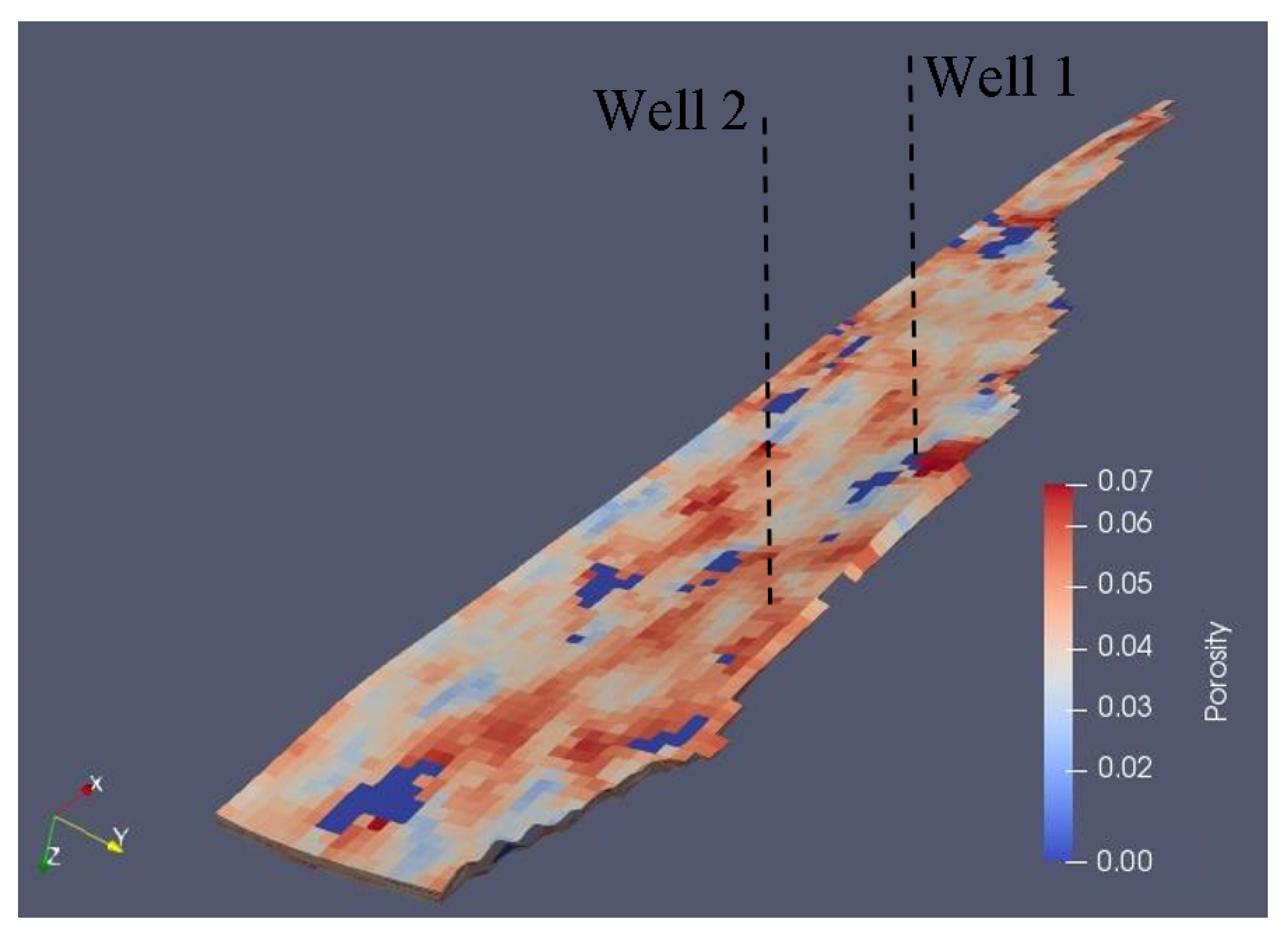
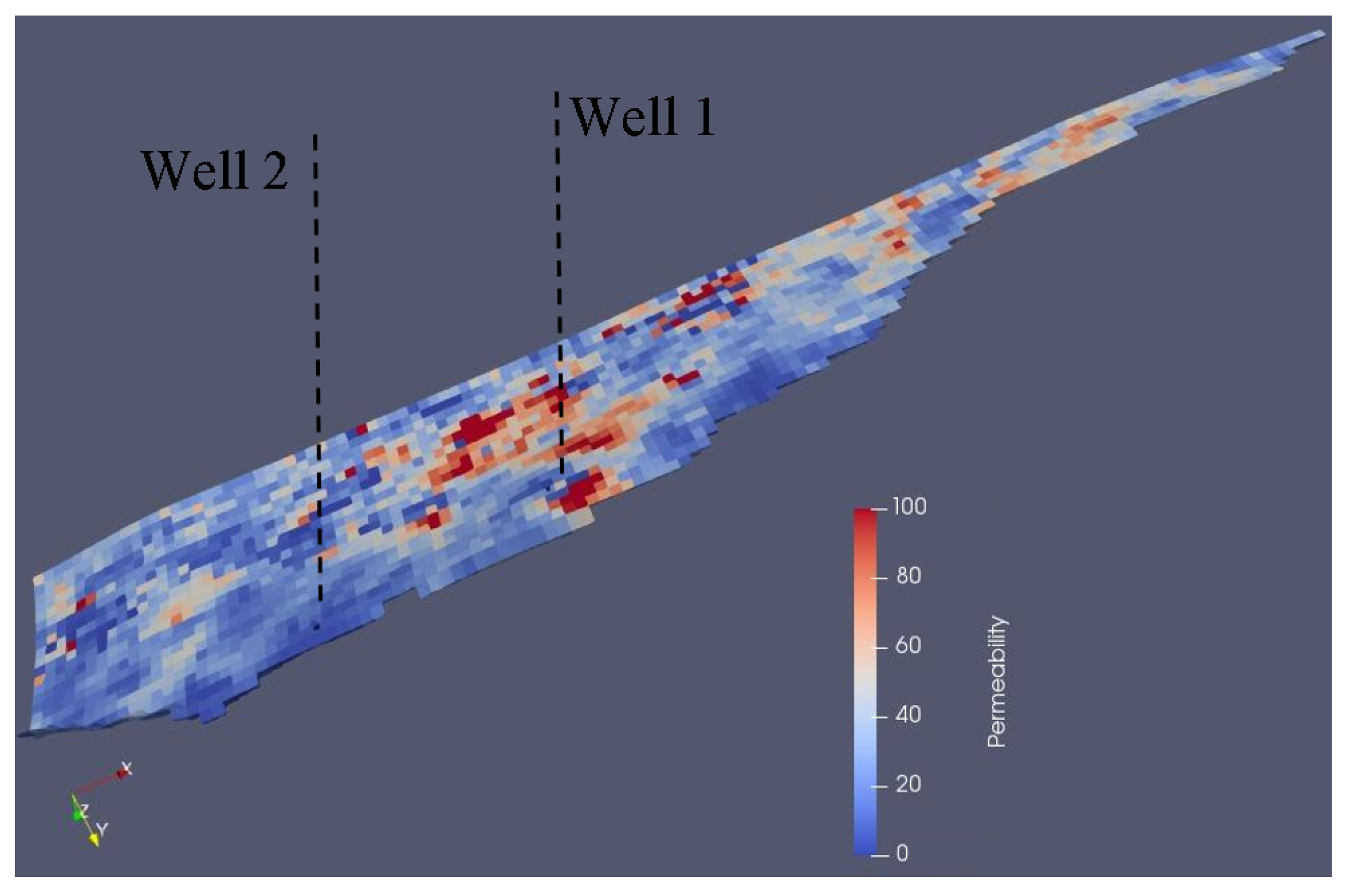
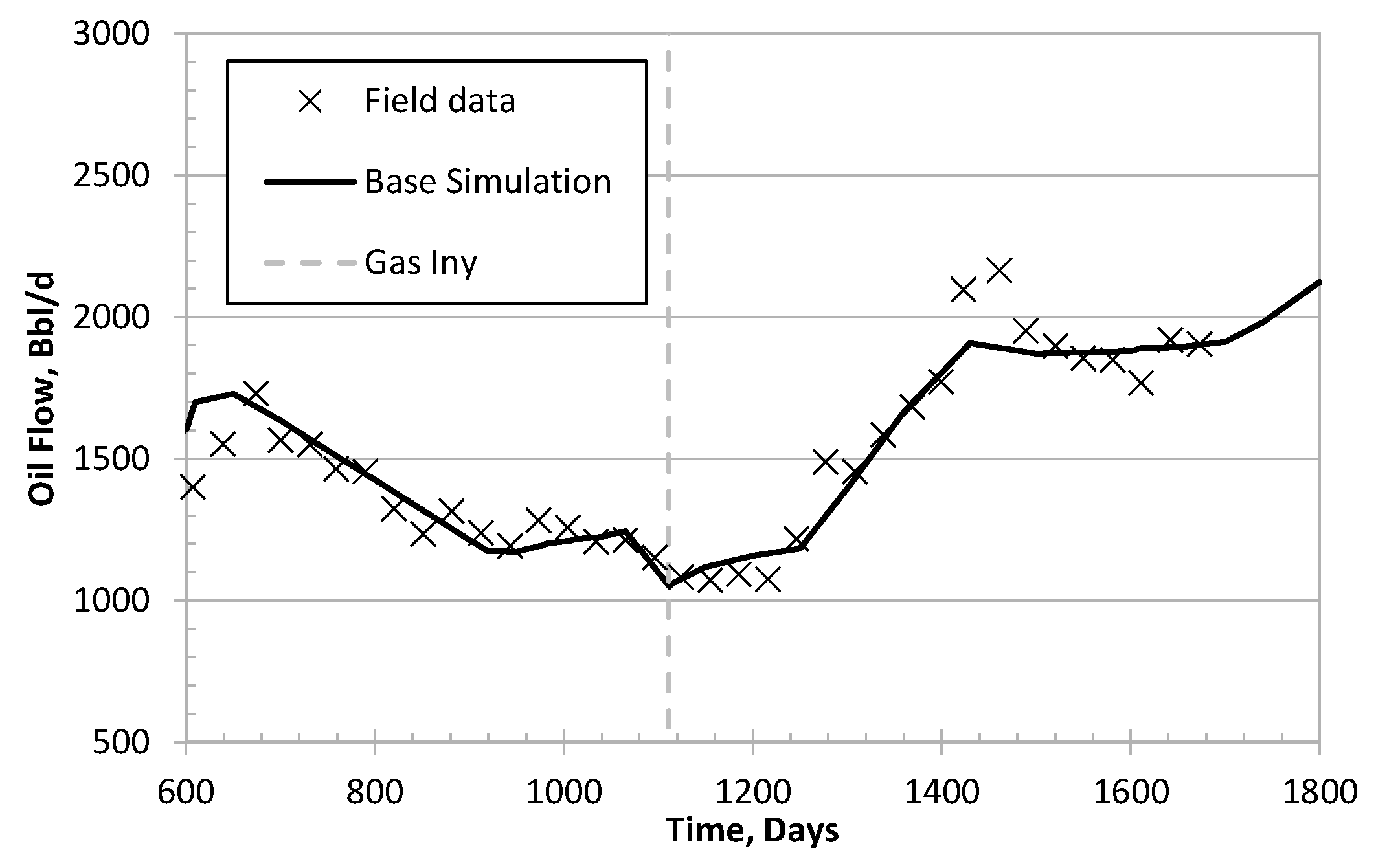
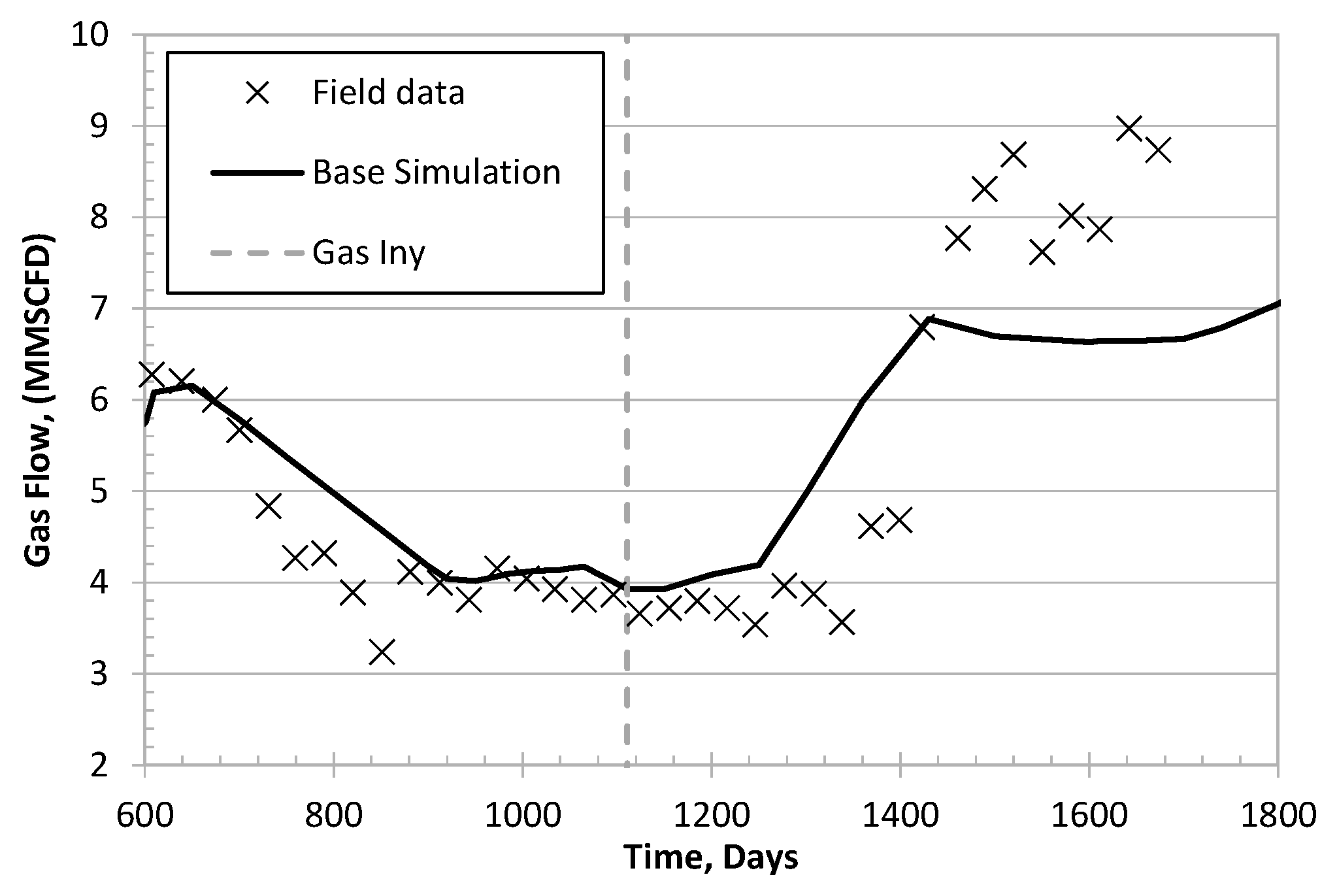

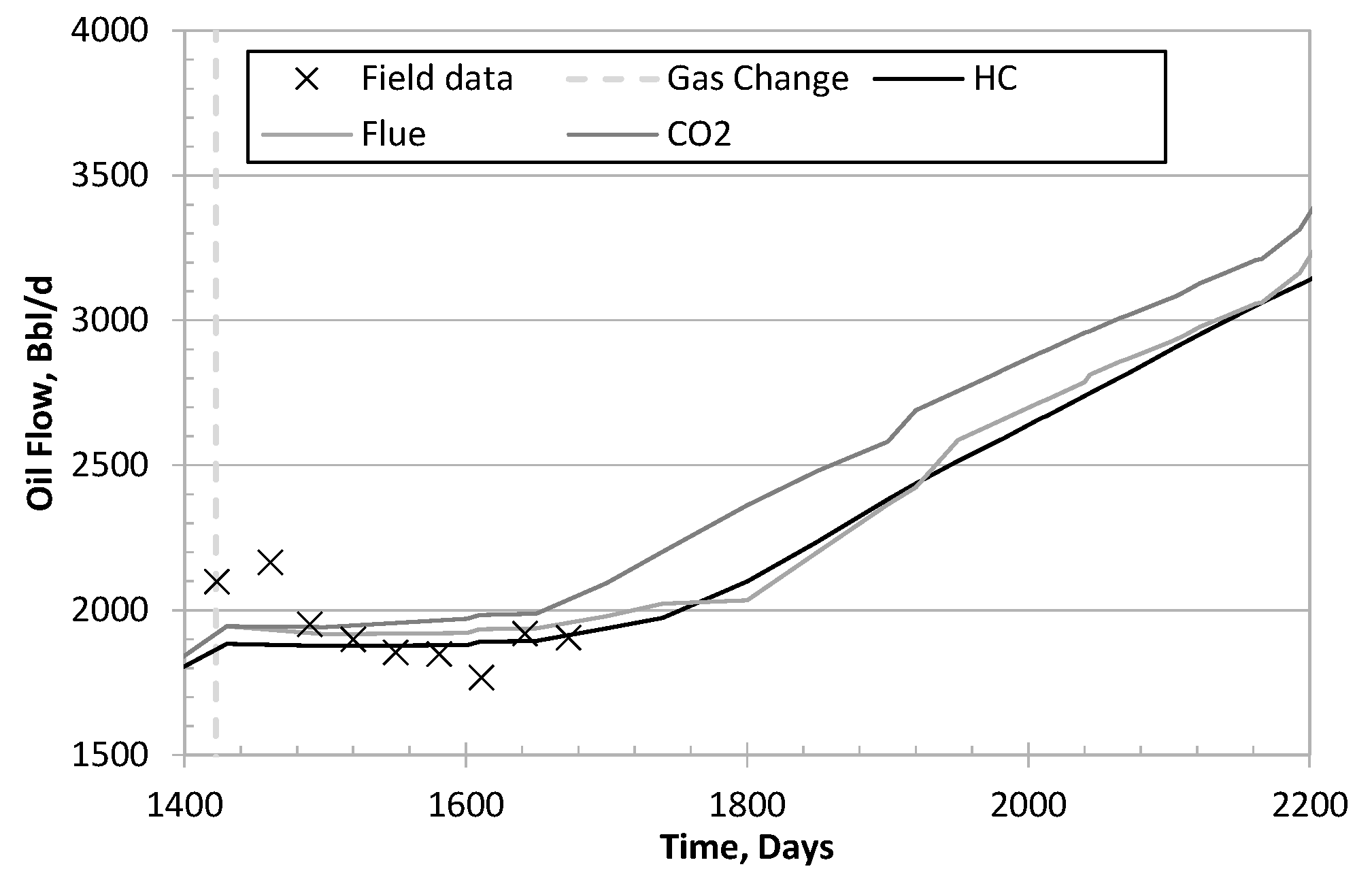
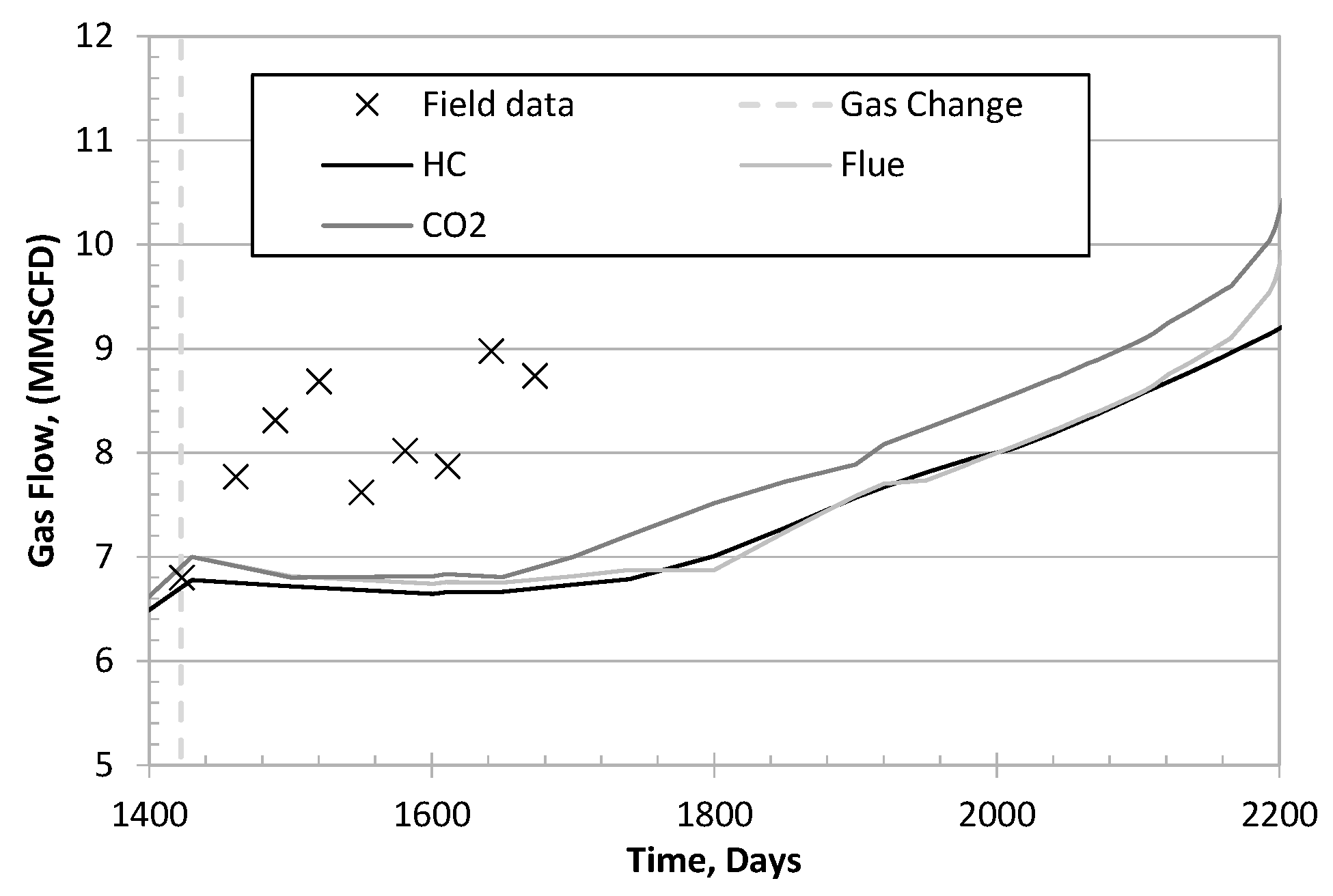
| k | Acentric Factor | (psi) | (R) | (ft/lbm) | |
|---|---|---|---|---|---|
| C | 0.0130 | 588.0 | 350.00 | 16.04 | 0.0988 |
| C | 0.0986 | 708.5 | 549.77 | 30.07 | 0.0788 |
| C | 0.1524 | 617.5 | 665.82 | 44.10 | 0.0727 |
| C | 0.2010 | 550.8 | 765.36 | 58.12 | 0.0703 |
| C | 0.2539 | 489.7 | 845.28 | 72.15 | 0.0690 |
| C | 0.3007 | 439.8 | 914.22 | 86.18 | 0.0684 |
| C | 0.3613 | 385.9 | 1032.21 | 114.43 | 0.0652 |
| C | 0.4501 | 340.8 | 1148.02 | 144.83 | 0.0630 |
| C | 0.5339 | 293.8 | 1234.35 | 177.78 | 0.0622 |
| C | 0.7244 | 184.5 | 1347.00 | 253.63 | 0.0610 |
| h | UC | UC | FOC | FOC | SOC | SOC |
|---|---|---|---|---|---|---|
| 70.9514 | 26.6976 | - | 7.2053 | - | 5.3999 | - |
| 47.8249 | 15.6275 | 1.3577 | 3.7519 | 1.6543 | 2.5007 | 1.9517 |
| 36.1943 | 10.7943 | 1.3279 | 2.3784 | 1.6358 | 1.4547 | 1.9444 |
| 29.2541 | 8.1559 | 1.3166 | 1.6669 | 1.6700 | 0.9448 | 2.0273 |
| 23.7852 | 6.5166 | 1.0843 | 1.2480 | 1.3982 | 0.6631 | 1.7104 |
| 20.9633 | 5.4088 | 1.4755 | 0.9782 | 1.9287 | 0.4903 | 2.3901 |
| 18.2621 | 4.6133 | 1.1531 | 0.7934 | 1.5179 | 0.3781 | 1.8835 |
| 16.1160 | 4.0165 | 1.1081 | 0.6596 | 1.4781 | 0.2992 | 1.8739 |
| 14.6520 | 3.5535 | 1.2862 | 0.5592 | 1.7327 | 0.2431 | 2.1808 |
| 12.2806 | 2.8821 | 1.1860 | 0.4213 | 1.6040 | 0.1698 | 2.0322 |
| 10.7534 | 2.4213 | 1.3119 | 0.3315 | 1.8053 | 0.1252 | 2.2939 |
| Pressure (Psia) | Bo (RB/STB) | ρo (lbm/) | (cp) | Rs (scf/STB) | Bg (Mcf/STB) | ρg (lbm/) | (cp) | Bw (Mcf/STB) | ρw (lbm/) | (cp) |
|---|---|---|---|---|---|---|---|---|---|---|
| 400 | 1.0120 | 46.497 | 1.17 | 165 | 5.90 | 2.119 | 0.0130 | 1.01303 | 62.212 | 0.96 |
| 800 | 1.0255 | 48.100 | 1.14 | 335 | 2.95 | 4.238 | 0.0135 | 1.01182 | 62.286 | 0.96 |
| 1200 | 1.0380 | 49.372 | 1.11 | 500 | 1.96 | 6.397 | 0.0140 | 1.01061 | 62.360 | 0.96 |
| 1600 | 1.0510 | 50.726 | 1.08 | 665 | 1.47 | 8.506 | 0.0145 | 1.00940 | 62.436 | 0.96 |
| 2000 | 1.0630 | 52.072 | 1.06 | 828 | 1.18 | 10.596 | 0.0150 | 1.00820 | 62.510 | 0.96 |
| 2400 | 1.0750 | 53.318 | 1.03 | 985 | 0.98 | 12.758 | 0.0155 | 1.00700 | 62.585 | 0.96 |
| 2800 | 1.0870 | 54.399 | 1.00 | 1130 | 0.84 | 14.885 | 0.0160 | 1.00580 | 62.659 | 0.96 |
| 3200 | 1.0985 | 55.424 | 0.98 | 1270 | 0.74 | 16.896 | 0.0165 | 1.00460 | 62.734 | 0.96 |
| 3600 | 1.1100 | 56.203 | 0.95 | 1390 | 0.65 | 19.236 | 0.0170 | 1.00341 | 62.808 | 0.96 |
| 4000 | 1.1200 | 56.930 | 0.94 | 1500 | 0.59 | 21.192 | 0.0175 | 1.00222 | 62.883 | 0.96 |
| 4400 | 1.1300 | 57.534 | 0.92 | 1600 | 0.54 | 23.154 | 0.0180 | 1.00103 | 62.958 | 0.96 |
| 4800 | 1.1400 | 57.864 | 0.91 | 1676 | 0.49 | 25.517 | 0.0185 | 0.99985 | 63.032 | 0.96 |
| 5200 | 1.1480 | 58.267 | 0.90 | 1750 | 0.45 | 27.785 | 0.0190 | 0.99866 | 63.107 | 0.96 |
| 5600 | 1.1550 | 58.564 | 0.89 | 1810 | 0.42 | 29.769 | 0.0195 | 0.99749 | 63.181 | 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Echavarría-Montaña, S.; Velásquez, S.; Bueno, N.; Valencia, J.D.; Solano, H.; Mejía, J.M. Semi-Implicit Finite Volume Procedure for Compositional Subsurface Flow Simulation in Highly Anisotropic Porous Media. Fluids 2021, 6, 341. https://doi.org/10.3390/fluids6100341
Echavarría-Montaña S, Velásquez S, Bueno N, Valencia JD, Solano H, Mejía JM. Semi-Implicit Finite Volume Procedure for Compositional Subsurface Flow Simulation in Highly Anisotropic Porous Media. Fluids. 2021; 6(10):341. https://doi.org/10.3390/fluids6100341
Chicago/Turabian StyleEchavarría-Montaña, Sebastián, Steven Velásquez, Nicolás Bueno, Juan David Valencia, Hillmert Alexander Solano, and Juan Manuel Mejía. 2021. "Semi-Implicit Finite Volume Procedure for Compositional Subsurface Flow Simulation in Highly Anisotropic Porous Media" Fluids 6, no. 10: 341. https://doi.org/10.3390/fluids6100341
APA StyleEchavarría-Montaña, S., Velásquez, S., Bueno, N., Valencia, J. D., Solano, H., & Mejía, J. M. (2021). Semi-Implicit Finite Volume Procedure for Compositional Subsurface Flow Simulation in Highly Anisotropic Porous Media. Fluids, 6(10), 341. https://doi.org/10.3390/fluids6100341






