Abstract
The performance of several engineering applications are strictly connected to the rheology of the working fluids and the Oldroyd-B model is widely employed to describe a linear viscoelastic behaviour. In the present paper, a buoyant Oldroyd-B flow in a vertical porous layer with permeable and isothermal boundaries is investigated. Seepage flow is modelled through an extended version of Darcy’s law which accounts for the Oldroyd-B rheology. The basic stationary flow is parallel to the vertical axis and describes a single-cell pattern where the cell has an infinite height. A linear stability analysis of such a basic flow is carried out to determine the onset conditions for a multicellular pattern. This analysis is performed numerically by employing the shooting method. The neutral stability curves and the values of the critical Rayleigh number are evaluated for different retardation time and relaxation time characteristics of the fluid. The study highlights the extent to which the viscoelasticity has a destabilising effect on the buoyant flow. For the limiting case of a Newtonian fluid, the known results available in the literature are recovered, namely a critical value of the Darcy–Rayleigh number equal to 197.081 and a corresponding critical wavenumber of 1.05950.
1. Introduction
The convective instability in a plane vertical porous layer saturated by a fluid is a topic of great interest for its applications spanning from geophysical systems to building insulation. Although the analysis of geophysical systems typically involves groundwater or hydrocarbons, the study of thermal insulation panels features air or another gas as a working fluid. Hydrocarbons saturating a porous medium may occasionally display a non-Newtonian viscoelastic behaviour. This circumstance will be that envisaged in the present study.
The classical paper by Gill [1] offered a rigorous mathematical proof that a vertical porous layer, saturated by a Newtonian fluid endowed with impermeable boundaries, kept at different uniform temperatures, displays a stationary conduction regime with a stable parallel vertical buoyant flow, regardless of the temperature gap between the boundaries. In other words, such basic buoyant flow is always stable for every value of the Rayleigh number. The linear stability analysis carried out by Gill [1] is relative to a Newtonian fluid subject to Darcy’s law. In the context of Newtonian fluids, other authors further developed Gill’s important result by including other features such as the non-linearity of the perturbation dynamics or other momentum transfer models of the seepage flow in the porous medium [2,3,4,5,6,7]. Further investigations provided evidence that the stability theorem proved by Gill does not hold when the hypothesis of impermeable boundaries for the porous layer is released [8,9,10,11,12]. As proved in these studies, with perfectly or partly permeable boundaries, the onset of convective instability is possible for sufficiently large values of the Rayleigh number.
Stability analyses of the buoyant flow in a vertical porous layer envisage a non-Newtonian saturating fluid only in a few instances [13,14,15]. Barletta and Alves [13] considered a power-law fluid, while Shankar and Shivakumara [14,15] considered a viscoelastic fluid described according to the Oldroyd-B model as developed, for saturated porous media, by Khuzhayorov et al. [16] and employed by other authors [17,18]. However, the non-Newtonian versions of the stability analysis of Gill’s system developed by Barletta and Alves [13] and by Shankar and Shivakumara [14,15] are relative to a layer with impermeable boundaries.
Following the path devised by Barletta [8], the aim of this paper is to relax the assumption of impermeable boundaries and reconsider the linear stability analysis of the vertical buoyant flow in a vertical layer saturated by a viscoelastic Oldroyd-B fluid. The special case analysed by Barletta [8] is retrieved when the relaxation time of the viscoelastic fluid coincides with the retardation time. On the other hand, the viscoelastic behaviour shows up when such times are different. In this case, the threshold to convective instability is affected by the viscoelastic rheology of the fluid. The neutral stability condition and the critical Rayleigh number will be obtained for different values of the characteristic governing parameters of viscoelasticity.
2. Mathematical Model
A vertical porous layer saturated by a viscoelastic fluid is studied. The layer is infinitely wide in the y and z directions and has thickness L in the horizontal direction x. A sketch of the layer is presented in Figure 1. The Oldroyd-B model is employed to describe the viscoelasticity. Darcy’s law for Oldroyd-B type of fluids [16] is written
where and are two characteristic relaxation/retardation times, respectively, with . The buoyancy force is modelled by the Oberbeck–Boussinesq approximation, is the Cartesian position vector, is the filtration velocity vector, T is the temperature and is the gravitational acceleration vector (opposite to the z direction).
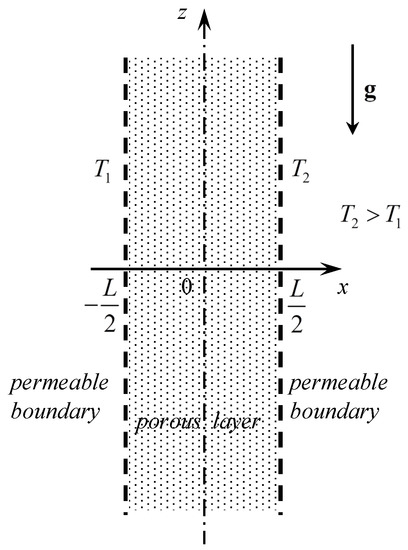
Figure 1.
A sketch of the vertical porous layer.
The energy balance equation employed to model the heat transfer is the convection/conduction equation where no source or sink term is considered.
The vertical boundaries of the layer are permeable and the external environments in the regions and are considered as isothermal fluid reservoirs in a motionless state, so that the pressure distribution along the boundaries is purely hydrostatic. Since the external fluid reservoirs are kept at different uniform temperatures and , where , the layer is subject to side heating, as depicted in Figure 1.
Thus, the governing equations are given by
where g and are the modulus of and the unit vector along the z direction, respectively, while is the reference hydrostatic pressure of the external environments. In Equation (2) is the dynamic viscosity of the fluid, K is the permeability of the porous medium, is the fluid density evaluated at the reference temperature , is the thermal expansion coefficient of the fluid, is the heat capacity ratio, is the ratio between the effective thermal conductivity of the fluid saturated porous medium and the volumetric heat capacity of the fluid, . The parameters , and are defined as [19]
where is the porosity, is the specific heat capacity of the fluid, is the specific heat capacity of the porous medium, is the density of the solid phase, is the thermal conductivity of the fluid and is the thermal conductivity of the solid phase.
The following scaling, where , is employed to obtain the dimensionless formulation of the problem:
By substituting Equation (4) in Equation (2), the following dimensionless governing equations are obtained
where
Basic State
Let us consider as basic state the steady and fully developed buoyant flow in the vertical direction z and adopt the subscript b to denote the quantities relative to the basic state. Thus, the only non-vanishing component of the filtration velocity vector is , along the z-direction. According to Equation (5), results in a solenoidal field. Thus, the basic stationary solution is characterised by a zero net mass flow rate throughout the layer, namely
The solution for the basic state describes the behaviour of a stationary flow which is parallel to the vertical axis, thus yielding a single-cell vertical pattern where the cell has an infinite vertical height.
3. Linear Stability Analysis
To perform a linear stability analysis, we proceed by perturbing the basic state just defined by applying small-amplitude disturbances, namely
where . By substituting Equation (8) into Equation (5) and by neglecting terms, one obtains
By applying the divergence operator to the perturbed momentum balance equation and by applying the linear differential operator to the perturbed energy balance equation, one obtains the following pressure–temperature formulation, which is more convenient than Equation (9) since the boundary conditions are relative to P and
We assume the pressure and temperature perturbations to have the form of normal modes,
where is the growth or decay rate, is the angular frequency and is the wave vector. The parameters are real while are, in general, complex functions. The growth rate marks the difference between stability and instability . The neutrally stable configuration is identified by . The condition of minimum R among the neutrally stable modes defines the critical values and .
By substituting definitions (11) into Equation (10), one obtains the following eigenvalue problem for neutrally stable modes,
where
We mention that where, according to Equation (1), the limiting case represents the case of a Newtonian fluid.
Moreover, the rescaled Darcy–Rayleigh number S accounts for the inclination of the wave vector to the vertical z axis. When , one has a transverse mode propagating along the z axis and . On the other hand, when , one has a longitudinal mode propagating along the y axis and . Since the latter result can be obtained also when , horizontally propagating modes are equivalent to transverse modes having a vanishing Darcy–Rayleigh number. Thus, modes having and a given value of S correspond to transverse modes with the same S and a larger value of R. As a consequence, the transverse modes necessarily are the most unstable.
4. Numerical Solution and Discussion of the Results
The eigenvalue problem formulated through the dimensionless governing Equation (12) can be solved numerically by means of the shooting method. In the considered approach, the associated initial value problem is solved with the Runge–Kutta method, while Brent’s method is adopted for the root searching procedure. The numerical solution of the problem is here found through the built-in functions NDSolve and FindRoot available within the Mathematica 12.0 environment.
In detail, the numerical approach used to solve the eigenvalue problem given by Equation (12) requires the input values and determines both and as eigenvalue data. The minimum of yields the critical values that define the onset of the convective instability.
The main requirement for an efficient solution of Equation (12) through the shooting method is an accurate initial guess for the eigenvalue quantities S and , for a given prescribed input dataset .
The investigated cases refer to wide ranges of values of the dimensionless parameters and . In detail, the considered cases are those obtained from the possible pairs among the values and . It is worth noticing that these values include the limiting case of Newtonian fluid and the special case of Boger’s fluid [20].
4.1. Limiting Case of a Newtonian Fluid
As already emphasised, the limiting case of a Newtonian fluid occurs when . In this case, regardless of the value of , the neutral stability curve, displayed in Figure 2, shows up a minimum in the plane for the critical values
which hold for every choice of . It is worth noticing that, as it can be inferred from Equation (12), such a neutral stability solution with is always present. In other words, among all the possible values assigned to , Equation (14) yields the maximum of .
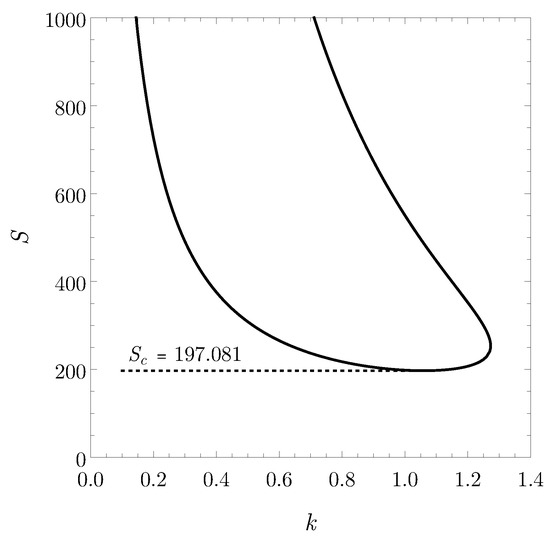
Figure 2.
Neutral stability curve for a Newtonian fluid.
4.2. Results for Viscoelastic Fluids
The neutral stability curves for the considered data are reported in Figure 3. Each frame refers to a different value of , while the solid lines are drawn for given values of . For decreasing values of , the curves move upward, as well as for increasing values of . It is worth noticing that the vertical axis has the range , since this value corresponds to the onset of instability for a Newtonian fluid, namely the maximum possible critical value of S.
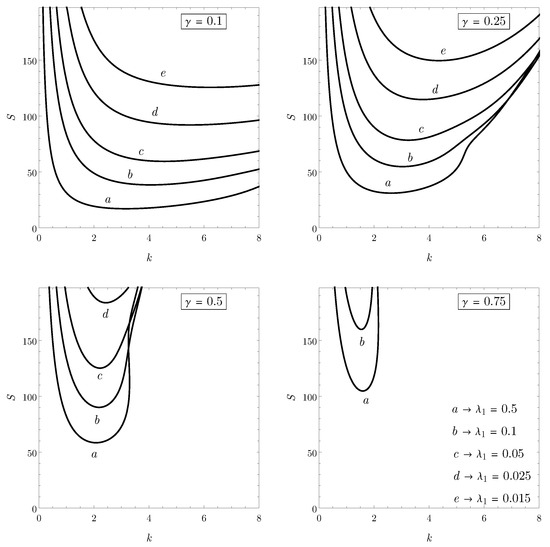
Figure 3.
Neutral stability curves for different values of and .
The threshold values of that have been found numerically are reported in Table 1. The obtained results are insensitive to the sign of . Thus, in Table 1, the values of are to be intended as . As can be inferred from Table 1, for a given value of , an increase in the dimensionless relaxation time leads to a decrease in the threshold values (at least, whenever ). The minimum of the neutral stability curve moves to the left and becomes smaller.

Table 1.
Critical values of versus .
5. Conclusions
The effects of viscoelasticity on the onset of convection in a fluid saturated vertical porous layer have been analysed. An extended version of Darcy’s law has been utilised in order to implement the Oldroyd-B rheological model for the seepage flow in the porous medium. The boundaries of the vertical porous layer have been considered as permeable to external fluid reservoirs kept at different temperatures. The boundary temperature difference causes a side-heating mechanism and, hence, a stationary buoyant flow driven by the uniform horizontal temperature gradient. Such conditions define the basic conduction state. The linear stability of this basic state has been studied by employing a three-dimensional normal mode scheme, with a suitable Squire transformation mapping all possible modes to equivalent transverse rolls. Finally, the stability eigenvalue problem has been formulated and solved numerically by employing the shooting method.
The main highlights of our study are the following:
- The dimensionless governing parameters identifying the viscoelastic behaviour are the relaxation parameter, , and the ratio between the retardation time and the relaxation time, . The physically significant domain is one where . When , the Newtonian fluid behaviour is recovered: the critical value of the modified Darcy–Rayleigh number is 197.081 and the corresponding critical value of the wavenumber is 1.05950;
- The neutral stability threshold to the convective instability obtained for the Newtonian case always exists, whatever is the choice of and . However, in most cases, the Newtonian branch of neutral stability is not the lowest one. In these cases, the neutral stability condition is characterised by travelling modes, i.e., modes with a non-zero angular frequency. Thus, the effect of viscoelasticity is generally destabilising with respect to the Newtonian fluid case;
- There exist input values of , with , such that the critical conditions for the onset of the convective instability coincide with those for a Newtonian fluid or, equivalently, the Newtonian branch of neutral stability is the lowest one.
There are several possible directions where the study presented in this paper can be extended. In Authors’ opinion, one of the most interesting developments of this study is the introduction of a model for partially permeable boundary conditions. With such a model one can investigate the gradual transition from permeable to perfectly impermeable boundaries, and its effects on the onset conditions for the instability.
Author Contributions
Conceptualization: S.L., M.C., and A.B.; Formal analysis: S.L., M.C., and A.B.; Funding acquisition: A.B.; Investigation: S.L., M.C., and A.B.; Methodology: S.L., M.C., and A.B.; Project administration: A.B.; Software: S.L.; Supervision: A.B.; Validation: S.L. and M.C.; Writing—original draft: S.L., M.C., and A.B.; Writing—review and editing: S.L., M.C., and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Italian Ministry of Education and Scientific Research grant number PRIN 2017F7KZWS.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Gill, A.E. A proof that convection in a porous vertical slab is stable. J. Fluid Mech. 1969, 35, 545–547. [Google Scholar] [CrossRef]
- Rees, D.A.S. The stability of Prandtl–Darcy convection in a vertical porous layer. Int. J. Heat Mass Transf. 1988, 31, 1529–1534. [Google Scholar] [CrossRef]
- Straughan, B. A nonlinear analysis of convection in a porous vertical slab. Geophys. Astrophys. Fluid Dyn. 1988, 42, 269–275. [Google Scholar] [CrossRef]
- Lewis, S.; Bassom, A.P.; Rees, D.A.S. The stability of vertical thermal boundary–layer flow in a porous medium. Eur. J. Mech. B Fluids 1995, 14, 395–407. [Google Scholar]
- Rees, D.A.S.; Lage, J.L. The effect of thermal stratification on natural convection in a vertical porous insulation layer. Int. J. Heat Mass Transf. 1996, 40, 111–121. [Google Scholar] [CrossRef]
- Rees, D.A.S. The effect of local thermal nonequilibrium on the stability of convection in a vertical porous channel. Transp. Porous Media 2011, 87, 459–464. [Google Scholar] [CrossRef]
- Scott, N.L.; Straughan, B. A Nonlinear stability analysis of convection in a porous vertical channel including local thermal nonequilibrium. J. Math. Fluid Mech. 2013, 15, 171–178. [Google Scholar] [CrossRef]
- Barletta, A. A proof that convection in a porous vertical slab may be unstable. J. Fluid Mech. 2015, 770, 273–288. [Google Scholar] [CrossRef]
- Celli, M.; Barletta, A.; Rees, D.A.S. Local thermal non–equilibrium analysis of the instability in a vertical porous slab with permeable sidewalls. Transp. Porous Media 2017, 119, 539–553. [Google Scholar] [CrossRef]
- Barletta, A.; Celli, M.; Ouarzazi, M.N. Unstable buoyant flow in a vertical porous layer with convective boundary conditions. Int. J. Therm. Sci. 2017, 120, 427–436. [Google Scholar] [CrossRef]
- Barletta, A.; Rees, D.A.S. On the onset of convection in a highly permeable vertical porous layer with open boundaries. Phys. Fluids 2019, 31, 074106. [Google Scholar] [CrossRef]
- Barletta, A.; Celli, M. Anisotropy and the onset of the thermoconvective instability in a vertical porous layer. ASME J. Heat Transf. 2021, 143, 102601. [Google Scholar] [CrossRef]
- Barletta, A.; de Alves, L.S.B. On Gill’s stability problem for non–Newtonian Darcy’s flow. Int. J. Heat Mass Transf. 2014, 79, 759–768. [Google Scholar] [CrossRef]
- Shankar, B.M.; Shivakumara, I.S. On the stability of natural convection in a porous vertical slab saturated with an Oldroyd–B fluid. Theor. Comput. Fluid Dyn. 2017, 31, 221–231. [Google Scholar] [CrossRef]
- Shankar, B.M.; Shivakumara, I.S. Effect of local thermal nonequilibrium on the stability of natural convection in an Oldroyd–B fluid saturated vertical porous layer. ASME J. Heat Transf. 2017, 139, 041001. [Google Scholar] [CrossRef]
- Khuzhayorov, B.; Auriault, J.L.; Royer, P. Derivation of macroscopic filtration law for transient linear viscoelastic fluid flow in porous media. Int. J. Eng. Sci. 2000, 38, 487–504. [Google Scholar] [CrossRef] [Green Version]
- Hirata, S.C.; Ouarzazi, M.N. Three–dimensional absolute and convective instabilities in mixed convection of a viscoelastic fluid through a porous medium. Phys. Lett. A 2010, 374, 2661–2666. [Google Scholar] [CrossRef]
- de Alves, L.S.B.; Barletta, A.; Hirata, S.; Ouarzazi, M.N. Effects of viscous dissipation on the convective instability of viscoelastic mixed convection flows in porous media. Int. J. Heat Mass Transf. 2014, 70, 586–598. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Boger, D.V. Viscoelastic flows through contractions. Annu. Rev. Fluid Mech. 1987, 19, 157–182. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).