1. Introduction
The flow of fluids in composite porous-clear domains is a prevalent phenomenon in many natural and industrial applications. Consequently, such has been the focus of several research studies, covering both laminar and turbulent flow considerations [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11].
In this work, attention is focused on the study of turbulent flow over a porous medium, and the concomitant effects on the flow through the coupled porous medium. Even so, the impact of such flows is far-reaching. Turbulent flow mechanisms are, for example, known to influence the hyporheic exchange of pollutants to regions below and adjacent to streams and rivers [
12]. In canopies of submerged aquatic vegetation, biogeochemical processes are regulated through unsteady inertial and turbulent exchanges of mass and momentum between the canopy (acting as a permeable medium) and the ambient water [
13]. Turbulent transport of wind within and above forest canopies also plays an integral role in the atmospheric exchange of carbon dioxide (therefore forcing climate change [
14]). They are also important in making site assessments for architectural structures and wind turbine performance [
15]. In industrial settings, on the other hand, porous assemblies in the form of pin fin arrays have been used to increase the turbulence and unsteadiness of coolant flow to guarantee efficient cooling [
16]. In the casting of alloys, turbulent flows generated due to electromagnetic stirring has been found to decrease channel formation in the mushy zone and associated patterns of segregation [
17].
While the range of studies varies considerably in the application, analyses of turbulent flows over porous media are facilitated by distinguishing the flow domain into a channel (or free or open) flow region, and a porous flow region [
18]. These two regions are separated by an interfacial zone that is sometimes discussed as a separate region [
6]. Concerning the open flow region, a great deal of what is presently known about the pertinent turbulent flow has been shaped by canopy flows [
13,
19,
20,
21]. From this perspective, the flow features are characterized by wall-normal variations of the mean streamwise velocities that inflect at the interfacial zone. Structurally, the flow in that region is conceived as similar to a mixing layer. However, the inflectional profile renders the flow prone to the development of vortices originating from an instability of the Kelvin–Helmholtz type. Indeed, these vortices grow into other secondary vorticial structures that often propagate a coherent wave-like oscillatory phenomenon. Nevertheless, the flow in this channel flow region is often considered to be dominated by large coherent structures. It is noteworthy that other related studies associated with permeable bed models (such as cubes, spheres, nets, and foams) have given insight into the dynamics of flow in the open region. Accordingly, compared to solid walls, friction factors, wall shear stress, momentum flux, and Reynolds stress were found to be enhanced at porous walls due to porous matrix factors such as porosity and permeability [
22,
23,
24,
25,
26]. By using a double-averaging method [
5,
27], the global effects of the porous medium factors were evaluated and found to be different from the roughness effects [
25]. In this regard, Suga et al. [
7] conducted extensive particle image velocimetry (PIV) measurements of the boundary layer above a porous boundary. Models of porous media of variant permeability were tested over a wide range of Reynolds numbers. The researchers demonstrated that the streamwise mean velocity did fit a log-law form after accounting for a displacement height and equivalent roughness height as well as a von Kármán coefficient (different from the 0.38–0.41 range conventionally applied to flows associated with smooth and rough walls). In various PIV experiments, the extent of the logarithmic layer has also been assessed, along with correlations of the log-law parameters with characteristic permeability Reynolds numbers [
7,
28,
29]. While these results are concrete, it must also be conceded that they were notably obtained from fully developed flows over porous media. Thus, they do not account for cases of compact porous media arrangements where, at least, the streamwise velocity variations are dependent of the streamwise location.
The interfacial zone is the transitional layer between the open and the porous regions where effects of the turbulent motion of the surface flow are persistent [
18]. It is therefore the region where momentum, energy, and scalers are exchanged [
6]. Despite the importance of the interfacial zone in the general flow dynamics, the information provided in the literature has been relatively sparse. The simulations of Breugem et al. [
25] indicate that there is a link between the sign of the flow across the interfacial zone with the transporting fluid; and that this is specified by the fluctuating velocity component. This was later confirmed by Kim et al. [
6] using PIV to provide velocities of a refractive-index-matched system of turbulent flow over a cubic-packed arrangement of uniform spheres. Before this confirmation, however, Manes et al. [
18] conducted velocity measurements in a turbulent open channel flow over cubically packed spheres. Instead of a gradual monotonic decay in streamwise mean velocity just below the interface between the open and porous regions, rather, they observed the velocity dampen to a minimum and then rise toward a constant value within the porous medium. In a subsequent study, Pokrajac et al. [
30] explained this to be the product of enhanced turbulence in the pores closer to the interface. They noted that this resulted in the viscous drag extracting momentum from the flow, thus allowing higher mean velocities to form in the lower pores. In another surprising discovery, the canopy flow studies of Florens et al. [
5] indicated that contrary to popular assumption, the dispersive stress near the top of the porous medium is not negligible. Such unexpected observations point to significant gaps in the current understanding of the flow at the interfacial zone.
For the flow within the porous region, the available data are still rare, and the information has been mixed. The numerical computations of Breugem et al. [
25] as well as Sharma and García-Mayoral [
31] showed an exponential decay in the mean velocity profile, turbulence intensities, and pressure fluctuations inside the porous medium. This was in part, corroboration of the experimental findings of Ruff and Gelhar [
22] and Vollmer et al. [
24]. Florens et al. [
5], on the other hand, reported linear variations of mean wall-normal velocity, mean spanwise velocity, and total stress in the wall-normal direction. Kim et al. [
6] also observed channeling of flow along the trough regions of their cubic-packed arrangements. They also noted that the crest region was the region of secondary motion resulting from neighboring trough channels. There are several studies on pin-fin heat transfer that have provided direct detailed measurements of the flow field within the arrays. These studies have provided valuable information on flow dynamics and structures such as vortex shedding strength with geometric changes [
32], near wake flow development [
33], and the nature of horseshoe vortex systems [
34]. However, such studies usually presume turbulent flow within the arrays and do not consider the case of the effects of turbulent flow over the arrays.
In summary, it is important to note that while several studies have been conducted on turbulent flow over porous media, most of these works have been focused on the open flow region [
7,
28,
29]. Experimental work on flow at the interfacial and porous regions, however, is scarce. Thus, while several conclusive observations have been made on the flow phenomena about changes in porosity, permeability, and Reynolds number, the same cannot be said about the interfacial and porous regions. Furthermore, it is worth noting that most of the studies on turbulent flows associated with porous boundaries appear to be focused on acquiring information from a fully developed section of the turbulent flow [
6,
7,
18,
28,
30]. Consequently, some of the definite conclusions in the literature regarding the variation of mean velocity, momentum, and turbulent statistics may not necessarily apply to cases associated with compact porous media. It must be emphasized that such a lack is not trivial, because some pertinent natural scenarios may only be suited for analyses when considered as turbulent flows over compact porous media. These include terrestrial or aquatic canopy flows over regions of land with small/confined arrangements of sparse vegetation or building structures. Additionally, the design and evaluation of engineering systems such as pin-fin arrays of rods for heat transfer enhancement may not be sufficiently helped by considering what is currently in the literature when there is a turbulent flow over the pin-fin array. Specifically, fundamental questions remain regarding the nature of boundary layer development, the spatial variations of the mean turbulence, and other statistics due to three-dimensional effects, the mode, and development of interactions between the open region and the porous region at the interfacial zone, and the porous flow phenomenon itself. To provide some answers to these questions, an experimental research program was designed to conduct velocity measurements of a turbulent flow over and penetrating through a compact model porous medium. In this particular work, the objectives were to study the turbulent boundary layer development over the porous medium and its penetration into the porous flow, three-dimensional effects, and Reynolds number effects of the flow. The physical system was achieved by using a square array of rods to model the three-dimensional porous medium and testing it in a flow channel. The porous medium was arranged to cover a single porosity value of 85%, and to fill 21% of the depth of the flow channel. The uniqueness of this work lies in the fact that the porous medium model used was designed to be compact, having only twelve columns and nine rows of rods. Furthermore, a planar PIV system was used to conduct detailed velocity measurements in several streamwise-wall-normal planes through and over the porous medium in a turbulent flow over a range of Reynolds numbers. The mean flow and turbulent statistics were assessed to characterize the flow through and over the compact porous medium.
3. Results and Discussion
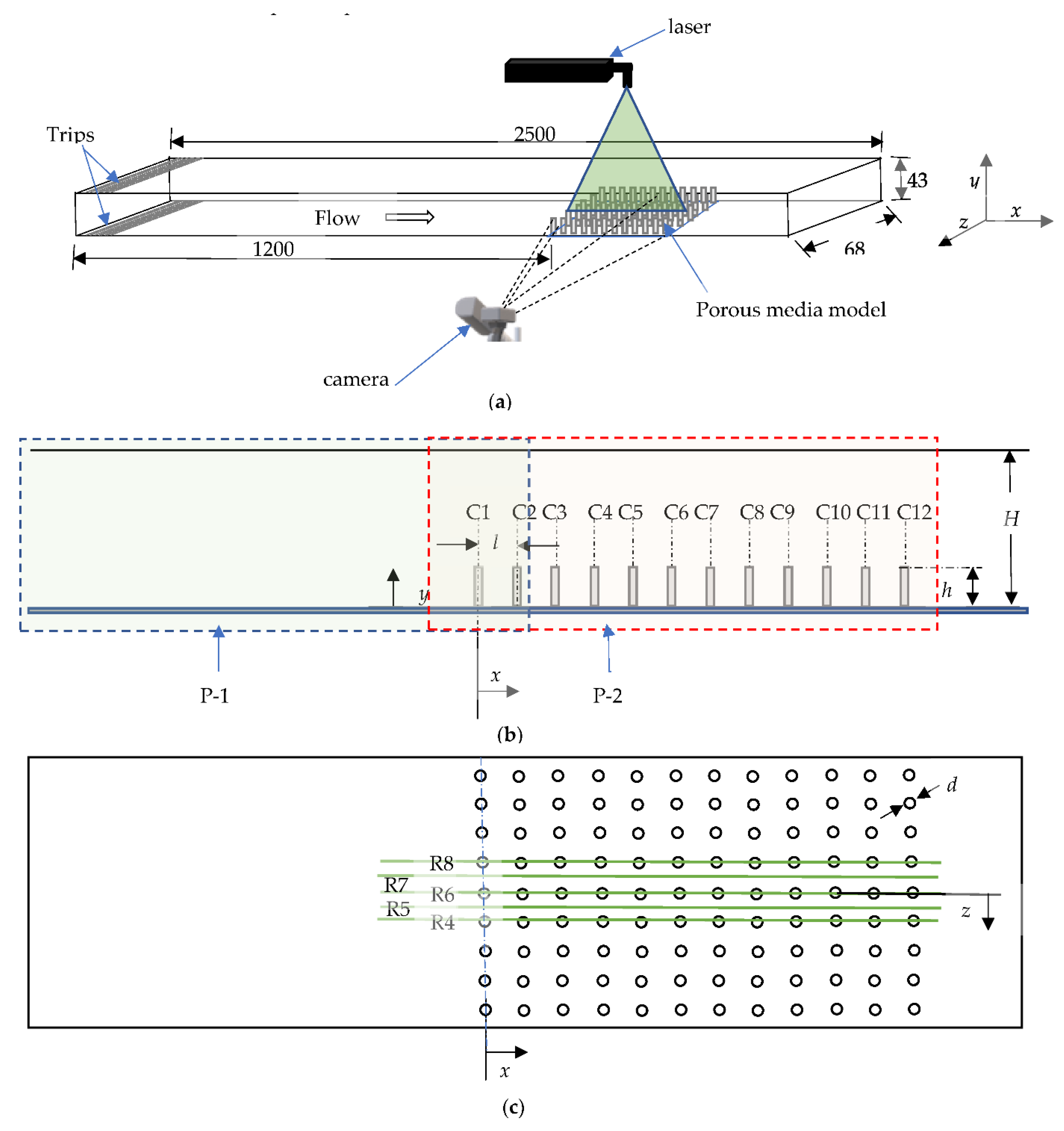
In this section, the results of the tests are presented by considering the flow within the porous region, at the interfacial region, and then in the open region, respectively. The presentation and discussion are illustrated with tabulated results, one-dimensional line-averaged plots, vector plots, and contour plots. However, to maintain brevity and clarity of presentation, for one-dimensional plots, streamwise variations of the flow phenomena are largely demonstrated using multiple line-averaged data obtained from measurements made in the
z = 0 plane. The line averages were conducted between adjacent centers of selected rods as schematized and denominated in
Figure 1b. The selected pair of columns of rods were columns 1 and 2 (labeled C1–2), columns 4 and 5 (labeled C4–5), columns 6 and 7 (labeled C6–7), columns 8 and 9 (labeled C8–9), and columns 11 and 12 (labeled C11–12). Likewise, for conciseness, assessments of spanwise variations were undertaken using one-dimensional plots that were largely limited to line-averaged data from multiple spanwise planar measurements. The line averages were carried out between columns 8 and 9, and the measurement planes from which data were extracted are
z =
l, 0.5
l, 0, −0.5
l, and −
l. These planes are respectively indicated by R4, R5, R6, R7, and R8 in the plots as previously shown in
Figure 1c. It should also be noted that for both vectors, streamlines, and contour plots, data/levels were respectively skipped to avoid congestion and to highlight prominent characteristics.
3.1. Flow within the Porous Region, Flow at Porous-Open Flow Interface
3.1.1. Mean Velocities, Vectors, Streamlines, and Vorticity
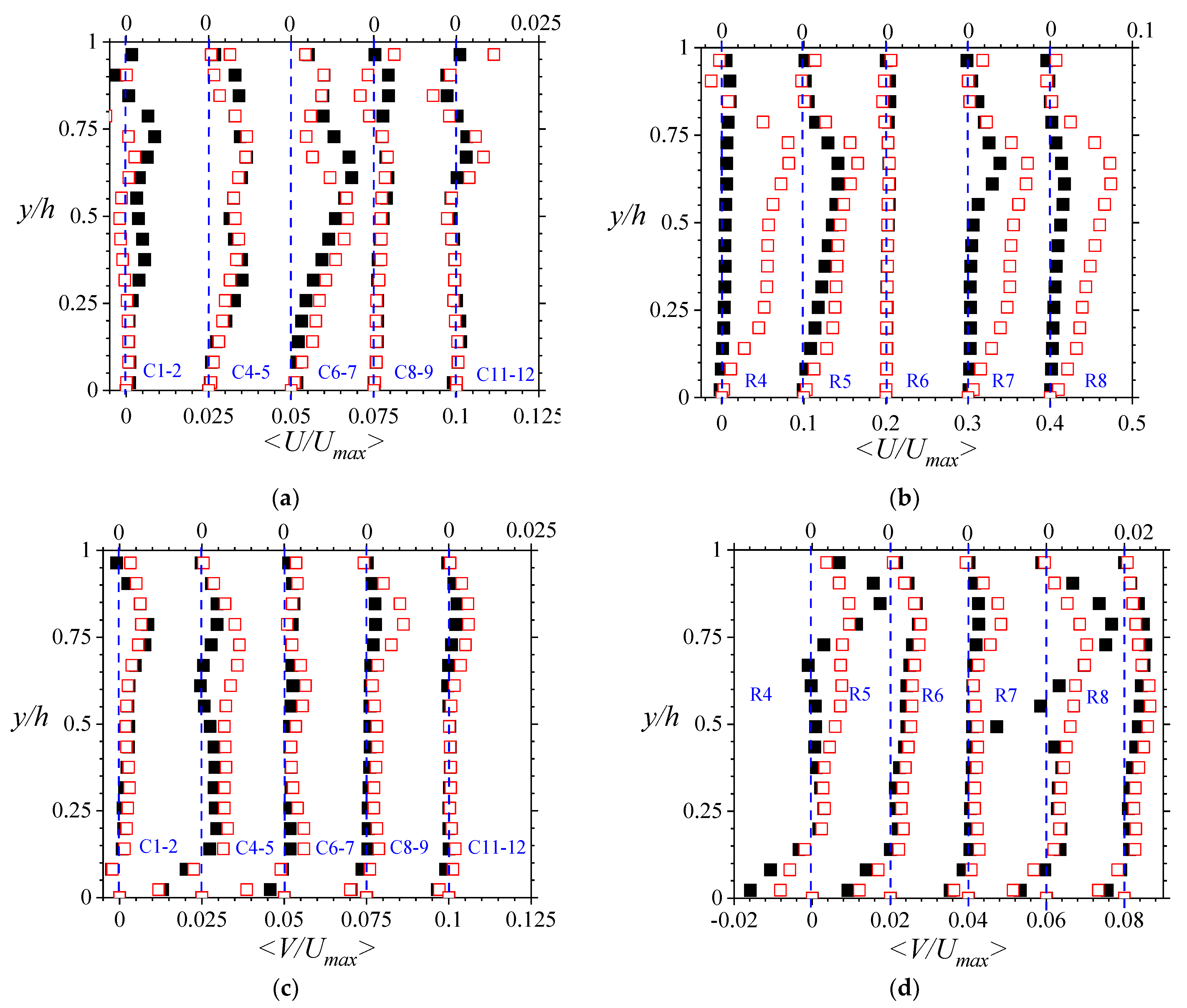
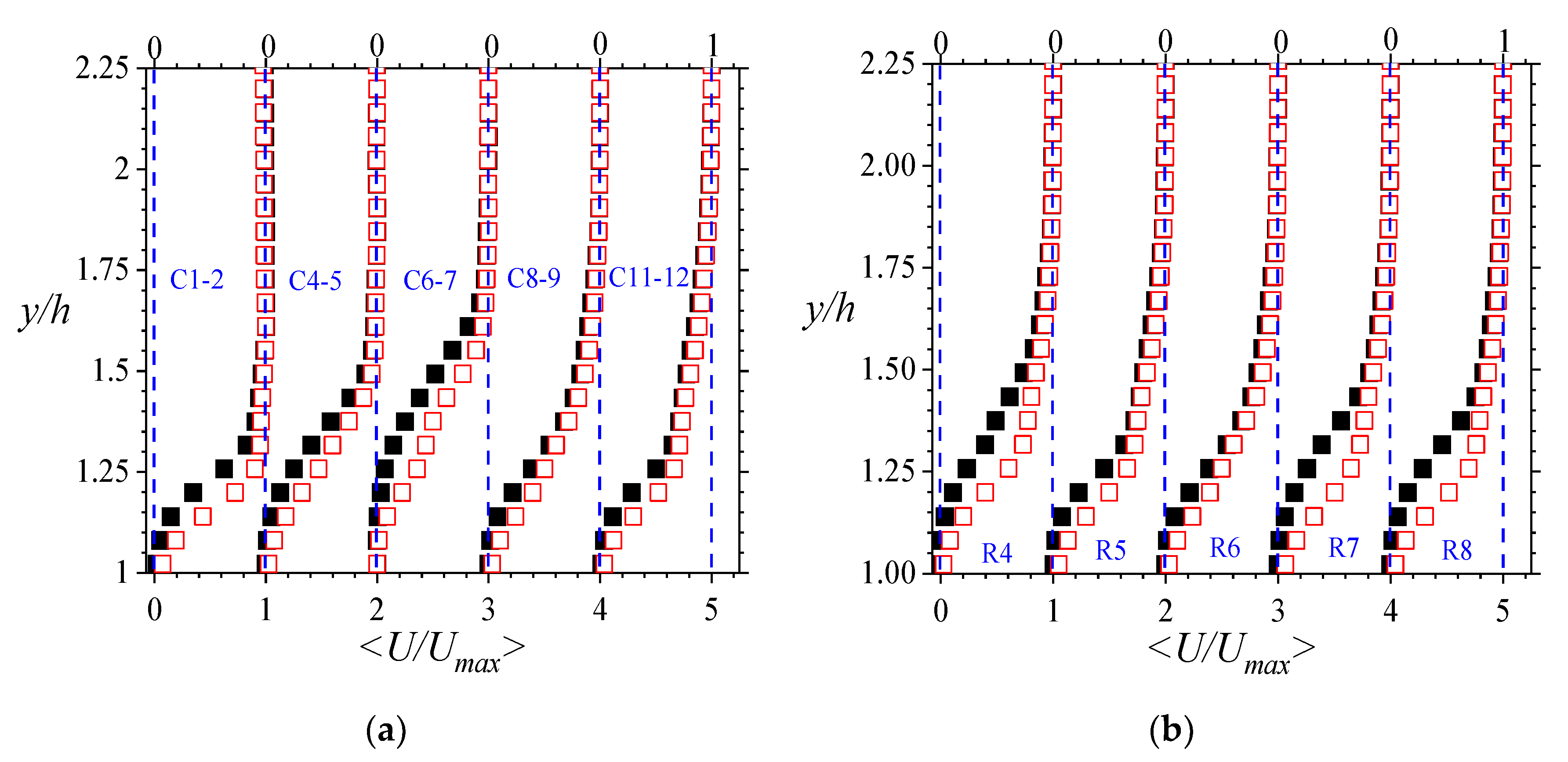
Some of the major aims of this study were to ascertain the extent to which the overlying mean turbulent flow influences the porous region, how that varies along the length and span of the compact porous medium, and how that varied with Reynolds number. To this end, line-averaged velocity plots of the mean streamwise and wall-normal velocities of the flow within the porous medium were first assessed. Notably, as indicated in
Figure 3, the mean velocities were found to be three-dimensional, and the magnitudes of the flow were relatively low. The low flow within the porous region was not a surprise, given the obstruction posed by the rods. However, the magnitudes measured are worth highlighting given the high porosity of the porous medium under consideration. Even at 85% porosity, less than 1% of the mass flow was diverted through the porous region when the overlying flow was turbulent (
Table 2 and
Table 3). Thus, the average streamwise velocity within the porous region (
<Ub,p>) was of the order of just 1 mm s
−1, and the streamwise velocities were no more than 8% of the corresponding local line-averaged maximum velocity <
Umax>.
It is also important to point out that the variation of the flow for the wall-normal coordinate is not uniformly linear. Even though the mid-plane flow is linear (as expected of flow in a plane passing through the rods), the majority of the cases indicated streamwise velocities that rose from zero at the lower wall. The velocities reached a maximum at about three-quarters of the depth of porous medium, and then dipped toward the interface. Contrary to observations by Florens et al. [
5], the wall-normal mean velocities also followed a similar non-linear variation with the wall-normal coordinate (albeit muted in magnitude). Conspicuously, this variation includes negative gradients particularly close to the lower wall and in the planes outside of the midspan. These phenomena are not suggestive of flow channeling within the pores of the porous medium, nor can they imply a two-dimensional system. Rather, they are indicative of a complex flow activity within the porous medium.
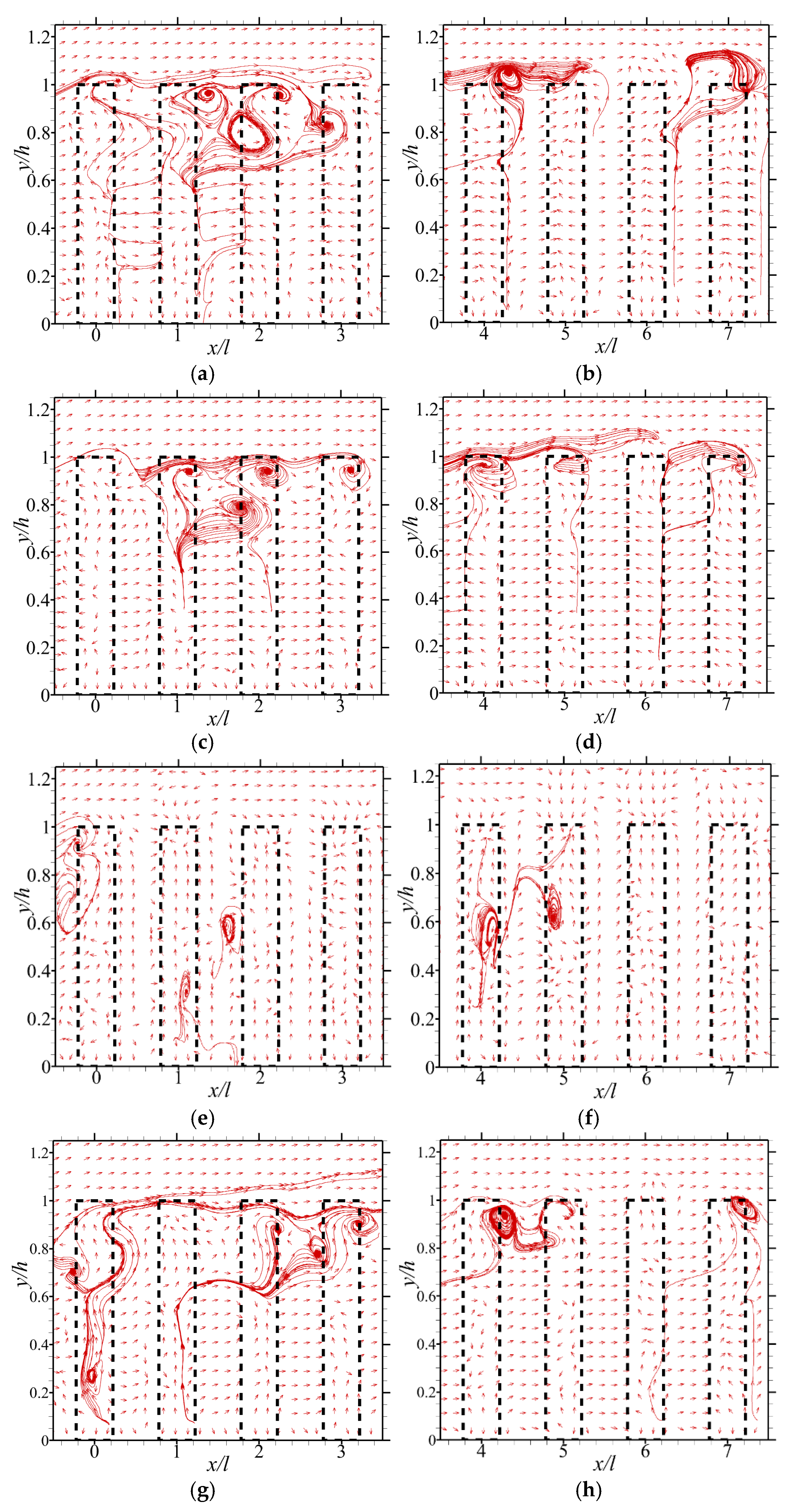
To investigate this complicated flow activity further, vector plots, streamlines, and contours were examined. The mean vector plots for the conditions of measurement planes passing through rods of the porous medium (i.e.,
z = 0, ±
l) are shown in
Figure 4. For both Reynolds numbers tested, the midspan vectors within the porous medium showed a combination of upwelling and downwelling events in no definite order. For the off-midspan planes, increasing the Reynolds number of the flow led to distinct patterns of flow circulation occurring at finite regions close to the lower wall and the interface. In
Figure 5, it is also noted from the streamlines that for spanwise planes of flow between rods (i.e.,
z = ±0.5
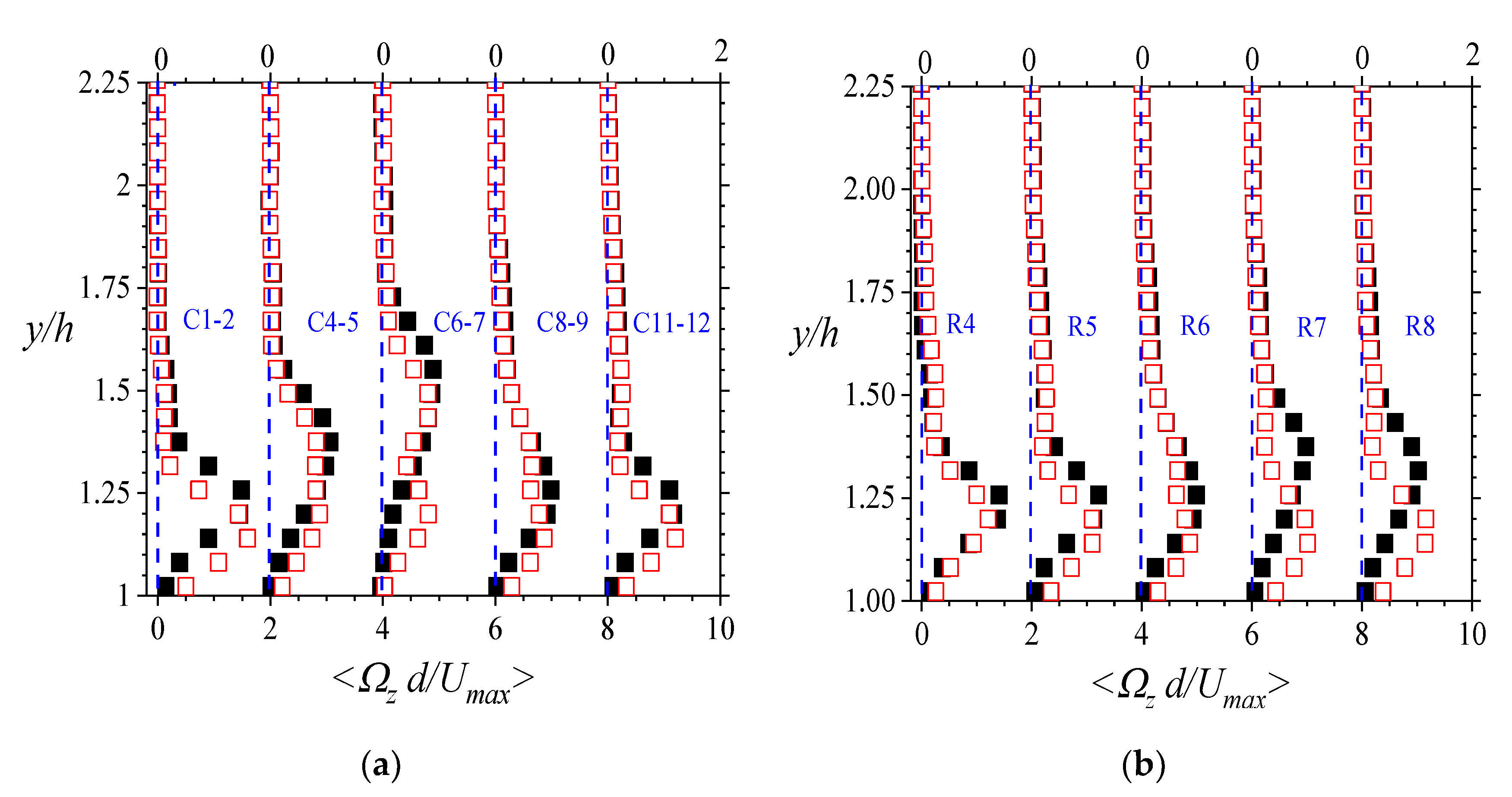
l), the vectors were of some structural order. Thus, vortices of different sizes and counter-rotating pairs were found in different locations of the flow in the porous region. The iso-contours of the mean spanwise vorticity (
Ωz = ∂
V/∂
x − ∂
U/∂
y) presented in
Figure 6 show that within the porous region, pockets of weak, but significant vorticity formed in both test cases, but in different spanwise locations. Of note, some of the spanwise vorticities were negative in value because the mean wall-normal velocity gradient in the streamwise coordinate (∂
V/∂
x) was less than the mean streamwise velocity gradient in the wall-normal direction (∂
U/∂
y) in those regions. Additionally, the vorticity pockets were also mostly located close to the lower wall, or at about two-thirds of the depth of the porous medium. The longitudinal extent of these pockets ranged from 10 to 30% of the depth of the porous medium. It is also important to point out that while the pockets of vorticity were longer in the upstream section of the porous medium, they shrunk and ultimately degenerated in the downstream section.
The source of these vorticial activities is open to debate. It is possible that these activities are entirely or partially characteristic of the flow behavior of the associated porous flow regime. Within the porous region, the interstitial velocities amount to a local hydraulic Reynolds number ranging from 18 to 668. Such a scope of Reynolds number translates to porous flow in a steady inertial flow regime, or in the extreme, a chaotic (turbulent) regime [
46]. These regimes are respectively characterized by vortex formation or sub-pore scale turbulence along with intense vortex shedding [
46,
47,
48,
49]. Thus, it is possible that with the present porous medium flow being in the inertial flow regime (at the very least), vortices are being generated by shear close to the particle surfaces. A reasonable alternative explanation about the origins of this vorticial activity may, however, be found in the turbulent flow at the unobstructed sections close to the porous region. At such sections, there are zones of strong shear in the velocity close to the edge of the porous medium. Such shear triggers an instability of the Kelvin–Helmholtz (K–H) type, generating the canopy-scale turbulence observed in this work [
13,
35]. It is worth pointing out that in the particular case of a compact porous medium, prospective vorticity-generating sources at the edge of the porous medium are of two kinds. There is the leading edge of the porous region (i.e., the most upstream rods at
x = −
d/2), and the interface between the porous region at the overlying open flow region (at
y =
h). As both locations are regions of intense shear layers, either of them is capable of inducing K–H vortices. From thence, the vortices are advected elsewhere within the porous medium.
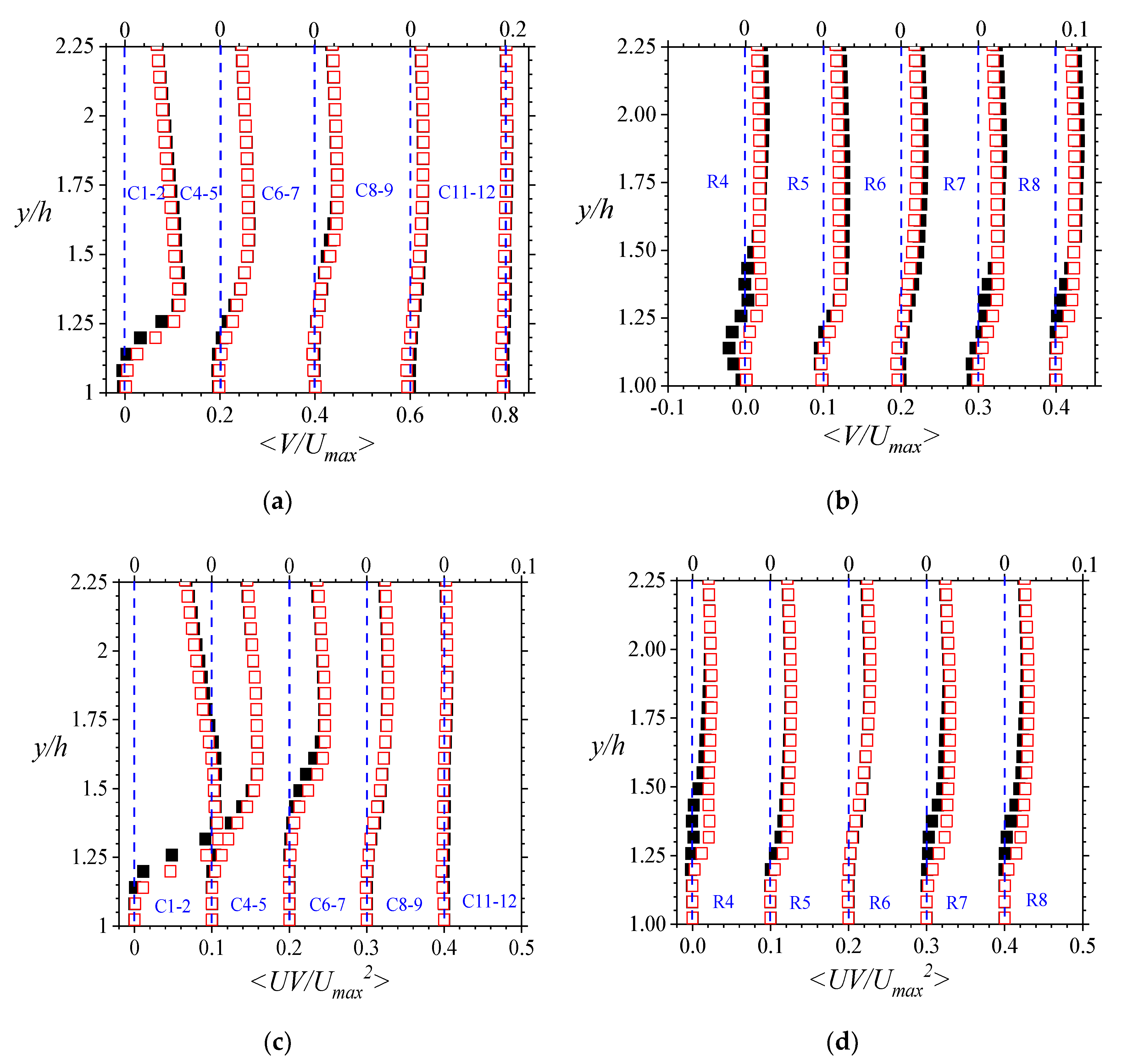
3.1.2. Turbulence Intensities and Reynolds Stresses
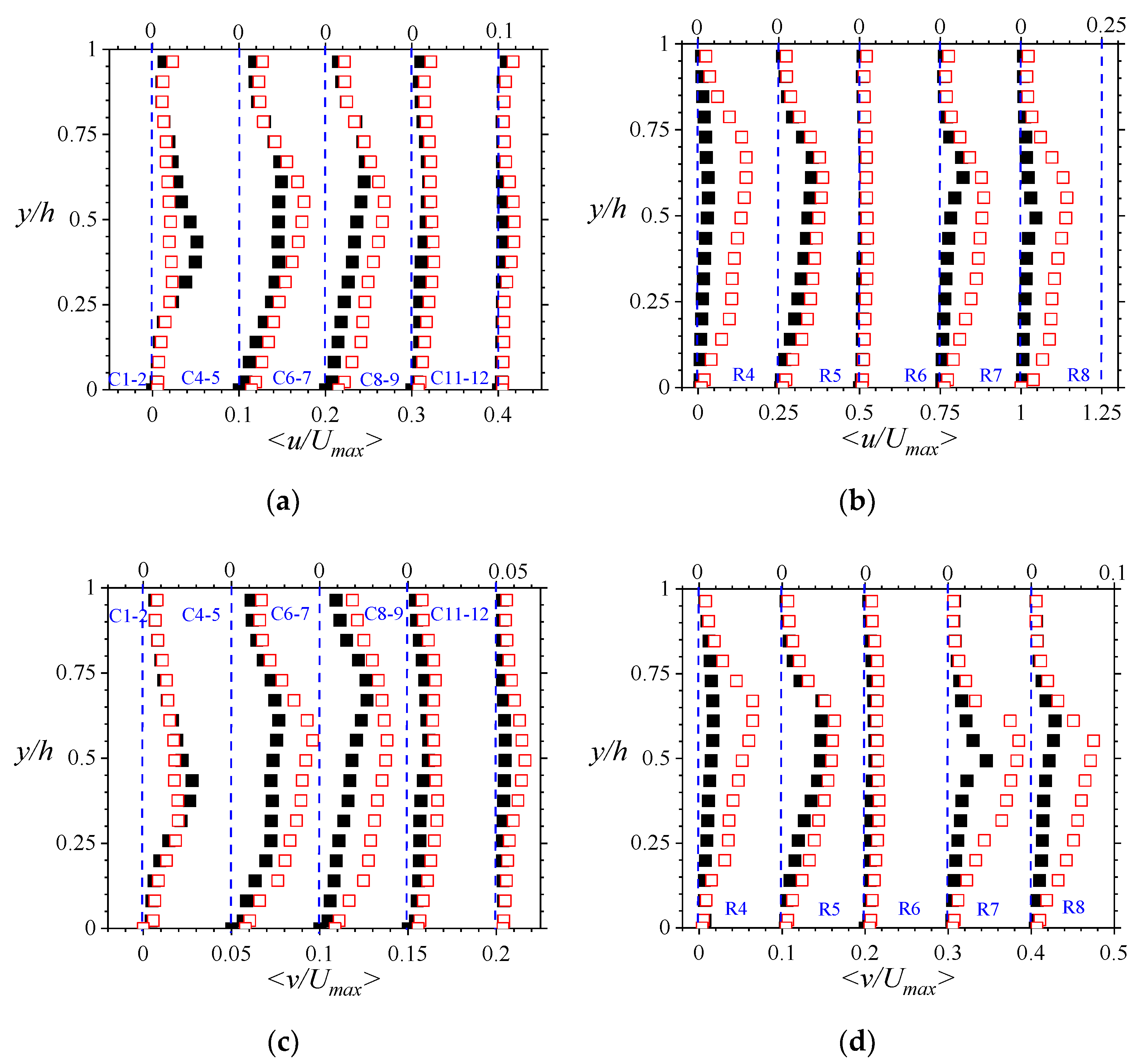
The nature of turbulence within the porous medium was first analyzed using plots such as those in
Figure 7. In that figure, the line-averaged turbulence intensities in the streamwise direction <
u>, and the corresponding component in the wall-normal direction <
v> are shown. While the pore-level turbulence intensities were less than 6% of the maximum line-averaged local streamwise mean velocity, they vary in the streamwise, wall-normal, and spanwise directions. Furthermore, they are Reynolds number dependent.
It is worth noting, however, that in all cases, the streamwise components of the turbulence intensities were larger than the wall-normal components. This is expected, given that the mean flow is predominantly driven in the streamwise direction, and the wall-normal components are going to be suppressed by the walls that are normal to it. Along the stream, however, the deviation of the velocity components from the mean increased over the first seven columns of rods. The profiles also showed that within the porous medium, the peak intensities were registered at about 0.5–0.6 of the depth of the porous medium. The observance of high intensities at rod mid-height and upstream rod areas can be explained by the compounding disturbance of the flow due to the rods as well as the vorticial activity close to those regions. Consequently, the turbulence intensities decline as the flow moves past the eighth column of rods where vortices devolve thereon, and the flow encounters an unobstructed domain downstream. These observations suggest then that the utmost utility of a rod arrangement such as a turbulence generator is gained using a limited number of columns of rods (<8) along the stream.
The spanwise variations of the turbulence intensities also revealed low turbulence levels at the midspan, compared with other spanwise locations. Indeed, the intensities in the midspan plane were so low that their variations with depth appeared to be linear. The reason for these differences in velocities in the present study may be rationally attributed to the side wall effects due to the narrow wall channel used in the tests. The sheer proximity of the solid side walls is expected to increase the turbulence intensities close to those walls. This explains why some of the highest intensities were recorded at measurements taken at z = ±l. Concerning Reynolds number variation, intensity increments are expected, as the random nature of the flow within the porous medium will only worsen as the flow speed (and consequently the Reynolds number) is increased.
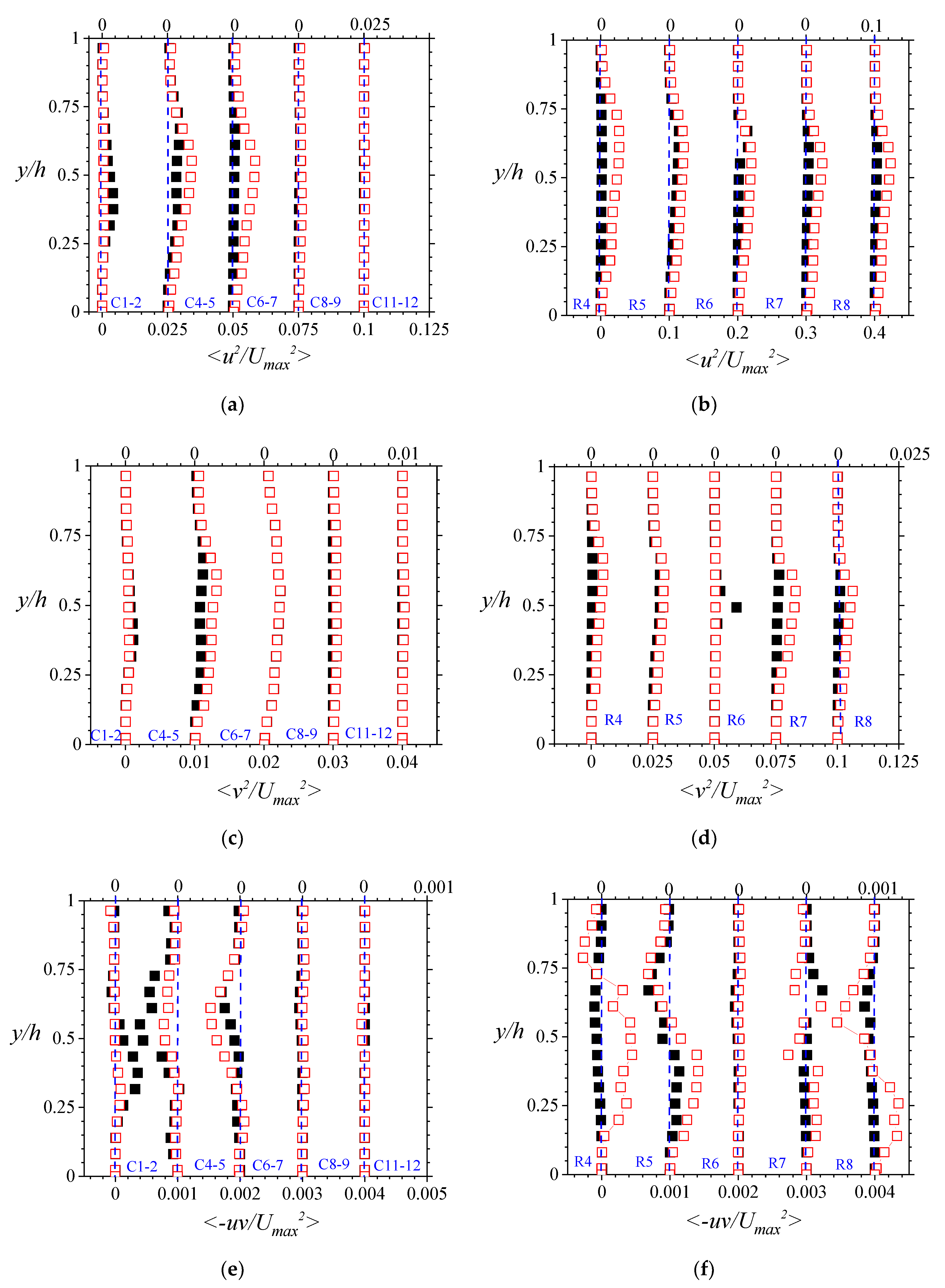
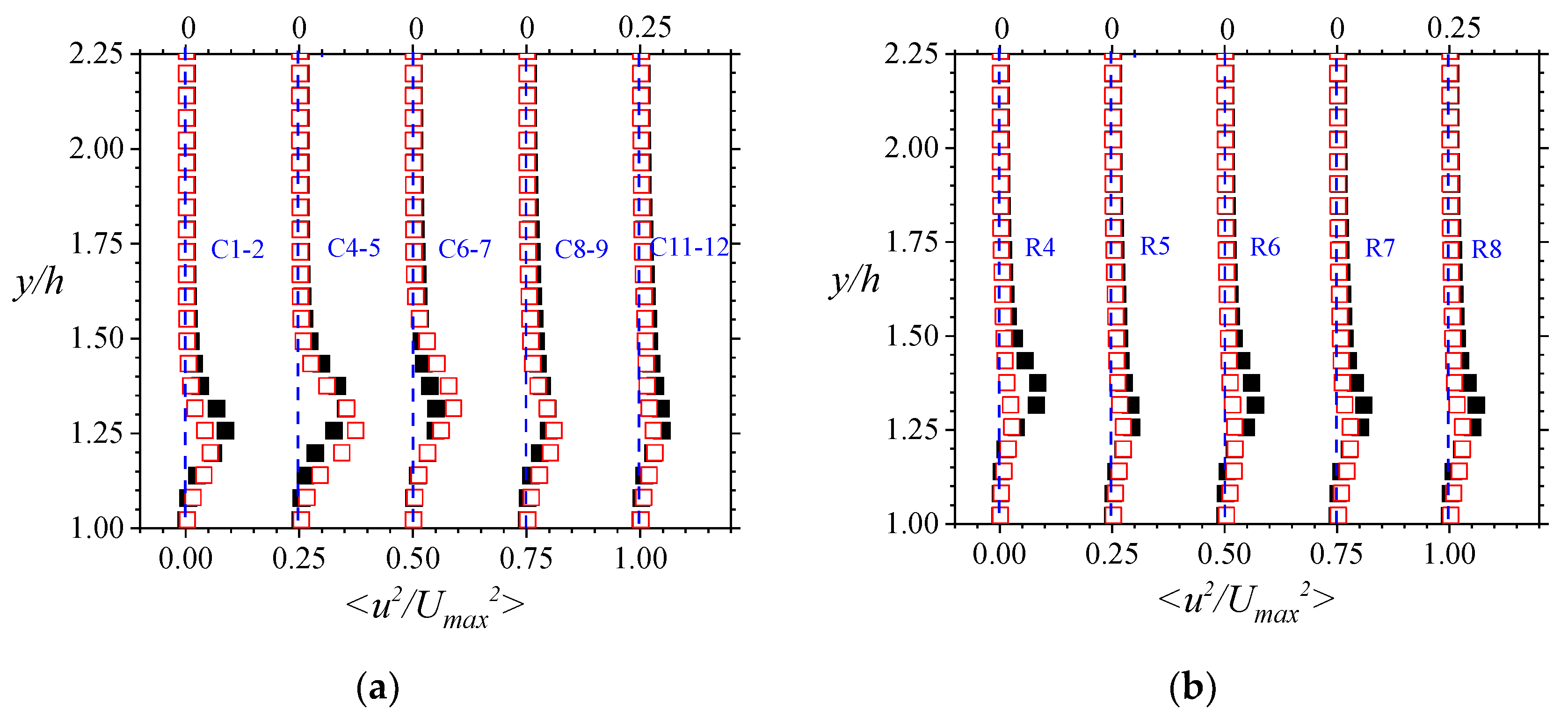
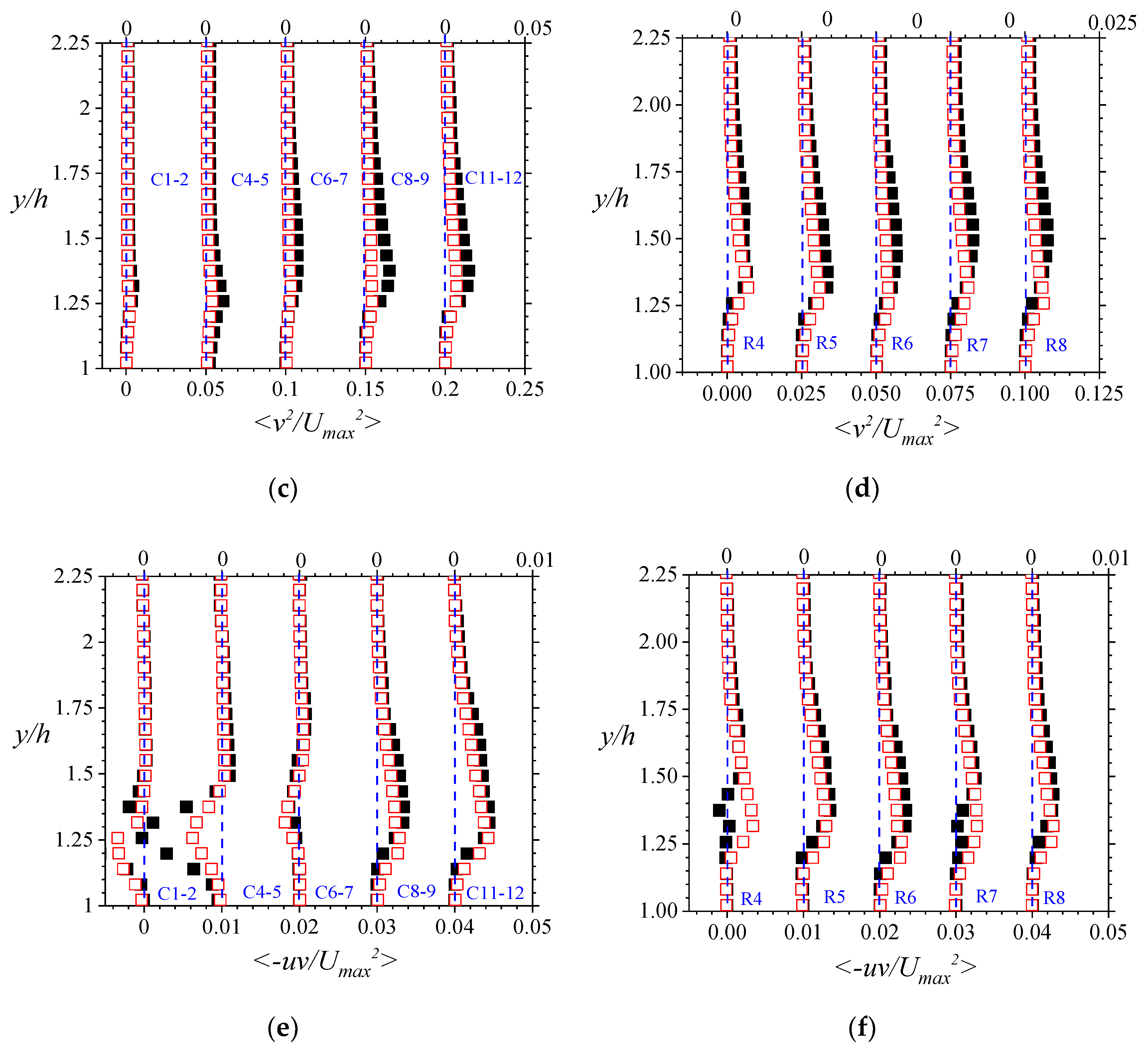
The normalized Reynolds stress distributions were considered to determine if there were any further significant turbulent features within the porous medium. These are plotted in
Figure 8a–d for line-averaged normal stresses in the streamwise direction <
u2> and wall-normal direction <
v2>, and in
Figure 8e,f for line-averaged shear stresses in the streamwise-wall-normal plane <−
uv>. With a greater presence of solid boundaries along the stream, it is expected that the velocities normal to those surfaces will be suppressed more than the component parallel to the surface [
50]. Hence, <
v2> was found to be less than <
u2>, suggesting an anisotropic turbulent field. It was also observed that some of the identifiable features of the turbulence intensities were present in the Reynolds normal stresses. The peak values were at approximately the same location as that of the turbulence intensities; additionally, the upstream columns of rods also showed some significant streamwise and wall-normal variations that were Reynolds number dependent. It is therefore reasonable to assume that some of the physics dictating the trends of the turbulence intensities and the Reynolds normal stresses are similar. The Reynolds shear stresses, however, were complex and very different from those reported by Manes et al. [
18]. For the upstream rods, the Reynolds shear stresses generally declined with porous medium depth to a negative value, and then resulted in a null value. While the downstream rods showed a linear profile, there were distinctive changes in the off-midspan plane profiles. As these Reynolds shear stresses were produced by the mean shear in the streamwise-wall-normal plane within the turbulent flow, they recorded significant values at regions of substantial shear such as observed at regions close to the sidewalls.
3.1.3. Interfacial Flow
For a dense submerged canopy such as that under study, the drag due to the porous medium is expected to be larger than that of the lower wall. Thus, the discontinuity in drag that occurs at the interfacial edge will give rise to a region of shear that resembles a free shear layer with an inflection point near the interface [
35]. The generation and propagation of K–H vortices from this shear layer suggest that the interface is a determinant of the degree of communication between the open and porous regional flows. Therefore, an understanding of the interfacial flow is integral to a proper view of the entire flow domain. The interfacial flow is known to be a function of several parameters including the specific permeability of the porous medium, average velocity within the porous medium, the velocity at that interface (i.e., the slip velocity), shear rate at the interface (i.e.,
Υ0 = dU/
dy|
y=h), and the channel’s local maximum velocity [
51]. In this work, the interfacial flow was analyzed by focusing attention on measurements (or interpolations) of the slip velocity and its associated shear rate. The spatial variations of these select parameters were then studied with regard to changes in the bulk Reynolds numbers of the flow.
The reported slip velocity <
Us> is defined as the line-averaged streamwise mean velocity at the plane tangent to the edges of the rods in most immediate contact with the open flow region (i.e.,
y =
h). Particle image velocimetry measured velocities over a finite interrogation area whose center was not located exactly at this defined interface. Thus, it was not possible to provide the averaged slip velocities at the interface. Consequently, in this study, slip velocities could only be determined within interfacial location uncertainties of ±0.27 mm (which is half the size of an interrogation window). The line-averaged interfacial mean shear rate <
Υ0> was also determined by using a curve of six or more streamwise velocity data points located at the region close to the interface. To assure some accuracy in the procedure, interpolations of the line-averaged data were first obtained. Differentiation of the curve was then performed smoothly over data points covering a distance of over 0.27 mm. The slip velocity and interfacial shear rates were then studied using three dimensionless parameters, namely
<Us/Ub,p>,
<Us/(Υ0 d)>, and
<Us/Umax>. By using
<Us/Ub,p> and
<Us/(Υ0 d)>, the line-averaged slip velocities were respectively assessed in terms of the streamwise bulk flow within the porous medium <
Ub,p> and the local penetration by the shear. On the other hand, by using
<Us/Umax>, the relative effects of the overlying turbulent flow on the line-averaged slip velocities were determined. The results are summarized in
Table 2 and
Table 3.
The data in both tables show that the interfacial velocities dropped from their initial values in the upstream columns of rods, and then rose again with downstream rods. The rate at which shearing was applied increased to a peak just over the columns of rods, and subsequently declined as the region of obstruction was approached. The results also indicate that there were sharp flow reversals at the interfacial region, resulting in negative slip velocities (in some cases). Furthermore, there were negative shear rates at the interfaces. The flow reversals are consistent with some of the observations made regarding vector plots in
Figure 4. While the negative shear rates were more confounding, they are still reasonable given that velocities higher than the slip velocities were identified just beneath the interface in
Figure 3a. On the whole, it is remarkable that relative to the bulk velocity within the porous medium, the slip velocities were dependent on the spatial location and the Reynolds number, and not a constant value as observed by Suga et al. [
7]. For
<Us/(Υ0 d)> and
<Us/Umax>, the slip velocities were also found to be greatest just after the most upstream rods. They also increased with Reynolds number. Across the span of the porous medium, however, both slip velocity and shear rates were dependent on the spatial location, and all the dimensionless parameters (
<Us/Ub,p>,
<Us/(Υ0 d)>, and
<Us/Umax>) tended to be symmetrical about the midspan at the higher Reynolds number.
The overall conclusions regarding the interfacial flow are that while the slip velocities recorded in this work were largely substantial in value compared to the bulk flow within the porous medium, they were mostly a small fraction of the maximum velocity (≤6%). If the absolute value of <Us/Υ0> is a measure of the depth of penetration of the turbulent flow, then the <Us/(Υ0 d)> parameter determined tells us that the average depth of such infiltration through the interfacial zone is small (~7% of the rod diameter). However, this penetration is effective in creating some significant measure of porous flow just beneath the interface.
3.2. Flow Development over the Porous Wall
In this section, the results of the flow above the porous wall are presented and discussed. Consideration of the flow is limited to 1.25 h above the porous wall.
3.2.1. Boundary Layer Characteristics
Having considered the flow within the porous medium, attention is now turned to the overlying turbulent flow. To characterize the boundary layers of the selected line-averaged streamwise velocities, values of the maximum streamwise component of the mean velocity <
Umax>, boundary layer thickness
δ, streamwise location of the edge of the boundary layer (i.e.,
y/h value at 0.99<
Umax>), displacement thickness
δ*, momentum thickness
θ*, Reynolds number based on momentum thickness and maximum velocity
Reθ, and shape parameter
H were determined from the line-averaged plots. These were obtained for selected locations, according to definitions of parameters given in
Section 2.3. Apart from <
Umax>, (which is summarized in
Table 2 and
Table 3), all the other relevant boundary layer values are presented in
Table 4 and
Table 5 and plotted in
Figure 9 and
Figure 10. It should be noted that for the convenience of analyses, the streamwise locations of the boundary layer data are taken as the center between the rods. Furthermore, the values of relevant entry flow boundary layer parameters are included in
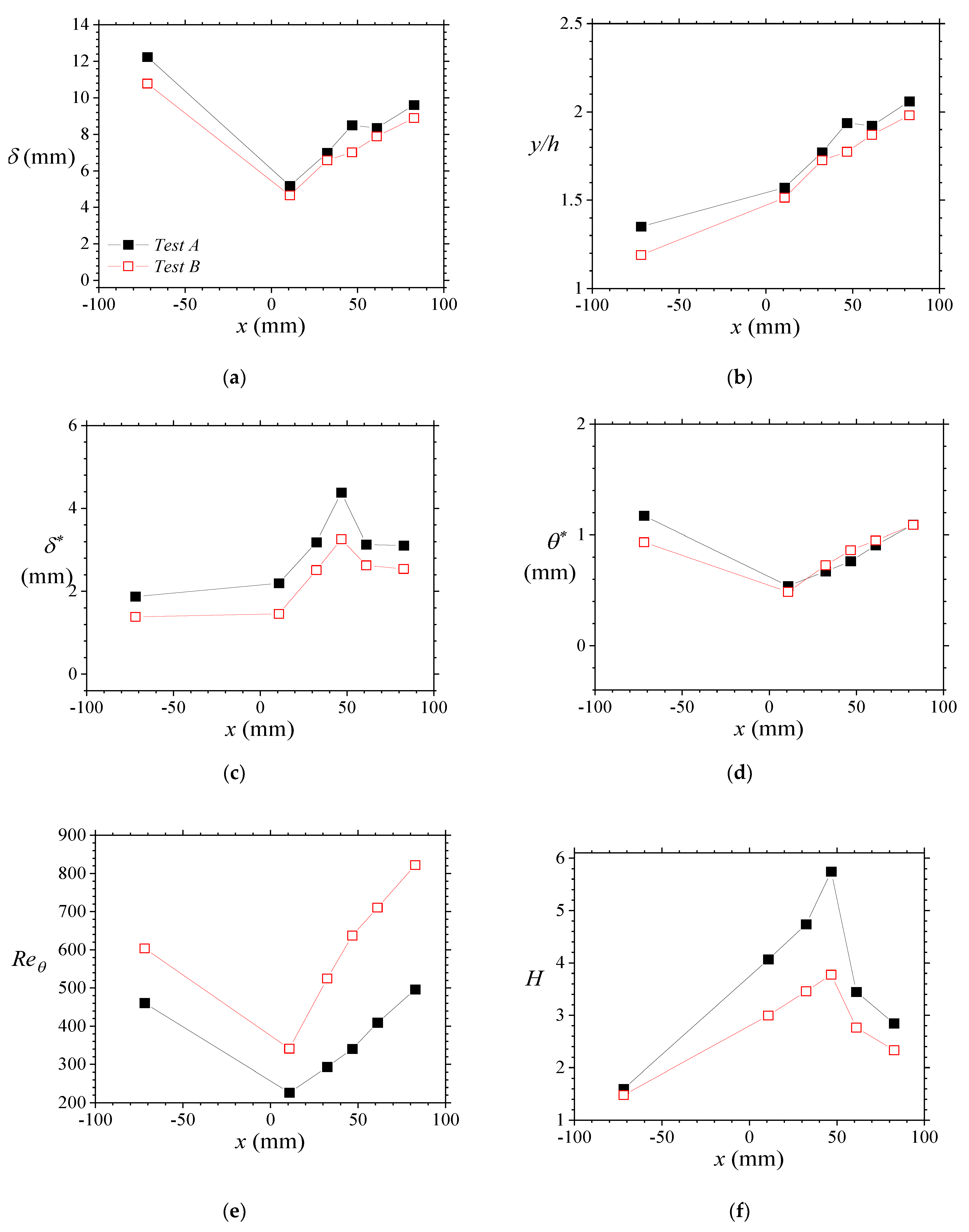
Figure 9 to show the effects of the porous medium on the flow.
By introducing the porous medium, a 21% blockage was created in the flow section, resulting in an increased acceleration of flow in the open region. Some of the results of this increment were a 27% to 32% rise in maximum velocities in the open region, and an upward shift in the location of the maximum flow. The latter can particularly be seen in
Figure 9b, where the edge of the boundary layer changes substantially from ~1.3
h at the entry flow to ~1.5
h at the upstream rods. There were also significant reductions in
δ and
θ*, especially at the most upstream rods relative to the entry flow, following the characteristics associated with flows undergoing favorable pressure gradient changes [
52,
53]. However, due to the opposing effects of the porous medium (in generating significant mass flux deficit), similar reductions in
δ* were resisted.
On the other hand, the porous boundary appeared to diffuse viscous effects into the mean turbulent flow in the open region. Thus, as the boundary layer developed over the porous medium, it thickened along the stream by about 90% at the trailing rods compared to its value over the leading rods. This boundary layer development also led to a monotonic increase in θ*, and an initial augmentation in δ*. It must be noted that both δ* and θ* are respectively indicators of the mass and momentum flux deficits. For the present tests, both parameters ultimately increased in value at the trailing rods (compared to that at the leading rods of the porous medium). Thus, it may be concluded that the current porous medium significantly enhanced mass and momentum deficit (by 42–102%). Consequently, with the 30% increase in maximum streamwise mean velocity, Reθ magnified much more significantly, and more prominently at the higher Reynolds number flow.
The relative effects of
δ* and
θ* in the flow arrangement are accounted for in the shape factor
H trends indicated in
Figure 9f and
Table 4. For the entry flow,
H compared well with previous results of turbulent flows over a smooth wall at zero pressure gradient and at similar
Reθ [
54]. However, along the streamwise direction on the porous wall, the values of
H were found to be high, and characterized by two distinct zonal attributes. There was the first zone upstream of the porous medium, marked by a sharp increase in mass deficit flux compared to momentum deficit flux along the stream. There was also the second zone where in anticipation of lower flux deficits in the unobstructed flow downstream, the displacement thickness dropped sharply to a constant value while the momentum deficit flux continued to increase incrementally toward the trailing edge of the porous medium. Thus,
H declined in the flow over the trailing rods of the porous medium. The value of
H measured between columns 11 and 12 of the porous medium rods showed that the porous medium more than doubled the shape parameter of the boundary layer relative to the entry flow. This is predictable for obstructions in flow that generate higher drag characteristics such as that expected of the porous medium in the current flow arrangement [
55].
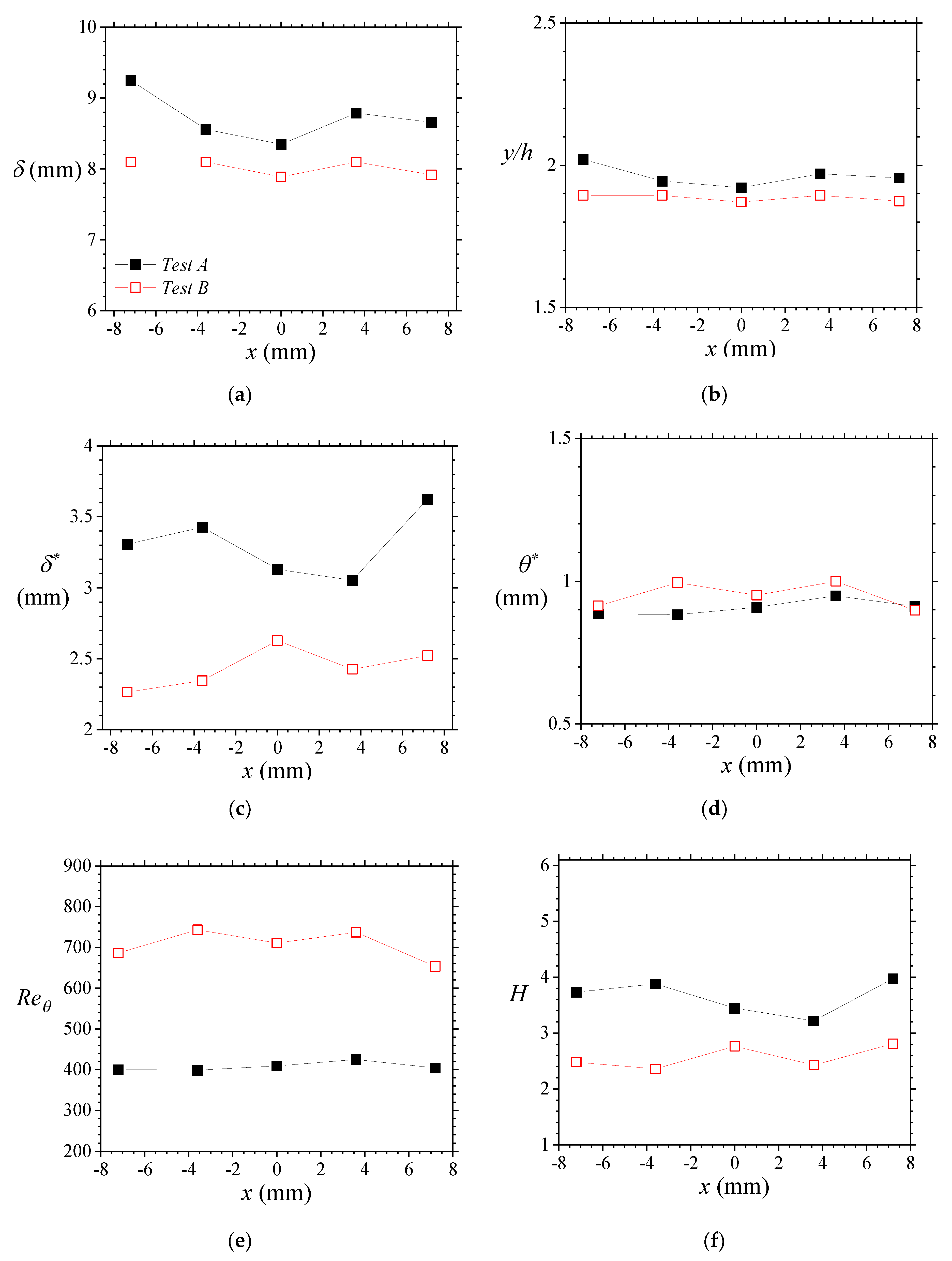
Regarding spanwise changes in boundary layer characteristics,
Figure 10 and
Table 5 reveal variations were less dramatic compared to the streamwise changes. However, it is noteworthy from the data that lower flow speeds tended to display three-dimensional effects. In the current arrangement, this resulted in relative deviations that were no more than 16% of the value at the mid-plane. Such maximum deviations occurred at locations closer to the sidewalls.
3.2.2. Mean Velocities, Momentum Flux, and Vorticity
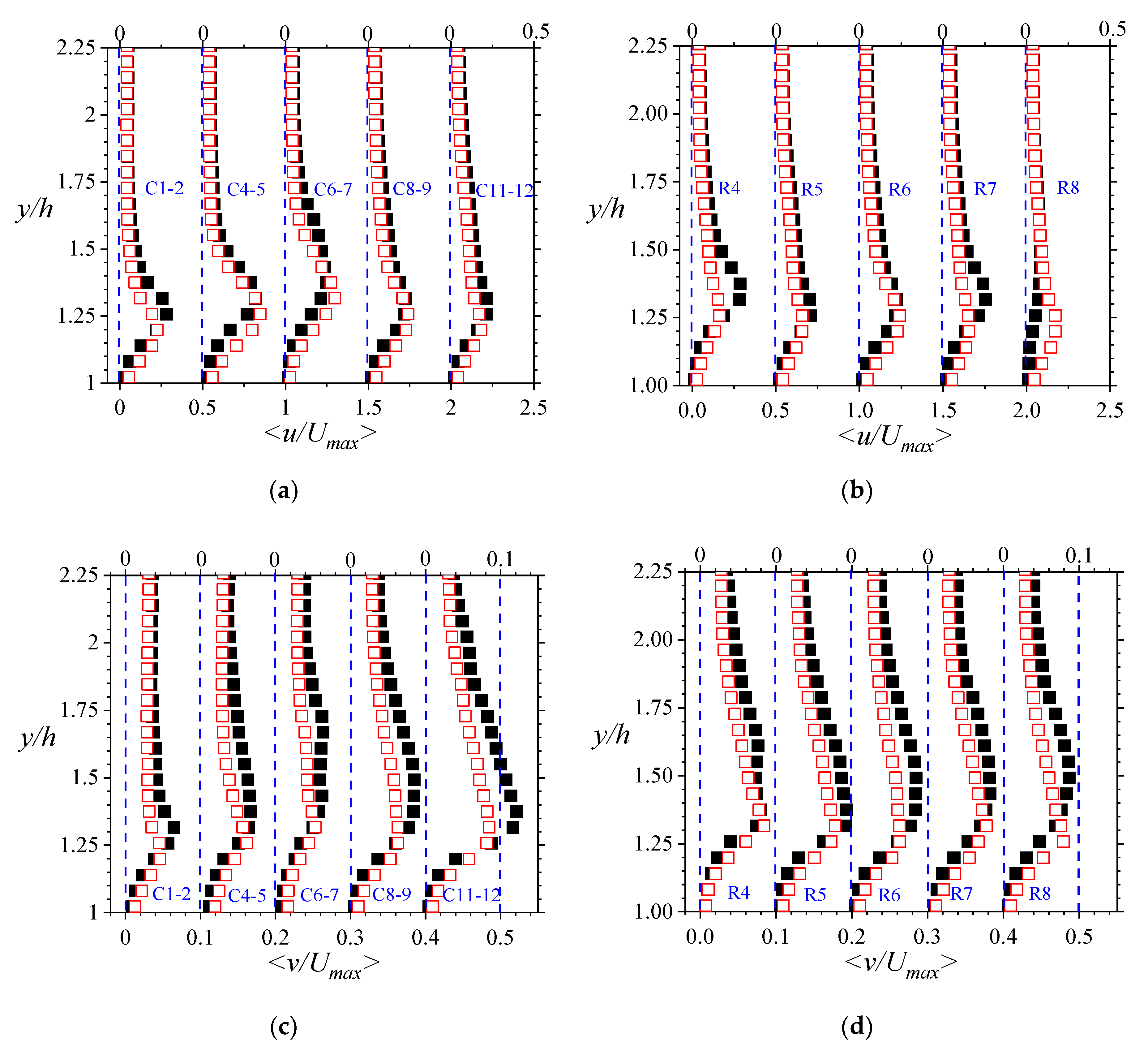
The mean velocity profiles in the streamwise directions are shown in the outer coordinates in
Figure 11. As indicated in
Section 3.1.3, there were flow reversals at the interface, specifically for mid-span line-averaged measurements between columns 4 and 5, and columns 8 and 9, respectively. The line averaged shear rates were also negative in value. All of these, along with the high
H values observed in
Figure 9 and
Figure 10, point to complications in flow characteristics similar to those observed in adverse pressure gradient flows [
55]. This behavior is possibly due to the intermittent pores on the surface of the porous medium.
The streamwise mean velocities were also critically examined to ascertain the validity of a logarithmic region in the flow profile over the porous wall during flow development. The associated friction velocities
Uτ were also determined. In doing this, a modified form of the procedure outlined in
Section 2.3 for rough wall turbulent flow [
6,
55,
56] was followed. The normalized mean plots were matched with the following modified log law [
42,
55].
where
U+ =
U/
Uτ and the von Kármán constant
κ and logarithmic constants
B were 0.41 and 5, respectively. It should be noted, however, that in this modified log law, the variable
y+ =
y Uτ/
ν is defined as (
+
yo)
Uτ/
ν. This is in line with the customary practice of rough wall experiments where the ‘roughness’ effects are considered in the definition of
y. In the current setup,
y is defined as the sum of the wall-normal distance from the top plane of the rods
and a virtual origin
. The parameter
B+ is a ‘roughness’ function that measures the increase in local drag due to the presence of roughness elements on the surface [
57]. Thus, it is seen as a downward shift of the log law profile of a comparable turbulent flow over a smooth wall. Following precedence then [
6,
55], the Clauser plot technique was used to simultaneously estimate
Uτ and
yo. Previous DNS results of turbulent flow over two-dimensional rods showed that at 1 <
x/
l < 9 (i.e., the initial developing flow region),
yo/h ranges from 0.51 to 0.52 [
58]. On this basis, an initial guess within this range was used. The optimized value of
yo = 0.515
h yielded
Uτ values listed in
Table 4 and
Table 5 with an uncertainty limit of ±10%. Selected streamwise mean velocity profiles in the inner coordinates are presented in
Figure 12. Clearly, the associated roughness functions were high; indeed, they were found to range from 21 to 24 for the streamwise variation plots, and 18 to 23 for the spanwise variation plots. These values are much higher than what was indicated in other turbulent flows over rough surfaces [
55,
57,
59], suggestive of the possibility of a different von Kármán constant than what was employed in this work.
From these assessments, it is evident that if existent, the logarithmic layer occupies a very limited region. The friction velocities
Uτ (in
Table 4 and
Table 5) were substantially (9 to 18 times) higher over the porous surface compared to the entry flow over the smooth wall. As the flow over the porous surface developed along the stream, this friction velocity increased to a peak and declined thereafter. This is consistent with the trends seen for the displacement thickness observed in
Figure 9, and mean velocity profiles in
Figure 11. A similar trend in
Uτ was reported in the simulations of Lee and Sung [
58] for a turbulent flow over two-dimensional rods. However, in that work, their peak value was just about a quarter of the value recorded in this work. The higher values observed in the present tests stem from the increased drag due to the three-dimensional porous medium rod arrangement. The lateral deviations of
Uτ, on the other hand, were insignificant considering the uncertainty limits.
Remarkably, the mean wall-normal profiles in
Figure 13a,b were not negligible as often observed in turbulent flows over smooth walls of zero pressure gradient [
55,
58]. Indeed, in the flow over the first seven columns of rods, the maximum values were 5 to 12% of the line-averaged local maximum mean streamwise velocity. Compared with
Figure 11, it is patent that the flow over those rods is three-dimensional, and that the wall-normal velocities contribute significantly to the mean momentum transport over the porous surface. Consequently, it is not surprising that mean momentum fluxes in
Figure 13c,d were also significant. The high fluxes imply that they are also important factors in the production of shear stresses in those regions [
57]. The dynamic roles of the mean wall-normal velocities and the momentum fluxes, however, declined downstream as the flow approached the unobstructed domain.
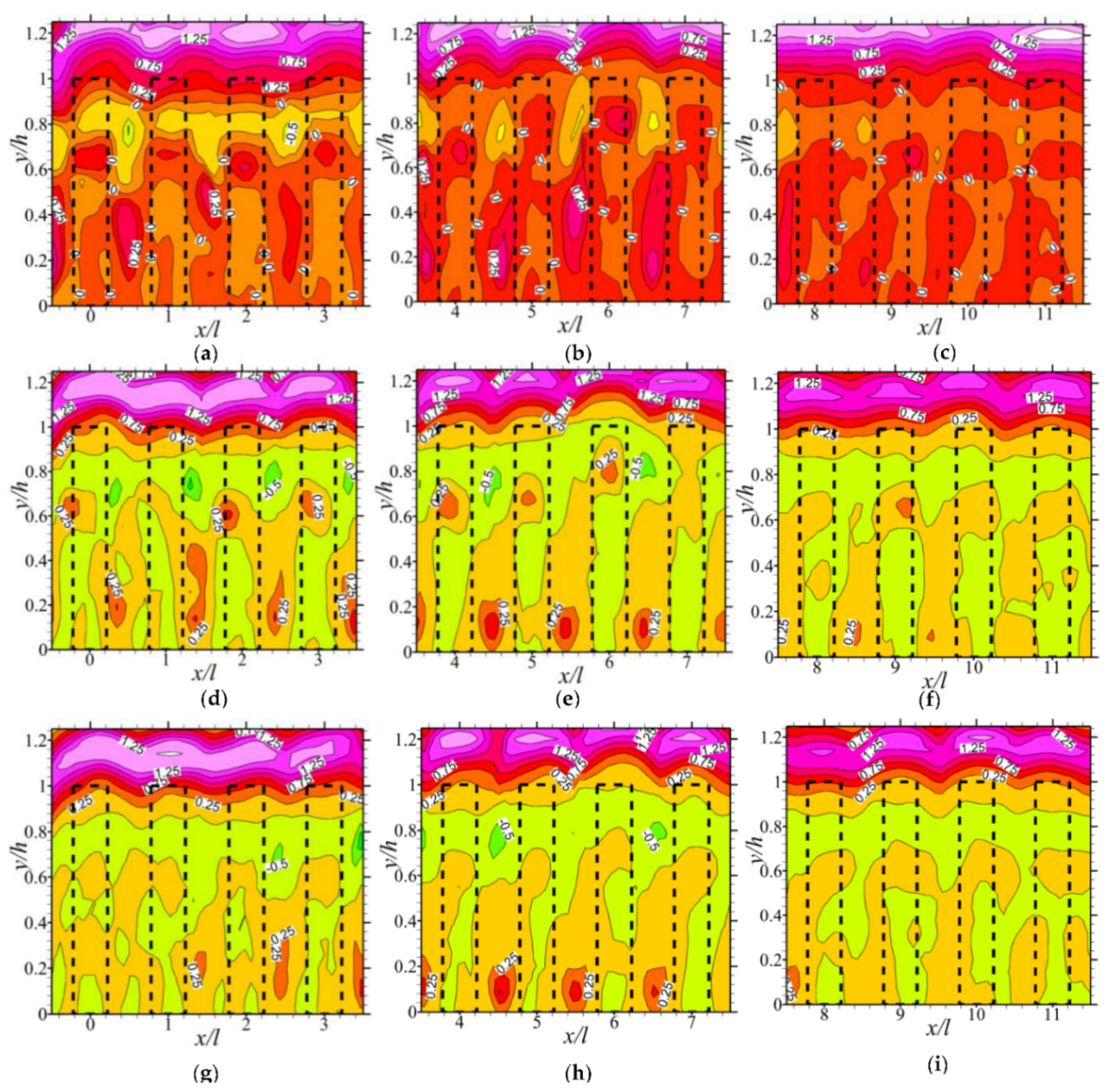
To illustrate the rotational regions of flow above the porous medium, the line-averaged mean spanwise vorticity <
Ωz> (<∂
V/∂
x − ∂
U/∂
y>) distributions are plotted in
Figure 14. They underscore the complex vorticial activity over the porous medium. These vortices are presumed to stem from Kelvin–Helmholtz (K–H) instabilities, and such are reported in other related studies [
7,
60]. In the current tests, the domination of these vortices were emphatic at the first seven columns of rods. For those domains, they were found to extend into increasing depth of the flow above the rods as they propagated through the flow. The location of the maximum vorticity also changed with the streamwise location. Compared with the flow through the porous medium, vortex motions over the rods were ~5 times more intense in magnitude, and more sustained. Moreover, the spatial variations along the span also showed that the presence of the side walls tended to heighten the vortex motions and more so at lower Reynolds number.
3.2.3. Turbulence Intensities, Reynolds Stresses, and Turbulent Energy
The turbulent intensities of the flow over the porous surface were also examined. They are plotted as line-averaged distributions in
Figure 15. The results indicate that compared with the local mean streamwise velocities, the maximum streamwise and wall-normal turbulent intensities were ~25% and ~12%, respectively. The Reynolds number effects were also apparent in the wall-normal turbulent intensities. The maximum turbulent intensities measured in the flow above the porous medium were much higher than those measured at the entry flow and within the porous medium. Indeed, the relative proportions of the streamwise and wall-normal components were found to be higher than that recorded in previous works [
7,
60]. It is also worth noting that the variation of the wall-normal locations of the maximum streamwise turbulent intensities was relatively small compared with other mean flow quantities (e.g., momentum flux). This indicates that the maximum turbulent intensities were not so much a factor of the mass and momentum dynamics of the turbulent flow as the static attributes of the flow section. Thus, it is reasonable to conclude that the turbulent intensities are mostly due to the porous boundary condition, and specifically the structural arrangements of the porous material.
The profiles of the line-averaged Reynolds normal and shear stresses are shown in
Figure 16. The Reynolds normal stresses were found to be qualitatively similar to the turbulent intensities. Thus, here also, as the wall-normal components were expected to be curbed by the porous wall, these values were smaller than the streamwise components. Additionally, the wall-normal locations of the maximum Reynolds normal stresses did not very much, consolidating the likelihood of the porous boundary being the main factor of influence of their magnitudes. The Reynolds shear stresses, on the other hand, were quite distinctive. The profiles of flow over the first six columns of rods had negative maximum values, while those over the downstream rods had positive maximum values. This observation of negative Reynolds shear stress measurements of turbulent flows over porous media is rare in the literature. However, it should be conceded that the literature has barely any record of turbulent boundary layer flow developments over porous media. Nevertheless, it is notable that Lee and Sung [
58] reported negative Reynolds shear stresses in their direct numerical simulations of the turbulent boundary layer over a rod-roughened wall. These negative values were also specifically located over the most upstream two-dimensional rod. Hence, this feature is not totally out of the bounds of possibility. This phenomenon requires further study. However, it is also reasonable to note that if the negative mean momentum flux <−
UV> is important in the production of the shear stress (as suggested in the streamwise momentum equation [
57]), then large pockets of positive mean momentum flux <
UV> (
Figure 13c,d) may be a factor in the sign change in <
−uv> [
57].
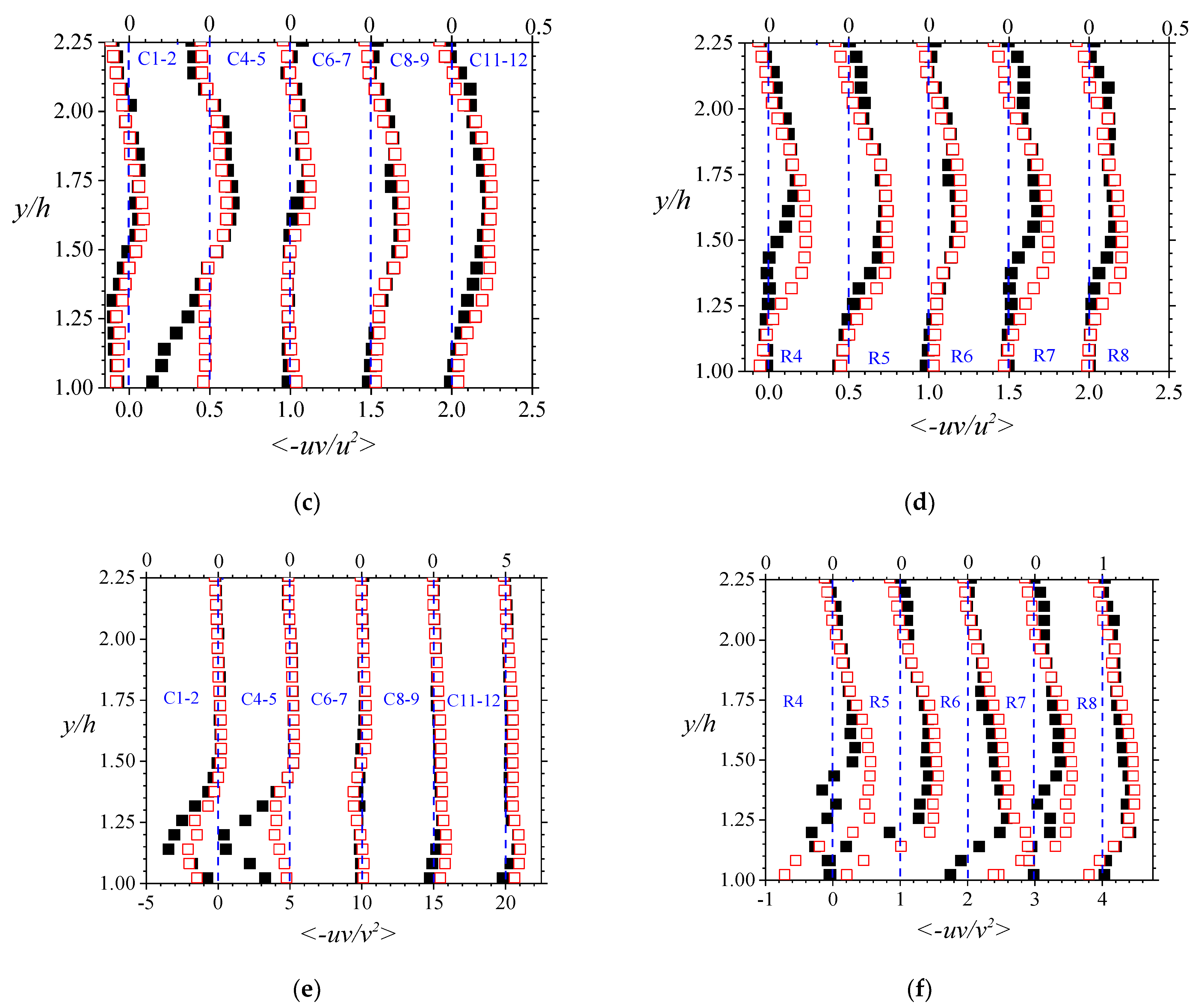
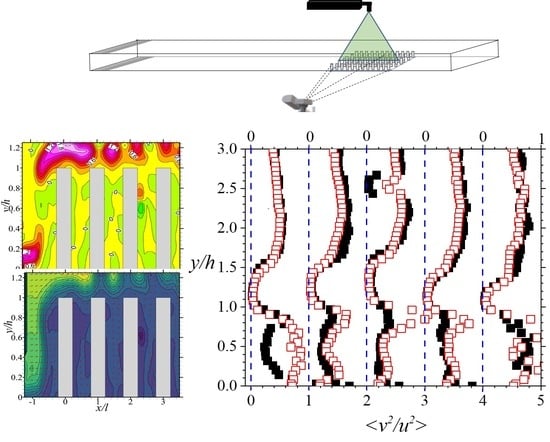
To study large-scale anisotropy, ratios of the Reynold stresses were analyzed. The plots are presented in
Figure 17. As shown, close to the porous boundary, the ratio of the normal stresses tended to decay and flatten to values other than unity. Further away from the walls, they increased to ~0.5. The ratios of the Reynolds shear stress and the normal stress, however, were complex. As the flow developed downstream, the ratio of the Reynolds shear stress and the streamwise component of the normal stress varied throughout the flow, with Reynolds effects apparent in the spanwise planes. As expected, the effects of negative Reynolds shear stresses were also present in the upstream rods. It has been reported that some researchers (e.g., Suga [
61]) have been able to develop turbulence models for fully developed flows over porous media with varying degrees of success. The results showed herein, however, indicate that the use of models (e.g.,
k-
ε and
k-
ω) that assume local isotropy do not apply to turbulent flows over compact porous media as tested in this work.
In another consideration, the turbulent kinetic energy
k was assessed. As the current measurement system is planar, the Reynolds normal stress in the spanwise direction
w2 could not be measured directly. Thus,
k was estimated as 0.75 (
u2 +
v2). The normalized line-averaged profiles are shown in
Figure 18. As the streamwise component of the Reynolds normal stress is the dominant contributor of
k, the profiles are qualitatively similar to the streamwise Reynolds normal stress distributions in
Figure 16. Clearly, there is significant turbulent kinetic energy at the domain where intense vorticial activity is prevalent. The ratio of the Reynolds shear stress to the kinetic energy is an important parameter that is used to calibrate turbulence model coefficient
Ck [
62,
63]. This constant (also called Townsend’s structure parameter, <−
uv/(2
k)> is used in the Kolmogorov–Prandtl expression associated with the eddy viscosity
vT (=
Ck k/
L, where
L is a length scale). De Lemos [
63] suggested a constant for turbulent flow over porous media. However,
Figure 19 indicates that this coefficient may vary from ~−0.3 to 0.1 depending on the wall-normal location above the porous medium.
4. Conclusions
The focus of the present work was the investigation of a turbulent flow through and over a compact porous medium. This research was conducted to measure the development of the flow over the porous boundary, the penetration of the turbulent flow into the porous domain, the attendant three-dimensional effects, and Reynolds number effects. These objectives were achieved by conducting particle image velocimetry measurements in a test section with turbulent flow through and over a compact model porous medium of porosity 85%, and filling fraction of 21%. The porous medium model was made of a square array of cylindrical rods of twelve columns and nine rows. The tests were carried out at Reynolds numbers (based on the bulk flow through the entire channel, and the depth of the channel) = 14,338 and 24,510.
Overall, this work indicates that the flow through and over a compact porous medium exhibits phenomenon different and somewhat complex compared to that associated with fully developed domains. The flow above the compact porous medium showed a complex flow development pattern with the boundary layer thickening along the stream by about 90% at the trailing rods, increasing monotonically in momentum thickness, and growing non-monotonically in displacement thickness and shape parameter. The spanwise variations, on the other hand, were no more than 16% from the value at the mid-plane. The mean velocities showed that if existent, the logarithmic layer occupied a very limited region. The friction velocities were 9 to 18 times higher over the porous surface compared to the entry flow over the smooth wall. There were significant complex vorticial activities over the porous medium, extending into an increasing depth of the flow above the rods as they propagate through the flow. The ratios of the Reynolds stresses showed a complex large-scale anisotropy in the flow over the porous medium. The implication then is that the use of turbulence models that assume local isotropy through and over porous media may not apply to turbulent flows over compact porous media. At the interface between the porous medium and the overlying turbulent flow, the slip velocities were no more than 6% of the maximum velocity. The shear rate obtained indicates that the average depth of such infiltration through the interfacial zone was only about 7% of the rod diameter. For the flow through the porous medium, the results showed that the streamwise velocities, in particular, had variations with negative gradients close to the lower wall and in the planes outside of the midspan. Pockets of variant sizes of the mean spanwise vortices appeared to be propagated from regions of shear through the porous medium, at the edge of the most upstream porous medium rods, and the interfacial region.
This work provides useful insight into the physics of flow pertinent to natural and industrial scenarios such as terrestrial or aquatic canopy flows over regions with small/confined arrangements of sparse vegetation, and flows associated with pin-fin arrays of rods for heat transfer enhancement. The data may serve as a useful resource for developing and validating numerical models.