1. Introduction
In geophysical fluid flows, the Lagrangian approach, where one follows fluid parcels as they move through time and space, provides a natural perspective to study the dynamics of motion and the patterns of transport [
1,
2,
3,
4,
5]. Even simple, time-periodic velocity fields can generate complicated trajectories and chaotic motion [
6,
7]. It thus comes as no surprise that Lagrangian transport in realistic oceanic flows, which are aperiodic, can be incredibly complex.
The Lagrangian structures that organize transport and govern coherent trajectory patterns are referred to as Lagrangian Coherent Structures (LCS), a term introduced by Haller and Yuan [
8]. These structures act as the hidden skeleton of a flow [
9,
10] that can be uncovered using techniques from the dynamical systems theory [
8,
11,
12]. Recent review papers of LCS detection methods include [
13,
14,
15,
16].
LCS methods can be classified into those looking to identify regions (two- and three-dimensional in 2D- and 3D-flows, respectively) with coherent Lagrangian motion, and those looking for the boundaries (one- and two-dimensional in 2D- and 3D-flows, respectively) between such regions. The majority of clustering methods, including our optimized-parameter spectral clustering presented in this paper, fall into the former category, whereas the latter category includes, for example, Finite-Time Lyapunov Exponent (FTLE) and Finite-Size Lyapunov Exponent (FSLE) ridges [
8,
17,
18,
19], geodesic and variational transport barriers [
14,
20,
21,
22], Lagrangian-Averaged Vorticity Deviation (LAVD) and Rotationally Coherent Lagrangian Vortices (RCLV) [
23,
24], and diffusive transport barriers [
25].
Cluster-based LCS methods take root in the field of unsupervised machine learning. Several algorithms have been adapted recently to LCS detection in geophysical flows [
26,
27,
28]. A recurring concern with these methods is that the results rely on a set of user-input parameters, making the outcome subjective. Hadjighasem et al. [
15] present a comparison of the number of parameters required by several clustering methods to construct a Lagrangian field and show how spectral clustering requires the least amount of user inputs. The authors describe how to “choose a reasonable set of parameters for each method” to yield “the most favorable outcome”. They describe a robust outcome as an outcome where “small variations in the parameters do not lead to drastic changes in the outcome”, which is a fair way to describe robustness. The reasonability of the parameters and the favorability of the outcome, however, suggest that in the end, the user will have to make decisions about the outcomes of the analyses that could be arbitrary and subjective. In this paper, we append the conventional spectral clustering method of HA16 (explained in
Section 2.1 and
Section 2.2) with an algorithm for the automatic identification of the optimal parameters within pre-defined parameter ranges (
Section 2.4). Our optimized-parameter spectral clustering method is still subject to all the usual limitations of the spectral approaches, including the need for a detectable spectral gap [
15,
29] and a tendency to favor clusters of equal size [
30]. In addition to the parameter optimization algorithm for spectral clustering, we also introduce a noise-based metric for quantifying the coherence of the resulting coherent clusters (
Section 2.4), which allows comparing the clusters to each other within the same flow, as well as inter-comparing the clusters between different flows. The optimized-parameter spectral clustering approach is then applied in
Section 3 to two idealized analytical flows, the Bickley Jet and the asymmetric Duffing oscillator, and to a realistic oceanic coastal flow. In the last example, the identified clusters are tested using observed trajectories of real drifters. The results are discussed in
Section 4.
2. Materials and Methods
Consider an unsteady flow that is known, either from measurements or simulations, over a finite-time window from to within a finite spatial domain. Our goal is to separate the domain into coherent clusters according to their Lagrangian behavior. Please note that the time window and the domain size should be considered part of the problem set up rather than parameters of the cluster detection method.
Below we review the conventional spectral clustering method, discuss its shortcomings associated with the need for user-input parameters, and then introduce a new and improved optimized-parameter spectral clustering method. We also review the Finite-Time-Lyapunov Exponents and Poincaré section techniques, which will be used in
Section 3 for comparisons with the spectral clusters.
2.1. Conventional Spectral Clustering Method
The spectral clustering approach to LCS detection by [
27], hereinafter referred to as HA16, partitions the dataset according to similarity between trajectories, such that intra-cluster similarity is maximized, and inter-cluster similarity is minimized. The similarity is determined from the pairwise distances between trajectories. Reviews of spectral clustering can be found in [
29,
31]. Below we briefly summarize the method.
Let
and
be two trajectories in
, where
for two- or three-dimensional flows, respectively, with positions at
n discrete times from
to
. The time-averaged distance
between trajectories is, following HA16:
with
denoting the spatial Euclidean norm and where it is assumed that during each time step
, the distance is constant and equal to the mean between the values at endpoints. Next, convert the pairwise distances
into the similarity weights
:
From the weights
, build the similarity graph
, with nodes
, edges
between nodes
and
, and similarity matrix
that associates the weights
to the edges
. Next, define the sparsification radius
r and sparsify
W by removing all weights
The advantage of sparsifying W is two-fold: first, it saves computational efforts by removing a large number of entries; second, it minimizes the influences of entries with insignificant similarities.
The optimal partition of the domain is one with maximal intra-cluster similarity and minimal inter-cluster similarity; the ideal case would be one in which the dissimilarity between subsets is absolute, or the similarity is zero. The partition of the domain into
k subsets that maximize the intra-cluster similarity and minimize the inter-cluster similarity can be achieved by minimizing the Ncut function,
, where
is a subset of the nodes within the domain,
is the complement of
and
is the volume of set
V, with
. For large datasets, however, minimizing Ncut is computationally expensive. Therefore, an approximate solution is often used, which can be efficiently constructed with the eigenvectors
of an eigenvalue problem for the graph Laplacian
(see [
29,
31] for derivations of this result):
where the diagonal degree matrix, D, contains degrees,
, for all nodes
. The solutions
s are the generalized eigenvectors associated with the unnormalized graph Laplacian
L from Equation (
4). As detailed in [
29], it is often advantageous to use a normalized Laplacian: normalized spectral clustering performs better in partitioning the graph such that within-cluster similarity is maximized, especially for irregular graphs with vertices of highly varying degrees. We thus use the normalized graph Laplacian
following the derivation in HA16. Hereinafter, the
’s refer to the eigenvectors of the normalized graph Laplacian
.
From perturbation theory and the Davis–Kahan theorem, which bounds the differences between eigenspaces of symmetric matrices under perturbations, the eigenvectors ’s are close to the vectors from the exact Ncut partition. The order of eigenvectors and eigenvalues is meaningful and the first k eigenvectors s can be used as approximate solutions for the k connected components of the graph. The optimal number of eigenvectors that are kept is retrieved by the heuristic argument of the spectral eigengap, i.e., the largest gap between successive eigenvalues of . This number equals the number of eigenvalues before the eigengap. The resulting partition separates the connected components from the rest of the domain, which is assigned to the ”incoherent background” subset. The wider the eigengap, the closer the approximate solution is to the exact solution of the graph cut minimization problem and the better the partition of the domain will be.
The final step is to extract the coherent clusters from the weighted graph data. To partition
N trajectories, or nodes, into
clusters (i.e., into
coherent clusters and 1 incoherent background cluster), the K-Means algorithm ([
32], summarized below) is applied to the matrix
of the first
eigenvectors
. Each eigenvector
has length
N (for the
N nodes), and the matrix
U has size
N-by-
.
U contains information about the connectivity between nodes within the connected part of the graph. The output of K-Means is an
N-by-1 vector that assigns a cluster index of each node. The clusters are mutually exclusive, i.e., each node only belongs to 1 cluster. For this reason, the K-Means is sometimes referred to as Hard C-Means, in contrast to the Fuzzy C-Means clustering, where a node can be assigned to different clusters with some probability.
The K-means iterative algorithm is applied to U as follows:
1. randomly assign each node to a cluster;
2. compute the cluster centers for all clusters:
where the first summation goes over all nodes
n belonging to cluster
k and where
is the number of nodes in cluster
k;
3. compute the sum of inter-cluster distances from the corresponding cluster centers:
4. compute distances from each node
to all cluster centers
and assign each node to the cluster with the closest center;
5. repeat steps 2–4 until the cluster assignment does not change or until the improvement in is below a tolerance threshold. Then, output the cluster assignment.
In the spectral clustering approach, the K-Means algorithm is not applied to the flow trajectories, but to the eigenvectors of the graph Laplacian
. The clustering of spectral vectors as opposed to a trajectory dataset is the key difference with other clustering methods for LCS detection, including the Fuzzy C-Means approach by [
26].
2.2. Challenges of Conventional Spectral Clustering
One important shortcoming of the conventional spectral clustering is the need for user-input parameters, including the sparsification radius
r in Equation (
1) and the percentage of sparsification in
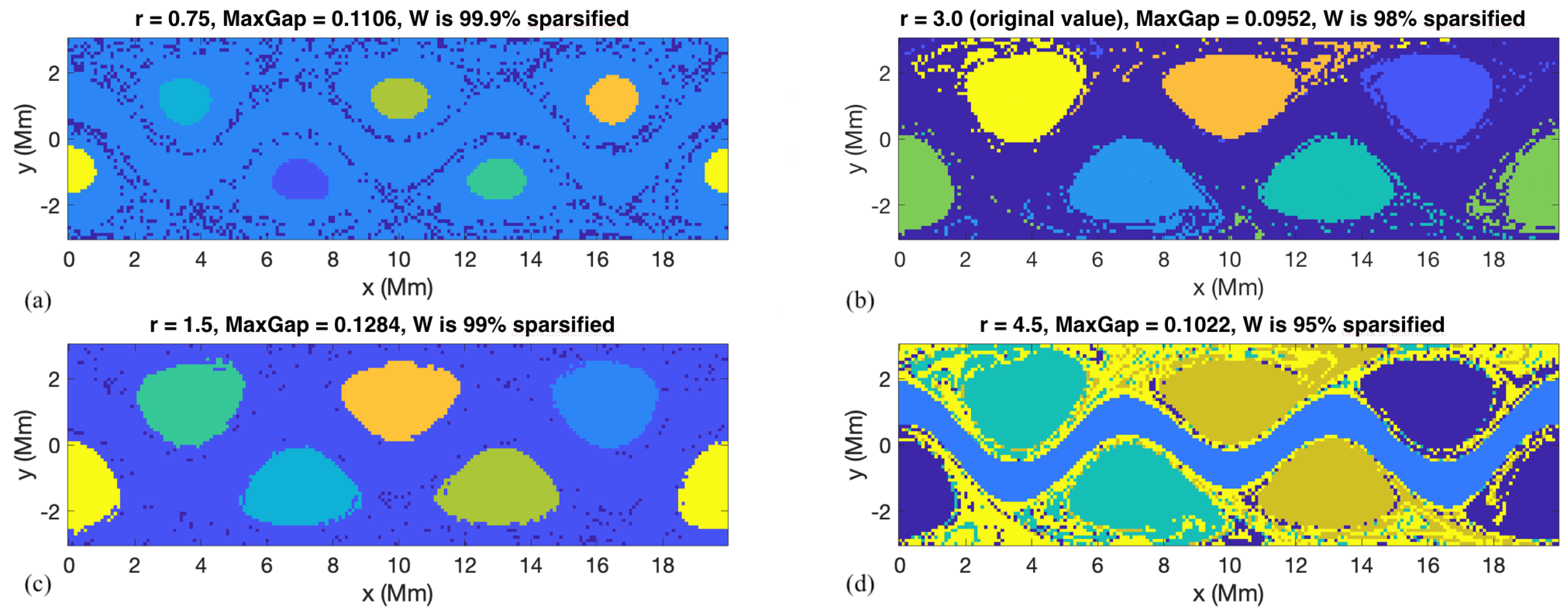
W, both of which significantly affect the spectral clustering results. For
r, HA16 advise to choose the
r value which, first, sparsifies the weights matrix by 5–10% (so that 90–95% entries are removed during the sparsification step), and second, the optimal
r should correspond to the largest eigengap. As illustrated in
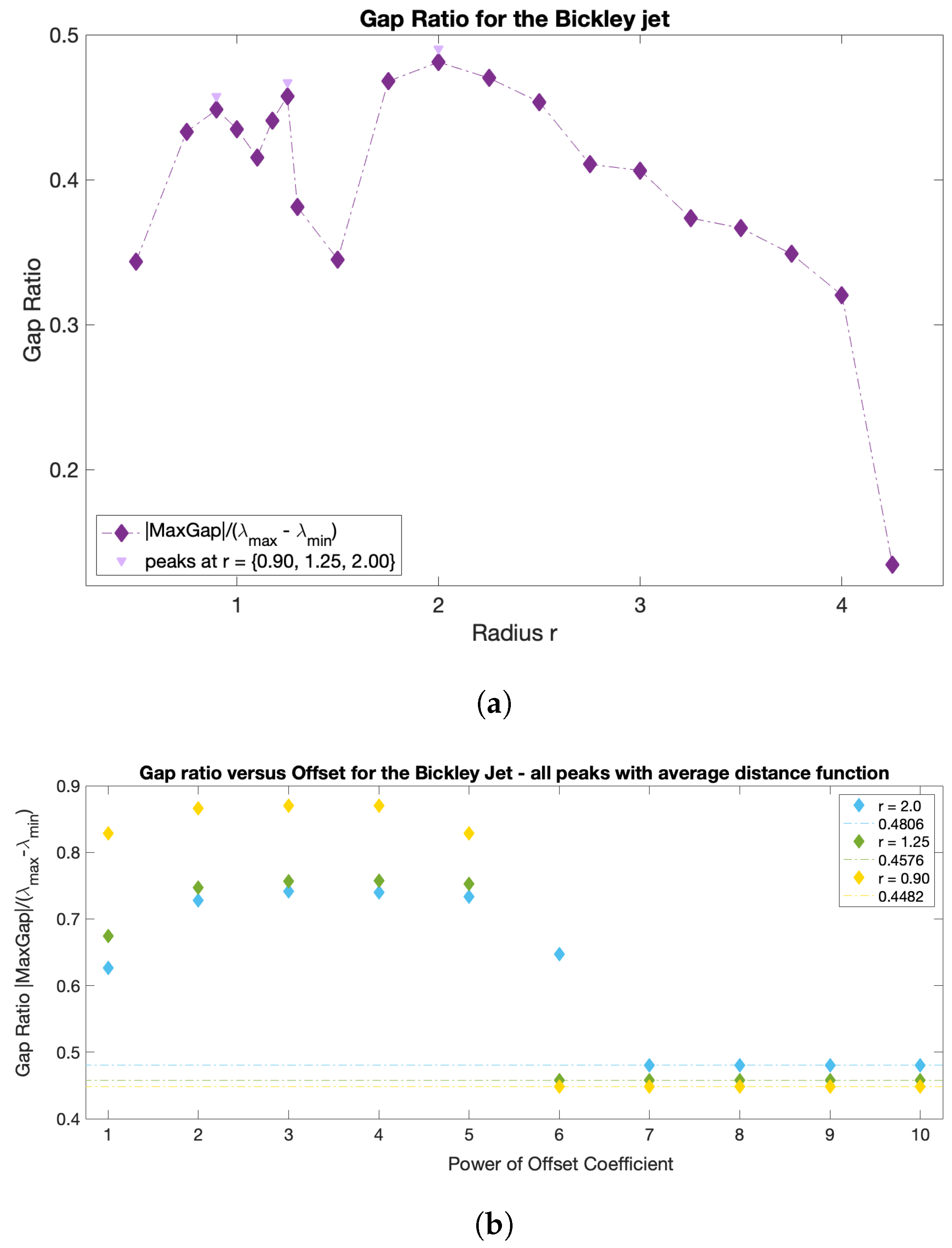
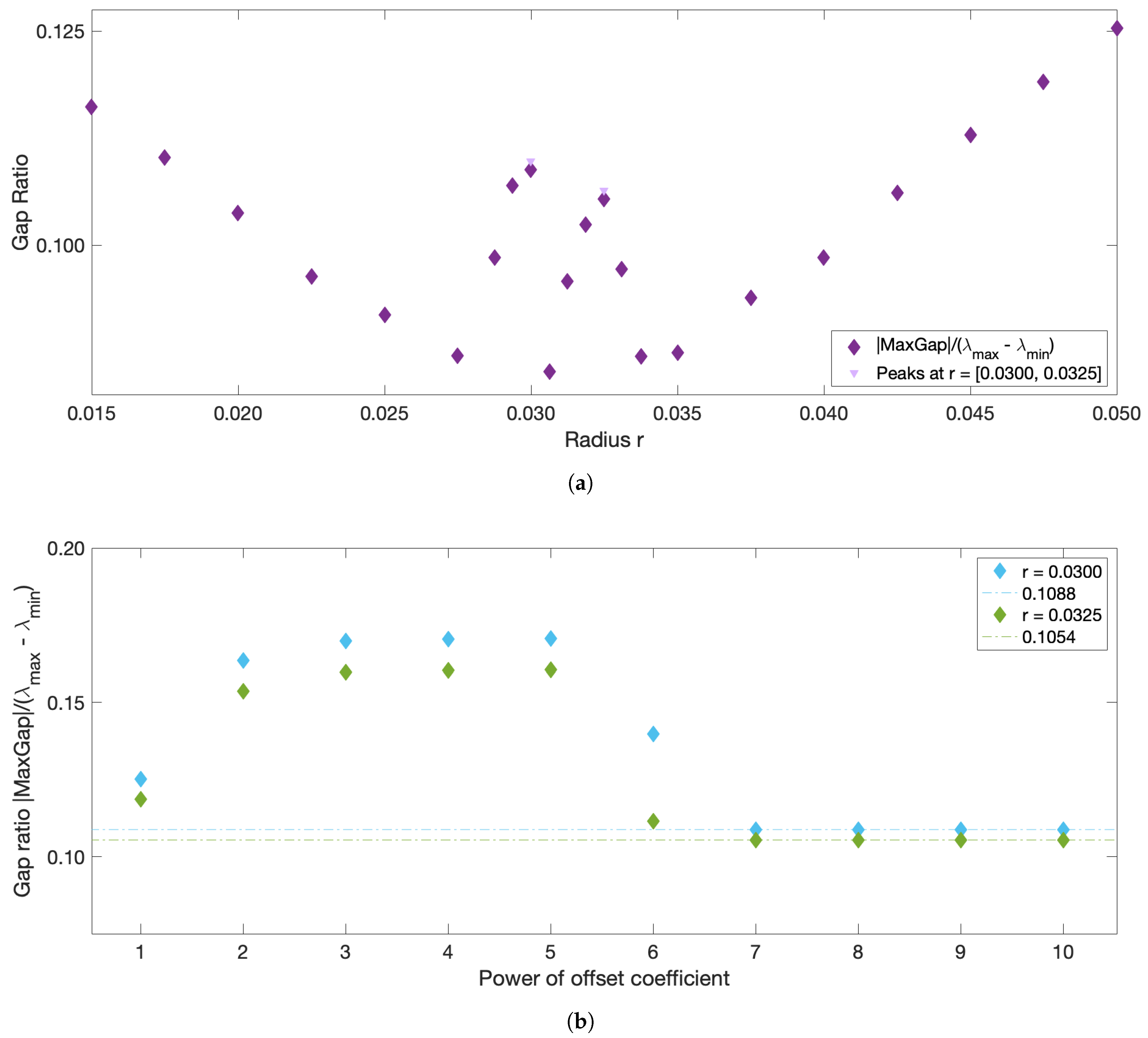
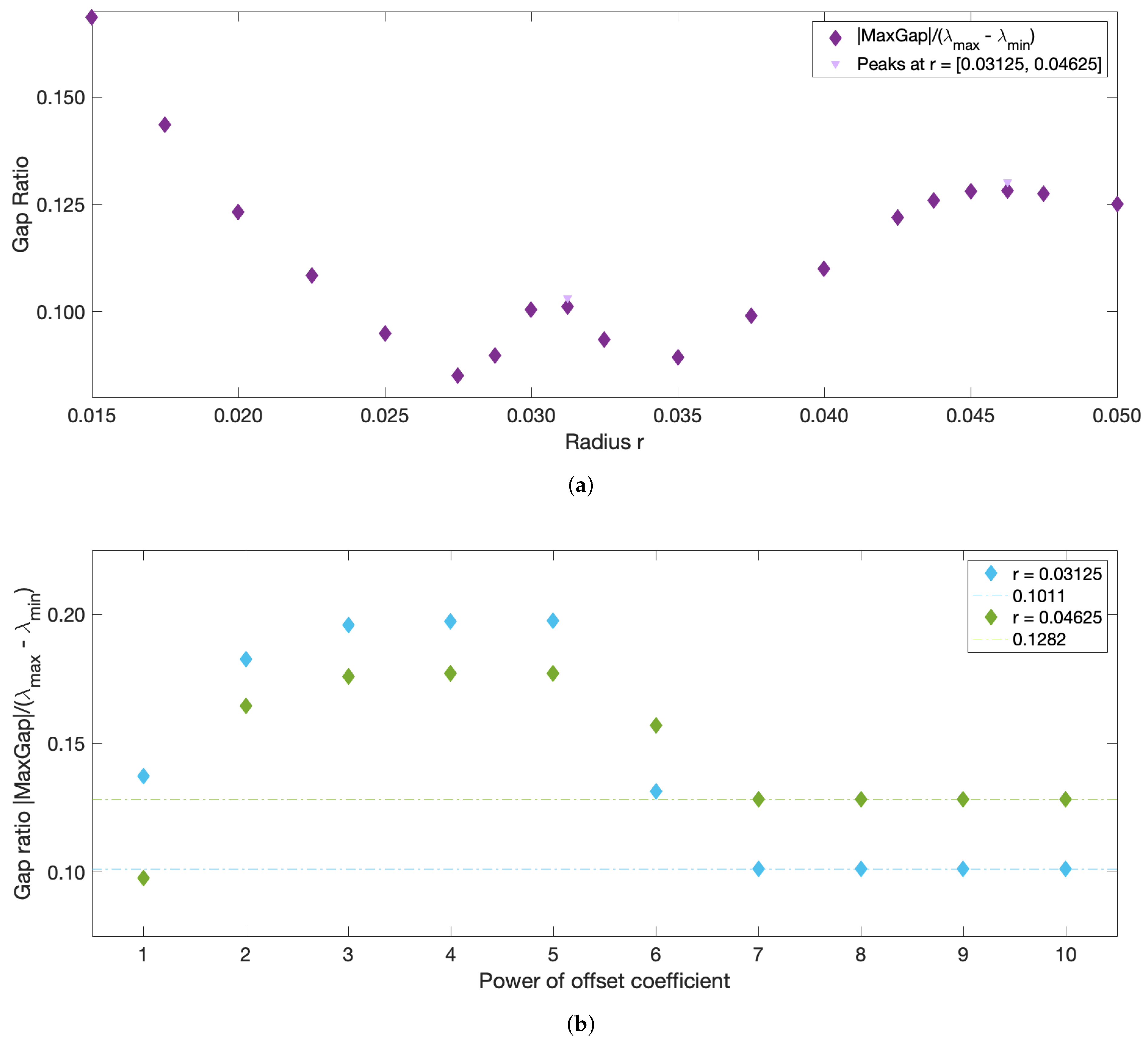
Figure 1, however, the largest eigengap is often achieved at an
r value that contradicts the 5–10% sparsification rule of thumb, and in many problems corresponds to the largest
r considered. Thus, in the end, the choice of
r is left entirely to the subjective judgement of the user and relies on the
a priori knowledge of the system under study.
Another user input is the distance function and, subsequently, how it impacts the diagonal elements
in
W. [
31] use a Gaussian kernel for the distance between nodes, a commonly chosen function in spectral clustering [
30], and choose an offset value for the diagonal of elements
in
W. HA16 use a different approach, where the distance function is described by Equation (
2) and the offset is added to
W before computing
D. This offset value in the diagonal elements is set to a large constant, which is immaterial for unnormalized graph Laplacians. Normalized Laplacians are however more common and adding the offset for the adjacency matrix
W before calculating
D does affect the eigenvalues and eigenvectors. The reader should thus be mindful of the scalar chosen for this diagonal offset, as it can impact the spectral clustering results.
Very large values (towards ) of the offset can introduce numerical errors due to the limits of double-precision. On the opposite, an offset value that is too small compared to the other ’s entries of W can yield erroneous results. Unlike r, the offset is not a real physical parameter, but rather a numerical manipulation to avoid infinity in the diagonal. A convergence in the spectral decomposition is expected for large values of the offset, as long as these scalar values are numerically reasonable. ‘Large’ values, however, will depend on the flow: for this reason, the proposed approach verifies the convergence of the results and sets the offset value as a coefficient related to the maximum entry in W, as described in more detail below.
2.3. Improved Optimized-Parameter Spectral Clustering
Here we propose an improvement to the conventional spectral clustering algorithm, which minimizes the need for user-input parameters. The optimal parameter choices are based on the notion of convergence (for ) and an argument involving the normalized spectral eigengap (for r). With and r obtained in a user-independent fashion within pre-defined ranges, the sparsification number is no longer needed. With these modifications, the only user input is the pre-defined range for parameters, within which the method automatically detects optimal parameter values. We also provide guidance for the choice of the parameter range that is most inclusive and worked well in all our examples.
The sparsification radius
r defines the largest allowed distance between trajectories, because all weights corresponding to larger distances are removed during sparsification. Thus,
r can be thought of as the parameter defining the size of the resulting clusters. It is tempting to use the same eigengap argument to define the optimal
r, which was used to define the optimal number of clusters
, namely that the optimal
r should yield the largest eigengap. The eigenvalues of the graph Laplacian, and thus the corresponding eigengap value, however, typically decrease with
r, as more and more entries are removed from the weight matrix during sparsification. Thus, the
r value that yields the largest eigengap is often the largest
r considered. To overcome this issue and use the spectral gap arguments for choosing the optimal
r, we introduce the normalized spectral eigengap by referencing the largest eigengap to the full dynamic range of the spectral values. Specifically, we define the normalized eigengap as the absolute value of the maximum eigengap divided by the difference between the largest and smallest eigenvalues,
:
This is similar in spirit to the recently proposed Normalized Maximum Eigengap by [
33], but in our approach the denominator is automatically calculated from the spectral decomposition and does not include any user-input coefficient. As normalization does not change the physical meaning of the eigengap, large values of the normalized eigengap still yield spectral clusters with high intra-cluster similarity and low inter-cluster similarity. The optimal
r should result in clusters with higher/lower intra-/inter-cluster similarity than those for both locally smaller or larger
r values. Thus, the optimal
r values should correspond to local maxima in the normalized eigengap. If several local maxima are present, we suggest proceeding with identifying coherent clusters for all the corresponding
r values. This will ensure that in flows with more than one dominant length scale, all coherent clusters of different sizes will be recovered. Since a reliable estimate of a coherent cluster requires at least several trajectories within it, the smallest
r considered should be dictated by the resolution, i.e., by the number of trajectories released in the domain and the distance between neighboring trajectories. In all our simulations, the simulated trajectories are released on a regular rectangular grid spanning the domain and the trajectory grid spacing is the initial distance between neighboring simulated trajectories. As a rule of thumb, we propose starting the
r search with a value 10 times larger than the trajectory grid spacing. At smaller values of
r, the number of nodes within the
r radius is very low, which can result in computations on subsets with new nodes only; such small clusters may be erroneous and numerically unstable. Finally,
r values approaching the domain size will result in the nearly entire domain being assigned to one cluster, and while this partition has high intra- and low inter-cluster similarity, it is trivial and not physically relevant. Choosing
r values that correspond to the local maxima in normalized eigengap (and not the largest value of the normalized eigengap) avoids this problem. Although the normalized eigengaps can be also high for both very small and very large values of
r, they are not peaks; peaks, rather, indicate that structures at the corresponding
r value are more connected in comparison to the incoherent background than the structures at neighboring values of
r. Thus, these are the structures that are of most interest to us.
We now describe the strategy for eliminating the need for choosing the user-input parameter
. In practice, the offset value chosen for the diagonal of
W impacts the spectral clustering results. Being the artificial parameter introduced for numerical stability considerations, convergence of results is expected for increasing values of
w (HA16). However, while
w should be substantially higher than the rest of the weights, excessively large
ws result in numerical errors due to the limits of double-precision. Insufficiently large values of the offset will also yield erroneous results. Finally, the offset depends on the flow under study, and what is large for one system may be small for the other. For this reason, we propose to seek the optimal flow-dependent offset value of the form:
with integer
n, and pick
n which corresponds to the smallest value at which convergence of the results, specifically, convergence of the normalized spectral eigengap, is achieved.
With w and r determined based on the normalized eigengap arguments as outlined above, and the number of clusters K defined by the number of eigenvalues before the eigengap (), the new spectral clustering protocol does not require any other user input to find the optimal partition of the domain. Note, however, that the user still needs to pre-define the range over which the algorithm will look for the optimal parameters, as well as to choose the parameter increment for the parameter sweeps, so our optimized-parameter method cannot be considered entirely parameter-free.
As with all spectral methods, the proposed optimized-parameter spectral clustering requires the existence of a detectable spectral gap. As detailed in [
29], the larger the eigengap, the better the spectral clustering partition will be in terms of yielding large/small intra-/inter-cluster similarity. Note, however, that we do not impose an explicit threshold on how large the spectral gap should be. Instead, we simply define the normalized spectral gap as the largest gap between successive eigenvalues of the normalized eigenspectrum. Thus, our optimized-parameter spectral clustering method can be applied to any flow (except the degenerate case when the eigenspectrum is completely flat) and will identify a partition of the domain into coherent clusters based on the eigengap heuristic, but the values of the normalized eigengap should be taken into consideration when interpreting the resulting clusters and the associated partition of the domain. Note also that in addition to the values of the normalized eigengap, the proposed noise-based coherence metric (introduced below in
Section 2.4) can also be used to quantify the robustness of the detected features and their sensitivity to numerical noise and observational or model uncertainty.
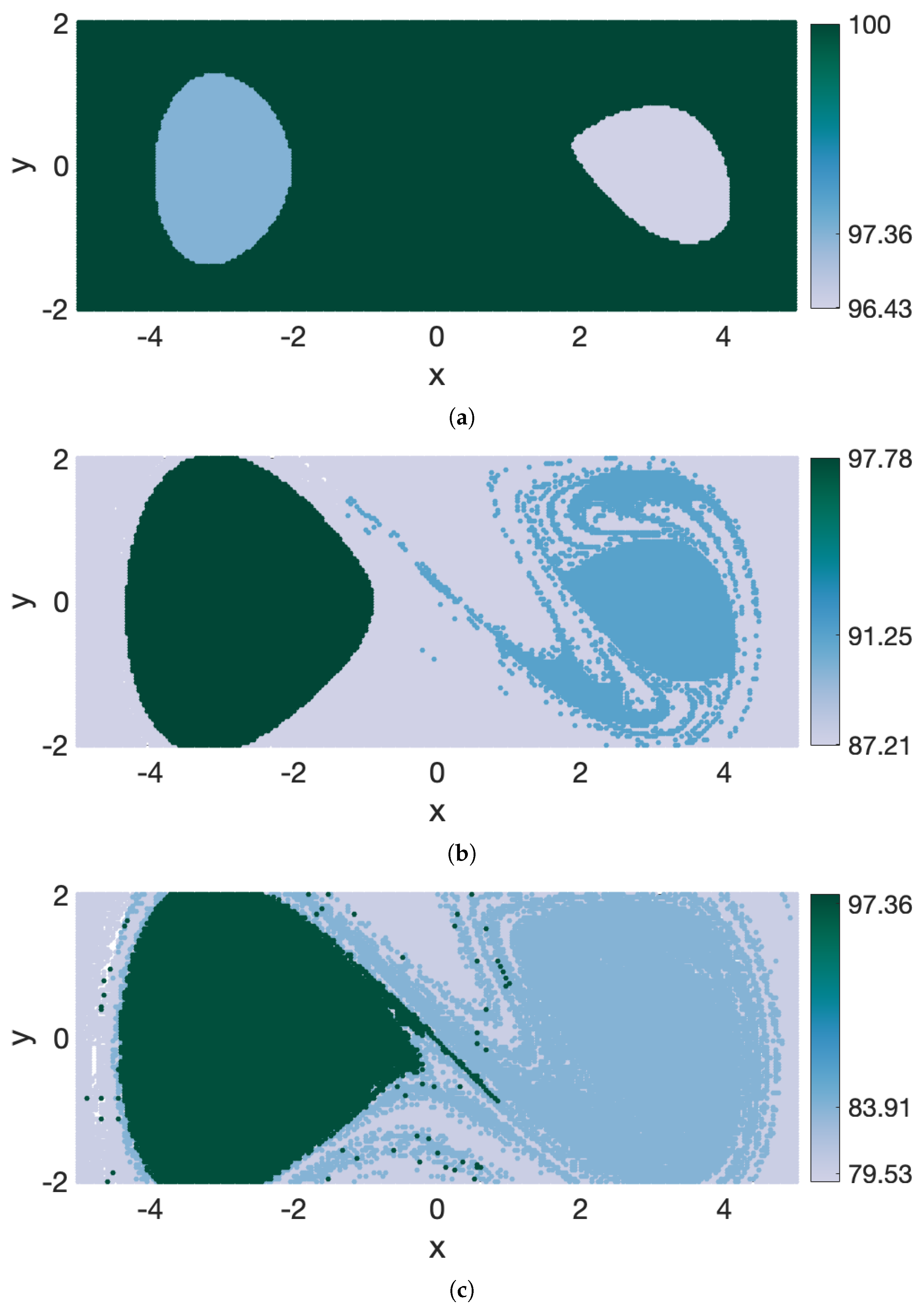
2.4. Noise-Based Cluster Coherence Metric
Once the spectral clustering analysis is conducted, how coherent are the resulting clusters? The eigenvalues of the graph Laplacian
contain information about coherence of eigenvectors but not of spectral clusters, because there is no one-to-one correspondence between former and latter. The spectral eigengap value, on the other hand, contains information about how optimal the partition is in terms of minimizing/maximizing inter-/intra-cluster similarity, but it does not provide information about the coherence of individual clusters. In many applications, such as identifying an optimal field experiment design or a strategy for a search-and-rescue operation, it is the coherence of individual clusters that determines the drifter release strategy or the search pattern. To determine how coherent the clusters are, we define below one possible coherence metric that is based on the robustness of the clusters with respect to a small random perturbation. This applied numerical noise can be representative, for example, of uncertainties in ocean circulation models. Our metric is similar, in spirit, to the approach by [
34]. The robustness to noise is computed as follows. For trajectories starting at
inside a given cluster, randomly perturb their final positions at time
, and advect trajectories backward in time to the start time
. The percentage of trajectories that return within the boundaries of their cluster is the proposed coherence metric. In all numerical simulations, we use the noise magnitude equal to
th of the trajectory grid spacing (here, the grid spacing is the initial distance between neighboring trajectories, as defined in
Section 2.3) but the results are similar for slightly larger or smaller perturbations. Essentially, our noise-based coherence metric favors coherent sets with large area-to-perimeter ratio and thus punishes small and filamentated clusters. Please note that because our coherence metric is not used to detect coherent clusters, it is not a parameter of our spectral clustering method. Rather, the coherence metric is computed after the clusters have been identified, and it allows us to interpret and inter-compare the robustness of the detected clusters with respect to noise.
2.5. Optimized-Parameter Spectral Clustering Algorithm Summary
The application of the optimized-parameter spectral clustering consists of 3 steps:
r-sweep: compute the normalized eigengap for variable sparsification radii r, from × (trajectory grid spacing) to (the domain size), keeping the fixed offset value (× worked well in all examples), and identify all local maxima. This choice of the upper limit, , is the most inclusive as it allows detecting clusters that are as large as the entire domain. This choice of the lower limit, , ensures that clusters contain at least 10 nodes (to avoid detecting of very small clusters that might be numerically unstable.)
w-sweep: for all local maxima, verify the convergence in the normalized eigengap by varying × , . In all our examples, convergence was observed at , but we cannot guarantee that this is true for all flows. If the normalized eigengap still varies between and , increase n past the value of 10 to ensure convergence.
identify coherent sets corresponding to all local eigengap maxima and compute noise-based coherence metrics for the resulting clusters.
2.6. Finite-Time Lyapunov Exponents and Poincaré Sections
In the next section, we also use Finite-Time Lyapunov Exponents (FTLE) and Poincaré sections to provide insight about the flow and to compare with the coherent clusters obtained using the optimized-parameter spectral clustering. For completeness, below we briefly describe both methods.
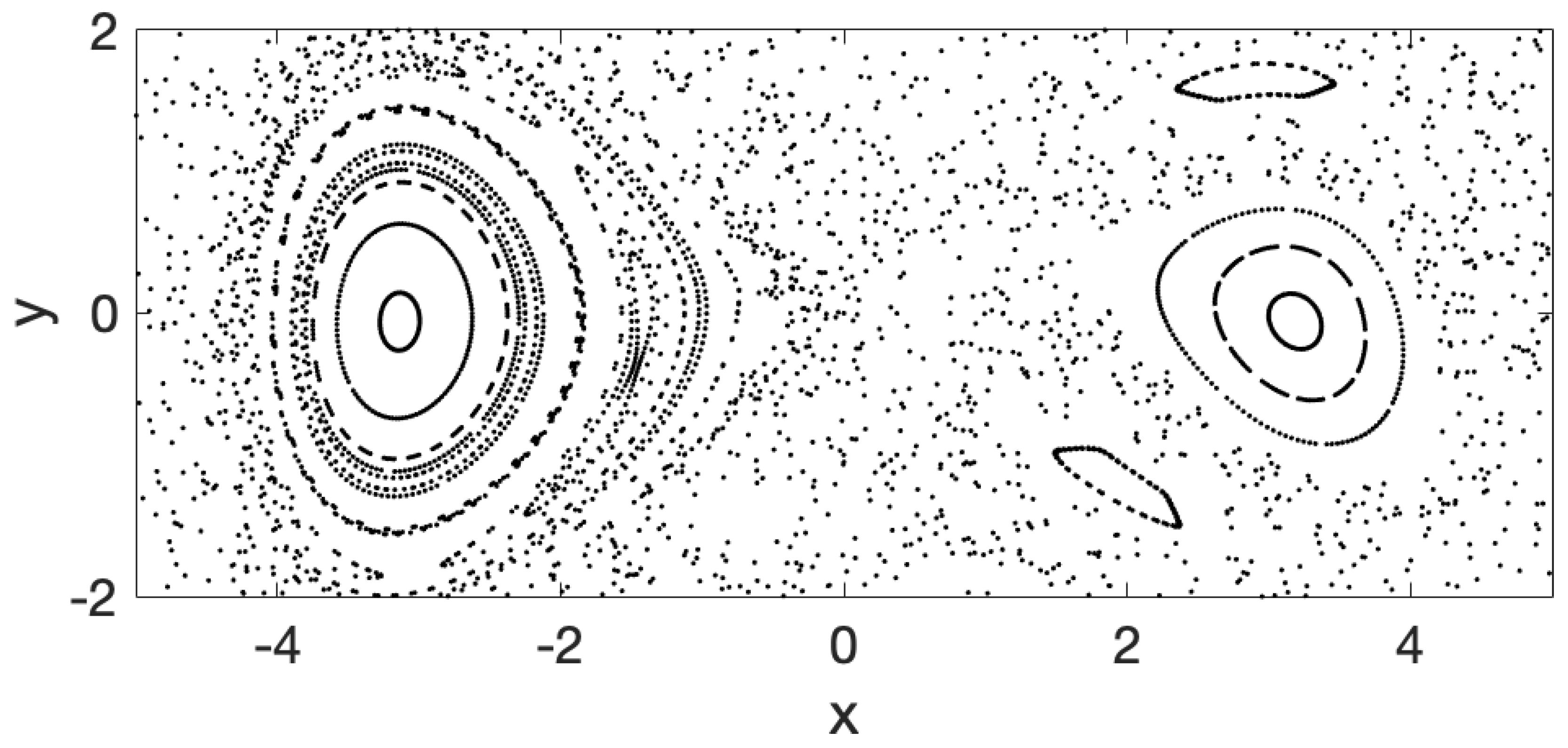
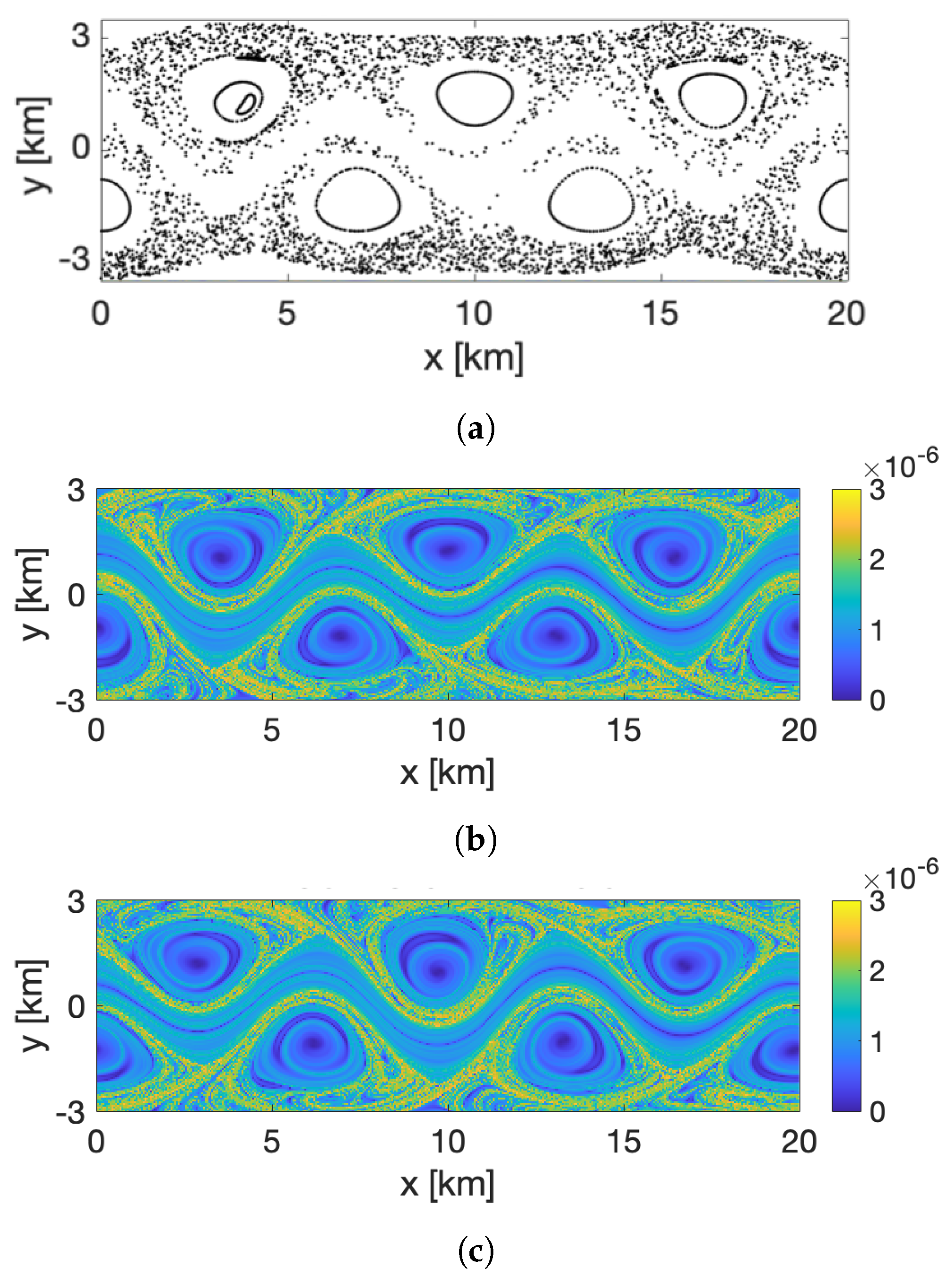
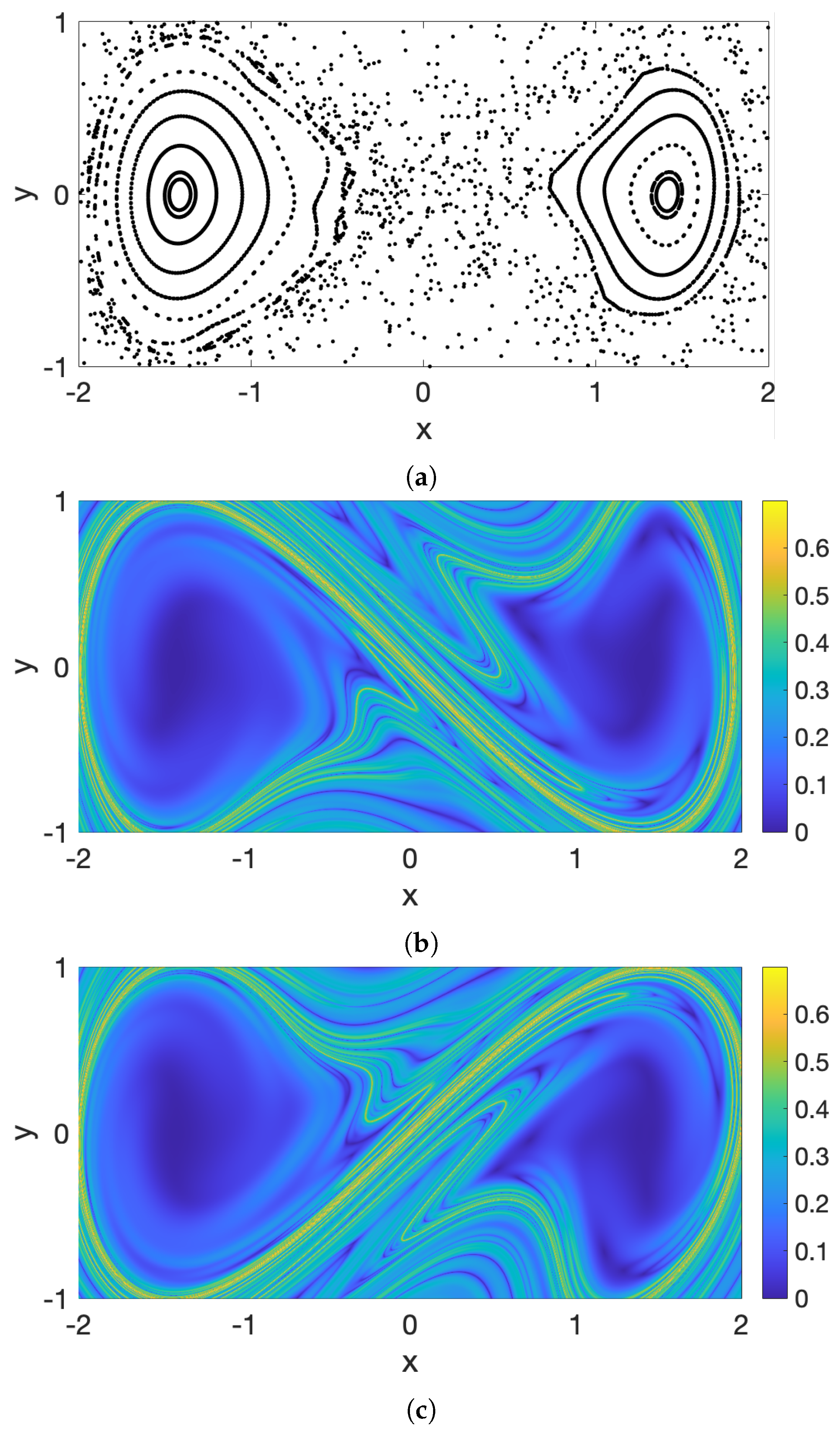
Poincaré section is a technique that allows mapping the chaotic and non-chaotic (regular) regions of the domain in time-periodic flows by stroboscopically sampling trajectories after each period of the perturbation. On the Poincaré section, regular trajectories appear as discretely sampled smooth curves, and chaotic trajectories appear as clouds of dots covering finite areas.
The FTLE approach [
8,
14,
17] is probably the most widely used LCS detection method due to its intuitive nature and numerical robustness. FTLE fields can be computed by the differentiation of the flow map,
, obtained from numerical trajectories
that start at
and advected by the flow over a finite integration time
. Specifically, the gradient of the flow map is used to compute the Cauchy-Green strain tensor,
, whose largest eigenvalue,
, quantifies the largest amount of stretching between neighboring trajectories and is then used to construct the FTLE field
Maximizing ridges of the FTLE field reveal the locally most repelling LCSs (provided that particle separation is dominated by strain and not shear; see Haller [
14]), which are the finite-time counterparts of the invariant stable manifolds of hyperbolic trajectories in time-periodic flows. Similarly, maximizing ridges of the backward FTLEs reveal the most attracting LCSs.
4. Discussion
A reliable method for identifying coherent clusters in oceanic flows is important for a variety of applications – from understanding of mixing and exchanges of biogeophysical tracers, to hazard mitigation and search-and-rescue operations. In studies of exchange processes, coherent clusters can help visualizing tracers that stay coherent over time. In hazard mitigation applications, clusters are useful for identifying areas where mitigation assets should be focused, and in the search-and-rescue operations, cluster geometries help narrow down on the optimal search-and-rescue pattern. The conventional spectral clustering algorithm has many of the desired qualities, yielding clusters that maximize inter-cluster similarity and intra-cluster differences of the underlying Lagrangian motion. Spectral clustering also has advantages over other techniques for LCS identification, such as FTLEs, in applications with sparse Lagrangian data. The major drawback of the conventional spectral clustering is the need for subjective user-defined choices for several method parameters, which requires a priori knowledge about the flow. The parameter choices vary between different flows and depend on flow characteristics such as intensity, spatial variability, and dominant spatio-temporal scales of the currents, which might not be known in real applications. Different parameter choices generally yield substantially different coherent clusters, which drastically complicates the applicability of this method.
In this paper, we describe a new optimized-parameter spectral clustering algorithm, which automatically identifies optimal parameters within pre-defined parameter ranges for a given flow(the pre-defined parameter range and the parameter increment for the sweeps still need to be specified by the user). The specific parameters of interest are the sparsification radius r, which is responsible for the sizes of the identified clusters, and the offset parameter , which is responsible for the numerical stability of the algorithm. Automated selection of optimal r and requires modifications of the conventional spectral clustering. Specifically, we introduce a normalized spectral eigengap, which allows inter-comparison between different r-choices, instead of the absolute eigengap used in the conventional method, which typically decreases with r. (As in the conventional spectral clustering, the optimal number of clusters is defined as the number of eigenvalues before the eigengap.) The optimal r value(s) is then identified as the value(s) that corresponds to the local maximum (or maxima) of the normalized eigengap. Specifying r in this manner ensures that for clusters of that particular size the inter-/intra-cluster similarity is largest/smallest compared to clusters that are either smaller and larger. Since many geophysical flows operate on multiple spatio-temporal scales, clusters of very different sizes could simultaneously exist within the same flow, and looking at all peaks in r ensures that we identify all of them. The second method parameter, , is chosen as the smallest at which convergence of the normalized eigengap is achieved. Finally, to evaluate the coherence of the clusters, we introduce a noise-based coherence metric that allows comparing clusters within the same flow or between different flows. This metric quantifies the relative robustness of the resulting clusters with respect to applied numerical noise.
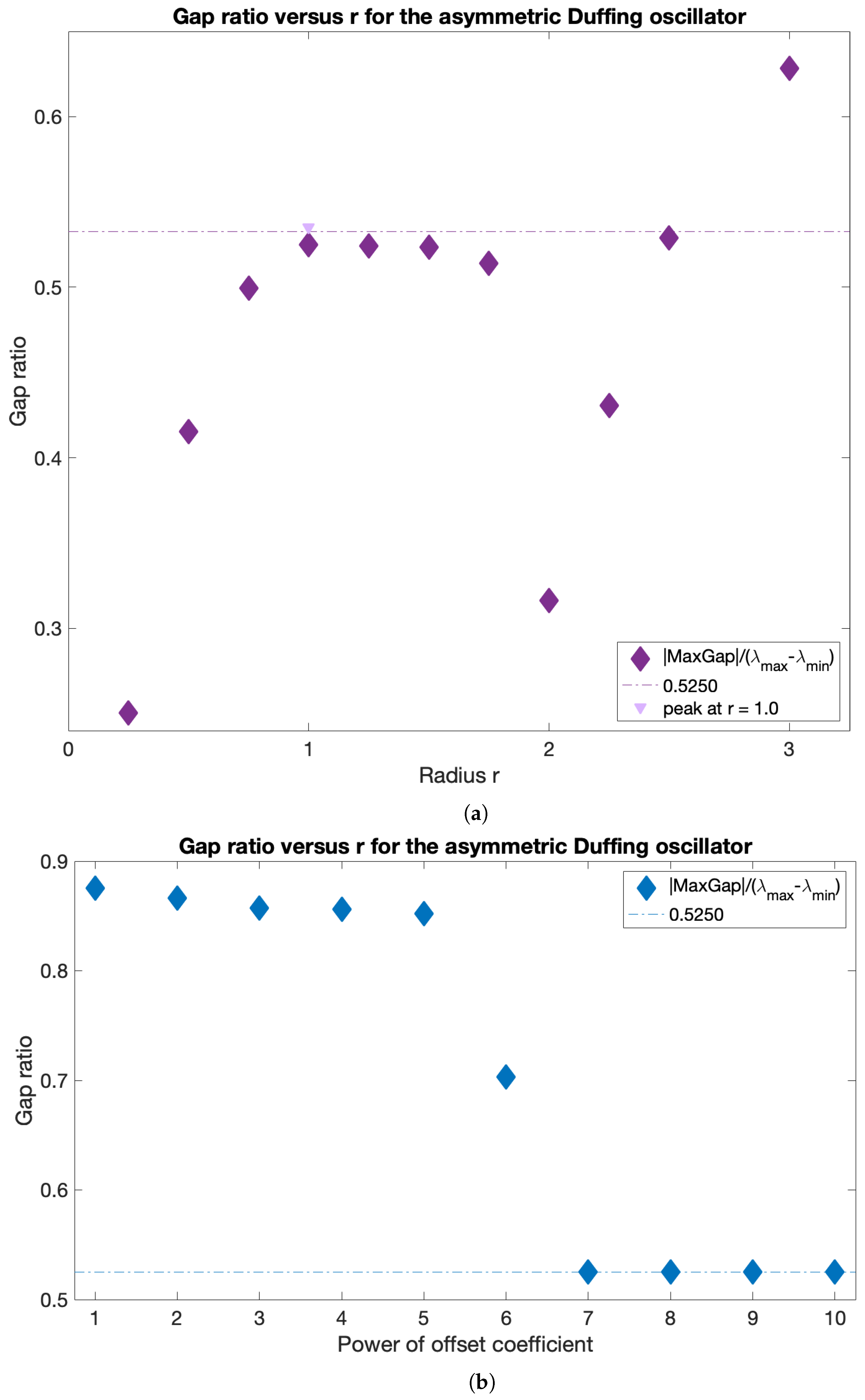
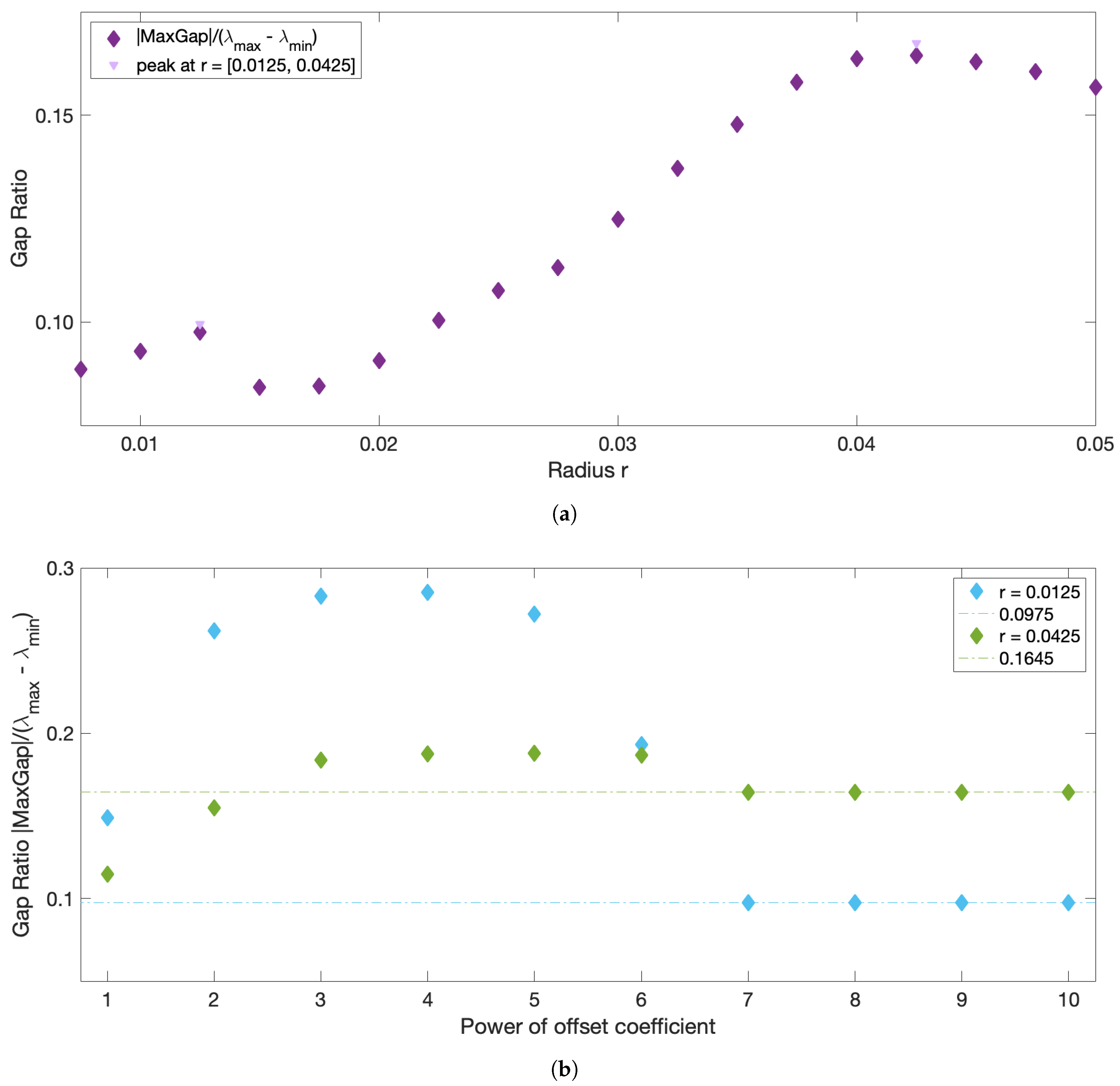
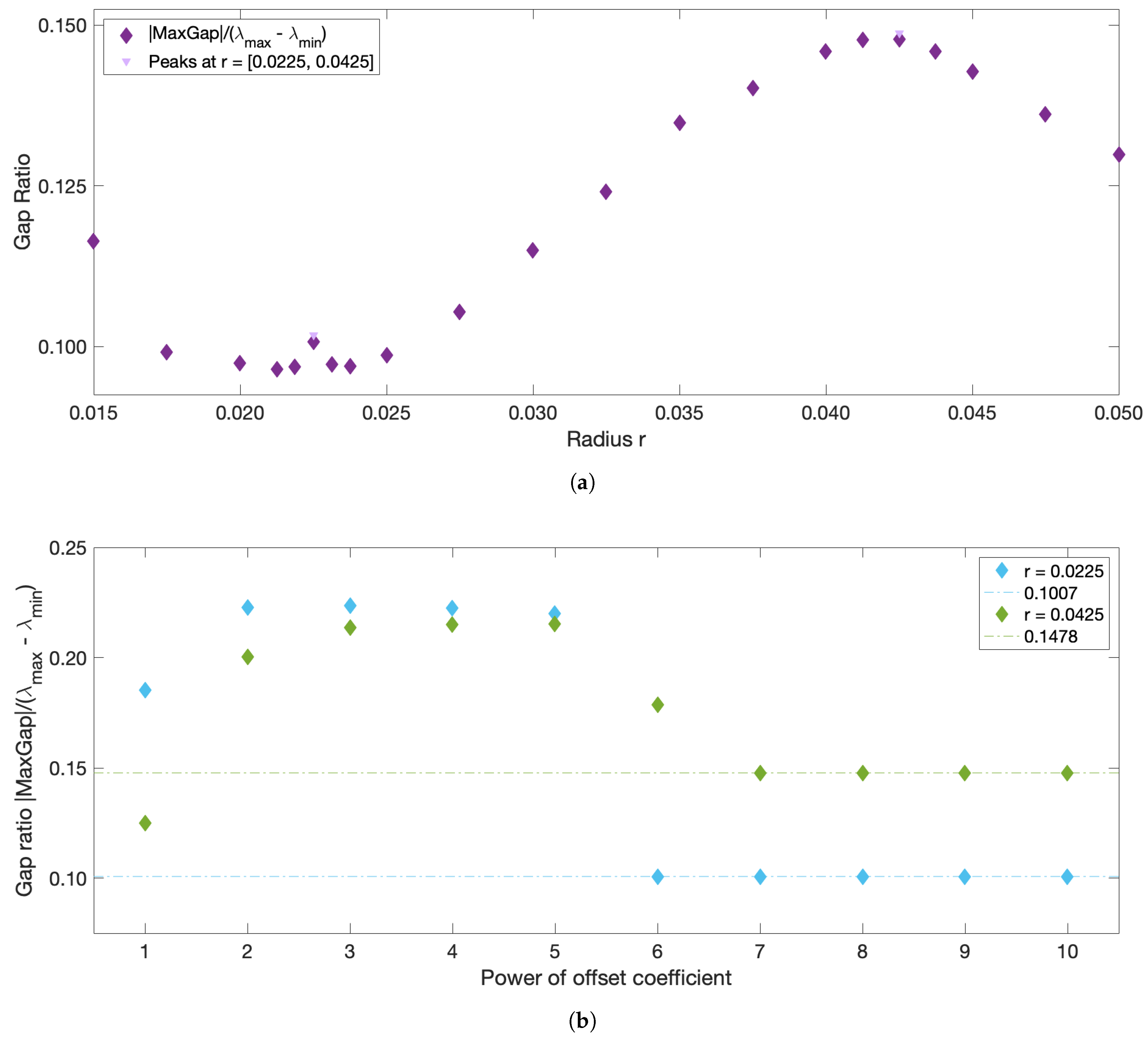
The automatic detection of multi-scale features is a well-known problem for conventional graph cut methods, including the normalized cut (which lies at the core of the spectral clustering) that favors clusters of equal size [
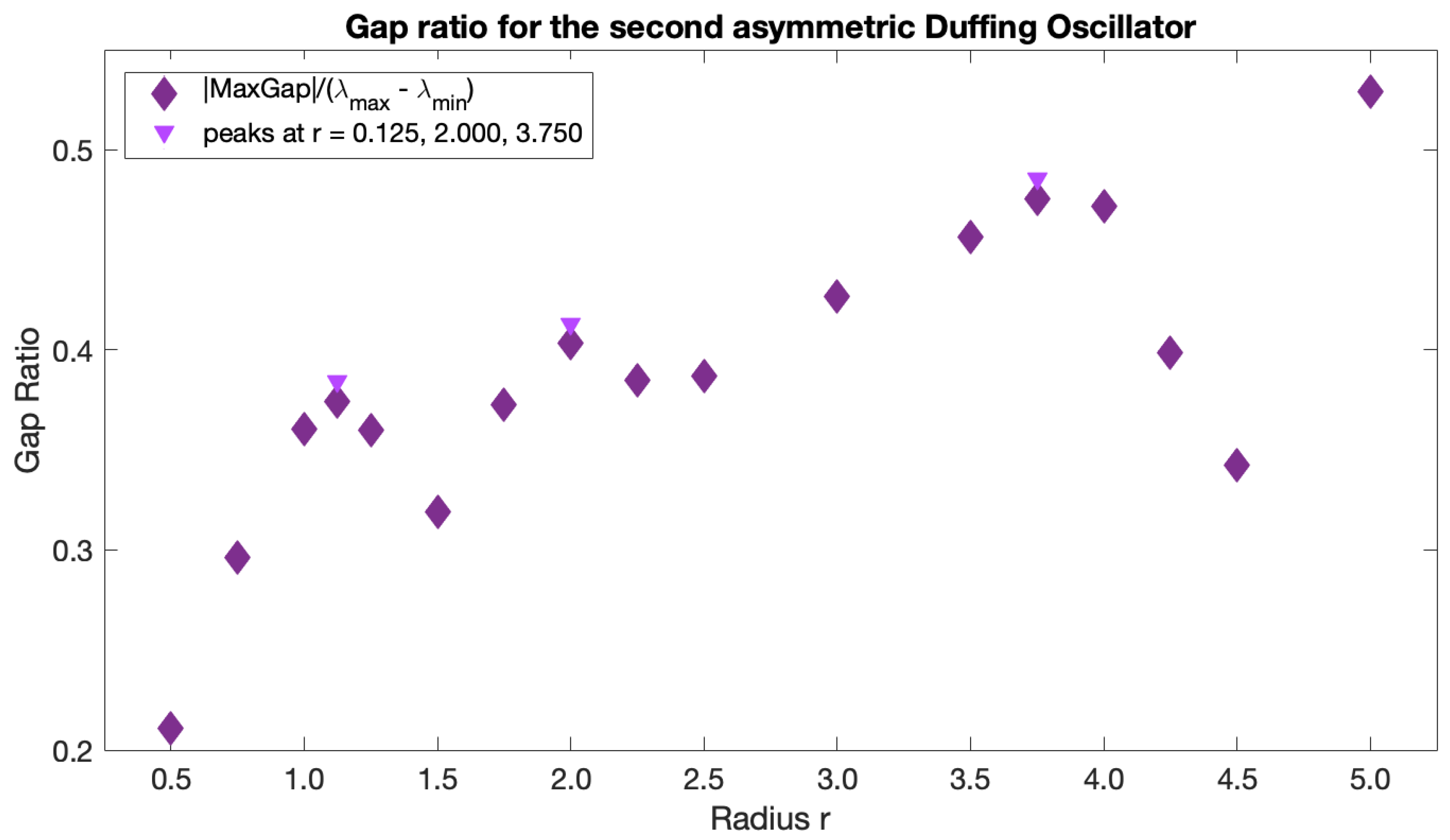
30]. When clusters are well separated from each other and their sizes are only slightly different, such as in the periodically forced pendulum example in HA16 or in our slightly asymmetric oscillator example, all clusters can be identified using a single
r value. However, when the clusters are sufficiently different in size, such as in our strongly asymmetric Duffing oscillator example, different
r values are needed to correctly identify all the coherent sets. Thus, in general, no single
r can be guaranteed to identify all the clusters. By doing sweeps in
r and identifying all the
r values that correspond to the local maxima in the normalized eigengaps, we can overcome this challenge and identify all the underlying coherent sets across a wide range of spatial scales. This is particularly important in oceanic applications, in which very little is known
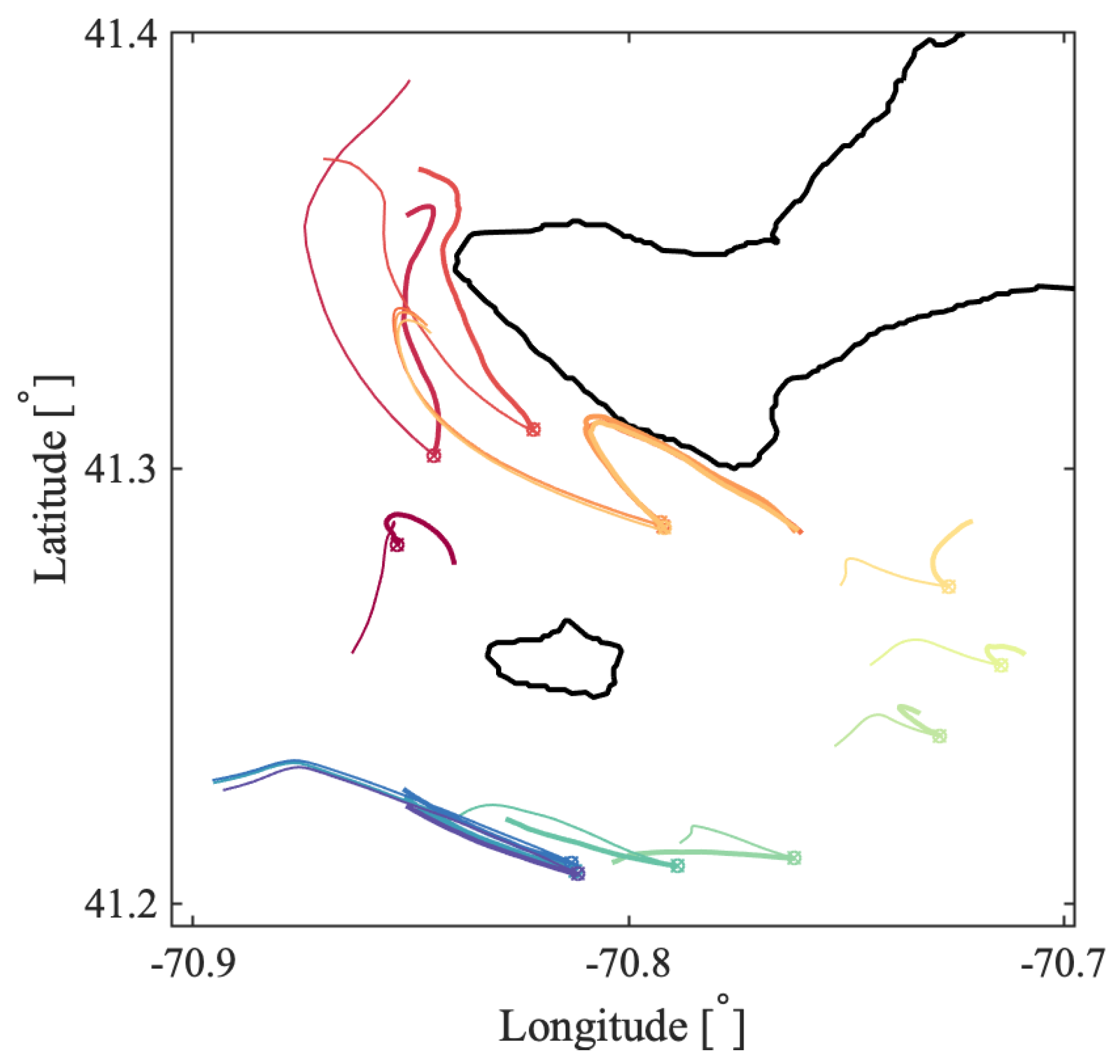
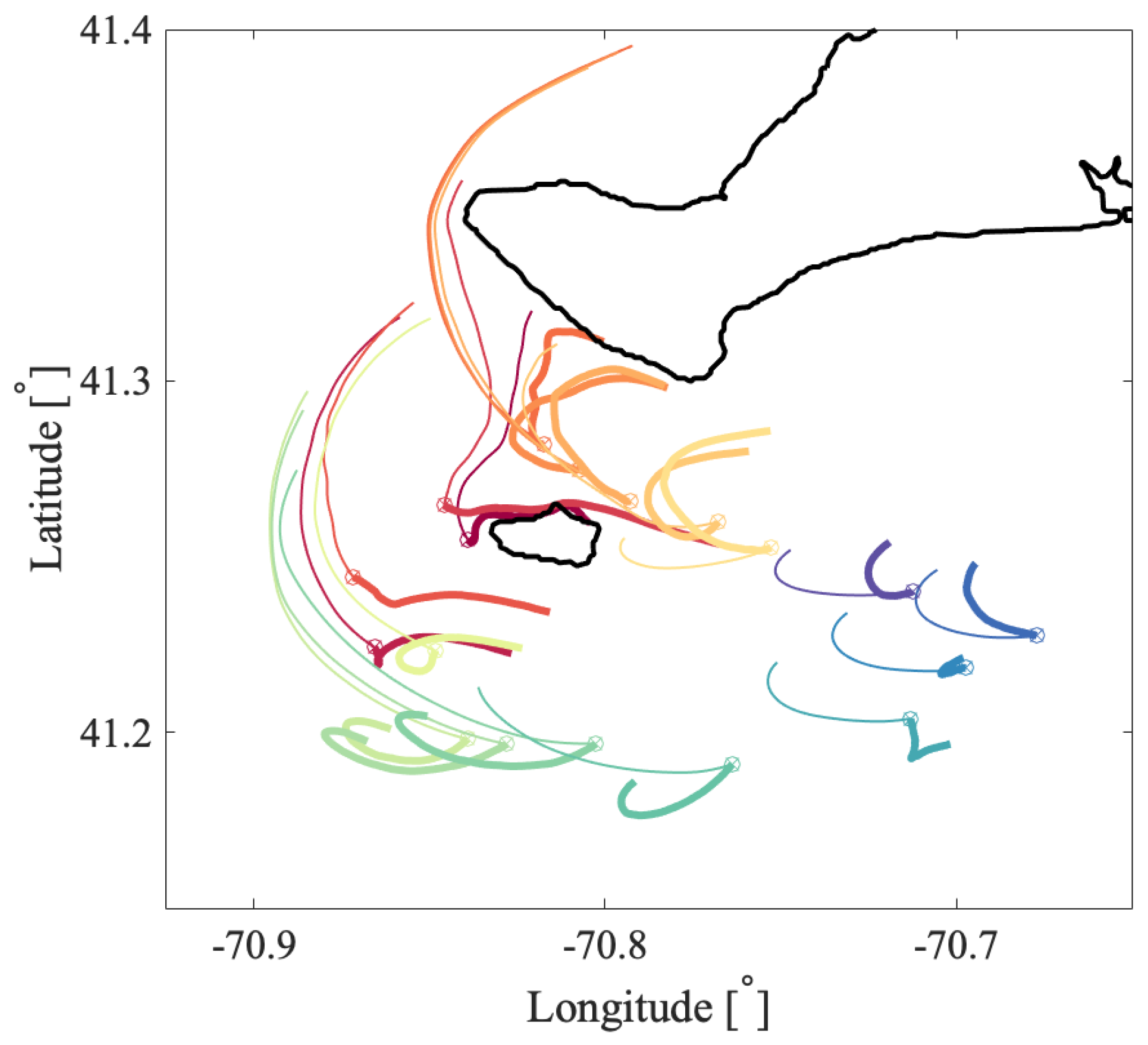
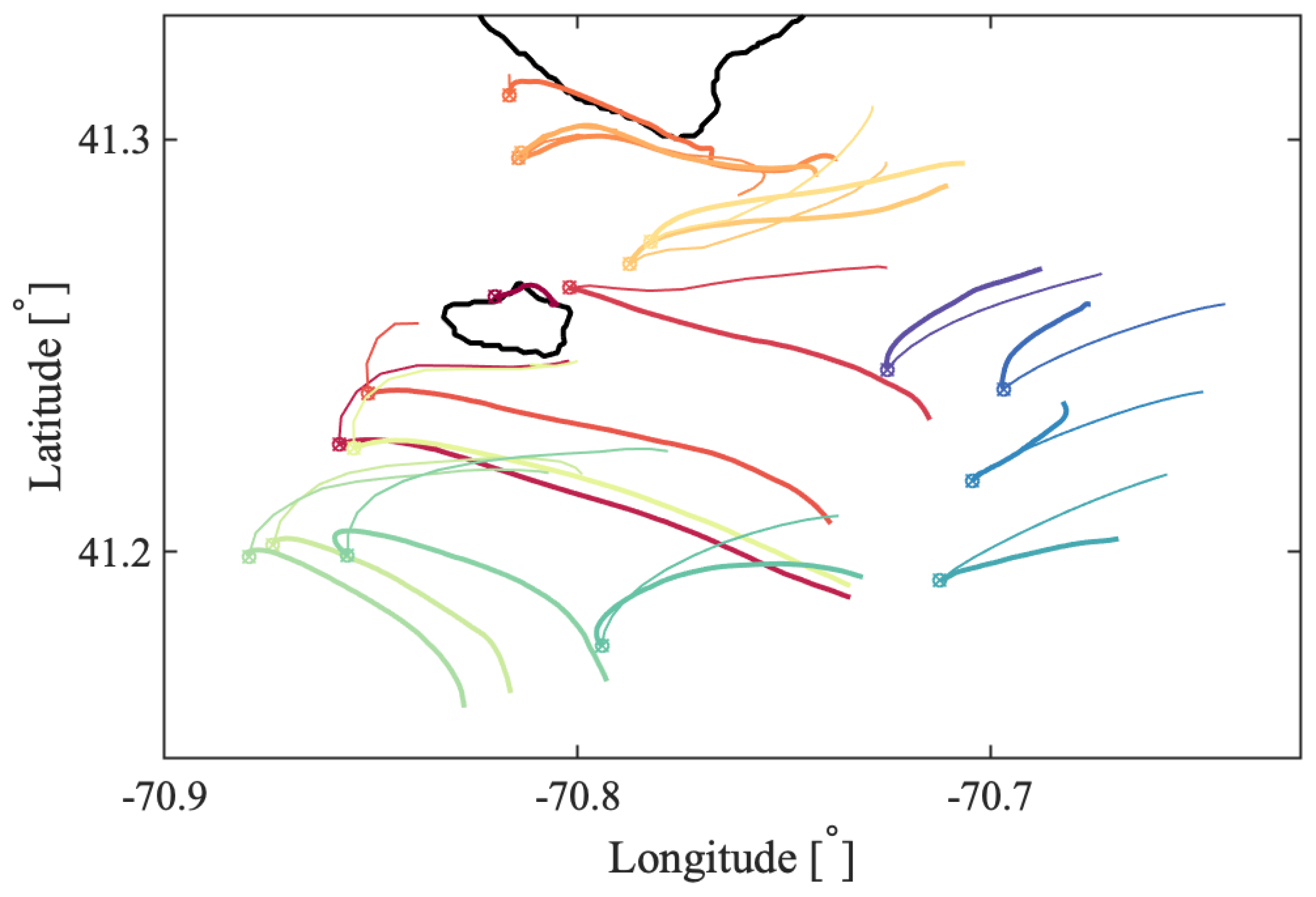
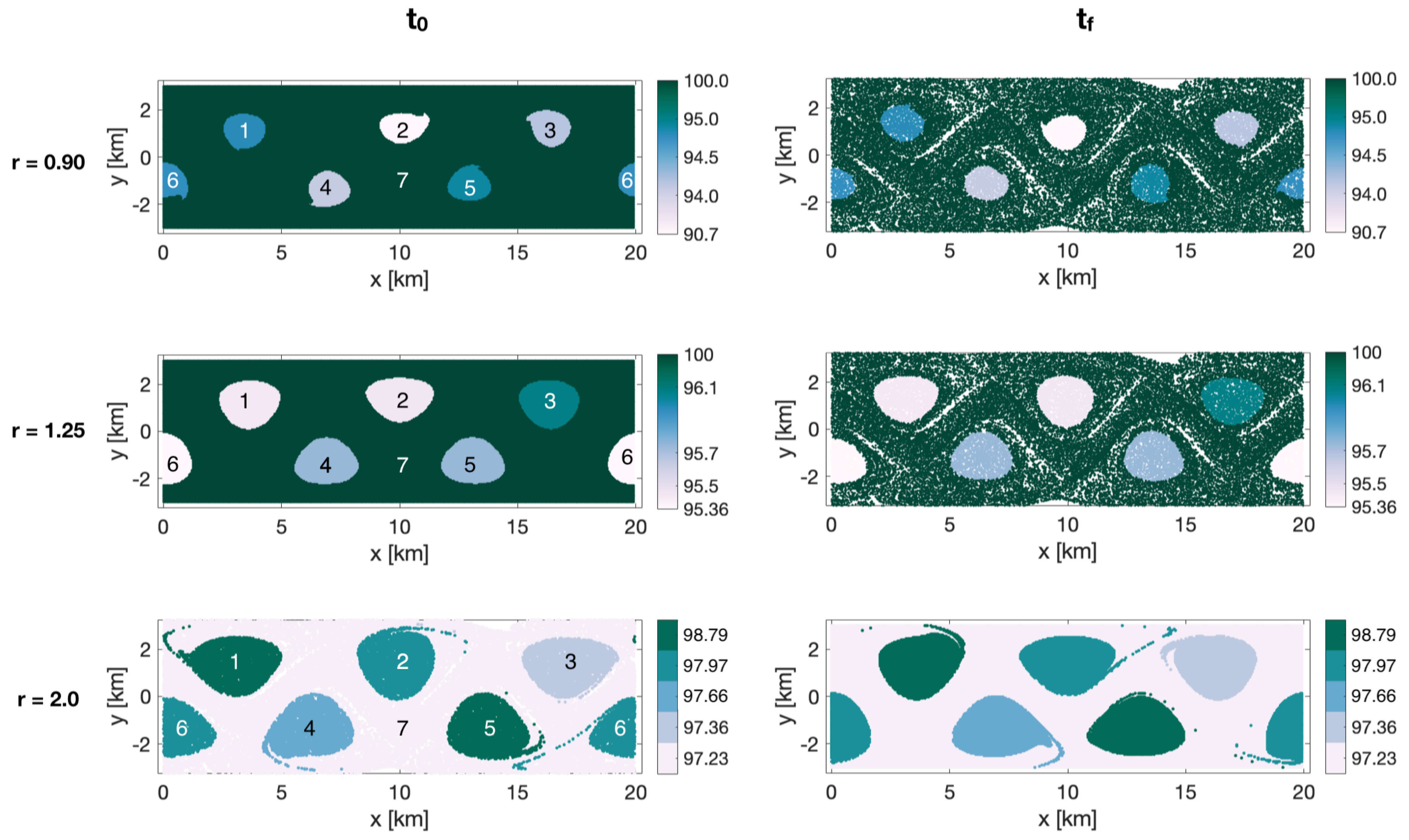
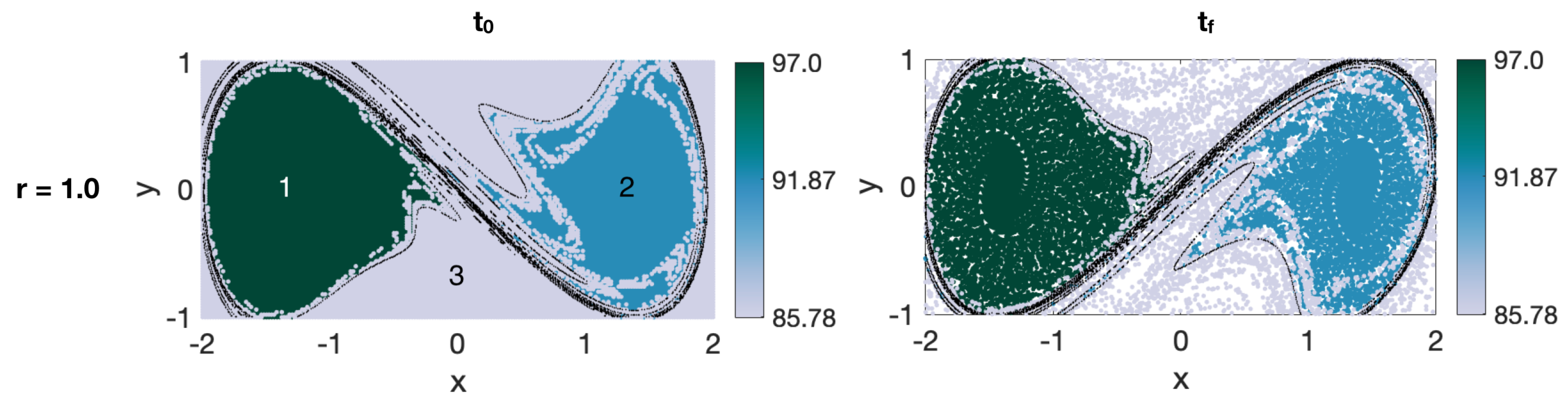
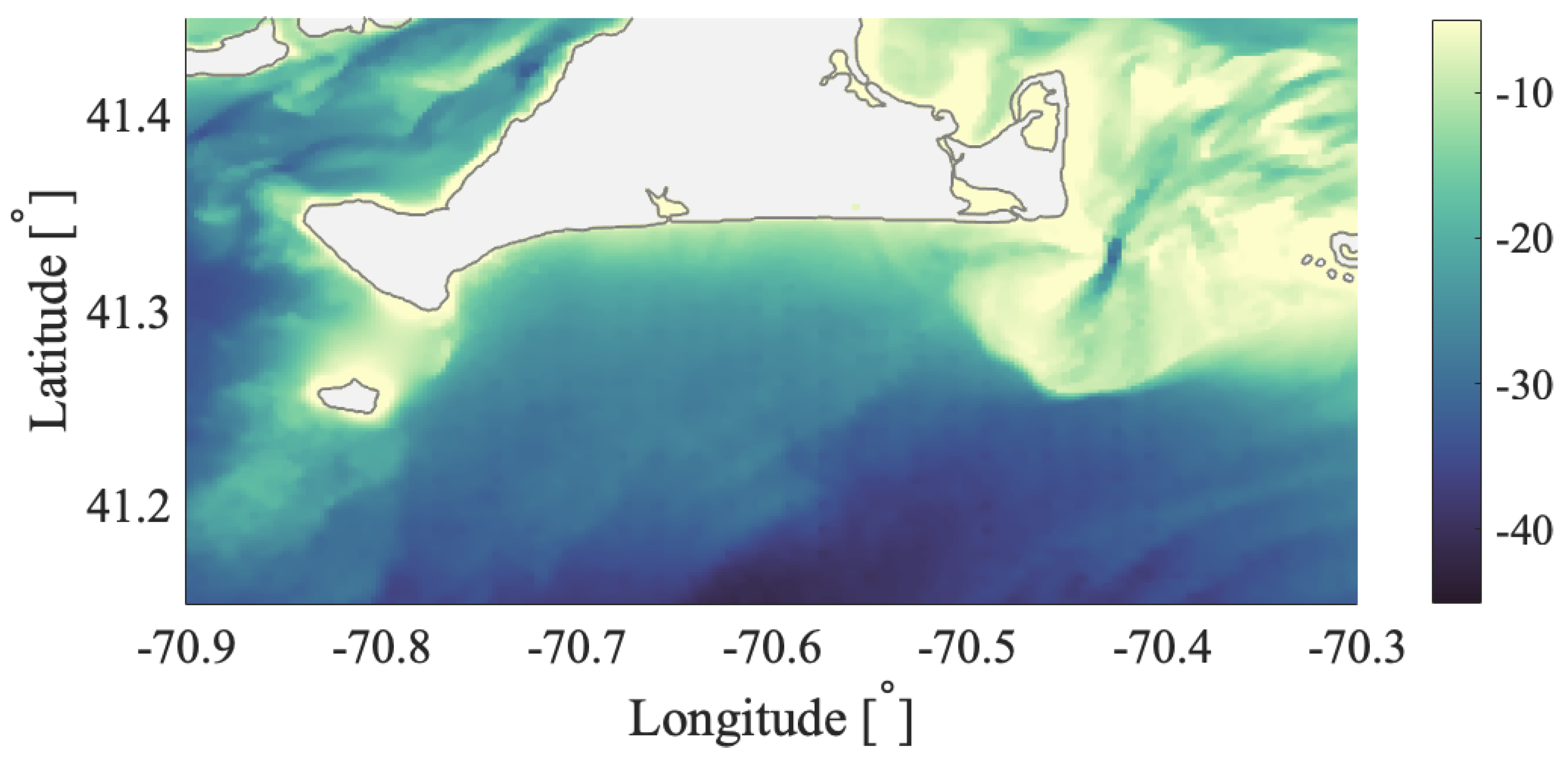
a priori about the flow and the scales of the coherent features. Oceanic flows often have more than one dominant length scale, and thus, multiple coherent clusters with different sizes may coexist within the same flow. This was indeed the case for the coastal flow south of Martha’s Vineyard. In all our oceanic examples, the optimized-parameter spectral clustering algorithm identified 2 optimal values of the sparsification radius,
r, yielding 2 different partitions of the domain into coherent clusters with different sizes.
The optimized set of parameters, as well as the specific noise-based metric of coherence that we have proposed here, present one possible way to reduce the user-input parameter choices and quantify the coherence of the resulting clusters. We explained the logical arguments underlying our proposed optimized-parameter algorithm, and we illustrated that our method reliably yields parameters and clusters that are optimal according to our specific definition. The strength of our optimized-parameter spectral clustering method is that it allows applying the method to any flow with minimal prior knowledge about it, and that the method automatically identifies clusters with minimal user input, along with a coherence value for each cluster.
Although optimized-parameter spectral clustering requires less user input than the conventional spectral clustering of HA16, we cannot claim that our method is completely parameter-free. Being of spectral nature, our optimized-parameter spectral clustering is also subject to all the limitations typical of other spectral methods. In our approach, the user still needs to specify the upper and lower limits for the parameter range, as well as the increment in the parameter values for the sweep. The method will then automatically identify the optimal parameters, detect the clusters and quantify their coherence. Since less information is needed for specifying the parameter range than specifying the exact parameter value, our method is easier to use in applications to the largely unknown oceanic flows, and it comes one step closer towards a parameter-free coherent structure identification.
We have tested the optimized-parameter spectral clustering in 2 commonly used benchmark analytic flows—Bickley Jet and Duffing oscillator—and in a real-life oceanic application to a high-resolution model-based surface flow in the coastal region south of Martha’s Vineyard, MA. The results are encouraging in that our method identified all known coherent clusters in both benchmark flows, and it identified reasonably looking clusters in the realistic oceanic example. Looking at the coherence of the clusters and the optimality of the resulting partition of the domain, both analytic flows had significantly larger values of normalized eigengaps (0.4–0.5) than the real oceanic flows (about 0.1), pointing to the poorer performance of the method in the latter examples. This is not surprising as both analytic flows have a stronger contrast in Lagrangian behavior between the coherent regions associated with the (more regular) gyre cores and the incoherent background that encompasses the well-mixed (chaotic) regions around the gyres, whereas in the realistic oceanic flows, this contrast between regular and chaotic motion is smeared. In all examples, however, our method still yielded clusters with relatively high values of noise-based coherence (above ), suggesting that even for the flow south of Martha’s Vineyard, the detected clusters were robust features of the flow that are not excessively sensitive to numerical noise and observational and model uncertainty. For the 2018 campaign, the 20:00–02:00 experiment exhibited particularly low gap ratios and the domain partitions were far from optimal, with numerous (≥17), small clusters adjacent to each other and an incoherent cluster that was indistinguishable from the coherent ones. This illustrates the limits of the method’s applicability: although the method did produce a partition into clusters, the flows need a certain amount of dissimilarity for the resulting clusters to be meaningful. This is discussed in HA16 and their notion of coherence, which exists in the presence of an incoherent background.
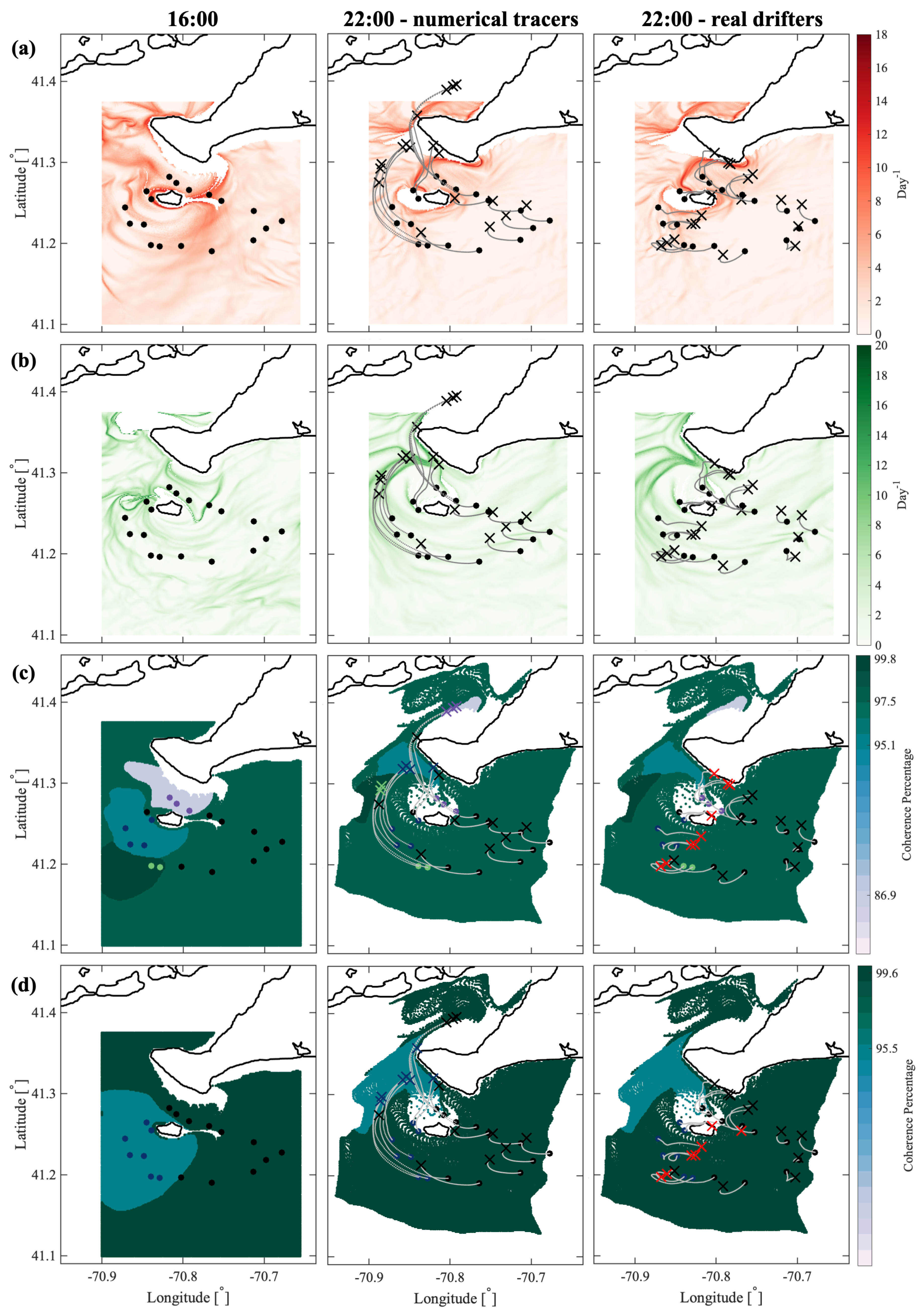
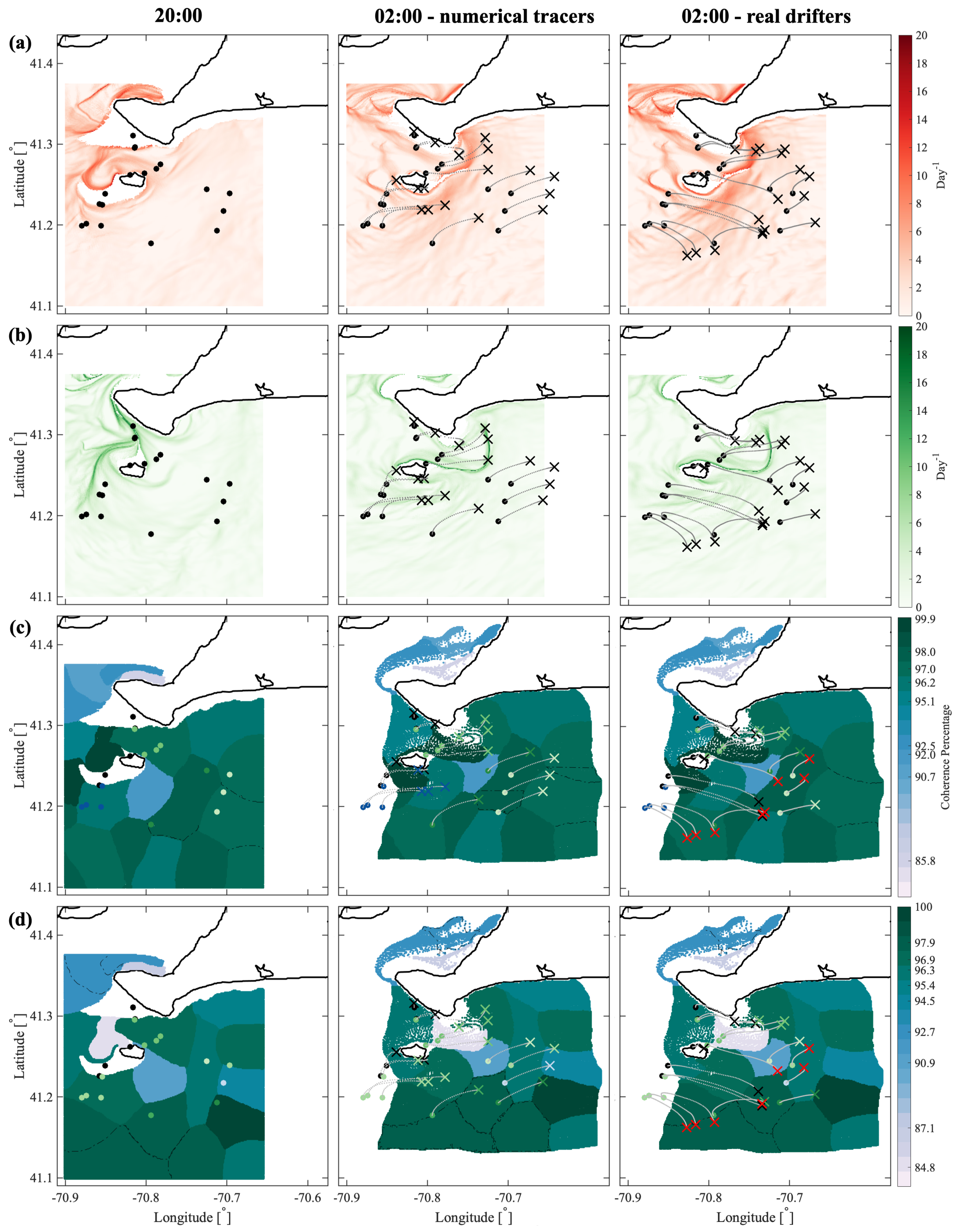
In the Martha’s Vineyard case study, since the flow south of the Vineyard has a strong tidal component, the resulting coherent clusters are qualitatively similar over the same phase of the tide on different days and even different years, whereas coherent clusters for the opposite tidal phase are qualitatively different. The strong dependence of the cluster geometry on the tidal phase has been also observed in tidally driven flow over an experiment in Scott Reef, Australia [
43]. Comparing the model-based clusters south of Martha’s Vineyard to the motion of real drifters, for most of the identified clusters, drifters deployed within a cluster stayed within the same cluster for 6 h, which was the time interval chosen for our analysis. Exceptions, i.e., clusters from which real drifters escaped in less than 6 h, include small clusters with lower coherence metric or clusters identified over the time interval with strong wind gusts that were not realistically represented in the numerical model of oceanic currents.
Comparing coherent clusters with FTLE fields reveals that cluster boundaries often have similarities with the forward-time FTLE ridges. This qualitative similarity is due to the repelling character of the forward FTLE ridges, which maximize separations between neighboring drifters and delineate regions of qualitatively different Lagrangian motion. In other cases, coherent clusters were identified in areas that shrink significantly over the subsequent 6 h, suggesting that these clusters might be dominated by the surface flow convergence. Finally, some of the coherent clusters were identified over the most quiescent regions with lowest FTLEs, which encompass groups of drifters that moved (and separated) less than others. Note, however, that because the spectral clustering method identifies clusters based on a specific criterion, i.e., by maximizing intra-/inter-cluster similarities/differences, one should not expect a one-to-one agreement between spectral clusters boundaries and FTLEs or other LCSs that use another underlying flow property. Thus, various complementary LCS techniques could be applied in concert to provide the most comprehensive view of the underlying Lagrangian transport.