Abstract
A recent predictive scenario of premixed flame propagation in unobstructed passages is extended to account for obstructions that can be encountered in facilities dealing with explosive materials such as in coalmines. Specifically, the theory of globally-spherical, self-accelerating premixed expanding flames and that of flame acceleration in obstructed conduits are combined to form a new analytical formulation. The coalmining configuration is imitated by two-dimensional and cylindrical passages of high aspect ratio, with a comb-shaped array of tightly placed obstacles attached to the walls. It is assumed that the spacing between the obstacles is much less or, at least, does not exceed the obstacle height. The passage has one extreme open end such that a flame is ignited at a closed end and propagates to an exit. The key stages of the flame evolution such as the velocity of the flame front and the run-up distance are scrutinized for variety of the flame and mining parameters. Starting with gaseous methane-air and propane-air flames, the analysis is subsequently extended to gaseous-dusty environments. Specifically, the coal (combustible, i.e., facilitating the fire) and inert (such as sand, moderating the process) dust and their combinations are considered, and the impact of the size and concentration of the dust particles on flame acceleration is quantified. Overall, the influence of both the obstacles and the combustion instability on the fire scenario is substantial, and it gets stronger with the blockage ratio.
1. Introduction
Historically, coal mining exhibits one of the highest fatality and injury rates among the industries dealing with flammable gases and combustible dust, with occupational hazards occurring on a regular basis [1]. For instance, not long ago an unfortunate mining accident in Soma, Turkey took hundreds of lives [2]. Among the causes of disasters, a spontaneous accidental explosion can lead to a catastrophic consequence. This happens, in particular, because methane is often present in the coal seams and can be accumulated inside a coal mining passage during the coal extraction process. If sufficient ventilation is not provided, a risk of violent methane/air/coal-dust explosion is viable. Consequently, in order to foresee potential risks and to install any safety measures against a fire accident, an understanding of the processes in a burning accident is essential. A predictive scenario of a coal mining fire [3] was a step in this direction. Specifically, the key characteristics of a fire such as the evolution of the shape and velocity of a premixed flame front, as well as the flame run-up distance were predicted by combining the mechanism of flame acceleration due to a “finger” flame shape [4] with another flame acceleration mechanism [5] devoted to self-similar accelerative outward propagation of a global spherical flame front, which is wrinkled because of the Darrieus–Landau (DL) instability (see [5] for more details on the dynamic and scalar fields associated with flame propagation and the fluid ahead of the flame front). However, [3] assumed smooth walls of a passage, while it was subsequently recognized by [6] that obstructions, which are inevitably present in a coal mine (such as mining equipment, belt conveyor systems, and piles of rubble), can block a noticeable part of the passage, thereby providing a significant impact on a fire scenario. Therefore, there is, a critical need to account for obstacles in a predictive coal mining fire scenario as addressed in the present work.
Previously, Silvestrini et al. [7] developed a simplified formulation for evaluating the flame run-up distance for smooth tubes, and then extended it to account for obstacles, and obtained that the obstacles promote flame acceleration, thereby leading to shorter run-up distances. Ciccarelli and Dorofeev [8] reviewed the knowledge on flame acceleration in smooth and obstructed channels, emphasizing the formation of a cellular flame structure due to the DL instability, as observed in the small-scale experiments for the flames in the obstructed channels [8]. Houim and Oran [9] considered a channel with smooth walls, filled with a coal dust or ash particles layered at the bottom of the channel. They demonstrated, computationally, that the flame interaction with the coal dust formed hot spots ahead of the flame front; and autoignition of these hot spots produced the jumps in the flame position and sharp spikes in the flame velocity. Seshadri et al. [10] considered the structure of a premixed flame propagating in environments where combustible particles were uniformly distributed and identified the effective equivalence ratio and laminar burning velocity of the mixture in terms of particle size and concentration. Xie et al. [11] showed, experimentally, that a small size of the combustible coal particles promoted the overall equivalence ratio of the fuel mixture, as well as the laminar flame speed in this mixture. Zheng et al. [12] investigated the effect of a distribution of a methane-air fuel mixture composition inside a two-dimensional (2D) obstructed channel on the deflagration-to-detonation transition (DDT), with the finding that the inhomogeneous distributions either did not produce a detonation or resulted in a detonation that was decoupled into a flame and a shock earlier as compared with the homogeneous distribution. The wall restrictions in the confined enclosures, as well as the shape and layout of the obstacles can significantly influence flame acceleration in the obstructed channels. In unconfined spaces, Ogawa et al. [13] showed that an array of square obstacles led to continuous detonation propagation. Bychkov et al. [14] provided an explanation of a physical mechanism of flame acceleration in a 2D obstructed channel, equipped with a comb-shaped array of tightly placed obstacles. Specifically, delayed burning in the pockets between the obstacles caused a jet flow along the centerline of the channel, thereby providing extremely powerful flame acceleration [14]. Subsequently, Valiev et al. [15] extended a 2D study [14] into cylindrical-axisymmetric geometry, with much stronger flame acceleration occurring in the cylindrical tubes [15] as compared with the 2D channels [14]. Unlike finger-flame acceleration [4], acceleration due to obstacles [14,15] is unlimited in time and it can eventually trigger a DDT constituting an extra, shock-based disaster for personnel and equipment in underground enclosures such as coal mines or subway tunnels.
In the present work, the coal mining passage is imitated by an obstructed channel/tube [14,15]. Specifically, we combine the formulation of a globally-spherical, self-accelerating expanding flame front, distorted by the DL instability [5] and the formulation of fast flame acceleration due to the obstacles in a channel/tube [14,15], thus, revisiting a predictive scenario of a burning accident in a coal mining passage [3]. It is shown that the obstacles play a key role in the coal mining fire scenario, and that the DL instability can significantly promote obstacle-based acceleration.
Starting with a homogeneous methane-air fuel mixture, the analysis is subsequently extended to a gaseous-dusty environment using a modified Seshadri formulation [3,10]. The parametric study involves variations of the blockage and equivalence ratios, and , as well as the size of the dust particles and their type (inert such as sand, combustible such as coal, and their combination).
2. Formulation
Here, we present our formulation, starting with the 2D geometry in Section 2.1, and then its counterpart, the approach for cylindrical-axisymmetric geometry in Section 2.2. First, we recall the basics of flame acceleration mechanism for a globally-spherical, expanding flame front corrugated due to the DL instability. Indeed, any large-scale premixed flame front is prone to this mode of instability such that the radius of a globally-spherical, expanding flame obeys the time-dependent power law [5]:
where a small quantity can be considered to be a fitting parameter that can account for the ignition uncertainty in the experiments or a critical flame radius at which self-similar acceleration visually starts [5]. In the present work, we neglect this parameter as negligible as compared with a passage height or an obstacle length, . The factor in Equation (1) can be evaluated as [3,5]:
with the thermal expansion ratio and the DL cutoff wavenumber ( is the DL critical wavelength), which is assumed to obey the relation (see [16] for details):
where is the conventional definition of the flame thickness, and is the thermal diffusivity coefficient of the fuel mixture. In the present work, Equation (3) is chosen because it was used in our previous works, such as in [3], and therefore it is natural to use the same formula here, for better comparison. It is nevertheless noted that there exist alternative formulas for as discussed in [17] and references therein. In this light, the present formulation is flexible with respect to the choice of the formula for , such that Equation (3) can be readily replaced by any alternative. The DL cutoff wavelength is a quantity, proportional to the flame thickness, , with a proportionality factor of the order of depending on thermal-chemical flame properties such as the expansion ratio [16,17]. Equation (3) is an example of such a dependence. Obviously, if , then ,
In [5], the authors developed an analytical theory describing self-similar accelerative outward propagation of a globally-spherical flame front. It is wrinkled because of the DL instability and obeys Equation (1). In particular, the dynamic and scalar fields associated with flame propagation, and the flow ahead of the flame, were analyzed, with a particular focus on (although not limited to) the flame-generated compression waves and the time evolution of the radial flow velocity. The exponent in Equation (1) has been reported to be in the range [18,19,20,21,22]. Similar to [3], in the present work, we employed in the majority of cases, although the impact of varying was also analyzed. According to Equation (1), instead of the unstretched laminar flame velocity , the instantaneous radial flame velocity with respect to the fuel mixture is
2.1. Two-Dimensional (2D) Geometry
We consider a 2D passage (channel) of width as illustrated in Figure 1, which is closed at one end, with a premixed flame front propagating towards the open end. The passage is blocked by the obstacles of length, , such that the central segment of the channel of width, , remains unobstructed. Theoretically, we adopt a limit of tightly placed obstacles, , which allows treating the flow between the obstacles as laminar. Nevertheless, it is noted that the Bychkov model [14] is applicable even far beyond the restriction ; namely, it is valid as long as or even as validated in the computational study [23]. Thus, it should be enough to keep the obstacle spacing less than the obstacle height, thereby having their ratio not exceeding unity, (although the tighter the better, of course). In this respect, the assumption of a laminar flow between the obstacles can be waved, to some extent. For instance, the Eulerian assumption of a non-viscous flow might lead to a similar x-direction velocity profile without imposing tightly placed obstacles. However, in that case, there would be additional effects of a vertical motion between the obstacles, presumably, leading to pulsations, which would need to be studied. Therefore, as of now, we assume a laminar flow in the pockets between the obstacles.
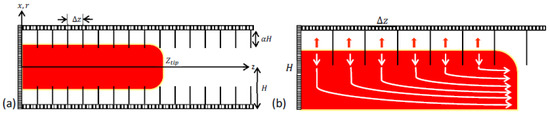
Figure 1.
Illustration of flame acceleration inside an obstructed passage (a) and delayed burning between obstacles (b).
With such a laminar flow approach, the flame front inside the pockets can be taken as locally planar all the time, thus, spreading in the x-direction with the instantaneous global flame velocity . As the burnt matter expands with a thermal expansion ratio , the flow is pushed out of the “pockets”. Coming into a central part of the passage, the flow changes its direction and pushes the flame forward in the z-direction towards the exit. This creates a positive feedback between the flame and the pockets as the flame is pushed forward, thereby creating new pockets behind it.
It is emphasized that the flame dynamics and morphology are controlled by the processes occurring in the obstructed segment of the passage and not in its unobstructed, central part. Indeed, although the flame tip is driven by a powerful jet flow; such a jet flow is generated due to delayed burning in the pockets between the obstacles. Moreover, the total burning rate (which grows extremely fast) correlates well with the total surface area of the flame front, which is mainly provided by the flame segments in the pockets between the obstacles. Consequently, the shape (surface area) of the flame tip does not seem to play a role in the flame surface area, and therefore the total burning rate (even if the tip would be very corrugated, this would not change the total flame surface area and the total burning rate). For this reason, the shape of the flame tip can be assumed to be planar all the time [14,15]. With this assumption, we can potentially neglect the effect of the flame growth at the initial stages of burning. Nevertheless, we accounted for the evolution of flame “skirt” described by Demir et al. [3], with a point ignition in our analysis,
With methane-air and propane-air laminar burning velocities not exceeding [24] and the respective speeds of sound circa , the initial Mach number associated with flame propagation appears to be very small, . This guides us to employ a low Mach number model of an incompressible flow, , similar to [3]. This model has been widely employed analytically and verified by fully compressible computational simulations in our previous works [4,15]. The model has been justified to work well at the initial, essentially subsonic stage of flame acceleration, and to provide reasonable evaluations even in the case of compressible flows. Nevertheless, it is recognized that the model would break when the burning velocity approaches near-sonic values. Such a limitation of the model and the way to overcome is commented on in Section 3.1. For a 2D geometry, the incompressible continuity equation reads as:
Similar to the Bychkov model [14,15], here, we employed the assumption of a potential flow in the burnt gas, which has been validated by the computational simulations in [15]. It is nevertheless noted that, in a real passage, obstacles generate vorticity at least in the central region close to the obstacles. At the same time, according to [23], although the flow in the burnt gas is generally rotational in practice, because of the curved flame shape, it can be treated as potentially close to the wall when the flame front is locally planar, which is enough to certify the Bychkov approach [23].
The question about vorticity and rotational region has been addressed, in part, in [23,25]. According to the simulations [25], vorticity provides a notable impact on the Bychkov mechanism only if the obstacle spacing exceeds the passage radius, , with the Bychkov model being fully broken if . Obviously, such is much larger than what usually means tightly placed obstacles, , say [23], thereby justifying the potential flow approach. As a result, considering the potential flow in the free part of the passage, with the boundary condition at , we find the velocity profiles in the burnt gas,
The flame tip obeys the evolution equation
which mathematically expresses the fact that the flame tip velocity in the laboratory reference frame equals the velocity of the burnt matter flow taken at the flame tip location, , plus the flame tip velocity with respect to this flow, . Accounting for Equation (7), Equation (8) can be rewritten as:
While both terms in the right-hand-side (RHS) of Equation (9) are, initially, of the same order, the first (“flow”) term soon dominates over the second (“flame”) term, because the value grows promptly with time. With the initial condition , the solution to Equation (9) reads as:
Then, the velocity of the flame tip is given by:
In the case of , the DL instability disappears and Equations (7)–(11) reproduce their counterparts of [14]. We next recognize that the DL instability should not provide an increase in the flame surface/velocity infinitely because the characteristic cross-sectional size of the flame eventually stops growing. Specifically, the characteristic length scale of the flame radius does not grow further after a flame skirt touches an obstacle in the case of point ignition. This instant can be calculated from a condition in Equation (5), namely:
after which the instantaneous global flame velocity remains constant. The respective flame tip position and the instantaneous global flame velocity at this instant are
Then, instead of the time-dependent quantity in Equation (9), we have a constant value
Integrating Equation (15) for , with the matching condition (13), we find
We also determine the flame run-up time, , which we evaluate as the time at which the flame velocity reaches the speed of sound of the reactants, . Namely, Equation (17) gives the run-up time as:
with the corresponding run-up distance being
2.2. Cylindrical Geometry
We next derive a similar formulation for the cylindrical geometry. Similarly, the passage radius is taken as . Evolution of the flame skirt in an unobstructed section is described as [3]:
where . The incompressible continuity equation in a cylindrical-axisymmetric geometry reads:
with a symmetric boundary condition at . Assuming that the flow in the unobstructed part of the passage is potential (and the shape of the flame front is not of significant importance), the velocity profile reads:
The propagation velocity of the flame tip with respect to burnt gas is given by:
Furthermore, an additional increase in the flame shape occurs in a cylindrical geometry, because the flame in an axisymmetric pocket expands with the radius as [15]:
where is the instant at which the fresh gas in the pocket between the obstacles at the position z starts burning and represents the radial coordinate of flame skirt in an obstructed passage. Averaging the last term in Equation (24) as (see [15] for details), we arrive at the following modified version of the evolution Equation (23) for :
Integrating Equation (25) with the initial condition , we find the solution in the form:
with the velocity of the flame tip being
Again, as in the 2D case, if , then the DL instability disappears, and the present formulation reproduces that of [15]. Furthermore, similar to the 2D formulation of the previous subsection, the average-in-mean radial flame size does not grow after the instant , which can be determined from the condition in Equation (20), namely:
The respective flame tip position and the instantaneous global flame velocity at this instant are
Then, instead of the time-dependent quantity in Equation (25), we have a constant value
Integrating the Equation (31) for , with the matching condition (29), we find
Similar to the 2D analysis, from the condition the run-up time in the cylindrical geometry can be evaluated from Equation (33) as:
with the corresponding run-up distance
Finally, it is recognized that a number of effects remained beyond consideration in the present work. For instance, only the DL flame instability is accounted for as the agent triggering unsteadiness, without considering turbulence or other combustion instability modes such as the diffusional-thermal (DT), Rayleigh–Taylor (RT), or Kevin–Helmholtz (KH) instabilities. In the future, these features could be potentially incorporated into the analysis by replacing the quantities (Equation (3)) and (Equation (4)) by the respective DT/RT/KH/turbulence-induced parameters. In addition, analysis of partly open obstructed duct, as in the pioneering Taylor–Bimson (TB) model [26], would be of interest. However, all such extensions of our work will be performed elsewhere.
3. Results and Discussion
In this section, we present and discuss the results of an intensive parametric study performed. Specifically, the first subsection is devoted to homogeneously-gaseous, methane-air and propane-air burning with the thermal-chemical parameters (such as and ) being the functions of the equivalence ratio , as tabulated in Table 1; see also [3,24]. In the second subsection, the analysis is extended to a gaseous-dusty environment.

Table 1.
The parameters for methane-air and propane-air combustion: the thermal expansion ratio, , the laminar burning velocity, , and the sound speed in the fuel mixture, , versus the equivalence ratio, .
3.1. Gaseous Combustion
We start with Figure 2 presenting the time evolutions of the flame tip position, , Figure 2a, and its velocity, , Figure 2b, in a 2D geometry, for stoichiometric methane (CH4)-air burning, as well as that of propane (C3H8)-air, for comparison, with various blockages employed. The horizontal dotted lines in Figure 2b show the speeds of sound for the methane-air, , and propane-air, , mixtures (Table 1). The case of no obstacles, , reproduces, completely, the situation of “finger + DL” flame acceleration [3]. It is noted that this acceleration is limited in time such that the flame would start decelerating when its skirt contacts a sidewall at and for methane-air and propane-air burning, respectively. It is also noted that by these times, the propane-air flame overcomes the sound threshold , whereas the methane-air flame stops at . In contrast, in an obstructed channel, , acceleration is unlimited in time until the flame approaches the speed of sound and can eventually trigger a detonation. We should recall, at this point, that approaching the near-sonic values by the flame front will eventually break the incompressible approach, adopted in Equation (6), and the entire present formulation. Indeed, to describe the DDT stage accurately, we have to incorporate the impacts of gas compressibility into the present analysis. This can be done by considering the formulation of Section 2 as the zeroth-order approach in , and then extending it to account for the finite according to the methodology employed earlier for unobstructed [27] and obstructed [28] geometries. However, such a rigorous extension of the present formulation to account for the compressibility effects requires a separate work and is presented elsewhere [29]. It is also noticed that the analytical incompressible formulation of Section 2 does not involve pressure as a parameter (except for the fact that pressure comes indirectly through the thermal-chemical parameters such as or , which are taken for ambient, atmospheric pressure indeed in the present section). However, if the present formulation is extended to account for a finite , as discussed above, then pressure, its variations and gradient, are directly involved in a revised formulation, with the ambient, atmospheric pressure imposed as the initial conditions and a boundary condition in the open side of the passage.
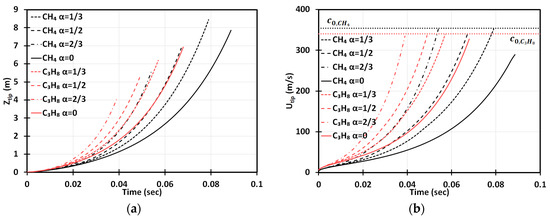
Figure 2.
Time evolution of the flame tip position (a) and velocity (b) in a 2D geometry for stoichiometric () methane (CH4)-air and propane (C3H8)-air burning with various blockage ratios .
Figure 3 is a counterpart of Figure 2 for the cylindrical geometry. It is seen that the flame accelerates faster in this case. Opposite to the situation of and methane-air burning in a 2D geometry, here, at the same conditions, the flame would overcome the sound speed at , i.e., slightly prior the deceleration stage starting at . To demonstrate this more clearly, in Figure 4 we have compared the results obtained in the 2D and cylindrical-axisymmetric geometries. Overall, Figure 2, Figure 3 and Figure 4 show that the obstacles influence a coal mine fire scenario significantly, making acceleration potentially unlimited in contrast to the case of no obstacles, which was considered in [3]. In addition, flame acceleration in Figure 2, Figure 3 and Figure 4 exceeds that of the original theories [14,15] by orders of magnitude, thereby certifying that the DL instability facilitates obstacle-based acceleration.

Figure 3.
Time evolution of the flame tip position (a) and velocity (b) in a cylindrical-axisymmetric geometry for stoichiometric CH4-air and C3H8-air burning with various blockage ratios, .
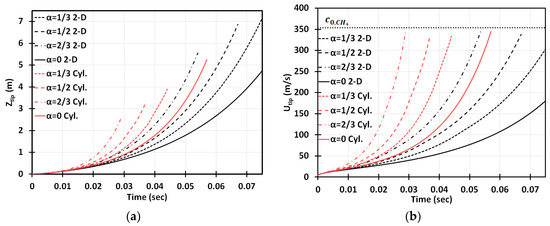
Figure 4.
Comparison of the 2D and cylindrical-axisymmetric geometries. Time evolution of the flame tip position (a) and velocity (b) for stoichiometric CH4-air burning with various blockage ratios .
It should be mentioned that everywhere except for Figure 5 we employed the exponent of Equation (1) to be the same as that in [3], i.e., . This is in order to compare the present work with the “unobstructed burning accident” theories [3] (as well as with the original Bychkov theories [14,15], which did not consider the DL instability, thereby having by default). It is noted, in this respect, that an appropriate choice of the factor is not yet finalized. Indeed, while various experimental studies such as Gostintsev et al. [18], Bradley et al. [19], Molkov et al. [20], Kim et al. [21] have reported , the Princeton experiments in a dual chamber at elevated pressures suggested ; see Jomaas et al. [22] and numerous references therein. The theoretical work [30] has provided an attempt to explain such a discrepancy between various experiments by the flame-acoustic coupling, which modifies . Moreover, the quantity of can also be potentially modified by turbulence and other combustion instability modes such as Rayleigh–Taylor instability (assuming that the general trend of Equation (1) remains).
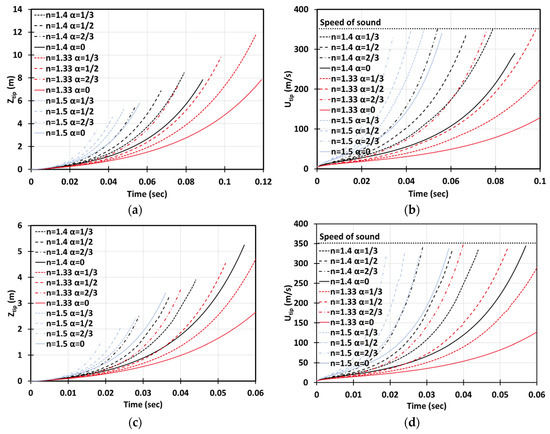
Figure 5.
Time evolution of the flame tip position (a,c) and velocity (b,d) in a 2D (a,b) and cylindrical-axisymmetric (c,d) geometry for stoichiometric CH4-air burning with various blockage ratios and various power factors .
We have considered in the range and scrutinized its impact on the present formulation. Specifically, Figure 5 compares the time evolutions of the flame tip positions (a, c) and velocities (b, d) for stoichiometric methane-air burning considering , and both 2D (Figure 5a,b) and cylindrical (Figure 5c,d), geometries are studied. It is seen that the variations of impact the flame position, velocity and acceleration substantially, although the effect is quantitative but not qualitative. As expected, flame acceleration in the case of proceeds noticeably faster than for , whereas a flame with accelerates noticeably slower as compared with that with (of course, provided that other combustion characteristics are kept the same). Nevertheless, without the final answer to the question about an appropriate choice for , in the rest of this work we keep using its median value, , the same as that in the unobstructed theories [3]. This allow us to make a comparison with [3], thereby separating the impact of obstacles.
Next, we extend the stoichiometric () gaseous methane-air combustion considered in Figure 2, Figure 3 and Figure 4 to the equivalence ratios in the range , see Figure 6, Figure 7, Figure 8 and Figure 9. In particular, Figure 6 presents the 2D configuration with various for . It is seen that a slightly fuel-lean flame with accelerates much slower than the flames, especially in the cases of and . This is because of a much lower (and thereby higher and lower ) inherent to such a slightly lean condition. However, it is recalled that flame acceleration in an obstructed passage is unlimited in time, and therefore it can eventually trigger a detonation in the case of sufficiently long passage and time. In particular, in this geometry, the approximate run-up times until the detonation initiation for the flame are evaluated as for and for . In the case of no obstacles, , no detonation is predicted for a flame in a 2D passage. Overall, among all equivalence ratios considered, the fastest flame acceleration is observed for a slightly rich flame of .
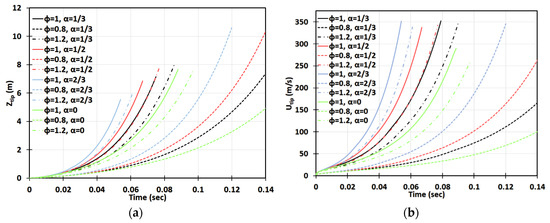
Figure 6.
Time evolution of the flame tip position (a) and velocity (b) in a 2D geometry for lean (), stoichiometric (), and rich () CH4-air burning with various blockage ratios .
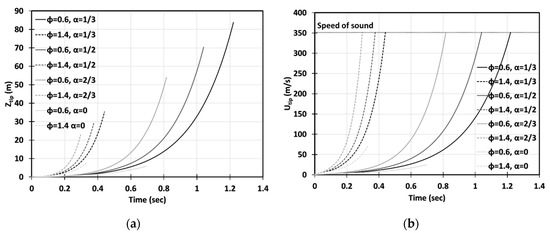
Figure 7.
Time evolution of the flame tip position (a) and velocity (b) in a 2D geometry for highly-lean () and highly-rich () CH4-air burning with various blockage ratios .
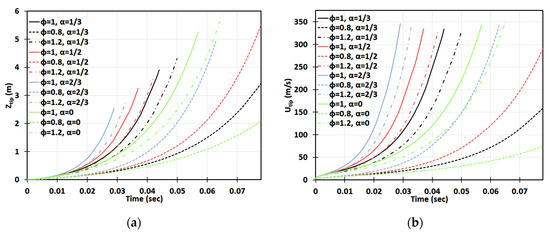
Figure 8.
Time evolution of the flame tip position (a) and velocity (b) in a cylindrical-axisymmetric geometry for lean (), stoichiometric (), and rich () CH4-air burning with various blockage ratios .
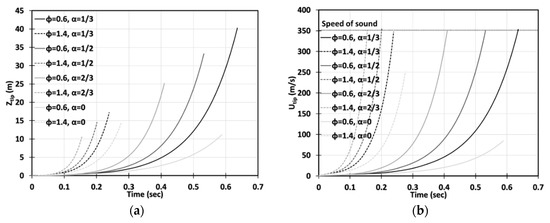
Figure 9.
Time evolution of the flame tip position (a) and velocity (b) in a cylindrical-axisymmetric geometry for highly-lean () and highly-rich () CH4-air burning with various blockage ratios .
The flame will propagate slower if we deviate further from stoichiometry, as depicted in Figure 7, showing the evolutions of the position and velocity of the and methane-air flames (to avoid messy, we split the plots for various equivalence ratios between Figure 6 and Figure 7). It is also seen that the duration of acceleration of the highly lean/rich flames in Figure 7 exceeds that of the stoichiometric or slightly lean/rich flames in Figure 6. In particular, without obstructions, the flame stops accelerating after advancing and attaining the maximal velocity of , before the flame skirt contacts the wall. Obviously, this acceleration scenario does not end thereafter, if the obstacles are added to the passage wall. In contrast, the flame front will keep accelerating until its speed reaches the speed of sound and, eventually, the detonation is triggered. It is noted that the obstacles facilitate flame acceleration as compared with that in an unobstructed passage, and the impact of obstacles seems to be more important for the flames than for the flames: the lines for with various go more widely than those for . It is also seen in Figure 7 that the rich flames, , accelerate faster than the lean flames, . With respect to the latter, the situation of highly non-stoichiometric combustion in Figure 7 qualitatively resembles slightly non-stoichiometric burning in Figure 6.
Figure 8 and Figure 9 are the cylindrical-axisymmetric counterparts of Figure 6 and Figure 7, respectively. Here, most of the 2D results discussed above remain qualitatively the same, although, quantitatively, the flames accelerate faster in the cylindrical passages. Here, the approximate run-up times until the detonation initiation for the flames appear for and for . A key difference between the two geometries is that whereas no detonation is predicted for the flame in a 2D case without obstacles, , in the cylindrical configuration with , the methane-air flame was able to reach the speed of sound, , at , thereby making a detonation possible. Again, further away from stoichiometry, see Figure 9, the and flames accelerate slower and the acceleration time lasts longer as compared to the flames in Figure 8. For example, in the case of , the flame stops accelerating when advancing and reaches the maximal velocity of s at the instant when the flame skirt contacts the side wall of the cylindrical passage. Similar to a 2D geometry, the highly rich flames () accelerate faster than the highly lean flames () in the cylindrical case, and the impact of obstacles seems to be more important for the flames (the lines corresponding to various blockage ratios go more widely).
Using Table 1, we next analyze the run-up times , Equations (18) and (34), and the respective run-up distances , Equations (19) and (35), for the methane (CH4)-air and propane (C3H8)-air flames of various equivalence ratios. Specifically, Figure 10 presents versus for various blockage ratios, including the case of no obstacles, , in the 2D (Figure 10a) and cylindrical (Figure 10b) geometries. Overall, Figure 10 agrees with our analysis above in that the shortest run-up distances are observed for a slightly fuel-rich methane-air flame of . In the 2D case, Figure 10a, we have , , and for , respectively. The case of in a 2D geometry is not relevant because a flame skirt contacts a sidewall and stops accelerating before the DDT event for all considered, which is in line with the findings of [3]. For the lean or rich methane-air flames, the run-up distances are much higher, namely, up to for and up to for (still in the 2D geometry). In the cylindrical-axisymmetric configuration, for the fastest methane-air flames with we found the run-up distances as small as , , , and for , respectively. For lean or rich methane-air burning, the run-up distances are much higher in the cylindrical geometry, i.e., up to for and up to for . It is noted that, unlike the 2D configuration, in the cylindrical-axisymmetric case, the detonation is predicted for methane-air burning even in the case of , when the equivalence ratio is in the range , which generally agrees with [3]. Overall, for the same geometry, and , the run-up distances are dramatically shorter for the C3H8-air flames as compared with the CH4-air flames; this would overcome the sound threshold for additional equivalence ratios in the case of , being within the ranges and for the 2D and cylindrical-axisymmetric geometries, respectively.
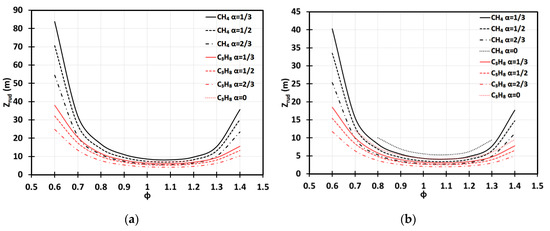
Figure 10.
The flame run-up distance versus the equivalence ratio for CH4-air and C3H8-air burning at various blockage ratios: in a 2D (a) and cylindrical-axisymmetric (b) geometries.
3.2. Validation of Gaseous Formulation
We have compared our analytical predictions with the data available in the literature such as the experiments by [31] and computational simulations (FAST and ALLA) in [6]. The results are shown in Figure 11 and Figure 12, where the flame tip velocity is shown versus its position, for various blockage ratios, such that the linear trend represents exponential acceleration. The simulation results [6] are shown by circles while the square markers present the experimental data [31]. The solid/dashed lines are devoted to the theoretical predictions. We observe reasonably good quantitative agreement between the 2D theory and the literature data. As for the cylindrical theory, our qualitative linear theoretical trend fits that of the markers very well.
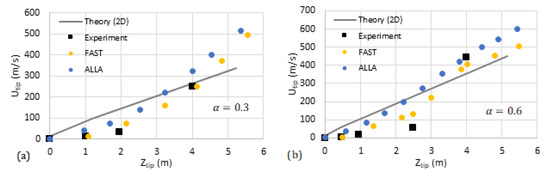
Figure 11.
Comparison of our theoretical formulation with the experiments [31] and computational simulations [6] (FAST, yellow, and ALLA, blue). The flame tip velocity vs. its position for the blockage ratios (a) and (b).
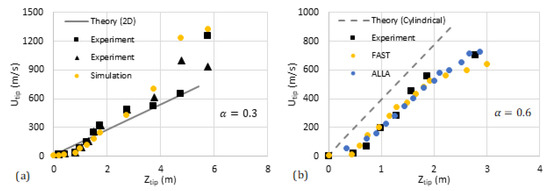
Figure 12.
Comparison of our theoretical formulation with the experiments [31] and computational simulations [6] (FAST, yellow, and ALLA, blue). The flame tip velocity vs. its position for the blockage ratios (a) and (b).
3.3. Extension to Gaseous-Dusty Environment
Starting with homogeneously gaseous combustion in the previous subsection, we next extend our analysis to a gaseous-dusty environment by using a modified version of the Seshadri formulation [10], which expresses the laminar flame velocity as a function of local thermal-chemical properties of the gas and dust particles (inert, such as sand; combustible, i.e., coal; and combined) in the form [3]:
where is the modified equivalence ratio of the gaseous-dusty-air mixture in the presence of combustible dust particles:
and are the respective molar masses; , and are the original masses per unit volume for a given equivalence ratio; is the specific heat of the whole mixture, containing the components for the gas, , and dust particles, ; is the density of a single dust particle, while is that for the gaseous-dusty fuel-air mixture, with the density of the gas and the concentration of the dust particles ; is the number of particles per unit volume, with being the volume of a single particle of radius ; is the universal gas constant; is the reactants temperature and is the adiabatic flame temperature based on the purely methane-air equivalence ratio. Similar to [3], here, is calculated as a fifth-order polynomial function of the equivalence ratio [32]:
valid in the range [32]. Knowing from Equation (37) and calculating a new flame temperature for the dusty-gaseous mixture, , one can find , Equation (36), to be employed in the formulation in the previous section.
We next employ the methodology of [3,11]. Unlike a combustible dust, an inert particle acts as a heat sink because it absorbs some heat from the flame and reduces the flame temperature. For , methane-air combustion, the global chemical reaction is described by the equation:
such that the heat release in the process of burning of moles of and moles of air is given by [3,11]:
where is the number of moles of the burning products, which depends on the equivalence ratio . Assuming that the entire heat released from the reaction is used to raise the temperature of the mixture, Equation (40) can be modified into an expression for the volumetric heat release from -air combustion of a given as follows [3]:
Next, it is assumed that a flame with particles releases the same amount of heat while it is also influenced by the temperature rise of particles [11]. Then Equation (41) can be extended as [3]:
where [11] is the heat of gasification per unit volume. From the last equation, the secondly revised flame temperature, , is calculated as:
Finally, the effect of the combination of the inert and combustible dust particles are accounted for by averaging the adiabatic flame temperature over those values associated with both effects separately, . Similar to a combustible dust case, and are used in Equation (36) to find a new laminar flame speed for the inert and combined dust particle incorporations, respectively. As of now, all the particles are assumed to be distributed uniformly inside a coal mining passage; non-uniform dust distributions can be considered elsewhere, for instance, following the method of [33].
It is even a more interesting question with respect to what happens with the DL cutoff wavelength when we go from the gaseous to the gaseous-dusty environment. To be self-consistent with the Seshadri formulation (which actually imitates a multi-phase system by an “effective” fluid with modified properties, adjusted due to the presence of solid particles), here, is considered to be the quantity devoted to such an effective fluid. Consequently, is given by the same formula, Equation (3), although the variables in this formula (, ) are adjusted due to the presence of dust particles.
We can also provide another justification for this approach, namely, because , if the flame thickness does not change much when the dust particles are laden, then the value , as well as the onset and emergence of the DL instability would also not change much. Nevertheless, we recognize that a rigorous analysis of the DL instability of gaseous-dusty flames would require a separate study, with extra features to be incorporated. In particular, the transport processes such as heat transfer could be modified in an intriguing way, in particular, due to radiation.
Figure 13 depicts the situation of gaseous-dusty combustion, with the dust of concentration and of dust particles radius in the 2D (a, b) and cylindrical-axisymmetric (c, d) geometries. We employed the lean () methane-air fuel mixture and various blockage ratios , including the case of no obstacles, . It is seen that combined (combustible + inert) and inert dust moderate flame acceleration, whereas combustible particles slightly facilitate flame propagation. The effect of obstacles is also noticeable (as compare with an unobstructed passage).
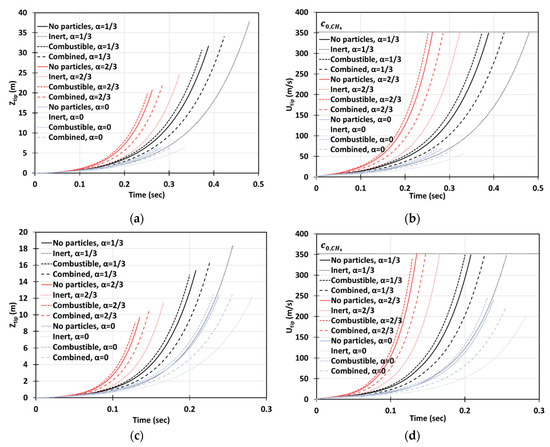
Figure 13.
Time evolution of the flame tip position (a,c) and velocity (b,d) in a 2D (a,b) and cylindrical-axisymmetric (c,d) geometries for lean CH4-air burning of , without and with dust particles (combustible, inert, and combined) of particle radius and concentration , for various blockage ratios, .
Next, we increase the dust concentration. Namely, in Figure 14, it is promoted to keeping the same particle radius, , and other characteristics and geometry, as in Figure 13. It is observed that combustible dust promotes flame acceleration, whereas inert dust and its combination with combustible dust moderate the acceleration process for the particles of radius . The impact of the blockage ratio is noticeable, especially in the cylindrical geometry. The flame velocity in the case of inert particles and is equivalent to the event of combustible dust but with no obstacles, , for ; and thereafter the flame accelerates faster in the presence of inert particles (Figure 14d). A relatively high concentration was also considered. Specifically, Figure 15 presents the case of , with the particle size , the same as in Figure 13 and Figure 14. This investigation reveals that if the dust particle size is kept constant while increasing the number of particles (i.e., the concentration), the effect of particles becomes more important. This is observed in Figure 13, Figure 14 and Figure 15 that the flames in gaseous-dusty environments departs from the case of no dust particles more widely as the concentration increases. Similar to the cases of and , the combustible particles promote flame acceleration, whereas the combined (combustible + inert) and inert particles also suppress it in the situation of .
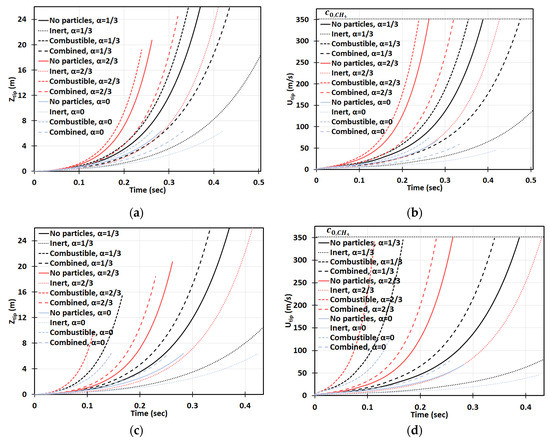
Figure 14.
Time evolution of the flame tip position (a,c) and velocity (b,d) in a 2D (a,b) and cylindrical-axisymmetric (c,d) geometries for lean CH4-air burning of , without and with dust particles (combustible, inert, and combined) of particle radius and concentration , for various blockage ratios, .
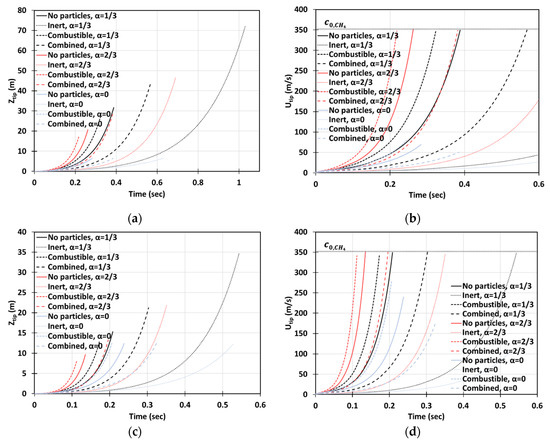
Figure 15.
Time evolution of the flame tip position (a,c) and velocity (b,d) in a 2D (a,b) and cylindrical-axisymmetric (c,d) geometries for lean CH4-air burning of , without and with dust particles (combustible, inert, and combined) of particle radius and concentration , for various blockage ratios, .
Figure 16a–d is the counterpart of Figure 14a–d, respectively, for a smaller particle radius, . It is observed, here, that smaller particles have a stronger impact on flame propagation. In the 2D geometry, while the flame velocities did not exceed for the particles of size , in the case of , the sound threshold of for methane-air burning was reached in the combustible coal gaseous-dusty environment with at the time instant (Figure 16b). In the cylindrical-axisymmetric geometry, the coal particles deviate noticeably larger from the case of no particles (Figure 16c,d). In fact, a particle type appears to be the most influential factor for flame acceleration in the obstructed passages. Namely, in any case of combustible dust present in any obstructed passages considered, , we obtained faster acceleration than in both respective cases of other dusts and no dust (Figure 16d). In contrast to the case in Figure 14, the combined combustible-inert particles promoted flame acceleration in the case of , Figure 16. These findings show that the impact of heat release on flame acceleration in a coal mining passage is significant, i.e., it facilitates the fire process, and, furthermore, it dominates over the impact of a heat sink when the particles are smaller. As for the inert particles, similar to the case of in Figure 14, they also suppress flame acceleration for . The aforementioned effects of all particles, i.e., combustible, inert, and combined, and particle sizes are found to grow with the blockage ratio .
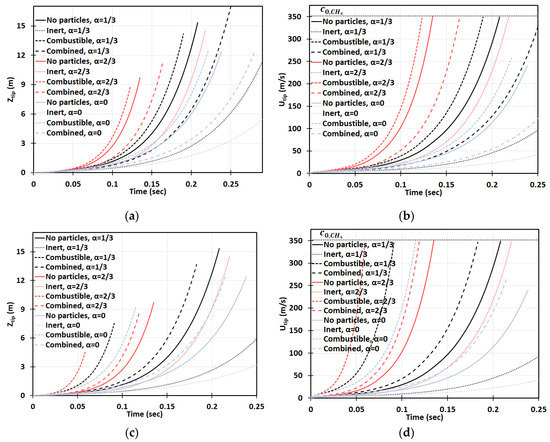
Figure 16.
Time evolution of the flame tip position (a,b) and velocity (c,d) in a 2D (a,b) and cylindrical-axisymmetric (c,d) geometries for lean CH4-air burning of with and without dust particles (combustible, inert, and combined) of particle radius and concentration , for various blockage ratios, .
4. Conclusions
Therefore, we have undertaken a step towards a predictive scenario of a burning accident in obstructed coal mining passage by developing a theoretical formulation, which combines the mechanism of flame acceleration in obstructed pipes [14,15] with that due to the DL instability [5]. Specifically, the 2D planar and cylindrical-axisymmetric geometries were considered, along with an assumption of incompressible flow for various passage configurations and the compositions of the combustible premixture. The newly identified flame propagation scenario was studied in terms of the evolution of the flame tip position and its velocity (in the laboratory reference frame) . The role of the obstacles, as well as the DL instability, on a fire scenario are found to be significant, with a stronger effect observed in the cylindrical geometry. Closer to the stoichiometric condition, a flame propagates and accelerates faster; and acceleration is also promoted with an increase in the blockage ratio . Starting with homogeneously gaseous combustion, the analysis was subsequently extended to incorporate dust particles in the passage. Namely, inert and combustible dust, as well as their combination, were considered. We found that the combustible dust particles of radii facilitate flame acceleration, while acceleration is moderated by the inert particles. The effect of particle size is significant in a manner that smaller particles lead to faster flame acceleration. While a combination of combustible and inert dust, of dust particle radius , moderates flame acceleration as compared with purely gaseous combustion, a combustible-inert combination of the particles of smaller radius, , promotes flame acceleration. The effect of a type and size of the particles increases with the blockage ratio.
Author Contributions
Conceptualization, F.K. and V.A.; funding acquisition, V.A.; investigation, F.K. and S.D.; methodology, F.K. and V.A.; project administration, V.A.; resources, V.A.; supervision, V.A. and D.V.; writing, F.K., V.A., and D.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by the Alpha Foundation for the Improvement of Mine Safety and Health, Inc., through Award #ASTI14FO-82 (V.A.), prior to which it was funded by the U.S. National Science Foundation (NSF) through CAREER Award No. 1554254 (V.A.), as well as by the West Virginia Higher Education Policy Commission through Grant #HEPC.dsr.18.7 (V.A.). The views, opinions, and recommendations expressed in this work are solely those of the authors and do not imply any endorsement by the Alpha Foundation, its directors and staff.
Acknowledgments
The authors dedicate this work to deceased Vitaly Bychkov (1968–2015) of Umea University, Sweden, whose role in analytical studies of premixed flame acceleration is hard to overestimate.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| radius of a global spherical expanding flame front | |
| constant defined in Equation (1) | |
| time | |
| Darrieus–Landau instability exponent | |
| Darrieus–Landau cutoff wavenumber | |
| laminar flame velocity | |
| density of fuel mixture | |
| density of burnt gas | |
| flame thickness | |
| thermal diffusivity coefficient | |
| instantaneous radial flame velocity | |
| half-width of a two-dimensional (2D) passage | |
| radius of a cylindrical passage | |
| obstacle spacing | |
| , r | radial direction |
| axial direction | |
| flame “skirt” | |
| obstacle spacing | |
| , | radial velocity |
| axial velocity | |
| flame tip position | |
| flame tip velocity | |
| the time flame skirt touches an obstacle | |
| flame “skirt” radius at | |
| flame tip position at | |
| global flame velocity at | |
| flame run-up time | |
| speed of sound | |
| flame run-up distance | |
| flame “skirt” in [15] | |
| the time instant at which the fresh gas between obstacles at the position starts burning | |
| laminar flame velocity in an “effective” gaseous-dusty environment | |
| specific heat of gaseous air-fuel mixture | |
| entire specific heat | |
| flame temperature with particles | |
| adiabatic flame temperature based on purely methane-air equivalence ratio | |
| unburnt gas temperature | |
| activation energy | |
| gas constant | |
| molar masses | |
| original masses | |
| specific heat of dust particles | |
| number of particles per unit volume | |
| volume of a single particle | |
| density of dust | |
| density of gaseous-dusty fuel-air mixture | |
| density of gas | |
| concentration of the particles | |
| radius of a particle | |
| volumetric heat release | |
| heat of gasification per unit volume | |
| number of moles of air per unit volume | |
| volume of methane | |
| volume of air | |
| number of moles of the burning products | |
| blockage ratio | |
| equivalence ratio | |
| Darrieus–Landau critical wavelength | |
| thermal expansion ratio | |
| defined as | |
| modified equivalence ratio in the gaseous-dusty air mixture | |
| flame | |
| Darrieus–Landau | |
| fuel mixture | |
| burnt gas | |
| thermal | |
| tip | |
| obstacle | |
| run-up distance | |
| initial | |
| flame in obstructed passage | |
| dust | |
| particle | |
| total | |
| burnt | |
| unburnt | |
| actual | |
| stoichiometric | |
| product |
References
- Ramani, R.V. Mining disasters caused and controlled by mankind: The case for coal mining and other mineral—Part 1: Causes of mining disasters. Nat. Resour. Forum 1995, 19, 233–242. [Google Scholar] [CrossRef]
- Lowen, M. Turkey Mine Disaster: Raw Anger in Soma a Year on. BBC World News. 13 May 2015. Available online: https://www.bbc.com/news/world-europe-32709431 (accessed on 1 June 2020).
- Demir, S.; Bychkov, V.; Chalagalla, S.H.R.; Akkerman, V. Towards a predictive scenario of a burning accident in a mining passage. Combust. Theory Model. 2017, 21, 997–1022. [Google Scholar] [CrossRef]
- Bychkov, V.; Akkerman, V.; Fru, G.; Petchenko, A.; Eriksson, L.-E. Flame acceleration at the early stages of burning in tubes. Combust. Flame 2007, 150, 263–276. [Google Scholar] [CrossRef]
- Akkerman, V.; Law, C.K.; Bychkov, V. Self-similar accelerative propagation of expanding wrinkled flames and explosion triggering. Phys. Rev. E 2011, 83, 026305. [Google Scholar] [CrossRef]
- Oran, E.S. Numerical Tools for Mitigation of Methane Explosions in Coalmines; Grant No. AFC215-20; The Alpha Foundation for the Improvement of Mine Safety and Health, Inc.: Philadelphia, PA, USA, 2017. [Google Scholar]
- Silvestrini, M.; Genova, B.; Parisi, G.; Trujillo, F.J.L. Flame acceleration and DDT run-up distance for smooth and obstacles filled tubes. J. Loss Prev. Process Ind. 2008, 21, 555–562. [Google Scholar] [CrossRef]
- Ciccarelli, G.; Dorofeev, S. Flame acceleration and transition to detonation in ducts. Prog. Energy Combust. Sci. 2008, 34, 499–550. [Google Scholar] [CrossRef]
- Houim, R.W.; Oran, E.S. Structure and flame speed of dilute and dense layered coal-dust explosion. J. Loss Prev. Process Ind. 2015, 36, 214–222. [Google Scholar] [CrossRef]
- Seshadri, K.; Berlad, A.L.; Tangirala, V. The structure of premixed particle-cloud flames. Combust. Flame 1992, 89, 333–342. [Google Scholar] [CrossRef]
- Xie, Y.; Raghavan, V.; Rangwala, A.S. Study of interaction of entrained coal dust particles in lean methane-air premixed flames. Combust. Flame 2012, 159, 2449–2456. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.; Kaplan, C.R.; Houim, R.W.; Oran, E.S. Flame acceleration and transition to detonation: Effects of a composition gradient in a mixture of methane and air. Proc. Combust. Inst. 2019, 37, 3521–3528. [Google Scholar] [CrossRef]
- Ogawa, T.; Gamezo, V.; Oran, E.S. Flame acceleration and transition to detonation in an array of square obstacles. J. Loss Prev. Process Ind. 2013, 26, 355–362. [Google Scholar] [CrossRef]
- Bychkov, V.; Valiev, D.; Eriksson, L.-E. Physical mechanism of ultrafast flame acceleration. Phys. Rev. Lett. 2008, 101, 164501. [Google Scholar] [CrossRef] [PubMed]
- Valiev, D.; Bychkov, V.; Akkerman, V.; Law, C.K.; Eriksson, L.-E. Flame acceleration in channels with obstacles in the deflagration-to-detonation transition. Combust. Flame 2010, 157, 1012–1021. [Google Scholar] [CrossRef] [Green Version]
- Pelce, P.; Clavin, P. Influence of hydrodynamics and diffusion upon the stability limit of laminar premixed flames. J. Fluid Mech. 1982, 124, 219–237. [Google Scholar] [CrossRef]
- Akkerman, V.; Bychkov, V. Velocity of weakly turbulent flames of finite thickness. Combust. Theory Model. 2005, 9, 323–351. [Google Scholar] [CrossRef]
- Gostintsev, Y.; Istratov, A.; Shulenin, Y. Self-similar propagation of a free turbulent flame in mixed gas mixtures. Combust. Explos. Shock Waves 1988, 24, 563–569. [Google Scholar] [CrossRef]
- Bradley, D.; Cresswell, T.; Puttock, J.S. Flame acceleration due to flame-induced instabilities in large-scale explosions. Combust. Flame 2001, 124, 551–559. [Google Scholar] [CrossRef]
- Molkov, V.V.; Makarov, D.V.; Schneider, H. Hydrogen-air deflagrations in open atmosphere: Large eddy simulation analysis of experimental data. Int. J. Hydrog. Energy 2007, 32, 2198–2205. [Google Scholar] [CrossRef]
- Kim, W.K.; Mogi, T.; Kuwana, K.; Dobashi, R. Self-similar propagation of expanding spherical flames in large-scale gas explosions. Proc. Combust. Inst. 2015, 35, 2051–2058. [Google Scholar] [CrossRef]
- Jomaas, G.; Law, C.K.; Bechtold, J. On transition to cellularity in expanding spherical flames. J. Fluid Mech. 2007, 583, 1–26. [Google Scholar] [CrossRef]
- Ugarte, O.; Bychkov, V.; Sadek, J.; Valiev, D.; Akkerman, V. Critical role of blockage ratio for flame acceleration in channels with tightly-spaced obstacles. Phys. Fluids 2016, 28, 093602. [Google Scholar] [CrossRef]
- Davis, S.G.; Quinard, J.; Searby, G. Markstein numbers in counterflow, methane- and propane-air flames: A computational study. Combust. Flame 2002, 130, 123–136. [Google Scholar] [CrossRef]
- Adebiyi, A.; Alkandari, R.; Valiev, D.; Akkerman, V. Effect of surface friction on ultrafast flame acceleration in obstructed cylindrical pipes. Aip Adv. 2019, 9, 035249. [Google Scholar] [CrossRef] [Green Version]
- Taylor, P.; Bimson, S.J. Flame propagation along a vented duct containing grids. Proc. Combust. Inst. 1988, 22, 1355–1362. [Google Scholar] [CrossRef]
- Demir, S.; Calavay, A.R.; Akkerman, V. Influence of gas compressibility on a burning accident in a mining passage. Combust. Theory Model. 2018, 22, 338–358. [Google Scholar] [CrossRef]
- Akkerman, V.; Valiev, D. Moderation of flame acceleration in obstructed cylindrical pipes due to Gas Compression. Phys. Fluids 2018, 30, 106101. [Google Scholar] [CrossRef]
- Kodakoglu, F.; Akkerman, V. Analytical study of an effect of gas compressibility on a burning accident in an obstructed passage. Phys. Fluids 2020, 32, 074602. [Google Scholar] [CrossRef]
- Akkerman, V.; Law, C.K. Effect of acoustic coupling on power-law flame acceleration in spherical confinement. Phys. Fluids 2013, 25, 013602. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Ciccarelli, G.; Dorofeev, S.; Alekseev, V.; Yankin, Y.; Kim, T. DDT in methane-air mixtures. Shock Waves 2002, 12, 215–220. [Google Scholar] [CrossRef]
- Morley, C. GASEQ—A Chemical Equilibrium Program. 2005. Available online: http://www.gaseq.co.uk/ (accessed on 1 May 2020).
- Demir, S.; Sezer, H.; Bush, T.; Akkerman, V. Promotion and mitigation of premixed flame propagation in a gaseous-dusty environment with various dust distributions. Fire Saf. J. 2019, 105, 270–276. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).