Scale-Resolving Simulation of a Propane-Fuelled Industrial Gas Turbine Combustor Using Finite-Rate Tabulated Chemistry
Abstract
1. Introduction
- (1)
- The investigated combustor includes important features of a realistic industrial-used gas turbine combustor, such as the multiple fuel holes, the swirler, the primary and secondary holes, the porous walls, etc.;
- (2)
- The SSTKWSAS approach is coupled with a finite-rate tabulated chemistry-based combustion model validated in our previous work [25];
- (3)
- Comprehensive comparisons of the SSTKWSAS model-produced results with experimental data are provided for the main flame region of the combustor;
- (4)
- The performances of different turbulence models are discussed and compared with LES results in the literature [26].
2. Mathematical Models
2.1. Turbulent Modeling
2.2. Combustion Modeling
3. Experimental Conditions and Numerical Methods
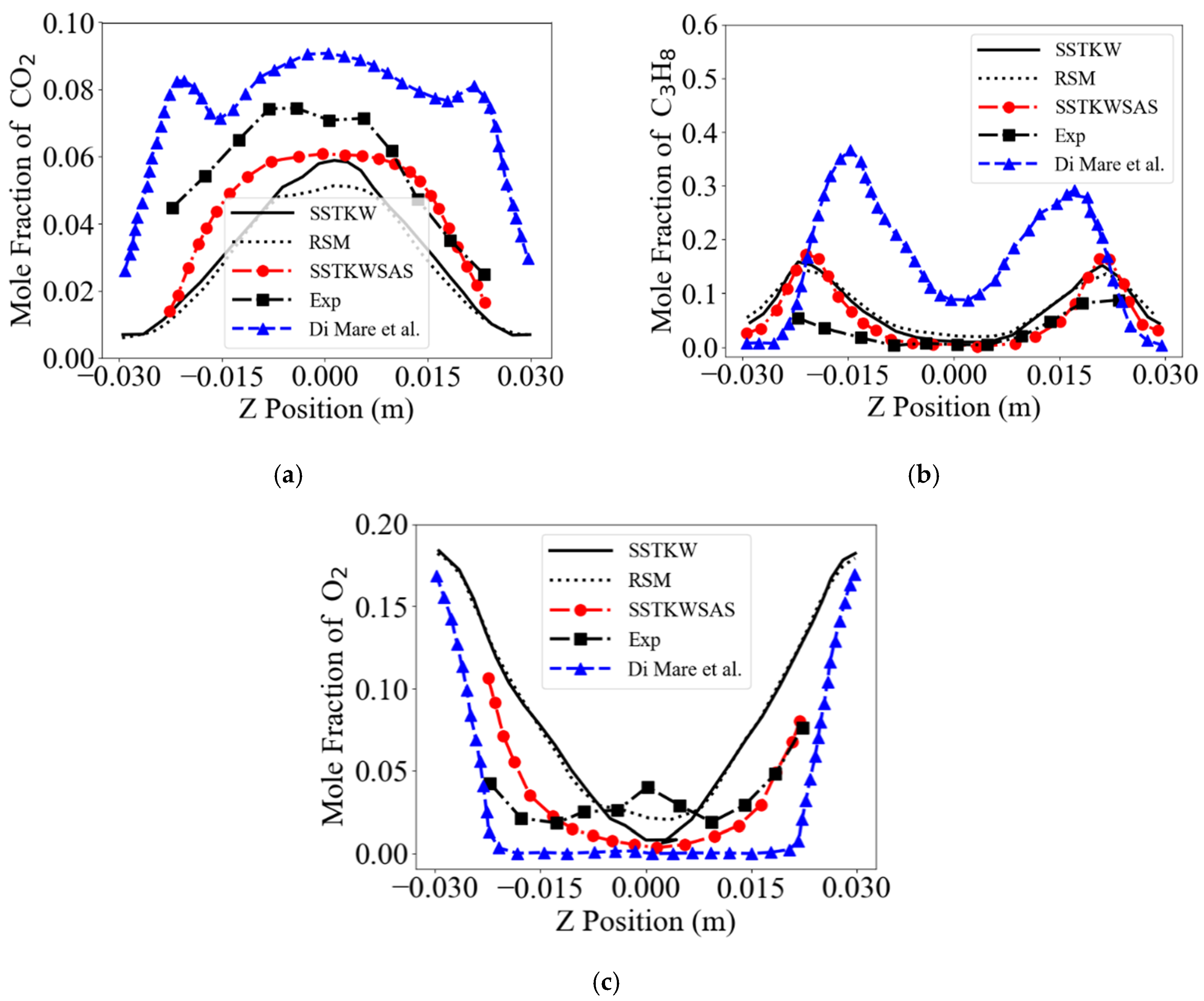
4. Results and Discussions
5. Conclusions
- (1)
- The spectrum-resolving SSTKWSAS model-based simulation is performed for the first time to predict the turbulent combustion in a practical industrial-used gas turbine combustor, by using a partially premixed, finite-rate chemistry combustion model.
- (2)
- The SSTKWSAS model-based simulation outperforms the URANS-based simulation by having provided a more accurate temperature and species concentration in the main flame region of the combustor, contributing to its ability to resolve turbulence eddies at high wavenumbers.
- (3)
- The inaccurate LES prediction of turbulent combustion in the main flame region of the combustor found in the literature is improved via the solutions discussed and provided.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclatures
| BCD | Bounded central differencing |
| CRZ | Center recirculation zone |
| CV | Control volume (m3) |
| C | Progress variable |
| Discharge coefficient | |
| d1, d2 | Inner and outer diameter of swirler (m) |
| b | Blockage factor |
| DES | Detached eddy simulation |
| , | Dissipation of and |
| Cross-diffusion term | |
| EDC | Eddy dissipation concept |
| , | Generation of and |
| turbulent kinetic energy (m2⋅s-2) | |
| Turbulent length scale (m) | |
| Von Karman length scale (m) | |
| LES | Large eddy simulation |
| Mass flow rate of air (Kg⋅s-1) | |
| Mass flow rate of propane (Kg⋅s-1) | |
| Probability density function | |
| q | Reacting flow quantity |
| RSM | Reynolds stress transport model |
| Swirl number | |
| SAS | Scale adaptive simulation |
| SLFM | Steady laminar flamelet modeling |
| Inlet temperature of mixtures (K) | |
| Turbulent flame speed (m⋅s-1) | |
| URANS | Unsteady Reynolds-averaged Navier–Stokes |
| ZTFSC | Zimont turbulent flame speed closure |
| Greek symbols | |
| , | Turbulent Prandtl and Schmidt number |
| Vortex frequency (s−1) | |
| Mesh size (m) | |
| , | Fluid, and unburnt mixture density (Kg⋅m−3) |
| Effective viscosity (kg⋅m−1⋅s−1) | |
| Von Karman constant | |
| Chemical reaction rate (Kg⋅m−3⋅s−1) | |
| Turning efficiency | |
| Geometric real angle (degree) | |
References
- Spalart, P.R. Strategies for turbulence modelling and simulations. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar] [CrossRef]
- Rutland, C.J. Large-eddy simulations for internal combustion engines–a review. Int. J. Engine Res. 2011, 12, 421–451. [Google Scholar] [CrossRef]
- Mehta, D.; Van Zuijlen, A.H.; Koren, B.; Holierhoek, J.G.; Bijl, H. Large Eddy Simulation of wind farm aerodynamics: A review. J. Wind Eng. Ind. Aerodyn. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Sivathanu, Y.R.; Faeth, G.M. Generalized state relationships for scalar properties in nonpremixed hydrocarbon/air flames. Combust. Flame 1990, 82, 211–230. [Google Scholar] [CrossRef]
- Peters, N. Laminar flamelet concepts in turbulent combustion. Int. Symp. Combust. 1988, 21, 1231–1250. [Google Scholar] [CrossRef]
- Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Spalart, P.R. Comments on the Feasibility of LES for Wings, and on Hybrid RANS/LES Approach, Advances in DNS/LES. In Proceedings of the 1st AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Menter, F.; Kuntz, M.; Bender, R.A. Scale-adaptive simulation model for turbulent flow predictions. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Menter, F.; Egorov, Y. A scale adaptive simulation model using two-equation models. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. Revisiting the turbulent scale equation. In Proceedings of the IUTAM Symposium on One Hundred Years of Boundary Layer Research, DLR-Göttingen, Germany, 12–14 August 2006; pp. 279–290. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. Turbulence models based on the length-scale equation. In TSFP Digital Library Online; Begel House Inc.: Williamsburg, Virginia, 2005. [Google Scholar]
- Menter, F.R.; Egorov, Y. SAS turbulence modelling of technical flows. In Direct and Large-Eddy Simulation VI; Springer: Dordrecht, The Nethelands, 2006; pp. 687–694. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y.; Rusch, D. Steady and unsteady flow modelling using the k−√kL model. In Ichmt Digital Library Online; Begel House Inc.: Dubrovnik, Croatia, 2006. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. Formulation of the Scale-Adaptive Simulation (SAS) model during the DESIDER Project. In DESider-A European Effort on Hybrid RANS-LES Modelling; Springer: Berlin, Germany, 2009; pp. 51–62. [Google Scholar]
- Menter, F.R.; Egorov, Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1: Theory and model description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Fröhlich, J.; Mellen, C.P.; Rodi, W.; Temmerman, L.; Leschziner, M.A. Highly resolved large-eddy simulation of separated flow in a channel with streamwise periodic constrictions. J. Fluid Mech. 2005, 526, 19–66. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F.R.; Lechner, R.; Cokljat, D. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 2: Application to complex flows. Flow Turbul. Combust. 2010, 85, 139–165. [Google Scholar] [CrossRef]
- Lourier, J.M.; Stöhr, M.; Noll, B.; Werner, S.; Fiolitakis, A. Scale Adaptive Simulation of a thermoacoustic instability in a partially premixed lean swirl combustor. Combust. Flame 2017, 183, 343–357. [Google Scholar] [CrossRef]
- Magnussen, B.F. Modeling of NOx and soot formation by the eddy dissipation concept. In Proceedings of the International Flame Research Foundation First Topic Oriented Technical Meeting, Amsterdam, The Netherlands, 17–19 October 1989; 1989; pp. 17–19. [Google Scholar]
- Gerlinger, P. Investigation of an assumed PDF approach for finite-rate chemistry. Combust. Sci. Technol. 2003, 175, 841–872. [Google Scholar] [CrossRef]
- Meier, W.E.I.G.A.N.D.; Weigand, P.; Duan, X.R.; Giezendanner-Thoben, R. Detailed characterization of the dynamics of thermoacoustic pulsations in a lean premixed swirl flame. Combust. Flame 2007, 150, 2–26. [Google Scholar] [CrossRef]
- Zhang, K.; Ghobadian, A.; Nouri, J.M. Comparative study of non-premixed and partially-premixed combustion simulations in a realistic Tay model combustor. Appl. Thermal Eng. 2017, 110, 910–920. [Google Scholar] [CrossRef]
- Di Mare, F.; Jones, W.P.; Menzies, K.R. Large eddy simulation of a model gas turbine combustor. Combust. Flame 2004, 137, 278–294. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Launder, B.E. Second-moment closure: Present… and future? Int. J. Heat Fluid Flow 1989, 10, 282–300. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Chemical-Kinetic Mechanisms for Combustion Applications, San Diego Mechanism web page, Mechanical and Aerospace Engineering (Combustion Research), University of California at San Diego. Available online: http://combustion.ucsd.edu (accessed on 1 January 2017).
- Müller, C.M.; Breitbach, H.; Peters, N. Partially premixed turbulent flame propagation in jet flames. Symp. Int. Combust. 1994, 25, 1099–1106. [Google Scholar] [CrossRef]
- Zimont, V.; Polifke, W.; Bettelini, M.; Weisenstein, W. An efficient computational model for premixed turbulent combustion at high Reynolds numbers based on a turbulent flame speed closure. J. Eng. Gas Turbines Power 1998, 120, 526–532. [Google Scholar] [CrossRef]
- Borghi, R.; Argueyrolles, B.; Gauffie, S.; Souhaite, P. Application of a “Presumed pdf” model of turbulent combustion to reciprocating engines. Symp. Int. Combust. 1988, 21, 1591–1599. [Google Scholar] [CrossRef]
- Bicen, A.F.; Tse, D.G.N.; Whitelaw, J.H. Combustion characteristics of a model can-type combustor. Combust. Flame 1990, 80, 111–125. [Google Scholar] [CrossRef]
- McGuirk, J.J.; Palma, J.L. The influence of numerical parameters in the calculation of gas turbine combustor flows. Comput. Methods Appl. Mech. Eng. 1992, 96, 65–92. [Google Scholar] [CrossRef]
- Crocker, D.S.; Fuller, E.J.; Smith, C.E. Fuel nozzle aerodynamic design using CFD analysis. J. Eng. Gas Turbines Power 1997, 119, 527–534. [Google Scholar] [CrossRef]
- Lefebvre, A.W. Gas Turbine Combustion; McGraw-Hill: New York, NY, USA, 1983; pp. 492–495. [Google Scholar]
- Bicen, A.F.; Palma, J.M.L.M. Flow Characteristics of Swirlers of a Model Tay Combustor; Tech. Rep. FS/86/36; Imperial College: London, UK, 1986. [Google Scholar]
- Jasak, H.; Weller, H.G.; Gosman, A.D. High resolution NVD differencing scheme for arbitrarily unstructured meshes. Int. J. Numer. Methods Fluids 1999, 31, 431–449. [Google Scholar] [CrossRef]
- Leonard, B.P. The ULTIMATE conservative difference scheme applied to unsteady one-dimensional advection. Comput. Methods Appl. Mech. Eng. 1991, 88, 17–74. [Google Scholar] [CrossRef]
- Barth, T.; Jespersen, D. The design and application of upwind schemes on unstructured meshes. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–14 January 1989. [Google Scholar] [CrossRef]
- Holmén, V. Methods for Vortex Identification. Master’s Thesis, Mathematical Sciences, Lund University, Lund, Sweden, 2012. [Google Scholar]
- Syred, N. A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 2006, 32, 93–161. [Google Scholar] [CrossRef]
- Lucca-Negro, O.; O’doherty, T. Vortex breakdown: A review. Prog. Energy Combust. Sci. 2001, 27, 431–481. [Google Scholar] [CrossRef]
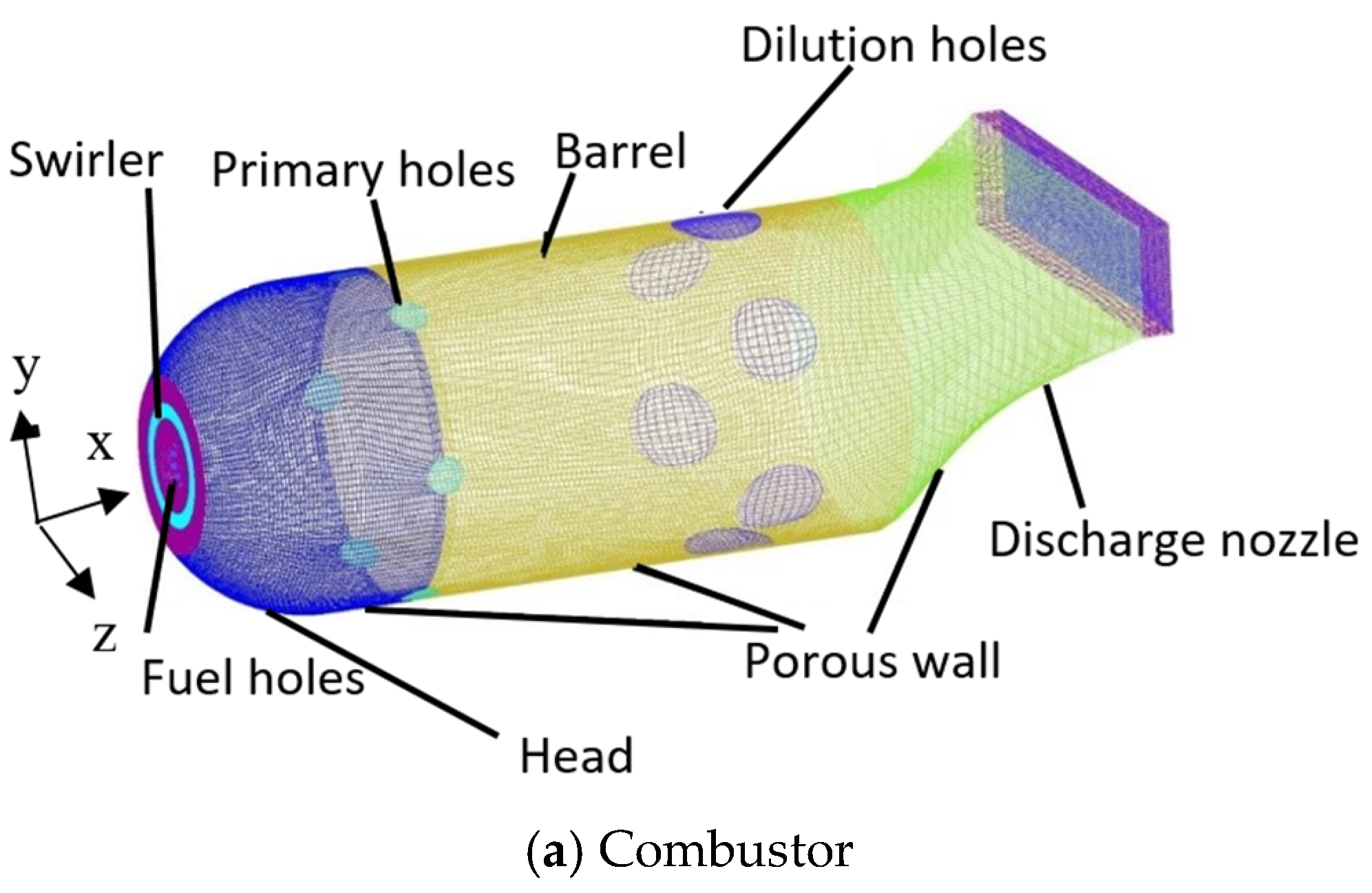


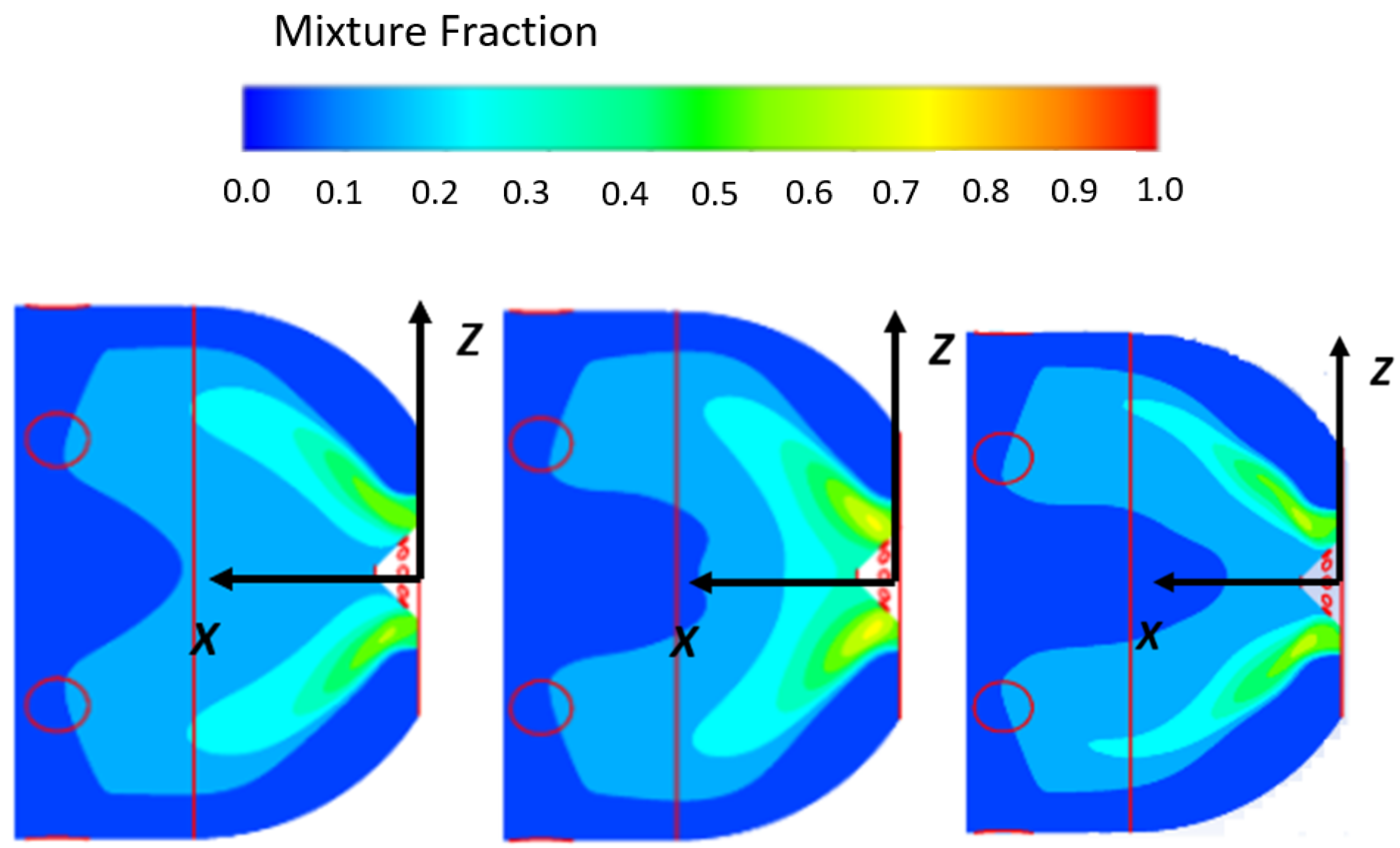

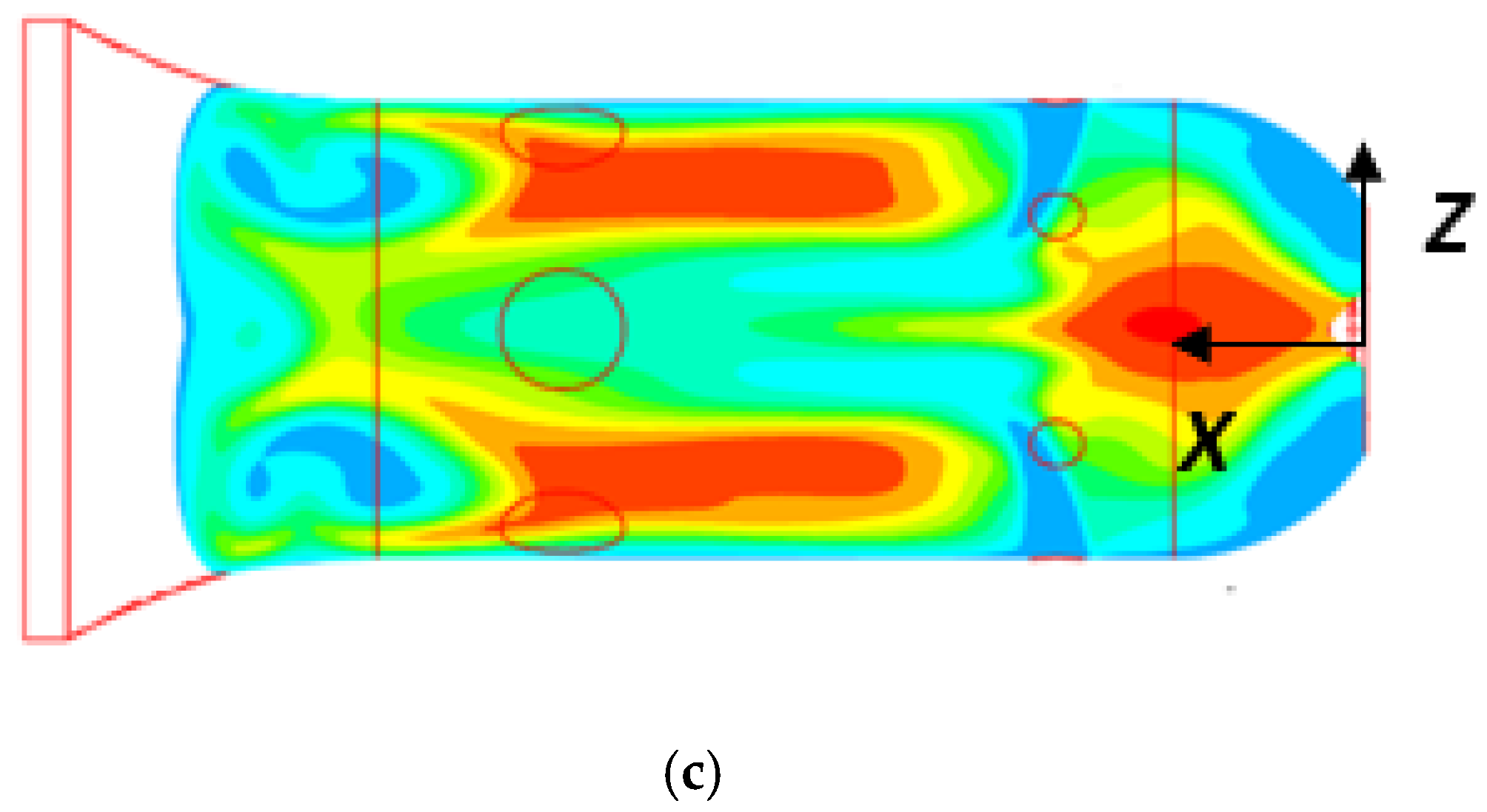
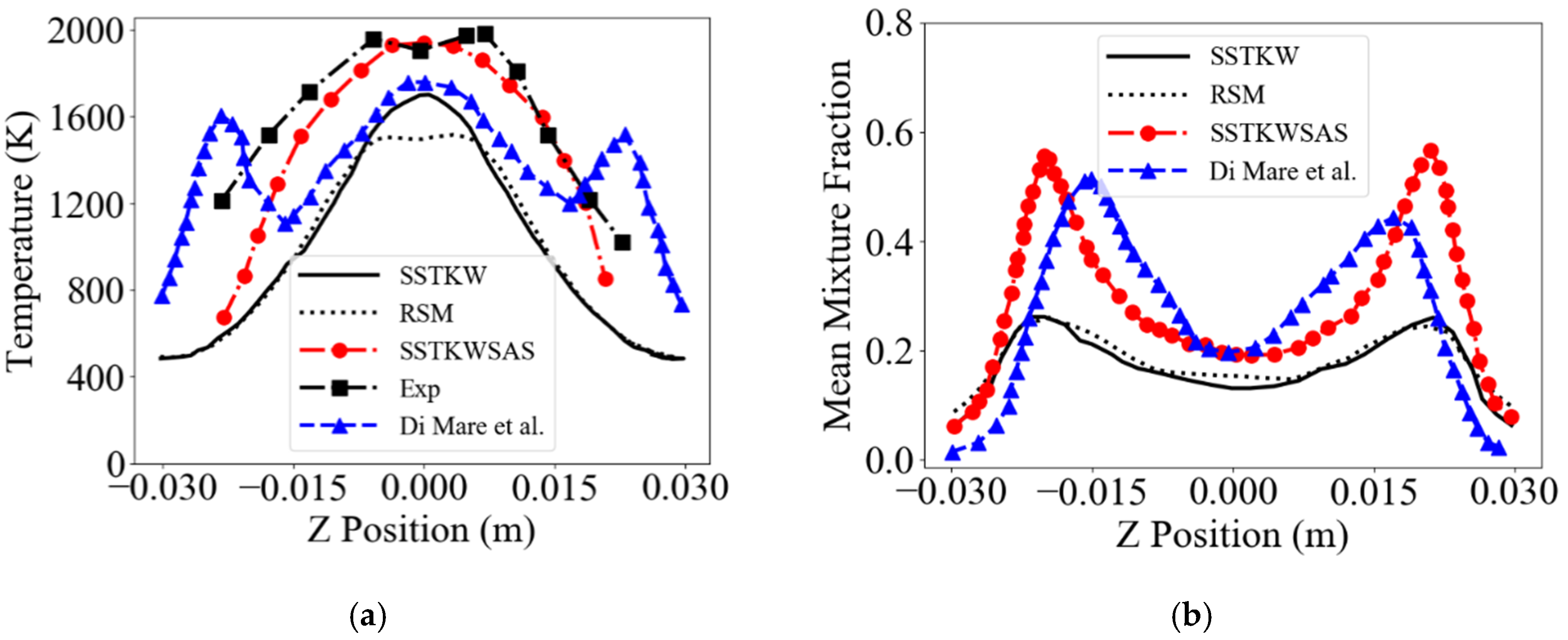
| Experiment | Swirler Vane Angle | P (atm) | Air-to-Fuel Ratio AFR | |||
|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.00176 | 45° | 1 | 315 | 57 |
| Primary Jets | Dilution Jets | Swirler Jets | Fuel Jets | Porous Wall Jet (Head) | Porous Wall Jet (Barrel) | Porous Wall Jet (Nozzle) | |
|---|---|---|---|---|---|---|---|
| (Kg/s) | 0.0136 | 0.0533 | 0.0069 | 0.00176 | 0.0066 | 0.0138 | 0.0058 |
| T (K) | 315 | 315 | 315 | 315 | 315 | 315 | 315 |
| nO2/nN2 | 0.21/ 0.79 | 0.21/ 0.79 | 0.21/ 0.79 | - | 0.21/ 0.79 | 0.21/ 0.79 | 0.21/ 0.79 |
| nC3H8 | - | - | - | 1 | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Ghobadian, A.; Nouri, J.M. Scale-Resolving Simulation of a Propane-Fuelled Industrial Gas Turbine Combustor Using Finite-Rate Tabulated Chemistry. Fluids 2020, 5, 126. https://doi.org/10.3390/fluids5030126
Zhang K, Ghobadian A, Nouri JM. Scale-Resolving Simulation of a Propane-Fuelled Industrial Gas Turbine Combustor Using Finite-Rate Tabulated Chemistry. Fluids. 2020; 5(3):126. https://doi.org/10.3390/fluids5030126
Chicago/Turabian StyleZhang, Kai, Ali Ghobadian, and Jamshid M. Nouri. 2020. "Scale-Resolving Simulation of a Propane-Fuelled Industrial Gas Turbine Combustor Using Finite-Rate Tabulated Chemistry" Fluids 5, no. 3: 126. https://doi.org/10.3390/fluids5030126
APA StyleZhang, K., Ghobadian, A., & Nouri, J. M. (2020). Scale-Resolving Simulation of a Propane-Fuelled Industrial Gas Turbine Combustor Using Finite-Rate Tabulated Chemistry. Fluids, 5(3), 126. https://doi.org/10.3390/fluids5030126






